SOUND

BY

JOHN TYNDALL, D.C.L., LL.D., F.R.S.

NEW YORK
P. F. COLLIER & SON
MCMII
7

SCIENCE

TO THE MEMORY

OF

MY FRIEND RICHARD DAWES

LATE DEAN OF HEREFORD

THIS BOOK IS DEDICATED

J. T.

CONTENTS

CHAPTER I

The Nerves and Sensation—Production and Propagation of Sonorous Motion—Experiments on Sounding Bodies placed in Vacuo—Deadening of Sound by Hydrogen—Action of Hydrogen on the Voice—Propagation of Sound through Air of Varying Density—Reflection of Sound—Echoes—Refraction of Sound—Diffraction of Sound; Case of Erith Village and Church—Influence of Temperature on Velocity—Influence of Density on Elasticity—Newton’s Calculation of Velocity—Thermal Changes Produced by the Sonorous Wave—Laplace’s Correction of Newton’s Formula—Ratio of Specific Heats at Constant Pressure and at Constant Volume deduced from Velocities of Sound—Mechanical Equivalent of Heat deduced from this Ratio—Inference that Atmospheric Air Possesses no Sensible Power to Radiate Heat—Velocity of Sound in Different Gases—Velocity in Liquids and Solids—Influence of Molecular Structure on the Velocity of Sound.

31 Summary of Chapter I 77

CHAPTER II

Physical Distinction between Noise and Music—A Musical Tone Produced by Periodic, Noise Produced by Unperiodic, Impulses—Production of Musical Sounds by Taps—Production of Musical Sounds by Puffs—Definition of Pitch in Music—Vibrations of a Tuning-Fork; their Graphic Representation on Smoked Glass—Optical Expression of the Vibrations of a Tuning-Fork—Description of the Siren—Limits of the Ear; Highest and Deepest Tones—Rapidity of Vibration Determined by the Siren—Determination of the Lengths of Sonorous Waves—Wave-Lengths of the Voice in Man and Woman—Transmission of Musical Sounds through Liquids and Solids.

82 Summary of Chapter II 117

CHAPTER III

Vibration of Strings—How employed in Music—Influence of Sound-Boards—Laws of Vibrating String—Combination of Direct and Reflected Pulses—Stationary and Progressive Waves—Nodes and Ventral Segments—Application of Results to the Vibrations of Musical Strings—Experiments of Melde—Springs set in Vibration by Tuning-Forks—Laws of Vibration thus demonstrated—Harmonic Tones of Strings—Definitions of Timbre or Quality, or Overtones and Clang—Abolition of Special Harmonies—Conditions which affect the Intensity of the Harmonic Tones—Optical Examination of the Vibrations of a Piano-Wire

120 Summary of Chapter III 161

CHAPTER IV

Vibrations of a Rod fixed at Both Ends: its Subdivisions and Corresponding Overtones—Vibrations of a Rod fixed at One End—The Kaleidophone—The Iron Fiddle and Musical Box—Vibrations of a Rod free at Both Ends—The Claque-bois and Glass Harmonica—Vibrations of a Tuning-Fork: its Subdivisions and Overtones—Vibrations of Square Plates—Chladni’s Discoveries—Wheatstone’s Analysis of the Vibrations of Plates—Chladni’s Figures—Vibrations of Disks and Bells—Experiments of Faraday and Strehlke.

165 Summary of Chapter IV 196

CHAPTER V

Longitudinal Vibrations of a Wire—Relative Velocities of Sound in Brass and Iron—Longitudinal Vibrations of Rods fixed at One End—Of Rods free at Both Ends—Divisions and Overtones of Rods vibrating longitudinally—Examination of Vibrating Bars by Polarized Light—Determination of Velocity of Sound in Solids—Resonance—Vibrations of Stopped Pipes: their Divisions and Overtones—Relation of the Tones of Stopped Pipes to those of Open Pipes—Condition of Column of Air within a Sounding Organ-Pipe—Reeds and Reed-Pipes—The Voice—Overtones of the Vocal Chords—The Vowel Sounds—Kundt’s Experiments—New Methods of determining the Velocity of Sound.

200 Summary of Chapter V 254

CHAPTER VI

Singing Flames—Influence of the Tube surrounding the Flame—Influence of Size of Flame—Harmonic Notes of Flames—Effect of Unisonant Notes on Singing Flames—Action of Sound on Naked Flames—Experiments with Fish-Tail and Bat’s-Wing Burners—Experiments on Tall Flames—Extraordinary Delicacy of Flames as Acoustic Reagents—The Vowel-Flame—Action of Conversational Tones upon Flames—Action of Musical Sounds on Smoke-Jets—Constitution of Water-Jets—Plateau’s Theory of the Resolution of a Liquid Vein into Drops—Action of Musical Sounds on Water-Jets—A Liquid Vein may compete in Point of Delicacy with the Ear

260 Summary of Chapter VI 301

CHAPTER VII

PART I

RESEARCHES ON THE ACOUSTIC TRANSPARENCY OF THE ATMOSPHERE IN RELATION TO THE QUESTION OF FOG-SIGNALLING

Introduction—Instruments and Observations—Contradictory Results from the 19th of May to the 1st of July inclusive—Solution of Contradictions—Aërial Reflection and its Causes—Aërial Echoes—Acoustic Clouds—Experimental Demonstration of Stoppage of Sound by Aërial Reflection

305

PART II

INVESTIGATION OF THE CAUSES WHICH HAVE HITHERTO BEEN SUPPOSED EFFECTIVE IN PREVENTING THE TRANSMISSION OF SOUND THROUGH THE ATMOSPHERE

Action of Hail and Rain—Action of Snow—Action of Fog; Observations in London—Experiments on Artificial Fogs—Observations on Fogs at the South Foreland—Action of Wind—Atmospheric Selection—Influence of Sound-Shadow

341 Summary of Chapter VII 374

CHAPTER VIII

Law of Vibratory Motions in Water and Air—Superposition of Vibrations—Interference of Sonorous Waves—Destruction of Sound by Sound—Combined Action of Two Sounds nearly in Unison with each other—Theory of Beats—Optical Illustration of the Principle of Interference—Augmentation of Intensity by Partial Extinction of Vibrations—Resultant Tones—Conditions of their Production—Experimental Illustrations—Difference-Tones and Summation-Tones—Theories of Young and Helmholtz

377 Summary of Chapter VIII 407

CHAPTER IX

Combination of Musical Sounds—The smaller the Two Numbers which express the Ratio of their Rates of Vibration, the more perfect is the Harmony of Two Sounds—Notions of the Pythagoreans regarding Musical Consonance—Euler’s Theory of Consonance—Theory of Helmholtz—Dissonance due to Beats—Interference of Primary Tones and of Overtones—Mechanism of Hearing—Schultze’s Bristles—The Otoliths—Corti’s Fibres—Graphic Representation of Consonance and Dissonance—Musical Chords—The Diatonic Scale—Optical Illustration of Musical Intervals—Lissajous’s Figures—Sympathetic Vibrations—Various Modes of illustrating the Composition of Vibrations

410 Summary of Chapter IX 450  

APPENDIX I

On the Influence of Musical Sounds on the Flame of a Jet of Coal-gas. By John le Conte, M.D.

454

APPENDIX II

On Acoustic Reversibility 461  

INDEX

471

ILLUSTRATION—

Fog-Siren Frontispiece

Fog-Siren

PREFACE TO THE THIRD EDITION

In preparing this new edition of “Sound,” I have carefully gone over the last one; amended, as far as possible, its defects of style and matter, and paid at the same time respectful attention to the criticisms and suggestions which the former editions called forth.

The cases are few in which I have been content to reproduce what I have read of the works of acousticians. I have sought to make myself experimentally familiar with the ground occupied; trying, in all cases, to present the illustrations in the form and connection most suitable for educational purposes.

Though bearing, it may be, an undue share of the imperfection which cleaves to all human effort, the work has already found its way into the literature of various nations of diverse intellectual standing. Last year, for example, a new German edition was published “under the special supervision” of Helmholtz and Wiedemann. That men so eminent, and so overladen with official duties, should add to these the labor of examining and correcting every proof-sheet of a work like this, shows that they consider it to be what it was meant to be—a serious attempt to improve the public knowledge of science. It is especially gratifying to me to be thus assured that not in England alone has the book met a public want, but also in that learned land to which I owe my scientific education.

Before me, on the other hand, lie two volumes of foolscap size, curiously stitched, and printed in characters the meaning of which I am incompetent to penetrate. Here and there, however, I notice the familiar figures of the former editions of “Sound.” For these volumes I am indebted to Mr. John Fryer, of Shanghai, who, along with them, favored me, a few weeks ago, with a letter from which the following is an extract: “One day,” writes Mr. Fryer, “soon after the first copy of your work on Sound reached Shanghai, I was reading it in my study, when an intelligent official, named Hsii-chung-hu, noticed some of the engravings and asked me to explain them to him. He became so deeply interested in the subject of Acoustics that nothing would satisfy him but to make a translation. Since, however, engineering and other works were then considered to be of more practical importance by the higher authorities, we agreed to translate your work during our leisure time every evening, and publish it separately ourselves. Our translation, however, when completed, and shown to the higher officials, so much interested them, and pleased them, that they at once ordered it to be published at the expense of the Government, and sold at cost price. The price is four hundred and eighty copper cash per copy, or about one shilling and eightpence. This will give you an idea of the cheapness of native printing.”

Mr. Fryer adds that his Chinese friend had no difficulty in grasping every idea in the book.

The new matter of greatest importance which has been introduced into this edition is an account of an investigation which, during the past two years, I have had the honor of conducting in connection with the Elder Brethren of the Trinity House. Under the title “Researches on the Acoustic Transparency of the Atmosphere, in Relation to the Question of Fog-signalling,” the subject is treated in Chapter VII. of this volume. It was only by Governmental appliances that such an investigation could have been made; and it gives me pleasure to believe that not only have the practical objects of the inquiry been secured, but that a crowd of scientific errors, which for more than a century and a half have surrounded this subject, have been removed, their place being now taken by the sure and certain truth of Nature. In drawing up the account of this laborious inquiry, I aimed at linking the observations so together that they alone should offer a substantial demonstration of the principles involved. Further labors enabled me to bring the whole inquiry within the firm grasp of experiment; and thus to give it a certainty which, without this final guarantee, it could scarcely have enjoyed.

Immediately after the publication of the first brief abstract of the investigation, it was subjected to criticism. To this I did not deem it necessary to reply, believing that the grounds of it would disappear in presence of the full account. The only opinion to which I thought it right to defer was to some extent a private one, communicated to me by Prof. Stokes. He considered that I had, in some cases, ascribed too exclusive an influence to the mixed currents of aqueous vapor and air, to the neglect of differences of temperature. That differences of temperature, when they come into play, are an efficient cause of acoustic opacity, I never doubted. In fact, aërial reflection arising from this cause is, in the present inquiry, for the first time made the subject of experimental demonstration. What the relative potency of differences of temperature and differences due to aqueous vapor, in the cases under consideration, may be, I do not venture to state; but as both are active, I have, in Chapter VII., referred to them jointly as concerned in the production of those “acoustic clouds” to which the stoppage of sound in the atmosphere is for the most part due.

Subsequently, however, to the publication of the full investigation another criticism appeared, to which, in consideration of its source, I would willingly pay all respect and attention. In this criticism, which reached me first through the columns of an American newspaper, differences in the amounts of aqueous vapor, and differences of temperature, are alike denied efficiency as causes of acoustic opacity. At a meeting of the Philosophical Society of Washington the emphatic opinion had, it was stated, been expressed that I was wrong in ascribing the opacity of the atmosphere to its flocculence, the really efficient cause being refraction. This view appeared to me so obviously mistaken that I assumed, for a time, the incorrectness of the newspaper account.

Recently, however, I have been favored with the “Report of the United States Lighthouse Board for 1874,” in which the account just referred to is corroborated. A brief reference to the Report will here suffice. Major Elliott, the accomplished officer and gentleman referred to at page 261, had published a record of his visit of inspection to this country, in which he spoke, with a perfectly enlightened appreciation of the facts, of the differences between our system of lighthouse illumination and that of the United States. He also embodied in his Report some account of the investigation on fog-signals, the initiation of which he had witnessed, and indeed aided, at the South Foreland.

On this able Report of their own officer the Lighthouse Board at Washington make the following remark: “Although this account is interesting in itself and to the public generally, yet, being addressed to the Lighthouse Board of the United States, it would tend to convey the idea that the facts which it states were new to the Board, and that the latter had obtained no results of a similar kind; while a reference to the appendix to this Report1 will show that the researches of our Lighthouse Board have been much more extensive on this subject than those of the Trinity House, and that the latter has established no facts of practical importance which had not been previously observed and used by the former.”

The “appendix” here referred to is from the pen of the venerable Prof. Joseph Henry, chairman of the Lighthouse Board at Washington. To his credit be it recorded that at a very early period in the history of fog-signalling Prof. Henry reported in favor of Daboll’s trumpet, though he was opposed by one of his colleagues on the ground that “fog-signals were of little importance, since the mariner should know his place by the character of his soundings.” In the appendix, he records the various efforts made in the United States with a view to the establishment of fog-signals. He describes experiments on bells, and on the employment of reflectors to reinforce their sound. These, though effectual close at hand, were found to be of no use at a distance. He corrects current errors regarding steam-whistles, which by some inventors were thought to act like ringing bells. He cites the opinion of the Rev. Peter Ferguson, that sound is better heard in fog than in clear air. This opinion is founded on observations of the noise of locomotives; in reference to which it may be said that others have drawn from similar experiments diametrically opposite conclusions. On the authority of Captain Keeney he cites an occurrence, “in the first part of which the captain was led to suppose that fog had a marked influence in deadening sound, though in a subsequent part he came to an opposite conclusion.” Prof. Henry also describes an experiment made during a fog at Washington, in which he employed “a small bell rung by clock-work, the apparatus being the part of a moderator lamp, intended to give warning to the keepers when the supply of oil ceased. The result of the experiment was, he affirms, contrary to the supposition of absorption of the sound by the fog.” This conclusion is not founded on comparative experiments, but on observations made in the fog alone; for, adds Prof. Henry, “the change in the condition of the atmosphere, as to temperature and the motion of the air, before the experiment could be repeated in clear weather, rendered the result not entirely satisfactory.”

This, I may say, is the only experiment on fog which I have found recorded in the appendix.

In 1867 the steam-siren was mounted at Sandy Hook, and examined by Prof. Henry. He compared its action with that of a Daboll trumpet, employing for this purpose a stretched membrane covered with sand, and placed at the small end of a tapering tube which concentrated the sonorous motion upon the membrane. The siren proved most powerful. “At a distance of 50, the trumpet produced a decided motion of the sand, while the siren gave a similar result at a distance of 58.” Prof. Henry also varied the pitch of the siren, and found that in association with its trumpet 400 impulses per second yielded the maximum sound; while the best result with the unaided siren was obtained when the impulses were 360 a second. Experiments were also made on the influence of pressure; from which it appeared that when the pressure varied from 100 lbs. to 20 lbs., the distance reached by the sound (as determined by the vibrating membrane) varied only in the ratio of 61 to 51. Prof. Henry also showed the sound of the fog-trumpet to be independent of the material employed in its construction; and he furthermore observed the decay of the sound when the angular distance from the axis of the instrument was increased. Further observations were made by Prof. Henry and his colleagues in August, 1873, and in August, and September, 1874. In the brief but interesting account of these experiments a hypothetical element appears, which is absent from the record of the earlier observations.

It is quite evident from the foregoing that, in regard to the question of fog-signalling, the Lighthouse Board of Washington have not been idle. Add to this the fact that their eminent chairman gives his services gratuitously, conducting without fee or reward experiments and observations of the character here revealed, and I think it will be conceded that he not only deserves well of his own country, but also sets his younger scientific contemporaries, both in his country and ours, an example of high-minded devotion.

I was quite aware, in a general way, that labors like those now for the first time made public had been conducted in the United States, and this knowledge was not without influence upon my conduct. The first instruments mounted at the South Foreland were of English manufacture; and I, on various accounts, entertained a strong sympathy for their able constructor, Mr. Holmes. From the outset, however, I resolved to suppress such feelings, as well as all other extraneous considerations, individual or national; and to aim at obtaining the best instruments, irrespective of the country which produced them. In reporting, accordingly, on the observations of May 19 and 20, 1873 (our first two days at the South Foreland), these were my words to the Elder Brethren of the Trinity House:

“In view of the reported performance of horns and whistles in other places, the question arises whether those mounted at the South Foreland, and to which the foregoing remarks refer, are of the best possible description.... I think our first duty is to make ourselves acquainted with the best instruments hitherto made, no matter where made; and then, if home genius can transcend them, to give it all encouragement. Great and unnecessary expense may be incurred, through our not availing ourselves of the results of existing experience.

“I have always sympathized, and I shall always sympathize, with the desire of the Elder Brethren to encourage the inventor who first made the magneto-electric light available for lighthouse purposes. I regard his aid and counsel as, in many respects, invaluable to the corporation. But, however original he may be, our duty is to demand that his genius shall be expended in making advances on that which has been already achieved elsewhere. If the whistles and horns that we heard on the 19th and 20th be the very best hitherto constructed, my views have been already complied with; but if they be not—and I am strongly inclined to think that they are not—then I would submit that it behooves us to have the best, and to aim at making the South Foreland, both as regards light and sound, a station not excelled by any other in the world.”

On this score it gives me pleasure to say that I never had a difficulty with the Elder Brethren. They agreed with me; and two powerful steam-whistles, the one from Canada, the other from the United States, together with a steam-siren—also an American instrument—were in due time mounted at the South Foreland. It will be seen in Chapter VII. that my strongest recommendation applies to an instrument for which we are indebted to the United States.

In presence of these facts, it will hardly be assumed that I wish to withhold from the Lighthouse Board of Washington any credit that they may fairly claim. My desire is to be strictly just; and this desire compels me to express the opinion that their Report fails to establish the inordinate claim made in its first paragraph. It contains observations, but contradictory observations; while as regards the establishment of any principle which should reconcile the conflicting results, it leaves our condition unimproved.

But I willingly turn aside from the discussion of “claims” to the discussion of science. Inserted, as a kind of intrusive element, into the Report of Prof. Henry, is a second Report by General Duane, founded on an extensive series of observations made by him in 1870 and 1871. After stating with distinctness the points requiring decision, the General makes the following remarks:

“Before giving the results of these experiments, some facts will be stated which will explain the difficulties of determining the power of a fog-signal.

“There are six steam fog-whistles on the coast of Maine: these have been frequently heard at a distance of twenty miles, and as frequently cannot be heard at the distance of two miles, and this with no perceptible difference in the state of the atmosphere.

“The signal is often heard at a great distance in one direction, while in another it will be scarcely audible at the distance of a mile. This is not the effect of wind, as the signal is frequently heard much further against the wind than with it.2 For example, the whistle on Cape Elizabeth can always be distinctly heard in Portland, a distance of nine miles, during a heavy northeast snowstorm, the wind blowing a gale directly from Portland toward the whistle.3

“The most perplexing difficulties, however, arise from the fact that the signal often appears to be surrounded by a belt, varying in radius from one mile to one mile and a half, from which the sound appears to be entirely absent. Thus, in moving directly from a station the sound is audible for the distance of a mile, is then lost for about the same distance, after which it is again distinctly heard for a long time. This action is common to all ear-signals, and has been at times observed at all the stations, at one of which the signal is situated on a bare rock twenty miles from the mainland, with no surrounding objects to affect the sound.”

It is not necessary to assume here the existence of a “belt,” at some distance from the station. The passage of an acoustic cloud over the station itself would produce the observed phenomenon.

Passing over the record of many other valuable observations in the Report of General Duane, I come to a few very important remarks which have a direct bearing upon the present question:

“From an attentive observation,” writes the General, “during three years, of the fog-signals on this coast, and from the reports received from the captains and pilots of coasting vessels, I am convinced that, in some conditions of the atmosphere, the most powerful signals will be at times unreliable.4

“Now it frequently occurs that a signal which, under ordinary circumstances, would be audible at the distance of fifteen miles, cannot be heard from a vessel at the distance of a single mile. This is probably due to the reflection mentioned by Humboldt.

“The temperature of the air over the land where the fog-signal is located being very different from that over the sea, the sound, in passing from the former to the latter, undergoes reflection at their surface of contact. The correctness of this view is rendered more probable by the fact that, when the sound is thus impeded in the direction of the sea, it has been observed to be much stronger inland.

“Experiments and observation lead to the conclusion that these anomalies in the penetration and direction of sound from fog-signals are to be attributed mainly to the want of uniformity in the surrounding atmosphere, and that snow, rain, and fog, and the direction of the wind, have much less influence than has been generally supposed.”

The Report of General Duane is marked throughout by fidelity to facts, rare sagacity, and soberness of speculation. The last three of the paragraphs just quoted exhibit, in my opinion, the only approach to a true explanation of the phenomena which the Washington Report reveals. At this point, however, the eminent Chairman of the Lighthouse Board strikes in with the following criticism:

“In the foregoing I differ entirely in opinion from General Duane as to the cause of extinction of powerful sounds being due to the unequal density of the atmosphere. The velocity of sound is not at all affected by barometric pressure; but if the difference in pressure is caused by a difference in heat, or by the expansive power of vapor mingled with the air, a slight degree of obstruction of sound may be observed. But this effect we think is entirely too minute to produce the results noted by General Duane and Dr. Tyndall, while we shall find in the action of currents above and below a true and efficient cause.”

I have already cited the remarkable observation of General Duane, that with a snowstorm from the northeast blowing against the sound, the signal at Cape Elizabeth is always heard at Portland, a distance of nine miles. The observations at the South Foreland, where the sound has-been proved to reach a distance of more than twelve miles against the wind, backed by decisive experiments, reduce to certainty the surmises of General Duane. It has, for example, been proved that a couple of gas-flames placed in a chamber can, in a minute or two, render its air so non-homogeneous as to cut a sound practically off; while the same sound passes without sensible impediment through showers of paper-scraps, seeds, bran, raindrops, and through fumes and fogs of the densest description. The sound also passes through thick layers of calico, silk, serge, flannel, baize, close felt, and through pads of cotton-net impervious to the strongest light.

As long, indeed, as the air on which snow, hail, rain or fog is suspended is homogeneous, so long will sound pass through the air, sensibly heedless of the suspended matter.5 This point is illustrated upon a large scale by my own observations on the Mer de Glace, and by those of General Duane, at Portland, which prove the snow-laden air from the northeast to be a highly homogeneous medium. Prof. Henry thus accounts for the fact that the northeast snow-wind renders the sound of Cape Elizabeth audible at Portland: In the higher regions of the atmosphere he places an ideal wind, blowing in a direction opposed to the real one, which always accompanies the latter, and which more than neutralizes its action. In speculating thus he bases himself on the reasoning of Prof. Stokes, according to which a sound-wave moving against the wind is tilted upward. The upper, and opposing wind, is invented for the purpose of tilting again the already lifted sound-wave downward. Prof. Henry does not explain how the sound-wave recrosses the hostile lower current, nor does he give any definite notion of the conditions under which it can be shown that it will reach the observer.

This, so far as I know, is the only theoretic gleam cast by the Washington Report on the conflicting results which have hitherto rendered experiments on fog-signals so bewildering. I fear it is an ignis fatuus, instead of a safe guiding light. Prof. Henry, however, boldly applies the hypothesis in a variety of instances. But he dwells with particular emphasis upon a case of non-reciprocity which he considers absolutely fatal to my views regarding the flocculence of the atmosphere. The observation was made on board the steamer “City of Richmond,” during a thick fog in a night of 1872. “The vessel was approaching Whitehead from the southwestward, when, at a distance of about six miles from the station, the fog-signal, which is a 10-inch steam-whistle, was distinctly perceived, and continued to be heard with increasing intensity of sound until within about three miles, when the sound suddenly ceased to be heard, and was not perceived again until the vessel approached within a quarter of a mile of the station, although from conclusive evidence, furnished by the keeper, it was shown that the signal had been sounding during the whole time.”

But while the 10-inch shore-signal thus failed to make itself heard at sea, a 6-inch whistle on board the steamer made itself heard on shore. Prof. Henry thus turns this fact against me. “It is evident,” he writes, “that this result could not be due to any mottled condition or want of acoustic transparency in the atmosphere, since this would absorb the sound equally in both directions.” Had the observation been made in a still atmosphere, this argument would, at one time, have had great force. But the atmosphere was not still, and a sufficient reason for the observed non-reciprocity is to be found in the recorded fact that the wind was blowing against the shore-signal, and in favor of the ship-signal.

But the argument of Prof. Henry, on which he places his main reliance, would be untenable, even had the air been still. By the very aërial reflection which he practically ignores, reciprocity may be destroyed in a calm atmosphere. In proof of this assertion I would refer him to a short paper on “Acoustic Reversibility,” printed at the end of this volume.6 The most remarkable case of non-reciprocity on record, and which, prior to the demonstration of the existence and power of acoustic clouds, remained an insoluble enigma, is there shown to be capable of satisfactory solution. These clouds explain perfectly the “abnormal phenomena” of Prof. Henry. Aware of their existence, the falling off and subsequent recovery of a signal-sound, as noticed by him and General Duane, is no more a mystery than the interception of the solar light by a common cloud, and its restoration after the cloud has moved or melted away.

The clew to all the difficulties and anomalies of this question is to be found in the aërial echoes, the significance of which has been overlooked by General Duane, and misinterpreted by Prof. Henry. And here a word might be said with regard to the injurious influence still exercised by authority in science. The affirmations of the highest authorities, that from clear air no sensible echo ever comes, were so distinct that my mind for a time refused to entertain the idea. Authority caused me for weeks to depart from the truth, and to seek counsel among delusions. On the day our observations at the South Foreland began I heard the echoes. They perplexed me. I heard them again and again, and listened to the explanations offered by some ingenious persons at the Foreland. They were an “ocean-echo”: this is the very phraseology now used by Prof. Henry. They were echoes “from the crests and slopes of the waves”: these are the words of the hypothesis which he now espouses. Through a portion of the month of May, through the whole of June, and through nearly the whole of July, 1873, I was occupied with these echoes; one of the phases of thought then passed through, one of the solutions then weighed in the balance and found wanting, being identical with that which Prof. Henry now offers for acceptation.

But though it thus deflected me from the proper track, shall I say that authority in science is injurious? Not without some qualification. It is not only injurious, but deadly, when it cows the intellect into fear of questioning it. But the authority which so merits our respect as to compel us to test and overthrow all its supports, before accepting a conclusion opposed to it, is not wholly noxious. On the contrary, the disciplines it imposes may be in the highest degree salutary, though they may end, as in the present case, in the ruin of authority. The truth thus established is rendered firmer by our struggles to reach it. I groped day after day, carrying this problem of aërial echoes in my mind; to the weariness, I fear, of some of my colleagues who did not know my object. The ships and boats afloat, the “slopes and crests of the waves,” the visible clouds, the cliffs, the adjacent lighthouses, the objects landward, were all in turn taken into account, and all in turn rejected.

With regard to the particular notion which now finds favor with Prof. Henry, it suggests the thought that his observations, notwithstanding their apparent variety and extent, were really limited as regards the weather. For did they, like ours, embrace weather of all kinds, it is not likely that he would have ascribed to the sea-waves an action which often reaches its maximum intensity when waves are entirely absent. I will not multiply instances, but confine myself to the definite statement that the echoes have often manifested an astonishing strength when the sea was of glassy smoothness. On days when the echoes were powerful, I have seen the southern cumuli mirrored in the waveless ocean, in forms almost as definite as the clouds themselves. By no possible application of the law of incidence and reflection could the echoes from such a sea return to the shore; and if we accept for a moment a statement which Prof. Henry seems to indorse, that sound-waves of great intensity, when they impinge upon a solid or liquid surface, do not obey the law of incidence and reflection, but “roll along the surface like a cloud of smoke,” it only increases the difficulty. Such a “cloud,” instead of returning to the coast of England, would, in our case, have rolled toward the coast of France. Nothing that I could say in addition could strengthen the case here presented. I will only add one further remark. When the sun shines uniformly on a smooth sea, thus producing a practically uniform distribution of the aërial currents to which the echoes are due, the direction in which the trumpet-echoes reach the shore is always that in which the axis of the instrument is pointed. At Dungeness this was proved to be the case throughout an arc of 210°—an impossible result, if the direction of reflection were determined by that of the ocean waves.

Rightly interpreted and followed out, these aërial echoes lead to a solution which penetrates and reconciles the phenomena from beginning to end. On this point I would stake the issue of the whole inquiry, and to this point I would, with special earnestness, direct the attention of the Lighthouse Board of Washington. Let them prolong their observations into calm weather: if their atmosphere resembles ours—which I cannot doubt—then I affirm that they will infallibly find the echoes strong on days when all thought of reflection “from the crests and slopes of the waves” must be discarded. The echoes afford the easiest access to the core of this question, and it is for this reason that I dwell upon them thus emphatically. It requires no refined skill or profound knowledge to master the conditions of their production; and these once mastered, the Lighthouse Board of Washington will find themselves in the real current of the phenomena, outside of which—I say it with respect—they are now vainly speculating. The acoustic deportment of the atmosphere in haze, fog, sleet, snow, rain, and hail will be no longer a mystery; even those “abnormal phenomena” which are now referred to an imaginary cause, or reserved for future investigation, will be found to fall naturally into place, as illustrations of a principle as simple as it is universal.

“With the instruments now at our disposal wisely established along our coasts, I venture to think that the saving of property, in ten years, will be an exceedingly large multiple of the outlay necessary for the establishment of such signals. The saving of life appeals to the higher motives of humanity.” Such were the words with which I wound up my Report on Fog-Signals.7 One year after their utterance, the “Schiller” goes to pieces on the Scilly rocks. A single calamity covers the predicted multiple, while the sea receives three hundred and thirty-three victims. As regards the establishment of fog-signals, energy has been hitherto paralyzed by their reputed uncertainty. We now know both the reason and the range of their variations; and such knowledge places it within our power to prevent disasters like the recent one. The inefficiency of bells, which caused their exclusion from our inquiry, was sadly illustrated in the case of the “Schiller.”

JOHN TYNDALL.

Royal institution, June, 1875.

PREFACE TO THE FIRST EDITION

In the following pages I have tried to render the science of Acoustics interesting to all intelligent persons, including those who do not possess any special scientific culture.

The subject is treated experimentally throughout, and I have endeavored so to place each experiment before the reader that he should realize it as an actual operation. My desire, indeed, has been to give distinct images of the various phenomena of acoustics, and to cause them to be seen mentally in their true relations.

I have been indebted to the kindness of some of my English friends for a more or less complete examination of the proof-sheets of this work. To my celebrated German friend Clausius, who has given himself the trouble of reading the proofs from beginning to end, my especial thanks are due and tendered.

There is a growing desire for scientific culture throughout the civilized world. The feeling is natural, and, under the circumstances, inevitable. For a power which influences so mightily the intellectual and material action of the age could not fail to arrest attention and challenge examination. In our schools and universities a movement in favor of science has begun which, no doubt, will end in the recognition of its claims, both as a source of knowledge and as a means of discipline. If by showing, however inadequately, the methods and results of physical science to men of influence, who derive their culture from another source, this book should indirectly aid in promoting the movement referred to, it will not have been written in vain.

SOUND

CHAPTER I

The Nerves and Sensation—Production and Propagation of Sonorous Motion—Experiments on Sounding Bodies placed in Vacuo—Deadening of Sound by Hydrogen—Action of Hydrogen on the Voice—Propagation of Sound through Air of Varying Density—Reflection of Sound—Echoes—Refraction of Sound—Diffraction of Sound; Case of Erith Village and Church—Influence of Temperature on Velocity—Influence of Density on Elasticity—Newton’s Calculation of Velocity—Thermal Changes Produced by the Sonorous Wave—Laplace’s Correction of Newton’s Formula—Ratio of Specific Heats at Constant Pressure and at Constant Volume deduced from Velocities of Sound—Mechanical Equivalent of Heat deduced from this Ratio—Inference that Atmospheric Air Possesses no Sensible Power to Radiate Heat—Velocity of Sound in Different Gases—Velocity in Liquids and Solids—Influence of Molecular Structure on the Velocity of Sound

§ 1. Introduction: Character of Sonorous Motion. Experimental Illustrations

THE various nerves of the human body have their origin in the brain, which is the seat of sensation. When the finger is wounded, the sensor nerves convey to the brain intelligence of the injury, and if these nerves be severed, however serious the hurt may be, no pain is experienced. We have the strongest reason for believing that what the nerves convey to the brain is in all cases motion. The motion here meant is not, however, that of the nerve as a whole, but of its molecules or smallest particles.8

Different nerves are appropriated to the transmission of different kinds of molecular motion. The nerves of taste, for example, are not competent to transmit the tremors of light, nor is the optic nerve competent to transmit sonorous vibrations. For these a special nerve is necessary, which passes from the brain into one of the cavities of the ear, and there divides into a multitude of filaments. It is the motion imparted to this, the auditory nerve, which, in the brain, is translated into sound.

Applying a flame to a small collodion balloon which contains a mixture of oxygen and hydrogen, the gases explode, and every ear in this room is conscious of a shock, which we name a sound. How was this shock transmitted from the balloon to our organs of hearing? Have the exploding gases shot the air-particles against the auditory nerve as a gun shoots a ball against a target? No doubt, in the neighborhood of the balloon, there is to some extent a propulsion of particles; but no particle of air from the vicinity of the balloon reached the ear of any person here present. The process was this: When the flame touched the mixed gases they combined chemically, and their union was accompanied by the development of intense heat. The heated air expanded suddenly, forcing the surrounding air violently away on all sides. This motion of the air close to the balloon was rapidly imparted to that a little further off, the air first set in motion coming at the same time to rest. The air, at a little distance, passed its motion on to the air at a greater distance, and came also in its turn to rest. Thus each shell of air, if I may use the term, surrounding the balloon took up the motion of the shell next preceding, and transmitted it to the next succeeding shell, the motion being thus propagated as a pulse or wave through the air.

The motion of the pulse must not be confounded with the motion of the particles which at any moment constitute the pulse. For while the wave moves forward through considerable distances, each particular particle of air makes only a small excursion to and fro.

Fig. 1.

The process may be rudely represented by the propagation of motion through a row of glass balls, such as are employed in the game of solitaire. Placing the balls along a groove thus, Fig. 1, each of them touching its neighbor, and urging one of them against the end of the row: the motion thus imparted to the first ball is delivered up to the second, the motion of the second is delivered up to the third, the motion of the third is imparted to the fourth; each ball, after having given up its motion, returning itself to rest. The last ball only of the row flies away. In a similar way is sound conveyed from particle to particle through the air. The particles which fill the cavity of the ear are finally driven against the tympanic membrane, which is stretched across the passage leading from the external ear toward the brain. This membrane, which closes outwardly the “drum” of the ear, is thrown into vibration, its motion is transmitted to the ends of the auditory nerve, and afterward along that nerve to the brain, where the vibrations are translated into sound. How it is that the motion of the nervous matter can thus excite the consciousness of sound is a mystery which the human mind cannot fathom.

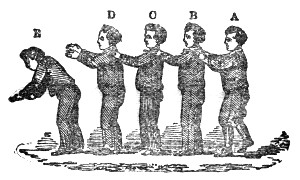
Fig. 2.

The propagation of sound may be illustrated by another homely but useful illustration. I have here five young assistants, A, B, C, D, and E, Fig. 2, placed in a row, one behind the other, each boy’s hands resting against the back of the boy in front of him. E is now foremost, and A finishes the row behind. I suddenly push A, A pushes B, and regains his upright position; B pushes C; C pushes D; D pushes E; each boy, after the transmission of the push, becoming himself erect. E, having nobody in front, is thrown forward. Had he been standing on the edge of a precipice, he would have fallen over; had he stood in contact with a window, he would have broken the glass; had he been close to a drumhead, he would have shaken the drum. “We could thus transmit a push through a row of a hundred boys, each particular boy, however, only swaying to and fro. Thus, also, we send sound through the air, and shake the drum of a distant ear, while each particular particle of the air concerned in the transmission of the pulse makes only a small oscillation.

But we have not yet extracted from our row of boys all that they can teach us. When A is pushed he may yield languidly, and thus tardily deliver up the motion to his neighbor B. B may do the same to C, C to D, and D to E. In this way the motion might be transmitted with comparative slowness along the line. But A, when pushed, may, by a sharp muscular effort and sudden recoil, deliver up promptly his motion to B, and come himself to rest; B may do the same to C, C to D, and D to E, the motion being thus transmitted rapidly along the line. Now this sharp muscular effort and sudden recoil is analogous to the elasticity of the air in the case of sound. In a wave of sound, a lamina of air, when urged against its neighbor lamina, delivers up its motion and recoils, in virtue of the elastic force exerted between them; and the more rapid this delivery and recoil, or in other words the greater the elasticity of the air, the greater is the velocity of the sound.

Fig. 3.

A very instructive mode of illustrating the transmission of a sound-pulse is furnished by the apparatus represented in Fig. 3, devised by my assistant, Mr. Cottrell. It consists of a series of wooden balls separated from each other by spiral springs. On striking the knob A, a rod attached to it impinges upon the first ball B, which transmits its motion to C, thence it passes to E, and so on through the entire series. The arrival at D is announced by the shock of the terminal ball against the wood, or, if we wish, by the ringing of a bell. Here the elasticity of the air is represented by that of the springs. The pulse may be rendered slow enough to be followed by the eye.

Scientific education ought to teach us to see the invisible as well as the visible in nature, to picture with the vision of the mind those operations which entirely elude bodily vision; to look at the very atoms of matter in motion and at rest, and to follow them forth, without ever once losing sight of them, into the world of the senses, and see them there integrating themselves in natural phenomena. With regard to the point now under consideration, we must endeavor to form a definite image of a wave of sound. We ought to see mentally the air-particles, when urged outward by the explosion of our balloon, crowding closely together; but immediately behind this condensation we ought to see the particles separated more widely apart. We must, in short, to be able to seize the conception that a sonorous wave consists of two portions, in the one of which the air is more dense, and in the other of which it is less dense than usual. A condensation and a rarefaction, then, are the two constituents of a wave of sound. This conception shall be rendered more complete in our next lecture.

§ 2. Experiments in Vacuo, in Hydrogen, and on Mountains

That air is thus necessary to the propagation of sound was proved by a celebrated experiment made before the Royal Society, by a philosopher named Hawksbee, in 1705.9 He so fixed a bell within the receiver of an air-pump that he could ring the bell when the receiver was exhausted. Before the air was withdrawn the sound of the bell was heard within the receiver; after the air was withdrawn the sound became so faint as to be hardly perceptible. An arrangement is before you which enables us to repeat in a very perfect manner the experiment of Hawksbee. Within this jar, G G′, Fig. 4, resting on the plate of an air-pump is a

Fig. 4. bell, B, associated with cloc-kwork.10 After the jar has been exhausted as perfectly as possible, I release, by means of a rod, r r′, which passes air-tight through the top of the vessel, the detent which holds the hammer. It strikes, and you see it striking, but only those close to the bell can hear the sound. Hydrogen gas, which you know is fourteen times lighter than air, is now allowed to enter the vessel. The sound of the bell is not augmented by the presence of this attenuated gas, though the receiver is now full of it. By working the pump, the atmosphere round the bell is rendered still more attenuated. In this way we obtain a vacuum more perfect than that of Hawksbee, and this is important, for it is the last traces of air that are chiefly effective in this experiment. You now see the hammer pounding the bell, but you hear no sound. Even when the ear is placed against the exhausted receiver not the faintest tinkle is heard. Observe also that the bell is suspended by strings, for if it were allowed to rest upon the plate of the air-pump the vibrations would be communicated to the plate, and thence transmitted to the air outside. Permitting the air to enter the jar with as little noise as possible, you immediately hear a feeble sound, which grows louder as the air becomes more dense, until finally every person in this large assembly distinctly hears the ringing of the bell.11

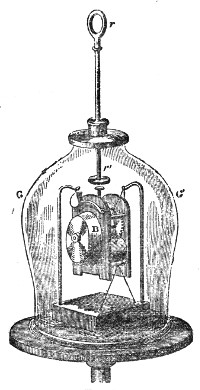
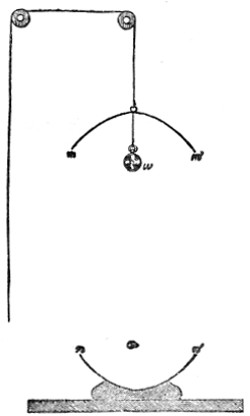
Sir John Leslie found hydrogen singularly incompetent to act as the vehicle of the sound of a bell rung in the gas. More than this, he emptied a receiver like that before you of half its air, and plainly heard the ringing of the bell. On permitting hydrogen to enter the half-filled receiver until it was wholly filled, the sound sank until it was scarcely audible. This result remained an enigma until it received a simple and satisfactory explanation at the hands of Prof. Stokes. When a common pendulum oscillates it tends to form a condensation in front and a rarefaction behind. But it is only a tendency; the motion is so slow, and the air is so elastic, that it moves away in front before it is sensibly condensed, and fills the space behind before it can become sensibly dilated. Hence waves or pulses are not generated by the pendulum. It requires a certain sharpness of shock to produce the condensation and rarefaction which constitute a wave of sound in air.

The more elastic and mobile the gas, the more able will it be to move away in front and to fill the space behind, and thus to oppose the formation of rarefactions and condensations by a vibrating body. Now hydrogen is much more mobile than air; and hence the production of sonorous waves in it is attended with greater difficulty than in air. A rate of vibration quite competent to produce sound-waves in the one may be wholly incompetent to produce them in the other. Both calculation and observation prove the correctness of this explanation, to which we shall again refer.

At great elevations in the atmosphere sound is sensibly diminished in loudness. De Saussure thought the explosion of a pistol at the summit of Mont Blanc to be about equal to that of a common cracker below. I have several times repeated this experiment; first, in default of anything better, with a little tin cannon, the torn remnants of which are now before you, and afterward with pistols. What struck me was the absence of that density and sharpness in the sound which characterize it at lower elevations. The pistol-shot resembled the explosion of a champagne bottle, but it was still loud. The withdrawal of half an atmosphere does not very materially affect our ringing bell, and air of the density found at the top of Mont Blanc is still capable of powerfully affecting the auditory nerve. That highly attenuated air is able to convey sound of great intensity is forcibly illustrated by the explosion of meteorites at elevations where the tenuity of the atmosphere must be almost infinite. Here, however, the initial disturbance must be exceedingly great.

The motion of sound, like all other motion, is enfeebled by its transference from a light body to a heavy one. When the receiver which has hitherto covered our bell is removed you hear how much more loudly it rings in the open air. When the bell was covered the aërial vibrations were first communicated to the heavy glass jar, and afterward by the jar to the air outside; a great diminution of intensity being the consequence. The action of hydrogen gas upon the voice is an illustration of the same kind. The voice is formed by urging air from the lungs through an organ called the larynx, where it is thrown into vibration by the vocal chords which thus generate sound. But when the lungs are filled with hydrogen, the vocal chords on speaking produce a vibratory motion in the hydrogen, which then transfers the motion to the outer air. By this transference from a light gas to a heavy one the voice is so weakened as to become a mere squeak.12

The intensity of a sound depends on the density of the air in which the sound is generated, and not on that of the air in which it is heard.13 Supposing the summit of Mont Blanc to be equally distant from the top of the Aiguille Verte and the bridge at Chamouni; and supposing two observers stationed, the one upon the bridge and the other upon the Aiguille: the report of a cannon fired on Mont Blanc would reach both observers with the same intensity, though in the one case the sound would pursue its way through the rare air above, while in the other it would descend though the denser air below. Again, let a straight line equal to that from the bridge at Chamouni to the summit of Mont Blanc be measured along the earth’s surface in the valley of Chamouni, and let two observers be stationed, the one on the summit and the other at the end of the line: the report of a cannon fired on the bridge would reach both observers with the same intensity, though in the one case the sound would be propagated through the dense air of the valley, and in the other case would ascend through the rarer air of the mountain. Finally, charge two cannon equally, and fire one of them at Chamouni and the other at the top of Mont Blanc: the one fired in the heavy air below may be heard above, while the one fired in the light air above is unheard below.

§ 3. Intensity of Sound. Law of Inverse Squares

In the case of our exploding balloon the wave of sound expands on all sides, the motion produced by the explosion being thus diffused over a continually augmenting mass of air. It is perfectly manifest that this cannot occur without an enfeeblement of the motion. Take the case of a thin shell of air with a radius of one foot, reckoned from the centre of explosion. A shell of air of the same thickness, but of two feet radius, will contain four times the quantity of matter; if its radius be three feet, it will contain nine times the quantity of matter; if four feet, it will contain sixteen times the quantity of matter, and so on. Thus the quantity of matter set in motion augments as the square of the distance from the centre of explosion. The intensity or loudness of sound diminishes in the same proportion. We express this law by saying that the intensity of the sound varies inversely as the square of the distance.

Let us look at the matter in another light. The mechanical effect of a ball striking a target depends on two things—the weight of the ball, and the velocity with which it moves. The effect is proportional to the weight simply; but it is proportional to the square of the velocity. The proof of this is easy, but it belongs to ordinary mechanics rather than to our present subject. Now what is true of the cannon-ball striking a target is also true of an air-particle striking the tympanum of the ear. Fix your attention upon a particle of air as the sound-wave passes over it; it is urged from its position of rest toward a neighbor particle, first with an accelerated motion, and then with a retarded one. The force which first urges it is opposed by the resistance of the air, which finally stops the particle and causes it to recoil. At a certain point of its excursion the velocity of the particle is its maximum. The intensity of the sound is proportional to the square of this maximum velocity.

The distance through which the air-particle moves to and fro, when the sound-wave passes it, is called the amplitude of the vibration. The intensity of the sound is proportional to the square of the amplitude.

§ 4. Confinement of Sound-waves in Tubes

This weakening of the sound, according to the law of inverse squares, would not take place if the sound-wave were so confined as to prevent its lateral diffusion. By sending it through a tube with a smooth interior surface we accomplish this, and the wave thus confined may be transmitted to great distances with very little diminution of intensity. Into one end of this tin tube, fifteen feet long, I whisper in a manner quite inaudible to the people nearest to me, but a listener at the other end hears me distinctly. If a watch be placed at one end of the tube, a person at the other end hears the ticks, though nobody else does. At the distant end of the tube is now placed a lighted candle, c, Fig. 5. When the hands are clapped at this end, the flame instantly ducks down at the other. It is not quite extinguished, but it is forcibly depressed. When two books, B B′, Fig. 5, are clapped together, the candle is blown out.14 You may here observe, in a rough way, the speed with which the sound-wave is propagated. The instant the clap is heard the flame is extinguished. I do not say that the time required by the sound to travel this tube is immeasurably short, but simply that the interval is too short for your senses to appreciate it.

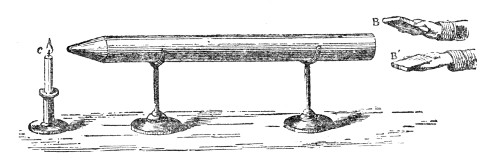
Fig. 5.

That it is a pulse and not a puff of air is proved by filling one end of the tube with the smoke of brown paper. On clapping the books together no trace of this smoke is ejected from the other end. The pulse has passed through both smoke and air without carrying either of them along with it.

An effective mode of throwing the propagation of a pulse through air has been devised by my assistant. The two ends of a tin tube fifteen feet long are stopped by sheet India-rubber stretched across them. At one end, e, a hammer with a spring handle rests against the India-rubber; at the other end is an arrangement for the striking of a bell, c. Drawing back the hammer e to a distance measured on the graduated circle and liberating it, the generated pulse is propagated through the tube, strikes the other end, drives away the cork termination a of the lever a b, and causes the hammer b to strike the bell. The rapidity of propagation is well illustrated here. When hydrogen (sent through the India-rubber tube H) is substituted for air the bell does not ring.

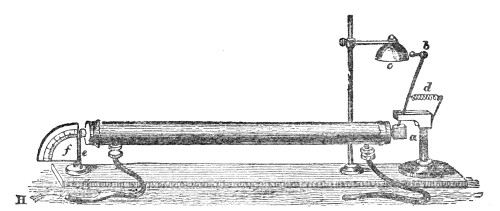
Fig. 6.

The celebrated French philosopher, Biot, observed the transmission of sound through the empty water-pipes of Paris, and found that he could hold a conversation in a low voice through an iron tube 3,120 feet in length. The lowest possible whisper, indeed, could be heard at this distance, while the firing of a pistol into one end of the tube quenched a lighted candle at the other.

§ 5. The Reflection of Sound. Resemblances to Light

The action of sound thus illustrated is exactly the same as that of light and radiant heat. They, like sound, are wave-motions. Like sound they diffuse themselves in space, diminishing in intensity according to the same law. Like sound also, light and radiant heat, when sent through a tube with a reflecting interior surface, may be conveyed to great distances with comparatively little loss. In fact, every experiment on the reflection of light has its analogy in the reflection of sound. On yonder gallery stands an electric lamp, placed close to the clock of this lecture-room. An assistant in the gallery ignites the lamp, and directs its powerful beam upon a mirror placed here behind the lecture-table. By the act of reflection the divergent beam is converted into this splendid luminous cone traced out upon the dust of the room. The point of convergence being marked and the lamp extinguished, I place my ear at that point. Here every sound-wave sent forth by the clock and reflected by the mirror is gathered up, and the ticks are heard as if they came, not from the clock, but from the mirror. Let us stop the clock, and place a watch w, Fig. 7, at the place occupied a moment ago by the electric light. At this great distance the ticking of the watch is distinctly heard. The hearing is much aided by introducing the end f of a glass funnel into the ear, the funnel here acting the part of an ear-trumpet. We know, moreover, that in optics the positions of a body and of its image are reversible. When a candle is placed at this lower focus, you see its image on the gallery above, and I have only to turn the mirror on its stand to make the image of the flame fall upon any one of the row of persons who occupy the front seat in the gallery. Removing the candle, and putting the watch, w, Fig. 8, in its place, the person on whom the light falls distinctly hears the sound. When the ear is assisted by the glass funnel, the reflected ticks of the clock in our first experiment are so powerful as to suggest the idea of something pounding against the tympanum, while the direct ticks are scarcely if at all, heard.

Fig. 7.

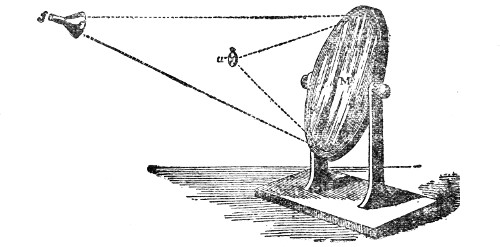
Fig. 8.

One of these two parabolic mirrors, n n′, Fig. 9, is placed upon the table, the other, m m′, being drawn up to the ceiling of this theatre; they are five-and-twenty feet apart. When the carbon-points of the electric light are placed in the focus a of the lower mirror and ignited, a fine luminous cylinder rises like a pillar to the upper

Fig. 9. mirror, which brings the parallel beam to a focus. At that focus is seen a spot of sunlike brilliancy, due to the reflection of the light from the surface of a watch, w, there suspended. The watch is ticking, but in my present position I do not hear it. At this lower focus, a, however, we have the energy of every sonorous wave converged. Placing the ear at a, the ticking is as audible as if the watch were at hand; the sound, as in the former case, appearing to proceed, not from the watch itself, but from the lower mirror.15

Curved roofs and ceilings and bellying sails act as mirrors upon sound. In our old laboratory, for example, the singing of a kettle seemed, in certain positions, to come, not from the fire on which it was placed, but from the ceiling. Inconvenient secrets have been thus revealed, an instance of which has been cited by Sir John Herschel.16 In one of the cathedrals in Sicily the confessional was so placed that the whispers of the penitents were reflected by the curved roof, and brought to a focus at a distant part of the edifice. The focus was discovered by accident, and for some time the person who discovered it took pleasure in hearing, and in bringing his friends to hear, utterances intended for the priest alone. One day, it is said, his own wife occupied the penitential stool, and both he and his friends were thus made acquainted with secrets which were the reverse of amusing to one of the party.

When a sufficient interval exists between a direct and a reflected sound, we hear the latter as an echo.

Sound, like light, may be reflected several times in succession, and, as the reflected light under these circumstances becomes gradually feebler to the eye, so the successive echoes become gradually feebler to the ear. In mountain regions this repetition and decay of sound produce wonderful and pleasing effects. Visitors to Killarney will remember the fine echo in the Gap of Dunloe. When a trumpet is sounded in the proper place in the Gap, the sonorous waves reach the ear in succession after one, two, three, or more reflections from the adjacent cliffs, and thus die away in the sweetest cadences. There is a deep cul-de-sac, called the Ochsenthal, formed by the great cliffs of the Engelhörner, near Rosenlaui, in Switzerland, where the echoes warble in a wonderful manner.

The sound of the Alpine horn, echoed from the rocks of the Wetterhorn or the Jungfrau, is in the first instance heard roughly. But by successive reflections the notes are rendered more soft and flute-like, the gradual diminution of intensity giving the impression that the source of sound is retreating further and further into the solitudes of ice and snow. The repetition of echoes is also in part due to the fact that the reflecting surfaces are at different distances from the hearer.

In large, unfurnished rooms the mixture of direct and reflected sound sometimes produces very curious effects. Standing, for example, in the gallery of the Bourse at Paris, you hear the confused vociferation of the excited multitude below. You see all the motions—of their lips as well as of their hands and arms. You know they are speaking—often, indeed, with vehemence—but what they say you know not. The voices mix with their echoes into a chaos of noise, out of which no intelligible utterance can emerge. The echoes of a room are materially damped by its furniture. The presence of an audience may also render intelligible speech possible where, without an audience, the definition of the direct voice is destroyed by its echoes. On the 16th of May, 1865, having to lecture in the Senate House of the University of Cambridge, I first made some experiments as to the loudness of voice necessary to fill the room, and was dismayed to find that a friend, placed at a distant part of the hall, could not follow me because of the echoes. The assembled audience, however, so quenched the sonorous waves that the echoes were practically absent, and my voice was plainly heard in all parts of the Senate House.

Sounds are also said to be reflected from the clouds. Arago reports that, when the sky is clear, the report of a cannon on an open plain is short and sharp, while a cloud is sufficient to produce an echo like the rolling of distant thunder. The subject of aërial echoes will be subsequently treated at length, when it will be shown that Arago’s conclusion requires correction.

Sir John Herschel, in his excellent article “Sound,” In the “Encyclopædia Metropolitana,” has collected with others the following instances of echoes. An echo in Woodstock Park repeats seventeen syllables by day and twenty by night; one, on the banks of the Lago del Lupo, above the fall of Terni, repeats fifteen. The tick of a watch may be heard from one end of the abbey church of St. Albans to the other. In Gloucester Cathedral, a gallery of an octagonal form conveys a whisper seventy-five feet across the nave. In the whispering-gallery of St. Paul’s, the faintest sound is conveyed from one side to the other of the dome, but is not heard at any intermediate point. At Carisbrook Castle, in the Isle of Wight, is a well two hundred and ten feet deep and twelve wide. The interior is lined by smooth masonry; when a pin is dropped into the well it is distinctly heard to strike the water. Shouting or coughing into this well produces a resonant ring of some duration.17

§ 6. Refraction of Sound

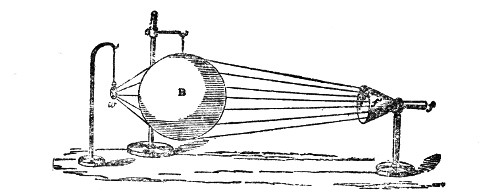
Fig. 10.

Another important analogy between sound and light has been established by M. Sondhauss.18 When a large lens is placed in front of our lamp, the lens compels the rays of light that fall upon it to deviate from their direct and divergent course, and to form a convergent cone behind it. This refraction of the luminous beam is a consequence of the retardation suffered by the light in passing through the glass. Sound may be similarly refracted by causing it to pass through a lens which retards its motion. Such a lens is formed when we fill a thin balloon with some gas heavier than air. A collodion balloon, B, Fig. 10, filled with carbonic-acid gas, the envelope being so thin as to yield readily to the pulses which strike against it, answers the purpose.19 A watch, w, is hung up close to the lens, beyond which, and at a distance of four or five feet from the lens, is placed the ear, assisted by the glass funnel f f′. By moving the head about, a position is soon discovered in which the ticking is particularly loud. This, in fact, is the focus of the lens. If the ear be moved from this focus the intensity of the sound falls; if, when the ear is at the focus, the balloon be removed, the ticks are enfeebled; on replacing the balloon their force is restored. The lens, in fact, enables us to hear the ticks distinctly when they are perfectly inaudible to the unaided ear.

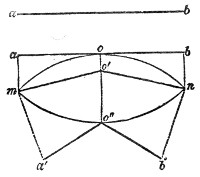
How a sound-wave is thus converged may be comprehended by reference to Fig. 11. Let m o n o″ be a section of the sound-lens, and a b a portion of a sonorous wave approaching it from a distance. The middle point, o, of the wave first touches the lens, and is first retarded

Fig. 11. by it. By the time the ends a and b, still moving through air, reach the balloon, the middle point o, pursuing its way through the heavier gas within, will have only reached o′. The wave is therefore broken at o; and the direction of motion being at right angles to the face of the wave, the two halves will encroach upon each other. This convergence of the two halves of the wave is augmented on quitting the lens. For when o′ has reached o″, the two ends a and b will have pushed forward to a greater distance, say to a′ and b′. Soon afterward the two halves of the wave will cross each other, or in other words come to a focus, the air at the focus being agitated by the sum of the motions of the two waves.20

§ 7. Diffraction of Sound: illustrations offered by great Explosions

When a long sea-roller meets an isolated rock in its passage, it rises against the rock and embraces it all round. Facts of this nature caused Newton to reject the undulatory theory of light. He contended that if light were a product of wave-motion we could have no shadows, because the waves of light would propagate themselves round opaque bodies as a wave of water round a rock. It has been proved since his time that the waves of light do bend round opaque bodies; but with that we have nothing now to do. A sound-wave certainly bends thus round an obstacle, though as it diffuses itself in the air at the back of the obstacle it is enfeebled in power, the obstacle thus producing a partial shadow of the sound. A railway train passing through cuttings and long embankments exhibits great variations in the intensity of the sound. The interposition of a hill in the Alps suffices to diminish materially the sound of a cataract; it is able sensibly to extinguish the tinkle of the cowbells. Still the sound-shadow is but partial, and the marker at the rifle-butts never fails to hear the explosion, though he is well protected from the ball. A striking example of this diffraction of a sonorous wave was exhibited at Erith after the tremendous explosion of a powder magazine which occurred there in 1864. The village of Erith was some miles distant from the magazine, but in nearly all cases the windows were shattered; and it was noticeable that the windows turned away from the origin of the explosion suffered almost as much as those which faced it. Lead sashes were employed in Erith Church, and these, being in some degree flexible, enabled the windows to yield to pressure without much fracture of the glass. As the sound-wave reached the church it separated right and left, and, for a moment, the edifice was clasped by a girdle of intensely compressed air, every window in the church, front and back, being bent inward. After compression, the air within the church no doubt dilated, tending to restore the windows to their first condition. The bending in of the windows, however, produced but a small condensation of the whole mass of air within the church; the recoil was therefore feeble in comparison with the pressure, and insufficient to undo what the latter had accomplished.

§ 8. Velocity of Sound: relation to Density and Elasticity of Air

Two conditions determine the velocity of propagation of a sonorous wave; namely, the elasticity and the density of the medium through which the wave passes. The elasticity of air is measured by the pressure which it sustains or can hold in equilibrium. At the sea-level this pressure is equal to that of a stratum of mercury about thirty inches high. At the summit of Mont Blanc the barometric column is not much more than half this height; and, consequently, the elasticity of the air upon the summit of the mountain is not much more than half what it is at the sea-level.

If we could augment the elasticity of air, without at the same time augmenting its density, we should augment the velocity of sound. Or, if allowing the elasticity to remain constant we could diminish the density, we should augment the velocity. Now, air in a closed vessel, where it cannot expand, has its elasticity augmented by heat, while its density remains unchanged. Through such heated air sound travels more rapidly than through cold air. Again, air free to expand has its density lessened by warming, its elasticity remaining the same, and through such air sound travels more rapidly than through cold air. This is the case with our atmosphere when heated by the sun.

The velocity of sound in air, at the freezing temperature, is 1,090 feet a second.

At all lower temperatures the velocity is less than this, and at all higher temperatures it is greater. The late M. Wertheim has determined the velocity of sound in air of different temperatures, and here are some of his results:

Temperature of air

    Velocity of sound

   0·5°

centigrade

 1,089 feet

  2·10

” 

1,091  ”  

  8·5

” 

1,109  ”  

12·0

” 

1,113  ”  

26·6

” 

1,140  ”  

At a temperature of half a degree above the freezing-point of water the velocity is 1,089 feet a second; at a temperature of 26·6 degrees, it is 1,140 feet a second, or a difference of 51 feet for 26 degrees; that is to say, an augmentation of velocity of nearly two feet for every single degree centigrade.

With the same elasticity the density of hydrogen gas is much less than that of air, and the consequence is that the velocity of sound in hydrogen far exceeds its velocity in air. The reverse holds good for heavy carbonic-acid gas. If density and elasticity vary in the same proportion, as the law of Boyle and Mariotte proves them to do in air when the temperature is preserved constant, they neutralize each other’s effects; hence, if the temperature were the same, the velocity of sound upon the summits of the highest Alps would be the same as that at the mouth of the Thames. But, inasmuch as the air above is colder than that below, the actual velocity on the summits of the mountains is less than that at the sea-level. To express this result in stricter language, the velocity is directly proportional to the square root of the elasticity of the air; it is also inversely proportional to the square root of the density of the air. Consequently, as in air of a constant temperature elasticity and density vary in the same proportion, and act oppositely, the velocity of sound is not affected by a change of density, if unaccompanied by a change of temperature.

There is no mistake more common than to suppose the velocity of sound to be augmented by density. The mistake has arisen from a misconception of the fact that in solids and liquids the velocity is greater than in gases. But it is the higher elasticity of those bodies, in relation to their density, that causes sound to pass rapidly through them. Other things remaining the same, an augmentation of density always produces a diminution of velocity. Were the elasticity of water, which is measured by its compressibility, only equal to that of air, the velocity of sound in water, instead of being more than quadruple the velocity in air, would be only a small fraction of that velocity. Both density and elasticity, then, must be always borne in mind; the velocity of sound being determined by neither taken separately, but by the relation of the one to the other. The effect of small density and high elasticity is exemplified in an astonishing manner by the luminiferous ether, which transmits the vibrations of light—not at the rate of so many feet, but at the rate of nearly two hundred thousand miles a second.

Those who are unacquainted with the details of scientific investigation have no idea of the amount of labor expended in the determination of those numbers on which important calculations or inferences depend. They have no idea of the patience shown by a Berzelius in determining atomic weights; by a Regnault in determining coefficients of expansion; or by a Joule in determining the mechanical equivalent of heat. There is a morality brought to bear upon such matters which, in point of severity, is probably without a parallel in any other domain of intellectual action. Thus, as regards the determination of the velocity of sound in air, hours might be filled with a simple statement of the efforts made to establish it with precision. The question has occupied the attention of experimenters in England, France, Germany, Italy, and Holland. But to the French and Dutch philosophers we owe the application of the last refinements of experimental skill to the solution of the problem. They neutralized effectually the influence of the wind; they took into account barometric pressure, temperature, and hygrometric condition. Sounds were started at the same moment from two distant stations, and thus caused to travel from station to station through the self-same air. The distance between the stations was determined by exact trigonometrical observations, and means were devised for measuring with the utmost accuracy the time required by the sound to pass from the one station to the other. This time, expressed in seconds, divided into the distance expressed in feet, gave 1,090 feet per second as the velocity of sound through air at the temperature of 0° centigrade.

The time required by light to travel over all terrestrial distances is practically zero; and in the experiments just referred to the moment of explosion was marked by the flash of a gun, the time occupied by the sound in passing from station to station being the interval observed between the appearance of the flash and the arrival of the sound. The velocity of sound in air once established, it is plain that we can apply it to the determination of distances. By observing, for example, the interval between the appearance of a flash of lightning and the arrival of the accompanying thunder-peal, we at once determine the distance of the place of discharge. It is only when the interval between the flash and peal is short that danger from lightning is to be apprehended.

§ 9. Theoretic Velocity calculated by Newton Laplace’s Correction

We now come to one of the most delicate points in the whole theory of sound. The velocity through air has been determined by direct experiment; but knowing the elasticity and density of the air, it is possible, without any experiment at all, to calculate the velocity with which a sound-wave is transmitted through it. Sir Isaac Newton made this calculation, and found the velocity at the freezing temperature to be 916 feet a second. This is about one-sixth less than actual observation had proved the velocity to be, and the most curious suppositions were made to account for the discrepancy. Newton himself threw out the conjecture that it was only in passing from particle to particle of the air that sound required time for its transmission; that it moved instantaneously through the particles themselves. He then supposed the line along which sound passes to be occupied by air-particles for one-sixth of its extent, and thus he sought to make good the missing velocity. The very art and ingenuity of this assumption were sufficient to throw doubt on it; other theories were therefore advanced, but the great French mathematician Laplace was the first

Fig. 12. to completely solve the enigma. I shall now endeavor to make you thoroughly acquainted with his solution.

Into this strong cylinder of glass, T U, Fig. 12, which is accurately bored, and quite smooth within, fits an air-tight piston. By pushing the piston down, I condense the air beneath it, heat being at the same time developed. A scrap of amadou attached to the bottom of the piston is ignited by the heat generated by compression. If a bit of cotton wool dipped into bisulphide of carbon be attached to the piston, when the latter is forced down, a flash of light, due to the ignition of the bisulphide of carbon vapor, is observed within the tube. It is thus proved that when air is compressed heat is generated. By another experiment it may be shown that when air is rarefied cold is developed. This brass box contains a quantity of condensed air. I open the cock, and permit the air to discharge itself against a suitable thermometer; the sinking of the instrument immediately declares the chilling of the air.

All that you have heard regarding the transmission of a sonorous pulse through air is, I trust, still fresh in your minds. As the pulse advances it squeezes the particles of air together, and two results follow from this compression. First, its elasticity is augmented through the mere augmentation of its density. Secondly, its elasticity is augmented by the heat of compression. It was the change of elasticity which resulted from a change of density that Newton took into account, and he entirely overlooked the augmentation of elasticity due to the second cause just mentioned. Over and above, then, the elasticity involved in Newton’s calculation, we have an additional elasticity due to changes of temperature produced by the sound-wave itself. When both are taken into account, the calculated and the observed velocities agree perfectly.

But here, without due caution, we may fall into the gravest error. In fact, in dealing with Nature, the mind must be on the alert to seize all her conditions; otherwise we soon learn that our thoughts are not in accordance with her facts. It is to be particularly noted that the augmentation of velocity due to the changes of temperature produced by the sonorous wave itself is totally different from the augmentation arising from the heating of the general mass of the air. The average temperature of the air is unchanged by the waves of sound. We cannot have a condensed pulse without having a rarefied one associated with it. But in the rarefaction, the temperature of the air is as much lowered as it is raised in the condensation. Supposing, then, the atmosphere parcelled out into such condensations and rarefactions, with their respective temperatures, an extraneous sound passing through such an atmosphere would be as much retarded in the latter as accelerated in the former, and no variation of the average velocity could result from such a distribution of temperature.

Fig. 13.

Whence, then, does the augmentation pointed out by Laplace arise? I would ask your best attention while I endeavor to make this knotty point clear to you. If air be compressed it becomes smaller in volume; if the pressure be diminished, the volume expands. The force which resists compression, and which produces expansion, is the elastic force of the air. Thus an external pressure squeezes the air-particles together; their own elastic force holds them asunder, and the particles are in equilibrium when these two forces are in equilibrium. Hence it is that the external pressure is a measure of the elastic force. Let the middle row of dots, Fig. 13, represent a series of air-particles in a state of quiescence between the points a and x. Then, because of the elastic force exerted between the particles, if any one of them be moved from its position of rest, the motion will be transmitted through the entire series. Supposing the particle a to be driven by the prong of a tuning-fork, or some other vibrating body, toward x, so as to be caused finally to occupy the position a′ in the lowest row of particles: at the instant the excursion of a commences, its motion begins to be transmitted to b. In the next following moments b transmits the motion to c, c to d, d to e, and so on. So that by the time a has reached the position a′, the motion will have been propagated to some point o′ of the line of particles more or less distant from a′. The entire series of particles between a′ and o′ is then in a state of condensation. The distance a′ o′, over which the motion has travelled during the excursion of a to a′, will depend upon the elastic force exerted between the particles. Fix your attention on any two of the particles, say a and b. The elastic force between them may be figured as a spiral spring, and it is plain that the more flaccid this spring the more sluggish would be the communication of the motion from a to b; while the stiffer the spring the more prompt would be the communication of the motion. What is true of a and b is true for every other pair of particles between a and o. Now the spring between every pair of these particles is suddenly stiffened by the heat developed along the line of condensation, and hence the velocity of propagation is augmented by this heat. Reverting to our old experiment with the row of boys, it is as if, by the very act of pushing his neighbor, the muscular rigidity of each boy’s arm was increased, thus enabling him to deliver his push more promptly than he would have done without this increase of rigidity. The condensed portion of a sonorous wave is propagated in the manner here described, and it is plain that the velocity of propagation is augmented by the heat developed in the condensation.

Let us now turn our thoughts for a moment to the propagation of the rarefaction. Supposing, as before, the middle row a x to represent the particles of air in equilibrium under the pressure of the atmosphere, and suppose the particle a to be suddenly drawn to the right, so as to occupy the position a″ in the highest line of dots: a″ is immediately followed by b″, b″ by c″, c″ by d″, d″ by e″; and thus the rarefaction is propagated backward toward x″, reaching a point o″ in the line of particles by the time a has completed its motion to the right. Now, why does b″ follow a″ when a″ is drawn away from it? Manifestly because the elastic force exerted between b″ and a″ is less than that between b″ and c″. In fact, b″ will be driven after a″ by a force equal to the difference of the two elasticities between a″ and b″ and between b″ and c″. The same remark applies to the motion of c″ after b″, to that of d″ after c″, in fact, to the motion of each succeeding particle when it follows its predecessor. The greater the difference of elasticity on the two sides of any particle the more promptly will it follow its predecessor. And here observe what the cold of rarefaction accomplishes. In addition to the diminution of the elastic force between a″ and b″ by the withdrawal of a″ to a greater distance, there is a further diminution due to the lowering of the temperature. The cold developed augments the difference of elastic force on which the propagation of the rarefaction depends. Thus we see that because the heat developed in the condensation augments the rapidity of the condensation, and because the cold developed in the rarefaction augments the rapidity of the rarefaction, the sonorous wave, which consists of a condensation and a rarefaction, must have its velocity augmented by the heat and the cold which it develops during its own progress.

It is worth while fixing your attention here upon the fact that the distance a′ o′, to which the motion has been propagated while a is moving to the position a′, may be vastly greater than that passed over in the same time by the particle itself. The excursion of a′ may not be more than a small fraction of an inch, while the distance to which the motion is transferred during the time required by a′ to perform this small excursion may be many feet, or even many yards. If this point should not appear altogether plain to you now, it will appear so by and by.

§ 10. Ratio of Specific Heats of Air deduced from Velocity of Sound

Having grasped this, even partially, I will ask you to accompany me to a remote corner of the domain of physics, with the view, however, of showing that remoteness does not imply discontinuity. Let a certain quantity of air at a temperature of 0°, contained in a perfectly inexpansible vessel, have its temperature raised 1°. Let the same quantity of air, placed in a vessel which permits the air to expand when it is heated—the pressure on the air being kept constant during its expansion—also have its temperature raised 1°. The quantities of heat employed in the two cases are different. The one quantity expresses what is called the specific heat of air at constant volume; the other the specific heat of air at constant pressure.21 It is an instance of the manner in which apparently unrelated natural phenomena are bound together, that from the calculated and observed velocities of sound in air we can deduce the ratio of these two specific heats. Squaring Newton’s theoretic velocity and the observed velocity, and dividing the greater square by the less, we obtain the ratio referred to. Calling the specific heat at constant volume C^v, and that at constant pressure C^p; calling, moreover, Newton’s calculated velocity V, and the observed velocity V′, Laplace proved that—

Inserting the values of V and V′ in this equation, and making the calculation, we find—

Thus, without knowing either the specific heat at constant volume or at constant pressure, Laplace found the ratio of the greater of them to the less to be 1·42. It is evident from the foregoing formulæ that the calculated velocity of sound, multiplied by the square root of this ratio, gives the observed velocity.

But there is one assumption connected with the determination of this ratio, which must be here brought clearly forth. It is assumed that the heat developed by compression remains in the condensed portion of the wave, and applies itself there to augment the elasticity; that no portion of it is lost by radiation. If air were a powerful radiator, this assumption could not stand. The heat developed in the condensation could not then remain in the condensation. It would radiate all round, lodging itself for the most part in the chilled and rarefied portion of the wave, which would be gifted with a proportionate power of absorption. Hence the direct tendency of radiation would be to equalize the temperatures of the different parts of the wave, and thus to abolish the increase of velocity which called forth Laplace’s correction.22

§ 11. Mechanical Equivalent of Heat deduced from Velocity of Sound

The question, then, of the correctness of this ratio involves the other and apparently incongruous question, whether atmospheric air possesses any sensible radiative power. If the ratio be correct, the practical absence of radiative power on the part of air is demonstrated. How then are we to ascertain whether the ratio is correct or not? By a process of reasoning which illustrates still further how natural agencies are intertwined. It was this ratio, looked at by a man of genius, named Mayer, which helped him to a clearer and a grander conception of the relation and interaction of the forces of inorganic and organic nature than any philosopher up to his time had attained. Mayer was the first to see that the excess 0·42 of the specific heat at constant pressure over that at constant volume was the quantity of heat consumed in the work performed by the expanding gas. Assuming the air to be confined laterally and to expand in a vertical direction, in which direction it would simply have to lift the weight of the atmosphere, he attempted to calculate the precise amount of heat consumed in the raising of this or any other weight. He thus sought to determine the “mechanical equivalent” of heat. In the combination of his data his mind was clear, but for the numerical correctness of these data he was obliged to rely upon the experimenters of his age. Their results, though approximately correct, were not so correct as the transcendent experimental ability of Regnault, aided by the last refinements of constructive skill, afterward made them. Without changing in the slightest degree the method of his thought or the structure of his calculation, the simple introduction of the exact numerical data into the formula of Mayer brings out the true mechanical equivalent of heat.

But how are we able to speak thus confidently of the accuracy of this equivalent? We are enabled to do so by the labors of an Englishman, who worked at this subject contemporaneously with Mayer; and who, while animated by the creative genius of his celebrated German brother, enjoyed also the opportunity of bringing the inspirations of that genius to the test of experiment. By the immortal experiments of Mr. Joule, the mutual convertibility of mechanical work and heat was first conclusively established. And “Joule’s equivalent,” as it is rightly called, considering the amount of resolute labor and skill expended in its determination, is almost identical with that derived from the formula of Mayer.

§ 12. Absence of Radiative Power of Air deduced from Velocity of Sound

Consider now the ground we have trodden, the curious labyrinth of reasoning and experiment through which we have passed. We started with the observed and calculated velocities of sound in atmospheric air. We found Laplace, by a special assumption, deducing from these velocities the ratio of the specific heat of air at constant pressure to its specific heat at constant volume. We found Mayer calculating from this ratio the mechanical equivalent of heat; finally, we found Joule determining the same equivalent by direct experiments on the friction of solids and liquids. And what is the result? Mr. Joule’s experiments prove the result of Mayer to be the true one; they therefore prove the ratio determined by Laplace to be the true ratio; and, because they do this, they prove at the same time the practical absence of radiative power in atmospheric air. It seems a long step from the stirring of water, or the rubbing together of iron plates in Joule’s experiments, to the radiation of the atoms of our atmosphere; both questions are, however, connected by the line of reasoning here followed out.

But the true physical philosopher never rests content with an inference when an experiment to verify or contravene it is possible. The foregoing argument is clinched by bringing the radiative power of atmospheric air to a direct test. When this is done, experiment and reasoning are found to agree; air being proved to be a body sensibly devoid of radiative and absorptive power.23

But here the experimenter on the transmission of sound through gases needs a word of warning. In Laplace’s day, and long subsequently, it was thought that gases of all kinds possessed only an infinitesimal power of radiation; but that this is not the case is now well established. It would be rash to assume that, in the case of such bodies as ammonia, aqueous vapor, sulphurous acid, and olefiant gas, their enormous radiative powers do not interfere with the application of the formula of Laplace. It behooves us to inquire whether the ratio of the two specific heats deduced from the velocity of sound in these bodies is the true ratio; and whether, if the true ratio could be found by other methods, its square root, multiplied into the calculated velocity, would give the observed velocity. From the moment heat first appears in the condensation and cold in the rarefaction of a sonorous wave in any of those gases, the radiative power comes into play to abolish the difference of temperature. The condensed part of the wave is on this account rendered more flaccid and the rarefied part less flaccid than it would otherwise be, and with a sufficiently high radiative power the velocity of sound, instead of coinciding with that derived from the formula of Laplace, must approximate to that derived from the more simple formula of Newton.

§ 13. Velocity of Sound through Gases, Liquids, and Solids

To complete our knowledge of the transmission of sound through gases, a table is here added from the excellent researches of Dulong, who employed in his experiments a method which shall be subsequently explained:

Velocity of Sound in Gases at the Temperature of 0° C.

 

Velocity

Air

1,092

feet

Oxygen

1,040

”

Hydrogen

4,164

”

Carbonic acid

858

”

Carbonic oxide

1,107

”

Protoxide of nitrogen

859

”

Olefiant gas

1,030

”

According to theory, the velocities of sound in oxygen and hydrogen are inversely proportional to the square roots of the densities of the two gases. We here find this theoretic deduction verified by experiment. Oxygen being sixteen times heavier than hydrogen, the velocity of sound in the latter gas ought, according to the above law, to be four times its velocity in the former; hence, the velocity in oxygen being 1,040, in hydrogen calculation would make it 4,160. Experiment, we see, makes it 4,164.

The velocity of sound in liquids may be determined theoretically, as Newton determined its velocity in air; for the density of a liquid is easily determined, and its elasticity can be measured by subjecting it to compression. In the case of water, the calculated and the observed velocities agree so closely as to prove that the changes of temperature produced by a sound-wave in water have no sensible influence upon the velocity. In a series of memorable experiments in the Lake of Geneva, MM. Colladon and Sturm determined the velocity of sound through water, and made it 4,708 feet a second. By a mode of experiment which you will subsequently be able to comprehend, the late M. Wertheim determined the velocity through various liquids, and in the following table I have collected his results:

Transmission of Sound through Liquids

Name of Liquid

Temperature

Velocity

River-water (Seine)

15° C.

4,714

feet

River

”

water (S

”

30

5,013

”

River

”

water (S

”

60

5,657

”

Sea-water (artificial)

20

4,768

”

Solution of common salt

18

5,132

”

Solution of sulphate of soda

20

5,194

”

Solution of carbonate of soda

22

5,230

”

Solution of nitrate of soda

21

5,477

”

Solution of chloride of calcium

23

6,493

”

Common alcohol

20

4,218

”

Absolute alcohol

23

3,804

”

Spirits of turpentine

24

3,976

”

Sulphuric ether

0

3,801

”

We learn from this table that sound travels with different velocities through different liquids; that a salt dissolved in water augments the velocity, and that the salt which produces the greatest augmentation is chloride of calcium. The experiments also teach us that in water, as in air, the velocity augments with the temperature. At a temperature of 15° C., for example, the velocity in Seine water is 4,714 feet, at 30° it is 5,013 feet, and at 60° 5,657 feet a second.

I have said that from the compressibility of a liquid, determined by proper measurements, the velocity of sound through the liquid may be deduced. Conversely, from the velocity of sound in a liquid, the compressibility of the liquid may be deduced. Wertheim compared a series of compressibilities deduced from his experiments on sound with a similar series obtained directly by M. Grassi. The agreement of both, exhibited in the following table, is a strong confirmation of the accuracy of the method pursued by Wertheim:

 

Cubic compressibility

 

╭———————^———————╮

 

from Wertheim’s

velocity of sound

from the direct

experiments of

M. Grassi

Sea-water

0·0000467

0·0000436

Solution of common salt

0·0000349

0·0000321

      ”       carbonate of soda

0·0000337

0·0000297

      ”       nitrate of soda

0·0000301

0·0000295

Absolute alcohol

0·0000947

0·0000991

Sulphuric ether

0·0001002

0·0001110

The greater the resistance which a liquid offers to compression, the more promptly and forcibly will it return to its original volume after it has been compressed. The less the compressibility, therefore, the greater is the elasticity, and consequently, other things being equal, the greater the velocity of sound through the liquid.

We have now to examine the transmission of sound through solids. Here, as a general rule, the elasticity, as compared with the density, is greater than in liquids, and consequently the propagation of sound is more rapid.

In the following table the velocity of sound through various metals, as determined by Wertheim, is recorded:

Velocity of Sound through Metals

Name of Metal

At 20° C.

At 100° C.

At 200° C.

Lead

4,030

3,951

......

Gold

5,717

5,640

5,619

Silver

8,553

8,658

8,127

Copper

11,666

10,802

9,690

Platinum

8,815

8,437

8,079

Iron

16,822

17,386

15,483

Iron wire (ordinary)

16,130

16,728

......

Cast steel

16,357

16,153

15,709

Steel wire (English)

15,470

17,201

16,394

Steel wire

16,023

16,443

......

As a general rule, the velocity of sound through metals is diminished by augmented temperature; iron is, however, a striking exception to this rule, but it is only within certain limits an exception. While, for example, a rise of temperature from 20° to 100° C. in the case of copper causes the velocity to fall from 11,666 to 10,802, the same rise produces in the case of iron an increase of velocity from 16,822 to 17,386. Between 100° and 200°, however, we see that iron falls from the last figure to 15,483. In iron, therefore, up to a certain point, the elasticity is augmented by heat; beyond that point it is lowered. Silver is also an example of the same kind.

The difference of velocity in iron and in air may be illustrated by the following instructive experiment: Choose one of the longest horizontal bars employed for fencing in Hyde Park; and let an assistant strike the bar at one end while the ear of the observer is held close to the bar at a considerable distance from the point struck. Two sounds will reach the ear in succession; the first being transmitted through the iron and the second through the air. This effect was obtained by M. Biot, in his experiments on the iron water-pipes of Paris.

The transmission of sound through a solid depends on the manner in which the molecules of the solid are arranged. If the body be homogeneous and without structure, sound is transmitted through it equally well in all directions. But this is not the case when the body, whether inorganic like a crystal or organic like a tree, possesses a definite structure. This is also true of other things than sound. Subjecting, for example, a sphere of wood to the action of a magnet, it is not equally affected in all directions. It is repelled by the pole of the magnet, but it is most strongly repelled when the force acts along the fibre. Heat also is conducted with different facilities in different directions through wood. It is most freely conducted along the fibre, and it passes more freely across the ligneous layers than along them. Wood, therefore, possesses three unequal axes of calorific conduction. These, established by myself, coincide with the axes of elasticity discovered by Savart. MM. Wertheim and Chevandier have determined the velocity of sound along these three axes and obtained the following results:

Velocity of Sound in Wood

  Name of Wood  

  Along Fibre  

  Across Rings  

  Along Rings  

Acacia

15,467

4,840

4,436

Fir

15,218

4,382

2,572

Beech

10,965

6,028

4,643

Oak

12,622

5,036

4,229

Pine

10,900

4,611

2,605

Elm

13,516

4,665

3,324

Sycamore

14,639

4,916

3,728

Ash

15,314

4,567

4,142

Alder

15,306

4,491

3,423

Aspen

16,677

5,297

2,987

Maple

13,472

5,047

3,401

Poplar

14,050

4,600

3,444

Separating a cube from the bark-wood of a good-sized tree, where the rings for a short distance may be regarded as straight: then, if A R, Fig. 14, be the section

Fig. 14. of the tree, the velocity of the sound in the direction m n, through such a cube, is greater than in the direction a b.

The foregoing table strikingly illustrates the influence of molecular structure. The great majority of crystals show differences of the same kind. Such bodies, for the most part, have their molecules arranged in different degrees of proximity in different directions, and where this occurs there are sure to be differences in the transmission and manifestation of heat, light, electricity, magnetism, and sound.

§ 14. Hooke’s Anticipation of the Stethoscope

I will conclude this lecture on the transmission of sound through gases, liquids, and solids, by a quaint and beautiful extract from the writings of that admirable thinker, Dr. Robert Hooke. It will be noticed that the philosophy of the stethoscope is enunciated in the following passage, and another could hardly be found which illustrates so well that action of the scientific imagination which, in all great investigators, is the precursor and associate of experiment:

“There may also be a possibility,” writes Hooke, “of discovering the internal motions and actions of bodies by the sound they make. Who knows but that, as in a watch, we may hear the beating of the balance, and the running of the wheels, and the striking of the hammers, and the grating of the teeth, and multitudes of other noises; who knows, I say, but that it may be possible to discover the motions of the internal parts of bodies, whether animal, vegetable, or mineral, by the sound they make; that one may discover the works performed in the several offices and shops of a man’s body, and thereby discover what instrument or engine is out of order, what works are going on at several times, and lie still at others, and the like; that in plants and vegetables one might discover by the noise the pumps for raising the juice, the valves for stopping it, and the rushing of it out of one passage into another, and the like? I could proceed further, but methinks I can hardly forbear to blush when I consider how the most part of men will look upon this: but, yet again, I have this encouragement, not to think all these things utterly impossible, though never so much derided by the generality of men, and never so seemingly mad, foolish, and fantastic, that as the thinking them impossible cannot much improve my knowledge, so the believing them possible may, perhaps, be an occasion of taking notice of such things as another would pass by without regard as useless. And somewhat more of encouragement I have also from experience, that I have been able to hear very plainly the beating of a man’s heart, and it is common to hear the motion of wind to and fro in the guts, and other small vessels; the stopping of the lungs is easily discovered by the wheezing, the stopping of the head by the humming and whistling noises, the slipping to and fro of the joints, in many cases, by crackling, and the like, as to the working or motion of the parts one among another; methinks I could receive encouragement from hearing the hissing noise made by a corrosive menstruum in its operation, the noise of fire in dissolving, of water in boiling, of the parts of a bell after that its motion is grown quite invisible as to the eye, for to me these motions and the other seem only to differ secundum magis minus, and so to their becoming sensible they require either that their motions be increased, or that the organ be made more nice and powerful to sensate and distinguish them.”

NOTE ON THE DIFFRACTION OF SOUND

The recent explosion of a powder-laden barge in the Regent’s Park produced effects similar to those mentioned in § 7. The sound-wave bent round houses and broke the windows at the back, the coalescence of different portions of the wave at special points being marked by intensified local action. Close to the place where the explosion occurred the unconsumed gunpowder was in the wave, and, as a consequence, the dismantled gatekeeper’s lodge was girdled all round by a black belt of carbon.

SUMMARY OF CHAPTER I

The sound of an explosion is propagated as a wave or pulse through the air.

This wave impinging upon the tympanic membrane causes it to shiver, its tremors are transmitted to the auditory nerve, and along the auditory nerve to the brain, where it announces itself as sound.

A sonorous wave consists of two parts, in one of which the air is condensed, and in the other rarefied.

The motion of the sonorous wave must not be confounded with the motion of the particles which at any moment form the wave. During the passage of the wave every particle concerned in its transmission makes only a small excursion to and fro.

The length of this excursion is called the amplitude of the vibration.

Sound cannot pass through a vacuum.

A certain sharpness of shock, or rapidity of vibration, is needed for the production of sonorous waves in air. It is still more necessary in hydrogen, because the greater mobility of this light gas tends to prevent the formation of condensations and rarefactions.

Sound is in all respects reflected like light; it is also refracted like light; and it may, like light, be condensed by suitable lenses.

Sound is also diffracted, the sonorous wave bending round obstacles; such obstacles, however, in part shade off the sound.

Echoes are produced by the reflected waves of sound.

In regard to sound and the medium through which it passes, four distinct things are to be borne in mind—intensity, velocity, elasticity, and density.

The intensity is proportional to the square of the amplitude as above defined.

It is also proportional to the square of the maximum velocity of the vibrating air-particles.

When sound issues from a small body in free air, the intensity diminishes as the square of the distance from the body increases.

If the wave of sound be confined in a tube with a smooth interior surface, it may be conveyed to great distances without sensible loss of intensity.

The velocity of sound in air depends on the elasticity of the air in relation to its density. The greater the elasticity the swifter is the propagation; the greater the density the slower is the propagation.

The velocity is directly proportional to the square root of the elasticity; it is inversely proportional to the square root of the density.

Hence, if elasticity and density vary in the same proportion, the one will neutralize the other as regards the velocity of sound.

That they do vary in the same proportion is proved by the law of Boyle and Mariotte; hence the velocity of sound in air is independent of the density of the air.

But that this law shall hold good, it is necessary that the dense air and the rare air should have the same temperature.

The intensity of a sound depends upon the density of the air in which it is generated, but not on that of the air in which it is heard.

The velocity of sound in air of the temperature 0° C. is 1,090 feet a second; it augments nearly 2 feet for every degree Centigrade added to its temperature.

Hence, given the velocity of sound in air, the temperature of the air may be readily calculated.

The distance of a fired cannon or of a discharge of lightning may be determined by observing the interval which elapses between the flash and the sound.

From the foregoing, it is easy to see that if a row of soldiers form a circle, and discharge their pieces all at the same time, the sound will be heard as a single discharge by a person occupying the centre of the circle.

But if the men form a straight row, and if the observer stand at one end of the row, the simultaneous discharge of the men’s pieces will be prolonged to a kind of roar.

A discharge of lightning along a lengthy cloud may in this way produce the prolonged roll of thunder. The roll of thunder, however, must in part at least be due to echoes from the clouds.

The pupil will find no difficulty in referring many common occurrences to the fact that sound requires a sensible time to pass through any considerable length of air. For example, the fall of the axe of a distant wood-cutter is not simultaneous with the sound of the stroke. A company of soldiers marching to music along a road cannot march in time, for the notes do not reach those in front and those behind simultaneously.

In the condensed portion of a sonorous wave the air is above, in the rarefied portion of the wave it is below, its average temperature.

This change of temperature, produced by the passage of the sound-wave itself, virtually augments the elasticity of the air, and makes the velocity of sound about one-sixth greater than it would be if there were no change of temperature.

The velocity found by Newton, who did not take this change of temperature into account, was 916 feet a second.

Laplace proved that by multiplying Newton’s velocity by the square root of the ratio of the specific heat of air at constant pressure to its specific heat at constant volume, the actual or observed velocity is obtained.

Conversely, from a comparison of the calculated and observed velocities, the ratio of the two specific heats may be inferred.

The mechanical equivalent of heat may be deduced from this ratio; it is found to be the same as that established by direct experiment.

This coincidence leads to the conclusion that atmospheric air is devoid of any sensible power to radiate heat. Direct experiments on the radiative power of air establish the same result.

The velocity of sound in water is more than four times its velocity in air.

The velocity of sound in iron is seventeen times its velocity in air.

The velocity of sound along the fibre of pine-wood is ten times its velocity in air.

The cause of this great superiority is that the elasticities of the liquid, the metal, and the wood, as compared with their respective densities, are vastly greater than the elasticity of air in relation to its density.

The velocity of sound is dependent to some extent upon molecular structure. In wood, for example, it is conveyed with different degrees of rapidity in different directions.

CHAPTER II

Physical Distinction between Noise and Music—A Musical Tone Produced by Periodic, Noise Produced by Unperiodic, Impulses—Production of Musical Sounds by Taps—Production of Musical Sounds by Puffs—Definition of Pitch in Music—Vibrations of a Tuning-Fork; their Graphic Representation on Smoked Glass—Optical Expression of the Vibrations of a Tuning-Fork—Description of the Siren—Limits of the Ear; Highest and Deepest Tones—Rapidity of Vibration Determined by the Siren—Determination of the Lengths of Sonorous Waves—Wave-Lengths of the Voice in Man and Woman—Transmission of Musical Sounds through Liquids and Solids

IN OUR last chapter we considered the propagation through air of a sound of momentary duration. We have to-day to consider continuous sounds, and to make ourselves in the first place acquainted with the physical distinction between noise and music. As far as sensation goes, everybody knows the difference between these two things. But we have now to inquire into the causes of sensation, and to make ourselves acquainted with the condition of the external air which in one case resolves itself into music and in another into noise.

We have already learned that what is loudness in our sensations is outside of us nothing more than width of swing, or amplitude, of the vibrating air-particles. Every other real sonorous impression of which we are conscious has its correlative without, as a mere form or state of the atmosphere. Were our organs sharp enough to see the motions of the air through which an agreeable voice is passing, we might see stamped upon that air the conditions of motion on which the sweetness of the voice depends. In ordinary conversation, also, the physical precedes and arouses the psychical; the spoken language, which is to give us pleasure or pain, which is to rouse us to anger or soothe us to peace, existing for a time, between us and the speaker, as a purely mechanical condition of the intervening air.

Noise affects us as an irregular succession of shocks. We are conscious while listening to it of a jolting and jarring of the auditory nerve, while a musical sound flows smoothly and without asperity or irregularity. How is this smoothness secured? By rendering the impulses received by the tympanic membrane perfectly periodic. A periodic motion is one that repeats itself. The motion of a common pendulum, for example, is periodic, but its vibrations are far too sluggish to excite sonorous waves. To produce a musical tone we must have a body which vibrates with the unerring regularity of the pendulum, but which can impart much sharper and quicker shocks to the air.

Imagine the first of a series of pulses following each other at regular intervals, impinging upon the tympanic membrane. It is shaken by the shock; and a body once shaken cannot come instantaneously to rest. The human ear, indeed, is so constructed that the sonorous motion vanishes with extreme rapidity, but its disappearance is not instantaneous; and if the motion imparted to the auditory nerve by each individual pulse of our series continues until the arrival of its successor, the sound will not cease at all. The effect of every shock will be renewed before it vanishes, and the recurrent impulses will link themselves together to a continuous musical sound. The pulses, on the contrary, which produce noise, are of irregular strength and recurrence. The action of noise upon the ear has been well compared to that of a flickering light upon the eye, both being painful through the sudden and abrupt changes which they impose upon their respective nerves.

The only condition necessary to the production of a musical sound is that the pulses should succeed each other in the same interval of time. No matter what its origin may be, if this condition be fulfilled the sound becomes musical. If a watch, for example, could be caused to tick with sufficient rapidity—say one hundred times a second—the ticks would lose their individuality and blend to a musical tone. And if the strokes of a pigeon’s wings could be accomplished at the same rate, the progress of the bird through the air would be accompanied by music. In the humming-bird the necessary rapidity is attained; and when we pass on from birds to insects, where the vibrations are more rapid, we have a musical note as the ordinary accompaniment of the insects’ flight.24 The puffs of a locomotive at starting follow each other slowly at first, but they soon increase so rapidly as to be almost incapable of being counted. If this increase could continue up to fifty or sixty puffs a second, the approach of the engine would be heralded by an organ-peal of tremendous power.

§ 2. Musical Sounds produced by Taps

Galileo produced a musical sound by passing a knife over the edge of a piastre. The minute serration of the coin indicated the periodic character of the motion, which consisted of a succession of taps quick enough to produce sonorous continuity. Every schoolboy knows how to produce a note with his slate-pencil. I will not call it

Fig. 15. musical, because this term is usually associated with pleasure, and the sound of the pencil is not pleasant.

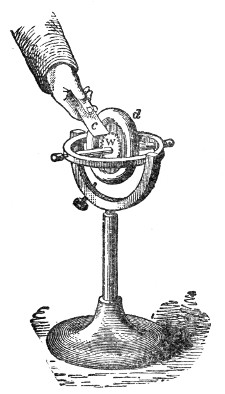
The production of a musical sound by taps is usually effected by causing the teeth of a rotating wheel to strike in quick succession against a card. This was first illustrated by the celebrated Robert Hooke,25 and nearer our own day by the eminent French experimenter Savart. We will confine ourselves to homelier modes of illustration. This gyroscope is an instrument consisting mainly of a heavy brass ring, d, Fig. 15, loading the circumference of a disk, through which and at right angles to its surface, passes a steel axis, delicately supported at its two ends. By coiling a string round the axis, and drawing it vigorously out, the ring is caused to spin rapidly; and along with it rotates a small-toothed wheel, w. On touching this wheel with the edge of a card c, a musical sound of exceeding shrillness is produced. I place my thumb for a moment against the ring; the rapidity of its rotation is thereby diminished, and this is instantly announced by a lowering of the pitch of the note. By checking the motion still more, the pitch is lowered still further. We are here made acquainted with the important fact that the pitch of a note depends upon the rapidity of its pulses.26 At the end of the experiment you hear the separate taps of the teeth against the card, their succession not being quick enough to produce that continuous flow of sound which is the essence of music. A screw with a milled head attached to a whirling table, and caused to rotate, produces by its taps against a card a note almost as clear and pure as that obtained from the toothed wheel of the gyroscope.

The production of a musical sound by taps may also be pleasantly illustrated in the following way: In this vise are fixed vertically two pieces of sheet-lead, with their horizontal edges a quarter of an inch apart. I lay a bar of brass across them, permitting it to rest upon the edges, and, tilting the bar a little, set it in oscillation like a see-saw. After a time, if left to itself, it comes to rest. But suppose the bar on touching the lead to be always tilted upward by a force issuing from the lead itself, it is plain that the vibrations would then be rendered permanent. Now such a force is brought into play when the bar is heated. On its then touching the lead the heat is communicated, a sudden jutting upward of the lead at the point of contact being the result. Hence an incessant tilting of the bar from side to side, so long as it continues sufficiently hot. Substituting for the brass bar the heated fire-shovel shown in Fig. 16, the same effect is produced.

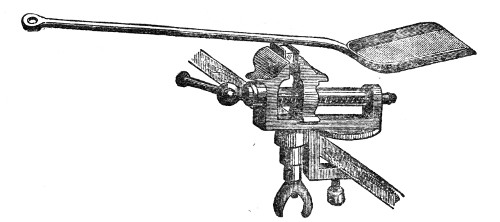
Fig. 16.

In its descent upon the lead the bar taps it gently, the taps being so slow that you may readily count them. But a mass of metal differently shaped may be caused to vibrate more briskly, and the taps to succeed each other more rapidly. When such a heated rocker, Fig. 17, is placed upon a block of lead, the taps hasten to a loud rattle. When, with the point of a file, the rocker is pressed against the lead, the vibrations are rendered more rapid, and the taps link themselves together to a deep musical tone. A second rocker, which oscillates more quickly than the last, produces music without any other pressure than that due to its own weight. Pressing it, however, with the file, the pitch rises, until a note of singular force and purity fills the room. Relaxing the pressure, the pitch instantly falls; resuming the pressure, it again rises; and thus by the alternation of the pressure we obtain great variations of tone. Nor are such rockers essential. Allowing one face of the clean, square end of a heated poker to rest upon the block of lead, a rattle is heard; causing another face to rest upon the block, a clear musical note is obtained. The two faces have been bevelled differently by a file, so as to secure different rates of vibration.27 This curious effect was discovered by Schwartz and Trevelyan.

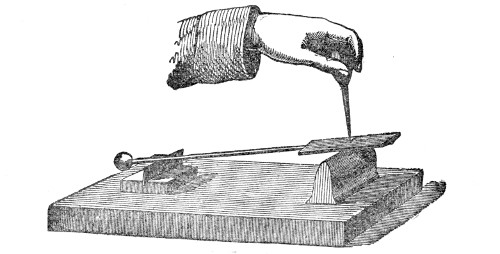
Fig. 17.

§ 3. Musical Sounds produced by Puffs

Prof. Robison was the first to produce a musical sound by a quick succession of puffs of air. His device was the first form of an instrument which will soon be introduced to you under the name of the siren. Robison describes his experiment in the following words: “A stop-cock was so constructed that it opened and shut the passage of a pipe 720 times in a second. The apparatus was fitted to the pipe of a conduit leading from the bellows to the wind-chest of an organ. The air was simply allowed to pass gently along this pipe by the opening of the cock. When this was repeated 720 times in a second, the sound g in alt was most smoothly uttered, equal in sweetness to a clear female voice. When the frequency was reduced to 360, the sound was that of a clear but rather a harsh man’s voice. The cock was now altered in such a manner that it never shut the hole entirely, but left about one-third of it open. When this was repeated 720 times in a second, the sound was uncommonly smooth and sweet. When reduced to 360, the sound was more mellow than any man’s voice of the same pitch.”

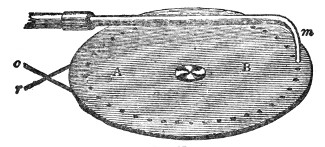
Fig. 18.

But the difficulty of obtaining the necessary speed renders another form of the experiment preferable. A disk of Bristol board, B, Fig. 18, twelve inches in diameter, is perforated at equal intervals along a circle near its circumference. The disk, being strengthened by a backing of tin, can be attached to a whirling table, and caused to rotate rapidly. The individual holes then disappear, blending themselves into a continuous shaded circle. Immediately over this circle is placed a bent tube, m, connected with a pair of acoustic bellows. The disk is now motionless, the lower end of the tube being immediately over one of the perforations of the disk. If, therefore, the bellows be worked, the wind will pass from m through the hole underneath. But if the disk be turned a little, an unperforated portion of the disk comes under the tube, the current of air being then intercepted. As the disk is slowly turned, successive perforations are brought under the tube, and whenever this occurs a puff of air gets through. On rendering the rotation rapid, the puffs succeed each other in very quick succession, producing pulses in the air which blend to a continuous musical note, audible to you all. Mark how the note varies. When the whirling table is turned rapidly the sound is shrill; when its motion is slackened the pitch immediately falls. If instead of a single glass tube there were two of them, as far apart as two of our orifices, so that whenever the one tube stood over an orifice, the other should stand over another, it is plain that if both tubes were blown through, we should, on turning the disk, get a puff through two holes at the same time. The intensity of the sound would be thereby augmented, but the pitch would remain unchanged. The two puffs issuing at the same instant would act in concert, and produce a greater effect than one upon the ear. And if instead of two tubes we had ten of them, or better still, if we had a tube for every orifice in the disk, the puffs from the entire series would all issue, and would be all cut off at the same time. These puffs would produce a note of far greater intensity than that obtained by the alternate escape and interruption of the air from a single tube. In the arrangement now before you, Fig. 19, there are nine tubes through which the air is urged—through nine apertures, therefore, puffs escape at once. On turning the whirling table, and alternately increasing and relaxing its speed, the sound rises and falls like the loud wail of a changing wind.

Fig. 19.

§ 4. Musical Sounds produced by a Tuning-fork

Various other means may be employed to throw the air into a state of periodic motion. A stretched string pulled aside and suddenly liberated imparts vibrations to the air which succeed each other in perfectly regular intervals. A tuning-fork does the same. When a bow is drawn across the prongs of this tuning-fork, Fig. 20, the resin of the bow enables the hairs to grip the prong, which is thus pulled aside. But the resistance of the prong soon becomes too strong, and it starts suddenly back; it is, however, immediately laid hold of again by the bow, to start back once more as soon as its resistance becomes great enough. This rhythmic process, continually repeated during the passage of the bow, finally throws the fork into a state of intense vibration, and the result is a musical note. A person close at hand could see the fork vibrating; a deaf person bringing his hand sufficiently near would feel the shivering of the air. Or causing its vibrating prong to touch a card, taps against the card link themselves, as in the case of the gyroscope, to a musical sound, the fork coming rapidly to rest. What we call silence expresses this absence of motion.

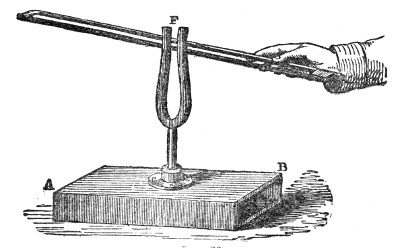
Fig. 20.

When the tuning-fork is first excited the sound issues from it with maximum loudness, becoming gradually feebler as the fork continues to vibrate. A person close to the fork can notice at the same time that the amplitude, or space through which the prongs oscillate, becomes gradually less and less. But the most expert ear in this assembly can detect no change in the pitch of the note. The lowering of the intensity of a note does not therefore imply the lowering of its pitch. In fact, though the amplitude changes, the rate of vibration remains the same. Pitch and intensity must therefore be held distinctly apart; the latter depends solely upon the amplitude, the former solely upon the rapidity of vibration.

This tuning-fork may be caused to write the story of its own motion. Attached to the side of one of its prongs, F, Fig. 21, is a thin strip of sheet-copper which tapers to a point. When the tuning-fork is excited it vibrates, and the strip of metal accompanies it in its vibration. The point of the strip being brought gently down upon a piece of smoked glass, it moves to and fro over the smoked surface, leaving a clear line behind. As long as the hand is kept motionless, the point merely passes to and fro over the same line; but it is plain that we have only to draw the fork along the glass to produce a sinuous line, Fig. 21.

Fig. 21.

When this process is repeated without exciting the fork afresh, the depth of the indentations diminishes. The sinuous line approximates more and more to a straight one. This is the visual expression of decreasing amplitude. When the sinuosities entirely disappear, the amplitude has become zero, and the sound, which depends upon the amplitude, ceases altogether.

Fig. 22.

To M. Lissajous we are indebted for a very beautiful method of giving optical expression to the vibrations of a tuning-fork. Attached to one of the prongs of a very large fork is a small metallic mirror, F, Fig. 22, the other prong being loaded with a piece of metal to establish equilibrium. Permitting a slender beam of intense light to fall upon the mirror, the beam is thrown back by reflection. In my hands is held a small looking-glass, which receives the reflected beam, and from which it is again reflected to the screen, forming a small luminous disk upon the white surface. The disk is perfectly motionless, but the moment the fork is set in vibration the reflected beam is tilted rapidly up and down, the disk describing a band of light three feet long. The length of the band depends on the amplitude of the vibration, and you see it gradually shorten as the motion of the fork is expended. It remains, however, a straight line as long as the glass is held in a fixed position. But on suddenly turning the glass so as to make the beam travel from left to right over the screen, you observe the straight line instantly resolved into a beautiful luminous ripple m n. A luminous impression once made upon the retina lingers there for the tenth of a second; if then the time required to transfer the elongated image from side to side of the screen be less than the tenth of a second, the wavy line of light will occupy for a moment the whole width of the screen. Instead of permitting the beam from the lamp to issue through a single aperture, it may be caused to issue through two apertures, about half an inch asunder, thus projecting two disks of light, one above the other, upon the screen. When the fork is excited and the mirror turned, we have a brilliant double sinuous line running over the dark surface, Fig. 23. turning the diaphragm so as to place the two disks beside each other, on exciting the fork and moving the mirror we obtain a beautiful interlacing of the two sinuous lines, Fig. 24.

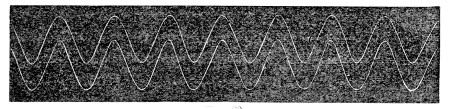
Fig. 23.

Fig. 24.

§ 5. The Waves of Sound

How are we to picture to ourselves the condition of the air through which this musical sound is passing? Imagine one of the prongs of the vibrating fork swiftly advancing; it compresses the air immediately in front of it, and when it retreats it leaves a partial vacuum behind, the process being repeated by every subsequent advance and retreat. The whole function of the tuning-fork is to carve the air into these condensations and rarefactions, and they, as they are formed, propagate themselves in succession through the air. A condensation with its associated rarefaction constitutes, as already stated, a sonorous wave. In water the length of a wave is measured from crest to crest; while, in the case of sound, the wave-length is the distance between two successive condensations. The condensation of the sound-wave corresponds to the crest, while the rarefaction of the sound-wave corresponds to the sinus, or depression, of the water-wave. Let the dark spaces, a, b, c, d, Fig. 25, represent the condensations, and the light ones, a′, b′, c′, d′, the rarefactions of the waves issuing from the fork a b: the wave-length would then be measured from a to b, from b to c, or from c to d.

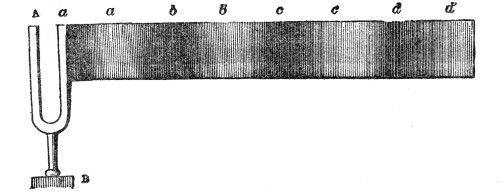
Fig. 25.

§ 6. Definition of Pitch: Determination of Rates of Vibration

When two notes from two distinct sources are of the same pitch, their rates of vibration are the same. If, for example, a string yield the same note as a tuning-fork, it is because they vibrate with the same rapidity; and if a fork yield the same note as the pipe of an organ or the tongue of a concertina, it is because the vibrations of the fork in the one case are executed in precisely the same time as the vibrations of the column of air, or of the tongue, in the other. The same holds good for the human voice. If a string and a voice yield the same note, it is because the vocal chords of the singer vibrate in the same time as the string vibrates. Is there any way of determining the actual number of vibrations corresponding to a musical note? Can we infer from the pitch of a string, of an organ-pipe, of a tuning-fork, or of the human voice, the number of waves which it sends forth in a second? This very beautiful problem is capable of the most complete solution.

§ 7. The Siren: Analysis of the Instrument

By the rotation of a perforated pasteboard disk, it has been proved to you that a musical sound is produced by a quick succession of puffs. Had we any means of registering the number of revolutions accomplished by that disk in a minute, we should have in it a means of determining the number of puffs per minute due to a note of any determinate pitch. The disk, however, is but a cheap substitute for a far more perfect apparatus, which requires no whirling table, and which registers its own rotations with the most perfect accuracy.

I will take the instrument asunder, so that you may see its various parts. A brass tube, t, Fig. 26, leads into a round box, C, closed at the top by a brass plate a b. This plate is perforated with four series of holes, placed along four concentric circles. The innermost series contains 8, the next 10, the next 12, and the outermost 16 orifices. When we blow into the tube t, the air escapes through the orifices, and the problem now before us is to convert these continuous currents into discontinuous puffs. This is accomplished by means of a brass disk d e, also perforated with 8, 10, 12, and 16 holes, at the same distances from the centre and with the same intervals between them as those in the top of the box C. Through the centre of the disk passes a steel axis, the two ends of which are smoothly bevelled off to points at p and p′. My object now is to cause this perforated disk to rotate over the perforated top a b of the box C. You will understand how this is done by observing how the instrument is put together.

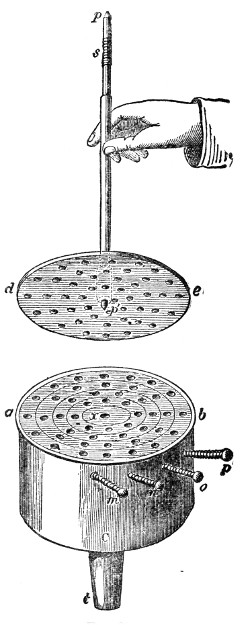
Fig. 26.

Fig. 27.

In the centre of a b, Fig. 26, is a depression x sunk in steel, smoothly polished and intended to receive the end p′ of the axis. I place the end p′ in this depression, and, holding the axis upright, bring down upon its upper end p a steel cap, finely polished within, which holds the axis at the top, the pressure both at top and bottom being so gentle, and the polish of the touching surfaces so perfect, that the disk can rotate with an exceedingly small amount of friction. At c, Fig. 27, is the cap which fits on to the upper end of the axis p p′. In this figure the disk d e is shown covering the top of the cylinder C. You may neglect for the present the wheel-work of the figure. Turning the disk d e slowly round, its perforations may be caused to coincide or not coincide with those of the cylinder underneath. As the disk turns, its orifices come alternately over the perforations of the cylinder and over the spaces between the perforations. Hence it is plain that if air were urged into C, and if the disk could be caused to rotate at the same time, we should accomplish our object, and carve into puffs the streams of air. In this beautiful instrument the disk is caused to rotate by the very air currents which it renders intermittent. This is done by the simple device of causing the perforations to pass obliquely through the top of the cylinder C, and also obliquely, but oppositely inclined, through the rotating disk d e. The air is thus caused to issue from C, not vertically, but in side currents, which impinge against the disk and drive it round. In this way, by its passage through the siren, the air is molded into sonorous waves.

Another moment will make you acquainted with the recording portion of the instrument. At the upper part of the steel axis p p′, Fig. 27, is a screw s, working into a pair of toothed wheels (seen when the back of the instrument is turned toward you). As the disk and its axis turn, these wheels rotate. In front you simply

Fig. 28. see two graduated dials, Fig. 28, each furnished with an index like the hand of a clock. These indexes record the number of revolutions executed by the disk in any given time. By pushing the button a or b the wheel-work is thrown into or out of action, thus starting or suspending, in a moment, the process of recording. Finally, by the pins m, n, o, p, Fig. 27, any series of orifices in the top of the cylinder C can be opened or closed at pleasure. By pressing m, one series is opened; by pressing n, another. By pressing two keys, two series of orifices are opened; by pressing three keys, three series; and by pressing all the keys, puffs are caused to issue from the four series simultaneously. The perfect instrument is now before you, and your knowledge of it is complete.

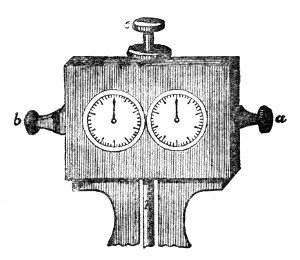
This instrument received the name of siren from its inventor, Cagniard de la Tour. The one now before you is the siren as greatly improved by Dove. The pasteboard siren, whose performance you have already heard, was devised by Seebeck, who gave the instrument various interesting forms, and executed with it many important experiments. Let us now make the siren sing. By pressing the key m, the outer series of apertures in the cylinder C is opened, and by working the bellows, the air is caused to impinge against the disk. It begins to rotate, and you hear a succession of puffs which follow each other so slowly that they may be counted. But as the motion augments, the puffs succeed each other with increasing rapidity, and at length you hear a deep musical note. As the velocity of rotation increases the note rises in pitch; it is now very clear and full, and as the air is urged more vigorously, it becomes so shrill as to be painful. Here we have a further illustration of the dependence of pitch on rapidity of vibration. I touch the side of the disk and lower its speed; the pitch falls instantly. Continuing the pressure the tone continues to sink, ending in the discontinuous puffs with which it began.

Were the blast sufficiently powerful and the siren sufficiently free from friction, it might be urged to higher and higher notes, until finally its sound would become inaudible to human ears. This, however, would not prove the absence of vibratory motion in the air; but would rather show that our auditory apparatus is incompetent to take up and translate into sound vibrations whose rapidity exceeds a certain limit. The ear, as we shall immediately learn, is in this respect similar to the eye.

By means of this siren we can determine with extreme accuracy the rapidity of vibration of any sonorous body. It may be a vibrating string, an organ-pipe, a reed, or the human voice. Operating delicately, we might even determine from the hum of an insect the number of times it flaps its wings in a second. I will illustrate the subject by determining in your presence a tuning-fork’s rapidity of vibration. From the acoustic bellows I urge the air through the siren, and, at the same time, draw my bow across the fork. Both now sound together, the tuning-fork yielding at present the highest note. But the pitch of the siren gradually rises, and at length you hear the “beats” so well known to musicians, which indicate that the two notes are not wide apart in pitch. These beats become slower and slower; now they entirely vanish, both notes blending as it were to a single stream of sound.

All this time the clockwork of the siren has remained out of action. As the second-hand of a watch crosses the number 60, the clockwork is set going by pushing the button a. We will allow the disk to continue its rotation for a minute, the tuning-fork being excited from time to time to assure you that the unison is preserved. The second-hand again approaches 60; as it passes that number the clockwork is stopped by pushing the button b; and then, recorded on the dials, we have the exact number of revolutions performed by the disk. The number is 1,440. But the series of holes open during the experiment numbers 16; for every revolution, therefore, we had 16 puffs of air, or 16 waves of sound. Multiplying 1,440 by 16, we obtain 23,040 as the number of vibrations executed by the tuning-fork in a minute. Dividing this by 60, we find the number of vibrations executed in a second to be 384.

§ 8. Determination of Wave-lengths: Time of Vibration

Having determined the rapidity of vibration, the length of the corresponding sonorous wave is found with the utmost facility. Imagine a tuning-fork vibrating in free air. At the end of a second from the time it commenced its vibrations the foremost wave would have reached a distance of 1,090 feet in air of the freezing temperature. In the air of a room which has a temperature of about 15° C., it would reach a distance of 1,120 in a second. In this distance, therefore, are embraced 384 sonorous waves. Dividing 1,120 by 384, we find the length of each wave to be nearly 3 feet. Determining in this way the rates of vibration of the four tuning-forks now before you, we find them to be 256, 320, 384, and 512; these numbers corresponding to wave-lengths of 4 feet 4 inches, 3 feet 6 inches, 2 feet 11 inches, and 2 feet 2 inches respectively. The waves generated by a man’s voice in common conversation are from 8 to 12 feet, those of a woman’s voice are from 2 to 4 feet in length. Hence a woman’s ordinary pitch in the lower sounds of conversation is more than an octave above a man’s; in the higher sounds it is two octaves.

And here it is important to note that by the term vibrations is meant complete ones; and by the term sonorous wave is meant a condensation and its associated rarefaction. By a vibration an excursion to and fro of the vibrating body is to be understood. Every wave generated by such a vibration bends the tympanic membrane once in and once out. These are the definitions of a vibration and of a sonorous wave employed in England and Germany. In France, however, a vibration consists of an excursion of the vibrating body in one direction, whether to or fro. The French vibrations, therefore, are only the halves of ours, and we therefore call them semi-vibrations. In all cases throughout these chapters, when the word vibration is employed without qualification, it refers to complete vibrations.

During the time required by each of those sonorous waves to pass entirely over a particle of air, that particle accomplishes one complete vibration. It is at one moment pushed forward into the condensation, while at the next moment it is urged back into the rarefaction. The time required by the particle to execute a complete oscillation is, therefore, that required by the sonorous wave to move through a distance equal to its own length. Supposing the length of the wave to be eight feet, and the velocity of sound in air of our present temperature to be 1,120 feet a second, the wave in question will pass over its own length of air in, 1/140th of a second: this is the time required by every air-particle that it passes to complete an oscillation.

In air of a definite density and elasticity a certain length of wave always corresponds to the same pitch. But supposing the density or elasticity not to be uniform; supposing, for example, the sonorous waves from one of our tuning-forks to pass from cold to hot air: an instant augmentation of the wave-length would occur, without any change of pitch, for we should have no change in the rapidity with which the waves would reach the ear. Conversely with the same length of wave the pitch would be higher in hot air than in cold, for the succession of the waves would be quicker. In an atmosphere of hydrogen, waves of a certain length would produce a note nearly two octaves higher than waves of the same length in air; for, in consequence of the greater rapidity of propagation, the number of impulses received in a given time in the one case would be nearly four times the number received in the other.

§ 9. Definition of an Octave

Opening the innermost and outermost series of the orifices of our siren, and sounding both of them, either together or in succession, the musical ears present at once detect the relationship of the two sounds. They notice immediately that the sound which issues from the circle of sixteen orifices is the octave of that which issues from the circle of eight. But for every wave sent forth by the latter, two waves are sent forth by the former. In this way we prove that the physical meaning of the term “octave” is, that it is a note produced by double the number of vibrations of its fundamental. By multiplying the vibrations of the octave by two, we obtain its octave, and by a continued multiplication of this kind we obtain a series of numbers answering to a series of octaves. Starting, for example, from a fundamental note of 100 vibrations, we should find, by this continual multiplication, that a note five octaves above it would be produced by 3,200 vibrations. Thus:

100

  Fundamental note.

2

 

——

 

200

  1st octave.

2

 

——

 

400

  2d octave.

2

 

——

 

800

  3d octave.

2

 

——

 

1600

  4th octave.

2

 

——

 

3200

  5th octave.

This result is more readily obtained by multiplying the vibrations of the fundamental note by the fifth power of two. In a subsequent chapter we shall return to this question of musical intervals. For our present purpose it is only necessary to define an octave.

§ 10. Limits of the Ear; and of Musical Sounds

The ear’s range of hearing is limited in both directions. Savart fixed the lower limit at eight complete vibrations a second; and to cause these slowly recurring vibrations to link themselves together he was obliged to employ shocks of great power. By means of a toothed wheel and an associated counter, he fixed the upper limit of hearing at 24,000 vibrations a second. Helmholtz has recently fixed the lower limit at 16 vibrations, and the higher at 38,000 vibrations, a second. By employing very small tuning-forks, the late M. Depretz showed that a sound corresponding to 38,000 vibrations a second is audible.28 Starting from the note 16, and multiplying continually by 2, or more compendiously raising 2 to the 11th power, and multiplying this by 16, we should find that at 11 octaves above the fundamental note the number of vibrations would be 32,768. Taking, therefore, the limit assigned by Helmholtz, the entire range of the human ear embraces about eleven octaves. But all the notes comprised within these limits cannot be employed in music. The practical range of musical sounds is comprised between 40 and 4,000 vibrations a second, which amounts, in round numbers, to seven octaves.29

The limits of hearing are different in different persons. While endeavoring to estimate the pitch of certain sharp sounds, Dr. Wollaston remarked in a friend a total insensibility to the sound of a small organ-pipe, which, in respect to acuteness, was far within the ordinary limits of hearing. The sense of hearing of this person terminated at a note four octaves above the middle E of the pianoforte. The squeak of the bat, the sound of a cricket, even the chirrup of the common house-sparrow, are unheard by some people who for lower sounds possess a sensitive ear. A difference of a single note is sometimes sufficient to produce the change from sound to silence. “The suddenness of the transition,” writes Wollaston, “from perfect hearing to total want of perception, occasions a degree of surprise which renders an experiment of this kind with a series of small pipes among several persons rather amusing. It is curious to observe the change of feeling manifested by various individuals of the party, in succession, as the sounds approach and pass the limits of their hearing. Those who enjoy a temporary triumph are often compelled, in their turn, to acknowledge to how short a distance their little superiority extends.” “Nothing can be more surprising,” writes Sir John Herschel, “than to see two persons, neither of them deaf, the one complaining of the penetrating shrillness of a sound, while the other maintains there is no sound at all. Thus, while one person mentioned by Dr. Wollaston could but just hear a note four octaves above the middle E of the pianoforte, others have a distinct perception of sounds full two octaves higher. The chirrup of the sparrow is about the former limit; the cry of the bat about an octave above it; and that of some insects probably another octave.” In “The Glaciers of the Alps” I have referred to a case of short auditory range, noticed by myself in crossing the Wengern Alps in company with a friend. The grass at each side of the path swarmed with insects, which to me rent the air with their shrill chirruping. My friend heard nothing of this, the insect-music lying beyond his limit of audition.

§ 11. Drum of the Ear. The Eustachian Tube

Behind the tympanic membrane exists a cavity—the drum of the ear—in part crossed by a series of bones, and in part occupied by air. This cavity communicates with the mouth by means of a duct called the Eustachian tube. This tube is generally closed, the air-space behind the tympanic membrane being thus shut off from the external air. If, under these circumstances, the external air becomes denser, it will press the tympanic membrane inward. If, on the other hand, the air outside becomes rarer, while the Eustachian tube remains closed, the membrane will be pressed outward. Pain is felt in both cases, and partial deafness is experienced. I once crossed the Stelvio Pass by night in company with a friend who complained of acute pain in the ears. On swallowing his saliva the pain instantly disappeared. By the act of swallowing, the Eustachian tube is opened, and thus equilibrium is established between the external and internal pressure.

It is possible to quench the sense of hearing of low sounds by stopping the nose and mouth, and trying to expand the chest, as in the act of inspiration. This effort partially exhausts the space behind the tympanic membrane, which is then thrown into a state of tension by the pressure of the outward air. A similar deafness to low sounds is produced when the nose and mouth are stopped, and a strong effort is made to expire. In this case air is forced through the Eustachian tube into the drum of the ear, the tympanic membrane being distended by the pressure of the internal air. The experiment may be made in a railway carriage, when the low rumble will vanish or be greatly enfeebled, while the sharper sounds are heard with undiminished intensity. Dr. Wollaston was expert in closing the Eustachian tube, and leaving the space behind the tympanic membrane occupied by either compressed or rarefied air. He was thus able to cause his deafness to continue for any required time without effort on his part, always, however, abolishing it by the act of swallowing. A sudden concussion may produce deafness by forcing air either into or out of the drum of the ear, and this may account for a fact noticed by myself in one of my Alpine rambles. In the summer of 1858, jumping from a cliff on to what was supposed to be a deep snowdrift, I came into rude collision with a rock which the snow barely covered. The sound of the wind, the rush of the glacier-torrents, and all the other noises which a sunny day awakes upon the mountains, instantly ceased. I could hardly hear the sound of my guide’s voice. This deafness continued for half an hour; at the end of which time the blowing of the nose opened, I suppose, the Eustachian tube, and restored, with the quickness of magic, the innumerable murmurs which filled the air around me.

Light, like sound, is excited by pulses or waves; and lights of different colors, like sounds of different pitch, are excited by different rates of vibration. But in its width of perception the ear exceedingly transcends the eye; for while the former ranges over eleven octaves, but little more than a single octave is possible to the latter. The quickest vibrations which strike the eye, as light, have only about twice the rapidity of the slowest;30 whereas the quickest vibrations which strike the ear, as a musical sound, have more than two thousand times the rapidity of the slowest.

§ 12. Helmholtz’s Double Siren

Prof. Dove, as we have seen, extended the utility of the siren of Cagniard de la Tour, by providing it with four series of orifices instead of one. By doubling all its parts, Helmholtz has recently added vastly to the power of the instrument. The double siren, as it is called, is now before you, Fig. 29 (next page). It is composed of two of Dove’s sirens, C and C′, one turned upside down. You will recognize in the lower siren the instrument with which you are already acquainted. The disks of the two sirens have a common axis, so that when one disk rotates the other rotates with it. As in the former case, the number of revolutions is recorded by clockwork (omitted in the figure). When air is urged through the tube t′ the upper siren alone sounds; when urged through t, the lower one only sounds; when it is urged simultaneously through t′ and t, both the sirens sound. With this instrument, therefore, we are able to introduce much more varied combinations than with the former one. Helmholtz has also contrived a means by which not only the disk of the upper siren, but the box C′ above the disk, can be caused to rotate. This is effected by a toothed wheel and pinion, turned by a handle. Underneath the handle is a dial with an index, the use of which will be subsequently illustrated.

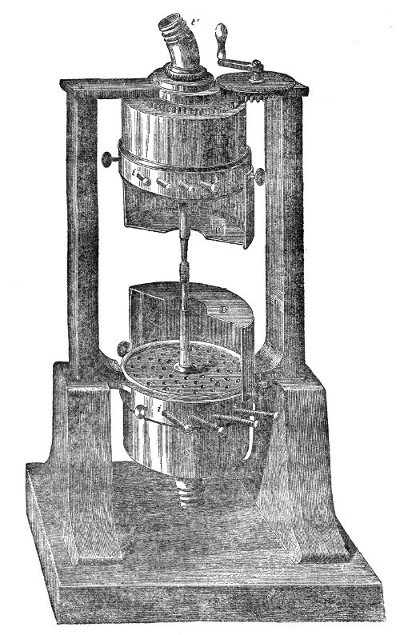
Fig. 29.

Let us direct our attention for the present to the upper siren. By means of an India-rubber tube, the orifice t′ is connected with an acoustic bellows, and air is urged into C′. Its disk turns round, and we obtain with it all the results already obtained with Dove’s siren. The pitch of the note is uniform. Turning the handle above, so as to cause the orifices of the cylinder C′ to meet those of the disk, the two sets of apertures pass each other more rapidly than when the cylinder stood still. An instant rise of pitch is the result. By reversing the motion, the orifices are caused to pass each other more slowly than when C′ is motionless, and in this case you notice an instant fall of pitch when the handle is turned. Thus, by imparting in quick alternation a right-handed and left-handed motion to the handle, we obtain successive rises and falls of pitch. An extremely instructive effect of this kind may be observed at any railway station on the passage of a rapid train. During its approach the sonorous waves emitted by the whistle are virtually shortened, a greater number of them being crowded into the ear in a given time. During its retreat we have a virtual lengthening of the sonorous waves. The consequence is, that, when approaching, the whistle sounds a higher note, and when retreating it sounds a lower note, than if the train were still. A fall of pitch, therefore, is perceived as the train passes the station.31 This is the basis of Doppler’s theory of the colored stars. He supposes that all stars are white, but that some of them are rapidly retreating from us, thereby lengthening their luminiferous waves and becoming red. Others are rapidly approaching us, thereby shortening their waves, and becoming green or blue. The ingenuity of this theory is extreme, but its correctness is more than doubtful.

§ 13. Transmission of Musical Sounds by Liquids and Solids

We have thus far occupied ourselves with the transmission of musical sounds through air. They are also transmitted by liquids and solids. When a tuning-fork screwed into a little wooden foot vibrates, nobody, except the persons closest to it, hears its sound. On dipping the foot into a glass of water a musical sound is audible: the vibrations having been transmitted through the water to the air. The tube M N, Fig. 30, three feet long, is set upright upon a wooden tray A B. The tube ends in a funnel at the top, and is now filled with water to the brim. The fork F is thrown into vibration, and on dipping its foot into the funnel at the top of the tube, a musical sound swells out. I must so far forestall matters as to remark that in this experiment the tray is the real sounding body. It has been thrown into vibration by the fork, but the vibrations have been conveyed to the tray by the water. Through the same medium vibrations

Fig. 30. are communicated to the auditory nerve, the terminal filaments of which are immersed in a liquid: substituting mercury for water, a similar result is obtained.

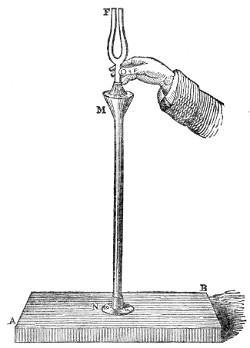
The siren has received its name from its capacity to sing under water. A vessel now in front of the table is half filled with water, in which a siren is wholly immersed. When a cock is turned, the water from the pipes which supply the house forces itself through the instrument. Its disk is now rotating, and a sound of rapidly augmenting pitch issues from the vessel. The pitch rises thus rapidly because the heavy and powerfully pressed water soon drives the disk up to its maximum speed of rotation. When the supply is lessened, the motion relaxes and the pitch falls. Thus, by alternately opening and closing the cock, the song of the siren is caused to rise and fall in a wild and melancholy manner. You would not consider such a sound likely to woo mariners to their doom.

The transmission of musical sounds through solid bodies is also capable of easy and agreeable illustration. Before you is a wooden rod, thirty feet long, passing from the table through a window in the ceiling, into the open air above. The lower end of the rod rests upon a wooden tray, to which the musical vibrations of a body applied to the upper end of the rod are to be transferred. An assistant is above, with a tuning-fork in his hand. He strikes the fork against a pad; it vibrates, but you hear nothing. He now applies the stem of the fork to the end of the rod, and instantly the wooden tray upon the table is rendered musical. The pitch of the sound, moreover, is exactly that of the tuning-fork; the wood has been passive as regards pitch, transmitting the precise vibrations imparted to it without any alteration. With another fork a note of another pitch is obtained. Thus fifty forks might be employed instead of two, and 300 feet of wood instead of 30; the rod would transmit the precise vibrations imparted to it, and no other.

We are now prepared to appreciate an extremely beautiful experiment, for which we are indebted to Sir Charles Wheatstone. In a room underneath this, and separated from it by two floors, is a piano. Through the two floors passes a tin tube 2-1/2 inches in diameter, and along the axis of this tube passes a rod of deal, the end of which emerges from the floor in front of the lecture-table. The rod is clasped by India-rubber bands, which entirely close the tin tube. The lower end of the rod rests upon the sound-board of the piano, its upper end being exposed before you. An artist is at this moment engaged at the instrument, but you hear no sound. When, however, a violin is placed upon the end of the rod, the instrument becomes instantly musical, not, however, with the vibrations of its own strings, but with those of the piano. When the violin is removed, the sound ceases; putting in its place a guitar, the music revives. For the violin and guitar we may substitute a plain wooden tray, which is also rendered musical. Here, finally, is a harp, against the sound-board of which the end of the deal rod is caused to press; every note of the piano is reproduced before you. On lifting the harp so as to break the connection with the piano, the sound vanishes; but the moment the sound-board is caused to press upon the rod the music is restored. The sound of the piano so far resembles that of the harp that it is hard to resist the impression that the music you hear is that of the latter instrument. An uneducated person might well believe that witchcraft or “spiritualism” is concerned in the production of this music.

What a curious transference of action is here presented to the mind! At the command of the musician’s will, the fingers strike the keys; the hammers strike the strings, by which the rude mechanical shock is converted into tremors. The vibrations are communicated to the sound-board of the piano. Upon that board rests the end of the deal rod, thinned off to a sharp edge to make it fit more easily between the wires. Through the edge, and afterward along the rod, are poured with unfailing precision the entangled pulsations produced by the shocks of those ten agile fingers. To the sound-board of the harp before you the rod faithfully delivers up the vibrations of which it is the vehicle. This second sound-board transfers the motion to the air, carving it and chasing it into forms so transcendently complicated that confusion alone could be anticipated from the shock and jostle of the sonorous waves. But the marvellous human ear accepts every feature of the motion, and all the strife and struggle and confusion melt finally into music upon the brain.32

SUMMARY OF CHAPTER II

A musical sound is produced by sonorous shocks which follow each other at regular intervals with a sufficient rapidity of succession.

Noise is produced by an irregular succession of sonorous shocks.

A musical sound may be produced by taps which rapidly and regularly succeed each other. The taps of a card against the cogs of a rotating wheel are usually employed to illustrate this point.

A musical sound may also be produced by a succession of puffs. The siren is an instrument by which such puffs are generated.

The pitch of a musical note depends solely on the number of vibrations concerned in its production. The more rapid the vibrations, the higher the pitch.

By means of the siren the rate of vibration of any sounding body may be determined. It is only necessary to render the sound of the siren and that of the body identical in pitch to maintain both sounds in unison for a certain time, and to ascertain, by means of the counter of the siren, how many puffs have issued from, the instrument in that time. This number expresses the number of vibrations executed by the sounding body.

When a body capable of emitting a musical sound—a tuning-fork, for example—vibrates, it molds the surrounding air into sonorous waves, each of which consists of a condensation and a rarefaction.

The length of the sonorous wave is measured from condensation to condensation, or from rarefaction to rarefaction.

The wave-length is found by dividing the velocity of sound per second by the number of vibrations executed by the sounding body in a second.

Thus a tuning-fork which vibrates 256 times in a second produces in air of 15° C., where the velocity is 1,120 feet a second, waves 4 feet 4 inches long. While two other forks, vibrating respectively 320 and 384 times a second, generate waves 3 feet 6 inches, and 2 feet 11 inches long.

A vibration, as defined in England and Germany, comprises a motion to and fro. It is a complete vibration. In France, on the contrary, a vibration comprises a movement to or fro. The French vibrations are with us semi-vibrations.

The time required by a particle of air over which a sonorous wave passes to execute a complete vibration is that required by the wave to move through a distance equal to its own length.

The higher the temperature of the air, the longer is the sonorous wave corresponding to any particular rate of vibration. Given the wave-length and the rate of vibration, we can readily deduce the temperature of the air.

The human ear is limited in its range of hearing musical sounds. If the vibrations number less than 16 a second, we are conscious only of the separate shocks. If they exceed 38,000 a second, the consciousness of sound ceases altogether. The range of the best ear covers about 11 octaves, but an auditory range limited to 6 or 7 octaves is not uncommon.

The sounds available in music are produced by vibrations comprised between the limits of 40 and 4,000 a second. They embrace 7 octaves.

The range of the ear far transcends that of the eye, which hardly exceeds an octave.

By means of the Eustachian tube, which is opened in the act of swallowing, the pressure of the air on both sides of the tympanic membrane is equalized.

By either condensing or rarefying the air behind the tympanic membrane, deafness to sounds of low pitch may be produced.

On the approach of a railway train the pitch of the whistle is higher, on the retreat of the train the pitch is lower, than it would be if the train were at rest.

Musical sounds are transmitted by liquids and solids. Such sounds may be transferred from one room to another; from the ground-floor to the garret of a house of many stories, for example, the sound being unheard in the rooms intervening between both, and rendered audible only when the vibrations are communicated to a suitable sound-board.

CHAPTER III

Vibration of Strings—How employed in Music—Influence of Sound-Boards—Laws of Vibrating Strings—Combination of Direct and Reflected Pulses—Stationary and Progressive Waves—Nodes and Ventral Segments—Application of Results to the Vibrations of Musical Strings—Experiments of Melde—Strings set in Vibration by Tuning-Forks—Laws of Vibration thus demonstrated—Harmonic Tones of Strings—Definitions of Timbre or Quality, or Overtones and Clang—Abolition of Special Harmonics—Conditions which affect the Intensity of the Harmonic Tones—Optical Examination of the Vibrations of a Piano-Wire.

§ 1. Vibrations of Strings: Use of Sound-Boards

WE HAVE to begin our studies to-day with the vibrations of strings or wires; to learn how bodies of this form are rendered available as sources of musical sounds, and to investigate the laws of their vibrations.

To enable a musical string to vibrate transversely, or at right angles to its length, it must be stretched between two rigid points. Before you, Fig. 31 (next page), is an instrument employed to stretch strings, and to render their vibrations audible. From the pin p, to which one end of it is firmly attached, a string passes across the two bridges B and B′, being afterward carried over the wheel H, which moves with great freedom. The string is finally stretched by a weight W, of 28 lbs., attached to its extremity. The bridges B and B′, which constitute the real ends of the string, are fastened on to the long wooden box M N. The whole instrument is called a monochord, or sonometer.

Fig. 31.

Taking hold of the stretched string B B′ at its middle and plucking it aside, it springs back to its first position, passes it, returns, and thus vibrates for a time to and fro across its position of equilibrium. You hear a sound, but the sonorous waves which at present strike your ears do not proceed immediately from the string. The amount of wave-motion generated by so thin a body is too small to be sensible at any distance. But the string is drawn tightly over the two bridges B B′; and when it vibrates, its tremors are communicated through these bridges to the entire mass of the box M N, and to the air within the box, which thus become the real sounding bodies.

That the vibrations of the string alone are not sufficient to produce the sound may be thus experimentally demonstrated: A B, Fig. 32 (next page), is a piece of wood placed across an iron bracket C. From each end of the piece of wood depends a rope ending in a loop, while stretching across from loop to loop is an iron bar m n. From the middle of the iron bar hangs a steel wire s s′, stretched by a weight W, of 28 lbs. By this

Fig. 32. arrangement the wire is detached from all large surfaces to which it could impart its vibrations. Plucking the wire s s′, it vibrates vigorously, but even those nearest to it do not hear any sound. The agitation imparted to the air is too inconsiderable to affect the auditory nerve at any distance. A second wire t t′, Fig. 33 (next page), of the same length, thickness, and material as s s′, has one of its ends attached to the wooden tray A B. This wire also carries a weight W, of 28 lbs. Finally, passing over the bridges B B′ of the sonometer, Fig. 31, is our third wire, in every respect like the two former, and, like them, stretched by a weight W, of 28 lbs. When the wire t t′, Fig. 33, is caused to vibrate, you hear its sound distinctly. Though one end only of the wire is connected with the tray A B, the vibrations transmitted to it are sufficient to convert the tray into a sounding body. Finally, when the wire of the sonometer M N, Fig. 31, is plucked, the sound is loud and full, because the instrument is specially constructed to take up the vibrations of the wire.

The importance of employing proper sounding apparatus in stringed instruments is rendered manifest by

Fig. 33. these experiments. It is not the strings of a harp, or a lute, or a piano, or a violin, that throw the air into sonorous vibrations. It is the large surfaces with which the strings are associated, and the air inclosed by these surfaces. The goodness of such instruments depends almost wholly upon the quality and disposition of their sound-boards.33

Take the violin as an example. It is, or ought to be, formed of wood of the most perfect elasticity. Imperfectly elastic wood expends the motion imparted to it in the friction of its own molecules; the motion is converted into heat, instead of sound. The strings of the violin pass from the “tail-piece” of the instrument over the “bridge,” being thence carried to the “pegs,” the turning of which regulates the tension of the strings. The bow is drawn across at a point about one-tenth of the length of the string from the bridge. The two “feet” of the bridge rest upon the most yielding portion of the “belly” of the violin, that is, the portion that lies between the two f-shaped orifices. One foot is fixed over a short rod, the “sound post,” which runs from belly to back through the interior of the violin. This foot of the bridge is thereby rendered rigid, and it is mainly through the other foot, which is not thus supported, that the vibrations are conveyed to the wood of the instrument, and thence to the air within and without. The sonorous quality of the wood of a violin is mellowed by age. The very act of playing also has a beneficial influence, apparently constraining the molecules

Fig. 34. of the wood, which in the first instance might be refractory, to conform at last to the requirements of the vibrating strings.

This is the place to make the promised reference (page 38) to Prof. Stokes’s explanation of the action of sound-boards. Although the amplitude of the vibrating board may be very small, still its larger area renders the abolition of the condensations and rarefactions difficult. The air cannot move away in front nor slip in behind before it is sensibly condensed and rarefied. Hence with such vibrating bodies sound-waves may be generated, and loud tones produced, while the thin strings that set them in vibration, acting alone, are quite inaudible.

The increase of sound, produced by the stoppage of lateral motion, has been experimentally illustrated by Prof. Stokes. Let the two black rectangles in Fig. 34 represent the section of a tuning-fork. After it has been made to vibrate, place a sheet of paper, or the blade of a broad knife, with its edge parallel to the axis of the fork, and as near to the fork as may be without touching. If the obstacle be so placed that the section of it is A or B, no effect is produced; but if it be placed at C, so as to prevent the reciprocating to-and-fro movement of the air, which tends to abolish the condensations and rarefactions, the sound becomes much stronger.

§ 2. Laws of Vibrating Strings

Having thus learned how the vibrations of strings are rendered available in music, we have next to investigate the laws of such vibrations. I pluck at its middle point the string B B′, Fig. 31. The sound heard is the fundamental or lowest note of the string, to produce which it swings, as a whole, to and fro. By placing a movable bridge under the middle of the string, and pressing the string against the bridge, it is divided into two equal parts. Plucking either of those at its centre, a musical note is obtained, which many of you recognize as the octave of the fundamental note. In all cases, and with all instruments, the octave of a note is produced by doubling the number of its vibrations. It can, moreover, be proved, both by theory and by the siren, that this half string vibrates with exactly twice the rapidity of the whole. In the same way it can be proved that one-third of the string vibrates with three times the rapidity, producing a note a fifth above the octave, while one-fourth of the string vibrates with four times the rapidity, producing the double octave of the whole string. In general terms, the number of vibrations is inversely proportional to the length of the string.

Again, the more tightly a string is stretched the more rapid is its vibration. When this comparatively slack string is caused to vibrate, you hear its low fundamental note. By turning a peg, round which one end of it is coiled, the string is tightened, and the pitch rendered higher. Taking hold with my left hand of the weight w, attached to the wire B B′ of our sonometer, and plucking the wire with the fingers of my right, I alternately press upon the weight and lift it. The quick variations of tension are expressed by a varying wailing tone. Now, the number of vibrations executed in the unit of time bears a definite relation to the stretching force. Applying different weights to the end of the wire B B′, and determining in each case the number of vibrations executed in a second, we find the numbers thus obtained to be proportional to the square roots of the stretching weights. A string, for example, stretched by a weight of one pound, executes a certain number of vibrations per second; if we wish to double this number, we must stretch it by a weight of four pounds; if we wish to treble the number, we must apply a weight of nine pounds, and so on.

The vibrations of a string also depend upon its thickness. Preserving the stretching weight, the length, and the material of the string constant, the number of vibrations varies inversely as the thickness of the string. If, therefore, of two strings of the same material, equally long and equally stretched, the one has twice the diameter of the other, the thinner string will execute double the number of vibrations of its fellow in the same time. If one string be three times as thick as another, the latter will execute three times the number of vibrations, and so on.

Finally, the vibrations of a string depend upon the density of the matter of which it is composed. A platinum wire and an iron wire, for example, of the same length and thickness, stretched by the same weight, will not vibrate with the same rapidity. For, while the specific gravity of iron, or in other words its density, is 7·8, that of platinum is 21·5. All other conditions remaining the same, the number of vibrations is inversely proportional to the square root of the density of the string. If the density of one string, therefore, be one-fourth that of another of the same length, thickness, and tension, it will execute its vibrations twice as rapidly; if its density be one-ninth that of the other, it will vibrate with three times the rapidity, and so on. The last two laws, taken together, may be expressed thus: The number of vibrations is inversely proportional to the square root of the weight of the string.

In the violin and other stringed instruments we avail ourselves of thickness instead of length to obtain the deeper tones. In the piano we not only augment the thickness of the wires intended to produce the bass notes, but we load them by coiling round them an extraneous substance. They resemble horses heavily jockeyed, and move more slowly on account of the greater weight imposed upon the force of tension.

§ 3. Mechanical Illustrations of Vibrations. Progressive and Stationary Waves. Ventral Segments and Nodes

These, then, are the four laws which regulate the transverse vibrations of strings. We now turn to certain allied phenomena, which, though they involve mechanical

Fig. 35. considerations of a rather complicated kind, may be completely mastered by an average Fig. 36. amount of attention. And they must be mastered if we would thoroughly comprehend the philosophy of stringed instruments.

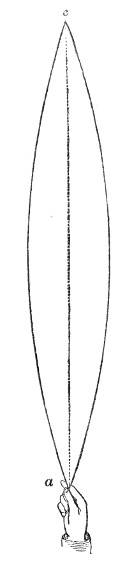
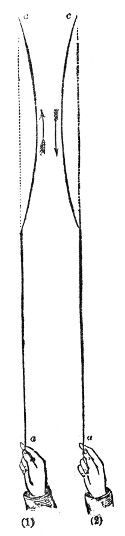
From the ceiling c, Fig. 35, of this room hangs an India-rubber tube twenty-eight feet long. The tube is filled with sand to render its motions slow and more easily followed by the eye. I take hold of its free end a, stretch the tube a little, and by properly timing my impulses cause it to swing to and fro as a whole, as shown in the figure. It has its definite period of vibration dependent on its length, weight, thickness, and tension, and my impulses must synchronize with that period.

I now stop the motion, and by a sudden jerk raise a hump upon the tube, which runs along it as a pulse toward its fixed end; here the hump reverses itself, and runs back to my hand. At the fixed end of the tube, in obedience to the law of reflection, the pulse reversed both its position and the direction of its motion. Supposing c, Fig. 36, to be the fixed end of the tube, and a the end held in the hand: if the pulse on reaching c have the position shown in (1), after reflection it will have the position shown in (2). The arrows mark the direction of progression. The time required for the pulse to pass from the hand to the fixed end and back is exactly that required to accomplish one complete vibration of the tube as a whole. It is indeed the addition of such impulses which causes the tube to continue to vibrate as a whole.

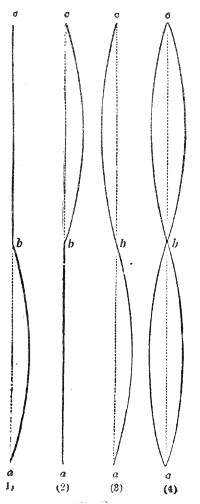
Fig. 37.

If, instead of a single jerk, a succession of jerks be imparted, thereby sending a series of pulses along the tube, every one of them will be reflected above, and we have now to inquire how the direct and reflected pulses behave toward each other.

Let the time required by the pulse to pass from my hand to the fixed end be one second; at the end of half a second it occupies the position a b (1), Fig. 37, its foremost point having reached the middle of the tube. At the end of a whole second it would have the position b c (2), its foremost point having reached the fixed end c of the tube. At the moment when reflection begins at c, let another jerk be imparted at a. The reflected pulse from c moving with the same velocity as this direct one from a, the foremost points of both will arrive at the centre b (3) at the same moment. What must occur? The hump a b wishes to move on to c, and to do so must move the point b to the right. The hump c b wishes to move toward a, and to do so must move the point b to the left. The point b, urged by equal forces in two opposite directions at the same time, will not move in either direction. Under these circumstances, the two halves, a b, b c of the tube will oscillate as if they were independent of each other (4). Thus by the combination of two progressive pulses, the one direct and the other reflected, we produce two stationary pulses on the tube a c.

The vibrating parts a b and b c are called ventral segments; the point of no vibration b is called a node.

The term “pulse” is here used advisedly, instead of the more usual term wave. For a wave embraces two of these pulses. It embraces both the hump and the depression which follows the hump. The length of a wave, therefore, is twice that of a ventral segment.

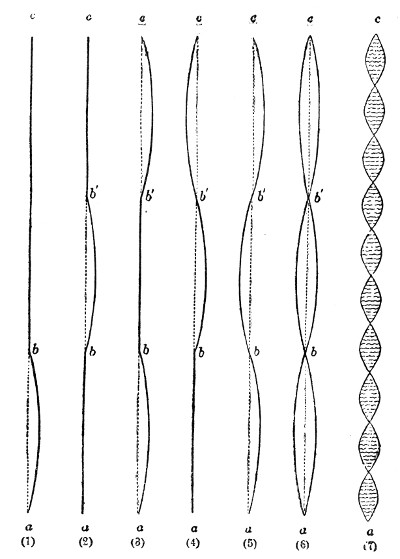
Fig. 38.

Supposing the jerks to be so timed as to cause each hump to be one-third of the tube’s length. At the end of one-third of a second from starting the pulse will be in the position a b (1), Fig. 38. In two-thirds of a second it will have reached the position b b′ (2), Fig. 38. At this moment let a new pulse be started at a; after the lapse of an entire second from the commencement we shall have two humps upon the tube, one occupying the position a b (3), the other the position b′ c (3). It is here manifest that the end of the reflected pulse from c, and the end of the direct one from a, will reach the point b′ at the same moment. We shall therefore have the state of things represented in (4), where b b′ wishes to move upward, and c b′ to move downward. The action of both upon the point b′ being in opposite directions, that point will remain fixed. And from it, as if it were a fixed point, the pulse b b′ will be reflected, while the segment b′ c will oscillate as an independent string. Supposing that at the moment b b′ (4) begins to be reflected at b′ we start another pulse from a, it will reach b at the same moment the pulse reflected from b′ reaches it. The pulses will neutralize each other at b, and we shall have there a second node. Thus, by properly timing our jerks, we divide the rope into three ventral segments, separated from each other by two nodal points. As long as the agitation continues the tube will vibrate as in (6).

There is no theoretic limit to the number of nodes and ventral segments that may be thus produced. By the quickening of the impulses, the tube is divided into four ventral segments separated by three nodes; quickening still more we have five ventral segments and four nodes. With this particular tube the hand may be caused to vibrate sufficiently quick to produce ten ventral segments, as shown in Fig. 38 (7). When the stretching force is constant, the number of ventral segments is proportional to the rapidity of the hand’s vibration. To produce 2, 3, 4, 10 ventral segments requires twice, three times, four times, ten times the rapidity of vibration necessary to make the tube swing as a whole. When the vibration is very rapid the ventral segments appear like a series of shadowy spindles, separated from each other by dark motionless nodes. The experiment is a beautiful one, and it is easily performed.

If, instead of moving the hand to-and fro, it be caused to describe a small circle, the ventral segments become “surfaces of revolution.” Instead of the hand, moreover, we may employ a hook turned by a whirling-table. Before you is a cord more rigid than the India-rubber tube, 25 feet long, with one of its ends attached to a freely-moving swivel fixed in the ceiling of the room. By turning the whirling-table to which the other end is attached, this cord may be divided into as many as 20 ventral segments, separated from each other by their appropriate nodes. In another arrangement a string of catgut 12 feet long, with silvered beads strung along it, is stretched horizontally between a vertical wheel and a free swivel fixed in a rigid stand. On turning the wheel, and properly regulating both the tension and the rapidity of rotation, the beaded cord may be caused to rotate as a whole, and to divide itself successively into 2, 3, 4, or 5 ventral segments. When we envelop the cord in a luminous beam, every spot of light on every bead describes a brilliant circle, and a very beautiful experiment is the result.

§ 4. Mechanical Illustrations of Damping Various Points of Vibrating Cord

The subject of stationary waves was first experimentally treated by the Messrs. Weber, in their excellent researches on wave-motion. It is a subject which will well repay your attention by rendering many of the most difficult phenomena of musical strings perfectly intelligible. It will make the connection of both classes of vibrations more obvious if we vary our last experiments. Before you is a piece of India-rubber tubing, 10 or 12 feet long, stretched from c to a, Fig. 39, and made fast to two pins at c and a. The tube is blackened, and behind it is placed a surface of white paper, to render its motions more visible. Encircling the tube at its centre b (1) by the thumb and forefinger of my left hand, and taking the middle of the lower half b a of the tube in my right, I pluck it aside. Not only does the lower half swing, but the upper half also is thrown into vibration. Withdrawing the hands wholly from the tube, its two halves a b and b c continue to vibrate, being separated from each other by a node b at the centre (2).

Fig. 39.

I now encircle the tube at a point b (3) one-third of its length from its lower end a, and, taking hold of a b at its centre, pluck it aside; the length b c above my hand instantly divides into two vibrating segments. Withdrawing the hands wholly, you see the entire tube divided into three ventral segments, separated from each other by two motionless nodes, b and b′ (4). I pass on to the point b (5), which marks off one-fourth of the length of the tube, encircle it, and pluck the shorter segment aside. The longer segment above my hand divides itself immediately into three vibrating parts. So that, on withdrawing the hand, the whole tube appears before you divided into four ventral segments, separated from each other by three nodes b b′ b″ (6). In precisely the same way the tube may be divided into five vibrating segments with four nodes.

This sudden division of the long upper segment of the tube, without any apparent cause, is very surprising; but if you grant me your attention for a moment, you will find that these experiments are essentially similar to those which illustrated the coalescence of direct and reflected undulations. Reverting for a moment to the latter, you observed that the to-and-fro motion of the hand through the space of a single inch was sufficient to make the middle points of the ventral segments vibrate through a foot or eighteen inches. By being properly timed the impulses accumulated, until the amplitude of the vibrating segments exceeded immensely that of the hand which produced them. The hand, in fact, constituted a nodal point, so small was its comparative motion. Indeed, it is usual, and correct, to regard the ends of the tube also as nodal points.

Consider now the case represented in (1), Fig. 39, where the tube was encircled at its middle, the lower segment a b being thrown into the vibration corresponding to its length and tension. The circle formed by the finger and thumb permitted the tube to oscillate at the point b through the space of an inch; and the vibrations at that point acted upon the upper half b c exactly as my hand acted when it caused the tube suspended from the ceiling to swing as a whole, as in Fig. 35. Instead of the timid vibrations of the hand, we have now the timid vibrations of the lower half of the tube; and these, though narrowed to an inch at the place clasped by the finger and thumb, soon accumulate, and finally produce an amplitude, in the upper half, far exceeding their own. The same reasoning applies to all the other cases of subdivision. If, instead of encircling a point by the finger and thumb, and plucking the portion of the tube below it aside, that same point were taken hold of by the hand and agitated in the period proper to the lower segment of the tube, precisely the same effect would be produced. We thus reduce both effects to one and the same cause; namely, the combination of direct and reflected undulations.

And here let me add that, when the tube was divided by the timid impulses of the hand, not one of its nodes was, strictly speaking, a point of no motion; for were the nodes not capable of vibrating through a very small amplitude, the motion of the various segments of the tube could not be maintained.

§ 5. Stationary Water-waves

What is true of the undulations of an India-rubber tube applies to all undulations whatsoever. Water-waves, for example, obey the same laws, and the coalescence of direct and reflected waves exhibits similar phenomena. This long and narrow vessel with glass sides, Fig. 40, is a copy of the wave-canal of the brothers Weber. It is filled to the level A B with colored water. By tilting the end A suddenly, a wave is generated, which moves on to B, and is there reflected. By sending forth fresh waves at the proper intervals, the surface is divided into two stationary undulations. Making the succession of impulses more rapid we can subdivide the surface into three, four (shown in the figure), or more stationary undulations, separated from each other by nodes. The step of a water-carrier is sometimes so timed as to throw the surface of the water in his vessel into stationary waves, which may augment in height until the water splashes over the brim. Practice has taught the water-carrier what to do; he changes his step, alters the period of his impulses, and thus stops the accumulation of the motion.

Fig. 40.

In travelling recently in the coupé of a French railway carriage, I had occasion to place a bottle half filled with water on one of the little coupé tables. It was interesting to observe it. At times it would be quite still; at times it would oscillate violently. To the passenger within the carriage there was no sensible change in the motion of the train to which the difference could be ascribed. But in the one case the tremor of the carriage contained no vibrations synchronous with the oscillating period of the water, while in the other case such vibrations were present. Out of the confused assemblage of tremors the water selected the particular constituent which belonged to itself, and declared its presence when the traveller was utterly unconscious of its introduction.

§ 6. Application of Mechanical Illustrations to Musical Strings

From these comparatively gross, but by no means unbeautiful, mechanical vibrations, we pass to those of a sounding string. In the experiments with our monochord, when the wire was to be shortened, a movable bridge was employed, against which the wire was pressed so as to deprive the point resting on the bridge of all possibility of motion. This strong pressure, however, is not necessary. Placing the feather-end of a goose-quill lightly against the middle of the string, and drawing a violin-bow over one of its halves, the string yields the octave of the note yielded by the whole string. The mere damping of the string at the centre, by the light touch of the feather, is sufficient to cause the string to divide into two vibrating segments. Nor is it necessary to hold the feather there throughout the experiment: after having drawn the bow, the feather may be removed; the string will continue to vibrate, emitting the same note as before. We have here a case exactly analogous to that in which the central point of our stretched India-rubber tube was damped, by encircling it with the finger and thumb as in Fig. 39 (1). Not only did the half plucked aside vibrate, but the other half vibrated also. We can, in fact, reproduce, with the vibrating string, every effect obtained with the tube. This, however, is a point of such importance as to demand full experimental illustration.

To prove that when the centre is damped, and the bow drawn across one of the halves of the string, the other half vibrates, I place across the middle of the untouched half a little rider of red paper. Damping the centre and drawing the bow, the string shivers, and the rider is overthrown, Fig. 41.

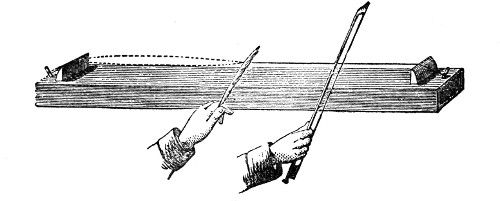
Fig. 41.

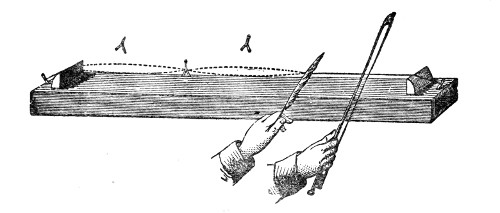
Fig. 42.

When the string is damped at a point which cuts off one-third of its length, and the bow drawn across the shorter section, not only is this section thereby thrown into vibration, but the longer section divides itself into two ventral segments with a node between them. This is proved by placing small riders of red paper on the ventral segments, and a rider of blue paper at the node. Passing the bow across the short segment you observe a fluttering of the red riders, and now they are completely tossed off, while the blue rider which crosses the node is undisturbed, Fig. 42.

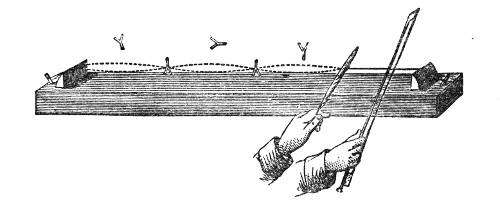
Fig. 43.

Damping the string at the end of one-fourth of its length, the bow is drawn across the shorter section; the remaining three-fourths divide themselves into three ventral segments, with two nodes between them. This is proved by the unhorsing of the three riders placed astride the ventral segments, the two at the nodes keeping their places undisturbed, Fig. 43.

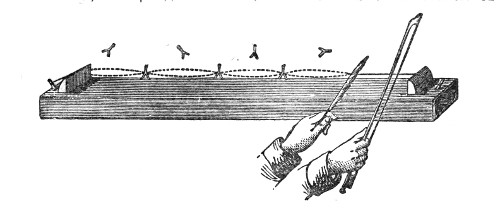
Fig. 44.

Finally, damping the string at the end of one-fifth of its length, and arranging, as before, the red riders on the ventral segments and the blue ones on the nodes, by a single sweep of the bow the four red riders are unhorsed, and the three blue ones left undisturbed, Fig. 44. In this way we perform with a sounding string the same series of experiments that were formerly executed with a stretched India-rubber tube, the results in both cases being identical.34

To make, if possible, this identity still more evident to you, a stout steel wire 28 feet in length is stretched behind the table from side to side of the room. I take the central point of this wire between my finger and thumb, and allow my assistant to pluck one-half of it aside. It vibrates, and the vibrations transmitted to the other half are sufficiently powerful to toss into the air a large sheet of paper placed astride the wire. With this long wire, and with riders not of one-eighth of a square inch, but of 30, 40, or 50 square inches in area, we may repeat all the experiments which you have witnessed with the musical string. The sheets of paper placed across the nodes remain always in their places, while those placed astride the ventral segments are tossed simultaneously into the air when the shorter segment of the wire is set in vibration. In this case, when close to it, you can actually see the division of the wire.

§ 7. Melde’s Experiments

It is now time to introduce to your notice some recent experiments on vibrating strings, which appeal to the eye with a beauty and a delicacy far surpassing anything attainable with our monochord. To M. Melde, of Marburg, we are indebted for this new method of exhibiting the vibrations of strings. The scale of the experiments will be here modified so as to suit our circumstances.

Fig. 45.

First, then, you observe here a large tuning-fork T, Fig. 45, with a small screw fixed into the top of one of its prongs, by which a silk string can be firmly attached to the prong. From the fork the string passes round a distant peg P, by turning which it may be stretched to any required extent. When the bow is drawn across the fork, an irregular flutter of the string is the only result. On tightening it, however, when at the proper tension it expands into a beautiful gauzy spindle six feet long, more than six inches across at its widest part, and shining with a kind of pearly lustre. The stretching force at the present moment is such that the string swings to and fro as a whole, its vibrations being executed in a vertical plane.

Relaxing the string gradually, when the proper tension has been reached, it suddenly divides into two ventral segments, separated from each other by a sharply-defined and apparently motionless node.

While the fork continues vibrating, if the string be relaxed still further, it divides into three vibrating parts. Slackening it still more, it divides into four vibrating parts. And thus we might continue to subdivide the string into ten, or even twenty ventral segments, separated from each other by the appropriate number of nodes.

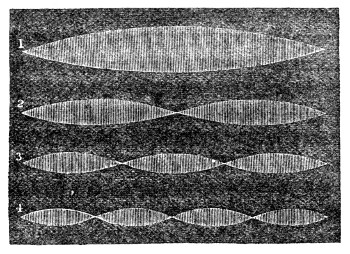
Fig. 46.

When white-silk strings vibrate thus, the nodes appear perfectly fixed, while the ventral segments form spindles of the most delicate beauty. Every protuberance of the twisted string, moreover, writes its motion in a more or less luminous line on the surface of the aërial gauze. The four nodes of vibration just illustrated are represented in Fig. 46, 1, 2, 3, 4.35

When the synchronism between fork and string is perfect, the vibrations of the string are steady and long-continued. A slight departure from synchronism, however, introduces unsteadiness, and the ventral segments, though they may show themselves for a time, quickly disappear.

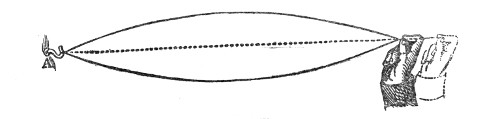
Fig. 47.

In the experiments just executed the fork vibrated in the direction of the length of the string. Every forward stroke of the fork raised a protuberance, which ran to the fixed end of the string, and was there reflected; so that when the longitudinal impulses were properly timed they produced a transverse vibration. Let us consider this further. One end of this heavy cord is attached to a hook A, Fig. 47, fixed in the wall. Laying hold of the other end I stretch the cord horizontally, and then move my hand to and fro in the direction of the cord. It swings as a whole, and you may notice that always, when the cord is at the limit of its swing, the hand is in its most forward position. If it vibrate in a vertical plane, the hand, in order to time the impulses properly, must be at its forward limit at the moment the cord reaches the upper boundary, and also at the moment it reaches the lower boundary of its excursion. A little reflection will make it plain that, in order to accomplish this, the hand must execute a complete vibration while the cord executes a semi-vibration; in other words, the vibrations of the hand must be twice as rapid as those of the cord.

Precisely the same is true of our tuning-fork. When the fork vibrates in the direction of the string, the number of vibrations which it executes in a certain time is twice the number executed by the string itself. And if, while arranged thus, a fork and string vibrate with sufficient rapidity to produce musical notes, the note of the fork will be an octave above that of the string.

But if, instead of the hand being moved to and fro in the direction of this heavy cord, it is moved at right angles to that direction, then every upward movement of the hand coincides with an upward movement of the cord; every downward movement of the hand with a downward movement of the cord. In fact, the vibrations of hand and string, in this case, synchronize perfectly; and if the hand could emit a musical note, the cord would, emit a note of the same pitch. The same holds good when a vibrating fork is substituted for the vibrating hand.

Hence, if the string vibrate as a whole when the vibrations of the fork are along it, it will divide into two ventral segments when the vibrations are across it; or, more generally expressed, preserving the tension constant, whatever be the number of ventral segments produced by the fork when its vibrations are in the direction of the string, twice that number will be produced when the vibrations are transverse to the string. The string A B, for example, Figs. 48 and 49, passing over a pulley B, is stretched by a definite weight (not shown in the figure). When the tuning-fork vibrates along it, as in Fig. 48, the string divides into two equal ventral segments. When the fork is turned so that it shall vibrate at right angles to the string, the number of ventral segments is four, Fig. 49, or double the former number. Attaching two strings of the same length to the same fork, the one parallel and the other perpendicular to the direction of vibration, and stretching both with equal weights, when the fork is caused to vibrate, one of them divides itself into twice the number of ventral segments exhibited by the other.

Fig. 48.

Fig. 49.

A number of exquisite effects may be obtained with these vibrating cords. The path described by any point of any one of them may be studied, after the manner of Dr. Young, by illuminating that point, and watching the line of light which it describes. This is well illustrated by a flat burnished silver wire, twisted so as to form a spiral surface, from which, at regular intervals, the light flashes when the wire is illuminated. When the vibration is steady, the luminous spots describe straight lines of sunlike brilliancy. On slackening the wire, but not so much as to produce its next higher subdivision, upon the larger motion of the wire are superposed a host of minor motions, the combination of all producing scrolls of marvellous complication and of indescribable splendor.

In reflecting on the best means of rendering these effects visible, the thought occurred to me of employing a fine platinum wire heated to redness by an electric current. Such a wire now stretches from a tuning-fork over a bridge of copper, and then passes round a peg. The copper bridge on the one hand and the tuning-fork on the other are the poles of a voltaic battery, from which a current passes through the wire and causes it to glow. On drawing the bow across the fork, the wire vibrates as a whole; its two ends are brilliant, while its middle is dark, being chilled by its rapid passage through the air. Thus you have a shading off of incandescence from the ends to the centre of the wire. On relaxing the tension, the wire divides itself into two ventral segments; on relaxing still further, we obtain three; still further, and the wire divides into four ventral segments, separated from each other by three brilliant nodes. Right and left from every node the incandescence shades away until it disappears. You notice also, when the wire settles into steady vibration, that the nodes shine out with greater brilliancy than that possessed by the wire before the vibration commenced. The reason is this. Electricity passes more freely along a cold wire than along a hot one. When, therefore, the vibrating segments are chilled by their swift passage through the air, their conductivity is improved, more electricity passes through the vibrating than through the motionless wire, and hence the augmented glow of the nodes. If, previous to the agitation of the fork, the wire be at a bright-red heat, when it vibrates its nodes may be raised to the temperature of fusion.

§ 8. New Mode of determining the Laws of Vibration

We may extend the experiments of M. Melde to the establishment of all the laws of vibrating strings. Here are four tuning-forks, which we may call a, b, c, d, whose rates of vibration are to each other as the numbers 1, 2, 4, 8. To the largest fork is attached a string, a, stretched by a weight, which causes it to vibrate as a whole. Keeping the stretching weight the same, I determine the lengths of the same string, which, when attached to the other three forks, b, c, d, swing as a whole. The lengths in the four respective cases are as the numbers 8, 4, 2, 1.

From this follows the first law of vibration, already established (p. 126) by another method; viz., the length of the string is inversely proportional to the rapidity of vibration.36

In this case the longest string vibrates as a whole when attached to the fork a. I now transfer the string to b, still keeping it stretched by the same weight. It vibrates when b vibrates; but how? By dividing into two equal ventral segments. In this way alone can it accommodate itself to the swifter vibrating period of b. Attached to c, the same string separates into four, while when attached to d, it divides into eight ventral segments. The number of the ventral segments is proportional to the rapidity of vibration. It is evident that we have here, in a more delicate form, a result which we have already established in the case of our India-rubber tube set in motion by the hand. It is also plain that this result might be deduced theoretically from our first law.

We may extend the experiment. Here are two tuning-forks separated from each other by the musical interval called a fifth. Attaching a string to one of the forks, I stretch the string until it divides into two ventral segments: attached to the other fork, and stretched by the same weight, it divides instantly into three segments when the fork is set in vibration. Now, to form the interval of a fifth, the vibrations of the one fork must be to those of the other in the ratio of 2:3. The division of the string, therefore, declares the interval. In, the same way the division of the string in relation to all other musical intervals may be illustrated.37

Again. Here are two tuning-forks, a and b, one of which (a) vibrates twice as rapidly as the other. A string of silk is attached to a, and stretched until it synchronizes with the fork, and vibrates as a whole. Here is a second string of the same length, formed by laying four strands of the first one side by side. I attach this compound thread to b, and, keeping the tension the same as in the last experiment, set b in vibration. The compound thread synchronizes with b, and swings as a whole. Hence, as the fork b vibrates with half the rapidity of a, by quadrupling the weight of the string we halved its rapidity of vibration. In the same simple way it might be proved that by augmenting the weight of the string nine times we reduce the number of its vibrations to one-third. We thus demonstrate the law:

The rapidity of vibration is inversely proportional to the square root of the weight of the string.

An instructive confirmation of this result is thus obtained: Attached to this tuning-fork is a silk string six feet long. Two feet of the string are composed of four strands of the single thread, placed side by side; the remaining four feet are a single thread. A stretching force is applied, which causes the string to divide into two ventral segments. But how does it divide? Not at its centre, as is the case when the string is of uniform thickness throughout, but at the precise point where the thick string terminates. This thick segment, two feet long, is now vibrating at the same rate as the thin segment four feet long, a result which follows by direct deduction from the two laws already established.

Here again are two strings of the same length and thickness. One of them is attached to the fork a, the other to the fork b, which vibrates with twice the rapidity of a. Stretched by a weight of 20 grains, the string attached to b vibrates as a whole. Substituting b for a, a weight of 80 grains causes the string to vibrate as a whole. Hence, to double the rapidity of vibration, we must quadruple the stretching weight. In the same way it might be proved that to treble the rapidity of vibration we should have to make the stretching weight ninefold. Hence our third law:

The rapidity of vibration is proportional to the square root of the tension.

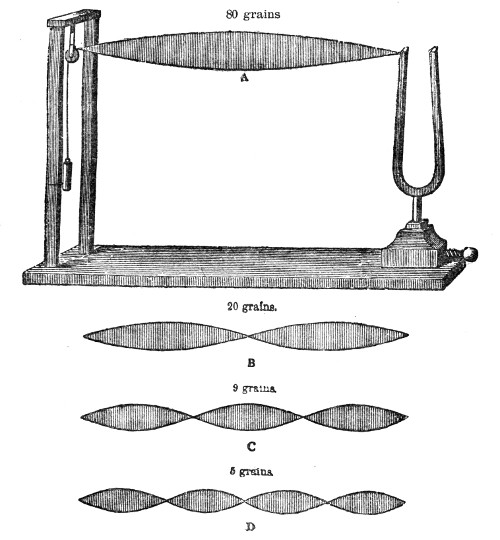
Fig. 50.

Let us vary this experiment. This silk cord is carried from the tuning-fork over the pulley, and stretched by a weight of 80 grains. The string vibrates as a whole as at A, Fig. 50. By diminishing the weight the string is relaxed, and finally divides sharply into two ventral segments, as at B, Fig. 50. What is now the stretching weight?—20 grains, or one-fourth of the first. With a stretching weight of almost exactly 9 grains it divides into three segments, as at C; while with a stretching weight of 5 grains it divides into four segments, as at D. Thus then, a tension of one-fourth doubles, a tension of one-ninth trebles, and a tension of one-sixteenth quadruples the number of ventral segments. In general terms, the number of segments is inversely proportional to the square root of the tension. This result may be deduced by reasoning from our first and third laws, and its realization here confirms their correctness.

Thus, by a series of reasonings and experiments totally different from those formerly employed, we arrive at the self-same laws. In science, different lines of reasoning often converge upon the same truth; and if we only follow them faithfully, we are sure to reach that truth at last. We may emerge, and often do emerge, from our reasoning with a contradiction in our hands; but on retracing our steps, we infallibly find the cause of the contradiction to be due, not to any lack of constancy in Nature, but of accuracy in man. It is the millions of experiences of this kind which science furnishes that give us our present faith in the stability of Nature.

HARMONIC SOUNDS OR OVERTONES

§ 9. Timbre; Klangfarbe; Clang-tint

We now approach a portion of our subject which will subsequently prove to be of the very highest importance. It has been shown by the most varied experiments that a stretched string can either vibrate as a whole, or divide itself into a number of equal parts, each of which vibrates as an independent string. Now it is not possible to sound the string as a whole without at the same time causing, to a greater or less extent, its subdivision; that is to say, superposed upon the vibrations of the whole string we have always, in a greater or less degree, the vibrations of its aliquot parts. The higher notes produced by these latter vibrations are called the harmonics of the string. And so it is with other sounding bodies; we have in all cases a coexistence of vibrations. Higher tones mingle with the fundamental one, and it is their intermixture which determines what, for want of a better term, we call the quality of the sound. The French call it timbre, and the Germans call it Klangfarbe.38 It is this union of high and low tones that enables us to distinguish one musical instrument from another. A clarinet and a violin, for example, though tuned to the same fundamental note, are not confounded; the auxiliary tones of the one are different from those of the other, and these latter tones, uniting themselves to the fundamental tones of the two instruments, destroy the identity of the sounds.

All bodies and instruments, then, employed for producing musical sounds emit, besides their fundamental tones, others due to higher orders of vibration. The Germans embrace all such sounds under the general term Obertöne. I think it will be an advantage if we in England adopt the term overtones as the equivalent of the term employed in Germany. One has occasion to envy the power of the German language to adapt itself to requirements of this nature. The term Klangfarbe, for example, employed by Helmholtz is exceedingly expressive, and we need its equivalent also. Color depends upon rapidity of vibration, blue light bearing to red the same relation that a high tone does to a low one. A simple color has but one rate of vibration, and it may be regarded as the analogue of a simple tone in music. A tone, then, may be defined as the product of a vibration which cannot be decomposed into more simple ones. A compound color, on the contrary, is produced by the admixture of two or more simple ones, and an assemblage of tones, such as we obtain when the fundamental tone and the harmonics of a string sound together, is called by the Germans a Klang. May we not employ the English word clang to denote the same thing, and thus give the term a precise scientific meaning akin to its popular one? And may we not, like Helmholtz, add the word color or tint, to denote the character of the clang, using the term clang-tint as the equivalent of Klangfarbe?

With your permission I shall henceforth employ these terms; and now it becomes our duty to look a little more closely than we have hitherto done into the subdivision of a string into its harmonic segments. Our monochord with its stretched wire is before you. The scale of the instrument is divided into 100 equal parts. At the middle point of the wire stands the number 50; at a point almost exactly one-third of its length from its end stands the number 33; while at distances equal to one-fourth and one-fifth of its length from its end stand the numbers 25 and 20 respectively. These numbers are sufficient for our present purpose. When the wire is plucked at 50 you hear its clang, rather hollow and dull. When plucked at 33, the clang is different. When plucked at 25, the clang is different from either of the former. As we retreat from the centre of the string, the clang-tint becomes more “brilliant,” the sound more brisk and sharp. What is the reason of these differences in the sound of the same wire?

The celebrated Thomas Young, once professor in this Institution, enables us to solve the question. He proved that when any point of a string is plucked, all the higher tones which require that point for a node vanish from the clang. Let me illustrate this experimentally. I pluck the point 50, and permit the string to sound. It may be proved that the first overtone, which corresponds to a division of the string into two vibrating parts, is now absent from the clang. If it were present, the damping of the point 50 would not interfere with it, for this point would be its node. But on damping the point 50 the fundamental tone is quenched, and no octave of that tone is heard. Along with the octave its whole progeny of overtones, with rates of vibration four times, six times, eight times—all even numbers of times—the rate of the fundamental tone, disappear from the clang. All these tones require that a node should exist at the centre, where, according to the principle of Young, it cannot now be formed. Let us pluck some other point, say 25, and damp 50 as before. The fundamental tone is now gone, but its octave, clear and full, rings in your ears. The point 50 in this case not being the one plucked, a node can form there; it has formed, and the two halves of the string continue to vibrate after the vibrations of the string as a whole have been extinguished. Plucking the point 33, the second harmonic or overtone is absent from the clang. This is proved by damping the point 33. If the second harmonic were on the string this would not affect it, for 33 is its node. The fundamental is quenched, but no tone corresponding to a division of the string into three vibrating parts is now heard. The tone is not heard because it was never there.

All the overtones which depend on this division, those with six times, nine times, twelve times the rate of vibration of the fundamental one, are also withdrawn from the clang. Let us now pluck 20, damping 33 as before. The second harmonic is not extinguished, but continues to sound clearly and fully after the extinction of the fundamental tone. In this case the point 33 not being that plucked, a node can form there, and the string can divide itself into three parts accordingly. In like manner, if 25 be plucked and then damped, the third harmonic is not heard; but when a point between 25 and the end of the wire is plucked, and the point 25 damped, the third harmonic is plainly heard. And thus we might proceed, the general rule enunciated by Young, and illustrated by these experiments, being, that when any point of a string is plucked or struck, or, as Helmholtz adds, agitated with a bow, the harmonic which requires that point for a node vanishes from the general clang of the string.

§ 10. Mingling of Overtones with Fundamental. The Æolian Harp

You are now in a condition to estimate the influence which these higher vibrations must have upon the quality of the tone emitted by the string. The sounds which ring in your ears so plainly after the fundamental tone is quenched mingled with that note before it was extinguished. It seems strange that tones of such power could be so masked by the fundamental one that even the disciplined ear of a musician is unable to separate the one from the other. But Helmholtz has shown that this is due to want of practice and attention. The musician’s faculties were never exercised in this direction. There are numerous effects which the musician can distinguish, because his art demands the habit of distinguishing them. But it is no necessity of his art to resolve the clang of an instrument into its constituent tones. By attention, however, even the unaided ear can accomplish this, particularly if the mind be informed beforehand what the ear has to bend itself to find.

And this reminds me of an occurrence which took place in this room at the beginning of my acquaintance with Faraday. I wished to show him a peculiar action of an electro-magnet upon a crystal. Everything was arranged, when just before the magnet was excited he laid his hand upon my arm and asked, “What am I to look for?” Amid the assemblage of impressions connected with an experiment, even this prince of experimenters felt the advantage of having his attention directed to the special point to be illustrated. Such help is the more needed when we attempt to resolve into its constituent parts an effect so intimately blended as the composite tones of a clang. When we desire to isolate a particular tone, one way of helping the attention is to sound that tone feebly on a string of the proper length. Thus prepared, the ear glides more readily from the single tone to that of the same pitch in a composite clang, and detaches it more readily from its companions. In the experiments executed a moment ago, where our aim in each respective case was to bring out the higher tone of the string in all its power, we entirely extinguished its fundamental tone. It may, however, be enfeebled without being destroyed. I pluck this string at 33, and lay the feather lightly for a moment on the string at 50. The fundamental tone is thereby so much lowered that its octave can make itself plainly heard. By again touching the string at 50, the fundamental tone is lowered still more; so that now its first harmonic is more powerful than itself. You hear the sound of both, and you might have heard them in the first instance by a sufficient stretch of attention.

The harmonics of a string may be augmented or subdued within wide limits. They may, as we have seen, be masked by the fundamental tone, and they may also effectually mask it. A stroke with a hard body is favorable, while a stroke with a soft body is unfavorable to their development. They depend, moreover, on the promptness with which the body striking the string retreats after striking. Thus they are influenced by the weight and elasticity of the hammers in the pianoforte. They also depend upon the place at which the shock is imparted. When, for example, a string is struck in the centre, the harmonics are less powerful than when it is struck near one end.

Helmholtz, who is equally eminent as a mathematician and as an experimental philosopher, has calculated the theoretic intensity of the harmonics developed in various ways; that is to say, the actual vis viva or energy of the vibration, irrespective of its effects upon the ear. A single example given by him will suffice to illustrate this subject. Calling the intensity of the fundamental tone, in each case, 100, that of the second harmonic, when the string was simply pulled aside at a point one-seventh of its length from its end and then liberated, was found to be 56·1, or a little better than one-half. When the string was struck with the hammer of a pianoforte, whose contact with the string endured for three-sevenths of the period of vibration of the fundamental tone, the intensity of the same tone was 9. In this case the second harmonic was nearly quenched. When, however, the duration of contact was diminished to three-twentieths of the period of the fundamental, the intensity of the harmonic rose to 357; while, when the string was sharply struck with a very hard hammer, the intensity mounted to 505, or to more than quintuple that of the fundamental tone.39 Pianoforte manufacturers have found that the most pleasing tone is excited by the middle strings of their instruments, when the point against which the hammer strikes is from one-seventh to one-ninth of the length of the wire from its extremity.

Why should this be the case? Helmholtz has given the answer. Up to the tones which require these points as nodes the overtones all form chords with the fundamental; but the sixth and eighth overtones of the wire do not enter into such chords; they are dissonant tones, and hence the desirability of doing away with them. This is accomplished by making the point at which a node is required that on which the hammer falls. The possibility of the tone forming is thereby shut out, and its injurious effect is avoided.

The strings of the Æolian harp are divided into harmonic parts by a current of air passing over them. The instrument is usually placed in a window between the sash and frame, so as to leave no way open to the entrance of the air except over the strings. Sir Charles Wheatstone recommends the stretching of a first violin-string at the bottom of a door which does not closely fit. When the door is shut, the current of air entering beneath sets the string in vibration, and when a fire is in the room, the vibrations are so intense that a great variety of sounds are simultaneously produced.40 A gentleman in Basel once constructed with iron wires a large instrument which he called the weather-harp or giant-harp, and which, according to its maker, sounded as the weather changed. Its sounds were also said to be evoked by changes of terrestrial magnetism. Chladni pointed out the error of these notions, and reduced the action of the instrument to that of the wind upon its strings.

§ 11. Young’s Optical Illustrations

Finally, with regard to the vibrations of a wire, the experiments of Dr. Young, who was the first to employ optical methods in such experiments, must be mentioned. He allowed a sheet of sunlight to cross a pianoforte-wire, and obtained thus a brilliant dot. Striking the wire he caused it to vibrate, the dot described a luminous line like that produced by the whirling of a burning coal in the air, and the form of this line revealed the character of the vibration. It was rendered manifest by these experiments that the oscillations of the wire were not confined to a single plane, but that it described in its vibrations curves of greater or less complexity. Superposed upon the vibration of the whole string were partial vibrations, which revealed themselves as loops and sinuosities. Some of the lines observed by Dr. Young are given in Fig. 51. Every one of these figures corresponds to a distinct impression made by the wire upon the surrounding air. The form of the sonorous wave is affected by these superposed vibrations, and thus they influence the clang-tint or quality of the sound.

Fig. 51.

SUMMARY OF CHAPTER III

The amount of motion communicated by a vibrating string to the air is too small to be perceived as sound, even at a small distance from the string.

When a broad surface vibrates in air, condensations and rarefactions are more readily formed than when the vibrating body is of small dimensions like a string. Hence, when strings are employed as sources of musical sounds, they are associated with surfaces of larger area which take up their vibrations, and transfer them to the surrounding air.

Thus the tone of a harp, a piano, a guitar, or a violin, depends mainly upon the sound-board of the instrument.

The following four laws regulate the vibrations of strings: The rate of vibrations is inversely proportional to the length; it is inversely proportional to the diameter; it is directly proportional to the square root of the stretching weight or tension; and it is inversely proportional to the square root of the density of the string.

When strings of different diameters and densities are compared, the law is, that the rate of vibration is inversely proportional to the square root of the weight of the string.

When a stretched rope, or an India-rubber tube filled with sand, with one of its ends attached to a fixed object, receives a jerk at the other end, the protuberance raised upon the tube runs along it as a pulse to the fixed end, and, being there reflected, returns to the hand by which the jerk was imparted.

The time required for the pulse to travel from the hand to the fixed end of the tube and back is that required by the whole tube to execute a complete vibration.

When a series of pulses are sent in succession along the tube, the direct and reflected pulses meet, and by their coalescence divide the tube into a series of vibrating parts, called ventral segments, which are separated from each other by points of apparent rest called nodes.

The number of ventral segments is directly proportional to the rate of vibration at the free end of the tube.

The hand which produces these vibrations may move through less than an inch of space; while by the accumulation of its impulses the amplitude of the ventral segments may amount to several inches, or even to several feet.

If an India-rubber tube, fixed at both ends, be encircled at its centre by the finger and thumb, when either of its halves is pulled aside and liberated, both halves are thrown into a state of vibration.

If the tube be encircled at a point one-third, one-fourth, or one-fifth of its length from one of its ends, on pulling the shorter segment aside and liberating it, the longer segment divides itself into two, three, or four vibrating parts, separated from each other by nodes.

The number of vibrating segments depends upon the rate of vibration at the point encircled by the finger and thumb.

Here also the amplitude of vibration at the place encircled by the finger and thumb may not be more than a fraction of an inch, while the amplitude of the ventral segments may amount to several inches.

A musical string damped by a feather at a point one-half, one-third, one-fourth, one-fifth, etc., of its length from one of its ends, and having its shorter segment agitated, divides itself exactly like the India-rubber tube. Its division may be rendered apparent by placing little paper riders across it. Those placed at the ventral segments are thrown off, while those placed at the nodes retain their places.

The notes corresponding to the division of a string into its aliquot parts are called the harmonics of the string.

When a string vibrates as a whole, it usually divides at the same time into its aliquot parts. Smaller vibrations are superposed upon the larger; the tones corresponding to those smaller vibrations, and which we have agreed to call overtones, mingling at the same time with the fundamental tone of the string.

The addition of these overtones to the fundamental tone determines the timbre or quality of the sound, or, as we have agreed to call it, the clang-tint.

It is the addition of such overtones to fundamental tones of the same pitch which enables us to distinguish the sound of a clarionet from that of a flute, and the sound of a violin from both. Could the pure fundamental tones of these instruments be detached, they would be indistinguishable from each other; but the different admixture of overtones in the different instruments renders their clang-tints diverse, and therefore distinguishable.

Instead of the heavy India-rubber tube in the experiment above referred to, we may employ light silk strings, and, instead of the vibrating hand, we may employ vibrating tuning-forks, and cause the strings to swing as a whole, or to divide themselves into any number of ventral segments. Effects of great beauty are thus obtained, and by experiments of this character all the laws of vibrating strings may be demonstrated.

When a stretched string is plucked aside or agitated by a bow, all the overtones which require the agitated point for a node vanish from the clang of the string.

The point struck by the hammer of the piano is from one-seventh to one-ninth of the length of the string from its end: by striking this point, the notes which require it as a node cannot be produced, a source of dissonance being thus avoided.

CHAPTER IV

Vibrations of a Rod fixed at Both Ends: its Subdivisions and Corresponding Overtones—Vibrations of a Rod fixed at One End—The Kaleidophone—The Iron Fiddle and Musical Box—Vibrations of a Rod free at Both Ends—The Claque-bois and Glass Harmonica—Vibrations of a Tuning-Fork: its Subdivisions and Overtones—Vibrations of Square Plates—Chladni’s Discoveries—Wheatstone’s Analysis of the Vibrations of Plates—Chladni’s Figures—Vibrations of Disks and Bells—Experiments of Faraday and Strehlke

§ 1. Transverse Vibrations of a Rod fixed at Both Ends

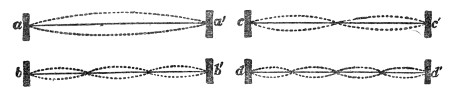
Fig. 52.

OUR last chapter was devoted to the transverse vibrations of strings. This one I propose devoting to the transverse vibrations of rods, plates, and bells, commencing with the case of a rod fixed at both ends. Its modes of vibration are exactly those of a string. It vibrates as a whole, and can also divide itself into two, three, four, or more vibrating parts. But, for a reason to be immediately assigned, the laws which regulate the pitch of the successive notes are entirely different in the two cases. Thus, when a string divides into two equal parts, each of its halves vibrates with twice the rapidity of the whole; while, in the case of the rod, each of its halves vibrates with nearly three times the rapidity of the whole. With greater strictness, the ratio of the two rates of vibration is as 9 is to 25, or as the square of 3 to the square of 5. In Fig. 52, a a′, c c′, b b′, d d′, are sketched the first four modes of vibration of a rod fixed at both ends: the successive rates of vibration, in the four cases bear to each other the following relation:

Number of nodes

0

1

2

3

Number of vibrations

9

25

49

81

the last row of figures being the squares of the odd numbers 3, 5, 7, 9.

In the case of a string, the vibrations are maintained by a tension externally applied; in the case of a rod, the vibrations are maintained by the elasticity of the rod itself. The modes of division are in both cases the same, but the forces brought into play are different, and hence also the successive rates of vibration.

§ 2. Transverse Vibrations of a Rod fixed at One End

Let us now pass on to the case of a rod fixed at one end and free at the other. Here also it is the elasticity of the material, and not any external tension, that sustains the vibrations. Approaching, as usual, sonorous vibrations through more grossly mechanical ones, I fix this long rod of iron, n o, Fig. 53, in a vise, draw it aside, and liberate it. To make its vibrations more evident, its shadow is thrown upon a screen. The rod oscillates as a whole to and fro, between the points p p′. But it is capable of other modes of vibration. Damping it at the point a, by holding it gently there between the finger and thumb, and striking it sharply between a and o, the rod divides into two vibrating parts, separated by a node as shown in Fig. 54. You see upon the screen a shadowy spindle between a and the vise below, and a shadowy fan above a, with a black node between both. The division may be effected without damping a, by merely imparting a sufficiently sharp shock to the rod between a and o. In this case, however, besides oscillating in parts, the rod oscillates as a whole, the partial oscillations being superposed upon the large one.

Fig. 53.

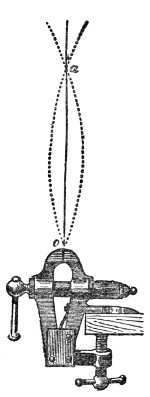
Fig. 54.

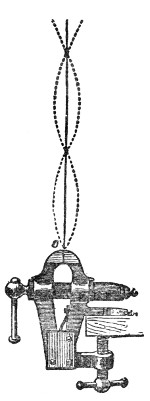
Fig. 55.

You notice, moreover, that the amplitude of the partial oscillations depends upon the promptness of the stroke. When the stroke is sluggish, the partial division is but feebly pronounced, the whole oscillation being most marked. But when the shock is sharp and prompt, the whole oscillation is feeble, and the partial oscillations are executed with vigor. If the vibrations of this rod were rapid enough to produce a musical sound, the oscillation of the rod as a whole would correspond to its fundamental tone, while the division of the rod into two vibrating parts would correspond to the first of its overtones. If, moreover, the rod vibrated as a whole and as a divided rod at the same time, the fundamental tone and the overtone would be heard simultaneously. By damping the proper point and imparting the proper shock, we can still further subdivide the rod, as shown in Fig. 55.

§ 3. Chladni’s Tonometer: the Iron Fiddle, Musical Box, and the Kaleidophone

And now let us shorten our rod, so as to bring its vibrations into proper relation to our ears. When it is about four inches long, it emits a low musical sound. When further shortened, the tone is higher; and, by continuing to shorten the rod, the speed of vibration is augmented, until finally the sound becomes painfully acute. These musical vibrations differ only in rapidity from the grosser oscillations which a moment ago appealed to the eye.

The increase in the rate of vibrations here observed is ruled by a definite law; the number of vibrations executed at a given time is inversely proportional to the square of the length of the vibrating rod. You hear the sound of this strip of brass, two inches long, as the fiddle-bow is passed over its end. Making the length of the strip one inch, the sound is the double octave of the last one; the rate of vibration is augmented four times. Thus, by doubling the length of the vibrating strip, we reduce its rate of vibration to one-fourth; by trebling the length, we reduce the rate of vibration to one-ninth; by quadrupling the length, we reduce the vibrations to one-sixteenth, and so on. It is plain that, by proceeding in this way, we should finally reach a length where the vibrations would be sufficiently slow to be counted. Or, it is plain that, beginning with a long strip whose vibrations could be counted, we might, by shortening, not only make the strip sound, but also determine the rates of vibration corresponding to its different tones. Supposing we start with a strip 36 inches long, which vibrates once in a second, the strip reduced to 12 inches would, according to the above law, execute 9 vibrations a second; reduced to 6 inches, it would execute 36, to 3 inches, 144; while, if reduced to 1 inch in length, it would execute 1,296 vibrations in a second. It is easy to fill the spaces between the lengths here given, and thus to determine the rate of vibration corresponding to any particular tone. This method was proposed and carried out by Chladni.

A musical instrument may be formed of short rods. Into this common wooden tray a number of pieces of stout iron wire of different lengths are fixed, being ranged in a semicircle. When the fiddle-bow is passed over the series, we obtain a succession of very pleasing notes. A competent performer could certainly extract very tolerable music from a sufficient number of these iron pins. The iron fiddle (violon de fer) is thus formed. The notes of the ordinary musical box are also produced by the vibrations of tongues of metal fixed at one end. Pins are fixed in a revolving, cylinder, the free ends of the tongues are lifted by these pins and then suddenly let go. The tongues vibrate, their length and strength being so arranged as to produce in each particular case the proper rapidity of vibration.

Sir Charles Wheatstone has devised a simple and ingenious optical method for the study of vibrating rods fixed at one end. Attaching light glass beads, silvered within, to the end of a metal rod, and allowing the light of a lamp or candle to fall upon the bead, he obtained a small spot intensely illuminated. When the rod vibrated, this spot described a brilliant line which showed the character of the vibration. A knitting-needle, fixed in a vise with a small bead stuck on to it by marine glue, answers perfectly as an illustration. In Wheatstone’s more complete instrument, which he calls a kaleidophone, the vibrating rods are firmly screwed into a massive stand. Extremely beautiful figures are obtained by this simple contrivance, some of which may now be projected on a magnified scale upon the screen before you.

Fixing the rod horizontally in the vise, a condensed beam is permitted to fall upon the silvered bead, a spot of sunlike brilliancy being thus obtained. Placing a lens in front of the bead, a bright image of the spot is thrown upon the screen, the needle is then drawn aside, and suddenly liberated. The spot describes a ribbon of light, at first straight, but speedily opening out into an ellipse, passing into a circle, and then again through a second ellipse back to a straight line. This is due to the fact that a rod held thus in a vise vibrates not only in the direction in which it is drawn aside, but also at right angles to this direction. The curve is due to the combination of two rectangular vibrations.41 While the rod is thus swinging as a whole, it may also divide itself into vibrating parts. By properly drawing a violin-bow across the needle, this serrated circle, Fig. 56, is obtained, a number of small undulations being superposed upon the large one. You moreover hear a musical tone, which you did not hear when the rod vibrated as a whole only; its oscillations, in fact, were then too slow to excite such a tone. The vibrations which produce these sinuosities, and which correspond to the first division of the rod, are executed with about 6-1/4 times the rapidity of the vibrations of the rod swinging as a whole. Again I draw the bow; the note rises in pitch, the serrations run more closely together, forming on the screen a luminous ripple more minute and, if possible, more beautiful than the last one, Fig. 57. Here we have the second division of the rod, the sinuosities of which correspond to 17-13/36 times its rate of vibration as a whole. Thus every change in the sound of the rod is accompanied by a change of the figure upon the screen.

Fig. 56.

         

Fig. 57.

The rate of vibration of the rod, as a whole, is to the rate corresponding to its first division nearly as the square of 2 is to the square of 5, or as 4:25. From the first division onward the rates of vibration are approximately proportional to the squares of the series of odd numbers 3, 5, 7, 9, 11, etc. Supposing the vibrations of the rod as a whole to number 36, then the vibrations corresponding to this and to its successive divisions would be expressed approximately by the following series of number’s:

36, 225, 625, 1225, 2025, etc.

In Fig. 58, a, b, c, d, e, are shown the modes of division corresponding to this series of numbers. You will not fail to observe that these overtones of a vibrating rod rise far more rapidly in pitch than the harmonics of a string.

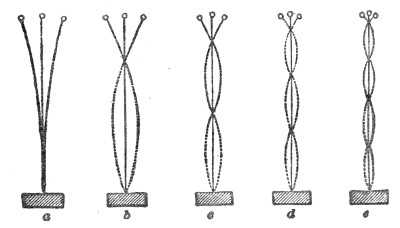
Fig. 58.

Other forms of vibration may be obtained by smartly striking the rod with the finger near its fixed end. In fact, an almost infinite variety of luminous scrolls can be thus produced, the beauty of which may be inferred from the subjoined figures (see next page) first obtained by Sir C. Wheatstone. They may be produced by illuminating the bead with sunlight, or with the light of a lamp or candle. The scrolls, moreover, may be doubled by employing two candles instead of one. Two spots of light then appear, each of which describes its own luminous line when the knitting-needle is set in vibration. In a subsequent lecture we shall become acquainted with Wheatstone’s application of his method to the study of rectangular vibrations.

Fig. 59.

§ 4. Transverse Vibrations of a Rod free at Both Ends. The Claque-bois and Glass Harmonica

Fig. 60.

From a rod or bar fixed at one end, we will now pass to rods or bars free at both ends; for such an arrangement has also been employed in music. By a method afterward to be described, Chladni, the father of modern acoustics, determined experimentally the modes of vibration possible to such bars. The simplest mode of division in this case occurs when the rod is divided by two nodes into three vibrating parts. This division is easily illustrated by a flexible box ruler, six feet long. Holding it at about twelve inches from its two ends between the forefinger and thumb of each hand, and shaking it, or causing its centre to be struck, it vibrates, the middle segment forming a shadowy spindle, and the two ends forming fans. The shadow of the ruler on the screen renders the mode of vibration very evident. In this case the distance of each node from the end of the ruler is about one-fourth of the distance between the two nodes. In its second mode of vibration the rod or ruler is divided into four vibrating parts by three nodes. In Fig. 60, 1 and 2, these respective modes of division are shown. Looking at the edge of the ruler 1, the dotted lines cutting a a′, b b′, show the manner in which the segments bend up and down when the first division occurs, while c c′, d d′, show the mode of vibration corresponding to the second division. The deepest tone of a rod free at both ends is higher than the deepest tone of a rod fixed at one end in the proportion of 4:25. Beginning with the first two nodes, the rates of vibration of the free bar rise in the following proportion:

Number of nodes

 

2, 3, 4, 5, 6, 7

Numbers to the squares of which the

}

3, 5, 7, 9, 11, 13

   pitch is approximately proportional

Here, also, we have a similarly rapid rise of pitch to that noticed in the last two cases.

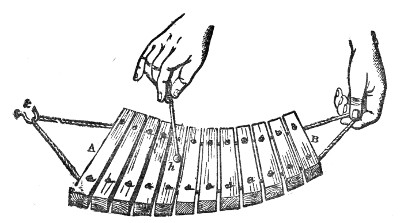
Fig. 61.

For musical purposes the first division only of a free rod has been employed. When bars of wood of different lengths, widths, and depths, are strung along a cord which passes through the nodes, we have the claque-bois of the French, an instrument now before you, A B, Fig. 61. Supporting the cord at one end by a hook k and holding it at the other in the left hand, I run the hammer h along the series of bars, and produce an agreeable succession of musical tones. Instead of using the cord, the bars may rest at their nodes on cylinders of twisted straw; hence the name “straw-fiddle,” sometimes applied to this instrument. Chladni informs us that it is introduced as a play of bells (Glockenspiel) into Mozart’s opera of “Die Zauberflöte.” If, instead of bars of wood, we employ strips of glass, we have the glass harmonica.

§ 5. Vibrations of a Tuning-fork

From the vibrations of a bar free at both ends it is easy to pass to the vibrations of a tuning-fork, as analyzed by Chladni. Supposing a a, Fig. 62, to represent a straight steel bar, with the nodal points corresponding to its first mode of division marked by the transverse dots. Let the bar be bent to the form b b; the two nodal points still remain, but they have approached nearer to each other. The tone of the bent bar is also somewhat lower than that of the straight one. Passing through various stages of bending, c c, d d, we at length convert the bar into a tuning-fork e e, with parallel prongs; it still retains its two nodal points, which, however, are much closer together than when the bar was straight.

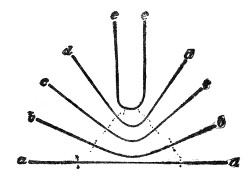
Fig. 62.

Fig. 63.

When such a fork sounds its deepest note, its free ends oscillate as in Fig. 63, where the prongs vibrate between the limits b and n, and f and m, and where p and q are the nodes. There is no division of a tuning-fork corresponding to the division of a straight bar by three nodes. In its second mode of division, which corresponds to the first overtone of the fork, we have a node on each prong, and two at the bottom. The principle of Young, referred to at page 155, extends also to tuning-forks. To free the fundamental tone from an overtone, you draw your bow across the fork at the place where the node is required to form the latter. In the third mode of division there are two nodes on each prong and one at the bottom; in the fourth division there are two nodes on each prong and two at the bottom; while in the fifth division there are three nodes on each prong and one at the bottom. The first overtone of the fork requires, according to Chladni, 6-1/4 times the number of vibrations of the fundamental tone.

It is easy to elicit the overtones of tuning-forks. Here, for example, is our old series, vibrating respectively 256, 320, 384, and 512 times in a second. In passing from the fundamental tone to the first overtone of each you notice that the interval is vastly greater than that between the fundamental tone and the first overtone of a stretched string. From the numbers just mentioned we pass at once to 1,600, 2,000, 2,400, and 3,200 vibrations a second. Chladni’s numbers, however, though approximately correct, are not always rigidly verified by experiment. A pair of forks, for example, may have their fundamental tones in perfect unison and their overtones discordant. Two such forks are now before you. When the fundamental tones of both are sounded, the unison is perfect; but when the first overtones of both are sounded, they are not in unison. You hear rapid “beats,” which grate upon the ear. By loading one of the forks with wax, the two overtones may be brought into unison; but now the fundamental tones produce loud beats when sounded together. This could not occur if the first overtone of each fork was produced by a number of vibrations exactly 6-1/4 times the rate of its fundamental. In a series of forks examined by Helmholtz, the number of vibrations of the first overtone varied from 5·6 to 6·6 times that of the fundamental.

Starting from the first overtone, and including it, the rates of vibration of the whole series of overtones are as the squares of the numbers 3, 5, 7, 9, etc. That is to say, in the time required by the first overtone to execute 9 vibrations, the second executes 25, the third 49, the fourth 81, and so on. Thus the overtones of the fork rise with far greater rapidity than those of a string. They also vanish more speedily, and hence adulterate to a less extent the fundamental tone by their admixture.

§ 6. Chladni’s Figures

The device of Chladni for rendering these sonorous vibrations visible has been of immense importance to the science of acoustics. Lichtenberg had made the experiment of scattering an electrified powder over an electrified resin-cake, the arrangement of the powder revealing the electric condition of the surface. This experiment suggested to Chladni the idea of rendering sonorous vibrations visible by means of sand strewed upon the surface of the vibrating body. Chladni’s own account of his discovery is of sufficient interest to justify its introduction here:

“As an admirer of music, the elements of which I had begun to learn rather late, that is, in my nineteenth year, I noticed that the science of acoustics was more neglected than most other portions of physics. This excited in me the desire to make good the defect, and by new discovery to render some service to this part of science. In 1785 I had observed that a plate of glass or metal gave different sounds when it was struck at different places, but I could nowhere find any information regarding the corresponding modes of vibration. At this time there appeared in the journals some notices of an instrument made in Italy by the Abbé Mazzochi, consisting of bells, to which one or two violin-bows were applied. This suggested to me the idea of employing a violin-bow to examine the vibrations of different sonorous bodies. When I applied the bow to a round plate of glass fixed at its middle it gave different sounds, which, compared with each other, were (as regards the number of their vibrations) equal to the squares of 2, 3, 4, 5, etc.; but the nature of the motions to which these sounds corresponded, and the means of producing each of them at will, were yet unknown to me. The experiments on the electric figures formed on a plate of resin, discovered and published by Lichtenberg, in the memoirs of the Royal Society of Göttingen, made me presume that the different vibratory motions of a sonorous plate might also present different appearances, if a little sand or some other similar substance were spread over the surface. On employing this means, the first figure that presented itself to my eyes upon the circular plate already mentioned resembled a star with ten or twelve rays, and the very acute sound, in the series alluded to, was that which agreed with the square of the number of diametrical lines.”

§ 7. Vibrations of Square Plates: Nodal Lines

I will now illustrate the experiments of Chladni, commencing with a square plate of glass held by a suitable clamp at its centre. The plate might be held with the finger and thumb, if they could only reach far enough. Scattering fine sand over the plate, the middle point of one of its edges is damped by touching it with the finger-nail, and a bow is drawn across the edge of the plate, near one of its corners. The sand is tossed away from certain parts of the surface, and collects along two nodal lines which divide the large square into four smaller ones, as in Fig. 64. This division of the plate corresponds to its deepest tone.

Fig. 64.

Fig. 65.

Fig. 66.

The signs + and - employed in these figures denote that the two squares on which they occur are always moving in opposite directions. When the squares marked + are above the average level of the plate those marked - are below it; and when those marked - are above the average level those marked + are below it. The nodal lines mark the boundaries of these opposing motions. They are the places of transition from the one motion to the other, and are therefore unaffected by either.

Scattering sand once more over its surface, I damp one of the corners of the plate, and excite it by drawing the bow across the middle of one of its sides. The sand dances over the surface, and finally ranges itself in two sharply-defined ridges along its diagonals, Fig. 65. The note here produced is a fifth above the last. Again damping two other points, and drawing the bow across the centre of the opposite side of the plate, we obtain a far shriller note than in either of the former cases, and the manner in which the plate vibrates to produce this note is represented in Fig. 66.

Fig. 67.

Thus far plates of glass have been employed held by a clamp at the centre. Plates of metal are still more suitable for such experiments. Here is a plate of brass, 12 inches square, and supported on a suitable stand. Damping it with the finger and thumb of my left hand at two points of its edge, and drawing the bow with my right across a vibrating portion of the opposite edge, the complicated pattern represented in Fig. 67 is obtained.

Fig. 68.

The beautiful series of patterns shown on page 182 were obtained by Chladni, by damping and exciting square plates in different ways. It is not only interesting but startling to see the suddenness with which these sharply-defined figures are formed by the sweep of the bow of a skilful experimenter.

§ 8. Wheatstone’s Analysis of the Vibrations of Square Plates

And now let us look a little more closely into the mechanism of these vibrations. The manner in which a bar free at both ends divides itself when it vibrates transversely has been already explained. Rectangular pieces of glass or of sheet metal—the glass strips of

Fig. 69. the harmonica, for example—also obey the laws of free rods and bars. In Fig. 69 is drawn a rectangle a, with the nodes corresponding to its first division marked upon it, and underneath it is placed a figure showing the manner in which the rectangle, looked at edgewise, bends up and down when it is set in vibration.42 For the sake of plainness the bending is greatly exaggerated. The figures b and c indicate that the vibrating parts of the plate alternately rise above and fall below the average level of the plate. At one moment, for example, the centre of the plate is above the level and its ends below it, as at b; while at the next moment its centre is below and its two ends above the average level, as at c. The vibrations of the plate consist in the quick successive assumption of these two positions. Similar remarks apply to all other modes of division.

Now suppose the rectangle gradually to widen, till it becomes a square. There then would be no reason why the nodal lines should form parallel to one pair of sides rather than to the other. Let us now examine what would be the effect of the coalescence of two such systems of vibrations.

To keep your conceptions clear, take two squares of glass and draw upon each of them the nodal lines belonging to a rectangle. Draw the lines on one plate in white, and on the other in black; this will help you to keep the plates distinct in your mind as you look at them. Now lay one square upon the other so that their nodal lines shall coincide, and then realize with perfect mental clearness both plates in a state of vibration. Let us assume, in the first instance, that the vibrations of the two plates are concurrent; that the middle segment and the end segments of each rise and fall together; and now suppose the vibrations of one plate transferred to the other. What would be the result? Evidently vibrations of a double amplitude on the part of the plate which has received this accession. But suppose the vibrations of the two plates, instead of being concurrent, to be in exact opposition to each other—that when the middle segment of the one rises the middle segment of the other falls—what would be the consequence of adding them together? Evidently a neutralization of all vibration.

Instead of placing the plates so that their nodal lines coincide, set these lines at right angles to each other. That is to say, push A over A′, Fig. 70. In these figures the letter P means positive, indicating, in the section where it occurs, a motion of the plate upward; while N means negative, indicating, where it occurs, a motion downward. You have now before you a kind of check pattern, as shown in the third square, consisting of a square s in the middle, a smaller square b at each corner, and four rectangles at the middle portions of the four sides. Let the plates vibrate, and let the vibrations of their corresponding sections be concurrent, as indicated by the letters P and N; and then suppose the vibrations of one of them transferred to the other. What must result? A moment’s reflection will show you that the big middle square s will vibrate with augmented energy; the same is true of the four smaller squares b, b, b, b, at the four corners; but you will at once convince yourselves that the vibrations in the four rectangles are in opposition, and that where their amplitudes are equal they will destroy each other. The middle point of each side of the plate of glass would therefore be a point of rest; the points where the nodal lines of the two plates cross each other would also be points of rest. Draw a line through every three of these points and you will obtain a second square inscribed in the first. The sides of this square are lines of no motion.

Fig. 70.

We have thus far been theorizing. Let us now clip a square plate of glass at a point near the centre of one of its edges, and draw the bow across the adjacent corner of the plate. When the glass is homogeneous, a close approximation to this inscribed square is obtained. The reason is that when the plate is agitated in this manner the two sets of vibrations which we have been considering actually coexist in the plate, and produce the figure due to their combination.

Again, place the squares of glass one upon the other exactly as in the last case; but now, instead of supposing them to concur in their vibrations, let their corresponding sections oppose each other: that is, let A cover A′, Fig. 71. Then it is manifest that on superposing the vibrations the middle point of our middle square must be a point of rest; for here the vibrations are equal and opposite. The intersections of the nodal lines are also points of rest, and so also is every corner of the plate itself, for here the added vibrations are also equal and opposite. We have thus fixed four points of rest on each diagonal of the square. Draw the diagonals, and they will represent the nodal lines consequent on the superposition of the two vibrations.

Fig. 71.

These two systems actually coexist in the same plate when the centre is clamped and one of the corners touched, while the fiddle-bow is drawn across the middle of one of the sides. In this case the sand which marks the lines of rest arranges itself along the diagonals. This, in its simplest possible form, is Sir C. Wheatstone’s analysis of these superposed vibrations.

§ 9. Vibrations of Circular Plates

Passing from square plates to round ones, we also obtain various beautiful effects. This disk of brass is supported horizontally upon an upright stand: it is blackened, and fine white sand is scattered lightly over it. The disk is capable of dividing itself in various ways, and of emitting notes of various pitch. I sound the lowest fundamental note of the disk by touching its edge at a certain point and drawing the bow across the edge at a point 45° distant from the damped one. You hear the note and you see the sand. It quits the four quadrants of the disk, and ranges itself along two of the diameters, Fig. 72, A (next page). When a disk divides itself thus into four vibrating segments, it sounds its deepest note. I stop the vibration, clear the disk, and once more scatter sand over it. Damping its edge, and drawing the bow across it at a point 30° distant from the damped one, the sand immediately arranges itself in a star. We have here six vibrating segments, separated from each other by their appropriate nodal lines, Fig. 72, B. Again I damp a point, and agitate another nearer to the damped one than in the last instance; the disk divides itself into eight vibrating segments with lines of sand between them, Fig. 72, C. In this way the disk may be subdivided into ten, twelve, fourteen, sixteen sectors, the number of sectors being always an even one. As the division becomes more minute the vibrations become more rapid, and the pitch consequently more high. The note emitted by the sixteen segments into which the disk is now divided is so acute as to be almost painful to the ear. Here you have Chladni’s first discovery. You can understand his emotion on witnessing this wonderful effect, “which no mortal had previously seen.” By rendering the centre of the disk free, and damping appropriate points of the surface, nodal circles and other curved lines may be obtained.

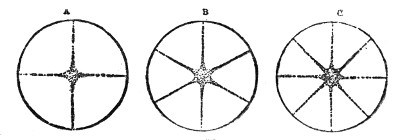
Fig. 72.

The rate of vibration of a disk is directly proportional to its thickness, and inversely proportional to the square of its diameter. Of these three disks two have the same diameter, but one is twice as thick as the other; two of them are of the same thickness, but one has half the diameter of the other. According to the law just enunciated, the rules of vibration of the disks are as the numbers 1, 2, 4. When they are sounded in succession, the musical ears present can testify that they really stand to each other in the relation of a note, its octave, and its double octave.

§ 10. Strehlke and Faraday’s Experiments: Deportment of Light Powders

The actual movement of the sand toward the nodal lines may be studied by clogging the sand with a semi-fluid substance. When gum is employed to retard the motion of the particles, the curves which they individually describe are very clearly drawn upon the plates. M. Strehlke has sketched these appearances, and from him the patterns A, B, C, Fig. 73, are borrowed.

Fig. 73.

Fig. 74.

Fig. 75.

Fig. 76.

An effect of vibrating plates which long perplexed experimenters is here to be noticed. When with the sand strewed over a plate a little fine dust is mingled, say the fine seed of lycopodium, this light substance, instead of collecting along the nodal lines, forms little heaps at the places of most violent motion. It is heaped at the four corners of the plate, Fig. 74, at the four sides of the plate, Fig. 75, and lodged between the nodal lines of the plate, Fig. 76. These three figures represent the three states of vibration illustrated in Figs. 64, 65, and 66. The dust chooses in all cases the place of greatest agitation. Various explanations of this effect had been given, but it was reserved for Faraday to assign its extremely simple cause. The light powder is entangled by the little whirlwinds of air produced by the vibrations of the plate: it cannot escape from the little cyclones, though the heavier sand particles are readily driven through them. When, therefore, the motion ceases, the light powder settles down at the places where the vibration was a maximum. In vacuo no such effect is observed: here all powders, light and heavy, move to the nodal lines.

§ 11. Vibration of Bells: Means of rendering them visible

The vibrating segments and nodes of a bell are similar to those of a disk. When a bell sounds its deepest note, the coalescence of its pulses causes it to divide into four vibrating segments, separated from each other by four nodal lines, which run up from the sound-bow to the

Fig. 77. crown of the bell. The place where the hammer strikes is always the middle of a vibrating segment; the point diametrically opposite is also the middle of such a segment. Ninety degrees from these points, we have also vibrating segments, while at 45 degrees right and left of them we come upon the nodal lines. Supposing the strong, dark circle in Fig. 77 to represent the circumference of the bell in a state of quiescence, then when the hammer falls on any one of the segments a, c, b, or d, the sound-bow passes periodically through the changes indicated by the dotted lines. At one moment it is an oval, with a b for its longest diameter; at the next moment it is an oval, with c d for its longest diameter. The changes from one oval to the other constitute, in fact, the vibrations of the bell. The four points n, n, n, n, where the two ovals intersect each other, are the nodes. As in the case of a disk, the number of vibrations executed by a bell in a given time varies directly as the thickness, and inversely as the square of the bell’s diameter.

Like a disk, also, a bell can divide itself into any even number of vibrating segments, but not into an odd number. By damping proper points in succession the bell can be caused to divide into 6, 8, 10, and 12 vibrating parts. Beginning with the fundamental note, the number of vibrations corresponding to the respective divisions of a bell, as of a disk, is as follows:

Number of divisions

 

4, 6, 8, 10, 12

Numbers the squares of which express the

}

2, 3, 4, 5, 6

   rates of vibration

Thus, if the vibrations of the fundamental tone be 40, that of the next higher tone will be 90, the next 160, the next 250, the next 360, and so on. If the bell be thin, the tendency to subdivision is so great that it is almost impossible to bring out the pure fundamental tone without the admixture of the higher ones.

I will now repeat before you a homely, but an instructive experiment. This common jug, when a fiddle-bow is drawn across its edge, divides into four vibrating segments exactly like a bell. The jug is provided with a handle; and you are to notice the influence of this handle upon the tone. When the fiddle-bow is drawn across the edge at a point diametrically opposite to the handle, a certain note is heard. When it is drawn at a point 90° from the handle, the same note is heard. In both these cases the handle occupies the middle of a vibrating segment, loading that segment by its weight. But I now draw the bow at an angular distance of 45° from the handle; the note is sensibly higher than before. The handle in this experiment occupies a node; it no longer loads a vibrating segment, and hence the elastic force, having to cope with less weight, produces a more rapid vibration. Chladni executed with a teacup the experiment here made with a jug. Now bells often exhibit round their sound-bows an absence of uniform thickness tantamount to the want of symmetry in the case of our jug; and we shall learn subsequently that the intermittent sound of many bells, noticed more particularly when their tones are dying out, is produced by the combination of two distinct rates of vibration, which have this absence of uniformity for their origin.

There are no points of absolute rest in a vibrating bell, for the nodes of the higher tones are not those of the fundamental one. But it is easy to show that the various parts of the sound-bow, when the fundamental tone is predominant, vibrate with very different degrees of intensity. Suspending a little ball of sealing-wax a, Fig. 78 (next page), by a string, and allowing it to rest gently against the interior surface of an inverted bell, it is tossed to and fro when the bell is thrown into vibration. But the rattling of the sealing-wax ball is far more violent when it rests against the vibrating segments than when it rests against the nodes. Permitting the ivory bob of a short pendulum to rest in succession against a vibrating segment and against a node of the “Great Bell” of Westminster, I found that in the former position it was driven away five inches, in the latter only two inches and three-quarters, when the hammer fell upon the bell.

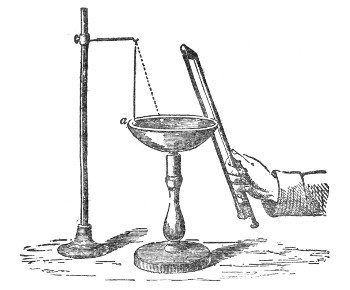
Fig. 78.

Could the “Great Bell” be turned upside down and filled with water, on striking it the vibrations would express themselves in beautiful ripples upon the liquid surface. Similar ripples may be obtained with smaller bells, or even with finger and claret glasses, but they would be too minute for our present purpose. Filling a large hemispherical glass with water, and passing the fiddle-bow across its edge, large crispations immediately cover its surface. When the bow is vigorously drawn, the water rises in spray from the four vibrating segments. Projecting, by means of a lens, a magnified image of the illuminated water-surface upon the screen, pass the bow gently across the edge of the glass, or rub the finger gently along the edge. You hear this low sound, and at the same time observe the ripples breaking, as it were, in visible music over the four sectors of the figure.

You know the experiment of Leidenfrost which proves that, if water be poured into a red-hot silver basin, it rolls about upon its own vapor. The same effect is produced if we drop a volatile liquid, like ether, on the surface of warm water. And, if a bell-glass be filled with ether or with alcohol, a sharp sweep of the bow over the edge of the glass detaches the liquid spherules, which, when they fall back, do not mix with the liquid, but are driven over the surface on wheels of vapor to the nodal lines. The warming of the liquid, as might be expected, improves the effect. M. Melde, to whom we are indebted for this beautiful experiment, has given the drawings, Figs. 79 and 80, representing what occurs when the surface is divided into four and into six vibrating parts. With a thin wineglass and strong brandy the effect may also be obtained.43

Fig. 79.

Fig. 80.

The glass and the liquid within it vibrate here together, and everything that interferes with the perfect continuity of the entire mass disturbs the sonorous effect. A crack in the glass passing from the edge downward extinguishes its sounding power. A rupture in the continuity of the liquid has the same effect. When a glass containing a solution of carbonate of soda is struck with a bit of wood, you hear a clear musical sound. But when a little tartaric acid is added to the liquid, it foams, and a dry, unmusical collision takes the place of the musical sound. As the foam disappears, the sonorous power returns, and now that the liquid is once more clear, you hear the musical ring as before.

Fig. 81.

The ripples of the tide leave their impressions upon the sand over which they pass. The ripples produced by sonorous vibrations have been proved by Faraday competent to do the same. Attaching a plate of glass to a long flexible board, and pouring a thin layer of water over the surface of the glass, on causing the board to vibrate its tremors chase the water into a beautiful mosaic of ripples. A thin stratum of sand strewed upon the plate is acted upon by the water, and carved into patterns, of which Fig. 81 is a reduced specimen.

SUMMARY OF CHAPTER IV

A rod fixed at both ends and caused to vibrate transversely divides itself in the same manner as a string vibrating transversely.

But the succession of its overtones is not the same as those of a string, for while the series of tones emitted by the string is expressed by the natural numbers 1, 2, 3, 4, 5, etc., the series of tones emitted by the rod is expressed by the squares of the odd numbers 3, 5, 7, 9, etc.

A rod fixed at one end can also vibrate as a whole, or can divide itself into vibrating segments separated from each other by nodes.

In this case the rate of vibration of the fundamental tone is to that of the first overtone as 4:25, or as the square of 2 to the square of 5. From the first division onward the rates of vibration are proportional to the squares of the odd numbers 3, 5, 7, 9, etc.

With rods of different lengths the rate of vibration is inversely proportional to the square of the length of the rod.

Attaching a glass bead silvered within to the free end of the rod, and illuminating the bead, the spot of light reflected from it describes curves of various forms when the rod vibrates. The kaleidophone of Wheatstone is thus constructed.

The iron fiddle and the musical box are instruments whose tones are produced by rods, or tongues, fixed at one end and free at the other.

A rod free at both ends can also be rendered a source of sonorous vibrations. In its simplest mode of division it has two nodes, the subsequent overtones correspond to divisions by 3, 4, 5, etc., nodes. Beginning with its first mode of division, the tones of such a rod are represented by the squares of the odd numbers 3, 5, 7, 9, etc.

The claque-bois, straw-fiddle, and glass harmonica are instruments whose tones are those of rods or bars free at both ends, and supported at their nodes.

When a straight bar, free at both ends, is gradually bent at its centre, the two nodes corresponding to its fundamental tone gradually approach each other. It finally assumes the shape of a timing-fork which, when it sounds its fundamental note, is divided by two nodes near the base of its two prongs into three vibrating parts.

There is no division of a tuning-fork by three nodes.

In its second mode of division, which corresponds to the first overtone of the fork, there is a node on each prong and two others at the bottom of the fork.

The fundamental tone of the fork is to its first overtone approximately as the square of 2 is to the square of 5. The vibrations of the first overtone are, therefore, about 6-1/4 times as rapid as those of the fundamental. From the first overtone onward the successive rates of vibration are as the squares of the odd numbers 3, 5, 7, 9, etc.

We are indebted to Chladni for the experimental investigation of all these points. He was enabled to conduct his inquiries by means of the discovery that, when sand is scattered over a vibrating surface, it is driven from the vibrating portions of the surface, and collects along the nodal lines.

Chladni embraced in his investigations plates of various forms. A square plate, for example, clamped at the centre, and caused to emit its fundamental tone, divides itself into four smaller squares by lines parallel to its sides.

The same plate can divide itself into four triangular vibrating parts, the nodal lines coinciding with the diagonals. The note produced in this case is a fifth above the fundamental note of the plate.

The plate may be further subdivided, sand-figures of extreme beauty being produced; the notes rise in pitch as the subdivision of the plate becomes more minute.

These figures may be deduced from the coalescence of different systems of vibration.

When a circular plate clamped at its centre sounds its fundamental tone, it divides into four vibrating parts, separated by four radial nodal lines.

The next note of the plate corresponds to a division into six vibrating sectors, the next note to a division into eight sectors; such a plate can divide into any even number of vibrating sectors, the sand-figures assuming beautiful stellar forms.

The rates of vibration corresponding to the divisions of a disk are represented by the squares of the numbers 2, 3, 4, 5, 6, etc. In other words, the rates of vibration are proportional to the squares of the numbers representing the sectors into which the disk is divided.

When a bell sounds its deepest note it is divided into four vibrating parts separated from each other by nodal lines, which run upward from the sound-bow and cross each other at the crown.

It is capable of the same subdivisions as a disk; the succession of its tones being also the same.

The rate of vibration of a disk or bell is directly proportional to the thickness and inversely proportional to the square of the diameter.

CHAPTER V

Longitudinal Vibrations of a Wire—Relative Velocities of Sound in Brass and Iron—Longitudinal Vibrations of Rods fixed at One End—Of Rods free at Both Ends—Divisions and Overtones of Rods vibrating longitudinally—Examination of Vibrating Bars by Polarized Light—Determination of Velocity of Sound in Solids—Resonance—Vibrations of Stopped Pipes: their Divisions and Overtones—Relation of the Tones of Stopped Pipes to those of Open Pipes—Condition of Column of Air within a Sounding Organ-Pipe—Reeds and Reed-Pipes—The Voice—Overtones of the Vocal Chords—The Vowel Sounds—Kundt’s Experiments—New Methods of determining the Velocity of Sound

§ 1. Longitudinal Vibrations of Wires and Rods: Conversion of Longitudinal into Transverse Vibrations

WE HAVE thus far occupied ourselves exclusively with transversal vibrations; that is to say, vibrations executed at right angles to the lengths of the strings, rods, plates, and bells subjected to examination. A string is also capable of vibrating in the direction of its length, but here the power which enables it to vibrate is not a tension applied externally, but the elastic force of its own molecules. Now this molecular elasticity is much greater than any that we can ordinarily develop by stretching the string, and the consequence is that the sounds produced by the longitudinal vibrations of a string are, as a general rule, much more acute than those produced by its transverse vibrations. These longitudinal vibrations may be excited by the oblique passage of a fiddle-bow; but they are more easily produced by passing briskly along the string a bit of cloth or leather on which powdered resin has been strewed. The resined fingers answer the same purpose.

When the wire of our monochord is plucked aside, you hear the sound produced by its transverse vibrations. When resined leather is rubbed along the wire, a note much more piercing than the last is heard. This is due to the longitudinal vibrations of the wire. Behind the table is stretched a stout iron wire 23 feet long. One end of it is firmly attached to an immovable wooden tray, the other end is coiled round a pin fixed firmly into one of our benches. With a key this pin can be turned, and the wire stretched so as to facilitate the passage of the rubber. Clasping the wire with the resined leather, and passing the hand to and fro along it, a rich, loud musical sound is heard. Halving the wire at its centre, and rubbing one of its halves, the note heard is the octave of the last: the vibrations are twice as rapid. When the wire is clipped at one-third of its length and the shorter segment rubbed, the note is a fifth above the octave. Taking one-fourth of its length and rubbing as before, the note yielded is the double octave of that of the whole wire, being produced by four times the number of vibrations. Thus, in longitudinal as well as in transverse vibrations, the number of vibrations executed in a given time is inversely proportional to the length of the wire.

And notice the surprising power of these sounds when the wire is rubbed vigorously. With a shorter length, the note is so acute, and at the same time so powerful, as to be hardly bearable. It is not the wire itself which produces this intense sound; it is the wooden tray at its end to which its vibrations are communicated. And, the vibrations of the wire being longitudinal, those of the tray, which is at right angles to the wire, must be transversal. We have here, indeed, an instructive example of the conversion of longitudinal into transverse vibrations.

§ 2. Longitudinal Pulses in Iron and Brass: their Relative Velocities determined

Causing the wire to vibrate again longitudinally through its entire length, my assistant shall at the same time turn the key at the end, thus changing the tension. You notice no variation of the note. The longitudinal vibrations of the wire, unlike the transverse ones, are independent of the tension. Beside the iron wire is stretched a second, of brass, of the same length and thickness. I rub them both. Their tones are not the same; that of the iron wire is considerably the higher of the two. Why? Simply because the velocity of the sound-pulse is greater in iron than in brass. The pulses in this case pass to and fro from end to end of the wire. At one moment the wire pushes the tray at its end; at the next moment it pulls the tray, this pushing and pulling being due to the passage of the pulse to and fro along the whole wire. The time required for a pulse to run from one end to the other and back is that of a complete vibration. In that time the wire imparts one push and one pull to the wooden tray at its end; the wooden tray imparts one complete vibration to the air, and the air bends once in and once out the tympanic membrane. It is manifest that the rapidity of vibration, or, in other words, the pitch of the note, depends upon the velocity with which the sound-pulse is transmitted through the wire.

And now the solution of a beautiful problem falls of itself into our hands. By shortening the brass wire we cause it to emit a note of the same pitch as that emitted by the other. You hear both notes now sounding in unison, and the reason is that the sound-pulse travels through these 23 feet of iron wire, and through these 15 feet 6 inches of brass wire, in the same time. These lengths are in the ratio of 11:17, and these two numbers express the relative velocities of sound in brass and iron. In fact, the former velocity is 11,000 feet, and the latter 17,000 feet a second. The same method is of course applicable to many other metals.

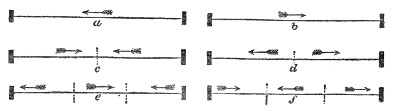
Fig. 82.

When a wire or string, vibrating longitudinally, emits its lowest note, there is no node whatever upon it; the pulse, as just stated, runs to and fro along the whole length. But, like a string vibrating transversely, it can also subdivide itself into ventral segments separated by nodes. By damping the centre of the wire we make that point a node. The pulses here run from both ends, meet in the centre, recoil from each other, and return to the ends, where they are reflected as before. The note produced is the octave of the fundamental note. The next higher note corresponds to the division of the wire into three vibrating segments, separated from each other by two nodes. The first of these three modes of vibration is shown in Fig. 82, a and b; the second at c and d; the third at e and f; the nodes being marked by dotted transverse lines, and the arrows in each case pointing out the direction in which the pulse moves. The rates of vibration follow the order of the numbers 1, 2, 3, 4, 5, etc., just as in the case of a wire vibrating transversely.

A rod or bar of wood or metal, with its two ends fixed, and vibrating longitudinally, divides itself in the same manner as the wire. The succession of tones is also the same in both cases.

§ 3. Longitudinal Vibrations of Rods fixed at One End: Musical Instruments formed on this Principle

Rods and bars with one end fixed are also capable of vibrating longitudinally. A smooth wooden or metal rod, for example, with one of its ends fixed in a vise, yields a musical note, when the resined fingers are passed along it. When such a note yields its lowest note, it simply elongates and shortens in quick alternation; there is, then, no node upon the rod. The pitch of the note is

Fig. 83. inversely proportional to the length of the rod. This follows necessarily from the fact that the time of a complete vibration is the time required for the sonorous pulse to run twice to and fro over the rod. The first overtone of a rod, fixed at one end, corresponds to its division by a node at a point one-third of its length from its free end. Its second overtone corresponds to a division by two nodes, the highest of which is at a point one-fifth of the length of the rod from its free end, the remainder of the rod being divided into two equal parts by the second node. In Fig. 83, a and b, c and d, e and f, are shown the conditions of the rod answering to its first three modes of vibration: the nodes, Fig. 84. as before, are marked by dotted lines, the arrows in the respective cases marking the direction of the pulses.

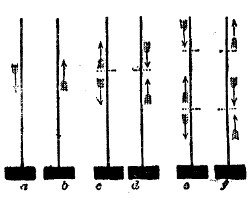
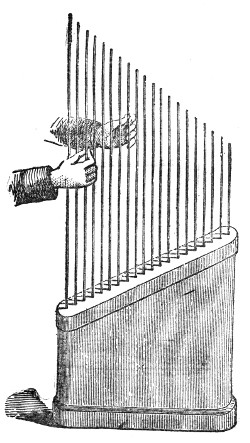
The order of the tones of a rod fixed at one end and vibrating longitudinally is that of the odd numbers 1, 3, 5, 7, etc. It is easy to see that this must be the case. For the time of vibration of c or d is that of the segment above the dotted line: and the length of this segment being only one-third that of the whole rod, its vibrations must be three times as rapid. The time of vibration in e or f is also that of its highest segment, and as this segment is one-fifth of the length of the whole rod, its vibrations must be five times as rapid. Thus the order of the tones must be that of the odd numbers.

Before you, Fig. 84, is a musical instrument, the sounds of which are due to the longitudinal vibrations of a number of deal rods of different lengths. Passing the resined fingers over the rods in succession, a series of notes of varying pitch is obtained. An expert performer might render the tones of this instrument very pleasant to you.

§ 4. Vibrations of Rods free at Both Ends

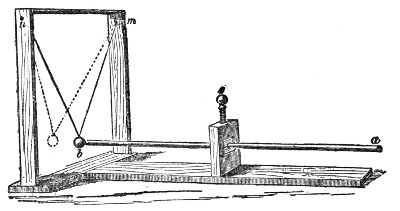
Fig. 85.

Rods with both ends free are also capable of vibrating longitudinally, and producing musical tones. The investigation of this subject will lead us to exceedingly important results. Clasping a long glass tube exactly at its centre, and passing a wetted cloth over one of its halves, a clear musical sound is the result. A solid glass rod of the same length would yield the same note. In this case the centre of the tube is a node, and the two halves elongate and shorten in quick alternation. M. König, of Paris, has provided us with an instrument which will illustrate this action. A rod of brass, a b, Fig. 85, is held at its centre by the clamp s, while an ivory ball, suspended by two strings from the points, m and n, of a wooden frame, is caused to rest against the end, b, of the brass rod. Drawing gently a bit of resined leather over the rod near a, it is thrown into longitudinal vibration. The centre, s, is a node; but the uneasiness of the ivory ball shows you that the end, b, is in a state of tremor. I apply the rubber still more briskly. The ball, b, rattles, and now the vibration is so intense that the ball is rejected with violence whenever it comes into contact with the end of the rod.

§ 5. Fracture of Glass Tube by Sonorous Vibrations

When the wetted cloth is passed over the surface of a glass tube the film of liquid left behind by the cloth is seen forming narrow tremulous rings all along the rod. Now this shivering of the liquid is due to the shivering of the glass underneath it, and it is possible so to augment the intensity of the vibration that the glass shall actually go to pieces. Savart was the first to show this. Twice in this place I have repeated this experiment, sacrificing in each case a fine glass tube 6 feet long and 2 inches in diameter. Seizing the tube at its centre C, Fig. 86, I swept my hand vigorously to and fro along C D, until finally the half most distant from my hand was shivered into annular fragments. On examining these it was found that, narrow as they were, many of them were marked by circular cracks indicating a still more minute subdivision.

In this case also the rapidity of vibration is inversely proportional to the length of the rod. A rod of half the length vibrates longitudinally with double the rapidity, a rod of one-third the length with treble the rapidity, and so on. The time of a complete vibration being that required by the pulse to travel to and fro over the rod, and that time being directly proportional to the length of the rod, the rapidity of vibration must, of necessity, be in the inverse proportion.

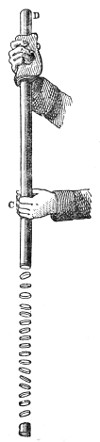
Fig. 86.

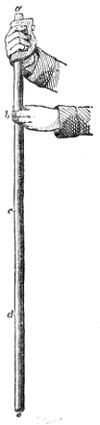
Fig. 87.

This division of a rod by a single node at its centre corresponds to the deepest tone produced by its longitudinal vibration. But, as in all other cases hitherto examined, such rods can subdivide themselves further. Holding the long glass rod a e, Fig. 87, at a point b, midway between its centre and one of its ends, and rubbing its short section, a b, with a wet cloth, the point b becomes a node, a second node, d, being formed at the same distance from the opposite end of the rod. Thus we have the rod divided into three vibrating parts, consisting of one whole ventral segment, b d, and two half ones, a b and d e. The sound corresponding to this division of the rod is the octave of its fundamental note.

You have now a means of checking me. For, if the second mode of division just described produces the octave of the fundamental note, and if a rod of half the length produces the same octave, then the whole rod held at a point one-fourth of its length from one of its ends ought to emit the same note as the half rod held in the middle. When both notes are sounded together they are heard to be identical in pitch.

Fig. 88.

Fig. 88, a and b, c and d, e and f, shows the three first divisions of a rod free at both ends and vibrating longitudinally. The nodes, as before, are marked by transverse dots, the direction of the pulses being shown by arrows. The order of the tones is that of the numbers, 1, 3, 4, etc.

§ 6. Action of Sonorous Vibrations on Polarized Light

When a tube or rod vibrating longitudinally yields its fundamental tone, its two ends are in a state of free vibration, the glass there suffering neither strain nor pressure. The case at the centre is exactly the reverse; here there is no vibration, but a quick alternation of tension and compression. When the sonorous pulses meet at the centre they squeeze the glass; when they recoil they strain it. Thus while at the ends we have the maximum of vibration, but no change of density, at the centre we have the maximum changes of density, but no vibration.

We have now cleared the way for the introduction of a very beautiful experiment made many years ago by Biot, but never, to my knowledge, repeated on the scale here presented to you. The beam from our electric lamp, L, Fig. 89, being sent through a prism, B, of bi-refracting spar, a beam of polarized light is obtained. This beam impinges on a second prism of spar, n, but, though both prisms are perfectly transparent, the light which has passed through the first cannot get through the second. By introducing a piece of glass between the two prisms, and subjecting the glass to either strain or pressure, the light is enabled to pass through the entire system.

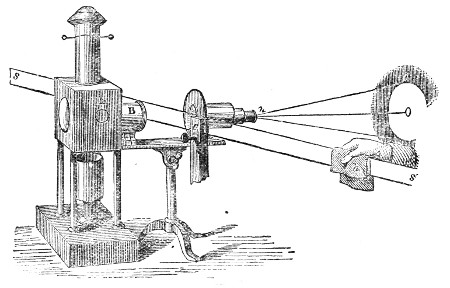
Fig. 89.

I now introduce between the prisms B and n a rectangle, s s′, of plate glass, 6 feet long, 2 inches wide, and one-third of an inch thick, which is to be thrown into longitudinal vibration. The beam from L passes through the glass at a point near its centre, which is held in a vise, c, so that when a wet cloth is passed over one of the halves, c s′, of the strip, the centre will be a node. During its longitudinal vibration the glass near the centre is, as already explained, alternately strained and compressed; and this successive strain and pressure so changes the condition of the light as to enable it to pass through the second prism. The screen is now dark; but on passing the wetted cloth briskly over the glass a brilliant disk of light, three feet in diameter, flashes out upon the screen. The vibration quickly subsides, and the luminous disk as quickly disappears, to be, however, revived at will by the passage of the wetted cloth along the glass.

The light of this disk appears to be continuous, but it is really intermittent, for it is only when the glass is under strain or pressure that the light can get through. In passing from strain to pressure, and from pressure to strain, the glass is for a moment in its natural state, which, if it continued, would leave the screen dark. But the impressions of brightness, due to the strains and pressures, remain far longer upon the retina than is necessary to abolish the intervals of darkness; hence the screen appears illuminated by a continuous light. When the glass rectangle is shifted so as to cause the beam of polarized light to pass through it close to its end, s, the longitudinal vibrations of the glass have no effect whatever upon the polarized beam.

Thus, by means of this subtile investigator, we demonstrate that, while the centre of the glass, where the vibration is nil, is subjected to quick alternations of strain and pressure, the ends of the rectangle, where the vibration is a maximum, suffer neither.44

§ 7. Vibrations of Rods of Wood: Determination of Relative Velocities in Different Woods

Rods of wood and metal also yield musical tones when they vibrate longitudinally. Here, however, the rubber employed is not a wet cloth, but a piece of leather covered with powdered resin. The resined fingers also elicit the music of the rods. The modes of vibration here are those already indicated, the pitch, however, varying with the velocity of the sonorous pulse in the respective substances. When two rods of the same length, the one of deal, the other of Spanish mahogany, are sounded together, the pitch of the one is much lower than that of the other. Why? Simply because the sonorous pulses pass more slowly through the mahogany than through the deal. Can we find the relative velocity of sound through both? With the greatest ease. We have only to carefully shorten the mahogany rod till it yields the same note as the deal one. The notes, rendered approximate by the first trials, are now identical. Through this rod of mahogany 4 feet long, and through this rod of deal 6 feet long, the sound-pulse passes in the same time, and these numbers express the relative velocities of sound through the two substances.

Modes of investigation, which could only be hinted at in our earlier lectures, are now falling naturally into our hands. When in the first lecture the velocity of sound in air was spoken of, many possible methods of determining this velocity must have occurred to your minds, because here we have miles of space to operate upon. Its velocity through wood or metal, where such distances are out of the question, is determined in the simple manner just indicated. From the notes which they emit when suitably prepared, we may infer with certainty the relative velocities of sound through different solid substances; and determining the ratio of the velocity in any one of them to its velocity in air, we are able to draw up a table of absolute velocities. But how is air to be introduced into the series? We shall soon be able to answer this question, approaching it, however, through a number of phenomena with which, at first sight, it appears to have no connection.

RESONANCE

§ 8. Experiments with Resonant Jars. Analysis and Explanation

The series of tuning-forks now before you have had their rates of vibration determined by the siren. One, you will remember, vibrates 256 times in a second, the length of its sonorous wave being 4 feet 4 inches. It is detached from its case, so that when struck against a pad you hardly hear it. When held over this glass jar, A B, Fig. 90, 18 inches deep, you still fail to hear the sound of the fork. Preserving the fork in its position, I pour water with the least possible noise into the jar. The column of air underneath the fork shortens, the sound augments in intensity, and when the water has reached a certain level it bursts forth with extraordinary power. A greater quantity of water causes the sound to sink, and become finally inaudible, as at first. By pouring the water carefully out, a point is reached where the reinforcement of the sound again occurs. Experimenting thus, we learn that there is one particular length of the column of air which, when the fork is placed above it, produces a maximum augmentation of the sound. This reinforcement of the sound is named resonance.

Operating in the same way with all the forks in succession, a column of air is found for each, which yields a maximum resonance. These columns become shorter as the rapidity of vibration increases. In Fig. 91 the series

Fig. 90. of jars is represented, the number of vibrations to which each resounds being placed above it.

What is the physical meaning of this very wonderful effect? To solve this question we must revive our knowledge of the relation of the motion of the fork itself to the motion of the sonorous wave produced by the fork. Supposing a prong of this fork, which executes 256 vibrations in a second, to vibrate between the points a and b, Fig. 92, in its motion from a to b the fork generates half a sonorous wave, and

Fig. 91. as the length of the whole wave emitted by this fork is 4 feet 4 inches, at the moment the prong reaches b the foremost point of the sonorous wave will be at C, 2 feet 2 inches distant from the fork. The motion of the wave, then, is vastly greater than that of the fork. In fact, the distance a b is, in this case, not more than one-twentieth of an inch, while the wave has passed over a distance of 26 inches. With forks of lower pitch the difference would be still greater.

Fig. 92.

Our next question is, what is the length of the column of air which resounds to this fork? By measurement with a two-foot rule it is found to be 13 inches. But the length of the wave emitted by the fork is 52 inches; hence the length of the column of air which resounds to the fork is equal to one-fourth of the length of the sound-wave produced by the fork. This rule is general, and might be illustrated by any other of the forks instead of this one.

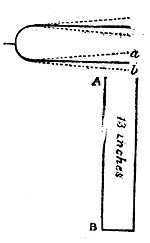
Fig. 93.

Let the prong, vibrating between the limits a and b, be placed over its resonant jar, A B, Fig. 93. In the time required by the prong to move from a to b, the condensation it produces runs down to the bottom of the jar, is there reflected, and, as the distance to the bottom and back is 26 inches, the reflected wave will reach the fork at the moment when it is on the point of returning from b to a. The rarefaction of the wave is produced by the retreat of the prong from b to a. This rarefaction will also run to the bottom of the jar and back, overtaking the prong just as it reaches the limit, a, of its excursion. It is plain from this analysis that the vibrations of the fork are perfectly synchronous with the vibrations of the aërial column A B; and in virtue of this synchronism the motion accumulates in the jar, spreads abroad in the room, and produces this vast augmentation of the sound.

When we substitute for the air in one of these jars a gas of different elasticity, we find the length of the resounding column to be different. The velocity of sound through coal-gas is to its velocity in air about as 8:5. Hence, to synchronize with our fork, a jar filled with coal-gas must be deeper than one filled with air. I turn this jar, 18 inches long, upside down, and hold close to its open mouth our agitated tuning-fork. It is scarcely audible. The jar, with air in it, is 5 inches too deep for this fork. Let coal-gas now enter the jar. As it ascends the note at a certain point swells out, proving that for the more elastic gas a depth of 18 inches is not too great. In fact, it is not great enough; for if too much gas be allowed to enter the jar the resonance is weakened. By suddenly turning the jar upright, still holding the fork close to its mouth, the gas escapes, and at the point of proper admixture of gas and air the note swells out again.45

§ 9. Reinforcement of Bell by Resonance

This fine, sonorous bell, Fig. 94, is thrown into intense vibration by the passage of a resined bow across its edge. You hear its sound, pure, but not very forcible. When, however, the open mouth of this large tube, which is closed at one end, is brought close to one of the vibrating segments of the bell, the tone swells into a musical roar. As the tube is alternately withdrawn and advanced, the sound sinks and swells in this extraordinary manner.

Fig. 94.

The second tube, open at both ends, is capable of being lengthened and shortened by a telescopic slider. When brought near the vibrating bell, the resonance is feeble. On lengthening the tube by drawing out the slider at a certain point, the tone swells out as before. If the tube be made longer, the resonance is again enfeebled. Note the fact, which shall be explained presently, that the open tube which gives the maximum resonance is exactly twice the length of the closed one. For these fine experiments we are indebted to Savart.

§ 10. Expenditure of Motion in Resonance

With the India-rubber tube employed in our third chapter it was found necessary to time the impulses properly, so as to produce the various ventral segments. I could then feel that the muscular work performed, when the impulses were properly timed, was greater than when they were irregular. The same truth may be illustrated by a claret-glass half filled with water. Endeavor to move your hand to and fro, in accordance with the oscillating period of the water: when you have thoroughly established synchronism, the work thrown upon the hand apparently augments the weight of the water. So likewise with our tuning-fork; when its impulses are timed to the vibrations of the column of air contained in this jar, its work is greater than when they are not so timed. As a consequence of this the tuning-fork comes sooner to rest when it is placed over the jar than when it is permitted to vibrate either in free air, or over a jar of a depth unsuited to its periods of vibration.46

Reflecting on what we have now learned, you would have little difficulty in solving the following beautiful problem: You are provided with a tuning-fork and a siren, and are required by means of these two instruments to determine the velocity of sound in air. To solve this problem you lack, if anything, the mere power of manipulation which practice imparts. You would first determine, by means of the siren, the number of vibrations executed by the tuning-fork in a second; you would then determine the length of the column of air which resounds to the fork. This length multiplied by 4 would give you, approximately, the wave-length of the fork, and the wave-length multiplied by the number of vibrations in a second would give you the velocity in a second. Without quitting your private room, therefore, you could solve this important problem. We will go on, if you please, in this fashion, making our footing sure as we advance.

§ 11. Resonators of Helmholtz

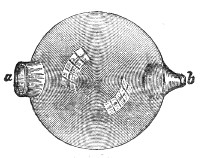
Fig. 94a.

Helmholtz has availed himself of the principle of resonance in analyzing composite sounds. He employs little hollow spheres, called resonators, one of which is shown in Fig. 94a. The small projection b, which has an orifice, is placed in the ear, while the sound-waves enter the hollow sphere through the wide aperture at a. Reinforced by the resonance of such a cavity, and rendered thereby more powerful than its companions, a particular note of a composite clang may be in a measure isolated and studied alone.

ORGAN-PIPES

§ 12. Principles of Resonance applied to Organ-Pipes

Thus disciplined we are prepared to consider the subject of organ-pipes, which is one of great importance. Before me on the table are two resonant jars, and in my right hand and my left are held two tuning-forks. I agitate both, and hold them over this jar. One of them only is heard. Held over the other jar, the other fork alone is heard. Each jar selects that fork whose periods of vibration synchronize with its own. And instead of two forks suppose several of them to be held over the jar; from the confused assemblage of pulses thus generated, the jar would select and reinforce that one which corresponds to its own period of vibration.

When I blow across the open mouth of the jar, or, better still, for the jar is too wide for this experiment, when I blow across the open end of a glass tube, t u, Fig. 95, of the same length as the jar, a fluttering of the air is thereby produced, an assemblage of pulses at the open mouth of the tube being generated. And what is the consequence? The tube selects that pulse of the flutter which is in synchronism with itself, and raises it to a musical sound. The sound, you perceive, is precisely that obtained when the proper tuning-fork is placed over the tube. The column of air within the tube has, in this case, virtually created its own tuning-fork; for by the reaction of its pulses upon the sheet of air issuing from the lips it has compelled that sheet to vibrate in synchronism with itself, and made it thus act the part of the tuning-fork.

Fig. 95.

Selecting for each of the other tuning-forks a resonant tube, in every case, on blowing across the open end of the tube, a tone is produced identical in pitch with that obtained through resonance.

When different tubes are compared, the rate of vibration is found to be inversely proportional to the length of the tube. These three tubes are 24, 12, and 6 inches long, respectively. I blow gently across the 24-inch tube, and bring out its fundamental note; similarly treated, the 12-inch tube yields the octave of the note of the 24-inch. In like manner the 6-inch tube yields the octave of the 12-inch. It is plain that this must be the case; for, the rate of vibration depending on the distance which the pulse has to travel to complete a vibration, if in one case this distance be twice what it is in another, the rate of vibration must be twice as slow. In general terms, the rate of vibration is inversely proportional to the length of the tube through which the pulse passes.

§ 13. Vibrations of Stopped Pipes: Modes of Division: Overtones

But that the current of air should be thus able to accommodate itself to the requirements of the tube, it must enjoy a certain amount of flexibility. A little reflection will show you that the power of the reflected pulse over the current must depend to some extent on the force of the current. A stronger current, like a more powerfully stretched string, requires a great force to deflect it, and when deflected vibrates more quickly. Accordingly, to obtain the fundamental note of this 24-inch tube, we must blow very gently across its open end; a rich, full, and forcible musical tone is then produced. With a little stronger blast the sound approaches a mere rustle; blowing stronger still, a tone is obtained of much higher pitch than the fundamental one. This is the first overtone of the tube, to produce which the column of air within it has divided itself into two vibrating parts, with a node between them. With a still stronger blast a still higher note is obtained. The tube is now divided into three vibrating parts, separated from each other by two nodes. Once more I blow with sudden strength; a higher note than any before obtained is the consequence.

In Fig. 96 are represented the divisions of the column of air corresponding to the first three notes of a tube stopped at one end. At a and b, which correspond to the fundamental note, the column is undivided; the bottom of the tube is the only node, and the pulse simply moves up and down from top to bottom, as denoted by the arrows. In c and d, which correspond to the first overtone of the tube, we have one nodal surface shown by dots at x, against which the pulses abut, and from which they are reflected as from a fixed surface. This nodal surface is situated at one-third of the length of the tube from its open end. In e and f, which correspond to the second overtone, we have two nodal surfaces, the upper one, x′, of which is at one-fifth of the length of the tube from its open end, the remaining four-fifths being divided into two equal parts by the second nodal surface. The arrows, as before, mark the directions of the pulses.

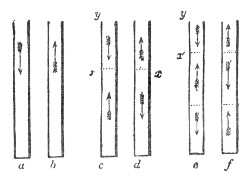
Fig. 96.

We have now to inquire into the relation of these successive notes to each other. The space from node to node has been called all through “a ventral segment”; hence the space between the middle of a ventral segment and a node is a semi-ventral segment. You will readily bear in mind the law that the number of vibrations is directly proportional to the number of semi-ventral segments into which the column of air within the tube is divided. Thus, when the fundamental note is sounded, we have but a single semi-ventral segment, as at a and b. The bottom here is a node, and the open end of the tube, where the air is agitated, is the middle of a ventral segment. The mode of division represented in c and d yields three semi-ventral segments; in e and f we have five. The vibrations, therefore, corresponding to this series of notes, augment in the proportion of the series of odd numbers 1:3:5. Could we obtain still higher notes, their relative rates of vibration would continue to be represented by the odd numbers 7, 9, 11, 13, etc.

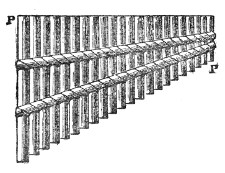
Fig. 97.

It is evident that this must be the law of succession. For the time of vibration in c or d is that of a stopped tube of the length x y; but this length is one-third of the length of the whole tube, consequently its vibrations must be three times as rapid. The time of vibration in e or f is that of a stopped tube of the length x′ y′, and inasmuch as this length is one-fifth that of the whole tube, its vibrations must be five times as rapid. We thus obtain the succession 1, 3, 5; if we pushed matters further we should obtain the continuation of the series of odd numbers.

And here it is once more in your power to subject my statements to an experimental test. Here are two tubes, one of which is three times the length of the other. I sound the fundamental note of the longest tube, and then the next note above the fundamental. The vibrations of these two notes are stated to be in the ratio of 1:3. This latter note, therefore, ought to be of precisely the same pitch as the fundamental note of the shorter of the two tubes. When both tubes are sounded their notes are identical.

It is only necessary to place a series of such tubes of different lengths thus together to form that ancient instrument, Pan’s pipes, p p′, Fig. 97 (page 223), with which we are so well acquainted.

The successive divisions, and the relation of the overtones of a rod fixed at one end (described in page 205), are plainly identical with those of a column of air in a tube stopped at one end, which we have been here considering.

§ 14. Vibrations of Open Pipes: Modes of Division: Overtones

From tubes closed at one end, and which, for the sake of brevity, may be called stopped tubes, we now pass to tubes open at both ends, which we shall call open tubes. Comparing, in the first instance, a stopped tube with an open one of the same length, we find the note of the latter an octave higher than that of the former. This result is general. To make an open tube yield the same note as a closed one, it must be twice the length of the latter. And, since the length of a closed tube sounding its fundamental note is one-fourth of the length of its sonorous wave, the length of an open tube is one-half that of the sonorous wave that it produces.

It is not easy to obtain a sustained musical note by blowing across the end of an open glass tube; but a mere puff of breath across the end reveals the pitch to the disciplined ear. In each case it is that of a closed tube half the length of the open one.

Fig. 98.

Fig. 99.

There are various ways of agitating the air at the ends of pipes and tubes, so as to throw the air-columns within them into vibration. In organ-pipes this is done by blowing a thin sheet of air against a sharp edge. You will have no difficulty in understanding the construction of an open organ-pipe, from this model, Fig. 98, one side of which has been removed so that you may see its inner parts. Through the tube t the air passes from the wind-chest into the chamber, C, which is closed at the top, save a narrow slit, e d, through which the compressed air of the chamber issues. This thin air-current breaks against the sharp edge, a b, and there produces a fluttering noise, and the proper pulse of this flutter is converted by the resonance of the pipe above into a musical sound. The open space between the edge, a b, and the slit below it is called the embouchure. Fig. 99 represents a stopped pipe of the same length as that shown in Fig. 98, and hence producing a note an octave lower.

Instead of a fluttering sheet of air, a tuning-fork whose rate of vibration synchronizes with that of the organ-pipe may be placed at the embouchure, as at a b, Fig. 100. The pipe will resound. Here, for example, are four open pipes of different lengths, and four tuning-forks of different rates of vibration. Striking the most slowly vibrating fork, and bringing it near the embouchure of the longest pipe, the pipe speaks powerfully. When blown into, the same pipe yields a tone identical with that of the tuning-fork. Going through all the pipes in succession, we find in each case that the note obtained

Fig. 100. by blowing into the pipe is exactly that produced when the proper tuning-fork is placed at the embouchure. Conceive now the four forks placed together near the same embouchure; we should have pulses of four different periods there excited; but out of the four the pipe would select only one. And if four hundred vibrating forks could be placed there instead of four, the pipe would still make the proper selection. This it also does when for the pulses of tuning-forks we substitute the assemblage of pulses created by the current of air when it strikes against the sharp upper edge of the embouchure.

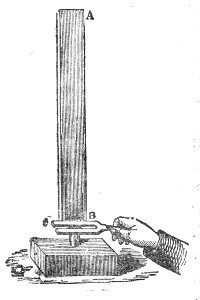
The heavy vibrating mass of the tuning-fork is practically uninfluenced by the motion of the air within the pipe. But this is not the case when air itself is the vibrating body. Here, as before explained, the pipe creates, as it were, its own tuning-fork, by compelling the fluttering stream at its embouchure to vibrate in periods answering to its own.

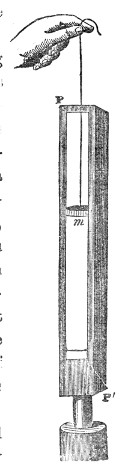
Fig. 101.

The condition of the air within an open organ-pipe, when its fundamental note is sounded, is that of a rod free at both ends, held at its centre, and caused to vibrate longitudinally. The two ends are places of vibration, the centre is a node. Is there any way of feeling the vibrating air-column so as to determine its nodes and its places of vibration? The late excellent William Hopkins has taught us the following mode of solving this problem: Over a little hoop is stretched a thin membrane, forming a little tambourine. The front of this organ-pipe, P P′, Fig. 101, is of glass, through which you can see the position of any body within it. By means of a string, the little tambourine, m, can be raised or lowered at pleasure through the entire length of the pipe. When held above the upper end of the pipe, you hear the loud buzzing of the membrane. When lowered into the pipe, it continues to buzz for a time; the sound becoming gradually feebler, and finally ceasing totally. It is now in the middle of the pipe, where it cannot vibrate, because the air around it is at rest. On lowering it still further, the buzzing sound instantly recommences, and continues down to the bottom of the pipe. Thus, as the membrane is raised and lowered in quick succession, during every descent and ascent, we have two periods of sound separated from each other by one of silence. If sand were strewed upon the membrane, it would dance above and below, but it would be quiescent at the centre. We thus prove experimentally that, when an organ-pipe sounds its fundamental note, it divides itself into two semi-ventral segments separated by a node.

Fig. 102.

What is the condition of the air at this node? Again, that of the middle of a rod, free at both ends, and yielding the fundamental note of its longitudinal vibration. The pulses reflected from both ends of the rod, or of the column of air, meet in the middle, and produce compression; they then retreat and produce rarefaction. Thus, while there is no vibration in the centre of an organ-pipe, the air there undergoes the greatest changes of density. At the two ends of the pipe, on the other hand, the air-particles merely swing up and down without sensible compression or rarefaction.

If the sounding pipe were pierced at the centre, and the orifice stopped by a membrane, the air, when condensed, would press the membrane outward, and, when rarefied, the external air would press the membrane inward. The membrane would therefore vibrate in unison with the column of air. The organ-pipe, Fig. 102, is so arranged that a small jet of gas, b, can be lighted opposite the centre of the pipe, and there acted upon by the vibrations of a membrane. Two other gas-jets, a and c, are placed nearly midway between the centre and the two ends of the pipe. The three burners, a, b, c, are fed in the following manner: through the tube, t, the gas enters the hollow chamber, e d, from which issue three little bent tubes, shown in the figure, each communicating with a capsule closed underneath by the membrane. This is in direct contact with the air of the organ-pipe. From the three capsules issue the three little burners, with their flames, a, b, c.

Blowing into the pipe so as to sound its fundamental note, the three flames are agitated, but the central one is most so. Lowering the flames so as to render them very small, and blowing again, the central flame, b, is extinguished, while the others remain lighted. The experiment may be performed half a dozen times in succession; the sounding of the fundamental note always quenches the middle flame.

By blowing more sharply into the pipe, it is caused to yield its first overtone. The middle node no longer exists. The centre of the pipe is now a place of maximum vibration, while two nodes are formed midway between the centre and the two ends. But if this be the case, and if the flame opposite the node be always blown out, then, when the first overtone of this pipe is sounded, the two flames a and c ought to be extinguished, while the central flame remains lighted. This is the case. When the first harmonic is sounded the two nodal flames are infallibly extinguished, while the flame b in the middle of the ventral segment is not sensibly disturbed.

There is no theoretic limit to the subdivision of an organ-pipe, either stopped or open. In stopped pipes we begin with 1 semi-ventral segment, and pass on to 3, 5, 7, etc., semi-ventral segments, the number of vibrations of the successive notes augmenting in the same ratio. In open pipes we begin with 2 semi-ventral segments, and pass on to 4, 6, 8, 10, etc., the number of vibrations of the successive notes augmenting in the same ratio; that is to say, in the ratio 1:2:3:4:5, etc. When, therefore, we pass from the fundamental tone to the first overtone in an open pipe, we obtain the octave of the fundamental.

Fig. 103. When we make the same passage in a stopped pipe, we obtain a note a fifth above the octave. No intermediate modes of vibration are in either case possible. If the fundamental tone of a stopped pipe be produced by 100 vibrations a second, the first overtone will be produced by 300 vibrations, the second by 500, and so on. Such a pipe, for example, cannot execute 200 or 400 vibrations in a second. In like manner the open pipe, whose fundamental note is produced by 100 vibrations a second, cannot vibrate 150 times in a second, but passes, at a jump, to 200, 300, 400, and so on.

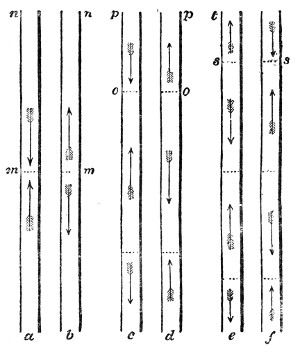
In open pipes, as in stopped ones, the number of vibrations executed in the unit of time is inversely proportional to the length of the pipe. This follows from the fact, already dwelt upon so often, that the time of a vibration is determined by the distance which the sonorous pulse has to travel to complete a vibration.

In Fig. 103, a and b (at the bottom) represent the division of an open pipe corresponding to its fundamental tone; c and d represent the division corresponding to its first, e and f the division corresponding to its second overtone, the dots marking the nodes. The distance m n is one-half, o p is one-fourth, and s t is one-sixth of the whole length of the pipe. But the pitch of a is that of a stopped pipe equal in length to m n; the pitch of c is that of a stopped pipe of the length o p; while the pitch of e is that of a stopped pipe of the length s t. Hence, as these lengths are in the ratio of 1/2:1/4:1/6, or as 1:1/2:1/3, the rates of vibration must be as the reciprocals of these, or as 3:2:1. From the mere inspection, therefore, of the respective modes of vibration, we can draw the inference that the succession of tones of an open pipe must correspond to the series of natural numbers.

The pipe a, Fig. 103, has been purposely drawn twice the length of a, Fig. 93 (p. 215). It is perfectly manifest that to complete a vibration the pulse has to pass over the same distance in both pipes, and hence that the pitch of the two pipes must be the same. The open pipe, a n, consists virtually of two stopped ones, with the central nodal surface at m as their common base. This shows the relation of a stopped pipe to an open one to be that which experiment establishes.

§ 15. Velocity of Sound in Gases, Liquids, and Solids determined by Musical Vibrations

We have already learned that the relative velocities of sound in different solid bodies may be determined from the notes which they emit when thrown into longitudinal vibration. It was remarked at the time that to draw up a table of absolute velocities we only required the accurate comparison of the velocity in any one of those solids with the velocity in air. We are now in a condition to supply this comparison. For we have learned that the vibrations of the air in an organ-pipe open at both ends are executed precisely as those of a rod free at both ends. Any difference of rapidity, therefore, between the vibrations of a rod and of an open organ-pipe of the same length must be due solely to the different velocities with which the sonorous pulses are propagated through them. Take therefore an organ-pipe of a certain length, emitting a note of a certain pitch, and find the length of a rod of pine which yields the same note. This length would be ten times that of the organ-pipe, which would prove the velocity of sound in pine to be ten times its velocity in air. But the absolute velocity in air is 1,090 feet a second; hence the absolute velocity in pine is 10,900 feet a second, which is that given in our first chapter (p. 74). To the celebrated Chladni we are indebted for this beautiful mode of determining the velocity of sound in solid bodies.

We had also in our first lecture a table of the velocities of sound in other gases than air. I am persuaded that you could tell me, after due reflection, how this table was constructed. It would only be necessary to find a series of organ-pipes which, when filled with the different gases, yield the same note; the lengths of these pipes would give the relative velocities of sound through the gases. Thus we should find the length of a pipe filled with hydrogen to be four times that of a pipe filled with oxygen, yielding the same note, and this would prove the velocity of sound in the former to be four times its velocity in the latter.

But we had also a table of velocities through various liquids. How was it constructed? By forcing the liquids through properly constructed organ-pipes, and comparing their musical tones. Thus, in water it requires a pipe a little better than four feet long to produce the note of an air-pipe one foot long; and this proves the velocity of sound in water to be somewhat more than four times its velocity in air. My object here is to give you a clear notion of the way in which scientific knowledge enables us to cope with these apparently insurmountable problems. It is not necessary to go into the niceties of these measurements. You will, however, readily comprehend that all the experiments with gases might be made with the same organ-pipe, the velocity of sound in each respective gas being immediately deduced from the pitch of its note. With a pipe of constant length the pitch, or, in other words, the number of vibrations, would be directly proportional to the velocity. Thus, comparing oxygen with hydrogen, we should find the note of the latter to be the double octave of that of the former, whence we should infer the velocity of sound in hydrogen to be four times its velocity in oxygen. The same remark applies to experiments with liquids. Here also the same pipe may be employed throughout, the velocities being inferred from the notes produced by the respective liquids.

In fact, the length of an open pipe being, as already explained, one-half the length of its sonorous wave, it is only necessary to determine, by means of the siren, the number of vibrations executed by the pipe in a second, and to multiply this number by twice the length of the pipe, in order to obtain the velocity of sound in the gas or liquid within the pipe. Thus, an open pipe 26 inches long and filled with air executes 256 vibrations in a second. The length of its sonorous wave is twice 26 inches, or 4-1/3 feet: multiplying 256 by 4-1/3 we obtain 1,120 feet per second as the velocity of sound through air of this temperature. Were the tube filled with carbonic-acid gas, its vibrations would be slower: were it filled with hydrogen, its vibrations would be quicker; and applying the same principle, we should find the velocity of sound in both these gases.

So likewise the length of a solid rod free at both ends, and sounding its fundamental note, is half that of the sonorous wave in the substance of the solid. Hence we have only to determine the rate of vibration of such a rod, and multiply it by twice the length of the rod, to obtain the velocity of sound in the substance of the rod. You can hardly fail to be impressed by the power which physical science has given us over these problems; nor will you refuse your admiration to that famous old investigator, Chladni, who taught us how to master them experimentally.

REEDS AND REED-PIPES

The construction of the siren and our experiments with that instrument are, no doubt, fresh in your recollection. Its musical sounds are produced by the cutting up into puffs of a series of air-currents. The same purpose is effected by a vibrating reed, as employed in the accordion, the concertina, and the harmonica. In these instruments it is not the vibrations of the reed itself which, imparted to the air, and transmitted through it to our organs of hearing, produce the music; the function of the reed is constructive, not generative; it molds into a series of discontinuous puffs that which without it would be a continuous current of air.

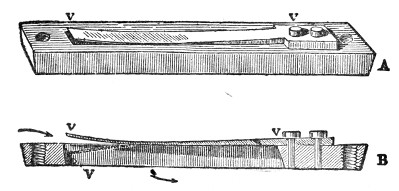
Fig. 104.

Reeds, if associated with organ-pipes, sometimes command, and are sometimes commanded by, the vibrations of the column of air. When they are stiff they rule the column; when they are flexible the column rules them. In the former case, to derive any advantage from the air-column, its length ought to be so regulated that either its fundamental tone or one of its overtones shall correspond to the rate of vibration of the reed. The metal reed commonly employed in organ-pipes is shown in Fig. 104, A and b, both in perspective and in section. It consists of a long and flexible strip of metal, V V, placed in a rectangular orifice, through which the current of air enters the pipe. The manner in which the reed and pipe are associated is shown in Fig. 105. The front, b c, of the space containing the flexible tongue is of glass, so that you may see the tongue within it. A conical pipe, A B, surmounts the reed.47 The wire w i, shown pressing

Fig. 105. against the reed, is employed to lengthen or shorten it, and thus to vary within certain limits its rate of vibration. At one time in the practice of music the reed closed the aperture by simply falling against its sides; every stroke of the reed produced a tap, and these linked themselves together to an unpleasant, screaming sound, which materially injured that of the associated organ-pipe. This was mitigated, but not removed, by permitting the reed to strike against soft leather; but the reed now employed is the free reed, which vibrates to and fro between the sides of the aperture, almost, but not quite, filling it. In this way the unpleasantness referred to is avoided. When reed and pipe synchronize perfectly, the sound is most pure and forcible; a certain latitude, however, is possible on both sides of perfect synchronism. But if the discordance be pushed too far, the pipe ceases to be of any use. We then obtain the sound due to the vibrations of the reed alone.

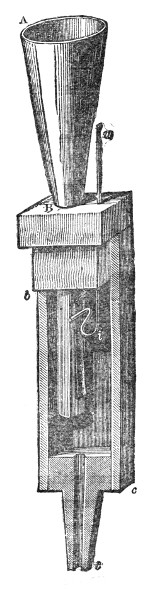
Flexible wooden reeds, which can accommodate themselves to the requirements of the pipes above them, are also employed in organ-pipes. Perhaps the simplest illustration of the action of the reed commanded by its aërial column is furnished by a common wheaten straw. At about an inch from a knot, at r, I bury my penknife in this straw, s r′, Fig. 106, to a depth of about one-fourth of the straw’s diameter, and, turning the blade flat, pass it upward toward the knot, thus raising a strip of the straw nearly an inch in length. This strip, r r′, is to be our reed, and the straw itself is to be our pipe. It is now eight inches long. When blown into, it emits this decidedly musical sound. When cut so as to make its length six inches, the pitch is higher; with a length of four inches, the pitch is higher still; and with a length of two inches, the sound is very shrill indeed. In these experiments the reed was compelled to accommodate itself throughout to the requirements of the vibrating column of air.

Fig. 106.

The clarinet is a reed-pipe. It has a single broad tongue, with which a long, cylindrical tube is associated. The reed-end of the instrument is grasped by the lips, and by their pressure the slit between the reed and its frame is narrowed to the required extent. The overtones of a clarinet are different from those of a flute. A flute is an open pipe, a clarinet a stopped one, the end at which the reed is placed answering to the closed end of the pipe. The tones of a flute follow the order of the natural numbers 1, 2, 3, 4, etc., or of the even numbers 2, 4, 6, 8, etc.; while the tones of a clarinet follow the order of the odd numbers 1, 3, 5, 7, etc. The intermediate notes are supplied by opening the lateral orifices of the instrument. Sir C. Wheatstone was the first to make known this difference between the flute and clarinet, and his results agree with the more thorough investigations of Helmholtz. In the hautboy and bassoon we have two reeds inclined to each other at a sharp angle, with a slit between them, through which the air is urged. The pipe of the hautboy is conical, and its overtones are those of an open pipe—different, therefore, from those of a clarinet. The pulpy end of a straw of green corn may be split by squeezing it, so as to form a double reed of this kind, and such a straw yields a musical tone. In the horn, trumpet, and serpent, the performer’s lips play the part of the reed. These instruments are formed of long, conical tubes, and their overtones are those of an open organ-pipe. The music of the older instruments of this class was limited to their overtones, the particular tone elicited depending on the force of the blast and the tension of the lips. It is now usual to fill the gaps between the successive overtones by means of keys, which enable the performer to vary the length of the vibrating column of air.

§ 16. The Voice

The most perfect of reed instruments is the organ of voice. The vocal organ in man is placed at the top of the trachea or wind-pipe, the head of which is adjusted for the attachment of certain elastic bands which almost close the aperture. When the air is forced from the lungs through the slit which separates these vocal chords, they are thrown into vibration; by varying their tension, the rate of vibration is varied, and the sound changed in pitch. The vibrations of the vocal chords are practically unaffected by the resonance of the mouth, though we shall afterward learn that this resonance, by reinforcing one or the other of the tones of the vocal chords, influences in a striking manner the quality of the voice. The sweetness and smoothness of the voice depend on the perfect closure of the slit of the glottis at regular intervals during the vibration.

Fig. 107.

The vocal chords may be illuminated and viewed in a mirror, placed suitably at the back of the mouth. Varied experiments of this kind have been executed by Sig. Garcia.48 I once sought to project the larynx of M. Czermak upon a screen in this room, but with only partial success. The organ may, however, be viewed directly in the laryngoscope; its motions, in singing, speaking, and coughing, being strikingly visible. It is represented at rest in Fig. 107. The roughness of the voice in colds is due, according to Helmholtz, to mucous flocculi, which get into the slit of the glottis, and which are seen by means of the laryngoscope. The squeaking falsetto voice, with which some persons are afflicted, Helmholtz thinks, may be produced by the drawing aside of the mucous layer which ordinarily lies under and loads the vocal chords. Their edges thus become sharper and their weight less; while, their elasticity remaining the same, they are shaken into more rapid tremors. The promptness and accuracy with which the vocal chords can change their tension, their form, and the width of the slit between them, to which must be added the elective resonance of the cavity of the mouth, render the voice the most perfect of musical instruments.

Fig. 108.

The celebrated comparative anatomist, John Müller, imitated the action of the vocal chords by means of bands of India-rubber. He closed the open end of a glass tube by two strips of this substance, leaving a slit between them. On urging air through the slit, the bands were thrown into vibration, and a musical tone produced. Helmholtz recommends the form shown in Fig. 108, where the tube, instead of ending in a section at right angles to its axis, terminates in two oblique sections, over which the bands of India-rubber are drawn. The easiest mode of obtaining sounds from reeds of this character is to roll round the end of a glass tube a strip of thin India-rubber, leaving about an inch of the substance projecting beyond the end of the tube. Taking two opposite portions of the projecting rubber in the fingers, and stretching it, a slit is formed, the blowing through which produces a musical sound, which varies in pitch, as the sides of the slit vary in tension.

§ 17. Vowel Sounds

The formation of the vowel sounds of the human voice excited long ago philosophic inquiry. We can distinguish one vowel sound from another, while assigning to both the same pitch and intensity. What, then, is the quality which renders the distinction possible? In the year 1779 this was made a prize question by the Academy of St. Petersburg, and Kratzenstein gained the prize for the successful manner in which he imitated the vowel sounds by mechanical arrangements. At the same time Von Kempelen, of Vienna, made similar and more elaborate experiments. The question was subsequently taken up by Mr. Willis, who succeeded beyond all his predecessors in the experimental treatment of the subject. The true theory of vowel sounds was first stated by Sir C. Wheatstone, and quite recently they have been made the subject of exhaustive inquiry by Helmholtz. You will find little difficulty in comprehending their origin.

Mounted on the acoustic bellows, without any pipe associated with it, when air is urged through its orifice, a free reed speaks in this forcible manner. When upon the frame of the reed a pyramidal pipe is fixed, you notice a change in the sound; and by pushing my flat hand over the open end of the pipe, the similarity between the sound produced and that of the human voice is unmistakable. Holding the palm of the hand over the end of the pipe so as to close it altogether, and then raising the hand twice in quick succession, the word “mamma” is heard as plainly as if it were uttered by an infant. For this pyramidal tube I now substitute a shorter one, and with it make the same experiment. The “mamma” now heard is exactly such as would be uttered by a child with a stopped nose. Thus, by associating with a vibrating reed a suitable pipe, we can impart to the sound the qualities of the human voice.

In the organ of voice, the reed is formed by the vocal chords, and associated with this reed is the resonant cavity of the mouth, which can so alter its shape as to resound, at will, either to the fundamental tone of the vocal chords or to any of their overtones. With the aid of the mouth, therefore, we can mix together the fundamental tone and the overtones of the voice in different proportions. Different vowel sounds are due to different admixtures of this kind. Striking one of this series of tuning-forks, and placing it before my mouth, I adjust the size of that cavity until it resounds forcibly to the fork. Then, without altering in the least the shape or size of my mouth, I urge air through the glottis. The vowel sound “U” (oo in hoop) is produced, and no other. I strike another fork, and, placing it in front of the mouth, adjust the cavity to resonance. Then removing the fork and urging air through the glottis, the vowel sound “O,” and it only, is heard. I strike a third fork, adjust my mouth to it, and then urge air through the larynx; the vowel sound ah! and no other, is heard. In all these cases the vocal chords have been in the same constant condition. They have generated throughout the same fundamental tone and the same overtones, the changes of sound which you have heard being due solely to the fact that different tones in the different cases were reinforced by the resonance of the mouth. Donders first proved that the mouth resounded differently for the different vowels.

In the formation of the different vowel sounds the resonant cavity of the mouth undergoes, according to Helmholtz, the following changes:

For the production of the sound “U” (oo in hoop), the lips must be pushed forward, so as to make the cavity of the mouth as deep as possible, and the orifice of the mouth, by the contraction of the lips, as small as possible. This arrangement corresponds to the deepest resonance of which the mouth is capable. The fundamental tone itself of the vocal chords is here reinforced, while the higher tones retreat.

The vowel “O” requires a somewhat wider opening of the mouth. The overtones which lie in the neighborhood of the middle b of the soprano come out strongly in the case of this vowel.

When “Ah” is sounded, the mouth assumes the shape of a funnel, widening outward. It is thus tuned to a note an octave higher than in the case of the vowel “O.” Hence, in sounding “Ah,” those overtones are most strengthened which lie near the higher b of the soprano. As the mouth is in this case wide open, all the other overtones are also heard, though feebly.

In sounding “A” and “E,” the hinder part of the mouth is deepened, while the front of the tongue rises against the gums and forms a tube; this yields a higher resonance-tone, rising gradually from “A” to “E,” while the hinder hollow space yields a lower resonance-tone, which is deepest when “E” is sounded.

These examples sufficiently illustrate the subject of vowel sounds. We may blend in various ways the elementary tints of the solar spectrum, producing innumerable composite colors by their admixture. Out of violet and red we produce purple, and out of yellow and blue we produce white. Thus also may elementary sounds be blended so as to produce all possible varieties of clang-tint. After having resolved the human voice into its constituent tones, Helmholtz was able to imitate these tones by tuning-forks, and, by combining them appropriately together, to produce the sounds of all the vowels.

§ 18. Kundt’s Experiments: New Modes of determining Velocity of Sound

Unwilling to interrupt the continuity of our reasonings and experiments on the sound of organ-pipes, and their relations to the vibrations of solid rods, I have reserved for the conclusion of this discourse some reflections and experiments which, in strictness, belong to an earlier portion of the chapter. You have already heard the tones, and made yourselves acquainted with the various modes of division of a glass tube, free at both ends, when thrown into longitudinal vibration. When it sounds its fundamental tone, you know that the two halves of such a tube lengthen and shorten in quick alternation. If the tube were stopped at its ends, the closed extremities would throw the air within the tube into a state of vibration; and if the velocity of sound in air were equal to its velocity in glass, the air of the tube would vibrate in synchronism with the tube itself. But the velocity of sound in air is far less than its velocity in glass, and hence, if the column of air is to synchronize with the vibrations of the tube, it can only do so by dividing itself into vibrating segments of a suitable length. In an investigation of great interest, recently published in “Poggendorff’s Annalen,” M. Kundt, of Berlin, has taught us how these segments may be rendered visible. Into this six-foot tube is introduced the light powder of lycopodium, being shaken all over the interior surface. A small quantity of the powder clings to that surface. Stopping the ends of the tube, holding its centre by a fixed clamp, and sweeping a wet cloth briskly over one of its halves, instantly the powder, which a moment ago clung to its interior surface, falls to the bottom of the tube in the forms shown in Fig. 109, the arrangement of the lycopodium marking the manner in which the column of air has been divided. Every node here is encircled by a ring of dust, while from node to node the dust arranges itself in transverse streaks along the ventral segments.

Fig. 109.

You will have little difficulty in seeing that we perform here, with air, substantially the same experiment as that of M. Melde with a vibrating string. When the string was too long to vibrate as a whole, it met the requirements of the tuning-fork to which it was attached by dividing into ventral segments. Now, in all cases, the length from a node to its next neighbor is half that of the sonorous wave: how many such half-waves then have we in our tube in the present instance? Sixteen (the figure shows only four of them). But the length of our glass tube vibrating thus longitudinally is also half that of the sonorous wave in glass. Hence, in the case before us, with the same rate of vibration, the length of the semi-wave in glass is sixteen times the length of the semi-wave in air. In other words, the velocity of sound in glass is sixteen times its velocity in air. Thus, by a single sweep of the wet rubber, we solve a most important problem. But, as M. Kundt has shown, we need not confine ourselves to air. Introducing any other gas into the tube, a single stroke of our wet cloth enables us to determine the relative velocity of sound in that gas and in glass. When hydrogen is introduced, the number of ventral segments is less than in air; when carbonic acid is introduced, the number is greater.

From the known velocity of sound in air, coupled with the length of one of these dust segments, we can immediately deduce the number of vibrations executed in a second by the tube itself. Clasping a glass tube at its centre and drawing my wetted cloth over one of its halves, I elicit this shrill note. The length of every dust segment, now within the tube, is 3 inches. Hence the length of the aërial sonorous wave corresponding to this note is 6 inches. But the velocity of sound in air of our present temperature is 1,120 feet per second; a distance which would embrace 2,240 of our sonorous waves. This number, therefore, expresses the number of vibrations per second executed by the glass tube now before us.

Instead of damping the centre of the tube, and making it a nodal point, we may employ any other of its subdivisions. Laying hold of it, for example, at a point midway between its centre and one of its ends, and rubbing it properly, it divides into three vibrating parts, separated by two nodes. We know that in this division the note elicited is the octave of that heard when a single node is formed at the middle of the tube; for the vibrations are twice as rapid. If therefore we divide the tube, having air within it, by two nodes instead of one, the number of ventral segments revealed by the lycopodium dust will be thirty-two instead of sixteen. The same remark applies, of course, to all other gases.

Filling a series of four tubes with air, carbonic acid, coal-gas, and hydrogen, and then rubbing each so as to produce two nodes, M. Kundt found the number of dust segments formed within the tube in the respective cases to be as follows:

Air

32

dust segments

Carbonic acid

40

”

Coal-gas

20

”

Hydrogen

9

”

Calling the velocity in air unity, the following fractions express the ratio of this velocity to those in the other gases:

 

32

 

Carbonic acid

—

= 0·8

 

40

         

32

 

Coal-gas

—

= 1·6

 

20

         

32

 

Hydrogen

—

= 3·56

 

9

 

Fig. 110.

Referring to a table introduced in our first chapter, we learn that Dulong by a totally different mode of experiment found the velocity in carbonic acid to be 0.86, and in hydrogen 3·8 times the velocity in air. The results of Dulong were deduced from the sounds of organ-pipes filled with the various gases; but here, by a process of the utmost simplicity, we arrive at a close approximation to his results. Dusting the interior surfaces of our tubes, filling them with the proper gases, and sealing their ends, they may be preserved for an indefinite time. By properly shaking one of them at any moment, its inner surface becomes thinly coated with the dust; and afterward a single stroke of the wet cloth produces the division from which the velocity of sound in the gas may be immediately inferred. Savart found that a spiral nodal line is formed round a tube or rod when it vibrates longitudinally, and Seebeck showed that this line was produced, not by longitudinal, but by secondary transverse vibrations. Now this spiral nodal line tends to complicate the division of the dust in our present experiments. It is, therefore, desirable to operate in a manner which shall altogether avoid the formation of this line; M. Kundt has accomplished this, by exciting the longitudinal vibrations in one tube, and producing the division into ventral segments in another, into which the first fits like a piston. Before you is a tube of glass, Fig. 110, seven feet long, and two inches internal diameter. One end of this tube is filled by the movable stopper b. The other end, K K, is also stopped by a cork, through the centre of which passes the narrower tube A a, which is firmly clasped at its middle by the cork, K K. The end of the interior tube, A a, is also closed with a projecting stopper, a, almost sufficient to fill the larger tube, but still fitting into it so loosely that the friction of a against the interior surface is too slight to interfere practically with its vibrations. The interior surface between a and b being lightly coated with the lycopodium dust, a wet cloth is passed briskly over A K; instantly the dust between a and b divides into a number of ventral segments. When the length of the column of air, a b, is equal to that of the glass tube, A a, the number of ventral segments is sixteen. When, as in the figure, a b is only one-half the length of A a, the number of ventral segments is eight.

But here you must perceive that the method of experiment is capable of great extension. Instead of the glass tube, A a, we may employ a rod of any other solid substance—of wood or metal, for example, and thus determine the relative velocity of sound in the solid and in air. In the place of the glass tube, for example, a rod of brass of equal length may be employed. Rubbing its external half by a resined cloth, it divides the column a b into the number of ventral segments proper to the metal’s rate of vibrations. In this way M. Kundt operated with brass, steel, glass, and copper, and his results prove the method to be capable of great accuracy. Calling, as before, the velocity of sound in air unity, the following numbers expressive of the ratio of the velocity of sound in brass to its velocity in air were obtained in three different series of experiments:

1st experiment

10·87

2d experiment

10·87

3d experiment

10·86

The coincidence is here extraordinary. To illustrate the possible accuracy of the method, the length of the individual dust segments was measured. In a series of twenty-seven experiments, this length was found to vary between 43 and 44 millimètres (each millimètre 1/25th of an inch), never rising so high as the latter and never falling so low as the former. The length of the metal rod, compared with that of one of the segments capable of this accurate measurement, gives us at once the velocity of sound in the metal, as compared with its velocity in air.

Three distinct experiments, performed in the same manner on steel, gave the following velocities, the velocity through air, as before, being regarded as unity:

1st experiment

15·34

2d experiment

15·33

3d experiment

15·34

Here the coincidence is quite as perfect as in the case of brass.

In glass, by this new mode of experiment, the velocity was found to be

15·25.49

Finally, in copper the velocity was found to be

11·96.

These results agree extremely well with those obtained by other methods. Wertheim, for example, found the velocity of sound in steel wire to be 15·108; M. Kundt finds it to be 15·34: Wertheim also found the velocity in copper to be 11·17; M. Kundt finds it to be 11·96. The differences are not greater than might be produced by differences in the materials employed by the two experimenters.

Fig. 111.

The length of the aërial column may or may not be an exact multiple of the wave-length, corresponding to the rod’s rate of vibration. If not, the dust segments usually take the form shown in Fig. 111. But if, by means of the stopper, b, the column of air be made an exact multiple of the wave-length, then the dust quits the vibrating segments altogether, and forms, as in Fig. 112, little isolated heaps at the nodes.

§ 19. Explanation of a Difficulty

And here a difficulty presents itself. The stopped end b of the tube Fig. 110 is, of course, a place of no vibration, where in all cases a nodal dust-heap is formed; but, whenever the column of air was an exact multiple of the wave-length, M. Kundt always found a dust-heap close to the end a of the vibrating rod also. Thus the point from which all the vibration emanated seemed itself to be a place of no vibration.

Fig. 112.

This difficulty was pointed out by M. Kundt, but he did not attempt its solution. We are now in a condition to explain it. In Lecture III. it was remarked that in strictness a node is not a place of no vibration; that it is a place of minimum vibration; and that, by the addition of the minute pulses which the node permits, vibrations of vast amplitude may be produced. The ends of M. Kundt’s tube are such points of minimum motion, the lengths of the vibrating segments being such that, by the coalescence of direct and reflected pulses, the air at a distance of half a ventral segment from the end of the tube vibrates much more vigorously than that at the end of the tube itself. This addition of impulses is more perfect when the aërial column is an exact multiple of the wave-length, and hence it is that, in this case, the vibrations become sufficiently intense to sweep the dust altogether away from the vibrating segments. The same point is illustrated by M. Melde’s tuning-forks, which, though they are the sources of all the motion, are themselves nodes.

An experiment of Helmholtz’s is here capable of instructive application. Upon the string of the sonometer described in our third lecture I place the iron stem of this tuning-fork, which executes 512 complete vibrations in a second. At present you hear no augmentation of the sound of the fork; the string remains quiescent. But on moving the fork along the string, at the number 33, a loud, swelling note issues from the string. At this particular tension the length 33 exactly synchronizes with the vibrations of the fork. By the intermediation of the string, therefore, the fork is enabled to transfer its motion to the sonometer, and through it to the air. The sound continues as long as the fork vibrates, but the least movement to the right or to the left from this point causes a sudden fall of the sound. Tightening the string, the note disappears; for it requires a greater length of this more highly tensioned string to respond to the fork. But, on moving the fork further away, at the number 36 the note again bursts forth. Tightening still more, 40 is found to be the point of maximum power. When the string is slackened, it must, of course, be shortened in order to make it respond to the fork. Moving the fork now toward the end of the string, at the number 25 the note is found as before. Again, shifting the fork to 35, nothing is heard; but, by the cautious turning of the key, the point of synchronism, if I may use the term, is moved further from the end of the string. It finally reaches the fork, and at that moment a clear, full note issues from the sonometer. In all cases, before the exact point is attained, and immediately in its vicinity, we hear “beats,” which, as we shall afterward understand, are due to the coalescence of the sound of the fork with that of the string, when they are nearly, but not quite, in unison with each other.

In these experiments, though the fork was the source of all the motion, the point on which it rested was a nodal point. It constituted the comparatively fixed extremity of the wire, whose vibrations synchronized with those of the fork. The case is exactly analogous to that of the hand holding the India-rubber tube, and to the tuning-fork in the experiments of M. Melde. It is also an effect precisely the same in kind as that observed by M. Kundt, where the part of the column of air in contact with the end of his vibrating rod proved to be a node instead of the middle of a ventral segment.

ADDENDUM REGARDING RESONANCE

The resonance of caves and of rocky inclosures is well known. Bunsen notices the thunder-like sound produced when one of the steam jets of Iceland breaks out near the mouth of a cavern. Most travellers in Switzerland have noticed the deafening sound produced by the fall of the Reuss at the Devil’s Bridge. The sound heard when a hollow shell is placed close to the ear is a case of resonance. Children think they hear in it the sound of the sea. The noise is really due to the reinforcement of the feeble sounds with which even the stillest air is pervaded, and also in part to the noise produced by the pressure of the shell against the ear itself. By using tubes of different lengths, the variation of the resonance with the length of the tube may be studied. The channel of the ear itself is also a resonant cavity. When a poker is held by two strings, and when the fingers of the hands holding the poker are thrust into the ears on striking the poker against a piece of wood, a sound is heard as deep and sonorous as that of a cathedral bell. When open, the channel of the ear resounds to notes whose periods of vibration are about 3,000 per second. This has been shown by Helmholtz, and Madame Seiler has found that dogs which howl to music are particularly sensitive to the same notes. We may expect from Mr. Francis Galton interesting results in connection with this subject.

SUMMARY OF CHAPTER V

When a stretched wire is suitably rubbed, in the direction of its length, it is thrown into longitudinal vibrations: the wire can either vibrate as a whole or divide itself into vibrating segments separated from each other by nodes.

The tones of such a wire follow the order of the numbers 1, 2, 3, 4, etc.

The transverse vibrations of a rod fixed at both ends do not follow the same order as the transverse vibrations of a stretched wire; for here the forces brought into play, as explained in Lecture IV., are different. But the longitudinal vibrations of a stretched wire do follow the same order as the longitudinal vibrations of a rod fixed at both ends, for here the forces brought into play are the same, being in both cases the elasticity of the material.

A rod fixed at one end vibrates longitudinally as a whole, or it divides into two, three, four, etc., vibrating parts, separated from each other by nodes. The order of the tones of such a rod is that of the odd numbers 1, 3, 5, 7, etc.

A rod free at both ends can also vibrate longitudinally. Its lowest note corresponds to a division of the rod into two vibrating parts by a node at its centre. The overtones of such a rod correspond to its division into three, four, five, etc., vibrating parts, separated from each other by two, three, four, etc., nodes. The order of the tones of such a rod is that of the numbers 1, 2, 3, 4, 5, etc.

We may also express the order by saying that while the tones of a rod fixed at both ends follow the order of the odd numbers 1, 3, 5, 7, etc., the tones of a rod free at both ends follow the order of the even numbers 2, 4, 6, 8, etc.

At the points of maximum vibration the rod suffers no change of density; at the nodes, on the contrary, the changes of density reach a maximum. This may be proved by the action of the rod upon polarized light.

Columns of air of definite length resound to tuning-forks of definite rates of vibration.

The length of a tube filled with air, and closed at one end, which resounds to a fork is one-fourth of the length of the sonorous wave produced by the fork.

This resonance is due to the synchronism which exists between the vibrating period of the fork and that of the column of air.

By blowing across the mouth of a tube closed at one end, we produce a flutter of the air, and some pulse of this flutter may be raised by the resonance of the tube to a musical sound.

The sound is the same as that obtained when a tuning-fork, whose rate of vibration is that of the tube, is placed over the mouth of the tube.

When a tube closed at one end—a stopped organ-pipe, for example—sounds its lowest note, the column of air within it is undivided by a node. The overtones of such a column correspond to its division into parts, like those of a rod fixed at one end and vibrating longitudinally. The order of its tones is that of the odd numbers 1, 3, 5, 7, etc. That this must be the order follows from the manner in which the column is divided.

In organ-pipes the air is agitated by causing it to issue from a narrow slit, and to strike upon a cutting edge. Some pulse of the flutter thus produced is raised by the resonance of the pipe to a musical sound.

When, instead of the aërial flutter, a tuning-fork of the proper rate of vibration is placed at the embouchure of an organ-pipe, the pipe speaks in response to the fork. In practice, the organ-pipe virtually creates its own tuning-fork, by compelling the sheet of air at its embouchure to vibrate in periods synchronous with its own.

An open organ-pipe yields a note an octave higher than that of a closed pipe of the same length. This relation is a necessary consequence of the respective modes of vibration.

When, for example, a stopped organ-pipe sounds its deepest note, the column of air, as already explained, is undivided. When an open pipe sounds its deepest note, the column is divided by a node at its centre. The open pipe in this case virtually consists of two stopped pipes with a common base. Hence it is plain that the fundamental note of an open pipe must be the same as that of a stopped pipe of half its length.

The length of a stopped pipe is one-fourth that of the sonorous wave which it produces, while the length of an open pipe is one-half that of its sonorous wave.

The order of the tones of an open pipe is that of the even numbers 2, 4, 6, 8, etc., or of the natural numbers 1, 2, 3, 4, etc.

In both stopped and open pipes the number of vibrations executed in a given time is inversely proportional to the length of the pipe.

The places of maximum vibration in organ-pipes are places of minimum changes of density; while at the places of minimum vibration the changes of density reach a maximum.

The velocities of sound in gases, liquids, and solids may be inferred from the tones which equal lengths of them produce; or they may be inferred from the lengths of these substances which yield equal tones.

Reeds, or vibrating tongues, are often associated with vibrating columns of air. They consist of flexible laminæ, which vibrate to and fro in a rectangular orifice, thus rendering intermittent the air-current passing through the orifice.

The action of the reed is the same as that of the siren.

The flexible wooden reeds sometimes associated with organ-pipes are compelled to vibrate in unison with the column of air in the pipe; other reeds are too stiff to be thus controlled by the vibrating air. In this latter case the column of air is taken of such a length that its vibrations synchronize with those of the reed.

By associating suitable pipes with reeds we impart to their tones the qualities of the human voice.

The vocal organ in man is a reed instrument, the vibrating reed in this case being elastic bands placed at the top of the trachea, and capable of various degrees of tension.

The rate of vibration of these vocal chords is practically uninfluenced by the resonance of the mouth; but the mouth, by changing its shape, can be caused to resound to the fundamental tone, or to any of the overtones of the vocal chords.

By the strengthening of particular tones through the resonance of the mouth, the clang-tint of the voice is altered.

The different vowel-sounds are produced by different admixtures of the fundamental tone and the overtones of the vocal chords.

When the solid substance of a tube stopped at one, or at both ends, is caused to vibrate longitudinally, the air within it is also thrown into vibration.

By covering the interior surface of the tube with a light powder, the manner in which the aërial column divides itself may be rendered apparent. From the division of the column the velocity of sound in the substance of the tube, compared with its velocity in air, may be inferred.

Other gases may be employed instead of air, and the velocity of sound in these gases, compared with its velocity in the substance of the tube, may be determined.

The end of a rod vibrating longitudinally may be caused to agitate a column of air contained in a tube, compelling the air to divide itself into ventral segments. These segments may be rendered visible by light powders, and from them the velocity of sound in the substance of the vibrating rod, compared with its velocity in air, may be inferred.

In this way the relative velocities of sound in all solid substances capable of being formed into rods, and of vibrating longitudinally, may be determined.

CHAPTER VI

Singing Flames—Influence of the Tube surrounding the Flame—Influence of Size of Flame—Harmonic Notes of Flames—Effect of Unisonant Notes on Singing Flames—-Action of Sound on Naked Flames—Experiments with Fish-Tail and Bat’s-Wing Burners—Experiments on Tall Flames—Extraordinary Delicacy of Flames as Acoustic Reagents—The Vowel-Flame—Action of Conversational Tones upon Flames—Action of Musical Sounds on Smoke-Jets—Constitution of Water-Jets—Plateau’s Theory of the Resolution of a Liquid Vein into Drops—Action of Musical Sounds on Water-Jets—A Liquid Vein may compete in Point of Delicacy with the Ear

§ 1. Rhythm of Friction: Musical Flow of a Liquid through a Small Aperture

FRICTION is always rhythmic. When a resined bow is passed across a string, the tension of the string secures the perfect rhythm of the friction. When the wetted finger is moved round the edge of a glass, the breaking up of the friction into rhythmic pulses expresses itself in music. Savart’s beautiful experiments on the flow of liquids through small orifices bear immediately upon this question. We have here the means of verifying his results. The tube A B, Fig. 113, is filled with water, its extremity, B, being closed by a plate of brass, which is pierced by a circular orifice of a diameter equal to the thickness of the plate. Removing a little peg which stops the orifice, the water issues from it, and as it sinks in the tube a musical note of great sweetness issues from the liquid column. This note is due to the intermittent flow of the liquid through the orifice, by which the whole column above it is thrown into vibration. The tendency to this effect shows itself when tea is poured from a teapot, in the circular ripples that cover the falling liquid. The same intermittence is observed in the black, dense smoke which rolls in rhythmic rings from the funnel of a steamer. The unpleasant noise of unoiled machinery is also a declaration of the fact that the friction is not uniform, but is due to the alternate “bite” and release of the rubbing surfaces.

Fig. 113.

Where gases are concerned, friction is of the same intermittent character. A rifle-bullet sings in its passage through the air; while to the rubbing of the wind against the boles and branches of the trees are to be ascribed the “waterfall tones” of an agitated pine-wood. Pass a steadily-burning candle rapidly through the air; an indented band of light, declaring intermittence, is often the consequence, while the almost musical sound which accompanies the appearance of this band is the audible expression of the rhythm. On the other hand, if you blow gently against a candle-flame, the fluttering noise announces a rhythmic action. We have already learned what can be done when a pipe is associated with such a flutter; we have learned that the pipe selects a special pulse from the flutter, and raises it by resonance to a musical sound. In a similar manner the noise of a flame may be turned to account. The blow-pipe flame of our laboratory, for example, when inclosed within an appropriate tube, has its flutter raised to a roar. The special pulse first selected soon reacts upon the flame so as to abolish in a great degree the other pulses, compelling the flame to vibrate in periods answering to the selected one. And this reaction can become so powerful—the timed shock of the reflected pulses may accumulate to such an extent—as to beat the flame, even when very large, into extinction.

§ 2. Musical Flames

Nor is it necessary to produce this flutter by any extraneous means. When a gas-flame is simply inclosed within a tube, the passage of the air over it is usually sufficient to produce the necessary rhythmic action, so as to cause the flame to burst spontaneously into song. This flame-music may be rendered exceedingly intense. Over a flame issuing from a ring burner with twenty-eight orifices, I place a tin tube 5 feet long and 2-1/2 inches in diameter. The flame flutters at first, but it soon chastens its impulses into perfect periodicity, and a deep and clear musical tone is the result. By lowering the gas the note now sounded is caused to cease, but, after a momentary interval of silence, another note, which is the octave of the last, is yielded by the flame. The first note was the fundamental note of the surrounding tube; this second note is its first harmonic. Here, as in the case of open organ-pipes, we have the aërial column dividing itself into vibrating segments, separated from each other by nodes.

Fig. 114. A still more striking effect is obtained with this larger tube, a b, Fig. 114, 15 feet long and 4 inches wide, which was made for a totally different purpose. It is supported by a steady stand, s s′, and into it is lifted the tall burner, shown enlarged at B. You hear the incipient flutter: you now hear the more powerful sound. As the flame is lifted higher the action becomes more violent, until finally a storm of music issues from the tube. And now all has suddenly ceased; the reaction of its own pulses upon the flame has beaten it into extinction. I relight the flame and make it very small. When raised within the tube, the flame again sings, but it is one of the harmonics of the tube that you now hear. On turning the gas fully on, the note ceases—all is silent for a moment; but the storm is brewing, and soon it bursts forth, as at first in a kind of hurricane of sound. By lowering the flame the fundamental note is abolished, and now you hear the first harmonic of the tube. Making the flame still smaller, the first harmonic disappears, and the second is heard. Your ears being disciplined to the apprehension of these sounds, I turn the gas once more fully on. Mingling with the deepest note you notice the harmonics, as if struggling to be heard amid the general uproar of the flame. With a large Bunsen’s rose burner, the sound of this tube becomes powerful enough to shake the floor and seats, and the large audience that occupies the seats of this room, while the extinction of the flame, by the reaction of the Fig. 115. sonorous pulses, announces itself by an explosion almost as loud as a pistol-shot. It must occur to you that a chimney is a tube of this kind upon a large scale, and that the roar of a flame in a chimney is simply a rough attempt at music.

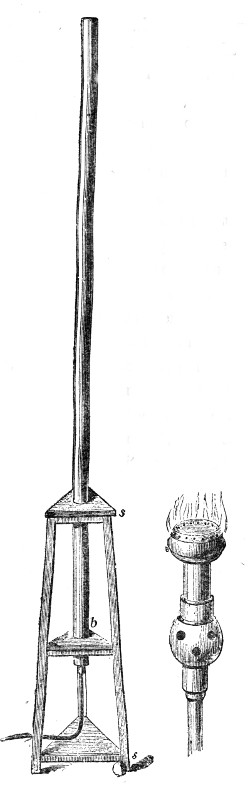
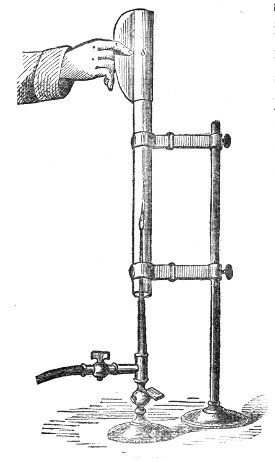
Let us now pass on to shorter tubes and smaller flames. Placing tubes of different lengths over eight small flames, each of them starts into song, and you notice that as the tubes lengthen the tones deepen. The lengths of these tubes are so chosen that they yield in succession the eight notes of the gamut. Round some of them you observe a paper slider, s, Fig. 115, by which the tube can be lengthened or shortened. If while the flame is sounding the slider be raised, the pitch instantly falls; if lowered, the pitch rises. These experiments prove the flame to be governed by the tube. By the reaction of the pulses, reflected back upon the flame, its flutter is rendered perfectly periodic, the length of that period being determined, as in the case of organ-pipes, by the length of the tube.

The fixed stars, especially those near the horizon, shine with an unsteady light, sometimes changing color as they twinkle. I have often watched at night, upon the plateaux of the Alps, the alternate flash of ruby and emerald in the lower and larger stars. If you place a piece of looking-glass so that you can see in it the image of such a star, on tilting the glass quickly to and

Fig. 116. fro, the line of light obtained will not be continuous, but will form a string of colored beads of extreme beauty. The same effect is obtained when an opera-glass is pointed to the star and shaken. This experiment shows that in the act of twinkling the light of the star is quenched at intervals; the dark spaces between the bright beads corresponding to the periods of extinction. Now, our singing flame is a twinkling flame. When it begins to sing you observe a certain quivering motion which may be analyzed with a looking-glass, or an opera-glass, as in the case of the star.50 I can now see the image of this flame in a small looking-glass. On tilting the glass, so as to cause the image to form a circle of light, the luminous band is not seen to be continuous, as it would be if the flame were perfectly steady; it is resolved into a beautiful chain of flames, Fig. 116.

§ 3. Experimental Analysis of Musical Flame