GROWTH AND FORM

CAMBRIDGE UNIVERSITY PRESS

C. F. CLAY, MANAGER

London: FETTER LANE, E.C.

Edinburgh: 100 PRINCES STREET

New York: G. P. PUTNAM’S SONS

Bombay, Calcutta and Madras: MACMILLAN AND Co., LTD.

Toronto: J. M. DENT AND SONS, LTD.

Tokyo: THE MARUZEN-KABUSHIKI-KAISHA

All rights reserved

ON

GROWTH AND FORM

BY

D’ARCY WENTWORTH THOMPSON

Cambridge:

at the University Press

1917

“The reasonings about the wonderful and intricate operations of nature are so full of uncertainty, that, as the Wise-man truly observes, hardly do we guess aright at the things that are upon earth, and with labour do we find the things that are before us.” Stephen Hales, Vegetable Staticks (1727), p. 318, 1738.

PREFATORY NOTE

This book of mine has little need of preface, for indeed it is “all preface” from beginning to end. I have written it as an easy introduction to the study of organic Form, by methods which are the common-places of physical science, which are by no means novel in their application to natural history, but which nevertheless naturalists are little accustomed to employ.

It is not the biologist with an inkling of mathematics, but the skilled and learned mathematician who must ultimately deal with such problems as are merely sketched and adumbrated here. I pretend to no math­e­mat­i­cal skill, but I have made what use I could of what tools I had; I have dealt with simple cases, and the math­e­mat­i­cal methods which I have introduced are of the easiest and simplest kind. Elementary as they are, my book has not been written without the help—the indispensable help—of many friends. Like Mr Pope translating Homer, when I felt myself deficient I sought assistance! And the experience which Johnson attributed to Pope has been mine also, that men of learning did not refuse to help me.

My debts are many, and I will not try to proclaim them all: but I beg to record my particular obligations to Professor Claxton Fidler, Sir George Greenhill, Sir Joseph Larmor, and Professor A. McKenzie; to a much younger but very helpful friend, Mr John Marshall, Scholar of Trinity; lastly, and (if I may say so) most of all, to my colleague Professor William Peddie, whose advice has made many useful additions to my book and whose criticism has spared me many a fault and blunder.

I am under obligations also to the authors and publishers of many books from which illustrations have been borrowed, and especially to the following:—

To the Controller of H.M. Stationery Office, for leave to reproduce a number of figures, chiefly of Foraminifera and of Radiolaria, from the Reports of the Challenger Expedition. {vi}

To the Council of the Royal Society of Edinburgh, and to that of the Zoological Society of London:—the former for letting me reprint from their Transactions the greater part of the text and illustrations of my concluding chapter, the latter for the use of a number of figures for my chapter on Horns.

To Professor E. B. Wilson, for his well-known and all but indispensable figures of the cell (figs. 42–51, 53); to M. A. Prenant, for other figures (41, 48) in the same chapter; to Sir Donald MacAlister and Mr Edwin Arnold for certain figures (335–7), and to Sir Edward Schäfer and Messrs Longmans for another (334), illustrating the minute trabecular structure of bone. To Mr Gerhard Heilmann, of Copenhagen, for his beautiful diagrams (figs. 388–93, 401, 402) included in my last chapter. To Professor Claxton Fidler and to Messrs Griffin, for letting me use, with more or less modification or simplification, a number of illustrations (figs. 339–346) from Professor Fidler’s Textbook of Bridge Construction. To Messrs Blackwood and Sons, for several cuts (figs. 127–9, 131, 173) from Professor Alleyne Nicholson’s Palaeontology; to Mr Heinemann, for certain figures (57, 122, 123, 205) from Dr Stéphane Leduc’s Mechanism of Life; to Mr A. M. Worthington and to Messrs Longmans, for figures (71, 75) from A Study of Splashes, and to Mr C. R. Darling and to Messrs E. and S. Spon for those (fig. 85) from Mr Darling’s Liquid Drops and Globules. To Messrs Macmillan and Co. for two figures (304, 305) from Zittel’s Palaeontology, to the Oxford University Press for a diagram (fig. 28) from Mr J. W. Jenkinson’s Experimental Embryology; and to the Cambridge University Press for a number of figures from Professor Henry Woods’s Invertebrate Palaeontology, for one (fig. 210) from Dr Willey’s Zoological Results, and for another (fig. 321) from “Thomson and Tait.”

Many more, and by much the greater part of my diagrams, I owe to the untiring help of Dr Doris L. Mackinnon, D.Sc., and of Miss Helen Ogilvie, M.A., B.Sc., of this College.

D’ARCY WENTWORTH THOMPSON.

UNIVERSITY COLLEGE, DUNDEE.

December, 1916.

CONTENTS

CHAP.

PAGE

I.

INTRODUCTORY 1

II.

ON MAGNITUDE 16

III.

THE RATE OF GROWTH 50

IV.

ON THE INTERNAL FORM AND STRUCTURE OF THE CELL 156

V.

THE FORMS OF CELLS 201

VI.

A

NOTE ON ADSORPTION 277

VII.

THE FORMS OF TISSUES, OR CELL-AGGREGATES 293

VIII.

THE SAME

(

continued

)

346

IX.

ON CONCRETIONS, SPICULES, AND SPICULAR SKELETONS 411

X.

A

PARENTHETIC NOTE ON GEODETICS 488

XI.

THE LOGARITHMIC SPIRAL 493

XII.

THE SPIRAL SHELLS OF THE FORAMINIFERA 587

XIII.

THE SHAPES OF HORNS, AND OF TEETH OR TUSKS: WITH A NOTE ON TORSION 612

XIV.

ON LEAF-ARRANGEMENT, OR PHYLLOTAXIS 635

XV.

ON THE SHAPES OF EGGS, AND OF CERTAIN OTHER HOLLOW STRUCTURES 652

XVI.

ON FORM AND MECHANICAL EFFICIENCY 670

XVII.

ON THE THEORY OF TRANSFORMATIONS, OR THE COMPARISON OF RELATED FORMS 719 EPILOGUE 778 INDEX 780

LIST OF ILLUSTRATIONS

Fig.

Page

1

.

Nerve-cells, from larger and smaller animals (Minot, after Irving Hardesty)

37

2

.

Relative magnitudes of some minute organisms (Zsigmondy)

39

3

.

Curves of growth in man (Quetelet and Bowditch)

61

4

, 5.

Mean annual increments of stature and weight in man (

do.

)

66, 69

6

.

The ratio, throughout life, of female weight to male (

do.

)

71

7

–9.

Curves of growth of child, before and after birth (His and Rüssow)

74–6

10

.

Curve of growth of bamboo (Ostwald, after Kraus)

77

11

.

Coefficients of variability in human stature (Boas and Wissler)

80

12

.

Growth in weight of mouse (Wolfgang Ostwald)

83

13

.

Do.

of silkworm (Luciani and Lo Monaco)

84

14

.

Do.

of tadpole (Ostwald, after Schaper)

85

15

.

Larval eels, or

Leptocephali

, and young elver (Joh. Schmidt)

86

16

.

Growth in length of

Spirogyra

(Hofmeister)

87

17

.

Pulsations of growth in

Crocus

(Bose)

88

18

.

Relative growth of brain, heart and body of man (Quetelet)

90

19

.

Ratio of stature to span of arms (

do.

)

94

20

.

Rates of growth near the tip of a bean-root (Sachs)

96

21

, 22.

The weight-length ratio of the plaice, and its annual periodic changes

99, 100

23

.

Variability of tail-forceps in earwigs (Bateson)

104

24

.

Variability of body-length in plaice

105

25

.

Rate of growth in plants in relation to temperature (Sachs)

109

26

.

Do.

in maize, observed (Köppen), and calculated curves

112

27

.

Do.

in roots of peas (Miss I. Leitch)

113

28

, 29.

Rate of growth of frog in relation to temperature (Jenkinson, after O. Hertwig), and calculated curves of

do.

115, 6

30

.

Seasonal fluctuation of rate of growth in man (Daffner)

119

31

.

Do.

in the rate of growth of trees (C. E. Hall)

120

32

.

Long-period fluctuation in the rate of growth of Arizona trees (A. E. Douglass)

122

33

, 34.

The varying form of brine-shrimps (

Artemia

), in relation to salinity (Abonyi)

128, 9

35

–39.

Curves of regenerative growth in tadpoles’ tails (M. L. Durbin)

140–145

40

.

Relation between amount of tail removed, amount restored, and time required for restoration (M. M. Ellis)

148

41

.

Caryokinesis in trout’s egg (Prenant, after Prof. P. Bouin)

169

42

–51.

Diagrams of mitotic cell-division (Prof. E. B. Wilson)

171–5

52

.

Chromosomes in course of splitting and separation (Hatschek and Flemming)

180

53

.

Annular chromosomes of mole-cricket (Wilson, after vom Rath)

181

54

–56.

Diagrams illustrating a hypothetic field of force in caryokinesis (Prof. W. Peddie)

182–4

57

.

An artificial figure of caryokinesis (Leduc)

186

58

.

A segmented egg of

Cerebratulus

(Prenant, after Coe)

189

59

.

Diagram of a field of force with two like poles

189

60

.

A budding yeast-cell

213

61

.

The roulettes of the conic sections

218

62

.

Mode of development of an unduloid from a cylindrical tube

220

63

–65.

Cylindrical, unduloid, nodoid and catenoid oil-globules (Plateau)

222, 3

66

.

Diagram of the nodoid, or elastic curve

224

67

.

Diagram of a cylinder capped by the cor­re­spon­ding portion of a sphere

226

68

.

A liquid cylinder breaking up into spheres

227

69

.

The same phenomenon in a protoplasmic cell of

Trianea

234

70

.

Some phases of a splash (A. M. Worthington)

235

71

.

A breaking wave (

do.

)

236

72

.

The calycles of some campanularian zoophytes

237

73

.

A flagellate monad,

Distigma proteus

(Saville Kent)

246

74

.

Noctiluca miliaris

, diagrammatic

246

75

.

Various species of

Vorticella

(Saville Kent and others)

247

76

.

Various species of

Salpingoeca

(

do.

)

248

77

.

Species of

Tintinnus

,

Dinobryon

and

Codonella

(

do.

)

248

78

.

The tube or cup of

Vaginicola

248

79

.

The same of

Folliculina

249

80

.

Trachelophyllum

(Wreszniowski)

249

81

.

Trichodina pediculus

252

82

.

Dinenymplia gracilis

(Leidy)

253

83

.

A “collar-cell” of

Codosiga

254

84

.

Various species of

Lagena

(Brady)

256

85

.

Hanging drops, to illustrate the unduloid form (C. R. Darling)

257

86

.

Diagram of a fluted cylinder

260

87

.

Nodosaria scalaris

(Brady)

262

88

.

Fluted and pleated gonangia of certain Campanularians (Allman)

262

89

.

Various species of

Nodosaria

,

Sagrina

and

Rheophax

(Brady)

263

90

.

Trypanosoma tineae

and

Spirochaeta anodontae

, to shew undulating membranes (Minchin and Fantham)

266

91

.

Some species of

Trichomastix

and

Trichomonas

(Kofoid)

267

92

.

Herpetomonas

assuming the undulatory membrane of a Trypanosome (D. L. Mackinnon)

268

93

.

Diagram of a human blood-corpuscle

271

94

.

Sperm-cells of decapod crustacea,

Inachus

and

Galathea

(Koltzoff)

273

95

.

The same, in saline solutions of varying density (

do.

)

274

96

.

A sperm-cell of

Dromia

(

do.

)

275

97

.

Chondriosomes in cells of kidney and pancreas (Barratt and Mathews)

285

98

.

Adsorptive concentration of potassium salts in various plant-cells (Macallum)

290

99

–101.

Equilibrium of surface-tension in a floating drop

294, 5

102

.

Plateau’s “bourrelet” in plant-cells; diagrammatic (Berthold)

298

103

.

Parenchyma of maize, shewing the same phenomenon

298

104

, 5.

Diagrams of the partition-wall between two soap-bubbles

299, 300

106

.

Diagram of a partition in a conical cell

300

107

.

Chains of cells in

Nostoc

,

Anabaena

and other low algae

300

108

.

Diagram of a symmetrically divided soap-bubble

301

109

.

Arrangement of partitions in dividing spores of

Pellia

(Campbell)

302

110

.

Cells of

Dictyota

(Reinke)

303

111

, 2.

Terminal and other cells of

Chara

, and young antheridium of

do.

303

113

.

Diagram of cell-walls and partitions under various conditions of tension

304

114

, 5.

The partition-surfaces of three interconnected bubbles

307, 8

116

.

Diagram of four interconnected cells or bubbles

309

117

.

Various con­fi­gur­a­tions of four cells in a frog’s egg (Rauber)

311

118

.

Another diagram of two conjoined soap-bubbles

313

119

.

A froth of bubbles, shewing its outer or “epidermal” layer

314

120

.

A tetrahedron, or tetrahedral system, shewing its centre of symmetry

317

121

.

A group of hexagonal cells (Bonanni)

319

122

, 3.

Artificial cellular tissues (Leduc)

320

124

.

Epidermis of

Girardia

(Goebel)

321

125

.

Soap-froth, and the same under compression (Rhumbler)

322

126

.

Epidermal cells of

Elodea canadensis

(Berthold)

322

127

.

Lithostrotion Martini

(Nicholson)

325

128

.

Cyathophyllum hexagonum

(Nicholson, after Zittel)

325

129

.

Arachnophyllum pentagonum

(Nicholson)

326

130

.

Heliolites

(Woods)

326

131

.

Confluent septa in

Thamnastraea

and

Comoseris

(Nicholson, after Zittel)

327

132

.

Geometrical construction of a bee’s cell

330

133

.

Stellate cells in the pith of a rush; diagrammatic

335

134

.

Diagram of soap-films formed in a cubical wire skeleton (Plateau)

337

135

.

Polar furrows in systems of four soap-bubbles (Robert)

341

136

–8.

Diagrams illustrating the division of a cube by partitions of minimal area

347–50

139

.

Cells from hairs of

Sphacelaria

(Berthold)

351

140

.

The bisection of an isosceles triangle by minimal partitions

353

141

.

The similar partitioning of spheroidal and conical cells

353

142

.

S-shaped partitions from cells of algae and mosses (Reinke and others)

355

143

.

Diagrammatic explanation of the S-shaped partitions

356

144

.

Development of

Erythrotrichia

(Berthold)

359

145

.

Periclinal, anticlinal and radial partitioning of a quadrant

359

146

.

Construction for the minimal partitioning of a quadrant

361

147

.

Another diagram of anticlinal and periclinal partitions

362

148

.

Mode of segmentation of an artificially flattened frog’s egg (Roux)

363

149

.

The bisection, by minimal partitions, of a prism of small angle

364

150

.

Comparative diagram of the various modes of bisection of a prismatic sector

365

151

.

Diagram of the further growth of the two halves of a quadrantal cell

367

152

.

Diagram of the origin of an epidermic layer of cells

370

153

.

A discoidal cell dividing into octants

371

154

.

A germinating spore of

Riccia

(after Campbell), to shew the manner of space-partitioning in the cellular tissue

372

155

, 6.

Theoretical arrangement of successive partitions in a discoidal cell

373

157

.

Sections of a moss-embryo (Kienitz-Gerloff)

374

158

.

Various possible arrangements of partitions in groups of four to eight cells

375

159

.

Three modes of partitioning in a system of six cells

376

160

, 1.

Segmenting eggs of

Trochus

(Robert), and of

Cynthia

(Conklin)

377

162

.

Section of the apical cone of

Salvinia

(Pringsheim)

377

163

, 4.

Segmenting eggs of

Pyrosoma

(Korotneff), and of

Echinus

(Driesch)

377

165

.

Segmenting egg of a cephalopod (Watase)

378

166

, 7.

Eggs segmenting under pressure: of

Echinus

and

Nereis

(Driesch), and of a frog (Roux)

378

168

.

Various arrangements of a group of eight cells on the surface of a frog’s egg (Rauber)

381

169

.

Diagram of the partitions and interfacial contacts in a system of eight cells

383

170

.

Various modes of aggregation of eight oil-drops (Roux)

384

171

.

Forms, or species, of

Asterolampra

(Greville)

386

172

.

Diagrammatic section of an alcyonarian polype

387

173

, 4.

Sections of

Heterophyllia

(Nicholson and Martin Duncan)

388, 9

175

.

Diagrammatic section of a ctenophore (

Eucharis

)

391

176

, 7.

Diagrams of the construction of a Pluteus larva

392, 3

178

, 9.

Diagrams of the development of stomata, in

Sedum

and in the hyacinth

394

180

.

Various spores and pollen-grains (Berthold and others)

396

181

.

Spore of

Anthoceros

(Campbell)

397

182

, 4, 9.

Diagrammatic modes of division of a cell under certain conditions of asymmetry

400–5

183

.

Development of the embryo of

Sphagnum

(Campbell)

402

185

.

The gemma of a moss (

do.

)

403

186

.

The antheridium of

Riccia

(

do.

)

404

187

.

Section of growing shoot of

Selaginella

, diagrammatic

404

188

.

An embryo of

Jungermannia

(Kienitz-Gerloff)

404

190

.

Development of the sporangium of

Osmunda

(Bower)

406

191

.

Embryos of

Phascum

and of

Adiantum

(Kienitz-Gerloff)

408

192

.

A section of

Girardia

(Goebel)

408

193

.

An antheridium of

Pteris

(Strasburger)

409

194

.

Spicules of

Siphonogorgia

and

Anthogorgia

(Studer)

413

195

–7.

Calcospherites, deposited in white of egg (Harting)

421, 2

198

.

Sections of the shell of

Mya

(Carpenter)

422

199

.

Concretions, or spicules, artificially deposited in cartilage (Harting)

423

200

.

Further illustrations of alcyonarian spicules:

Eunicea

(Studer)

424

201

–3.

Associated, aggregated and composite cal­co­sphe­rites (Harting)

425, 6

204

.

Harting’s “conostats”

427

205

.

Liesegang’s rings (Leduc)

428

206

.

Relay-crystals of common salt (Bowman)

429

207

.

Wheel-like crystals in a colloid medium (

do.

)

429

208

.

A concentrically striated calcospherite or spherocrystal (Harting)

432

209

.

Otoliths of plaice, shewing “age-rings” (Wallace)

432

210

.

Spicules, or cal­co­sphe­rites, of

Astrosclera

(Lister)

436

211

. 2.

C- and S-shaped spicules of sponges and holothurians (Sollas and Théel)

442

213

.

An amphidisc of

Hyalonema

442

214

–7.

Spicules of calcareous, tetractinellid and hexactinellid sponges, and of various holothurians (Haeckel, Schultze, Sollas and Théel)

445–452

218

.

Diagram of a solid body confined by surface-energy to a liquid boundary-film

460

219

.

Astrorhiza limicola

and

arenaria

(Brady)

464

220

.

A nuclear “

reticulum plasmatique

” (Carnoy)

468

221

.

A spherical radiolarian,

Aulonia hexagona

(Haeckel)

469

222

.

Actinomma arcadophorum

(

do.

)

469

223

.

Ethmosphaera conosiphonia

(

do.

)

470

224

.

Portions of shells of

Cenosphaera favosa

and

vesparia

(

do.

)

470

225

.

Aulastrum triceros

(

do.

)

471

226

.

Part of the skeleton of

Cannorhaphis

(

do.

)

472

227

.

A Nassellarian skeleton,

Callimitra carolotae

(

do.

)

472

228

, 9.

Portions of

Dictyocha stapedia

(

do.

)

474

230

.

Diagram to illustrate the conformation of

Callimitra

476

231

.

Skeletons of various radiolarians (Haeckel)

479

232

.

Diagrammatic structure of the skeleton of

Dorataspis

(

do.

)

481

233

, 4.

Phatnaspis cristata

(Haeckel), and a diagram of the same

483

235

.

Phractaspis prototypus

(Haeckel)

484

236

.

Annular and spiral thickenings in the walls of plant-cells

488

237

.

A radiograph of the shell of

Nautilus

(Green and Gardiner)

494

238

.

A spiral foraminifer,

Globigerina

(Brady)

495

239

–42.

Diagrams to illustrate the development or growth of a logarithmic spiral

407–501

243

.

A helicoid and a scorpioid cyme

502

244

.

An Archimedean spiral

503

245

–7.

More diagrams of the development of a logarithmic spiral

505, 6

248

–57.

Various diagrams illustrating the math­e­mat­i­cal theory of gnomons

508–13

258

.

A shell of

Haliotis

, to shew how each increment of the shell constitutes a gnomon to the preexisting structure

514

259

, 60.

Spiral foraminifera,

Pulvinulina

and

Cristellaria

, to illustrate the same principle

514, 5

261

.

Another diagram of a logarithmic spiral

517

262

.

A diagram of the logarithmic spiral of

Nautilus

(Moseley)

519

263

, 4.

Opercula of

Turbo

and of

Nerita

(Moseley)

521, 2

265

.

A section of the shell of

Melo ethiopicus

525

266

.

Shells of

Harpa

and

Dolium

, to illustrate generating curves and gene

526

267

.

D’Orbigny’s Helicometer

529

268

.

Section of a nautiloid shell, to shew the “protoconch”

531

269

–73.

Diagrams of logarithmic spirals, of various angles

532–5

274

, 6, 7.

Constructions for determining the angle of a logarithmic spiral

537, 8

275

.

An ammonite, to shew its corrugated surface pattern

537

278

–80.

Illustrations of the “angle of retardation”

542–4

281

.

A shell of

Macroscaphites

, to shew change of curvature

550

282

.

Construction for determining the length of the coiled spire

551

283

.

Section of the shell of

Triton corrugatus

(Woodward)

554

284

.

Lamellaria perspicua

and

Sigaretus haliotoides

(

do.

)

555

285

, 6.

Sections of the shells of

Terebra maculata

and

Trochus niloticus

559, 60

287

–9.

Diagrams illustrating the lines of growth on a lamellibranch shell

563–5

290

.

Caprinella adversa

(Woodward)

567

291

.

Section of the shell of

Productus

(Woods)

567

292

.

The “skeletal loop” of

Terebratula

(

do.

)

568

293

, 4.

The spiral arms of

Spirifer

and of

Atrypa

(

do.

)

569

295

–7.

Shells of

Cleodora

,

Hyalaea

and other pteropods (Boas)

570, 1

298

, 9.

Coordinate diagrams of the shell-outline in certain pteropods

572, 3

300

.

Development of the shell of

Hyalaea tridentata

(Tesch)

573

301

.

Pteropod shells, of

Cleodora

and

Hyalaea

, viewed from the side (Boas)

575

302

, 3.

Diagrams of septa in a conical shell

579

304

.

A section of

Nautilus

, shewing the logarithmic spirals of the septa to which the shell-spiral is the evolute

581

305

.

Cast of the interior of the shell of

Nautilus

, to shew the contours of the septa at their junction with the shell-wall

582

306

.

Ammonites Sowerbyi

, to shew septal outlines (Zittel, after Steinmann and Döderlein)

584

307

.

Suture-line of

Pinacoceras

(Zittel, after Hauer)

584

308

.

Shells of

Hastigerina

, to shew the “mouth” (Brady)

588

309

.

Nummulina antiquior

(V. von Möller)

591

310

.

Cornuspira foliacea

and

Operculina complanata

(Brady)

594

311

.

Miliolina pulchella

and

linnaeana

(Brady)

596

312

, 3.

Cyclammina cancellata

(

do.

), and diagrammatic figure of the same

596, 7

314

.

Orbulina universa

(Brady)

598

315

.

Cristellaria reniformis

(

do.

)

600

316

.

Discorbina bertheloti

(

do.

)

603

317

.

Textularia trochus

and

concava

(

do.

)

604

318

.

Diagrammatic figure of a ram’s horns (Sir V. Brooke)

615

319

.

Head of an Arabian wild goat (Sclater)

616

320

.

Head of

Ovis Ammon

, shewing St Venant’s curves

621

321

.

St Venant’s diagram of a triangular prism under torsion (Thomson and Tait)

623

322

.

Diagram of the same phenomenon in a ram’s horn

623

323

.

Antlers of a Swedish elk (Lönnberg)

629

324

.

Head and antlers of

Cervus duvauceli

(Lydekker)

630

325

, 6.

Diagrams of spiral phyllotaxis (P. G. Tait)

644, 5

327

.

Further diagrams of phyllotaxis, to shew how various spiral appearances may arise out of one and the same angular leaf-divergence

648

328

.

Diagrammatic outlines of various sea-urchins

664

329

, 30.

Diagrams of the angle of branching in blood-vessels (Hess)

667, 8

331

, 2.

Diagrams illustrating the flexure of a beam

674, 8

333

.

An example of the mode of arrangement of bast-fibres in a plant-stem (Schwendener)

680

334

.

Section of the head of a femur, to shew its trabecular structure (Schäfer, after Robinson)

681

335

.

Comparative diagrams of a crane-head and the head of a femur (Culmann and H. Meyer)

682

336

.

Diagram of stress-lines in the human foot (Sir D. MacAlister, after H. Meyer)

684

337

.

Trabecular structure of the

os calcis

(

do.

)

685

338

.

Diagram of shearing-stress in a loaded pillar

686

339

.

Diagrams of tied arch, and bowstring girder (Fidler)

693

340

, 1.

Diagrams of a bridge: shewing proposed span, the cor­re­spon­ding stress-diagram and reciprocal plan of construction (

do.

)

696

342

.

A loaded bracket and its reciprocal construction-diagram (Culmann)

697

343

, 4.

A cantilever bridge, with its reciprocal diagrams (Fidler)

698

345

.

A two-armed cantilever of the Forth Bridge (

do.

)

700

346

.

A two-armed cantilever with load distributed over two pier-heads, as in the quadrupedal skeleton

700

347

–9.

Stress-diagrams. or diagrams of bending moments, in the backbones of the horse, of a Dinosaur, and of

Titanotherium

701–4

350

.

The skeleton of

Stegosaurus

707

351

.

Bending-moments in a beam with fixed ends, to illustrate the mechanics of chevron-bones

709

352

, 3.

Coordinate diagrams of a circle, and its deformation into an ellipse

729

354

.

Comparison, by means of Cartesian coordinates, of the cannon-bones of various ruminant animals

729

355

, 6.

Logarithmic coordinates, and the circle of Fig. 352 inscribed therein

729, 31

357

, 8.

Diagrams of oblique and radial coordinates

731

359

.

Lanceolate, ovate and cordate leaves, compared by the help of radial coordinates

732

360

.

A leaf of

Begonia daedalea

733

361

.

A network of logarithmic spiral coordinates

735

362

, 3.

Feet of ox, sheep and giraffe, compared by means of Cartesian coordinates

738, 40

364

, 6.

“Proportional diagrams” of human physiognomy (Albert Dürer)

740, 2

365

.

Median and lateral toes of a tapir, compared by means of rectangular and oblique coordinates

741

367

, 8.

A comparison of the copepods

Oithona

and

Sapphirina

742

369

.

The carapaces of certain crabs,

Geryon

,

Corystes

and others, compared by means of rectilinear and curvilinear coordinates

744

370

.

A comparison of certain amphipods,

Harpinia

,

Stegocephalus

and

Hyperia

746

371

.

The calycles of certain campanularian zoophytes, inscribed in cor­re­spon­ding Cartesian networks

747

372

.

The calycles of certain species of

Aglaophenia

, similarly compared by means of curvilinear coordinates

748

373

, 4.

The fishes

Argyropelecus

and

Sternoptyx

, compared by means of rectangular and oblique coordinate systems

748

375

, 6.

Scarus

and

Pomacanthus

, similarly compared by means of rectangular and coaxial systems

749

377

–80.

A comparison of the fishes

Polyprion

,

Pseudopriacanthus

,

Scorpaena

and

Antigonia

750

381

, 2.

A similar comparison of

Diodon

and

Orthagoriscus

751

383

.

The same of various crocodiles:

C. porosus

,

C. americanus

and

Notosuchus terrestris

753

384

.

The pelvic girdles of

Stegosaurus

and

Camptosaurus

754

385

, 6.

The shoulder-girdles of

Cryptocleidus

and of

Ichthyosaurus

755

387

.

The skulls of

Dimorphodon

and of

Pteranodon

756

388

–92.

The pelves of

Archaeopteryx

and of

Apatornis

compared, and a method illustrated whereby intermediate con­fi­gur­a­tions may be found by interpolation (G. Heilmann)

757–9

393

.

The same pelves, together with three of the intermediate or interpolated forms

760

394

, 5.

Comparison of the skulls of two extinct rhinoceroses,

Hyrachyus

and

Aceratherium

(Osborn)

761

396

.

Occipital views of various extinct rhinoceroses (

do.

)

762

397

–400.

Comparison with each other, and with the skull of

Hyrachyus

, of the skulls of

Titanotherium

, tapir, horse and rabbit

763, 4

401

, 2.

Coordinate diagrams of the skulls of

Eohippus

and of

Equus

, with various actual and hypothetical intermediate types (Heilmann)

765–7

403

.

A comparison of various human scapulae (Dwight)

769

404

.

A human skull, inscribed in Cartesian coordinates

770

405

.

The same coordinates on a new projection, adapted to the skull of the chimpanzee

770

406

.

Chimpanzee’s skull, inscribed in the network of Fig. 405

771

407

, 8.

Corresponding diagrams of a baboon’s skull, and of a dog’s

771, 3

“Cum formarum naturalium et corporalium esse non consistat nisi in unione ad materiam, ejusdem agentis esse videtur eas producere cujus est materiam transmutare. Secundo, quia cum hujusmodi formae non excedant virtutem et ordinem et facultatem principiorum agentium in natura, nulla videtur necessitas eorum originem in principia reducere altiora.” Aquinas, De Pot. Q. iii, a, 11. (Quoted in Brit. Assoc. Address, Section D, 1911.)

“...I would that all other natural phenomena might similarly be deduced from mechanical principles. For many things move me to suspect that everything depends upon certain forces, in virtue of which the particles of bodies, through forces not yet understood, are either impelled together so as to cohere in regular figures, or are repelled and recede from one another.” Newton, in Preface to the Principia. (Quoted by Mr W. Spottiswoode, Brit. Assoc. Presidential Address, 1878.)

“When Science shall have subjected all natural phenomena to the laws of Theoretical Mechanics, when she shall be able to predict the result of every combination as unerringly as Hamilton predicted conical refraction, or Adams revealed to us the existence of Neptune,—that we cannot say. That day may never come, and it is certainly far in the dim future. We may not anticipate it, we may not even call it possible. But none the less are we bound to look to that day, and to labour for it as the crowning triumph of Science:—when Theoretical Mechanics shall be recognised as the key to every physical enigma, the chart for every traveller through the dark Infinite of Nature.” J. H. Jellett, in Brit. Assoc. Address, Section A, 1874.

CHAPTER I INTRODUCTORY

Of the chemistry of his day and generation, Kant declared that it was “a science, but not science,”—“eine Wissenschaft, aber nicht Wissenschaft”; for that the criterion of physical science lay in its relation to mathematics. And a hundred years later Du Bois Reymond, profound student of the many sciences on which physiology is based, recalled and reiterated the old saying, declaring that chemistry would only reach the rank of science, in the high and strict sense, when it should be found possible to explain chemical reactions in the light of their causal relation to the velocities, tensions and conditions of equi­lib­rium of the component molecules; that, in short, the chemistry of the future must deal with molecular mechanics, by the methods and in the strict language of mathematics, as the astronomy of Newton and Laplace dealt with the stars in their courses. We know how great a step has been made towards this distant and once hopeless goal, as Kant defined it, since van’t Hoff laid the firm foundations of a math­e­mat­i­cal chemistry, and earned his proud epitaph, Physicam chemiae adiunxit1.

We need not wait for the full realisation of Kant’s desire, in order to apply to the natural sciences the principle which he urged. Though chemistry fall short of its ultimate goal in math­e­mat­i­cal mechanics, nevertheless physiology is vastly strengthened and enlarged by making use of the chemistry, as of the physics, of the age. Little by little it draws nearer to our conception of a true science, with each branch of physical science which it {2} brings into relation with itself: with every physical law and every math­e­mat­i­cal theorem which it learns to take into its employ. Between the physiology of Haller, fine as it was, and that of Helmholtz, Ludwig, Claude Bernard, there was all the difference in the world.

As soon as we adventure on the paths of the physicist, we learn to weigh and to measure, to deal with time and space and mass and their related concepts, and to find more and more our knowledge expressed and our needs satisfied through the concept of number, as in the dreams and visions of Plato and Pythagoras; for modern chemistry would have gladdened the hearts of those great philosophic dreamers.

But the zoologist or morphologist has been slow, where the physiologist has long been eager, to invoke the aid of the physical or math­e­mat­i­cal sciences; and the reasons for this difference lie deep, and in part are rooted in old traditions. The zoologist has scarce begun to dream of defining, in math­e­mat­i­cal language, even the simpler organic forms. When he finds a simple geometrical construction, for instance in the honey-comb, he would fain refer it to psychical instinct or design rather than to the operation of physical forces; when he sees in snail, or nautilus, or tiny foraminiferal or radiolarian shell, a close approach to the perfect sphere or spiral, he is prone, of old habit, to believe that it is after all something more than a spiral or a sphere, and that in this “something more” there lies what neither physics nor mathematics can explain. In short he is deeply reluctant to compare the living with the dead, or to explain by geometry or by dynamics the things which have their part in the mystery of life. Moreover he is little inclined to feel the need of such explanations or of such extension of his field of thought. He is not without some justification if he feels that in admiration of nature’s handiwork he has an horizon open before his eyes as wide as any man requires. He has the help of many fascinating theories within the bounds of his own science, which, though a little lacking in precision, serve the purpose of ordering his thoughts and of suggesting new objects of enquiry. His art of clas­si­fi­ca­tion becomes a ceaseless and an endless search after the blood-relationships of things living, and the pedigrees of things {3} dead and gone. The facts of embryology become for him, as Wolff, von Baer and Fritz Müller proclaimed, a record not only of the life-history of the individual but of the annals of its race. The facts of geographical distribution or even of the migration of birds lead on and on to speculations regarding lost continents, sunken islands, or bridges across ancient seas. Every nesting bird, every ant-hill or spider’s web displays its psychological problems of instinct or intelligence. Above all, in things both great and small, the naturalist is rightfully impressed, and finally engrossed, by the peculiar beauty which is manifested in apparent fitness or “adaptation,”—the flower for the bee, the berry for the bird.

Time out of mind, it has been by way of the “final cause,” by the teleological concept of “end,” of “purpose,” or of “design,” in one or another of its many forms (for its moods are many), that men have been chiefly wont to explain the phenomena of the living world; and it will be so while men have eyes to see and ears to hear withal. With Galen, as with Aristotle, it was the physician’s way; with John Ray, as with Aristotle, it was the naturalist’s way; with Kant, as with Aristotle, it was the philosopher’s way. It was the old Hebrew way, and has its splendid setting in the story that God made “every plant of the field before it was in the earth, and every herb of the field before it grew.” It is a common way, and a great way; for it brings with it a glimpse of a great vision, and it lies deep as the love of nature in the hearts of men.

Half overshadowing the “efficient” or physical cause, the argument of the final cause appears in eighteenth century physics, in the hands of such men as Euler2 and Maupertuis, to whom Leibniz3 had passed it on. Half overshadowed by the mechanical concept, it runs through Claude Bernard’s Leçons sur les {4} phénomènes de la Vie4, and abides in much of modern physiology5. Inherited from Hegel, it dominated Oken’s Naturphilosophie and lingered among his later disciples, who were wont to liken the course of organic evolution not to the straggling branches of a tree, but to the building of a temple, divinely planned, and the crowning of it with its polished minarets6.

It is retained, somewhat crudely, in modern embryology, by those who see in the early processes of growth a significance “rather prospective than retrospective,” such that the embryonic phenomena must be “referred directly to their usefulness in building the body of the future animal7”:—which is no more, and no less, than to say, with Aristotle, that the organism is the τέλος, or final cause, of its own processes of generation and development. It is writ large in that Entelechy8 which Driesch rediscovered, and which he made known to many who had neither learned of it from Aristotle, nor studied it with Leibniz, nor laughed at it with Voltaire. And, though it is in a very curious way, we are told that teleology was “refounded, reformed or rehabilitated9” by Darwin’s theory of natural selection, whereby “every variety of form and colour was urgently and absolutely called upon to produce its title to existence either as an active useful agent, or as a survival” of such active usefulness in the past. But in this last, and very important case, we have reached a “teleology” without a τέλος, {5} as men like Butler and Janet have been prompt to shew: a teleology in which the final cause becomes little more, if anything, than the mere expression or resultant of a process of sifting out of the good from the bad, or of the better from the worse, in short of a process of mechanism10. The apparent manifestations of “purpose” or adaptation become part of a mechanical philosophy, according to which “chaque chose finit toujours par s’accommoder à son milieu11.” In short, by a road which resembles but is not the same as Maupertuis’s road, we find our way to the very world in which we are living, and find that if it be not, it is ever tending to become, “the best of all possible worlds12.”

But the use of the teleological principle is but one way, not the whole or the only way, by which we may seek to learn how things came to be, and to take their places in the harmonious complexity of the world. To seek not for ends but for “antecedents” is the way of the physicist, who finds “causes” in what he has learned to recognise as fundamental properties, or inseparable concomitants, or unchanging laws, of matter and of energy. In Aristotle’s parable, the house is there that men may live in it; but it is also there because the builders have laid one stone upon another: and it is as a mechanism, or a mechanical construction, that the physicist looks upon the world. Like warp and woof, mechanism and teleology are interwoven together, and we must not cleave to the one and despise the other; for their union is “rooted in the very nature of totality13.”

Nevertheless, when philosophy bids us hearken and obey the lessons both of mechanical and of teleological interpretation, the precept is hard to follow: so that oftentimes it has come to pass, just as in Bacon’s day, that a leaning to the side of the final cause “hath intercepted the severe and diligent inquiry of all {6} real and physical causes,” and has brought it about that “the search of the physical cause hath been neglected and passed in silence.” So long and so far as “fortuitous variation14” and the “survival of the fittest” remain engrained as fundamental and satisfactory hypotheses in the philosophy of biology, so long will these “satisfactory and specious causes” tend to stay “severe and diligent inquiry,” “to the great arrest and prejudice of future discovery.”

The difficulties which surround the concept of active or “real” causation, in Bacon’s sense of the word, difficulties of which Hume and Locke and Aristotle were little aware, need scarcely hinder us in our physical enquiry. As students of math­e­mat­i­cal and of empirical physics, we are content to deal with those antecedents, or concomitants, of our phenomena, without which the phenomenon does not occur,—with causes, in short, which, aliae ex aliis aptae et necessitate nexae, are no more, and no less, than conditions sine quâ non. Our purpose is still adequately fulfilled: inasmuch as we are still enabled to correlate, and to equate, our particular phenomena with more and ever more of the physical phenomena around, and so to weave a web of connection and interdependence which shall serve our turn, though the metaphysician withhold from that interdependence the title of causality. We come in touch with what the schoolmen called a ratio cognoscendi, though the true ratio efficiendi is still enwrapped in many mysteries. And so handled, the quest of physical causes merges with another great Aristotelian theme,—the search for relations between things apparently disconnected, and for “similitude in things to common view unlike.” Newton did not shew the cause of the apple falling, but he shewed a similitude between the apple and the stars.

Moreover, the naturalist and the physicist will continue to speak of “causes,” just as of old, though it may be with some mental reservations: for, as a French philosopher said, in a kindred difficulty: “ce sont là des manières de s’exprimer, {7} et si elles sont interdites il faut renoncer à parler de ces choses.”

The search for differences or essential contrasts between the phenomena of organic and inorganic, of animate and inanimate things has occupied many mens’ minds, while the search for community of principles, or essential similitudes, has been followed by few; and the contrasts are apt to loom too large, great as they may be. M. Dunan, discussing the “Problème de la Vie15” in an essay which M. Bergson greatly commends, declares: “Les lois physico-chimiques sont aveugles et brutales; là où elles règnent seules, au lieu d’un ordre et d’un concert, il ne peut y avoir qu’incohérence et chaos.” But the physicist proclaims aloud that the physical phenomena which meet us by the way have their manifestations of form, not less beautiful and scarce less varied than those which move us to admiration among living things. The waves of the sea, the little ripples on the shore, the sweeping curve of the sandy bay between its headlands, the outline of the hills, the shape of the clouds, all these are so many riddles of form, so many problems of morphology, and all of them the physicist can more or less easily read and adequately solve: solving them by reference to their antecedent phenomena, in the material system of mechanical forces to which they belong, and to which we interpret them as being due. They have also, doubtless, their immanent teleological significance; but it is on another plane of thought from the physicist’s that we contemplate their intrinsic harmony and perfection, and “see that they are good.”

Nor is it otherwise with the material forms of living things. Cell and tissue, shell and bone, leaf and flower, are so many portions of matter, and it is in obedience to the laws of physics that their particles have been moved, moulded and conformed16. {8} They are no exception to the rule that Θεὸς ἀεὶ γεωμετρεῖ. Their problems of form are in the first instance math­e­mat­i­cal problems, and their problems of growth are essentially physical problems; and the morphologist is, ipso facto, a student of physical science.

Apart from the physico-chemical problems of modern physiology, the road of physico-math­e­mat­i­cal or dynamical in­ves­ti­ga­tion in morphology has had few to follow it; but the pathway is old. The way of the old Ionian physicians, of Anaxagoras17, of Empedocles and his disciples in the days before Aristotle, lay just by that highwayside. It was Galileo’s and Borelli’s way. It was little trodden for long afterwards, but once in a while Swammerdam and Réaumur looked that way. And of later years, Moseley and Meyer, Berthold, Errera and Roux have been among the little band of travellers. We need not wonder if the way be hard to follow, and if these wayfarers have yet gathered little. A harvest has been reaped by others, and the gleaning of the grapes is slow.

It behoves us always to remember that in physics it has taken great men to discover simple things. They are very great names indeed that we couple with the explanation of the path of a stone, the droop of a chain, the tints of a bubble, the shadows in a cup. It is but the slightest adumbration of a dynamical morphology that we can hope to have, until the physicist and the mathematician shall have made these problems of ours their own, or till a new Boscovich shall have written for the naturalist the new Theoria Philosophiae Naturalis.

How far, even then, mathematics will suffice to describe, and physics to explain, the fabric of the body no man can foresee. It may be that all the laws of energy, and all the properties of matter, and all the chemistry of all the colloids are as powerless to explain the body as they are impotent to comprehend the soul. For my part, I think it is not so. Of how it is that the soul informs the body, physical science teaches me nothing: consciousness is not explained to my comprehension by all the nerve-paths and “neurones” of the physiologist; nor do I ask of physics how goodness shines in one man’s face, and evil betrays itself in another. But of the construction and growth and working {9} of the body, as of all that is of the earth earthy, physical science is, in my humble opinion, our only teacher and guide18.

Often and often it happens that our physical knowledge is inadequate to explain the mechanical working of the organism; the phenomena are superlatively complex, the procedure is involved and entangled, and the in­ves­ti­ga­tion has occupied but a few short lives of men. When physical science falls short of explaining the order which reigns throughout these manifold phenomena,—an order more char­ac­ter­is­tic in its totality than any of its phenomena in themselves,—men hasten to invoke a guiding principle, an entelechy, or call it what you will. But all the while, so far as I am aware, no physical law, any more than that of gravity itself, not even among the puzzles of chemical “stereometry,” or of physiological “surface-action” or “osmosis,” is known to be transgressed by the bodily mechanism.

Some physicists declare, as Maxwell did, that atoms or molecules more complicated by far than the chemist’s hypotheses demand are requisite to explain the phenomena of life. If what is implied be an explanation of psychical phenomena, let the point be granted at once; we may go yet further, and decline, with Maxwell, to believe that anything of the nature of physical complexity, however exalted, could ever suffice. Other physicists, like Auerbach19, or Larmor20, or Joly21, assure us that our laws of thermodynamics do not suffice, or are “inappropriate,” to explain the maintenance or (in Joly’s phrase) the “accelerative absorption” {10} of the bodily energies, and the long battle against the cold and darkness which is death. With these weighty problems I am not for the moment concerned. My sole purpose is to correlate with math­e­mat­i­cal statement and physical law certain of the simpler outward phenomena of organic growth and structure or form: while all the while regarding, ex hypothesi, for the purposes of this correlation, the fabric of the organism as a material and mechanical configuration.

Physical science and philosophy stand side by side, and one upholds the other. Without something of the strength of physics, philosophy would be weak; and without something of philosophy’s wealth, physical science would be poor. “Rien ne retirera du tissu de la science les fils d’or que la main du philosophe y a introduits22.” But there are fields where each, for a while at least, must work alone; and where physical science reaches its limitations, physical science itself must help us to discover. Meanwhile the appropriate and legitimate postulate of the physicist, in approaching the physical problems of the body, is that with these physical phenomena no alien influence interferes. But the postulate, though it is certainly legitimate, and though it is the proper and necessary prelude to scientific enquiry, may some day be proven to be untrue; and its disproof will not be to the physicist’s confusion, but will come as his reward. In dealing with forms which are so concomitant with life that they are seemingly controlled by life, it is in no spirit of arrogant assertiveness that the physicist begins his argument, after the fashion of a most illustrious exemplar, with the old formulary of scholastic challenge,—An Vita sit? Dico quod non.

The terms Form and Growth, which make up the title of this little book, are to be understood, as I need hardly say, in their relation to the science of organisms. We want to see how, in some cases at least, the forms of living things, and of the parts of living things, can be explained by physical con­si­de­ra­tions, and to realise that, in general, no organic forms exist save such as are in conformity with ordinary physical laws. And while growth is a somewhat vague word for a complex matter, which may {11} depend on various things, from simple imbibition of water to the complicated results of the chemistry of nutrition, it deserves to be studied in relation to form, whether it proceed by simple increase of size without obvious alteration of form, or whether it so proceed as to bring about a gradual change of form and the slow development of a more or less complicated structure.

In the Newtonian language of elementary physics, force is recognised by its action in producing or in changing motion, or in preventing change of motion or in maintaining rest. When we deal with matter in the concrete, force does not, strictly speaking, enter into the question, for force, unlike matter, has no independent objective existence. It is energy in its various forms, known or unknown, that acts upon matter. But when we abstract our thoughts from the material to its form, or from the thing moved to its motions, when we deal with the subjective conceptions of form, or movement, or the movements that change of form implies, then force is the appropriate term for our conception of the causes by which these forms and changes of form are brought about. When we use the term force, we use it, as the physicist always does, for the sake of brevity, using a symbol for the magnitude and direction of an action in reference to the symbol or diagram of a material thing. It is a term as subjective and symbolic as form itself, and so is appropriately to be used in connection therewith.

The form, then, of any portion of matter, whether it be living or dead, and the changes of form that are apparent in its movements and in its growth, may in all cases alike be described as due to the action of force. In short, the form of an object is a “diagram of forces,” in this sense, at least, that from it we can judge of or deduce the forces that are acting or have acted upon it: in this strict and particular sense, it is a diagram,—in the case of a solid, of the forces that have been impressed upon it when its conformation was produced, together with those that enable it to retain its conformation; in the case of a liquid (or of a gas) of the forces that are for the moment acting on it to restrain or balance its own inherent mobility. In an organism, great or small, it is not merely the nature of the motions of the living substance that we must interpret in terms of force (according to kinetics), but also {12} the conformation of the organism itself, whose permanence or equi­lib­rium is explained by the interaction or balance of forces, as described in statics.

If we look at the living cell of an Amoeba or a Spirogyra, we see a something which exhibits certain active movements, and a certain fluctuating, or more or less lasting, form; and its form at a given moment, just like its motions, is to be investigated by the help of physical methods, and explained by the invocation of the math­e­mat­i­cal conception of force.

Now the state, including the shape or form, of a portion of matter, is the resultant of a number of forces, which represent or symbolise the manifestations of various kinds of energy; and it is obvious, accordingly, that a great part of physical science must be understood or taken for granted as the necessary preliminary to the discussion on which we are engaged. But we may at least try to indicate, very briefly, the nature of the principal forces and the principal properties of matter with which our subject obliges us to deal. Let us imagine, for instance, the case of a so-called “simple” organism, such as Amoeba; and if our short list of its physical properties and conditions be helpful to our further discussion, we need not consider how far it be complete or adequate from the wider physical point of view23.

This portion of matter, then, is kept together by the intermolecular force of cohesion; in the movements of its particles relatively to one another, and in its own movements relative to adjacent matter, it meets with the opposing force of friction. It is acted on by gravity, and this force tends (though slightly, owing to the Amoeba’s small mass, and to the small difference between its density and that of the surrounding fluid), to flatten it down upon the solid substance on which it may be creeping. Our Amoeba tends, in the next place, to be deformed by any pressure from outside, even though slight, which may be applied to it, and this circumstance shews it to consist of matter in a fluid, or at least semi-fluid, state: which state is further indicated when we observe streaming or current motions in its interior. {13} Like other fluid bodies, its surface, whatsoever other substance, gas, liquid or solid, it be in contact with, and in varying degree according to the nature of that adjacent substance, is the seat of molecular force exhibiting itself as a surface-tension, from the action of which many important consequences follow, which greatly affect the form of the fluid surface.

While the protoplasm of the Amoeba reacts to the slightest pressure, and tends to “flow,” and while we therefore speak of it as a fluid, it is evidently far less mobile than such a fluid, for instance, as water, but is rather like treacle in its slow creeping movements as it changes its shape in response to force. Such fluids are said to have a high viscosity, and this viscosity obviously acts in the way of retarding change of form, or in other words of retarding the effects of any disturbing action of force. When the viscous fluid is capable of being drawn out into fine threads, a property in which we know that the material of some Amoebae differs greatly from that of others, we say that the fluid is also viscid, or exhibits viscidity. Again, not by virtue of our Amoeba being liquid, but at the same time in vastly greater measure than if it were a solid (though far less rapidly than if it were a gas), a process of molecular diffusion is constantly going on within its substance, by which its particles interchange their places within the mass, while surrounding fluids, gases and solids in solution diffuse into and out of it. In so far as the outer wall of the cell is different in character from the interior, whether it be a mere pellicle as in Amoeba or a firm cell-wall as in Protococcus, the diffusion which takes place through this wall is sometimes distinguished under the term osmosis.

Within the cell, chemical forces are at work, and so also in all probability (to judge by analogy) are electrical forces; and the organism reacts also to forces from without, that have their origin in chemical, electrical and thermal influences. The processes of diffusion and of chemical activity within the cell result, by the drawing in of water, salts, and food-material with or without chemical transformation into protoplasm, in growth, and this complex phenomenon we shall usually, without discussing its nature and origin, describe and picture as a force. Indeed we shall manifestly be inclined to use the term growth in two senses, {14} just indeed as we do in the case of attraction or gravitation, on the one hand as a process, and on the other hand as a force.

In the phenomena of cell-division, in the attractions or repulsions of the parts of the dividing nucleus and in the “caryokinetic” figures that appear in connection with it, we seem to see in operation forces and the effects of forces, that have, to say the least of it, a close analogy with known physical phenomena; and to this matter we shall afterwards recur. But though they resemble known physical phenomena, their nature is still the subject of much discussion, and neither the forms produced nor the forces at work can yet be satisfactorily and simply explained. We may readily admit, then, that besides phenomena which are obviously physical in their nature, there are actions visible as well as invisible taking place within living cells which our knowledge does not permit us to ascribe with certainty to any known physical force; and it may or may not be that these phenomena will yield in time to the methods of physical in­ves­ti­ga­tion. Whether or no, it is plain that we have no clear rule or guide as to what is “vital” and what is not; the whole assemblage of so-called vital phenomena, or properties of the organism, cannot be clearly classified into those that are physical in origin and those that are sui generis and peculiar to living things. All we can do meanwhile is to analyse, bit by bit, those parts of the whole to which the ordinary laws of the physical forces more or less obviously and clearly and indubitably apply.

Morphology then is not only a study of material things and of the forms of material things, but has its dynamical aspect, under which we deal with the interpretation, in terms of force, of the operations of Energy. And here it is well worth while to remark that, in dealing with the facts of embryology or the phenomena of inheritance, the common language of the books seems to deal too much with the material elements concerned, as the causes of development, of variation or of hereditary transmission. Matter as such produces nothing, changes nothing, does nothing; and however convenient it may afterwards be to abbreviate our nomenclature and our descriptions, we must most carefully realise in the outset that the spermatozoon, the nucleus, {15} the chromosomes or the germ-plasm can never act as matter alone, but only as seats of energy and as centres of force. And this is but an adaptation (in the light, or rather in the conventional symbolism, of modern physical science) of the old saying of the philosopher: ἀρχὴ γὰρ ἡ φύσις μᾶλλον τῆς ὕλης.

CHAPTER II. ON MAGNITUDE

To terms of magnitude, and of direction, must we refer all our conceptions of form. For the form of an object is defined when we know its magnitude, actual or relative, in various directions; and growth involves the same conceptions of magnitude and direction, with this addition, that they are supposed to alter in time. Before we proceed to the consideration of specific form, it will be worth our while to consider, for a little while, certain phenomena of spatial magnitude, or of the extension of a body in the several dimensions of space24.

We are taught by elementary mathematics that, in similar solid figures, the surface increases as the square, and the volume as the cube, of the linear dimensions. If we take the simple case of a sphere, with radius r, the area of its surface is equal to 4πr² , and its volume to (⁴⁄₃)πr³ ; from which it follows that the ratio of volume to surface, or ^V⁄_S , is (¹⁄₃)r. In other words, the greater the radius (or the larger the sphere) the greater will be its volume, or its mass (if it be uniformly dense throughout), in comparison with its superficial area. And, taking L to represent any linear dimension, we may write the general equations in the form

S ∝ L² , V ∝ L³ ,

or

S = k · L² , and V = k′ · L³ ;

and

^V⁄_S ∝ L.

From these elementary principles a great number of consequences follow, all more or less interesting, and some of them of great importance. In the first place, though growth in length (let {17} us say) and growth in volume (which is usually tantamount to mass or weight) are parts of one and the same process or phenomenon, the one attracts our attention by its increase, very much more than the other. For instance a fish, in doubling its length, multiplies its weight by no less than eight times; and it all but doubles its weight in growing from four inches long to five.

In the second place we see that a knowledge of the correlation between length and weight in any particular species of animal, in other words a determination of k in the formula W = k · L³ , enables us at any time to translate the one magnitude into the other, and (so to speak) to weigh the animal with a measuring-rod; this however being always subject to the condition that the animal shall in no way have altered its form, nor its specific gravity. That its specific gravity or density should materially or rapidly alter is not very likely; but as long as growth lasts, changes of form, even though inappreciable to the eye, are likely to go on. Now weighing is a far easier and far more accurate operation than measuring; and the measurements which would reveal slight and otherwise imperceptible changes in the form of a fish—slight relative differences between length, breadth and depth, for instance,—would need to be very delicate indeed. But if we can make fairly accurate determinations of the length, which is very much the easiest dimension to measure, and then correlate it with the weight, then the value of k, according to whether it varies or remains constant, will tell us at once whether there has or has not been a tendency to gradual alteration in the general form. To this subject we shall return, when we come to consider more particularly the rate of growth.

But a much deeper interest arises out of this changing ratio of dimensions when we come to consider the inevitable changes of physical relations with which it is bound up. We are apt, and even accustomed, to think that magnitude is so purely relative that differences of magnitude make no other or more essential difference; that Lilliput and Brobdingnag are all alike, according as we look at them through one end of the glass or the other. But this is by no means so; for scale has a very marked effect upon physical phenomena, and the effect of scale constitutes what is known as the principle of similitude, or of dynamical similarity. {18}

This effect of scale is simply due to the fact that, of the physical forces, some act either directly at the surface of a body, or otherwise in proportion to the area of surface; and others, such as gravity, act on all particles, internal and external alike, and exert a force which is proportional to the mass, and so usually to the volume, of the body.

The strength of an iron girder obviously varies with the cross-section of its members, and each cross-section varies as the square of a linear dimension; but the weight of the whole structure varies as the cube of its linear dimensions. And it follows at once that, if we build two bridges geometrically similar, the larger is the weaker of the two25. It was elementary engineering experience such as this that led Herbert Spencer26 to apply the principle of similitude to biology.

The same principle had been admirably applied, in a few clear instances, by Lesage27, a celebrated eighteenth century physician of Geneva, in an unfinished and unpublished work28. Lesage argued, for instance, that the larger ratio of surface to mass would lead in a small animal to excessive transpiration, were the skin as “porous” as our own; and that we may hence account for the hardened or thickened skins of insects and other small terrestrial animals. Again, since the weight of a fruit increases as the cube of its dimensions, while the strength of the stalk increases as the square, it follows that the stalk should grow out of apparent due proportion to the fruit; or alternatively, that tall trees should not bear large fruit on slender branches, and that melons and pumpkins must lie upon the ground. And again, that in quadrupeds a large head must be supported on a neck which is either {19} excessively thick and strong, like a bull’s, or very short like the neck of an elephant.

But it was Galileo who, wellnigh 300 years ago, had first laid down this general principle which we now know by the name of the principle of similitude; and he did so with the utmost possible clearness, and with a great wealth of illustration, drawn from structures living and dead29. He showed that neither can man build a house nor can nature construct an animal beyond a certain size, while retaining the same proportions and employing the same materials as sufficed in the case of a smaller structure30. The thing will fall to pieces of its own weight unless we either change its relative proportions, which will at length cause it to become clumsy, monstrous and inefficient, or else we must find a new material, harder and stronger than was used before. Both processes are familiar to us in nature and in art, and practical applications, undreamed of by Galileo, meet us at every turn in this modern age of steel.

Again, as Galileo was also careful to explain, besides the questions of pure stress and strain, of the strength of muscles to lift an increasing weight or of bones to resist its crushing stress, we have the very important question of bending moments. This question enters, more or less, into our whole range of problems; it affects, as we shall afterwards see, or even determines the whole form of the skeleton, and is very important in such a case as that of a tall tree31.

Here we have to determine the point at which the tree will curve under its own weight, if it be ever so little displaced from the perpendicular32. In such an in­ves­ti­ga­tion we have to make {20} some assumptions,—for instance, with regard to the trunk, that it tapers uniformly, and with regard to the branches that their sectional area varies according to some definite law, or (as Ruskin assumed33) tends to be constant in any horizontal plane; and the math­e­mat­i­cal treatment is apt to be somewhat difficult. But Greenhill has shewn that (on such assumptions as the above), a certain British Columbian pine-tree, which yielded the Kew flagstaff measuring 221 ft. in height with a diameter at the base of 21 inches, could not possibly, by theory, have grown to more than about 300 ft. It is very curious that Galileo suggested precisely the same height (dugento braccia alta) as the utmost limit of the growth of a tree. In general, as Greenhill shews, the diameter of a homogeneous body must increase as the power 3 ⁄ 2 of the height, which accounts for the slender proportions of young trees, compared with the stunted appearance of old and large ones34. In short, as Goethe says in Wahrheit und Dichtung, “Es ist dafür gesorgt dass die Bäume nicht in den Himmel wachsen.” But Eiffel’s great tree of steel (1000 feet high) is built to a very different plan; for here the profile of the tower follows the logarithmic curve, giving equal strength throughout, according to a principle which we shall have occasion to discuss when we come to treat of “form and mechanical efficiency” in connection with the skeletons of animals.

Among animals, we may see in a general way, without the help of mathematics or of physics, that exaggerated bulk brings with it a certain clumsiness, a certain inefficiency, a new element of risk and hazard, a vague preponderance of disadvantage. The case was well put by Owen, in a passage which has an interest of its own as a premonition (somewhat like De Candolle’s) of the “struggle for existence.” Owen wrote as follows35: “In proportion to the bulk of a species is the difficulty of the contest which, as a living organised whole, the individual of such species {21} has to maintain against the surrounding agencies that are ever tending to dissolve the vital bond, and subjugate the living matter to the ordinary chemical and physical forces. Any changes, therefore, in such external conditions as a species may have been originally adapted to exist in, will militate against that existence in a degree proportionate, perhaps in a geometrical ratio, to the bulk of the species. If a dry season be greatly prolonged, the large mammal will suffer from the drought sooner than the small one; if any alteration of climate affect the quantity of vegetable food, the bulky Herbivore will first feel the effects of stinted nourishment.”

But the principle of Galileo carries us much further and along more certain lines.

The tensile strength of a muscle, like that of a rope or of our girder, varies with its cross-section; and the resistance of a bone to a crushing stress varies, again like our girder, with its cross-section. But in a terrestrial animal the weight which tends to crush its limbs or which its muscles have to move, varies as the cube of its linear dimensions; and so, to the possible magnitude of an animal, living under the direct action of gravity, there is a definite limit set. The elephant, in the dimensions of its limb-bones, is already shewing signs of a tendency to disproportionate thickness as compared with the smaller mammals; its movements are in many ways hampered and its agility diminished: it is already tending towards the maximal limit of size which the physical forces permit. But, as Galileo also saw, if the animal be wholly immersed in water, like the whale, (or if it be partly so, as was in all probability the case with the giant reptiles of our secondary rocks), then the weight is counterpoised to the extent of an equivalent volume of water, and is completely counterpoised if the density of the animal’s body, with the included air, be identical (as in a whale it very nearly is) with the water around. Under these circumstances there is no longer a physical barrier to the indefinite growth in magnitude of the animal36. Indeed, {22} in the case of the aquatic animal there is, as Spencer pointed out, a distinct advantage, in that the larger it grows the greater is its velocity. For its available energy depends on the mass of its muscles; while its motion through the water is opposed, not by gravity, but by “skin-friction,” which increases only as the square of its dimensions; all other things being equal, the bigger the ship, or the bigger the fish, the faster it tends to go, but only in the ratio of the square root of the increasing length. For the mechanical work (W) of which the fish is capable being proportional to the mass of its muscles, or the cube of its linear dimensions: and again this work being wholly done in producing a velocity (V) against a resistance (R) which increases as the square of the said linear dimensions; we have at once

W = l³ ,

and also

W = RV² = l²V² .

Therefore

l³ = l²V² ,  and  V = √l.

This is what is known as Froude’s Law of the cor­re­spon­dence of speeds.

But there is often another side to these questions, which makes them too complicated to answer in a word. For instance, the work (per stroke) of which two similar engines are capable should obviously vary as the cubes of their linear dimensions, for it varies on the one hand with the surface of the piston, and on the other, with the length of the stroke; so is it likewise in the animal, where the cor­re­spon­ding variation depends on the cross-section of the muscle, and on the space through which it contracts. But in two precisely similar engines, the actual available horse-power varies as the square of the linear dimensions, and not as the cube; and this for the obvious reason that the actual energy developed depends upon the heating-surface of the boiler37. So likewise must there be a similar tendency, among animals, for the rate of supply of kinetic energy to vary with the surface of the {23} lung, that is to say (other things being equal) with the square of the linear dimensions of the animal. We may of course (departing from the condition of similarity) increase the heating-surface of the boiler, by means of an internal system of tubes, without increasing its outward dimensions, and in this very way nature increases the respiratory surface of a lung by a complex system of branching tubes and minute air-cells; but nevertheless in two similar and closely related animals, as also in two steam-engines of precisely the same make, the law is bound to hold that the rate of working must tend to vary with the square of the linear dimensions, according to Froude’s law of steamship comparison. In the case of a very large ship, built for speed, the difficulty is got over by increasing the size and number of the boilers, till the ratio between boiler-room and engine-room is far beyond what is required in an ordinary small vessel38; but though we find lung-space increased among animals where greater rate of working is required, as in general among birds, I do not know that it can be shewn to increase, as in the “over-boilered” ship, with the size of the animal, and in a ratio which outstrips that of the other bodily dimensions. If it be the case then, that the working mechanism of the muscles should be able to exert a force proportionate to the cube of the linear bodily dimensions, while the respiratory mechanism can only supply a store of energy at a rate proportional to the square of the said dimensions, the singular result ought to follow that, in swimming for instance, the larger fish ought to be able to put on a spurt of speed far in excess of the smaller one; but the distance travelled by the year’s end should be very much alike for both of them. And it should also follow that the curve of fatigue {24} should be a steeper one, and the staying power should be less, in the smaller than in the larger individual. This is the case of long-distance racing, where the big winner puts on his big spurt at the end. And for an analogous reason, wise men know that in the ’Varsity boat-race it is judicious and prudent to bet on the heavier crew.

Leaving aside the question of the supply of energy, and keeping to that of the mechanical efficiency of the machine, we may find endless biological illustrations of the principle of similitude.

In the case of the flying bird (apart from the initial difficulty of raising itself into the air, which involves another problem) it may be shewn that the bigger it gets (all its proportions remaining the same) the more difficult it is for it to maintain itself aloft in flight. The argument is as follows:

In order to keep aloft, the bird must communicate to the air a downward momentum equivalent to its own weight, and therefore proportional to the cube of its own linear dimensions. But the momentum so communicated is proportional to the mass of air driven downwards, and to the rate at which it is driven: the mass being proportional to the bird’s wing-area, and also (with any given slope of wing) to the speed of the bird, and the rate being again proportional to the bird’s speed; accordingly the whole momentum varies as the wing-area, i.e. as the square of the linear dimensions, and also as the square of the speed. Therefore, in order that the bird may maintain level flight, its speed must be proportional to the square root of its linear dimensions.

Now the rate at which the bird, in steady flight, has to work in order to drive itself forward, is the rate at which it communicates energy to the air; and this is proportional to mV² , i.e. to the mass and to the square of the velocity of the air displaced. But the mass of air displaced per second is proportional to the wing-area and to the speed of the bird’s motion, and therefore to the power 2½ of the linear dimensions; and the speed at which it is displaced is proportional to the bird’s speed, and therefore to the square root of the linear dimensions. Therefore the energy communicated per second (being proportional to the mass and to the square of the speed) is jointly proportional to the power 2½ of the linear dimensions, as above, and to the first power thereof: {25} that is to say, it increases in proportion to the power 3½ of the linear dimensions, and therefore faster than the weight of the bird increases.

Put in math­e­mat­i­cal form, the equations are as follows:

(m = the mass of air thrust downwards; V its velocity, proportional to that of the bird; M its momentum; l a linear dimension of the bird; w its weight; W the work done in moving itself forward.)

M = w = l³ .

But

M = m V,  and  m = l² V.

Therefore

M = l² V² ,   and

l² V² = l³ ,   or

V = √l.

But, again,

W = m V²

= l² V × V²

= l² × √l × l

= l^3½ .

The work requiring to be done, then, varies as the power 3½ of the bird’s linear dimensions, while the work of which the bird is capable depends on the mass of its muscles, and therefore varies as the cube of its linear dimensions39. The disproportion does not seem at first sight very great, but it is quite enough to tell. It is as much as to say that, every time we double the linear dimensions of the bird, the difficulty of flight is increased in the ratio of 2³ : 2^3½ , or 8 : 11·3, or, say, 1 : 1·4. If we take the ostrich to exceed the sparrow in linear dimensions as 25 : 1, which seems well within the mark, we have the ratio between 25^3½ and 25³ , or between 5⁷ : 5⁶ ; in other words, flight is just five times more difficult for the larger than for the smaller bird40.

The above in­ves­ti­ga­tion includes, besides the final result, a number of others, explicit or implied, which are of not less importance. Of these the simplest and also the most important is {26} contained in the equation V = √l, a result which happens to be identical with one we had also arrived at in the case of the fish. In the bird’s case it has a deeper significance than in the other; because it implies here not merely that the velocity will tend to increase in a certain ratio with the length, but that it must do so as an essential and primary condition of the bird’s remaining aloft. It is accordingly of great practical importance in aeronautics, for it shews how a provision of increasing speed must accompany every enlargement of our aeroplanes. If a given machine weighing, say, 500 lbs. be stable at 40 miles an hour, then one geometrically similar which weighs, say, a couple of tons must have its speed determined as follows:

W : w :: L³ : l³ :: 8 : 1.

Therefore

L : l :: 2 : 1.

But

V² : v² :: L : l.

Therefore

V : v :: √2 : 1 = 1·414 : 1.

That is to say, the larger machine must be capable of a speed equal to 1·414 × 40, or about 56½ miles per hour.

It is highly probable, as Lanchester41 remarks, that Lilienthal met his untimely death not so much from any intrinsic fault in the design or construction of his machine, but simply because his engine fell somewhat short of the power required to give the speed which was necessary for stability. An arrow is a very imperfectly designed aeroplane, but nevertheless it is evidently capable, to a certain extent and at a high velocity, of acquiring “stability” and hence of actual “flight”: the duration and consequent range of its trajectory, as compared with a bullet of similar initial velocity, being correspondingly benefited. When we return to our birds, and again compare the ostrich with the sparrow, we know little or nothing about the speed in flight of the latter, but that of the swift is estimated42 to vary from a minimum of 20 to 50 feet or more per second,—say from 14 to 35 miles per hour. Let us take the same lower limit as not far from the minimal velocity of the sparrow’s flight also; and it {27} would follow that the ostrich, of 25 times the sparrow’s linear dimensions, would be compelled to fly (if it flew at all) with a minimum velocity of 5 × 14, or 70 miles an hour.

The same principle of necessary speed, or the indispensable relation between the dimensions of a flying object and the minimum velocity at which it is stable, accounts for a great number of observed phenomena. It tells us why the larger birds have a marked difficulty in rising from the ground, that is to say, in acquiring to begin with the horizontal velocity necessary for their support; and why accordingly, as Mouillard43 and others have observed, the heavier birds, even those weighing no more than a pound or two, can be effectively “caged” in a small enclosure open to the sky. It tells us why very small birds, especially those as small as humming-birds, and à fortiori the still smaller insects, are capable of “stationary flight,” a very slight and scarcely perceptible velocity relatively to the air being sufficient for their support and stability. And again, since it is in all cases velocity relative to the air that we are speaking of, we comprehend the reason why one may always tell which way the wind blows by watching the direction in which a bird starts to fly.

It is not improbable that the ostrich has already reached a magnitude, and we may take it for certain that the moa did so, at which flight by muscular action, according to the normal anatomy of a bird, has become physiologically impossible. The same reasoning applies to the case of man. It would be very difficult, and probably absolutely impossible, for a bird to fly were it the bigness of a man. But Borelli, in discussing this question, laid even greater stress on the obvious fact that a man’s pectoral muscles are so immensely less in proportion than those of a bird, that however we may fit ourselves with wings we can never expect to move them by any power of our own relatively weaker muscles; so it is that artificial flight only became possible when an engine was devised whose efficiency was extraordinarily great in comparison with its weight and size.

Had Leonardo da Vinci known what Galileo knew, he would not have spent a great part of his life on vain efforts to make to himself wings. Borelli had learned the lesson thoroughly, and {28} in one of his chapters he deals with the proposition, “Est impossible, ut homines propriis viribus artificiose volare possint44.”

But just as it is easier to swim than to fly, so is it obvious that, in a denser atmosphere, the conditions of flight would be altered, and flight facilitated. We know that in the carboniferous epoch there lived giant dragon-flies, with wings of a span far greater than nowadays they ever attain; and the small bodies and huge extended wings of the fossil pterodactyles would seem in like manner to be quite abnormal according to our present standards, and to be beyond the limits of mechanical efficiency under present conditions. But as Harlé suggests45, following upon a suggestion of Arrhenius, we have only to suppose that in carboniferous and jurassic days the terrestrial atmosphere was notably denser than it is at present, by reason, for instance, of its containing a much larger proportion of carbonic acid, and we have at once a means of reconciling the apparent mechanical discrepancy.

Very similar problems, involving in various ways the principle of dynamical similitude, occur all through the physiology of locomotion: as, for instance, when we see that a cockchafer can carry a plate, many times his own weight, upon his back, or that a flea can jump many inches high.

Problems of this latter class have been admirably treated both by Galileo and by Borelli, but many later writers have remained ignorant of their work. Linnaeus, for instance, remarked that, if an elephant were as strong in proportion as a stag-beetle, it would be able to pull up rocks by the root, and to level mountains. And Kirby and Spence have a well-known passage directed to shew that such powers as have been conferred upon the insect have been withheld from the higher animals, for the reason that had these latter been endued therewith they would have “caused the early desolation of the world46.” {29}

Such problems as that which is presented by the flea’s jumping powers, though essentially physiological in their nature, have their interest for us here: because a steady, progressive diminution of activity with increasing size would tend to set limits to the possible growth in magnitude of an animal just as surely as those factors which tend to break and crush the living fabric under its own weight. In the case of a leap, we have to do rather with a sudden impulse than with a continued strain, and this impulse should be measured in terms of the velocity imparted. The velocity is proportional to the impulse (x), and inversely proportional to the mass (M) moved: V = x ⁄ M. But, according to what we still speak of as “Borelli’s law,” the impulse (i.e. the work of the impulse) is proportional to the volume of the muscle by which it is produced47, that is to say (in similarly constructed animals) to the mass of the whole body; for the impulse is proportional on the one hand to the cross-section of the muscle, and on the other to the distance through which it contracts. It follows at once from this that the velocity is constant, whatever be the size of the animals: in other words, that all animals, provided always that they are similarly fashioned, with their various levers etc., in like proportion, ought to jump, not to the same relative, but to the same actual height48. According to this, then, the flea is not a better, but rather a worse jumper than a horse or a man. As a matter of fact, Borelli is careful to point out that in the act of leaping the impulse is not actually instantaneous, as in the blow of a hammer, but takes some little time, during which the levers are being extended by which the centre of gravity of the animal is being propelled forwards; and this interval of time will be longer in the case of the longer levers of the larger animal. To some extent, then, this principle acts as a corrective to the more general one, {30} and tends to leave a certain balance of advantage, in regard to leaping power, on the side of the larger animal49.

But on the other hand, the question of strength of materials comes in once more, and the factors of stress and strain and bending moment make it, so to speak, more and more difficult for nature to endow the larger animal with the length of lever with which she has provided the flea or the grasshopper.

To Kirby and Spence it seemed that “This wonderful strength of insects is doubtless the result of something peculiar in the structure and arrangement of their muscles, and principally their extraordinary power of contraction.” This hypothesis, which is so easily seen, on physical grounds, to be unnecessary, has been amply disproved in a series of excellent papers by F. Plateau50.

A somewhat simple problem is presented to us by the act of walking. It is obvious that there will be a great economy of work, if the leg swing at its normal pendulum-rate; and, though this rate is hard to calculate, owing to the shape and the jointing of the limb, we may easily convince ourselves, by counting our steps, that the leg does actually swing, or tend to swing, just as a pendulum does, at a certain definite rate51. When we walk quicker, we cause the leg-pendulum to describe a greater arc, but we do not appreciably cause it to swing, or vibrate, quicker, until we shorten the pendulum and begin to run. Now let two individuals, A and B, walk in a similar fashion, that is to say, with a similar angle of swing. The arc through which the leg swings, or the amplitude of each step, will therefore vary as the length of leg, or say as a ⁄ b; but the time of swing will vary as the square {31} root of the pendulum-length, or √a ⁄ √b. Therefore the velocity, which is measured by amplitude ⁄ time, will also vary as the square-roots of the length of leg: that is to say, the average velocities of A and B are in the ratio of √a : √b.

The smaller man, or smaller animal, is so far at a disadvantage compared with the larger in speed, but only to the extent of the ratio between the square roots of their linear dimensions: whereas, if the rate of movement of the limb were identical, irrespective of the size of the animal,—if the limbs of the mouse for instance swung at the same rate as those of the horse,—then, as F. Plateau said, the mouse would be as slow or slower in its gait than the tortoise. M. Delisle52 observed a “minute fly” walk three inches in half-a-second. This was good steady walking. When we walk five miles an hour we go about 88 inches in a second, or 88 ⁄ 6 = 14·7 times the pace of M. Delisle’s fly. We should walk at just about the fly’s pace if our stature were 1 ⁄ (14·7)² , or 1 ⁄ 216 of our present height,—say 72 ⁄ 216 inches, or one-third of an inch high.

But the leg comprises a complicated system of levers, by whose various exercise we shall obtain very different results. For instance, by being careful to rise upon our instep, we considerably increase the length or amplitude of our stride, and very considerably increase our speed accordingly. On the other hand, in running, we bend and so shorten the leg, in order to accommodate it to a quicker rate of pendulum-swing53. In short, the jointed structure of the leg permits us to use it as the shortest possible pendulum when it is swinging, and as the longest possible lever when it is exerting its propulsive force.

Apart from such modifications as that described in the last paragraph,—apart, that is to say, from differences in mechanical construction or in the manner in which the mechanism is used,—we have now arrived at a curiously simple and uniform result. For in all the three forms of locomotion which we have attempted {32} to study, alike in swimming, in flight and in walking, the general result, attained under very different conditions and arrived at by very different modes of reasoning, is in every case that the velocity tends to vary as the square root of the linear dimensions of the organism.

From all the foregoing discussion we learn that, as Crookes once upon a time remarked54, the form as well as the actions of our bodies are entirely conditioned (save for certain exceptions in the case of aquatic animals, nicely balanced with the density of the surrounding medium) by the strength of gravity upon this globe. Were the force of gravity to be doubled, our bipedal form would be a failure, and the majority of terrestrial animals would resemble short-legged saurians, or else serpents. Birds and insects would also suffer, though there would be some compensation for them in the increased density of the air. While on the other hand if gravity were halved, we should get a lighter, more graceful, more active type, requiring less energy and less heat, less heart, less lungs, less blood.

Throughout the whole field of morphology we may find examples of a tendency (referable doubtless in each case to some definite physical cause) for surface to keep pace with volume, through some alteration of its form. The development of “villi” on the inner surface of the stomach and intestine (which enlarge its surface much as we enlarge the effective surface of a bath-towel), the various valvular folds of the intestinal lining, including the remarkable “spiral fold” of the shark’s gut, the convolutions of the brain, whose complexity is evidently correlated (in part at least) with the magnitude of the animal,—all these and many more are cases in which a more or less constant ratio tends to be maintained between mass and surface, which ratio would have been more and more departed from had it not been for the alterations of surface-form55. {33}

In the case of very small animals, and of individual cells, the principle becomes especially important, in consequence of the molecular forces whose action is strictly limited to the superficial layer. In the cases just mentioned, action is facilitated by increase of surface: diffusion, for instance, of nutrient liquids or respiratory gases is rendered more rapid by the greater area of surface; but there are other cases in which the ratio of surface to mass may make an essential change in the whole condition of the system. We know, for instance, that iron rusts when exposed to moist air, but that it rusts ever so much faster, and is soon eaten away, if the iron be first reduced to a heap of small filings; this is a mere difference of degree. But the spherical surface of the raindrop and the spherical surface of the ocean (though both happen to be alike in math­e­mat­i­cal form) are two totally different phenomena, the one due to surface-energy, and the other to that form of mass-energy which we ascribe to gravity. The contrast is still more clearly seen in the case of waves: for the little ripple, whose form and manner of propagation are governed by surface-tension, is found to travel with a velocity which is inversely as the square root of its length; while the ordinary big waves, controlled by gravitation, have a velocity directly proportional to the square root of their wave-length. In like manner we shall find that the form of all small organisms is largely independent of gravity, and largely if not mainly due to the force of surface-tension: either as the direct result of the continued action of surface tension on the semi-fluid body, or else as the result of its action at a prior stage of development, in bringing about a form which subsequent chemical changes have rendered rigid and lasting. In either case, we shall find a very great tendency in small organisms to assume either the spherical form or other simple forms related to ordinary inanimate surface-tension phenomena; which forms do not recur in the external morphology of large animals, or if they in part recur it is for other reasons. {34}

Now this is a very important matter, and is a notable illustration of that principle of similitude which we have already discussed in regard to several of its manifestations. We are coming easily to a conclusion which will affect the whole course of our argument throughout this book, namely that there is an essential difference in kind between the phenomena of form in the larger and the smaller organisms. I have called this book a study of Growth and Form, because in the most familiar illustrations of organic form, as in our own bodies for example, these two factors are inseparably associated, and because we are here justified in thinking of form as the direct resultant and consequence of growth: of growth, whose varying rate in one direction or another has produced, by its gradual and unequal increments, the successive stages of development and the final configuration of the whole material structure. But it is by no means true that form and growth are in this direct and simple fashion correlative or complementary in the case of minute portions of living matter. For in the smaller organisms, and in the individual cells of the larger, we have reached an order of magnitude in which the intermolecular forces strive under favourable conditions with, and at length altogether outweigh, the force of gravity, and also those other forces leading to movements of convection which are the prevailing factors in the larger material aggregate.

However we shall require to deal more fully with this matter in our discussion of the rate of growth, and we may leave it meanwhile, in order to deal with other matters more or less directly concerned with the magnitude of the cell.

The living cell is a very complex field of energy, and of energy of many kinds, surface-energy included. Now the whole surface-energy of the cell is by no means restricted to its outer surface; for the cell is a very heterogeneous structure, and all its protoplasmic alveoli and other visible (as well as invisible) heterogeneities make up a great system of internal surfaces, at every part of which one “phase” comes in contact with another “phase,” and surface-energy is accordingly manifested. But still, the external surface is a definite portion of the system, with a definite “phase” of its own, and however little we may know of the distribution of the total energy of the system, it is at least plain that {35} the conditions which favour equi­lib­rium will be greatly altered by the changed ratio of external surface to mass which a change of magnitude, unaccompanied by change of form, produces in the cell. In short, however it may be brought about, the phenomenon of division of the cell will be precisely what is required to keep ap­prox­i­mate­ly constant the ratio between surface and mass, and to restore the balance between the surface-energy and the other energies of the system. When a germ-cell, for instance, divides or “segments” into two, it does not increase in mass; at least if there be some slight alleged tendency for the egg to increase in mass or volume during segmentation, it is very slight indeed, generally imperceptible, and wholly denied by some56. The development or growth of the egg from a one-celled stage to stages of two or many cells, is thus a somewhat peculiar kind of growth; it is growth which is limited to increase of surface, unaccompanied by growth in volume or in mass.

In the case of a soap-bubble, by the way, if it divide into two bubbles, the volume is actually diminished57 while the surface-area is greatly increased. This is due to a cause which we shall have to study later, namely to the increased pressure due to the greater curvature of the smaller bubbles.

An immediate and remarkable result of the principles just described is a tendency on the part of all cells, according to their kind, to vary but little about a certain mean size, and to have, in fact, certain absolute limitations of magnitude.

Sachs58 pointed out, in 1895, that there is a tendency for each nucleus to be only able to gather around itself a certain definite amount of protoplasm. Driesch59, a little later, found that, by artificial subdivision of the egg, it was possible to rear dwarf sea-urchin larvae, one-half, one-quarter, or even one-eighth of their {36} normal size; and that these dwarf bodies were composed of only a half, a quarter or an eighth of the normal number of cells. Similar observations have been often repeated and amply confirmed. For instance, in the development of Crepidula (a little American “slipper-limpet,” now much at home on our own oyster-beds), Conklin60 has succeeded in rearing dwarf and giant individuals, of which the latter may be as much as twenty-five times as big as the former. But nevertheless, the individual cells, of skin, gut, liver, muscle, and of all the other tissues, are just the same size in one as in the other,—in dwarf and in giant61. Driesch has laid particular stress upon this principle of a “fixed cell-size.”

We get an excellent, and more familiar illustration of the same principle in comparing the large brain-cells or ganglion-cells, both of the lower and of the higher animals62.

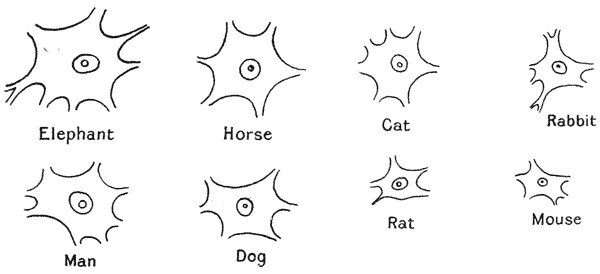
Fig. 1. Motor ganglion-cells, from the cervical spinal cord.

(From Minot, after Irving Hardesty.)

In Fig. 1 we have certain identical nerve-cells taken from various mammals, from the mouse to the elephant, all represented on the same scale of magnification; and we see at once that they are all of much the same order of magnitude. The nerve-cell of the elephant is about twice that of the mouse in linear dimensions, and therefore about eight times greater in volume, or mass. But making some allowance for difference of shape, the linear dimensions of the elephant are to those of the mouse in a ratio certainly not less than one to fifty; from which it would follow that the bulk of the larger animal is something like 125,000 times that of the less. And it also follows, the size of the nerve-cells being {37} about as eight to one, that, in cor­re­spon­ding parts of the nervous system of the two animals, there are more than 15,000 times as many individual cells in one as in the other. In short we may (with Enriques) lay it down as a general law that among animals, whether large or small, the ganglion-cells vary in size within narrow limits; and that, amidst all the great variety of structural type of ganglion observed in different classes of animals, it is always found that the smaller species have simpler ganglia than the larger, that is to say ganglia containing a smaller number of cellular elements63. The bearing of such simple facts as this upon the cell-theory in general is not to be disregarded; and the warning is especially clear against exaggerated attempts to correlate physiological processes with the visible mechanism of associated cells, rather than with the system of energies, or the field of force, which is associated with them. For the life of {38} the body is more than the sum of the properties of the cells of which it is composed: as Goethe said, “Das Lebendige ist zwar in Elemente zerlegt, aber man kann es aus diesen nicht wieder zusammenstellen und beleben.”

Among certain lower and microscopic organisms, such for instance as the Rotifera, we are still more palpably struck by the small number of cells which go to constitute a usually complex organ, such as kidney, stomach, ovary, etc. We can sometimes number them in a few units, in place of the thousands that make up such an organ in larger, if not always higher, animals. These facts constitute one among many arguments which combine to teach us that, however important and advantageous the subdivision of organisms into cells may be from the constructional, or from the dynamical point of view, the phenomenon has less essential importance in theoretical biology than was once, and is often still, assigned to it.

Again, just as Sachs shewed that there was a limit to the amount of cytoplasm which could gather round a single nucleus, so Boveri has demonstrated that the nucleus itself has definite limitations of size, and that, in cell-division after fertilisation, each new nucleus has the same size as its parent-nucleus64.

In all these cases, then, there are reasons, partly no doubt physiological, but in very large part purely physical, which set limits to the normal magnitude of the organism or of the cell. But as we have already discussed the existence of absolute and definite limitations, of a physical kind, to the possible increase in magnitude of an organism, let us now enquire whether there be not also a lower limit, below which the very existence of an organism is impossible, or at least where, under changed conditions, its very nature must be profoundly modified.

Among the smallest of known organisms we have, for instance, Micromonas mesnili, Bonel, a flagellate infusorian, which measures about ·34 µ, or ·00034 mm., by ·00025 mm.; smaller even than this we have a pathogenic micrococcus of the rabbit, M. progrediens, Schröter, the diameter of which is said to be only ·00015 mm. or ·15 µ, or 1·5 × 10⁻⁵ cm.,—about equal to the thickness of {39} the thinnest gold-leaf; and as small if not smaller still are a few bacteria and their spores. But here we have reached, or all but reached the utmost limits of ordinary microscopic vision; and there remain still smaller organisms, the so-called “filter-passers,” which the ultra-microscope reveals, but which are mainly brought within our ken only by the maladies, such as hydrophobia, foot-and-mouth disease, or the “mosaic” disease of the tobacco-plant, to which these invisible micro-organisms give rise65. Accordingly, since it is only by the diseases which they occasion that these tiny bodies are made known to us, we might be tempted to suppose that innumerable other invisible organisms, smaller and yet smaller, exist unseen and unrecognised by man.

Fig. 2. Relative magnitudes of: A, human blood-corpuscle (7·5 µ in diameter); B, Bacillus anthracis (4 – 15 µ × 1 µ); C, various Micrococci (diam. 0·5 – 1 µ, rarely 2 µ); D, Micromonas progrediens, Schröter (diam. 0·15 µ).

To illustrate some of these small magnitudes I have adapted the preceding diagram from one given by Zsigmondy66. Upon the {40} same scale the minute ultramicroscopic particles of colloid gold would be represented by the finest dots which we could make visible to the naked eye upon the paper.

A bacillus of ordinary, typical size is, say, 1 µ in length. The length (or height) of a man is about a million and three-quarter times as great, i.e. 1·75 metres, or 1·75 × 10⁶ µ; and the mass of the man is in the neighbourhood of five million, million, million (5 × 10¹⁸) times greater than that of the bacillus. If we ask whether there may not exist organisms as much less than the bacillus as the bacillus is less than the dimensions of a man, it is very easy to see that this is quite impossible, for we are rapidly approaching a point where the question of molecular dimensions, and of the ultimate divisibility of matter, begins to call for our attention, and to obtrude itself as a crucial factor in the case.

Clerk Maxwell dealt with this matter in his article “Atom67,” and, in somewhat greater detail, Errera discusses the question on the following lines68. The weight of a hydrogen molecule is, according to the physical chemists, somewhere about 8·6 × 2 × 10⁻²² milligrammes; and that of any other element, whose molecular weight is M, is given by the equation

(M) = 8·6 × M × 10⁻²² .

Accordingly, the weight of the atom of sulphur may be taken as

8·6 × 32 × 10⁻²² mgm. = 275 × 10⁻²² mgm.

The analysis of ordinary bacteria shews them to consist69 of about 85% of water, and 15% of solids; while the solid residue of vegetable protoplasm contains about one part in a thousand of sulphur. We may assume, therefore, that the living protoplasm contains about

¹⁄₁₀₀₀ × ¹⁵⁄₁₀₀ = 15 × 10⁻⁵

parts of sulphur, taking the total weight as = 1.

But our little micrococcus, of 0·15 µ in diameter, would, if it were spherical, have a volume of

^π⁄₆ × 0·15³ µ = 18 × 10⁻⁴ cubic microns; {41}

and therefore (taking its density as equal to that of water), a weight of

18 × 10⁻⁴ × 10⁻⁹ = 18 × 10⁻¹³ mgm.

But of this total weight, the sulphur represents only

18 × 10⁻¹³ × 15 × 10⁻⁵ = 27 × 10⁻¹⁷ mgm.

And if we divide this by the weight of an atom of sulphur, we have

(27 × 10⁻¹⁷) ÷ (275 × 10⁻²²) = 10,000, or thereby.

According to this estimate, then, our little Micrococcus progrediens should contain only about 10,000 atoms of sulphur, an element indispensable to its protoplasmic constitution; and it follows that an organism of one-tenth the diameter of our micrococcus would only contain 10 sulphur-atoms, and therefore only ten chemical “molecules” or units of protoplasm!

It may be open to doubt whether the presence of sulphur be really essential to the constitution of the proteid or “protoplasmic” molecule; but Errera gives us yet another illustration of a similar kind, which is free from this objection or dubiety. The molecule of albumin, as is generally agreed, can scarcely be less than a thousand times the size of that of such an element as sulphur: according to one particular determination70, serum albumin has a constitution cor­re­spon­ding to a molecular weight of 10,166, and even this may be far short of the true complexity of a typical albuminoid molecule. The weight of such a molecule is

8·6 × 10166 × 10⁻²² = 8·7 × 10⁻¹⁸ mgm.

Now the bacteria contain about 14% of albuminoids, these constituting by far the greater part of the dry residue; and therefore (from equation (5)), the weight of albumin in our micrococcus is about

¹⁴⁄₁₀₀ × 18 × 10⁻¹³ = 2·5 × 10⁻¹³ mgm.

If we divide this weight by that which we have arrived at as the weight of an albumin molecule, we have

2·5 × 10⁻¹³ ÷ (8·7 × 10⁻¹⁸) = 2·9 × 10⁻⁴ ,

in other words, our micrococcus apparently contains something less than 30,000 molecules of albumin. {42}

According to the most recent estimates, the weight of the hydrogen molecule is somewhat less than that on which Errera based his calculations, namely about 16 × 10⁻²² mgms. and according to this value, our micrococcus would contain just about 27,000 albumin molecules. In other words, whichever determination we accept, we see that an organism one-tenth as large as our micrococcus, in linear dimensions, would only contain some thirty molecules of albumin; or, in other words, our micrococcus is only about thirty times as large, in linear dimensions, as a single albumin molecule71.

We must doubtless make large allowances for uncertainty in the assumptions and estimates upon which these calculations are based; and we must also remember that the data with which the physicist provides us in regard to molecular magnitudes are, to a very great extent, maximal values, above which the molecular magnitude (or rather the sphere of the molecule’s range of motion) is not likely to lie: but below which there is a greater element of uncertainty as to its possibly greater minuteness. But nevertheless, when we shall have made all reasonable allowances for uncertainty upon the physical side, it will still be clear that the smallest known bodies which are described as organisms draw nigh towards molecular magnitudes, and we must recognise that the subdivision of the organism cannot proceed to an indefinite extent, and in all probability cannot go very much further than it appears to have done in these already discovered forms. For, even, after giving all due regard to the complexity of our unit (that is to say the albumin-molecule), with all the increased possibilities of interrelation with its neighbours which this complexity implies, we cannot but see that physiologically, and comparatively speaking, we have come down to a very simple thing.

While such con­si­de­ra­tions as these, based on the chemical composition of the organism, teach us that there must be a definite lower limit to its magnitude, other con­si­de­ra­tions of a purely physical kind lead us to the same conclusion. For our discussion of the principle of similitude has already taught us that, long before we reach these almost infinitesimal magnitudes, the {43} diminishing organism will have greatly changed in all its physical relations, and must at length arrive under conditions which must surely be incompatible with anything such as we understand by life, at least in its full and ordinary development and manifestation.

We are told, for instance, that the powerful force of surface-tension, or capillarity, begins to act within a range of about 1 ⁄ 500,000 of an inch, or say 0·05 µ. A soap-film, or a film of oil upon water, may be attenuated to far less magnitudes than this; the black spots upon a soap-bubble are known, by various concordant methods of measurement, to be only about 6 × 10⁻⁷ cm., or about ·006 µ thick, and Lord Rayleigh and M. Devaux72 have obtained films of oil of ·002 µ, or even ·001 µ in thickness.

But while it is possible for a fluid film to exist in these almost molecular dimensions, it is certain that, long before we reach them, there must arise new conditions of which we have little knowledge and which it is not easy even to imagine.

It would seem that, in an organism of ·1 µ in diameter, or even rather more, there can be no essential distinction between the interior and the surface layers. No hollow vesicle, I take it, can exist of these dimensions, or at least, if it be possible for it to do so, the contained gas or fluid must be under pressures of a formidable kind73, and of which we have no knowledge or experience. Nor, I imagine, can there be any real complexity, or heterogeneity, of its fluid or semi-fluid contents; there can be no vacuoles within such a cell, nor any layers defined within its fluid substance, for something of the nature of a boundary-film is the necessary condition of the existence of such layers. Moreover, the whole organism, provided that it be fluid or semi-fluid, can only be spherical in form. What, then, can we attribute, in the way of properties, to an organism of a size as small as, or smaller than, say ·05 µ? It must, in all probability, be a homogeneous, structureless sphere, composed of a very small number of albuminoid or other molecules. Its vital properties and functions must be extraordinarily limited; its specific outward characters, even if we could see it, must be nil; and its specific properties must be little more than those of an ion-laden corpuscle, enabling it to perform {44} this or that chemical reaction, or to produce this or that pathogenic effect. Even among inorganic, non-living bodies, there must be a certain grade of minuteness at which the ordinary properties become modified. For instance, while under ordinary circumstances cry­stal­li­sa­tion starts in a solution about a minute solid fragment or crystal of the salt, Ostwald has shewn that we may have particles so minute that they fail to serve as a nucleus for cry­stal­li­sa­tion,—which is as much as to say that they are too minute to have the form and properties of a “crystal”; and again, in his thin oil-films, Lord Rayleigh has noted the striking change of physical properties which ensues when the film becomes attenuated to something less than one close-packed layer of molecules74.

Thus, as Clerk Maxwell put it, “molecular science sets us face to face with physiological theories. It forbids the physiologist from imagining that structural details of infinitely small dimensions [such as Leibniz assumed, one within another, ad infinitum] can furnish an explanation of the infinite variety which exists in the properties and functions of the most minute organisms.” And for this reason he reprobates, with not undue severity, those advocates of pangenesis and similar theories of heredity, who would place “a whole world of wonders within a body so small and so devoid of visible structure as a germ.” But indeed it scarcely needed Maxwell’s criticism to shew forth the immense physical difficulties of Darwin’s theory of Pangenesis: which, after all, is as old as Democritus, and is no other than that Promethean particulam undique desectam of which we have read, and at which we have smiled, in our Horace.

There are many other ways in which, when we “make a long excursion into space,” we find our ordinary rules of physical behaviour entirely upset. A very familiar case, analysed by Stokes, is that the viscosity of the surrounding medium has a relatively powerful effect upon bodies below a certain size. A droplet of water, a thousandth of an inch (25 µ) in diameter, cannot fall in still air quicker than about an inch and a half per second; and as its size decreases, its resistance varies as the diameter, and not (as with larger bodies) as the surface of the {45} drop. Thus a drop one-tenth of that size (2·5 µ), the size, apparently, of the drops of water in a light cloud, will fall a hundred times slower, or say an inch a minute; and one again a tenth of this diameter (say ·25 µ, or about twice as big, in linear dimensions, as our micrococcus), will scarcely fall an inch in two hours. By reason of this principle, not only do the smaller bacteria fall very slowly through the air, but all minute bodies meet with great proportionate resistance to their movements in a fluid. Even such comparatively large organisms as the diatoms and the foraminifera, laden though they are with a heavy shell of flint or lime, seem to be poised in the water of the ocean, and fall in it with exceeding slowness.

The Brownian movement has also to be reckoned with,—that remarkable phenomenon studied nearly a century ago (1827) by Robert Brown, facile princeps botanicorum. It is one more of those fundamental physical phenomena which the biologists have contributed, or helped to contribute, to the science of physics.

The quivering motion, accompanied by rotation, and even by translation, manifested by the fine granular particles issuing from a crushed pollen-grain, and which Robert Brown proved to have no vital significance but to be manifested also by all minute particles whatsoever, organic and inorganic, was for many years unexplained. Nearly fifty years after Brown wrote, it was said to be “due, either directly to some calorical changes continually taking place in the fluid, or to some obscure chemical action between the solid particles and the fluid which is indirectly promoted by heat75.” Very shortly after these last words were written, it was ascribed by Wiener to molecular action, and we now know that it is indeed due to the impact or bombardment of molecules upon a body so small that these impacts do not for the moment, as it were, “average out” to ap­prox­i­mate equality on all sides. The movement becomes manifest with particles of somewhere about 20 µ in diameter, it is admirably displayed by particles of about 12 µ in diameter, and becomes more marked the smaller the particles are. The bombardment causes our particles to behave just like molecules of uncommon size, and this {46} behaviour is manifested in several ways76. Firstly, we have the quivering movement of the particles; secondly, their movement backwards and forwards, in short, straight, disjointed paths; thirdly, the particles rotate, and do so the more rapidly the smaller they are, and by theory, confirmed by observation, it is found that particles of 1 µ in diameter rotate on an average through 100° per second, while particles of 13 µ in diameter turn through only 14° per minute. Lastly, the very curious result appears, that in a layer of fluid the particles are not equally distributed, nor do they all ever fall, under the influence of gravity, to the bottom. But just as the molecules of the atmosphere are so distributed, under the influence of gravity, that the density (and therefore the number of molecules per unit volume) falls off in geometrical progression as we ascend to higher and higher layers, so is it with our particles, even within the narrow limits of the little portion of fluid under our microscope. It is only in regard to particles of the simplest form that these phenomena have been theoretically investigated77, and we may take it as certain that more complex particles, such as the twisted body of a Spirillum, would show other and still more complicated manifestations. It is at least clear that, just as the early microscopists in the days before Robert Brown never doubted but that these phenomena were purely vital, so we also may still be apt to confuse, in certain cases, the one phenomenon with the other. We cannot, indeed, without the most careful scrutiny, decide whether the movements of our minutest organisms are intrinsically “vital” (in the sense of being beyond a physical mechanism, or working model) or not. For example, Schaudinn has suggested that the undulating movements of Spirochaete pallida must be due to the presence of a minute, unseen, “undulating membrane”; and Doflein says of the same species that “sie verharrt oft mit eigenthümlich zitternden Bewegungen zu einem Orte.” Both movements, the trembling or quivering {47} movement described by Doflein, and the undulating or rotating movement described by Schaudinn, are just such as may be easily and naturally interpreted as part and parcel of the Brownian phenomenon.

While the Brownian movement may thus simulate in a deceptive way the active movements of an organism, the reverse statement also to a certain extent holds good. One sometimes lies awake of a summer’s morning watching the flies as they dance under the ceiling. It is a very remarkable dance. The dancers do not whirl or gyrate, either in company or alone; but they advance and retire; they seem to jostle and rebound; between the rebounds they dart hither or thither in short straight snatches of hurried flight; and turn again sharply in a new rebound at the end of each little rush. Their motions are wholly “erratic,” independent of one another, and devoid of common purpose. This is nothing else than a vastly magnified picture, or simulacrum, of the Brownian movement; the parallel between the two cases lies in their complete irregularity, but this in itself implies a close resemblance. One might see the same thing in a crowded market-place, always provided that the bustling crowd had no business whatsoever. In like manner Lucretius, and Epicurus before him, watched the dust-motes quivering in the beam, and saw in them a mimic representation, rei simulacrum et imago, of the eternal motions of the atoms. Again the same phenomenon may be witnessed under the microscope, in a drop of water swarming with Paramoecia or suchlike Infusoria; and here the analogy has been put to a numerical test. Following with a pencil the track of each little swimmer, and dotting its place every few seconds (to the beat of a metronome), Karl Przibram found that the mean successive distances from a common base-line obeyed with great exactitude the “Einstein formula,” that is to say the particular form of the “law of chance” which is applicable to the case of the Brownian movement78. The phenomenon is (of course) merely analogous, and by no means identical with the Brownian movement; for the range of motion of the little active organisms, whether they be gnats or infusoria, is vastly greater than that of the minute particles which are {48} passive under bombardment; but nevertheless Przibram is inclined to think that even his comparatively large infusoria are small enough for the molecular bombardment to be a stimulus, though not the actual cause, of their irregular and interrupted movements.

There is yet another very remarkable phenomenon which may come into play in the case of the minutest of organisms; and this is their relation to the rays of light, as Arrhenius has told us. On the waves of a beam of light, a very minute particle (in vacuo) should be actually caught up, and carried along with an immense velocity; and this “radiant pressure” exercises its most powerful influence on bodies which (if they be of spherical form) are just about ·00016 mm., or ·16 µ in diameter. This is just about the size, as we have seen, of some of our smallest known protozoa and bacteria, while we have some reason to believe that others yet unseen, and perhaps the spores of many, are smaller still. Now we have seen that such minute particles fall with extreme slowness in air, even at ordinary atmospheric pressures: our organism measuring ·16 µ would fall but 83 metres in a year, which is as much as to say that its weight offers practically no impediment to its transference, by the slightest current, to the very highest regions of the atmosphere. Beyond the atmosphere, however, it cannot go, until some new force enable it to resist the attraction of terrestrial gravity, which the viscosity of an atmosphere is no longer at hand to oppose. But it is conceivable that our particle may go yet farther, and actually break loose from the bonds of earth. For in the upper regions of the atmosphere, say fifty miles high, it will come in contact with the rays and flashes of the Northern Lights, which consist (as Arrhenius maintains) of a fine dust, or cloud of vapour-drops, laden with a charge of negative electricity, and projected outwards from the sun. As soon as our particle acquires a charge of negative electricity it will begin to be repelled by the similarly laden auroral particles, and the amount of charge necessary to enable a particle of given size (such as our little monad of ·16 µ) to resist the attraction of gravity may be calculated, and is found to be such as the actual conditions can easily supply. Finally, when once set free from the entanglement of the earth’s {49} atmosphere, the particle may be propelled by the “radiant pressure” of light, with a velocity which will carry it.—like Uriel gliding on a sunbeam,—as far as the orbit of Mars in twenty days, of Jupiter in eighty days, and as far as the nearest fixed star in three thousand years! This, and much more, is Arrhenius’s contribution towards the acceptance of Lord Kelvin’s hypothesis that life may be, and may have been, disseminated across the bounds of space, throughout the solar system and the whole universe!

It may well be that we need attach no great practical importance to this bold conception; for even though stellar space be shewn to be mare liberum to minute material travellers, we may be sure that those which reach a stellar or even a planetary bourne are infinitely, or all but infinitely, few. But whether or no, the remote possibilities of the case serve to illustrate in a very vivid way the profound differences of physical property and potentiality which are associated in the scale of magnitude with simple differences of degree.