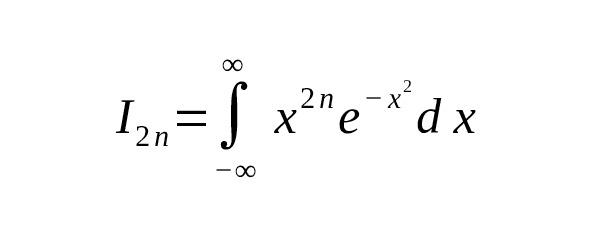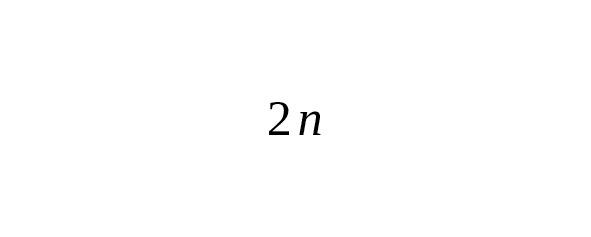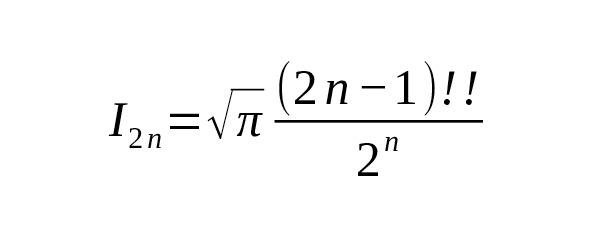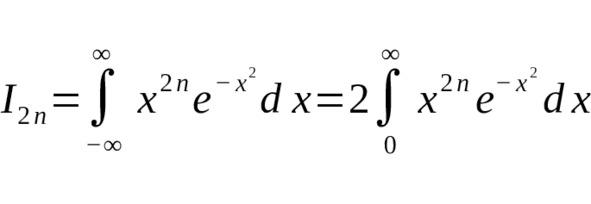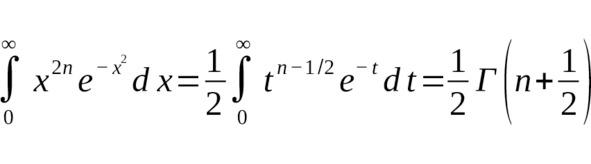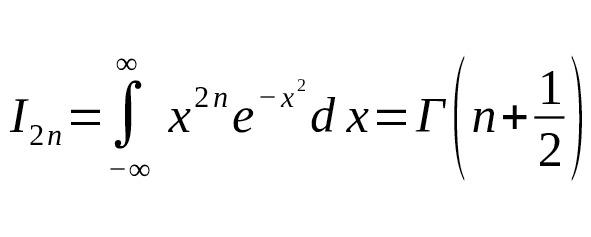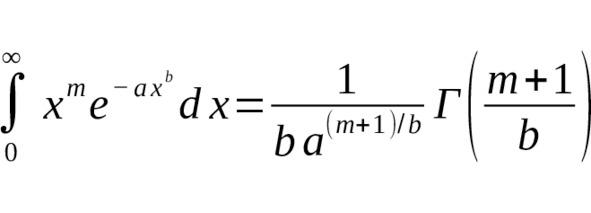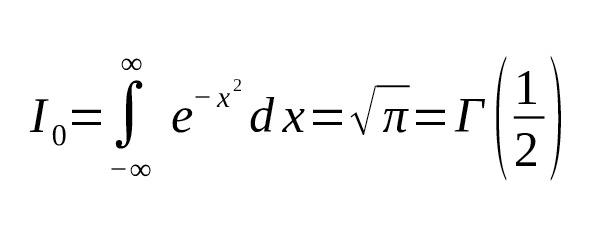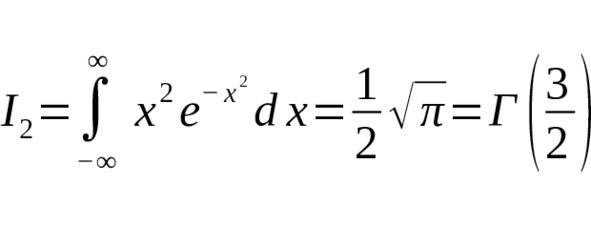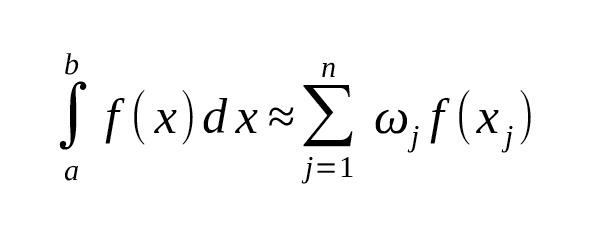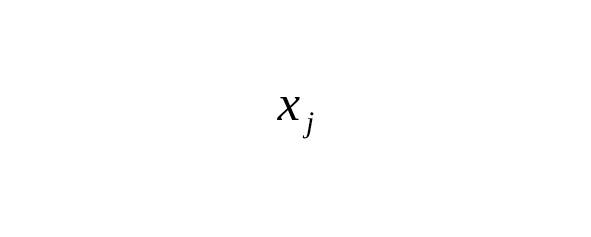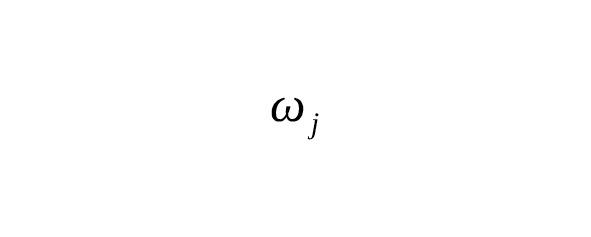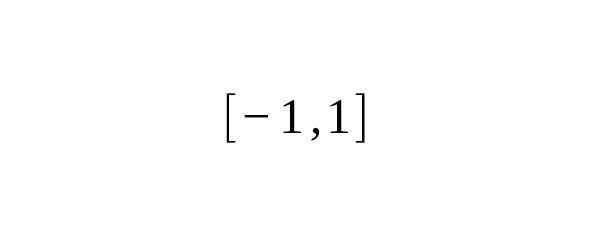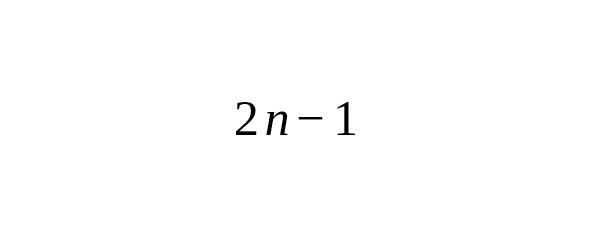Оглавление

Четные степени Интеграла Гаусса связь с гамма-функцией

Связь чётных степеней интеграла Гаусса с гамма-функцией выражается следующим образом:

Рассмотрим интеграл вида

где — чётная степень.

Этот интеграл выражается через гамма-функцию так:

или, используя свойства гамма-функции:

Замена переменной $ t = x^2 $ приводит к гамма-функции:

Таким образом,

— Чётные моменты гауссового интеграла выражаются через гамма-функцию от полуцелого аргумента.

— Для общего случая: где для стандартного Гаусса $ m=2n,,a=1,,b=2 $ [1] [2].

Это показывает прямую связь между чётными степенями интеграла Гаусса и значениями гамма-функции, и объясняет, почему значения при полуцелых аргументах выражаются через $ \sqrt {\pi} $ [1] [2].

— Например, для $ n=0 $ (то есть стандартный интеграл Гаусса):

— Для $ n=1 $:

То есть значения чётных моментных интегралов Гаусса прямо выражаются через гамма-функцию для полуцелых аргументов [1] [2].

Примеры использования:

⁂

Перечисли литературу на данную тему

Основные источники по теме интегралов Гаусса с четными степенями и связанных с этим тем квадартур, вычисления и применения:

— Фихтенгольц Г. М. «Курс дифференциального и интегрального исчисления», т.2. Классический учебник, подробно рассматривает гауссовы интегралы, их свойства и вычисления ^[3].

— Крайнов В. А. «Численные методы вычисления определенного интеграла». В пособии разбираются методы точного и приближенного вычисления интегралов, в том числе гауссовых, обсуждается точность для многочленов четной степени и приводятся формулы ^[4].

— Fedotov A.A. «Численные методы интегрирования». Современное пособие с практическими примерами численного вычисления гауссовых интегралов и их приложениями ^[5].

— Пастухов Д. Ф. «Квадратуры Гаусса. Интегральные уравнения». Методические указания по построению и применению квадратурных формул Гаусса для вычисления интегралов от многочленов даже высокой степени ^[6].

— Добрынина С. В. «Квадратурные и кубатурные формулы». Пособие содержит практические задания и разбор правил приближенного интегрирования, в том числе формулы Гаусса для интегралов с весами и многочленами ^[7].

— Арушанян И. О. «Алгоритмы приближенного вычисления интегралов». Обсуждаются методы вычисления интегралов с различными степенями точности, включая использование четных степеней в гауссовых интегралах ^[8].

Эти книги и пособия подходят для углубленного изучения вычисления и теории гауссовых интегралов, их свойств и приложений.

⁂
Теоретические основы квадратурных формул

Квадратурные формулы — это классический математический инструмент для приближённого вычисления определённых интегралов по значениям функции в конечном числе точек. Их основная задача — заменить вычисление интеграла суммой, где коэффициенты и точки выбора (узлы) подбираются для достижения максимальной точности на определённом классе функций [9] [10] [11].

Общий вид квадратурной формулы

Любая квадратурная формула обычно имеет следующий вид:

где:

— — узлы формулы (точки, в которых вычисляется функция),

— — веса (коэффициенты, с которыми берется значение функции в узлах).

Теоретические положения

— Точность квадратурной формулы определяется тем, для какого класса функций формула дает точное значение интеграла. Обычно это многочлены степени не выше некоторого значения.

— Погрешность (остаточный член) квадратурной формулы показывает, насколько точно аппроксимируется интеграл [10] [12].

— Выбор узлов и весов: Например, в формулах Ньютона–Котеса узлы равноотстоящие, а в формулах Гаусса — это корни ортогональных многочленов (например, многочленов Лежандра для классического интеграла на отрезке), что позволяет добиться наивысшей алгебраической степени точности — для узлов ^[11].