АВТОМАТИЗАЦИЯ СВАРКИ ПРОМЫШЛЕННЫМИ РОБОТАМИ
Промышленные роботы в сварочном производстве.
Понятие «Роботы в сварочном производстве» огромно и объёмно. Во многих отраслях промышленности сейчас используются роботы того или иного назначения. Широк спектр роботов-штабелёров, сборщиков, лаборантов.
Сложность выбора часто заключается не в том, чтобы узнать, нужен ли робот вообще, а в том, какие из имеющихся задач лучше всего подходят для улучшения производительности данного производства с помощью роботизации. Инновационный подход заключается в том, чтобы не искать задачу для роботов, а разделить производственный цикл на задачи, под которые уже адаптировать роботов.
В семействе сварочных роботов выделить отдельно по видам сварки почти невозможно. Все промышленные роботы изготавливаются сейчас универсальными. А именно, со сменными рабочими головками.
Технологические возможности промышленных роботов, используемых в сварочном производстве, характеризуются следующими параметрами:
* грузоподъемность (общая грузоподъемность сварочной головки);
* количество степеней мобильности (свободы) рабочего механизма;
* кинематическая схема;
* точность позиционирования;
• форма и размеры рабочей зоны — это пространство, в котором может располагаться сварочный робот, выполняющий сварку;
* система координат, определяющая кинематику основных движений и форму рабочей области.;
* Система управления PR (циклическая или контурная).
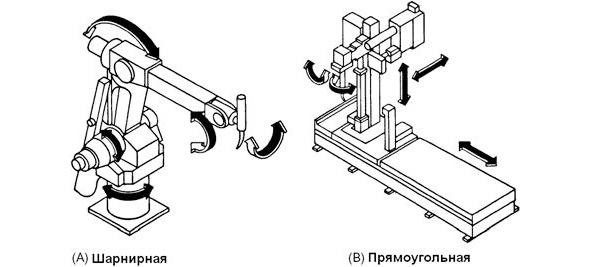
Промышленные роботы имеют разные системы координат: прямоугольно-цилиндрическую, сферическую и шарнирную.
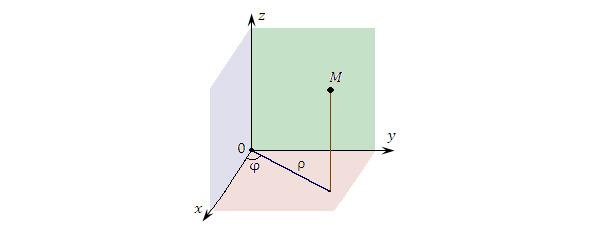
Цилиндрическая система координат представляет собой трёхмерную систему координат, являющуюся обобщением полярной системы координат посредством добавления третьей координаты, которая задаёт смещение произвольной точки M вдоль оси 0z относительно координатной плоскости 0xy.
Положение точки M в цилиндрической системе координат определяется тройкой чисел ρ, φ и z, где ρ — расстояние от точки M до оси 0z (); φ — угол, образованный проекцией радиус-вектора точки M на плоскость 0ху с положительным направлением оси 0х;
z — проекция точки M на ось 0z.
Рис. 1. Цилиндрические координаты точки M.
Связь между декартовыми и цилиндрическими координатами описывается формулами
Поверхность, на которой одна из координат сохраняет постоянное значение, называется координатной поверхностью.
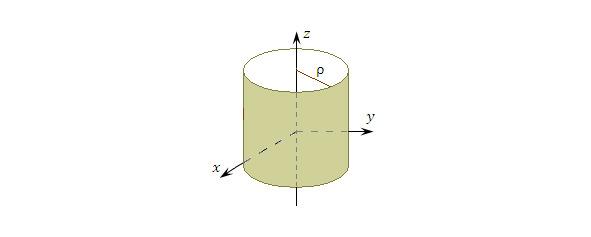
Рис. 2. Координатные поверхности цилиндрической системы координат:
круговой цилиндр (ρ = const);
полуплоскость (φ = const);
плоскость (z = const).