Введение
В данной книге приведена теоретическая часть для каждого задания и рассмотрены основные подходы к решению задач компьютерного ЕГЭ по информатике. Книгу можно использовать как справочник по теории на те или иные задания или как тренажер для нарешивания задач. Наилучшим психологическим подходом на экзамене считается такой: вы решаете все задания, которые легко вам даются, а более сложные пропускаете. После чего, воодушевленные своими успехами в решении задач, приступаете к решению задач, более сложных на ваш взгляд. Далее, если осталось время, то начинаете проверку заданий, которые решили. И напоследок при наличии времени начинаете прорешивать все задания вторым способом и сверяетесь с тем, что у вас получилось при решении первым способом. Если выявились расхождения в ответах, то ищите ошибку. Такая тактика позволит вам набрать максимальное число баллов на экзамене. В книге рассмотрено решение задачи на языке Python, т.к. на нем код получается более коротким в сравнении с другими языками, что поможет сэкономить время на экзамене и набрать более высокий балл. Если вы хотите решать задачи без языков программирования, то читайте книгу в любой последовательности по номерам: 1, 4, 7, 11, 10 — можно решать в любом порядке. Остальные задачи 2, 6, 12, 14, 16, 17, 22, 23, 8, 5, 19—21, 17, 5, 13, 3, 9, 18, 25, 24, 26, 27 лучше осваивать в указанном порядке. В конце каждой задачи есть раздел: «задачи для самостоятельного решения. Пробуйте самостоятельно написать код, стараясь не подглядывать на похожее решение, и также решать вторым аналитическим способом, в тех заданиях, где это возможно.
Каждый вариант экзаменационной работы включает в себя 27 заданий, различающихся уровнем сложности и необходимым для их выполнения программным обеспечением. В ответах на экзамене не нужно вводить отрицательные числа в качестве ответа и дробные числа. Если таковые числа у вас получились, то нужно прочитать еще раз условие задачи, возможно пересмотреть решение и ввести ответ, отличный от отрицательного и дробного числа, т.к. экзаменом такой формат ввода не предусмотрен.
Ответы на все задания представляют собой одно или несколько чисел, или последовательности символов (букв или цифр).
С 2021 г. ЕГЭ по информатике и ИКТ проводится в компьютерной форме, что позволило включить в КИМ задания на практическое программирование (составление и отладка программы в выбранной участником среде программирования), работу с электронными таблицами и информационный поиск.
Общее время выполнения работы — 235 мин.
В книге задания разбиты по темам на основании кодификатора и спецификации контрольных измерительных материалов для проведения в 2025 г. единого государственного экзамена по информатике и ИКТ, подготовленных Федеральным государственным бюджетным научным учреждением «Федеральный институт педагогических измерений». В книге рассмотрены все основные типы задач, которые встречались в тренировочных, репетиционных и диагностических работах, ЕГЭ по информатике основной и досрочной волны 2021–2025 годах.
Книга не отменяет занятия с репетитором, и другого обучения, а дополняет эту работу. Если захотите позаниматься со мной онлайн или у Вас остались вопросы, то пишите мне на мои контакты, что указаны в заключении книги. В 2024—2025 годах подготовил 6 выпускников по информатике к ЕГЭ, ОГЭ, результаты баллов на ЕГЭ, ОГЭ, было, стало: 15 — 74, 45−87, 35- 90, 56- 87, 29−76, 28- 85 баллов. Средний балл 83 балла
Глава 1. Моделирование и компьютерный эксперимент. Задача №1. Анализ информационных моделей
Граф — это способ графического представления информации. Объекты в нем — это вершины (узлы), а связи между объектами — ребра (дуги). То есть граф — это набор вершин и связывающих их ребер. Путь в графе — это конечная последовательность вершин, каждая из которых (кроме последней) соединена со следующим ребром. Граф может содержать циклы (первая вершина пути может совпадать с последней). Обычно в задачах используют взвешенный граф, т.е. граф, в котором с каждым ребром связано число (вес). Например, расстояние, стоимость и т. д. Граф обычно задается таблицей, в которой на пересечении строки и столбца с наименованиями вершин записано числовое значение (вес) ребра, соединяющего эти вершины.
Задачи на графы лучше всего решать вручную аналитически, хотя есть и программное решение, которое часто у моих учеников приводит к ошибкам ввиду ее неоднозначной сложности для учеников (поэтому здесь мы приводить ее не будем). Рекомендую программу «Ножницы», которая стандартно будет у вас открываться на экзамене в среде Windows. Вы можете скопировать картинку, нажать пуск/ найти/ввести слово «ножницы» и в открывшейся программе попытаться рисовать, решая данные задачи тем методом, что будет предложено ниже. Рассмотрим их.
Пример 1.1
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число — так, как оно указано в таблице. Решение: Из вершины B выходит 5 ребер, значит, в таблице соответствующий пункт должен иметь дороги в 5 других (строка должна содержать 5 заполненных клеток). Такой пункт в таблице один: П6. На графе из вершины Е выходит 4 ребра, значит, в таблице соответствующий пункт должен иметь дороги в 4 других (строка должна содержать 4 заполненные клетки). Такой пункт в таблице один: П4. Таким образом, нам нужно найти расстояние между П6 и П4. На пересечении П6 и П4 находится цифра 20. Ответ: 20.
Пример 1.2
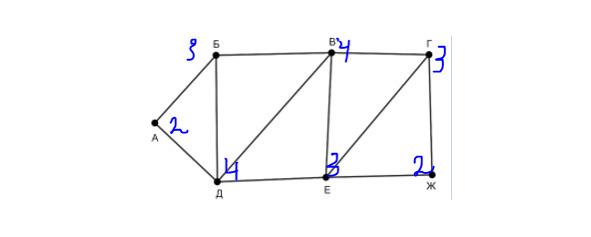
На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Известно, что длина дороги ВД меньше дороги ВЕ. Определите длину дороги ГЖ.
Решение: для начала расставим количество путей, которые выходят из каждой вершины. Минимальное число путей — это 2.
Им соответствует вершина А и Ж. Мы видим в таблице, что в П5 есть два пути. Поэтому предположим, что П5=А, тогда П4=Ж. Т. к. П5 пересекается в значении 10 с П6 и П6=3, то П6=Б. Аналогично получаем, что П7=Д. Далее П7 пересекается с П3, то П3=В. Т. к. П6 пересекается с П2, то П2=В, остается, что П3=Е. Осталась одна вершина — это П1=Г. Условие, что ВЕ> ВД, 23> 16. Это условие истинно, значит, наше предположение изначальное, что П5=А, а П4=Ж, а не наоборот — истинное. А если бы было ложное, тогда что? Тогда бы пришлось рисовать заново, предполагая, что П5=Ж, а П4=А. Смотрим по таблице пересечение П1 и П4 — это число 2. Ответ: 2.
Пример 1.3
На рисунке слева схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите номера пунктов, соответствующих пунктам З и Ж на графе. В качестве ответа запишите два числа в порядке возрастания без разделителей — найденные номера.
Решение:
Пункт К соединяется с вершинами Г (4 вершины) и В (4 вершины). П8 соединяется как раз с двумя вершинами П1 и П2, каждая из которых имеет по 4 дороги, значит, П8=К. Т. к. П8 соединяется с П1 и П2 имеет четыре вершины, то можно предположить, что П1=В, а П2=Г. П1 соединяется с П5, и т. к. П5 имеет 2 вершины, то П5=З. Ранее выяснили, что П2=Г и П2 пересекается с П3, которая имеет 2 вершины, значит, П3=Ж. Ответ: 35.
Задачи для самостоятельного решения
Задача 1.4. На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите длину кратчайшего пути из пункта А в пункт В, если передвигаться можно только по указанным дорогам. В ответе запишите целое число — длину пути в километрах.
Задача 1.5. На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами.
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно без пробелов и знаков препинания, указанные на графе буквенные обозначения пунктов от П1 до П8: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
Задача 1.6. На рисунке схема дорог N-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова сумма протяжённостей дорог из пункта A в пункт G и из пункта D в пункт E.