Новейший справочник школьника
Авторы-составители: Богомолова И. В., Гераськина И. Ю., Давыдова О. С. и др.

Алгебра

АРИФМЕТИКА

Натуральные числа – это те числа, которые возникают в процессе счета, целые положительные числа 1, 2, 3... Ряд таких чисел является бесконечным и называется натуральным рядом. Положительное число – это число больше нуля. Отрицательные числа появляются при вычитании большего числа из меньшего. Целые числа – это натуральные числа и ноль: 0, 1, 2, 3, 4, 5.

Арифметические операции

Сложение – это операция нахождения суммы двух или нескольких чисел, где под суммой понимается общее количество единиц, содержащихся в рассматриваемых числах вместе. Эти числа называются слагаемыми. Например: 5 + 6 = 11, где 5 и 6 – слагаемые, 11 – сумма.

Вычитание – это действие, обратное к сложению, так как это операция нахождения одного из слагаемых по сумме и другому слагаемому. Вычесть из одного числа (уменьшаемого) другое (вычитаемое) – значит найти такое третье число (разность), которое при сложении с вычитаемым дает уменьшаемое: 11–6 = 5. Здесь 11 – уменьшаемое, 6 – вычитаемое, 5 – разность.

Умножение. Умножить одно число а (множимое) на другое целое число b (множитель) – значит повторить множимое а в качестве слагаемого b раз. Результат умножения называется произведением. Например: 2×4 = 2 + + 2 + 2 + 2 = 8.

Деление является действием, обратным к умножению. Разделим одно число (делимое) на другое (делитель) и найдем такое третье число (частное), которое при умножении на делитель дает делимое: 8: 4 = 2.

Возведение в степень. Возвести число (основание степени) в целую степень (показатель степени) – значит повторить его сомножителем столько раз, каков показатель степени. Результат операции называется степенью. Например: 2⁴ = 2×2×2×2=16.

Извлечение корня является действием, обратным к возведению в степень, так как это операция нахождения основания степени по степени и ее показателю. Извлечь корень k-ой степени (к – показатель корня) из числа а (подкоренное число) – значит найти третье число, k-ая степень которого равна а. Результат называется корнем. Например:

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня являются попарно взаимно-обратными операциями.

Результат выполнения нескольких операций зависит от порядка действий. Рассмотрим следующий пример: 10–6 + 4 = 8, но если сначала сложить 6 и 4, а затем вычесть полученный результат из 10, то получим 0. Таким образом, можно сделать следующий вывод: для получения правильного результата должен быть установлен определенный порядок действий. Для того чтобы указать, в каком порядке должны выполняться действия, пользуются скобками. Если скобки отсутствуют, действия выполняются в следующем порядке:

1) возведение в степень и извлечение корня (в порядке их следования);

2) умножение и деление (в порядке их следования);

3) сложение и вычитание (в порядке их следования).

При наличии скобок сначала выполняются действия в скобках в указанном выше порядке, а затем все остальные действия вне скобок с соблюдением указанного выше порядка.

Законы сложения и умножения

Переместительный (коммутативный) закон сложения:

m + n=n + m.

Переместительный (коммутативный) закон умножения:

m × n=n × m.

Сочетательный (ассоциативный) закон сложения:

(m+n)+k=m+ (n+k)=m+n+k.

Сочетательный (ассоциативный) закон умножения:

(m x n) × k=m × (n × k)=m × n × k.

Распределительный (дистрибутивный) закон умножения относительно сложения:

(m+n) × k=m × k+n × k.

Признаки делимости:

1) на 2: если последняя цифра числа – ноль или делится на 2. Числа, делящиеся на два, называются четными, не делящиеся на два – нечетными;

2) на 4: если две последние цифры числа – нули или образуют число, которое делится на 4;

3) на 8: если три последние цифры числа – нули или образуют число, которое делится на 8;

4) на 3 и 9: число делится на 3, если его сумма цифр делится на 3. Число делится на 9, если его сумма цифр делится на 9;

5) на 6: если число делится на 2 и на 3;

6) на 5: число делится на 5, если его последняя цифра – ноль или 5;

7) на 25: если две последние цифры числа – нули или число, которое делится на 25;

8) на 10: если последняя цифра числа – ноль;

9) на 100: если две последние цифры – нули;

10) на 11: это только те числа, у которых сумма цифр, стоящих на нечетных местах, либо равна сумме цифр, стоящих на четных местах, либо отличается от нее на число, делящееся на 11.

Все целые числа (кроме 0 и 1) имеют минимум два делителя: 1 и самого себя. Числа, не имеющие других делителей, называются простыми числами. Числа, имеющие другие делители, называются составными (или сложными) числами.

Общим делителем нескольких чисел называется число, которое является делителем каждого из них. Например, рассмотрим числа 36, 42, 72. Среди всех общих делителей всегда есть наибольший. Чтобы найти наибольший общий делитель (НОД) нескольких чисел, необходимо выполнить следующие действия:

1) представить каждое число как произведение его простых множителей, в нашем случае:

36=2×2×3×3;

42=2×3×7;

72=2×2×2×3×3;

2) записать степени всех простых множителей: 36=2²×3²;

42=2¹×3¹×7¹;

72=2³×3²;

3) выписать все общие делители (множители) этих чисел: 2 и 3;

4) выбрать наименьшую степень каждого из них, встретившуюся во всех произведениях: 2¹ и 3¹;

5) перемножить эти степени: 2¹×3¹=6.

Таким образом, числа 36, 42 и 72 имеют общие делители 2, 3 и 6. Наибольший общий делитель (НОД) в этом случае равен 6.

Общим кратным нескольких чисел называется число, которое делится на каждое из этих чисел. Среди всех общих кратных всегда есть наименьшее (НОК). Рассмотрим числа 18, 27 и 45. Чтобы найти наименьшее общее кратное (НОК) нескольких чисел:

1) представить каждое число как произведение его простых множителей, например:

18=2×3×3;

27=3×3×3;

45=3×3×5;

2) записать степени всех простых множителей: 18=2¹×3²;

27=3³;

45=3²×5¹;

3) выписать все простые делители (множители) каждого из этих чисел: 2, 3, 5;

4) выбрать наибольшую степень каждого из них, встретившуюся во всех разложениях этих чисел: 2¹, 3³, 5¹;

5) перемножить эти степени: 2¹×3³×5¹=270.

Таким образом, 270 – НОК.

ДРОБИ

Часть единицы или несколько ее частей называют простой или обыкновенной дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей – числителем. Дробь записывается в виде:

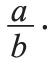
В данном случае а – числитель, b – знаменатель.

Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью. Если числитель больше знаменателя, то дробь больше 1, тогда дробь называется неправильной.

Если числитель и знаменатель дроби равны, то дробь равна 1. Если числитель можно разделить на знаменатель, то эта дробь равна частному от деления:

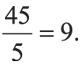
В случае если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом, например:

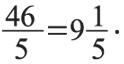
Тогда 9 – неполное частное (целая часть смешанного числа), 1 – остаток (числитель дробной части), 5 – знаменатель. Для того чтобы обратить смешанное число в дробь, необходимо умножить целую часть смешанного числа на знаменатель и прибавить числитель дробной части. Полученный результат будет числителем обыкновенной дроби, а знаменатель останется прежним.

Действия с дробями

Расширение дроби. Значение дроби не меняется, если умножить ее числитель и знаменатель на одно и то же число, отличное от нуля. Например:

Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля. Например,

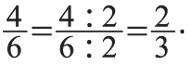
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

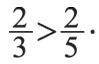
Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

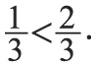
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, то есть привести к общему знаменателю. Рассмотрим, например, следующие дроби:

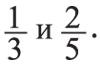
Таким образом, 

а следовательно 

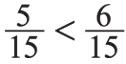
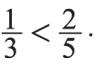
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то, для того чтобы сложить дроби, необходимо сложить их числители, а для того чтобы вычесть дроби, надо вычесть их числители. Полученная сумма, или разность, будет числителем результата, а знаменатель останется прежним. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел сначала необходимо преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.

Умножение дробей. Для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.

Деление дробей. Для того чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь.

Десятичная дробь – это результат деления единицы на десять, сто, тысячу и т. д. частей. Сначала пишется целая часть числа, затем справа ставится десятичная точка. Первая цифра после десятичной точки означает число десятых, вторая – число сотых, третья – число тысячных и т. д. Цифры, расположенные после десятичной точки, называются десятичными знаками, например:

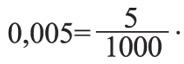
Свойства десятичных дробей

1. Десятичная дробь не меняется, если справа добавить нули: 4,5 = 4,5000.

2. Десятичная дробь не меняется, если удалить нули, расположенные в конце десятичной дроби: 0,0560000 = 0,056.

3. Десятичная дробь возрастает в 10, 100, 1000 и т. д. раз, если перенести десятичную точку на одну, две, три и т. д. позиции вправо: 4,5 → 45 (дробь возросла в 10 раз).

4. Десятичная дробь уменьшается в 10, 100, 1000 и т. д. раз, если перенести десятичную точку на одну, две, три и т. д. позиции влево: 4,5 → 0,45 (дробь уменьшилась в 10 раз).

Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, называемую периодом: 0,321321321321.. .=0, (321)

Действия с десятичными дробями

Сложение и вычитание десятичных дробей выполняются так же, как и сложение и вычитание целых чисел, необходимо только записать соответствующие десятичные знаки один под другим. Например,

Умножение десятичных дробей проводится в несколько этапов:

1) перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку;

2) применяется правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях.

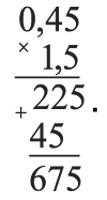
Сумма чисел десятичных знаков в сомножителях равна: 2+1=3. Теперь необходимо с конца получившегося числа отсчитать три знака и поставить десятичную точку: 0,675.

Деление десятичных дробей. Деление десятичной дроби на целое число: если делимое меньше делителя, тогда нужно записать ноль в целой части частного и поставить после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединить к его целой части следующую цифру дробной части и опять сравнить полученную целую часть делимого с делителем. Если новое число опять меньше делителя, надо повторить операцию. Этот процесс повторяется до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему, сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.

Деление одной десятичной дроби на другую: сначала переносятся десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом, и выполняются действия, описанные выше.

Для того чтобы обратить десятичную дробь в обыкновенную, необходимо в качестве числителя взять число, стоящее после десятичной точки, а в качестве знаменателя взять k-ю степень десяти (к – количество десятичных знаков). Отличная от нуля целая часть сохраняется в обыкновенной дроби; нулевая целая часть опускается. Например:

Для того чтобы обратить обыкновенную дробь в десятичную, надо разделить числитель на знаменатель в соответствии с правилами деления.

Процент – это сотая часть единицы, например: 5 % означает 0,05.

Отношение – это частное от деления одного числа на другое.

Пропорция – это равенство двух отношений. Например:

Основное свойство пропорции: произведение крайних членов пропорции равно произведению ее средних членов, то есть 5×30=6×25. Две взаимно зависимые величины называются пропорциональными, если отношение их величин сохраняется неизменным (коэффициент пропорциональности).

Таким образом, выявлены следующие арифметические действия:

1)

2)

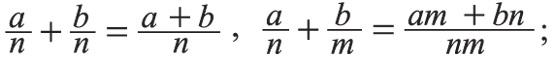
3)

4)

5)

6)

7)

8)

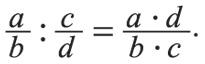
Множество рациональных чисел включает в себя положительные и отрицательные числа (целые и дробные) и ноль. Более точное определение рациональных чисел, принятое в математике, следующее: число называется рациональным, если оно может быть представлено в виде обыкновенной несократимой дроби вида:

где а и b целые числа.

Для отрицательного числа абсолютная величина (модуль) – это положительное число, получаемое от перемены его знака с «–» на «+»; для положительного числа и нуля – само это число. Для обозначения модуля числа используются две прямые черты, внутри которых записывается это число, например: |-5 |=5.

Свойства абсолютной величины

Пусть дан модуль числа

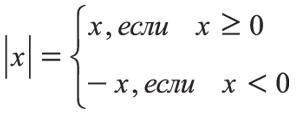
для которого справедливы свойства:

1) |х| = |– x|;

2) |x| ≥ х, |x| ≥ –х;

3) |х + y|≤|x| + |y|;

4) |х – y|≥|x| – |y|;

5) |х · y|≥|x| · |y|;

6)

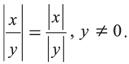
Одночлен – это произведение двух или нескольких сомножителей, каждый из которых либо число, либо буква, либо степень буквы: ЗхахЬ. Коэффициентом чаще всего называют лишь числовой множитель. Одночлены называются подобными, если они одинаковы или отличаются лишь коэффициентами. Степень одночлена – это сумма показателей степеней всех его букв. Если среди суммы одночленов есть подобные, то сумма может быть приведена к более простому виду: 3×а×b+6×а = 3×а× (b+2). Эта операция называется приведением подобных членов или вынесением за скобки.

Многочлен – это алгебраическая сумма одночленов. Степень многочлена есть наибольшая из степеней одночленов, входящих в данный многочлен.

Существуют следующие формулы сокращенного умножения:

(а ± b)²=а² ± 2ab+b²;

(a+b)(a-b)=a²-b²;

(а ± b)³=а³ ± 3а²b+3аb² ± b³:

(а ± b)(а² ± аb+b²)=а³ ± b³.

Методы разложения на множители:

1) вынесение одного множителя за скобки: ac + bc = (a + b)c.

2) использование формул сокращенного умножения.

3) использование формулы разложения квадратного трехчлена на множители:

ах²+bх+с=а(х – x₁)(x – x₂), а ≠ 0,

где х₁, х₂ – корни квадратного трехчлена

D=b²– 4ас≥0 (при ах²+bх + с).

4) использование теоремы Безу.

Алгебраическая дробь – это выражение вида

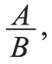
где A и B могут быть числом, одночленом, многочленом.

Если два выражения (числовые и буквенные) соединены знаком «=», то говорят, что они образуют равенство. Любое верное равенство, справедливое при всех допустимых числовых значениях входящих в него букв, называется тождеством.

Уравнение – это буквенное равенство, которое справедливо при определенных значениях входящих в него букв. Эти буквы называются неизвестными (переменными), а их значения, при которых данное уравнение обращается в тождество, – корнями уравнения.

Решить уравнение – значит найти все его корни. Два или несколько уравнений называются равносильными, если они имеют одни и те же корни.

Областью определения уравнения f(x)=g(x) называется множество D(f)⋂D(g). Это множество обозначается ОДЗ, поэтому корнями уравнения могут быть только числа из ОДЗ.

Уравнение f(x)= g(x)+h(x) равносильно уравнению f(x)-h(x)=g{x).

Уравнение f(x)g(x)=0 равносильно совокупности систем:

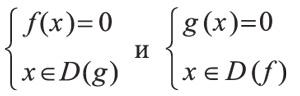
Если D(f)–D(g), то уравнение f(x)g(x)=0 равно совокупности

Уравнение 

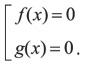
равносильно системе

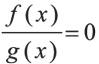
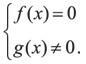
Однородное уравнение второго порядка

аf² (x) + bf (x)g (x) + cg ² (x) =0, а ≠ 0, b ² + c ² > 0;

равносильно совокупности:

Если функция f (x) является монотонно возрастающей, а g (x) – монотонно убывающей на Q (область ОДЗ), тогда уравнение f (x) =g (x) может иметь не более одного корня.

Если f (x) – четная функция, тогда для того, чтобы множество коней уравнения f (x) = 0 было нечетным, необходимо и достаточно, чтобы:

1) ноль являлся корнем уравнения;

2) уравнение имело только конечное число корней.

Основные типы алгебраических уравнений:

1) линейное: ax + b = 0;

2) квадратное: ax ² + bx + c = 0, a ≠ 0;

3) биквадратное: ax ⁴ + bx ² + c = 0, a ≠ 0;

4) двучленное уравнение n-го порядка: xⁿ = a, n ∈ N;

5) возвратное:

а) третьего порядка: ах ³ + bx ² + bx + а = 0, a, b ≠ 0;

б) четвертого порядка: ах ⁴ + bx ³ + cx ² ± bx + а = 0, a, b ≠ 0

6) однородное уравнение второго порядка: аf² (x) + bf (x)g (x) + cg ² (x) =0, а ≠ 0, b ² + c ² > 0;

7) уравнение вида: f (x)g (x) = 0;

8) уравнение вида:

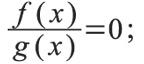
9) уравнение вида: f (φ (x)) = 0.

У линейного уравнения ax + b = 0:

1) если а ≠ 0, имеется единственный корень x = -b/а;

2) если а = 0, b ≠ 0, нет корней;

3) если а = 0, b = 0, корнем является любое действительное число.

Уравнение xⁿ = а, n ∈ N:

1) если n – нечетное число, имеет при любом а действительный корень, равный

2) если n – четное число, то при а < 0 не имеет корней, при а = 0 имеет единственный корень x = 0, если а > 0, то имеет два корня 

Основные тождественные преобразования: замена одного выражения другим, тождественно равным ему; перенос членов уравнения из одной стороны в другую с обратными знаками; умножение или деление обеих частей уравнения на одно и то же выражение (число), отличное от нуля.

Линейным уравнением с одним неизвестным называется уравнение вида: ax+b=0, где а и b – известные числа, а x – неизвестная величина.

Системы двух линейных уравнений с двумя неизвестными имеют вид:

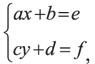
где а, b, c, d, e, f – заданные числа; x, y – неизвестные.

Числа а, b, c, d – коэффициенты при неизвестных; e, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами: метод подстановки: из одного уравнения выражаем одно из неизвестных через коэффициенты и другое неизвестное, а затем подставляем во второе уравнение, решая последнее уравнение, находим сначала одно неизвестное, затем подставляем найденное значение в первое уравнение и находим второе неизвестное; метод сложения или вычитания одного уравнения из другого.

Операции со степенями:

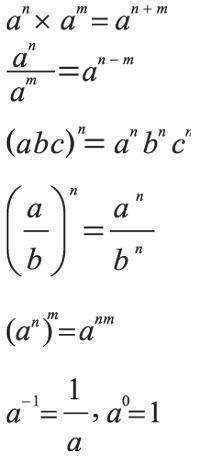
Операции с корнями:

Арифметическим корнем n-й степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Алгебраическим корнем n-й степени из данного числа называется множество всех корней из этого числа.

Иррациональные числа в отличие от рациональных не могут быть представлены в виде обыкновенной несократимой дроби вида m/n, где m и n – целые числа. Это числа нового типа, которые могут быть вычислены с любой точностью, но не могут быть заменены рациональным числом. Они могут появиться как результат геометрических измерений, например: отношение длины диагонали квадрата к длине его стороны равно

Квадратное уравнение есть алгебраическое уравнение второй степени ax²+bx+c=0, где a, b, c – заданные числовые или буквенные коэффициенты, x – неизвестное. Если разделить все члены этого уравнения на а, в результате получим x ²+px+q=0 – приведенное уравнение p=b/a, q=c/a. Его корни находятся по формуле:

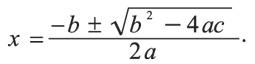
Если b ²-4ac>0, тогда имеются два различных корня, b ²-4ac=0, тогда имеются два равных корня; b ²-4ac<0, тогда имеются два комплексных корня. Выражение b ²-4ac называется дискриминантом и обозначается через D.

Уравнения, содержащие модули

Основные типы уравнений, содержащие модули:

1) If (x)l = lg (x)l;

2) If (x)l = g (x);

3) f (x)lg1 (x)l + f₂ (x)lg₂ (x)l + ... + f_n (x)lg_n (x)l =0, n ∈ N, где f (x), g (x), f_k (x), g_k (x) – заданные функции.

Уравнение If (x)l = lg (x)l равносильно совокупности уравнений

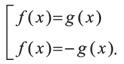
Уравнение If (x)l = lg (x)l равносильно любой из совокупностей систем:

Система 

равносильна

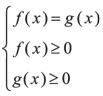
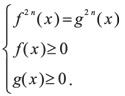
Иррациональные уравнения

Основные типы иррациональных уравнений:

1)

2)

3)

4)

5)

6)

Решение иррациональных уравнений

Уравнение f (x) = g (x) равносильно системе

Уравнение f (x) = g (x) равносильно уравнению

f^{2n +1}(x)=g^{2n +1}(x), n ∈ N.

Уравнение 

равносильно любой из систем:

Уравнение 

равносильно уравнению f (x) = g (x).

Уравнение 

равносильно системе

Показательные уравнения

Основные типы показательных уравнений:

1) a^{f (x)} = a^{g (x)}, a > 0, a≠ 1;

2) c₀a ² + c₁a^x + c₂ = 0, c₀ ≠ 0, a>0, a ≠ 1 – приводящееся к квадратному;

3) однородные:

а) первого порядка c₁a^x = c₂b^x = 0, c₁, c₂ ≠ 0, a, b ≠ 1;

б) второго порядка c₀a ^2x = c₁a^xb^x + c₂b ² = 0, c₀ ≠ 0, c2 + + c2 ≠ 0, a, b > 0, a, b ≠ 1;

4) a^{f (x)} = b, a>0, a ≠ 1;

5) (h (x))^{f (x)} = (H (x))^{g (x)};

Свойства показательных уравнений Уравнение a^{f (x)} = a^{g (x)} равносильно уравнению f (x) = g(x).

Уравнения c₁a^x = c₂b^x = 0 и c₀a ^2x + c₁a^xb^x + c₂b ^2x = 0 равносильны соответственно уравнениям c₁ (a/b)^x +c₂ = 0 и c₀ (a/b) ^2x + + c₁ (a/b)^x +c₂ = 0.

Уравнение a^f(x) = b равносильно уравнению f (x) = log_ab, если b>0, и не имеет корней в противном случае.

НЕРАВЕНСТВА

Теорема Виета. Сумма корней приведенного квадратного уравнения равна коэффициенту при первой степени неизвестного, взятому с обратным знаком: x₁+x₂=-p, а произведение равно свободному члену: x₁*x₂=q. Два выражения (числовые или буквенные), соединенные одним из знаков: «больше» (>), «меньше» (<), «больше или равно» (>), «меньше или равно» («), образуют неравенство. Два неравенства, содержащие одни и те же неизвестные, называются равносильными, если они справедливы при одних и тех же значениях этих неизвестных. Такое же определение используется для равносильности двух систем неравенств. Неравенства могут быть алгебраическими (содержащими только многочлены) и трансцендентными (например, логарифмическими или тригонометрическими).

Доказательство неравенств. Существует несколько методов доказательства неравенств.

1) использование известного или ранее доказанного неравенства;

2) оценка знака разности между частями неравенства;

3) доказательство от противного;

4) метод неопределенного неравенства. Неравенство называется неопределенным, если у него знак или, то есть когда неизвестно, в какую сторону следует повернуть этот знак, чтобы получить справедливое неравенство. В этом случае действуют те же правила, что и с обычными неравенствами.

Решить неравенство – значит найти границы, внутри которых должны находиться неизвестные, так чтобы неравенство было справедливым. Решить систему неравенств – значит найти границы, внутри которых должны находиться неизвестные, так чтобы все неравенства, входящие в систему, были справедливы одновременно.

Чтобы решить систему неравенств, необходимо решить каждое из них, и совместить их решения. Это совмещение приводит к одному из двух возможных случаев: либо система имеет решение, либо нет.

Основные типы алгебраических неравенств:

1) линейное: ax + b < 0;

2) квадратное: ax ² + bx + c < 0, a ≠ 0;

3) двучленное x_n < a, n = 2,3,..;

4) неравенство вида: f (x)g (x) < 0;

5) неравенство вида:

где f (x) и g (x) – заданные рациональные функции.

Основные свойства неравенств:

1. Если a<b, то b>a; или если a>b, то b<a.

2. Если a>b, то a+c>b+c; или если a<b, то a+c<b+c.

3. Если a>b и c>d, то a+c>b+d.

4. Если a>b и c<d, то a – c>b – d. Или если a<b и c>d, то a – c<b – d.

5. Если a>b и m>0, то ma>mb и a/m>b/m.

6. Если a>b и m<0, то ma<mb и a/m<b/m.

Некоторые важные неравенства:

1. lа+bl < lаl + lbl.

2. а+1/а ≤ 2, (а – положительно). Равенство будет только при а=1.

3. 

(а и b – положительны).

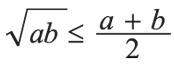
Равенство только при a=b.

Неравенства, содержащие модули

Основные типы неравенств, содержащих модули:

1) lf (x)l < g (x)

2) lf (x)l > g (x)

3) lf (x)l < \g (x)\

4) f₁ (x) l g₁ (x) l +.. + f_n (x) l g_n (x) l < 0, n = 2,3.., где f (x), g (x), f_k (x), g_k (x) – заданные функции.

Свойства неравенств, содержащих модули:

Неравенство lf (x)l < g (x) равносильно любой из систем:

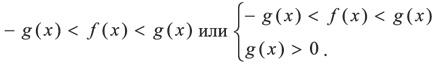
Неравенство lf (x)l > g(x) равносильно совокупности:

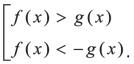
Неравенство lf (x)l > |g(x)| равносильно совокупности систем:

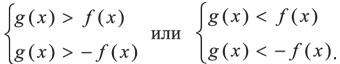
Неравенство lf (x)l < |g(x)| равносильно неравенству f²(x) < g²(x):

Иррациональные неравенства

Основные типы иррациональных неравенств:

1)

2)

3)

4)

5)

Свойства иррациональных неравенств

Системы неравенств

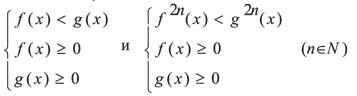
равносильны.

Неравенства f (x) < g (x) и f (x)²ⁿ+¹ < g ²ⁿ+¹ (x), n ∈ N, равносильны.

Неравенство

, равносильно любой из систем:

Неравенство

равносильны.

Неравенство 

равносильно системе

Неравенство 

равносильно совокупности систем:

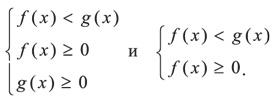
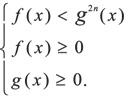
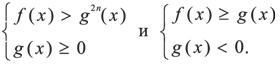
Неравенство типа

равносильно совокупности

Показательные неравенства

Основные типы показательных неравенств:

1) a^{f (x)} < a^{g (x)}, a > 0, a ≠ 1;

2) c₀a ^2x + c₁a^x + c₂ < 0, c₀ ≠ 0, a ≠ 1, c₀ ≠ 0 – приводящееся к квадратному;

3) однородные:

а) первого порядка c₁a^x + c₂b^x < 0, c₁, c₂ ≠ 0, a, b >0, a, b ≠ 1;

б) второго порядка c₀a ^2x + c₁a^xb^x + c₂b ^2x < 0, c₀ ≠ 0, c₁ ² + c₂ ² ≠ 0;

4) a^x < b (a^x > b), a > 0, a ≠ 1, b ∈ R;

5) (h (x))^{f (x)} = (h (x))^{g (x)}.

Свойства показательных неравенств

Неравенство a^{f (x)} < a^{g (x)} равносильно:

1) если 0 < a < 1, то неравенству f (x) > g (x);

2) если a > 1, то – f (x) < g (x).

При b ≤ 0 неравенство a^x < b не имеет решений, если же b > 0, то при 0<a<1 решением является множество (log_ab;+∞), при a>1 – (–∞; log_ab).

Решением неравенства a^x > b при b < 0 является множество (–∞; +∞), если же b > 0, то при 0 < a < 1 решением является множество (–∞; log_ab), при a > 1 – множество (log_ab; +∞).

Неравенство (h (x))^{f (x)} = (h (x))^{g (x)} равносильно совокупности систем:

...