E-text prepared by Sonya Schermann, Charlie Howard,
and the Online Distributed Proofreading Team
(http://www.pgdp.net)
from page images generously made available by
Internet Archive
(https://archive.org)

Note:

Images of the original pages are available through Internet Archive. See

https://archive.org/details/56010330R.nlm.nih.gov

HARPER’S FAMILY LIBRARY.
DESIGNED FOR ADULT PERSONS.

“Books that you may carry to the fire, and hold readily in your hand, are the most useful after all. A man will often look at them, and be tempted to go on, when he would have been frightened at books of a larger size, and of a more erudite appearance.”—Dr. Johnson.

The proprietors of the Family Library feel themselves stimulated to increased exertions by the distinguished favour with which it has already been received.

The volumes now before the public may be confidently appealed to as proofs of zeal on the part of the publishers to present to their readers a series of productions, which, as they are connected, not with ephemeral, but with permanent subjects, may, years hence as well as now, be consulted for lively amusement as well as solid instruction.

To render this Library still more worthy of patronage, the proprietors propose incorporating in it such works of interest and value as may appear in the various Libraries and Miscellanies now preparing in Europe, particularly “Constable’s Miscellany,” the “Edinburgh Cabinet” Library, &c. All these productions, as they emanate from the press, will be submitted to literary gentlemen for inspection; and none will be reprinted but such as shall be found calculated to sustain the exalted character which this Library has already acquired.

Several well-known authors have been engaged to prepare for it original works of an American character, on History, Biography, Travels, &c. &c.

Every distinct subject will in general be comprehended in one volume, or at most in three volumes, which may form either a portion of the series or a complete work by itself; and each volume will be embellished with appropriate engravings.

The entire series will be the production of authors of eminence, who have acquired celebrity by their literary labours, and whose names, as they appear in succession, will afford the surest guarantee to the public for the satisfactory manner in which the subjects will be treated.

Such is the plan by which it is intended to form an American Family Library, comprising all that is valuable in those branches of knowledge which most happily unite entertainment with instruction. The utmost care will be taken, not only to exclude whatever can have an injurious influence on the mind, but to embrace every thing calculated to strengthen the best and most salutary impressions.

With these arrangements and facilities, the publishers flatter themselves that they shall be able to present to their fellow-citizens a work of unparalleled merit and cheapness, embracing subjects adapted to all classes of readers, and forming a body of literature deserving the praise of having instructed many, and amused all; and above every other species of eulogy, of being fit to be introduced, without reserve or exception, by the father of a family to the domestic circle. Meanwhile, the very low price at which it is charged renders more extensive patronage necessary for its support and prosecution. The immediate encouragement, therefore, of those who approve its plan and execution is respectfully solicited. The work may be obtained in complete sets, or in separate numbers, from the principal booksellers throughout the United States.

OPINIONS OF THE FAMILY LIBRARY.

“The publishers have hitherto fully deserved their daily increasing reputation by the good taste and judgment which have influenced the selections of works for the Family Library.”—Albany Daily Advertiser.

“The Family Library—A title which, from the valuable and entertaining matter the collection contains, as well as from the careful style of its execution, it well deserves. No family, indeed, in which there are children to be brought up, ought to be without this Library, as it furnishes the readiest resources for that education which ought to accompany or succeed that of the boarding-school or the academy, and is infinitely more conducive than either to the cultivation of the intellect.”—Monthly Review.

“It is the duty of every person having a family to put this excellent Library into the hands of his children.”—N. Y. Mercantile Advertiser.

“It is one of the recommendations of the Family Library, that it embraces a large circle of interesting matter, of important information and agreeable entertainment, in a concise manner and a cheap form. It is eminently calculated for a popular series—published at a price so low, that persons of the most moderate income may purchase it—combining a matter and a style that the most ordinary mind may comprehend it, at the same time that it is calculated to raise the moral and intellectual character of the people.”—Constellation.

“We have repeatedly borne testimony to the utility of this work. It is one of the best that has ever been issued from the American press, and should be in the library of every family desirous of treasuring up useful knowledge.”—Boston Statesman.

“We venture the assertion that there is no publication in the country more suitably adapted to the taste and requirements of the great mass of community, or better calculated to raise the intellectual character of the middling classes of society, than the Family Library.”—Boston Masonic Mirror.

“We have so often recommended this enterprising and useful publication (the Family Library), that we can here only add, that each successive number appears to confirm its merited popularity.”—N. Y. American.

“The little volumes of this series truly comport with their title, and are in themselves a Family Library.”—N. Y. Commercial Advertiser.

“We recommend the whole set of the Family Library as one of the cheapest means of affording pleasing instruction, and imparting a proper pride in books, with which we are acquainted.”—U. S. Gazette.

“It will prove instructing and amusing to all classes. We are pleased to learn that the works comprising this Library have become, as they ought to be, quite popular among the heads of families.”—N. Y. Gazette.

“The Family Library is, what its name implies, a collection of various original works of the best kind, containing reading useful and interesting to the family circle. It is neatly printed, and should be in every family that can afford it—the price being moderate.”—New-England Palladium.

“We are pleased to see that the publishers have obtained sufficient encouragement to continue their valuable Family Library.”—Baltimore Republican.

“The Family Library presents, in a compendious and convenient form, well-written histories of popular men, kingdoms, sciences, &c. arranged and edited by able writers, and drawn entirely from the most correct and accredited authorities. It is, as it professes to be, a Family Library, from which, at little expense, a household may prepare themselves for a consideration of those elementary subjects of education and society, without a due acquaintance with which neither man nor woman has claim to be well bred, or to take their proper place among those with whom they abide.”—Charleston Gazette.

BOY’S AND GIRL’S LIBRARY.
PROSPECTUS.

The Publishers of the “Boy’s and Girl’s Library” propose, under this title, to issue a series of cheap but attractive volumes, designed especially for the young. The undertaking originates not in the impression that there does not already exist in the treasures of the reading world a large provision for this class of the community. They are fully aware of the deep interest excited at the present day on the subject of the mental and moral training of the young, and of the amount of talent and labour bestowed upon the production of works aiming both at the solid culture and the innocent entertainment of the inquisitive minds of children. They would not therefore have their projected enterprise construed into an implication of the slightest disparagement of the merits of their predecessors in the same department. Indeed it is to the fact of the growing abundance rather than to the scarcity of useful productions of this description that the design of the present work is to be traced; as they are desirous of creating a channel through which the products of the many able pens enlisted in the service of the young may be advantageously conveyed to the public.

The contemplated course of publications will more especially embrace such works as are adapted, not to the extremes of early childhood or of advanced youth, but to that intermediate space which lies between childhood and the opening of maturity, when the trifles of the nursery and the simple lessons of the school-room have ceased to exercise their beneficial influence, but before the taste for a higher order of mental pleasure has established a fixed ascendency in their stead. In the selection of works intended for the rising generation in this plastic period of their existence, when the elements of future character are receiving their moulding impress, the Publishers pledge themselves that the utmost care and scrupulosity shall be exercised. They are fixed in their determination that nothing of a questionable tendency on the score of sentiment shall find admission into pages consecrated to the holy purpose of instructing the thoughts, regulating the passions, and settling the principles of the young.

In fine, the Publishers of the “Boy’s and Girl’s Library” would assure the Public that an adequate patronage alone is wanting to induce and enable them to secure the services of the most gifted pens in our country in the proposed publication, and thus to render it altogether worthy of the age and the object which calls it forth, and of the countenance which they solicit for it.

SIR. G. KNELLER PINX.

ENG.^d BY GIMBER.

SIR ISAAC NEWTON.

HARPER’S FAMILY LIBRARY

Printed by R. Miller

Harper’s Stereotype Edition.

THE
LIFE
OF
SIR ISAAC NEWTON.

BY
DAVID BREWSTER, LL.D. F.R.S.

Ergo vivida vis animi pervicit, et extra Processit longe flammantia mœnia mundi; Atque omne immensum peragravit mente amimoque.

Lucret. lib. i. 1. 73.

The Birthplace of Newton.

NEW-YORK:

PRINTED AND PUBLISHED BY J. & J. HARPER;
NO. 82 CLIFF-STREET,
AND SOLD BY THE BOOKSELLERS GENERALLY THROUGHOUT
THE UNITED STATES.

1833.

TO
THE RIGHT HONOURABLE
LORD BRAYBROOKE.

The kindness with which your lordship intrusted to me some very valuable materials for the composition of this volume has induced me to embrace the present opportunity of publicly acknowledging it. But even if this personal obligation had been less powerful, those literary attainments and that enlightened benevolence which reflect upon rank its highest lustre would have justified me in seeking for it the patronage of a name which they have so justly honoured.

DAVID BREWSTER.

Allerly, June 1st, 1831.

PREFACE.

As this is the only Life of Sir Isaac Newton on any considerable scale that has yet appeared, I have experienced great difficulty in preparing it for the public. The materials collected by preceding biographers were extremely scanty; the particulars of his early life, and even the historical details of his discoveries, have been less perfectly preserved than those of his illustrious predecessors; and it is not creditable to his disciples that they have allowed a whole century to elapse without any suitable record of the life and labours of a master who united every claim to their affection and gratitude.

In drawing up this volume, I have obtained much assistance from the account of Sir Isaac Newton in the Biographia Britannica; from the letters to Oldenburg, and other papers in Bishop Horsley’s edition of his works; from Turnor’s Collections for the History of the Town and Soke of Grantham; from M. Biot’s excellent Life of Newton in the Biographie Universelle; and from Lord King’s Life and Correspondence of Locke.

Although these works contain much important information respecting the Life of Newton, yet I have been so fortunate as to obtain many new materials of considerable value.

To the kindness of Lord Braybrooke I have been indebted for the interesting correspondence of Newton, Mr. Pepys, and Mr. Millington, which is now published for the first time, and which throws much light upon an event in the life of our author that has recently acquired an unexpected and a painful importance. These letters, when combined with those which passed between Newton and Locke, and with a curious extract from the manuscript diary of Mr. Abraham Pryme, kindly furnished to me by his collateral descendant Professor Pryme of Cambridge, fill up a blank in his history, and have enabled me to delineate in its true character that temporary indisposition which, from the view that has been taken of it by foreign philosophers, has been the occasion of such deep distress to the friends of science and religion.

To Professor Whewell, of Cambridge, I owe very great obligations for much valuable information. Professor Rigaud, of Oxford, to whose kindness I have on many other occasions been indebted, supplied me with several important facts, and with extracts from the diary of Hearne in the Bodleian Library, and from the original correspondence between Newton and Flamstead, which the president of Corpus Christi College had for this purpose committed to his care; and Dr. J. C. Gregory, of Edinburgh, the descendant of the illustrious inventor of the reflecting telescope, allowed me to use his unpublished account of an autograph manuscript of Sir Isaac Newton, which was found among the papers of David Gregory, Savilian Professor of Astronomy at Oxford, and which throws some light on the history of the Principia.

I have been indebted to many other friends for the communication of books and facts, but especially to Sir William Hamilton, Bart., whose liberality in promoting literary inquiry is not limited to the circle of his friends.

D. B.

Allerly, June 1st, 1831.

CONTENTS.

Page

CHAPTER I.

The Pre-eminence of Sir Isaac Newton’s Reputation—The Interest attached to the Study of his Life and Writings—His Birth and Parentage—His early Education—Is sent to Grantham School—His early Attachment to Mechanical Pursuits—His Windmill—His Water-clock—His Self-moving Cart—His Sun-dials—His Preparation for the University

17

CHAPTER II.

Newton enters Trinity College, Cambridge—Origin of his Propensity for Mathematics—He studies the Geometry of Descartes unassisted—Purchases a Prism—Revises Dr. Barrow’s Optical Lectures—Dr. Barrow’s Opinion respecting Colours—Takes his Degrees—Is appointed a Fellow of Trinity College—Succeeds Dr. Barrow in the Lucasian Chair of Mathematics

26

CHAPTER III.

Newton occupied in grinding Hyperbolical Lenses—His first Experiments with the Prism made in 1666—He discovers the Composition of White Light, and the different Refrangibility of the Rays which compose it—Abandons his Attempts to improve Refracting Telescopes, and resolves to attempt the Construction of Reflecting ones—He quits Cambridge on account of the Plague—Constructs two Reflecting Telescopes in 1668, the first ever executed—One of them examined by the Royal Society, and shown to the King—He constructs a Telescope with Glass Specula—Recent History of the Reflecting Telescope—Mr. Airy’s Glass Specula—Hadley’s Reflecting Telescopes—Short’s—Herschel’s—Ramage’s—Lord Oxmantown’s

30

CHAPTER IV.

He delivers a Course of Optical Lectures at Cambridge—Is elected Fellow of the Royal Society—He communicates to them his Discoveries on the different Refrangibility and Nature of Light—Popular Account of them—They involve him in various Controversies—His Dispute with Pardies—Linus—Lucas—Dr. Hooke and Mr. Huygens—The Influence of these Disputes on the mind of Newton

47

CHAPTER V.

Mistake of Newton in supposing that the Improvement of Refracting

Telescopes was hopeless—Mr. Hall invents the Achromatic Telescope—Principles of the Achromatic Telescope explained—It is reinvented by Dollond, and improved by future Artists—Dr. Blair’s Aplanatic Telescope—Mistakes in Newton’s Analysis of the Spectrum—Modern Discoveries respecting the Structure of the Spectrum

63

CHAPTER VI.

Colours of thin Plates first studied by Boyle and Hooke—Newton determines the Law of their Production—His Theory of Fits of easy Reflection and Transmission—Colours of thick Plates

75

CHAPTER VII.

Newton’s Theory of the Colours of Natural Bodies explained—Objections to it stated—New Classification of Colours—Outline of a new Theory proposed

82

CHAPTER VIII.

Newton’s Discoveries respecting the Inflection or Diffraction of Light—Previous Discoveries of Grimaldi and Dr. Hooke—Labours of succeeding Philosophers—Law of Interference of Dr. Young—Fresnel’s Discoveries—New Theory of Inflection on the Hypothesis of the Materiality of Light

98

CHAPTER IX.

Miscellaneous Optical Researches of Newton—His Experiments on Refraction—His Conjecture respecting the Inflammability of the Diamond—His Law of Double Refraction—His Observations on the Polarization of Light—Newton’s Theory of Light—His “Optics”

106

CHAPTER X.

Astronomical Discoveries of Newton—Necessity of combined Exertion to the completion of great Discoveries—Sketch of the History or Astronomy previous to the time of Newton—Copernicus, 1473–1543—Tycho Brahe, 1546–1601—Kepler, 1571–1631—Galileo, 1564–1642

110

CHAPTER XI.

The first Idea of Gravity occurs to Newton in 1666—His first Speculations upon it—Interrupted by his Optical Experiments—He resumes the Subject in consequence of a Discussion with Doctor Hooke—He discovers the true Law of Gravity and the Cause of the Planetary Motions—Dr. Halley urges him to publish his Principia—His Principles of Natural Philosophy—Proceedings of the Royal Society on this Subject—The Principia appears in 1687—General Account of it, and of the Discoveries it contains—They meet with great Opposition, owing to the Prevalence of the Cartesian System—Account of the Reception and Progress of the Newtonian Philosophy in Foreign Countries—Account of its Progress and Establishment in England

140

CHAPTER XII.

Doctrine of Infinite Quantities—Labours of Pappus—Kepler—Cavaleri—Roberval—Fermat—Wallis—Newton discovers the Binomial Theorem and the Doctrine of Fluxions in 1606—His Manuscript Work containing this Doctrine communicated to his Friends—His Treatise on Fluxions—His Mathematical Tracts—His Universal Arithmetic—His Methodus Differentialis—His Geometria Analytica—His Solution of the Problems proposed by Bernouilli and Leibnitz—Account of the celebrated Dispute respecting the Invention of Fluxions—Commercium Epistolicum—Report of the Royal Society—General View of the Controversy

168

CHAPTER XIII.

James II. attacks the Privileges of the University of Cambridge—Newton chosen one of the Delegates to resist this Encroachment—He is elected a Member of the Convention Parliament—Burning of his Manuscript—His supposed Derangement of Mind—View taken of this by foreign Philosophers—His Correspondence with Mr. Pepys and Mr. Locke at the time of his Illness—Mr. Millington’s Letter to Mr. Pepys on the subject of Newton’s Illness—Refutation of the Statement that he laboured under Mental Derangement

200

CHAPTER XIV.

No Mark of National Gratitude conferred upon Newton—Friendship between him and Charles Montague, afterward Earl of Halifax—Mr. Montague appointed Chancellor of the Exchequer in 1694—He resolves upon a Recoinage—Nominates Mr. Newton Warden of the Mint in 1695—Mr. Newton appointed Master of the Mint in 1699—Notice of the Earl of Halifax—Mr. Newton elected Associate of the Academy of Sciences in 1699—Member for Cambridge in 1701—and President of the Royal Society in 1703—Queen Anne confers upon him the Honour of Knighthood in 1705—Second Edition of the Principia, edited by Cotes—His Conduct respecting Mr. Ditton’s Method of finding the Longitude

223

CHAPTER XV.

Respect in which Newton was held at the Court of George I.—The Princess of Wales delighted with his Conversation—Leibnitz endeavours to prejudice the Princess against Sir Isaac and Locke—Controversy occasioned by his Conduct—The Princess obtains a Manuscript Abstract of his System of Chronology—The Abbé Conti is, at her request, allowed to take a Copy of it on the promise of Secrecy—He prints it surreptitiously in French, accompanied with a Refutation by M. Freret—Sir Isaac’s Defence of his System—Father Souciet attacks it, and is answered by Dr. Halley—Sir Isaac’s larger Work on Chronology published after his Death—Opinions respecting it—Sir Isaac’s Paper on the Form of the most ancient Year

234

CHAPTER XVI.

Theological Studies of Sir Isaac—Their Importance to Christianity—Motives to which they have been ascribed—Opinions of Biot

and La Place considered—His Theological Researches begun before his supposed Mental Illness—The Date of these Works fixed—Letters to Locke—Account of his Observations on Prophecy—His Lexicon Propheticum—His Four Letters to Dr. Bentley—Origin of Newton’s Theological Studies—Analogy between the Book of Nature and that of Revelation

242

CHAPTER XVII.

The Minor Discoveries and Inventions of Newton—His Researches on Heat—On Fire and Flame—On Elective Attraction—On the Structure of Bodies—His supposed Attachment to Alchymy—His Hypothesis respecting Ether as the Cause of Light and Gravity—On the Excitation of Electricity in Glass—His Reflecting Sextant invented before 1700—His Reflecting Microscope—His Prismatic Reflector as a Substitute for the small Speculum of Reflecting Telescopes—His Method of varying the Magnifying Power of Newtonian Telescopes—His Experiments on Impressions on the Retina

265

CHAPTER XVIII.

His Acquaintance with Dr. Pemberton—Who edits the Third Edition of the Principia—His first Attack of ill Health—His Recovery—He is taken ill in consequence of attending the Royal Society—His Death on the 20th March, 1727—His Body lies in state—His Funeral—He is buried in Westminster Abbey—His Monument described—His Epitaph—A Medal struck in honour of him—Roubiliac’s full-length Statue of him erected in Cambridge—Division of his Property—His Successors

284

CHAPTER XIX.

Permanence of Newton’s Reputation—Character of his Genius—His Method of Investigation similar to that used by Galileo—Error in ascribing his Discoveries to the Use of the Methods recommended by Lord Bacon—The Pretensions of the Baconian Philosophy examined—Sir Isaac Newton’s Social Character—His great Modesty—The Simplicity of his Character—His Religious and Moral Character—His Hospitality and Mode of Life—His Generosity and Charity—His Absence—His Personal Appearance—Statues and Pictures of him—Memorials and Recollections of him

292

Appendix, No. I.

—Observations on the Family of Sir Isaac Newton

307

Appendix, No. II.

—Letter from Sir Isaac Newton to Francis Aston, Esq., a young Friend who was on the eve of setting out on his Travels

316

Appendix, No. III.

—“A Remarkable and Curious Conversation between Sir Isaac Newton and Mr. Conduit.”

320

LIFE OF SIR ISAAC NEWTON.

CHAPTER I.

The Pre-eminence of Sir Isaac Newton’s Reputation—The Interest attached to the Study of his Life and Writings—His Birth and Parentage—His early Education—Is sent to Grantham School—His early Attachment to Mechanical Pursuits—His Windmill—His Waterclock—His Self-moving Cart—His Sundials—His Preparation for the University.

The name of Sir Isaac Newton has by general consent been placed at the head of those great men who have been the ornaments of their species. However imposing be the attributes with which time has invested the sages and the heroes of antiquity, the brightness of their fame has been eclipsed by the splendour of his reputation; and neither the partiality of rival nations, nor the vanity of a presumptuous age, has ventured to dispute the ascendency of his genius. The philosopher,1 indeed, to whom posterity will probably assign the place next to Newton, has characterized the Principia as pre-eminent above all the productions of human intellect, and has thus divested of extravagance the contemporary encomium upon its author,

Nec fas est propius mortali attingere Divos.

Halley.

So near the gods—man cannot nearer go.

The biography of an individual so highly renowned cannot fail to excite a general interest. Though his course may have lain in the vale of private life, and may have been unmarked with those dramatic events which throw a lustre even round perishable names, yet the inquiring spirit will explore the history of a mind so richly endowed,—will study its intellectual and moral phases, and will seek the shelter of its authority on those great questions which reason has abandoned to faith and hope.

If the conduct and opinions of men of ordinary talent are recorded for our instruction, how interesting must it be to follow the most exalted genius through the incidents of common life;—to mark the steps by which he attained his lofty pre-eminence; to see how he performs the functions of the social and the domestic compact; how he exercises his lofty powers of invention and discovery; how he comports himself in the arena of intellectual strife; and in what sentiments, and with what aspirations he quits the world which he has adorned.

In almost all these bearings, the life and writings of Sir Isaac Newton abound with the richest counsel. Here the philosopher will learn the art by which alone he can acquire an immortal name. The moralist will trace the lineaments of a character adjusted to all the symmetry of which our imperfect nature is susceptible; and the Christian will contemplate with delight the high-priest of science quitting the study of the material universe,—the scene of his intellectual triumphs,—to investigate with humility and patience the mysteries of his faith.

* * * * *

Sir Isaac Newton was born at Woolsthorpe, a hamlet in the parish of Colsterworth, in Lincolnshire, about six miles south of Grantham, on the 25th December, O. S., 1642, exactly one year after Galileo died, and was baptized at Colsterworth on the 1st January, 1642–3. His father, Mr. Isaac Newton, died at the early age of thirty-six, a little more than a year after the death of his father Robert Newton, and only a few months after his marriage to Harriet Ayscough, daughter of James Ayscough of Market Overton in Rutlandshire. This lady was accordingly left in a state of pregnancy, and appears to have given a premature birth to her only and posthumous child. The helpless infant thus ushered into the world was of such an extremely diminutive size,2 and seemed of so perishable a frame, that two women who were sent to Lady Pakenham’s at North Witham, to bring some medicine to strengthen him, did not expect to find him alive on their return. Providence, however, had otherwise decreed; and that frail tenement which seemed scarcely able to imprison its immortal mind was destined to enjoy a vigorous maturity, and to survive even the average term of human existence. The estate of Woolsthorpe, in the manor-house of which this remarkable birth took place, had been more than a hundred years in the possession of the family, who came originally from Newton in Lancashire, but who had, previous to the purchase of Woolsthorpe, settled at Westby, in the county of Lincoln. The manor-house, of which we have given an engraving, is situated in a beautiful little valley, remarkable for its copious wells of pure spring water, on the west side of the river Witham, which has its origin in the neighbourhood, and commands an agreeable prospect to the east towards Colsterworth. The manor of Woolsthorpe was worth only 30l. per annum; but Mrs. Newton possessed another small estate at Sewstern,3 which raised the annual value of their property to about 80l.; and it is probable that the cultivation of the little farm on which she resided somewhat enlarged the limited income upon which she had to support herself, and educate her child.

For three years Mrs. Newton continued to watch over her tender charge with parental anxiety; but in consequence of her marriage to the Reverend Barnabas Smith, rector of North Witham, about a mile south of Woolsthorpe, she left him under the care of her own mother. At the usual age he was sent to two day-schools at Skillington and Stoke, where he acquired the education which such seminaries afforded; but when he reached his twelfth year he went to the public school at Grantham, taught by Mr. Stokes, and was boarded at the house of Mr. Clark, an apothecary in that town. According to information which Sir Isaac himself gave to Mr. Conduit, he seems to have been very inattentive to his studies, and very low in the school. The boy, however, who was above him, having one day given him a severe kick upon his stomach, from which he suffered great pain, Isaac laboured incessantly till he got above him in the school, and from that time he continued to rise till he was the head boy. From the habits of application which this incident had led him to form, the peculiar character of his mind was speedily displayed. During the hours of play, when the other boys were occupied with their amusements, his mind was engrossed with mechanical contrivances, either in imitation of something which he had seen, or in execution of some original conception of his own. For this purpose he provided himself with little saws, hatchets, hammers, and all sorts of tools, which he acquired the art of using with singular dexterity. The principal pieces of mechanism which he thus constructed were a windmill, a waterclock, and a carriage put in motion by the person who sat in it. When a windmill was erecting near Grantham on the road to Gunnerby, Isaac frequently attended the operations of the workmen, and acquired such a thorough knowledge of the machinery that he completed a working model of it, which excited universal admiration. This model was frequently placed on the top of the house in which he lodged at Grantham, and was put in motion by the action of the wind upon its sails. Not content with this exact imitation of the original machine, he conceived the idea of driving it by animal power, and for this purpose he enclosed in it a mouse which he called the miller, and which, by acting upon a sort of treadwheel, gave motion to the machine. According to some accounts, the mouse was made to advance by pulling a string attached to its tail, while others allege that the power of the little agent was called forth by its unavailing attempts to reach a portion of corn placed above the wheel.

His waterclock was formed out of a box which he had solicited from Mrs. Clark’s brother. It was about four feet high, and of a proportional breadth, somewhat like a common houseclock. The index of the dialplate was turned by a piece of wood, which either fell or rose by the action of dropping water. As it stood in his own bedroom he supplied it every morning with the requisite quantity of water, and it was used as a clock by Mr. Clark’s family, and remained in the house long after its inventor had quitted Grantham.4 His mechanical carriage was a vehicle with four wheels, which was put in motion with a handle wrought by the person who sat in it, but, like Merlin’s chair, it seems to have been used only on the smooth surface of a floor, and not fitted to overcome the inequalities of a road. Although Newton was at this time “a sober, silent, thinking lad,” who scarcely ever joined in the ordinary games of his schoolfellows, yet he took great pleasure in providing them with amusements of a scientific character. He introduced into the school the flying of paper kites; and he is said to have been at great pains in determining their best forms and proportions, and in ascertaining the position and number of the points by which the string should be attached. He made also paper lanterns, by the light of which he went to school in the winter mornings, and he frequently attached these lanterns to the tails of his kites in a dark night, so as to inspire the country people with the belief that they were comets.

In the house where he lodged there were some female inmates in whose company he appears to have taken much pleasure. One of these, a Miss Storey, sister to Dr. Storey, a physician at Buckminster, near Colsterworth, was two or three years younger than Newton, and to great personal attractions she seems to have added more than the usual allotment of female talent. The society of this young lady and her companions was always preferred to that of his own schoolfellows, and it was one of his most agreeable occupations to construct for them little tables and cupboards, and other utensils for holding their dolls and their trinkets. He had lived nearly six years in the same house with Miss Storey, and there is reason to believe that their youthful friendship gradually rose to a higher passion; but the smallness of her portion and the inadequacy of his own fortune appear to have prevented the consummation of their happiness. Miss Storey was afterward twice married, and under the name of Mrs. Vincent, Dr. Stukely visited her at Grantham in 1727, at the age of eighty-two, and obtained from her many particulars respecting the early history of our author. Newton’s esteem for her continued unabated during his life. He regularly visited her when he went to Lincolnshire, and never failed to relieve her from little pecuniary difficulties which seem to have beset her family.

Among the early passions of Newton we must recount his love of drawing; and even of writing verses. His own room was furnished with pictures drawn, coloured, and framed by himself, sometimes from copies, but often from life.5 Among these were portraits of Dr. Donne, Mr. Stokes, the master of Grantham school, and King Charles I. under whose picture were the following verses.

A secret art my soul requires to try, If prayers can give me what the wars deny. Three crowns distinguished here, in order do Present their objects to my knowing view. Earth’s crown, thus at my feet I can disdain, Which heavy is, and at the best but vain. But now a crown of thorns I gladly greet, Sharp is this crown, but not so sharp as sweet; The crown of glory that I yonder see Is full of bliss and of eternity.

These verses were repeated to Dr. Stukely by Mrs. Vincent, who believed them to be written by Sir Isaac, a circumstance which is the more probable, as he himself assured Mr. Conduit, with some expression of pleasure, that he “excelled in making verses,” although he had been heard to express a contempt for poetical composition.

But while the mind of our young philosopher was principally occupied with the pursuits which we have now detailed, it was not inattentive to the movements of the celestial bodies, on which he was destined to throw such a brilliant light. The imperfections of his waterclock had probably directed his thoughts to the more accurate measure of time which the motion of the sun afforded. In the yard of the house where he lived, he traced the varying movements of that luminary upon the walls and roofs of the buildings, and by means of fixed pins he had marked out the hourly and half-hourly subdivisions. One of these dials, which went by the name of Isaac’s dial, and was often referred to by the country people for the hour of the day, appears to have been drawn solely from the observations of several years; but we are not informed whether all the dials which he drew on the wall of his house at Woolsthorpe, and which existed after his death, were of the same description, or were projected from his knowledge of the doctrine of the sphere.

Upon the death of the Reverend Mr. Smith in the year 1656, his widow left the rectory of North Witham, and took up her residence at Woolsthorpe along with her three children, Mary, Benjamin, and Hannah Smith. Newton had now attained the fifteenth year of his age, and had made great progress in his studies; and as he was thought capable of being useful in the management of the farm and country business at Woolsthorpe, his mother, chiefly from a motive of economy, recalled him from the school at Grantham. In order to accustom him to the art of selling and buying, two of the most important branches of rural labour, he was frequently sent on Saturday to Grantham market to dispose of grain and other articles of farm produce, and to purchase such necessaries as the family required. As he had yet acquired no experience, an old trustworthy servant generally accompanied him on these errands. The inn which they patronised was the Saracen’s Head at West Gate; but no sooner had they put up their horses than our young philosopher deserted his commercial concerns, and betook himself to his former lodging in the apothecary’s garret, where a number of Mr. Clark’s old books afforded him abundance of entertainment till his aged guardian had executed the family commissions, and announced to him the necessity of returning. At other times he deserted his duties at an earlier stage, and intrenched himself under a hedge by the way-side, where he continued his studies till the servant returned from Grantham. The more immediate affairs of the farm were not more prosperous under his management than would have been his marketings at Grantham. The perusal of a book, the execution of a model, or the superintendence of a waterwheel of his own construction, whirling the glittering spray from some neighbouring stream, absorbed all his thoughts when the sheep were going astray, and the cattle were devouring or treading down the corn.

Mrs. Smith was soon convinced from experience that her son was not destined to cultivate the soil, and as his passion for study, and his dislike for every other occupation increased with his years, she wisely resolved to give him all the advantages which education could confer. He was accordingly sent back to Grantham school, where he continued for some months in busy preparation for his academical studies. His uncle, the Reverend W. Ayscough, who was rector of Burton Coggles, about three miles east of Woolsthorpe, and who had himself studied at Trinity College, recommended to his nephew to enter that society, and it was accordingly determined that he should proceed to Cambridge at the approaching term.6

CHAPTER II.

Newton enters Trinity College, Cambridge—Origin of his Propensity for Mathematics—He studies the Geometry of Descartes unassisted—Purchases a Prism—Revises Dr. Harrow’s Optical Lectures—Dr. Barrow’s Opinion respecting Colours—Takes his Degrees—Is appointed a Fellow of Trinity College—Succeeds Dr. Barrow in the Lucasian Chair of Mathematics.

To a young mind thirsting for knowledge, and ambitious of the distinction which it brings, the transition from a village school to a university like that of Cambridge,—from the absolute solitude of thought to the society of men imbued with all the literature and science of the age,—must be one of eventful interest. To Newton it was a source of peculiar excitement. The history of science affords many examples where the young aspirant had been early initiated into her mysteries, and had even exercised his powers of invention and discovery before he was admitted within the walls of a college; but he who was to give philosophy her laws did not exhibit such early talent; no friendly counsel regulated his youthful studies, and no work of scientific eminence seems to have guided him in his course. In yielding to the impulse of his mechanical genius, his mind obeyed the laws of its own natural expansion, and, following the line of least resistance, it was thus drawn aside from the strongholds with which it was destined to grapple.

When Newton, therefore, arrived at Trinity College, he brought with him a more slender portion of science than falls to the lot of ordinary scholars; but this state of his acquirements was perhaps not unfavourable to the development of his powers. Unexhausted by premature growth, and invigorated by healthful repose, his mind was the better fitted to make those vigorous and rapid shoots which soon covered with foliage and with fruit the genial soil to which it had been transferred.

Cambridge was consequently the real birthplace of Newton’s genius. Her teachers fostered his earliest studies;—her institutions sustained his mightiest efforts;—and within her precincts were all his discoveries made and perfected. When he was called to higher official functions, his disciples kept up the pre-eminence of their master’s philosophy, and their successors have maintained this seat of learning in the fulness of its glory, and rendered it the most distinguished among the universities of Europe.

It was on the 5th of June, 1660, in the 18th year of his age, that Newton was admitted into Trinity College, Cambridge, during the same year that Dr. Barrow was elected professor of Greek in the university. His attention was first turned to the study of mathematics by a desire to inquire into the truth of judicial astrology; and he is said to have discovered the folly of that study by erecting a figure with the aid of one or two of the problems of Euclid. The propositions contained in this ancient system of geometry he regarded as self-evident truths; and without any preliminary study he made himself master of Descartes’s Geometry by his genius and patient application. This neglect of the elementary truths of geometry he afterward regarded as a mistake in his mathematical studies, and he expressed to Dr. Pemberton his regret that “he had applied himself to the works of Descartes, and other algebraic writers, before he had considered the elements of Euclid with that attention which so excellent a writer deserved.7 Dr. Wallis’s Arithmetic of Infinites, Saunderson’s Logic, and the Optics of Kepler were among the books which he had studied with care. On these works he wrote comments during their perusal; and so great was his progress, that he is reported to have found himself more deeply versed in some branches of knowledge than the tutor who directed his studies.

Neither history nor tradition has handed down to us any particular account of his progress during the first three years that he spent at Cambridge. It appears from a statement of his expenses, that in 1664 he purchased a prism, for the purpose, as has been said, of examining Descartes’s theory of colours; and it is stated by Mr. Conduit, that he soon established his own views on the subject, and detected the errors in those of the French philosopher. This, however, does not seem to have been the case. Had he discovered the composition of light in 1664 or 1665, it is not likely that he would have withheld it, not only from the Royal Society, but from his own friends at Cambridge till the year 1671. His friend and tutor, Dr. Barrow, was made Lucasian Professor of Mathematics in 1663, and the optical lectures which he afterward delivered were published in 1669. In the preface of this work he acknowledges his obligations to his colleague, Mr. Isaac Newton,8 for having revised the MSS., and corrected several oversights, and made some important suggestions. In the twelfth lecture there are some observations on the nature and origin of colours, which Newton could not have permitted his friend to publish had he been then in possession of their true theory. According to Dr. Barrow, White is that which discharges a copious light equally clear in every direction; Black is that which does not emit light at all, or which does it very sparingly. Red is that which emits a light more clear than usual, but interrupted by shady interstices. Blue is that which discharges a rarified light, as in bodies which consist of white and black particles arranged alternately. Green is nearly allied to blue. Yellow is a mixture of much white and a little red; and Purple consists of a great deal of blue mixed with a small portion of red. The blue colour of the sea arises from the whiteness of the salt which it contains, mixed with the blackness of the pure water in which the salt is dissolved; and the blueness of the shadows of bodies, seen at the same time by candle and daylight, arises from the whiteness of the paper mixed with the faint light or blackness of the twilight. These opinions savour so little of genuine philosophy that they must have attracted the observation of Newton, and had he discovered at that time that white was a mixture of all the colours, and black a privation of them all, he could not have permitted the absurd speculations of his master to pass uncorrected.

That Newton had not distinguished himself by any positive discovery so early as 1664 or 1665, may be inferred also from the circumstances which attended the competition for the law fellowship of Trinity College. The candidates for this appointment were himself and Mr. Robert Uvedale; and Dr. Barrow, then Master of Trinity, having found them perfectly equal in their attainments, conferred the fellowship on Mr. Uvedale as the senior candidate.

In the books of the university, Newton is recorded as having been admitted sub-sizer in 1661. He became a scholar in 1664. In 1665 he took his degree of Bachelor of Arts, and in 1666, in consequence of the breaking out of the plague, he retired to Woolsthorpe. In 1667 he was made Junior Fellow. In 1668 he took his degree of Master of Arts, and in the same year he was appointed to a Senior Fellowship. In 1669, when Dr. Barrow had resolved to devote his attention to theology, he resigned the Lucasian Professorship of Mathematics in favour of Newton, who may now be considered as having entered upon that brilliant career of discovery the history of which will form the subject of some of the following chapters.

CHAPTER III.

Newton, occupied in grinding Hyperbolical Lenses—His first Experiments with the Prism made in 1666—He discovers the Composition of White Light, and the different Refrangibility of the Rays which compose it—Abandons his Attempts to improve Refracting Telescopes and resolves to attempt the Construction of Reflecting ones—He quits Cambridge on account of the Plague—Constructs two Reflecting Telescopes in 1668, the first ever executed—One of them examined by the Royal Society, and shown to the King—He constructs a Telescope with Glass Specula—Recent History of the Reflecting Telescope—Mr. Airy’s Glass Specula—Hadley’s Reflecting Telescopes—Short’s—Herschel’s—Ramage’s—Lord Oxmantown’s.

The appointment of Newton to the Lucasian chair at Cambridge seems to have been coeval with his grandest discoveries. The first of these of which the date is well authenticated is that of the different refrangibility of the rays of light, which he established in 1666. The germ of the doctrine of universal gravitation seems to have presented itself to him in the same year, or at least in 1667; and “in the year 1666 or before”9 he was in possession of his method of fluxions, and he had brought it to such a state in the beginning of 1669, that he permitted Dr. Barrow to communicate it to Mr. Collins on the 20th of June in that year.

Although we have already mentioned, on the authority of a written memorandum of Newton himself, that he purchased a prism at Cambridge in 1664, yet he does not appear to have made any use of it, as he informs us that it was in 1666 that he “procured a triangular glass prism to try therewith the celebrated phenomena of colours.”10 During that year he had applied himself to the grinding of “optic glasses, of other figures than spherical,” and having, no doubt, experienced the impracticability of executing such lenses, the idea of examining the phenomena of colour was one of those sagacious and fortunate impulses which more than once led him to discovery. Descartes in his Dioptrice, published in 1629, and more recently James Gregory in his Optica Promota published in 1663, had shown that parallel and diverging rays could be reflected or refracted, with mathematical accuracy, to a point or focus, by giving the surface a parabolic, an elliptical, or a hyperbolic form, or some other form not spherical. Descartes had even invented and described machines by which lenses of these shapes could be ground and polished, and the perfection of the refracting telescope was supposed to depend on the degree of accuracy with which they could be executed.

In attempting to grind glasses that were not spherical, Newton seems to have conjectured that the defects of lenses, and consequently of refracting telescopes, might arise from some other cause than the imperfect convergency of rays to a single point, and this conjecture was happily realized in those fine discoveries of which we shall now endeavour to give some account.

When Newton began this inquiry, philosophers of the highest genius were directing all the energies of their mind to the subject of light, and to the improvement of the refracting telescope. James Gregory of Aberdeen had invented his reflecting telescope. Descartes had explained the theory and exerted himself in perfecting the construction of the common refracting telescope, and Huygens had not only executed the magnificent instruments by which he discovered the ring and the satellites of Saturn, but had begun those splendid researches respecting the nature of light, and the phenomena of double refraction, which have led his successors to such brilliant discoveries. Newton, therefore, arose when the science of light was ready for some great accession, and at the precise time when he was required to propagate the impulse which it had received from his illustrious predecessors.

The ignorance which then prevailed respecting the nature and origin of colours is sufficiently apparent from the account we have already given of Dr. Barrow’s speculations on this subject. It was always supposed that light of every colour was equally refracted or bent out of its direction when it passed through any lens or prism, or other refracting medium; and though the exhibition of colours by the prism had been often made previous to the time of Newton, yet no philosopher seems to have attempted to analyze the phenomena.

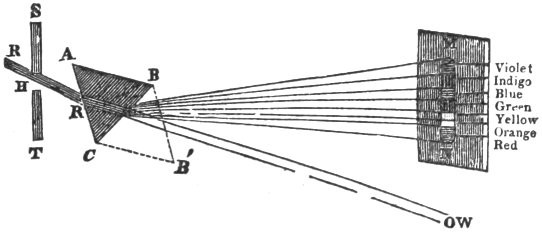
Fig. 1.

When he had procured his triangular glass prism, a section of which is shown at ABC, (fig. 1,) he made a hole H in one of his window-shutters, SHT, and having darkened his chamber, he let in a convenient quantity of the sun’s light RR, which, passing through the prism ABC, was so refracted as to exhibit all the different colours on the wall at MN, forming an image about five times as long as it was broad. “It was at first,” says our author, “a very pleasing divertisement to view the vivid and intense colours produced thereby,” but this pleasure was immediately succeeded by surprise at various circumstances which he had not expected. According to the received laws of refraction, he expected the image MN to be circular, like the white image at W, which the sunbeam RR had formed on the wall previous to the interposition of the prism; but when he found it to be no less than five times larger than its breadth, it “excited in him a more than ordinary curiosity to examine from whence it might proceed. He could scarcely think that the various thickness of the glass, or the termination with shadow or darkness, could have any influence on light to produce such an effect: yet he thought it not amiss first to examine those circumstances, and so find what would happen by transmitting light through parts of the glass of divers thicknesses, or through holes in the window of divers bignesses, or by setting the prism without (on the other side of ST), so that the light might pass through it and be refracted before it was terminated by the hole; but he found none of these circumstances material. The fashion of the colours was in all those cases the same.”

Newton next suspected that some unevenness in the glass, or other accidental irregularity, might cause the dilatation of the colours. In order to try this, he took another prism BCB′, and placed it in such a manner that the light RRW passing through them both might be refracted contrary ways, and thus returned by BCB′ into that course RRW, from which the prism ABC had diverted it, for by this means he thought the regular effects of the prism ABC would be destroyed by the prism BCB′, and the irregular ones more augmented by the multiplicity of refractions. The result was, that the light which was diffused by the first prism ABC into an oblong form, was reduced by the second prism BCB′ into a circular one W, with as much regularity as when it did not pass through them at all; so that whatever was the cause of the length of the image MN, it did not arise from any irregularity in the prism.

Our author next proceeded to examine more critically what might be effected by the difference of the incidence of the rays proceeding from different parts of the sun’s disk: but by taking accurate measures of the lines and angles, he found that the angle of the emergent rays should be 31 minutes equal to the sun’s diameter, whereas the real angle subtended by MN at the hole H was 2° 49′. But as this computation was founded on the hypothesis, that the sine of the angle of incidence was proportional to the sine of the angle of refraction, which from his own experience he could not imagine to be so erroneous as to make that angle but 31′, which was in reality 2° 49′, yet “his curiosity caused him again to take up his prism” ABC, and having turned it round in both directions, so as to make the rays RR fall both with greater and with less obliquity upon the face AC, he found that the colours on the wall did not sensibly change their place; and hence he obtained a decided proof that they could not be occasioned by a difference in the incidence of the light radiating from different parts of the sun’s disk.

Newton then began to suspect that the rays, after passing through the prism, might move in curve lines, and, in proportion to the different degrees of curvature, might tend to different parts of the wall; and this suspicion was strengthened by the recollection that he had often seen a tennis-ball struck with an oblique racket describe such a curve line. In this case a circular and a progressive motion is communicated to the ball by the stroke, and in consequence of this, the direction of its motion was curvilineal, so that if the rays of light were globular bodies, they might acquire a circulating motion by their oblique passage out of one medium into another, and thus move like the tennis-ball in a curve line. Notwithstanding, however, “this plausible ground of suspicion,” he could discover no such curvature in their direction, and, what was enough for his purpose, he observed that the difference between the length MN of the image, and the diameter of the hole H, was proportional to their distance HM, which could not have happened had the rays moved in curvilineal paths.

These different hypotheses, or suspicions, as Newton calls them, being thus gradually removed, he was at length led to an experiment which determined beyond a doubt the true cause of the elongation of the coloured image. Having taken a board with a small hole in it, he placed it behind the face BC of the prism, and close to it, so that he could transmit through the hole any one of the colours in MN, and keep back all the rest. When the hole, for example, was near C, no other light but the red fell upon the wall at N. He then placed behind N another board with a hole in it, and behind this board he placed another prism, so as to receive the red light at N, which passed through this hole in the second board. He then turned round the first prism ABC so as to make all the colours pass in succession through these two holes, and he marked their places on the wall. From the variation of these places, he saw that the red rays at N were less refracted by the second prism than the orange rays, the orange less than the yellow, and so on, the violet being more refracted than all the rest.

Hence he drew the grand conclusion, that light was not homogeneous, but consisted of rays, some of which were more refrangible than others.

As soon as this important truth was established, Sir Isaac saw that a lens which refracts light exactly like a prism must also refract the differently coloured rays with different degrees of force, bringing the violet rays to a focus nearer the glass than the red rays. This is shown in fig. 2, where LL is a convex lens, and S, L, SL rays of the sun falling upon it in parallel directions. The violet rays existing in the white light SL being more refrangible than the rest, will be more refracted or bent, and will meet at V, forming there a violet image of the sun. In like manner the yellow rays will form an image of the sun at Y, and so on, the red rays, which are the least refrangible, being brought to a focus at R, and there forming a red image of the sun.

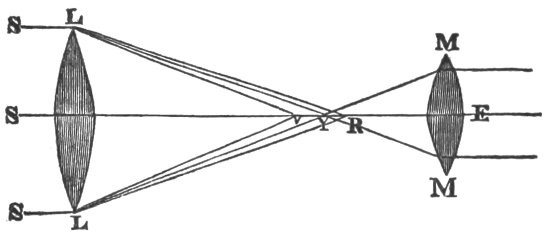
Fig. 2.

Hence, if we suppose LL to be the object-glass of a telescope directed to the sun, and MM an eye-glass through which the eye at E sees magnified the image or picture of the sun formed by LL, it cannot see distinctly all the different images between R and V. If it is adjusted so as to see distinctly the yellow image at Y, as it is in the figure, it will not see distinctly either the red or violet images, nor indeed any of them but the yellow one. There will consequently be a distinct yellow image, with indistinct images of all the other colours, producing great confusion and indistinctness of vision. As soon as Sir Isaac perceived this result of his discovery, he abandoned his attempts to improve the refracting telescope, and took into consideration the principle of reflection; and as he found that rays of all colours were reflected regularly, so that the angle of reflection was equal to the angle of incidence, he concluded that, upon this principle, optical instruments might be brought to any degree of perfection imaginable, provided a reflecting substance could be found which could polish as finely as glass, and reflect as much light as glass transmits, and provided a method of communicating to it a parabolic figure could be obtained. These difficulties, however, appeared to him very great, and he even thought them insuperable when he considered that, as any irregularity in a reflecting surface makes the rays deviate five or six times more from their true path than similar irregularities in a refracting surface, a much greater degree of nicety would be required in figuring reflecting specula than refracting lenses.

Such was the progress of Newton’s optical discoveries, when he was forced to quit Cambridge in 1666 by the plague which then desolated England, and more than two years elapsed before he proceeded any farther. In 1668 he resumed the inquiry, and having thought of a delicate method of polishing, proper for metals, by which, as he conceived, “the figure would be corrected to the last,” he began to put this method to the test of experiment. At this time he was acquainted with the proposal of Mr. James Gregory, contained in his Optica Promota, to construct a reflecting telescope with two concave specula, the largest of which had a hole in the middle of the larger speculum, to transmit the light to an eye-glass;11 but he conceived that it would be an improvement on this instrument to place the eye-glass at the side of the tube, and to reflect the rays to it by an oval plane speculum. One of these instruments he actually executed with his own hands; and he gave an account of it in a letter to a friend, dated February 23d, 1668–9, a letter which is also remarkable for containing the first allusion to his discoveries respecting colours. Previous to this he was in correspondence on the subject with Mr. Ent, afterward Sir George Ent, one of the original council of the Royal Society, an eminent medical writer of his day, and President of the College of Physicians. In a letter to Mr. Ent he had promised an account of his telescope to their mutual friend, and the letter to which we now allude contained the fulfilment of that promise. The telescope was six inches long. It bore an aperture in the large speculum something more than an inch, and as the eye-glass was a plano-convex lens, whose focal length was one-sixth or one-seventh of an inch, it magnified about forty times, which, as Newton remarks, was more than any six-foot tube (meaning refracting telescopes) could do with distinctness. On account of the badness of the materials, however, and the want of a good polish, it represented objects less distinct than a six-feet tube, though he still thought it would be equal to a three or four feet tube directed to common objects. He had seen through it Jupiter distinctly with his four satellites, and also the horns or moon-like phases of Venus, though this last phenomenon required some niceness in adjusting the instrument.

Although Newton considered this little instrument as in itself contemptible, yet he regarded it as an “epitome of what might be done;” and he expressed his conviction that a six-feet telescope might be made after this method, which would perform as well as a sixty or a hundred feet telescope made in the common way; and that if a common refracting telescope could be made of the “purest glass exquisitely polished, with the best figure that any geometrician (Descartes, &c.) hath or can design,” it would scarcely perform better than a common telescope. This, he adds, may seem a paradoxical assertion, yet he continues, “it is the necessary consequence of some experiments which I have made concerning the nature of light.”

The telescope now described possesses a very peculiar interest, as being the first reflecting one which was ever executed and directed to the heavens. James Gregory, indeed, had attempted, in 1664 or 1665, to construct his instrument. He employed Messrs. Rives and Cox, who were celebrated glass-grinders of that time, to execute a concave speculum of six feet radius, and likewise a small one; but as they had failed in polishing the large one, and as Mr. Gregory was on the eve of going abroad, he troubled himself no farther about the experiment, and the tube of the telescope was never made. Some time afterward, indeed, he “made some trials both with a little concave and convex speculum,” but, “possessed with the fancy of the defective figure, he would not be at the pains to fix every thing in its due distance.”

Such were the earliest attempts to construct the reflecting telescope, that noble instrument which has since effected such splendid discoveries in astronomy. Looking back from the present advanced state of practical science, how great is the contrast between the loose specula of Gregory and the fine Gregorian telescopes of Hadley, Short, and Veitch,—between the humble six-inch tube of Newton and the gigantic instruments of Herschel and Ramage.

The success of this first experiment inspired Newton with fresh zeal, and though his mind was now occupied with his optical discoveries, with the elements of his method of fluxions, and with the expanding germ of his theory of universal gravitation, yet with all the ardour of youth he applied himself to the laborious operation of executing another reflecting telescope with his own hands. This instrument, which was better than the first, though it lay by him several years, excited some interest at Cambridge; and Sir Isaac himself informs us, that one of the fellows of Trinity College had completed a telescope of the same kind, which he considered as somewhat superior to his own. The existence of these telescopes having become known to the Royal Society, Newton was requested to send his instrument for examination to that learned body. He accordingly transmitted it to Mr. Oldenburg in December, 1671, and from this epoch his name began to acquire that celebrity by which it has been so peculiarly distinguished.

On the 11th of January, 1672, it was announced to the Royal Society that his reflecting telescope had been shown to the king, and had been examined by the president, Sir Robert Moray, Sir Paul Neale, Sir Christopher Wren, and Mr. Hook. These gentlemen entertained so high an opinion of it, that, in order to secure the honour of the contrivance to its author, they advised the inventor to send a drawing and description of it to Mr. Huygens at Paris. Mr. Oldenburg accordingly drew up a description of it in Latin, which, after being corrected by Mr. Newton, was transmitted to that eminent philosopher. This telescope, of which the annexed is an accurate drawing, is carefully preserved in the library of the Royal Society of London, with the following inscription:—

“Invented by Sir Isaac Newton and made with his own hands, 1671.”

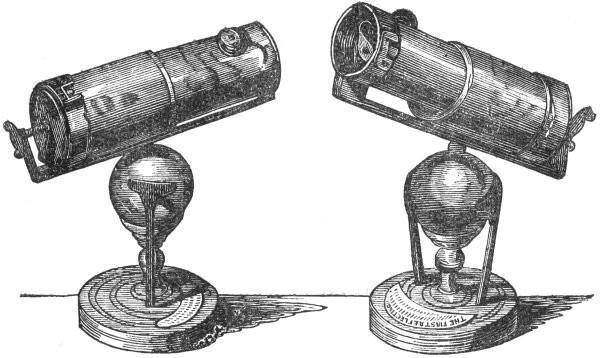
Fig. 3.

Sir Isaac Newton’s Reflecting Telescope.

It does not appear that Newton executed any other reflecting telescopes than the two we have mentioned. He informs us that he repolished and greatly improved a fourteen-feet object-glass, executed by a London artist, and having proposed in 1678 to substitute glass reflectors in place of metallic specula, he tried to make a reflecting telescope on this principle four feet long, and with a magnifying power of 150. The glass was wrought by a London artist, and though it seemed well finished, yet, when it was quicksilvered on its convex side, it exhibited all over the glass innumerable inequalities, which gave an indistinctness to every object. He expresses, however, his conviction that nothing but good workmanship is wanting to perfect these telescopes, and he recommends their consideration “to the curious in figuring glasses.”

For a period of fifty years this recommendation excited no notice. At last Mr. James Short of Edinburgh, an artist of consummate skill, executed about the year 1730 no fewer than six reflecting telescopes with glass specula, three of fifteen inches, and three of nine inches in focal length. He found it extremely troublesome to give them a true figure with parallel surfaces; and several of them when finished turned out useless, in consequence of the veins which then appeared in the glass. Although these instruments performed remarkably well, yet the light was fainter than he expected, and from this cause, combined with the difficulty of finishing them, he afterward devoted his labours solely to those with metallic specula.

At a later period, in 1822, Mr. G. B. Airy of Trinity College, and one of the distinguished successors of Newton in the Lucasian chair, resumed the consideration of glass specula, and demonstrated that the aberration both of figure and of colour might be corrected in these instruments. Upon this ingenious principle Mr. Airy executed more than one telescope, but though the result of the experiment was such as to excite hopes of ultimate success, yet the construction of such instruments is still a desideratum in practical science.

Such were the attempts which Sir Isaac Newton made to construct reflecting telescopes; but notwithstanding the success of his labours, neither the philosopher nor the practical optician seems to have had courage to pursue them. A London artist, indeed, undertook to imitate these instruments; but Sir Isaac informs us, that “he fell much short of what he had attained, as he afterward understood by discoursing with the under workmen he had employed.” After a long period of fifty years, John Hadley, Esq. of Essex, a Fellow of the Royal Society, began in 1719 or 1720 to execute a reflecting telescope. His scientific knowledge and his manual dexterity fitted him admirably for such a task, and, probably after many failures, he constructed two large telescopes about five feet three inches long, one of which, with a speculum six inches in diameter, was presented to the Royal Society in 1723. The celebrated Dr. Bradley and the Rev. Mr. Pound compared it with the great Huygenian refractor 123 feet long. It bore as high a magnifying power as the Huygenian telescope: it showed objects equally distinct, though not altogether so clear and bright, and it exhibited every celestial object that had been discovered by Huygens,—the five satellites of Saturn, the shadow of Jupiter’s satellites on his disk, the black list in Saturn’s ring, and the edge of his shadow cast on the ring. Encouraged and instructed by Mr. Hadley, Dr. Bradley began the construction of reflecting telescopes, and succeeded so well that he would have completed one of them, had he not been obliged to change his residence. Some time afterward he and the Honourable Samuel Molyneux undertook the task together at Kew, and attempted to execute specula about twenty-six inches in focal length; but notwithstanding Dr. Bradley’s former experience, and Mr. Hadley’s frequent instructions, it was a long time before they succeeded. The first good instrument which they finished was in May, 1724. It was twenty-six inches in focal length; but they afterward completed a very large one of eight feet, the largest that had ever been made. The first of these instruments was afterward elegantly fitted up by Mr. Molyneux, and presented to his majesty John V. King of Portugal.

The great object of these two able astronomers was to reduce the method of making specula to such a degree of certainty that they could be manufactured for public sale. Mr. Hauksbee had indeed made a good one about three and a half feet long, and had proceeded to the execution of two others, one of six feet, and another of twelve feet in focal length; but Mr. Scarlet and Mr. Hearne, having received all the information which Mr. Molyneux had acquired, constructed them for public sale; and the reflecting telescope has ever since been an article of trade with every regular optician.

As Sir Isaac Newton was at this time President of the Royal Society, he had the high satisfaction of seeing his own invention become an instrument of public use, and of great advantage to science, and he no doubt felt the full influence of this triumph of his skill. Still, however, the reflecting telescope had not achieved any new discovery in the heavens. The latest accession to astronomy had been made by the ordinary refractors of Huygens, labouring under all the imperfections of coloured light; and this long pause in astronomical discovery seemed to indicate that man had carried to its farthest limits his power of penetrating into the depths of the universe. This, however, was only one of those stationary positions from which human genius takes a new and a loftier elevation. While the English opticians were thus practising the recent art of grinding specula, Mr. James Short of Edinburgh was devoting to the subject all the energies of his youthful mind. In 1732, and in the 22d year of his age, he began his labours, and he carried to such high perfection the art of grinding and polishing specula, and of giving them the true parabolic figure, that, with a telescope fifteen inches in focal length, he read in the Philosophical Transactions at the distance of 500 feet, and frequently saw the five satellites of Saturn together,—a power which was beyond the reach even of Hadley’s six-feet instrument. The celebrated Maclaurin compared the telescopes of Short with those made by the best London artists, and so great was their superiority, that his small telescopes were invariably superior to larger ones from London. In 1742, after he had settled as an optician in the metropolis, he executed for Lord Thomas Spencer a reflecting telescope, twelve feet in focal length, for 630l.; in 1752 he completed one for the King of Spain, at the expense of 1200l.; and a short time before his death, which took place in 1768, he finished the specula of the large telescope which was mounted equatorially for the observatory of Edinburgh by his brother Thomas Short, who was offered twelve hundred guineas for it by the King of Denmark.

Although the superiority of these instruments, which were all of the Gregorian form, demonstrated the value of the reflecting telescope, yet no skilful hand had yet directed it to the heavens; and it was reserved for Dr. Herschel to employ it as an instrument of discovery, to exhibit to the eye of man new worlds and new systems, and to bring within the grasp of his reason those remote regions of space to which his imagination even had scarcely ventured to extend its power. So early as 1774 he completed a five-feet Newtonian reflector, and he afterward executed no fewer than two hundred 7 feet, one hundred and fifty 10 feet, and eighty 20 feet specula. In 1781 he began a reflector thirty feet long, and having a speculum thirty-six inches in diameter; and under the munificent patronage of George III. he completed, in 1789, his gigantic instrument forty feet long, with a speculum forty-nine and a half inches in diameter. The genius and perseverance which created instruments of such transcendent magnitude were not likely to terminate with their construction. In the examination of the starry heavens, the ultimate object of his labours, Dr. Herschel exhibited the same exalted qualifications, and in a few years he rose from the level of humble life to the enjoyment of a name more glorious than that of the sages and warriors of ancient times, and as immortal as the objects with which it will be for ever associated. Nor was it in the ardour of the spring of life that these triumphs of reason were achieved. Dr. Herschel had reached the middle of his course before his career of discovery began, and it was in the autumn and winter of his days that he reaped the full harvest of his glory. The discovery of a new planet at the verge of the solar system was the first trophy of his skill, and new double and multiple stars, and new nebulæ, and groups of celestial bodies were added in thousands to the system of the universe. The spring-tide of knowledge which was thus let in upon the human mind continued for a while to spread its waves over Europe; but when it sank to its ebb in England, there was no other bark left upon the strand but that of the Deucalion of Science, whose home had been so long upon its waters.

During the life of Dr. Herschel, and during the reign, and within the dominions of his royal patron, four new planets were added to the solar system, but they were detected by telescopes of ordinary power; and we venture to state, that since the reign of George III. no attempt has been made to keep up the continuity of Dr. Herschel’s discoveries.

Mr. Herschel, his distinguished son, has indeed completed more than one telescope of considerable size; Mr. Ramage, of Aberdeen, has executed reflectors rivalling almost those of Slough;—and Lord Oxmantown, an Irish nobleman of high promise, is now engaged on an instrument of great size. But what avail the enthusiasm and the efforts of individual minds in the intellectual rivalry of nations? When the proud science of England pines in obscurity, blighted by the absence of the royal favour, and of the nation’s sympathy;—when its chivalry fall unwept and unhonoured;—how can it sustain the conflict against the honoured and marshalled genius of foreign lands?

CHAPTER IV.

He delivers a Course of Optical Lectures at Cambridge—Is elected Fellow of the Royal Society—He communicates to them his Discoveries on the different Refrangibility and Nature of Light—Popular Account of them—They involve him in various Controversies—His Dispute with Pardies—Linus—Lucas—Dr. Hooke and Mr. Huygens—The Influence of these Disputes on the Mind of Newton.

Although Newton delivered a course of lectures on optics in the University of Cambridge in the years 1669, 1670, and 1671, containing his principal discoveries relative to the different refrangibility of light, yet it is a singular circumstance, that these discoveries should not have become public through the conversation or correspondence of his pupils. The Royal Society had acquired no knowledge of them till the beginning of 1672, and his reputation in that body was founded chiefly on his reflecting telescope. On the 23d December, 1671, the celebrated Dr. Seth Ward, Lord Bishop of Sarum, who was the author of several able works on astronomy, and had filled the astronomical chair at Oxford, proposed Mr. Newton as a Fellow of the Royal Society. The satisfaction which he derived from this circumstance appears to have been considerable; and in a letter to Mr. Oldenburg, of the 6th January, he says, “I am very sensible of the honour done me by the Bishop of Sarum in proposing me a candidate; and which, I hope, will be further conferred upon me by my election into the Society; and if so, I shall endeavour to testify my gratitude, by communicating what my poor and solitary endeavours can effect towards the promoting your philosophical designs.” His election accordingly took place on the 11th January, the same day on which the Society agreed to transmit a description of his telescope to Mr. Huygens at Paris. The notice of his election, and the thanks of the Society for the communication of his telescope, were conveyed in the same letter, with an assurance that the Society “would take care that all right should be done him in the matter of this invention.” In his next letter to Oldenburg, written on the 18th January, 1671–2, he announces his optical discoveries in the following remarkable manner: “I desire that in your next letter you would inform me for what time the Society continue their weekly meetings; because if they continue them for any time, I am purposing them, to be considered of and examined, an account of a philosophical discovery which induced me to the making of the said telescope; and I doubt not but will prove much more grateful than the communication of that instrument; being in my judgment the oddest, if not the most considerable detection which hath hitherto been made in the operations of nature.”

This “considerable detection” was the discovery of the different refrangibility of the rays of light which we have already explained, and which led to the construction of his reflecting telescope. It was communicated to the Royal Society in a letter to Mr. Oldenburg, dated February 6th, and excited great interest among its members. The “solemn thanks” of the meeting were ordered to be transmitted to its author for his “very ingenious discourse.” A desire was expressed to have it immediately printed, both for the purpose of having it well considered by philosophers, and for “securing the considerable notices thereof to the author against the arrogations of others;” and Dr. Seth Ward, Bishop of Salisbury, Mr. Boyle, and Dr. Hooke were desired to peruse and consider it, and to bring in a report upon it to the Society.

The kindness of this distinguished body, and the anxiety which they had already evinced for his reputation, excited on the part of Newton a corresponding feeling, and he gladly accepted of their proposal to publish his discourse in the monthly numbers in which the Transactions were then given to the world. “It was an esteem,” says he,12 “of the Royal Society for most candid and able judges in philosophical matters, encouraged me to present them with that discourse of light and colours, which since they have so favourably accepted of, I do earnestly desire you to return them my cordial thanks. I before thought it a great favour to be made a member of that honourable body; but I am now more sensible of the advantages; for believe me, sir, I do not only esteem it a duty to concur with you in the promotion of real knowledge; but a great privilege, that, instead of exposing discourses to a prejudiced and common multitude, (by which means many truths have been baffled and lost), I may with freedom apply myself to so judicious and impartial an assembly. As to the printing of that letter, I am satisfied in their judgment, or else I should have thought it too straight and narrow for public view. I designed it only to those that know how to improve upon hints of things; and, therefore, to spare tediousness, omitted many such remarks and experiments as might be collected by considering the assigned laws of refractions; some of which I believe, with the generality of men, would yet be almost as taking as any I described. But yet, since the Royal Society have thought it fit to appear publicly, I leave it to their pleasure: and perhaps to supply the aforesaid defects, I may send you some more of the experiments to second it (if it be so thought fit), in the ensuing Transactions.”

Following the order which Newton himself adopted, we have, in the preceding chapter, given an account of the leading doctrine of the different refrangibility of light, and of the attempts to improve the reflecting telescope which that discovery suggested. We shall now, therefore, endeavour to make the reader acquainted with the other discoveries respecting colours which he at this time communicated to the Royal Society.

Fig. 4.

Having determined, by experiments already described, that a beam of white light, as emitted from the sun, consisted of seven different colours, which possess different degrees of refrangibility, he measured the relative extent of the coloured spaces, and found them to have the proportions shown in fig. 4, which represents the prismatic spectrum, and which is nothing more than an elongated image of the sun produced by the rays being separated in different degrees from their original direction, the red being refracted least, and the violet most powerfully.

If we consider light as consisting of minute particles of matter, we may form some notion of its decomposition by the prism from the following popular illustration. If we take steel filings of seven different degrees of fineness and mix them together, there are two ways in which we may conceive the mass to be decomposed, or, what is the same thing, all the seven different kinds of filings separated from each other. By means of seven sieves of different degrees of fineness, and so made that the finest will just transmit the finest powder and detain all the rest, while the next in fineness transmits the two finest powders and detains all the rest, and so on, it is obvious that all the powders may be completely separated from each other. If we again mix all the steel filings, and laying them upon a table, hold high above them a flat bar magnet, so that none of the filings are attracted, then if we bring the magnet nearer and nearer, we shall come to a point where the finest filings are drawn up to it. These being removed, and the magnet brought nearer still, the next finest powders will be attracted, and so on till we have thus drawn out of the mass all the powders in a separate state. We may conceive the bar magnet to be inclined to the surface of the steel filings, and so moved over the mass, that at the end nearest to them the heaviest or coarsest will be attracted, and all the remotest and the finest or lighter filings, while the rest are attracted to intermediate points, so that the seven different filings are not only separated, but are found adhering in separate patches to the surface of the flat magnet. The first of these methods, with the sieves, may represent the process of decomposing light, by which certain rays of white light are absorbed, or stifled, or stopped in passing through bodies, while certain other rays are transmitted. The second method may represent the process of decomposing light by refraction, or by the attraction of certain rays farther from their original direction than other rays, and the different patches of filings upon the flat magnet may represent the spaces on the spectrum.

When a beam of white light is decomposed into the seven different colours of the spectrum, any particular colour, when once separated from the rest, is not susceptible of any change, or farther decomposition, whether it is refracted through prisms or reflected from mirrors. It may become fainter or brighter, but Newton never could, by any process, alter its colour or its refrangibility.

Among the various bodies which act upon light, it is conceivable that there might have been some which acted least upon the violet rays and most upon the red rays. Newton, however, found that this never took place; but that the same degree of refrangibility always belonged to the same colour, and the same colour to the same degree of refrangibility.

Having thus determined that the seven different colours of the spectrum were original or simple, he was led to the conclusion that whiteness or white light is a compound of all the seven colours of the spectrum, in the proportions in which they are represented in fig. 4. In order to prove this, or what is called the recomposition of white light out of the seven colours, he employed three different methods.

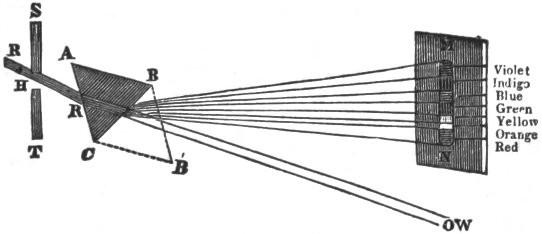
Fig. 5.

When the beam RR was separated into its elementary colours by the prism ABC, he received the colours on another prism BCB′, held either close to the first or a little behind it, and by the opposite refraction of this prism they were all refracted back into a beam of white light BW, which formed a white circular image on the wall at W, similar to what took place before any of the prisms were placed in its way.

The other method of recomposing white light consisted in making the spectrum fall upon a lens at some distance from it. When a sheet of white paper was held behind the lens, and removed to a proper distance, the colours were all refracted into a circular spot, and so blended as to reproduce light so perfectly white as not to differ sensibly from the direct light of the sun.

The last method of recomposing white light was one more suited to vulgar apprehension. It consisted in attempting to compound a white by mixing the coloured powders used by painters. He was aware that such colours, from their very nature, could not compose a pure white; but even this imperfection in the experiment he removed by an ingenious device. He accordingly mixed one part of red lead, four parts of blue bice, and a proper proportion of orpiment and verdigris. This mixture was dun, like wood newly cut, or like the human skin. He now took one-third of the mixture and rubbed it thickly on the floor of his room, where the sun shone upon it through the opened casement, and beside it, in the shadow, he laid a piece of white paper of the same size. “Then going from them to the distance of twelve or eighteen feet, so that he could not discern the unevenness of the surface of the powder nor the little shadows let fall from the gritty particles thereof; the powder appeared intensely white, so as to transcend even the paper itself in whiteness.” By adjusting the relative illumination of the powders and the paper, he was able to make them both appear of the very same degree of whiteness. “For,” says he, “when I was trying this, a friend coming to visit me, I stopped him at the door, and before I told him what the colours were, or what I was doing, I asked him which of the two whites were the best, and wherein they differed! And after he had at that distance viewed them well, he answered, that they were both good whites, and that he could not say which was best, nor wherein their colours differed.” Hence Newton inferred that perfect whiteness may be compounded of different colours.

As all the various shades of colour which appear in the material world can be imitated by intercepting certain rays in the spectrum, and uniting all the rest, and as bodies always appear of the same colour as the light in which they are placed, he concluded, that the colours of natural bodies are not qualities inherent in the bodies themselves, but arise from the disposition of the particles of each body to stop or absorb certain rays, and thus to reflect more copiously the rays which are not thus absorbed.

No sooner were these discoveries given to the world than they were opposed with a degree of virulence and ignorance which have seldom been combined in scientific controversy. Unfortunately for Newton, the Royal Society contained few individuals of pre-eminent talent capable of appreciating the truth of his discoveries, and of protecting him against the shafts of his envious and ignorant assailants. This eminent body, while they held his labours in the highest esteem, were still of opinion that his discoveries were fair subjects of discussion, and their secretary accordingly communicated to him all the papers which were written in opposition to his views. The first of these was by a Jesuit named Ignatius Pardies, Professor of Mathematics at Clermont, who pretended that the elongation of the sun’s image arose from the inequal incidence of the different rays on the first face of the prism, although Newton had demonstrated in his own discourse that this was not the case. In April, 1672, Newton transmitted to Oldenburg a decisive reply to the animadversions of Pardies; but, unwilling to be vanquished, this disciple of Descartes took up a fresh position, and maintained that the elongation of the spectrum might be explained by the diffusion of light on the hypothesis of Grimaldi, or by the diffusion of undulations on the hypothesis of Hook. Newton again replied to these feeble reasonings; but he contented himself with reiterating his original experiments, and confirming them by more popular arguments, and the vanquished Jesuit wisely quitted the field.

Another combatant soon sprung up in the person of one Francis Linus, a physician in Liege,13 who, on the 6th October, 1674, addressed a letter to a friend in London, containing animadversions on Newton’s doctrine of colours. He boldly affirms, that in a perfectly clear sky the image of the sun made by a prism is never elongated, and that the spectrum observed by Newton was not formed by the true sunbeams, but by rays proceeding from some bright cloud. In support of these assertions, he appeals to frequently repeated experiments on the refractions and reflections of light which he had exhibited thirty years before to Sir Kenelm Digby, “who took notes upon them;” and he unblushingly states, that, if Newton had used the same industry as he did, he would never have “taken so impossible a task in hand, as to explain the difference between the length and breadth of the spectrum by the received laws of refraction.” When this letter was shown to Newton, he refused to answer it; but a letter was sent to Linus referring him to the answer to Pardies, and assuring him that the experiments on the spectrum were made when there was no bright cloud in the heavens. This reply, however, did not satisfy the Dutch experimentalist. On the 25th February, 1675, he addressed another letter to his friend, in which he gravely attempts to prove that the experiment of Newton was not made in a clear day;—that the prism was not close to the hole,—and that the length of the spectrum was not perpendicular, or parallel to the length of the prism. Such assertions could not but irritate even the patient mind of Newton. He more than once declined the earnest request of Oldenburg to answer these observations; he stated, that, as the dispute referred to matters of fact, it could only be decided before competent witnesses, and he referred to the testimony of those who had seen his experiments. The entreaties of Oldenburg, however, prevailed over his own better judgment, and, “lest Mr. Linus should make the more stir,” this great man was compelled to draw up a long and explanatory reply to reasonings utterly contemptible, and to assertions altogether unfounded. This answer, dated November 13th, 1675, could scarcely have been perused by Linus, who was dead on the 15th December, when his pupil Mr. Gascoigne, took up the gauntlet, and declared that Linus had shown to various persons in Liege the experiment which proved the spectrum to be circular, and that Sir Isaac could not be more confident on his side than they were on the other. He admitted, however, that the different results might arise from different ways of placing the prism. Pleased with the “handsome genius of Mr. Gascoigne’s letter,” Newton replied even to it, and suggested that the spectrum seen by Linus may have been the circular one, formed by one reflexion, or, what he thought more probable, the circular one formed by two refractions, and one intervening reflection from the base of the prism, which would be coloured if the prism was not an isosceles one. This suggestion seems to have enlightened the Dutch philosophers. Mr. Gascoigne, having no conveniences for making the experiments pointed out by Newton, requested Mr. Lucas of Liege to perform them in his own house. This ingenious individual, whose paper gave great satisfaction to Newton, and deserves the highest praise, confirmed the leading results of the English philosopher; but though the refracting angle of his prism was 60° and the refractions equal, he never could obtain a spectrum whose length was more than from three to three and a half times its breadth, while Newton found the length to be five times its breadth. In our author’s reply, he directs his attention principally to this point of difference. He repeated his measures with each of the three angles of three different prisms, and he affirmed that Mr. Lucas might make sure to find the image as long or longer than he had yet done, by taking a prism with plain surfaces, and with an angle of 66° or 67°. He admitted that the smallness of the angle in Mr. Lucas’s prism, viz. 60°, did not account for the shortness of the spectrum which he obtained with it; and he observed in one of his own prisms that the length of the image was greater in proportion to the refracting angle than it should have been; an effect which he ascribes to its having a greater refractive power. There is every reason to believe that the prism of Lucas had actually a less dispersive power than that of Newton; and had the Dutch philosopher measured its refractive power instead of guessing it, or had Newton been less confident than he was14 that all other prisms must give a spectrum of the same length as his in relation to its refracting angle and its index of refraction, the invention of the achromatic telescope would have been the necessary result. The objections of Lucas drove our author to experiments which he had never before made,—to measure accurately the lengths of the spectra with different prisms of different angles and different refractive powers; and had the Dutch philosopher maintained his position with more obstinacy, he would have conferred a distinguished favour upon science, and would have rewarded Newton for all the vexation which had sprung from the minute discussion of his optical experiments.

Such was the termination of his disputes with the Dutch philosophers, and it can scarcely be doubted that it cost him more trouble to detect the origin of his adversaries’ blunders, than to establish the great truths which they had attempted to overturn.

Harassing as such a controversy must have been to a philosopher like Newton, yet it did not touch those deep-seated feelings which characterize the noble and generous mind. No rival jealousy yet pointed the arguments of his opponents;—no charges of plagiarism were yet directed against his personal character. These aggravations of scientific controversy, however, he was destined to endure; and in the dispute which he was called to maintain both against Hooke and Huygens, the agreeable consciousness of grappling with men of kindred powers was painfully imbittered by the personality and jealousy with which it was conducted.

Dr. Robert Hooke was about seven years older than Newton, and was one of the ninety-eight original or unelected members of the Royal Society. He possessed great versatility of talent, yet, though his genius was of the most original cast, and his acquirements extensive, he had not devoted himself with fixed purpose to any particular branch of knowledge. His numerous and ingenious inventions, of which it is impossible to speak too highly, gave to his studies a practical turn which unfitted him for that continuous labour which physical researches so imperiously demand. The subjects of light, however, and of gravitation seem to have deeply occupied his thoughts before Newton appeared in the same field, and there can be no doubt that he had made considerable progress in both of these inquiries. With a mind less divergent in its pursuits, and more endowed with patience of thought, he might have unveiled the mysteries in which both these subjects were enveloped, and preoccupied the intellectual throne which was destined for his rival; but the infirm state of his health, the peevishness of temper which this occasioned, the number of unfinished inventions from which he looked both for fortune and fame, and, above all, his inordinate love of reputation, distracted and broke down the energies of his powerful intellect. In the more matured inquiries of his rivals he recognised, and often truly, his own incompleted speculations; and when he saw others reaping the harvest for which he had prepared the ground, and of which he had sown the seeds, it was not easy to suppress the mortification which their success inspired. In the history of science, it has always been a difficult task to adjust the rival claims of competitors, when the one was allowed to have completed what the other was acknowledged to have begun. He who commences an inquiry, and publishes his results, often goes much farther than he has announced to the world, and, pushing his speculations into the very heart of the subject, frequently submits them to the ear of friendship. From the pedestal of his published labours his rival begins his researches, and brings them to a successful issue; while he has in reality done nothing more than complete and demonstrate the imperfect speculations of his predecessor. To the world, and to himself, he is no doubt in the position of the principal discoverer: but there is still some apology for his rival when he brings forward his unpublished labours; and some excuse for the exercise of personal feeling, when he measures the speed of his rival by his own proximity to the goal.

The conduct of Dr. Hooke would have been viewed with some such feeling, had not his arrogance on other occasions checked the natural current of our sympathy. When Newton presented his reflecting telescope to the Royal Society, Dr. Hooke not only criticised the instrument with undue severity, but announced that he possessed an infallible method of perfecting all kinds of optical instruments, so that “whatever almost hath been in notion and imagination, or desired in optics, may be performed with great facility and truth.”

Hooke had been strongly impressed with the belief, that light consisted in the undulations of a highly elastic medium pervading all bodies; and, guided by his experimental investigation of the phenomena of diffraction, he had even announced the great principle of interference, which has performed such an important part in modern science. Regarding himself, therefore, as in possession of the true theory of light, he examined the discoveries of Newton in their relation to his own speculative views, and, finding that their author was disposed to consider that element as consisting of material particles, he did not scruple to reject doctrines which he believed to be incompatible with truth. Dr. Hooke was too accurate an observer not to admit the general correctness of Newton’s observations. He allowed the existence of different refractions, the unchangeableness of the simple colours, and the production of white light by the union of all the colours of the spectrum; but he maintained that the different refractions arose from the splitting and rarefying of ethereal pulses, and that there are only two colours in nature, viz. red and violet, which produce by their mixture all the rest, and which are themselves formed by the two sides of a split pulse or undulation.

In reply to these observations, Newton wrote an able letter to Oldenburg, dated June 11, 1672, in which he examined with great boldness and force of argument the various objections of his opponent, and maintained the truth of his doctrine of colours, as independent of the two hypotheses respecting the origin and production of light. He acknowledged his own partiality to the doctrine of the materiality of light; he pointed out the defects of the undulatory theory; he brought forward new experiments in confirmation of his former results; and he refuted the opinions of Hooke respecting the existence of only two simple colours. No reply was made to the powerful arguments of Newton; and Hooke contented himself with laying before the Society his curious observations on the colours of soap-bubbles, and of plates of air, and in pursuing his experiments on the diffraction of light, which, after an interval of two years, he laid before the same body.

After he had thus silenced the most powerful of his adversaries, Newton was again called upon to defend himself against a new enemy. Christian Huygens, an eminent mathematician and natural philosopher, who, like Hooke, had maintained the undulatory theory of light, transmitted to Oldenburg various animadversions on the Newtonian doctrine; but though his knowledge of optics was of the most extensive kind, yet his objections were nearly as groundless as those of his less enlightened countryman. Attached to his own hypothesis respecting the nature of light, namely, to the system of undulation, he seems, like Dr. Hooke, to have regarded the discoveries of Newton as calculated to overturn it; but his principal objections related to the composition of colours, and particularly of white light, which he alleged could be obtained from the union of two colours, yellow and blue. To and similar objections, Newton replied that the colours in question were not simple yellows and blues, but were compound colours, in which, together, all the colours of the spectrum were themselves blended; and though he evinced some strong traces of feeling at being again put upon his defence, yet his high respect for Huygens induced him to enter with patience on a fresh development of his doctrine. Huygens felt the reproof which the tone of this answer so gently conveyed, and in writing to Oldenburg, he used the expression, that Mr. Newton “maintained his doctrine with some concern.” To this our author replied, “As for Mr. Huygens’s expression, I confess it was a little ungrateful to me, to meet with objections which had been answered before, without having the least reason given me why those answers were insufficient.” But though Huygens appears in this controversy as a rash objector to the Newtonian doctrine, it was afterward the fate of Newton to play a similar part against the Dutch philosopher. When Huygens published his beautiful law of double refraction in Iceland spar, founded on the finest experimental analysis of the phenomena, though presented as a result of the undulatory system, Newton not only rejected it, but substituted for it another law entirely inconsistent with the experiments of Huygens, which Newton himself had praised, and with those of all succeeding philosophers.

The influence of these controversies on the mind of Newton seems to have been highly exciting. Even the satisfaction of humbling all his antagonists he did not feel as a sufficient compensation for the disturbance of his tranquillity. “I intend,” says he,15 “to be no farther solicitous about matters of philosophy. And therefore I hope you will not take it ill if you find me never doing any thing more in that kind; or rather that you will favour me in my determination, by preventing, so far as you can conveniently, any objections or other philosophical letters that may concern me.” In a subsequent letter in 1675, he says, “I had some thoughts of writing a further discourse about colours, to be read at one of your assemblies; but find it yet against the grain to put pen to paper any more on that subject;” and in a letter to Leibnitz, dated December the 9th, 1675, he observes, “I was so persecuted with discussions arising from the publication of my theory of light, that I blamed my own imprudence for parting with so substantial a blessing as my quiet to run after a shadow.”

CHAPTER V.

Mistake of Newton in supposing that the Improvement of Refracting Telescopes was hopeless—Mr. Hall invents the Achromatic Telescope—Principles of the Achromatic Telescope explained—It is re-invented by Dollond, and improved by future Artists—Dr. Blair’s Aplanatic Telescope—Mistakes in Newton’s Analysis of the Spectrum—Modern Discoveries respecting the Structure of the Spectrum.

The new doctrines of the composition of light, and of the different refrangibility of the rays which compose it, having been thus established upon an impregnable basis, it will be interesting to take a general view of the changes which they have undergone since the time of Newton, and of their influence on the progress of optical discovery.

There is no fact in the history of science more singular than that Newton should have believed that all bodies produced spectra of equal length, or separated the red and violet rays to equal distances when the refraction of the mean rays was the same. This opinion, unsupported by experiments, and not even sanctioned by any theoretical views, seems to have been impressed upon his mind with all the force of an axiom.16 Even the shortness of the spectrum observed by Lucas did not rouse him to further inquiry; and when, under the influence of this blind conviction he pronounced the improvement of the refracting telescope to be desperate, he checked for a long time the progress of this branch of science, and furnished to future philosophers a lesson which cannot be too deeply studied.

In 1729, about two years after the death of Sir Isaac, an individual unknown to science broke the spell in which the subject of the spectrum had been so singularly bound. Mr. Chester More Hall, of More Hall in Essex, while studying the mechanism of the human eye, was led to suppose that telescopes might be improved by a combination of lenses of different refractive powers, and he actually completed several object-glasses upon this principle. The steps by which he arrived at such a construction have not been recorded; but it is obvious that he must have discovered what escaped the sagacity of Newton, that prisms made of different kinds of glass produced different degrees of separation of the red and violet rays, or gave spectra of different lengths when the refraction of the middle ray of the spectrum was the same.

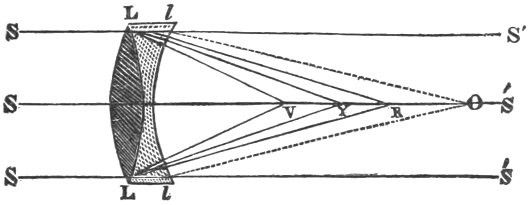
Fig. 6.

In order to explain how such a property led him to the construction of a telescope without colour, or an achromatic telescope, let us take a lens LL of crown or plate glass, whose focal length LY is about twelve inches. When the sun’s rays SL, SL fall upon it, the red will be refracted to R, the yellow to Y, and the violet to V. If we now place behind it a concave lens ll of the same glass, and of the same focus or curvature, it will be found, both by experiment and by drawing the refracted rays, according to the rules given in elementary works, that the concave glass ll will refract the rays LR, LR into LS′, LS′, and the rays LV, LV into LS′, LS′ free of all colour; but as these rays will be parallel, the two lenses will not have a focus, and consequently cannot form an image so as to be used as the object-glass of a telescope. This is obvious from another consideration; for since the curvatures of the convex and concave lenses are the same, the two put together will be exactly the same as if they were formed out of a single piece of glass, having parallel surfaces like a watch-glass, so that the parallel rays of light SL, SL will pass on in the same direction LS′, LS′ affected by equal and opposite refractions as in a piece of plane glass.

Now, since the convex lens LL separated the white light SL, SL into its component coloured rays, LV, LV being the extreme violet, and LR, LR the extreme red; it follows that a similar concave lens of the same glass is capable of uniting into white light LS′, LS′ rays, as much separated as LV, LR are. Consequently, if we take a concave lens ll of the same, or of a greater refractive power than the convex one, and having the power of uniting rays farther separated than LV, LR are, a less concavity in the lens ll will be sufficient to unite the rays LV, LR into a white ray LS′; but as the lens ll is now less concave than the lens LL is convex, the concavity will predominate, and the uncoloured rays LS′, LS′ will no longer be parallel, but will converge to some point O, where they will form a colourless or achromatic image of the sun.

The effect now described may be obtained by making the convex lens LL of crown or of plate glass, and the concave one of flint glass, or that of which wineglasses are made. If the concave lens ll has a greater refractive power than LL, which is always the case, the only effect of it will be to make the rays converge to a focus more remote than O, or to render a less curvature necessary in ll, if O is fixed for the focus of the combined lenses.

Such is the principle of the achromatic telescope as constructed by Mr. Hall. This ingenious individual employed working opticians to grind his lenses, and he furnished them with the radii of the surfaces, which were adjusted to correct the aberration of figure as well as of colour. His invention, therefore, was not an accidental combination of a convex and a concave lens of different kinds of glass, which might have been made merely for experiment; but it was a complete achromatic telescope, founded on a thorough knowledge of the different dispersive powers of crown and flint glass. It is a curious circumstance, however, in the history of the telescope, that this invention was actually lost. Mr. Hall never published any account of his labours, and it is probable that he kept them secret till he should be able to present his instrument to the public in a more perfect form; and it was not till John Dollond had discovered the property of light upon which the instrument depends, and had actually constructed many fine telescopes, that the previous labours of Mr. Hall were laid before the public.17 From this period the achromatic telescope underwent gradual improvement, and by the successive labours of Dollond, Ramsden, Blair, Tulley, Guinand, Lerebours, and Fraunhofer, it has become one of the most valuable instruments in physical science.

Although the achromatic telescope, as constructed by Dollond, was founded on the principle that the spectra formed by crown and flint glass differed only in their relative lengths, when the refraction of the mean ray was the same, yet by a more minute examination of the best instruments, it was found that they exhibited white or luminous objects tinged on one side with a green fringe, and on the other with one of a claret colour. These colours, which did not arise from any defect of skill in the artist, were found to arise from a difference in the extent of the coloured spaces in two equal spectra formed by crown and by flint glass. This property was called the irrationality of the coloured spaces, and the uncorrected colours which remained when the primary spectrum of the crown glass was corrected by the primary spectrum of the flint glass were called the secondary or residual spectrum. By a happy contrivance, which it would be out of place here to describe, Dr. Blair succeeded in correcting this secondary spectrum, or in removing the green and claret-coloured fringes which appeared in the best telescopes, and to this contrivance he gave the name of the Aplanatic Telescope.

But while Newton thus overlooked these remarkable properties of the prismatic spectrum, as formed by different bodies, he committed some considerable mistakes in his examination of the spectrum which was under his own immediate examination. It does not seem to have occurred to him that the relations of the coloured spaces must be greatly modified by the angular magnitude of the sun or the luminous body, or aperture from which the spectrum is obtained; and misled by an apparent analogy between the length of the coloured spaces and the divisions of a musical chord,18 he adopted the latter, as representing the proportion of the coloured spaces in every beam of white light. Had two other observers, one situated in Mercury, and the other in Jupiter, studied the prismatic spectrum of the sun by the same instruments, and with the same sagacity as Newton, it is demonstrable that they would have obtained very different results. On account of the apparent magnitude of the sun in Mercury, the observer there would obtain a spectrum entirely without green, having red, orange, and yellow at one end, the white in the middle, and terminated at the other end with blue and violet. The observer in Jupiter would, on the contrary, have obtained a spectrum in which the colours were much more condensed. On the planet Saturn a spectrum exactly similar would have been obtained, notwithstanding the greater diminution of the sun’s apparent diameter. It may now be asked, which of all these spectra are we to consider as exhibiting the number, and arrangement, and extent of the coloured spaces proper to be adopted as the true analysis of a solar ray.

The spectrum observed by Newton has surely no claim to our notice, merely because it was observed upon the surface of the earth. The spectrum obtained in Mercury affords no analysis at all of the incident beam, the colours being almost all compound, and not homogeneous, and that of Newton is liable to the same objection. Had Newton examined his spectrum under the very same circumstances in winter and in summer, he would have found the analysis of the beam more complete in summer, on account of the diminution of the sun’s diameter; and, therefore, we are entitled to say that neither the number nor the extent of the coloured spaces, as given by Newton, are those which belong to homogeneous and uncompounded light.

The spectrum obtained in Jupiter and Saturn is the only one where the analysis is complete, as it is incapable of having its character altered by any farther diminution of the sun’s diameter. Hence we are forced to conclude, not only that the number and extent of the primitive homogeneous colours, as given by Newton, are incorrect; but that if he had attempted to analyze some of the primitive tints in the spectrum, he would have found them decidedly composed of heterogeneous rays. There is one consequence of these observations which is somewhat interesting. A rainbow formed in summer, when the sun’s diameter is least, must have its colours more condensed and homogeneous than in winter, when the size of its disk is a maximum, and when the upper or the under limb of the sun is eclipsed, a rainbow formed at that time will lose entirely the yellow rays, and have the green and the red in perfect contact. For the same reason, a rainbow formed in Venus and Mercury will be destitute of green rays, and have a brilliant bow of white light separating two coloured arches; while in Mars, Jupiter, Saturn, and the Georgian planet, the bow will exhibit only four homogeneous colours.

From his analysis of the solar spectrum, Newton concluded, “that to the same degree of refrangibility ever belonged the same colour, and to the same colour ever belonged the same degree of refrangibility;” and hence he inferred, that red, orange, yellow, green, blue, indigo, and violet were primary and simple colours. He admitted, indeed, that “the same colours in specie with these primary ones may be also produced by composition. For a mixture of yellow and blue makes green, and of red and yellow makes orange;” but such compound colours were easily distinguished from the simple colours of the spectrum by the circumstance, that they are always capable of being resolved by the action of the prism into the two colours which compose them.

This view of the composition of the spectrum might have long remained unchallenged, had we not been able to apply to it a new mode of analysis. Though we cannot separate the green rays of the spectrum into yellow and blue by the refraction of prisms, yet if we possessed any substance which had a specific attraction for blue rays, and which stopped them in their course, and allowed the yellow rays to pass, we should thus analyze the green as effectually as if they were separated by refraction. The substance which possesses this property is a purplish blue glass, similar to that of which finger-glasses are made. When we view through a piece of this glass, about the twentieth of an inch thick, a brilliant prismatic spectrum, we find that it has exercised a most extraordinary absorptive action on the different colours which compose it. The red part of the spectrum is divided into two red spaces, separated by an interval entirely devoid of light. Next to the inner red space comes a space of bright yellow, separated from the red by a visible interval. After the yellow comes the green, with an obscure space between them, then follows the blue and the violet, the last of which has suffered little or no diminution. Now it is very obvious, that in this experiment, the blue glass has actually absorbed the red rays, which, when mixed with the yellow on one side, constituted orange, and the blue rays, which, when mixed with the yellow on the other side, constituted green, so that the insulation of the yellow rays thus effected, and the disappearance of the orange, and of the greater part of the green light, proves beyond a doubt that the orange and green colours in the spectrum are compound colours, the former consisting of red and yellow rays, and the latter of yellow and blue rays of the very same refrangibility. If we compare the two red spaces of the spectrum seen through the blue glass with the red space seen without the blue glass, it will be obvious that the red has experienced such an alteration in its tint by the action of the blue glass, as would be effected by the absorption of a small portion of yellow rays; and hence we conclude, that the red of the spectrum contains a slight tinge of yellow, and that the yellow space extends over more than one-half of the spectrum, including the red, orange, yellow, green, and blue spaces.

I have found also that red light exists in the yellow space, and it is certain that in the violet space red light exists in a state of combination with the blue rays. From these and other facts which it would be out of place here to explain, I conclude that the prismatic spectrum consists of three different spectra, viz. red, yellow, and blue, all having the same length, and all overlapping each other. Hence red, yellow, and blue rays of the very same refrangibility coexist at every point of the spectrum; but the colour at any one point will be that of the predominant ray, and will depend upon the relative distance of the point from the maximum ordinate of the curve which represents the intensity of the light of each of the three spectra.

Fig. 7.

This structure of the spectrum, which harmonizes with the old hypothesis of three simple colours, will be understood from the annexed diagram, where MN is the spectrum of seven colours, all compounded of the three simple ones, red, yellow, and blue. The ordinates of the curves R, Y, and B will express the intensities of each colour at different points of the spectrum. At the red extremity M of the spectrum, the pure red is scarcely altered by the very slight intermixture of yellow and blue. Farther on in the red space, the yellow begins to make the red incline to scarlet. It then exists in sufficient quantity to form orange, and, as the red declines, the yellow predominates over the feeble portion of red and blue which are mixed with it. As the yellow decreases in intensity, the increasing blue forms with it a good green, and the blue rising to its maximum speedily overpowers the small portion of yellow and red. When the blue becomes very faint, the red exhibits its influence in converting it into violet, and the yellow ceases to exercise a marked influence on the tint. The influence of the red over the blue space is scarcely perceptible, on account of the great intensity of the blue light; but we may easily conceive it to reappear and form the violet light, not only from the rapid decline of the blue light, but from the greater influence of the red rays upon the retina.

These views may, perhaps, be more clearly understood by supposing that a certain portion of white light is actually formed at every point of the spectrum by the union of the requisite number of the three coloured rays that exist at any point. The white light thus formed will add to the brilliancy without affecting the tint of the predominant colour.

In the violet space we may conceive the small portion of yellow which exists there to form white light with a part of the blue and a part of the red, so that the resulting tint will be violet, composed of the blue and the small remaining portion of red, mixed with the white light. This white light will possess the remarkable property of not being susceptible of decomposition by the analysis of the prism, as it is composed of red, yellow, and blue rays of the very same refrangibility. The insulation of this white light by the absorption of the predominant colours I have effected in the green, yellow, and red spaces, and by the use of new absorbing media we may yet hope to exhibit it in some of the other colours, particularly in the brightest part of the blue space, where an obvious approximation to it takes place.

Among the most important modern discoveries respecting the spectrum we must enumerate that of fixed dark and coloured lines, which we owe to the sagacity of Dr. Wollaston and M. Fraunhofer. Two or three of these lines were discovered by Dr. Wollaston, but nearly 600 have been detected by means of the fine prisms and the magnificent apparatus of the Bavarian optician. These lines are parallel to one another, and perpendicular to the length of the spectrum. The largest occupy a space from 5″ to 10″ in breadth. Sometimes they occur in well-defined lines, and at other times in groups; and in all spectra formed from solar light, they preserve the same order and intensity, and the same relative position to the coloured spaces, whatever be the nature of the prism by which they are produced. Hence these lines are fixed points, by which the relative dispersive powers of different media may be ascertained with a degree of accuracy hitherto unknown in this branch of science. In the light of the fixed stars, and in that of artificial flames, a different system of lines is produced, and this system remains unaltered, whatever be the nature of the prism by which the spectrum is formed.

The most important fixed lines in the spectrum formed by light emitted from the sun, whether it is reflected from the sky, the clouds, or the moon, may be easily seen by looking at a narrow slit in the window-shutter of a dark room, through a hollow prism formed of plates of parallel glass, and filled with any fluid of a considerable dispersive power. The slit should not greatly exceed the twentieth of an inch, and the eye should look through the thinnest edge of the prism where there is the least thickness of fluid. These lines I have found to be the boundaries of spaces within which the rays have particular affinities for particular bodies.

CHAPTER VI.

Colours of thin Plates first studied by Boyle and Hooke—Newton determines the Law of their Production—His Theory of Fits of Easy Reflection and Transmission—Colours of thick Plates.

In examining the nature and origin of colours as the component parts of white light, the attention of Newton was directed to the curious subject of the colours of thin plates, and to its application to explain the colours of natural bodies. His earliest researches on this subject were communicated, in his Discourse on Light and Colours, to the Royal Society, on the 9th December, 1675, and were read at subsequent meetings of that body. This discourse contained fuller details respecting the composition and decomposition of light than he had given in his letter to Oldenburg, and was concluded with nine propositions, showing how the colours of thin transparent plates stand related to those of all natural bodies.

The colours of thin plates seem to have been first observed by Mr. Boyle. Dr. Hooke afterward studied them with some care, and gave a correct account of the leading phenomena, as exhibited in the coloured rings upon soap-bubbles, and between plates of glass pressed together. He recognised that the colour depended upon some certain thickness of the transparent plate, but he acknowledges that he had attempted in vain to discover the relation between the thickness of the plate and the colour which it produced.

Dr. Hooke succeeded in splitting a mineral substance, called mica, into films of such extreme thinness as to give brilliant colours. One plate, for example, gave a yellow colour, another a blue colour, and the two together a deep purple; but, as plates which produced those colours were always less than the 12,000th part of an inch thick, it was quite impracticable, by any contrivance yet discovered, to measure their thickness, and determine the law according to which the colour varied with the thickness of the film. Newton surmounted this difficulty by laying a double convex lens, the radius of curvature of each side of which was fifty feet, upon the flat surface of a plano-convex object-glass, and in this way he obtained a plate of air or of space varying from the thinnest possible edge at the centre of the object-glass where it touched the plane surface, to a considerable thickness at the circumference of the lens. When light was allowed to fall upon the object-glass, every different thickness of the plate of air between the object-glass gave different colours, so that the point where the two object-glasses touched one another was the centre of a number of concentric coloured rings. Now, as the curvature of the object-glass was known, it was easy to calculate the thickness of the plate of air at which any particular colour appeared, and thus to determine the law of the phenomena.

In order to understand how he proceeded, let CED be the convex surface of the one object-glass, and AEB the flat surface of the other. Let them touch at the point E, and let homogeneous red rays fall upon them, as shown in the figure. At the point of contact E, where the plate of air is inconceivably thin, not a single ray of the pencil RE is reflected. The light is wholly transmitted, and, consequently, to an eye above E, there will appear at E a black spot. At a, where the plate of air is thicker, the red light ra is reflected in the direction aa′, and as the air has the same thickness in a circle round the point E, the eye above E, at a, will see next the black spot E a ring of red light. At m, where the thickness of the air is a little greater than at a, the light r′m is all transmitted as at E, and not a single ray suffers reflection, so that to an eye above E at m′ there will be seen without the red ring a a dark ring m. In like manner, at greater thicknesses of the plate of air, there is a succession of red and dark rings, diminishing in breadth as shown in the diagram.

Fig. 8.

When the same experiment was repeated in orange, yellow, green, blue, indigo, and violet light, the very same phenomenon was observed; with this difference only, that the rings were largest in red light, and smallest in violet light, and had intermediate magnitudes in the intermediate colours.

If the observer now places his eye below E, so as to see the transmitted rays, he will observe a set of rings as before, but they will have a bright spot in their centre at E, and the luminous rings will now correspond with those which were dark when seen by reflection, as will be readily understood from inspecting the preceding diagram.

When the object-glasses are illuminated by white light, the seven systems of rings, formed by all the seven colours which compose white light, will now be seen at once. Had the rings in each colour been all of the same diameter they would all have formed brilliant white rings, separated by dark intervals; but, as they have all different diameters, they will overlap one another, producing rings of various colours by their mixture. These colours, reckoning from the centre E, are as follows:—

1st Order. Black, blue, white, yellow, orange, red.

2d Order. Violet, blue, green, yellow, orange, red.

3d Order. Purple, blue, green, yellow, red, bluish-red.

4th Order. Bluish-green, green, yellowish-green, red.

5th Order. Greenish-blue, red.

6th Order. Greenish-blue, red.

By accurate measurements, Sir Isaac found that the thicknesses of air at which the most luminous parts of the first rings were produced, were in parts of an inch 1/178000, 3/178000, 5/178000, 7/178000, 9/178000, 11/178000. If the medium or the substance of the thin plate is water, as in the case of the soap-bubble, which produces beautiful colours according to its different degrees of thinness, the thicknesses at which the most luminous parts of the rings appear are produced at 1/1·336 of the thickness at which they are produced in air, and in the case of glass or mica at 1/1·525 of that thickness; the numbers 1.336, 1.525 expressing the ratio of the sines of the angles of incidence and refraction in the substances which produce the colours.

From the phenomena thus briefly described, Sir Isaac Newton deduces that ingenious, though hypothetical, property of light, called its fits of easy reflection and transmission. This property consists in supposing that every particle of light from its first discharge from a luminous body possesses, at equally distant intervals, dispositions to be reflected from, and transmitted through, the surfaces of bodies upon which it is incident. Hence, if a particle of light reaches a reflecting surface of glass when it is in its fit of reflection, or in its disposition to be reflected, it will yield more readily to the reflecting force of the surface; and, on the contrary, if it reaches the same surface while in a fit of easy transmission, or in a disposition to be transmitted, it will yield with more difficulty to the reflecting force. Sir Isaac has not ventured to inquire into the cause of this property; but we may form a very intelligible idea of it by supposing, that the particles of light have two attractive and two repulsive poles at the extremities of two axes at right angles to each other, and that the particles revolve round their axes, and at equidistant intervals bring one or other of these axes into the line of the direction in which the particle is moving. If the attractive axis is in the line of the direction in which the particle moves when it reaches the refracting surface, the particle will yield to the attractive force of the medium, and be refracted and transmitted; but if the repulsive axis is in the direction of the particle’s motion when it reaches the surface, it will yield to the repulsive force of the medium, and be reflected from it.

The application of the theory of alternate fits of reflection and transmission to explain the colours of thin plates is very simple. When the light falls upon the first surface AB, Fig. 8 of the plate of air between AB and CED, the rays that are in a fit of reflection are reflected, and those that are in a fit of transmission are transmitted. Let us call F the length of a fit, or the distance through which the particle of light moves while it passes from the state of being in a fit of reflection to the state of being in a fit of transmission. Now, as all the particles of light transmitted through AB were in a state of easy transmission when they entered AB, it is obvious, that, if the plate of air at E is so thin as to be less than one-half of F, the particles of light will still be in their disposition to be transmitted, and consequently the light will be all transmitted, and none reflected at the curve surface at E. When the plate becomes thicker towards a, so that its thickness exceeds half of F, the light will not reach the surface CE till it has come under its fit of reflection, and consequently at a the light will be all reflected, and none transmitted. As the thickness increases towards m, the light will have come under its fit of transmission, and so on, the light being reflected at a, l, and transmitted at E, m. This will perhaps be still more easily understood from fig. 9, where we may suppose AEC to be a thin wedge of glass or any other transparent body. When light is incident on the first surface AE, all the particles of it that are in a fit of easy reflection will be reflected, and all those in a fit of easy transmission will be transmitted. As the fits of transmission all commence at AE, let the first fit of transmission end when the particles of light have reached ab, and the second when they have reached ef; and let the fits of reflection commence at cd and gh. Then, as the fit of transmission continues from AE to ab, all the light that falls upon the portion mE of the second surface will be transmitted and none reflected, so that to an eye above E the space mE will appear black. As the fit of reflection commences at ab, and continues to cd, all the light which falls upon the portion nm will be reflected, and none transmitted; and so on, the light being transmitted at mE and pn, and reflected at nm and qp. Hence to an eye above E the wedge-shaped film of which AEC is a section will be covered with parallel bands or fringes of light separated by dark fringes of the same breadth, and they will be all parallel to the thin edge of the plate, a dark fringe corresponding to the thinnest edge. To an eye placed below CE, similar fringes will be seen, but the one corresponding to the thinnest edge mE will be luminous.

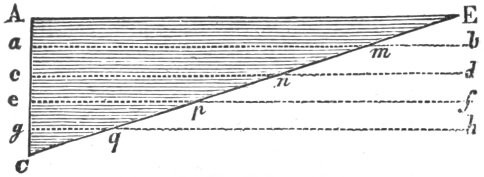
Fig. 9.

If the thickness of the plate does not vary according to a regular law as in fig. 9, but if, like a film of blown glass, it has numerous inequalities, then the alternate fringes of light and darkness will vary with the thickness of the film, and throughout the whole length of each fringe the thickness of the film will be the same.

We have supposed in the preceding illustration that the light employed is homogeneous. If it is white, then the differently coloured fringes will form by their superposition a system of fringes analogous to those seen between two object-glasses, as already explained.

The same periodical colours which we have now described as exhibited by thin plates were discovered by Newton in thick plates, and he has explained them by means of the theory of fits; but it would lead us beyond the limits of a popular work like this to enter into any details of his observations, or to give an account of the numerous and important additions which this branch of optics has received from the discoveries of succeeding authors.

CHAPTER VII.

Newton’s Theory of the Colours of Natural Bodies explained—Objections to it stated—New Classification of Colours—Outline of a New Theory proposed.

If the objects of the material world had been illuminated with white light, all the particles of which possessed the same degree of refrangibility, and were equally acted upon by the bodies on which they fall, all nature would have shone with a leaden hue, and all the combinations of external objects, and all the features of the human countenance, would have exhibited no other variety but that which they possess in a pencil sketch or a China-ink drawing. The rainbow itself would have dwindled into a narrow arch of white light,—the stars would have shone through a gray sky,—and the mantle of a wintry twilight would have replaced the golden vesture of the rising and the setting sun. But He who has exhibited such matchless skill in the organization of material bodies, and such exquisite taste in the forms upon which they are modelled, has superadded that ethereal beauty which enhances their more permanent qualities, and presents them to us in the ever-varying colours of the spectrum. Without this the foliage of vegetable life might have filled the eye and fostered the fruit which it veils,—but the youthful green of its spring would have been blended with the dying yellow of its autumn. Without this the diamond might have displayed to science the beauty of its forms, and yielded to the arts its adamantine virtues;—but it would have ceased to shine in the chaplet of beauty, and to sparkle in the diadem of princes. Without this the human countenance might have expressed all the sympathies of the heart, but the “purple light of love” would not have risen on the cheek, nor the hectic flush been the herald of its decay.

The gay colouring with which the Almighty has decked the pale marble of nature is not the result of any quality inherent in the coloured body, or in the particles by which it may be tinged, but is merely a property of the light in which they happen to be placed. Newton was the first person who placed this great truth in the clearest evidence. He found that all bodies, whatever were their peculiar colours, exhibited these colours only in white light. When they were illuminated by homogeneous red light they appeared red, by homogeneous yellow light, yellow, and so on, “their colours being most brisk and vivid under the influence of their own daylight colours.” The leaf of a plant, for example, appeared green in the white light of day, because it had the property of reflecting that light in greater abundance than any other. When it was placed in homogeneous red light, it could no longer appear green, because there was no green light to reflect; but it reflected a portion of red light, because there was some red in the compound green which it had the property of reflecting. Had the leaf originally reflected a pure homogeneous green, unmixed with red, and reflected no white light from its outer surface, it would have appeared quite black in pure homogeneous red light, as this light does not contain a single ray which the leaf was capable of reflecting. Hence the colours of material bodies are owing to the property which they possess of stopping certain rays of white light, while they reflect or transmit to the eye the rest of the rays of which white light is composed.

So far the Newtonian doctrine of colours is capable of rigid demonstration; but its author was not content with carrying it thus far: he sought to determine the manner in which particular rays are stopped, while others are reflected or transmitted; and the result of this profound inquiry was his theory of the colours of natural bodies, which was communicated to the Royal Society on the 10th February, 1675. This theory is perhaps the loftiest of all his speculations; and though, as a physical generalization, it stands on a perishable basis, and must soon be swept away in the progress of science, it yet bears the deepest impress of the grasp of his powerful intellect.

The principles upon which this theory is founded are the following:—

1. Bodies that have the greatest refractive powers reflect the greatest quantity of light; and at the confines of equally refracting media there is no reflection.

2. The least particles of almost all natural bodies are in some measure transparent.

3. Between the particles of bodies are many pores or spaces, either empty or filled with media of less density than the particles.

4. The particles of bodies and their pores, or the spaces between the particles, have some definite size.

Upon these principles Newton explains the origin of transparency, opacity, and colour.

Transparency he considers as arising from the particles and their intervals or pores being too small to cause reflection at their common surfaces,19 so that all the light which enters transparent bodies passes through them without any portion of it being turned from its path by reflection. If we could obtain, for example, a film of mica whose thickness does not exceed two-thirds of the millionth part of an inch, all the light which fell upon it would pass through it, and none would be reflected. If this film was then cut into fragments, a number of such fragments would constitute a bundle, which would also transmit all the light which fell upon it, and be perfectly transparent.

Opacity in bodies arises, he thinks, from an opposite cause, viz. when the parts of bodies are of such a size as to be capable of reflecting the light which falls upon them, in which case the light is “stopped or stifled” by the multitude of reflections.

The colours of natural bodies have, in the Newtonian hypothesis, the same origin as the colours of thin plates, their transparent particles, according to their several sizes, reflecting rays of one colour, and transmitting those of another. “For if a thinned or plated body which, being of an uneven thickness, appears all over of one uniform colour, should be slit into threads, or broken into fragments of the same thickness with the plate or film, every thread or fragment should keep its colour, and consequently, a heap of such threads or fragments should constitute a mass or powder of the same colour which the plate exhibited before it was broken: and the parts of all natural bodies being like so many fragments of a plate, must, on the same grounds, exhibit the same colour.”

Such is the theory of the colours of natural bodies, stated as clearly and briefly as we can. It has been very generally admitted by philosophers, both of our own and of other countries, and has been recently illustrated and defended by a French philosopher of distinguished eminence. That this theory affords the true explanation of certain colours, or, to speak more correctly, that certain colours in natural bodies are the colours of thin plates, cannot be doubted; but it will not be difficult to show that it is quite inapplicable to that great class of phenomena which may be considered as representing the colours of natural bodies.

The first objection to the Newtonian theory is the total absence of all reflected light from the particles of transparent coloured media, such as coloured gems, coloured glasses, and coloured fluids. This objection was urged long ago by Mr. Delaval, who placed coloured fluids on black grounds, and never could perceive the least trace of the reflected tints. I have repeated the experiment with every precaution, and with every variation that I could think of, and I consider it as an established fact, that in such coloured bodies the complementary reflected colour cannot be rendered visible. If the fluid, for example, be red, the green light from which the red has been separated ought to appear either directly by looking into the coloured mass, or ought to be recognised by its influence in modifying the light really reflected; but as it cannot be seen, we must conclude that it has not been reflected, but has been destroyed by some other property of the coloured body.

A similar objection may be drawn from the disappearance of the transmitted complementary colour in the leaves of plants and petals of flowers. I have ascertained from numerous experiments, that the transmitted colour is almost invariably the same with the reflected colour, and that the same holds true with the coloured juices expressed from them. The complementary tints are never seen, and wherever there has been any thing like an approximation to two tints, I have invariably found that it arose from there being two different coloured juices existing in different sides of the leaf.

In the phenomena of the light transmitted by coloured glasses, there are some peculiarities which, we think, demonstrate that their colours are not those of thin plates. The light, for example, transmitted through a particular kind of blue glass, has a blue colour of such a peculiar composition that there is no blue in any of the orders of colours in thin plates which has any resemblance to it. It is entirely destitute of the red rays which form the middle of the red space in the spectrum; so that the particles on which the colour depends must reflect the middle red rays, and transmit those on each side of it,—a property which cannot be deduced from the Newtonian doctrine.

The explanation of opacity, as arising from a multitude of reflections, is liable to the same objection which we have urged against the explanation of colour. In order to appreciate its weight, we must distinguish opacity into two kinds, namely, the opacity of whiteness and the opacity of blackness. Those bodies which possess the power of reflection in the highest degree, such as white metals, chalk, and plaster of Paris, never reflect more than one-half of the light which falls upon them. The other half of the incident light is, according to Newton, lost by a multitude of reflections. But how is it lost? Reflection merely changes the direction of the particles of light, so that they must again emerge from the body, unless they are reflected into fixed returning orbits, which detain them for ever in a state of motion within the body. In the case of black opacity, such as that of coal, which reflects from its first surface only 1/25th of the white light, the difficulty is still greater, and we cannot conceive how any system of interior reflections could so completely stifle 24/25ths of the whole incident light, without some of it returning to the eye in a visible form.

In determining the constitution of bodies that produce transparency and blackness, the Newtonian theory encounters a difficulty which its author has by no means surmounted. Transparency, as we have already seen, arises from the “particles and their interstices being too small to cause reflections in their common surfaces,” that is, they must be “less than any of those which exhibit colours,” or “less than is requisite to reflect the white and very faint blue of the first order. But this is the very same constitution which produces blackness by reflection, and in order to explain the cause of blackness by transmission, or black opacity, Newton is obliged to introduce a new principle.

“For the production of black,” says he, “the corpuscles must be less than any of those which exhibit colours. For at all greater sizes there is too much light reflected to constitute this colour. But if they be supposed a little less than is requisite to reflect the white and very faint blue of the first order, they will reflect so very little light as to appear intensely black, and yet may perhaps variously refract20 it to and fro within themselves so long, until it happens to be stifled and lost, by which means they will appear black in all positions of the eye, without any transparency.”

This very remarkable passage exhibits, in a striking manner, the perplexity in which our author was involved by the difficulties of his subject. As the particles which produce blackness by reflection are necessarily so small as to exclude the existence of any reflective forces, he cannot ascribe the loss of the intromitted light, as he does in the case of white opacity, to “a multitude of reflections;” and therefore he is compelled to have recourse to refracting forces to perform the same office. The reluctance with which he avails himself of this expedient is well marked in the mode of expression which he adopts; and I am persuaded that when he wrote the above passage, he felt the full force of the objections to this hypothesis, which cannot fail to present themselves. As the size of the particles which produce blackness are intermediate between those which produce transparency and those which produce colour, approaching closely to the latter, it is difficult to conceive why they should refract the intromitted light, while the greater and smaller particles, and even those almost of the same size, should be destitute of that property. It is, besides, not easy to understand how a refraction can take place within bodies which shall stifle all the light, and prevent it from emerging. Nay, we may admit the existence of such refractions, and yet understand how, by a compensation in their direction, the refracted rays may all emerge from the opaque body.

The force of these objections is tacitly recognised in Pemberton’s View of Sir Isaac Newton’s Philosophy;21 and as Newton not only read and approved of that work, but even perused a great part of it along with its author, we may fairly consider the opinion there stated to be his own.

“For producing black, the particles ought to be smaller than for exhibiting any of the colours, viz. of a size answering to the thickness of the bubble, whereby reflecting little or no light, it appears colourless; but yet they must not be too small, for that will make them transparent through deficiency of reflections in the inward parts of the body, sufficient to stop the light from going through it; but they must be of a size bordering upon that disposed to reflect the faint blue of the first order, which affords an evident reason why blacks usually partake a little of that colour.” In this passage all idea of refraction is abandoned, and that precise degree of size is assumed for the particles which leaves a small power of reflection, which is deemed sufficient to prevent the body from becoming transparent; that is, sufficient to render it opaque or black.

The last objection which we shall state to this theory is one to which we attach great weight, and, as it is founded on discoveries and views which have been published since the time of Newton, we venture to believe, that, had he been aware of them, he would never have proposed the theory which we are considering.

When light falls upon a thin film such as AEC, fig. 9, p. 80, so as to produce the colours of thin plates, it follows, from Sir Isaac Newton’s theory of fits, that a portion of the light is, as usual, reflected at the first surface AE,22 while the light which forms the coloured image is that which is reflected from the second surface EC, so that all the colours of thin plates are diluted with the white light reflected from the first surface. Now, in the modern theory, which ascribes the colours of thin plates to the interference of the light reflected from the second surface EC, with the light reflected from the first surface AE, the resulting tint arises from the combination of these two pencils, and consequently there is no white light reflected from the surface AE. In like manner, when the thickness of the film is such that the two interfering pencils completely destroy one another, and produce black, there is not a ray of light reflected from the first surface. Here, then, we have a criterion for deciding between the theory of fits and the theory of interference; for if there is no white light reflected from the first surface AE, the theory of fits must be rejected. In a remarkable phenomenon of blackness arising from minute fibres, which I have had occasion to describe, there was no perceptible reflection from the surface of the fibres;23 and M. Fresnel describes an experiment made to determine the same point, and states the result of it to have been unequivocally in favour of the doctrine of interference.

In order to apply this important fact, let us take a piece of coal, one of the blackest and most opaque of all substances, and which does not reflect to the eye a single ray out of those which enter its substance. The size of its particles is so small, that they are incapable of reflecting light. When a number of these particles are placed together, so as to form a surface, and other particles behind them, so as to form a solid, they will not acquire by this process the power of reflection; and consequently, a piece of coal so composed should be destitute of the property of reflecting light from its first surface. But this is not the case,—light is abundantly reflected from the first surface of the coal, and consequently, its elementary particles must possess the same power. Hence the blackness of coal must be ascribed to some other cause than to the minuteness of its transparent atoms.

To transparent bodies this argument has a similar application. As their atoms are still less than those of black bodies, their inability to reflect light is still greater, and hence arises their transparency. But the particles forming the surface of such bodies do reflect light, and, therefore, their transparency must have another origin.

In the case of coloured bodies, too, the particles forming their surfaces reflect white light like those of all other bodies, so that these particles cannot produce colour on the same principles as those of thin plates. In many of those cases of colour which seem to depend upon the minuteness of the particles of the body, the reflection of white light may nevertheless be observed, but this will be found to arise from a thin transparent film, behind which the colorific particles are placed.

Whatever answer may be given to these objections, we think it will be admitted by those who have studied the subject most profoundly, that a satisfactory theory of the colours of natural bodies is still a desideratum in science. How far we may be able to approach to it in the present state of optics the reader will judge from the following views.

Colours may be arranged into seven classes, each of which depends upon different principles.

1. Transparent coloured fluids—transparent coloured gems—transparent coloured glasses—coloured powders—and the colours of the leaves and flowers of plants.

2. Oxidations on metals—colours of Labrador feldspar—colours of precious and hydrophanous opal, and other opalescences—the colours of the feathers of birds, of the wings of insects, and of the scales of fishes.

3. Superficial colours, as those of mother-of-pearl and striated surfaces.

4. Opalescences and colours in composite crystals having double refraction.

5. Colours from the absorption of common and polarized light by doubly refracting crystals.

6. Colours at the surfaces of media of different dispersive powers.

7. Colours at the surface of media in which the reflecting forces extend to different distances, or follow different laws.

The first two of these classes are the most important. The Newtonian theory appears to be strictly applicable to the phenomena of the second class; but those of the first class cannot, we conceive, be referred to the same cause.

* * * * *

The rays of solar light possess several remarkable physical properties: They heat—they illuminate—they promote chymical combination—they effect chymical decompositions—they impart magnetism to steel—they alter the colours of bodies—they communicate to plants and flowers their peculiar colours, and are in many cases necessary to the development of their characteristic qualities. It is impossible to admit for a moment that these varied effects are produced by a mere mechanical action, or that they arise from the agitation of the particles of bodies by the vibration of the ether which is considered to be the cause of light. Whatever be the difficulties which attach to the theory which supposes light to consist of material particles, we are compelled, by its properties, to admit that light acts as if it were material, and that it enters into combinations with bodies, in order to produce the effects which we have enumerated.

When a beam of light falls upon a body, and the whole or a part of that which enters its substance totally disappears, we are entitled to say, that it is detained by some power exercised by the particles of the body over the particles of light. When this light is said to be lost by a multitude of reflections or refractions, the statement is not only hypothetical, but it is an hypothesis incompatible with optical principles. That the light detained within bodies has been stopped by the attractive force of the particles seems to be highly probable, and the mind will not feel any repugnance to admit that the particles of all bodies, whether solid, fluid, or aëriform, have a specific affinity for the particles of light. Considering light, therefore, as material, it is not difficult to comprehend how it should, like other elementary substances, enter into combination with bodies, and produce many chymical and physical effects, but particularly the phenomena of transparency, opacity, and colour.

In transparent colourless bodies, such as water and glass, the intromitted light experiences a considerable loss, because a certain number of its particles are attracted and detained by the atoms of the water or glass, and the light which emerges is colourless, because the particles exercise a proportional action over all the simple colours which compose white light.

When the transparent body has any decided colour, such as those enumerated in Class I., then the particles of the body have exercised a specific attraction over those rays of white light which are complementary to those which compose the colour of the transmitted light. If the transparent body, for example, is red, then its particles have detained the green rays which entered into the incident light, or certain other rays, which with the red are necessary to compose white light. In compound bodies, like some of the artificial glasses, the particles will attract and detain rays of light of different colours, as may be seen by analyzing the transmitted light with a prism, which will exhibit a spectrum deprived of all the rays which have been detained. In black bodies the particles exercise a powerful attraction over light, and detain all the intromitted rays.

When coloured bodies are opaque, so as to exhibit their colours principally by reflection, the light which is reflected back to the observer has received its colour from transmission through part of the thickness of the body, or, what is the same thing, the colour reflected to the eye is complementary to that which has been detained by the particles of the body while the light is passing and repassing through a thickness terminated by the reflecting surfaces; and as only a part of this light is reflected, as in the case of leaves and flowers, the transmitted light must have the same colour as the reflected light.

When coloured bodies exhibit two different colours complementary to each other, the one seen by reflection and the other by transmission, it is then highly probable that the colours are those of thin plates, though there are still other optical principles to which they may be referred. As the particles of bodies, and the medium which unites them, or, as the different atoms of a compound body may have different dispersive powers, while they exercise the same refractive force over a particular part of the spectrum, the rays for which this compensation takes place will be transmitted, while part of the complementary light is reflected.24 Or in cases where the refractive and dispersive powers are the same, the reflective forces of the particles may vary according to a different law, so that at the separating surfaces either white or coloured light may be reflected.25

In those cases of colour where the reflected and the transmitted tints are not complementary, as in leaf-gold, where the former is yellow and the latter green;—in leaf-silver, where they are white and blue, and in certain pieces of fir-wood, where the reflected light is whitish yellow, and the transmitted light a brilliant homogeneous red, we may explain the separation of the colours either by the principles we have already laid down or by the doctrine of thin plates. On the first principle, the colour of the reflected light, which is supposed to be the same as that of the transmitted light, will be modified by the law according to which the particles of the body attract different rays out of the beam of white light. In pitch, for example, the blue rays are first absorbed, so that at small thicknesses the transmitted light is a fine yellow, while, by the action of a greater thickness, the yellow itself is absorbed, and the transmitted light is a bright homogeneous red. Now in leaf-gold the transmitted colour of thinner films than we can obtain may be yellow, and, consequently, the light reflected from the first strata of interrupting faces will be yellow, and will determine the predominant tint of the reflected light. On the Newtonian doctrine, Mr. Herschel has explained it by saying, “that the transmitted rays have traversed the whole thickness of the medium, and therefore undergo many more times the action of its atoms than those reflected, especially those near the first surface to which the brighter part of the reflected colour is due.”

The phenomena of the absorption of common and polarized light, which I have described in another place,26 throw much light on the subject of coloured bodies. The relation of the absorbent action to the axes of double refraction, and, consequently, to the poles of the molecules of the crystal, shows how the particles of light attracted by the molecules of the body will vary, both in their nature and number, according to the direction in which they approach the molecules; and explains how the colour of a body may be changed, either temporarily or permanently, by heat, according as it produces a temporary or a permanent change in the relative position of the molecules. This is not the place to enlarge on this subject; but we may be permitted to apply the idea to the curious experiment of Thenard on phosphorus. When this substance is rendered pure by repeated distillation, it is transparent, and transmits yellow light; but when it is thrown in a melted state into cold water, it becomes jet black. When again melted, it resumes its original colour and transparency. According to the Newtonian theory, we must suppose that the atoms of the phosphorus have been diminished in size by sudden cooling,—an effect which it is not easy to comprehend; but, according to the preceding views, we may suppose that the atoms of the phosphorus have been forced by sudden cooling into relative positions quite different from those which they take when they slowly assume the solid state, and their poles of maximum attraction, in place of being turned to one another, are turned in different directions, and then allowed to exercise their full action in attracting the intromitted light, and detaining it wholly within the body.27

Before concluding this chapter, there is one topic peculiarly deserving our notice, namely, the change of colour produced in bodies by continued exposure to light. The general effect of light is to diminish or dilute the colours of bodies, and in many cases to deprive them entirely of their colour. Now, it is not easy to understand how repeated undulations propagated through a body could diminish the size of its particles, or how the same effect could be produced by a multitude of reflections from particle to particle. But if light is attracted by the particles of bodies, and combines with them, it is easy to conceive that, when the molecules of a body have combined with a great number of particles of a green colour, for example, their power of combination with others will be diminished, and, consequently, the number of particles of any colour absorbed or detained must diminish with the time that the body has been exposed to light; that is, these particles must enter into the transmitted and reflected pencils, and diminish the intensity of their colour. If the body, for example, absorbs red light, and transmits and reflects green, then if the quantity of absorbed red light is diminished, it will enter into the reflected and transmitted pencils, and, forming white light by its mixture with a portion of the green rays, will actually dilute them in the same manner as if a portion of white light had been added.28

CHAPTER VIII.

Newton’s Discoveries respecting the Inflection or Diffraction of Light—Previous Discoveries of Grimaldi and Dr. Hooke—Labours of succeeding Philosophers—Law of Interference of Dr. Young—Fresnel’s Discoveries—New Theory of Inflection on the Hypothesis of the Materiality of Light.

Although the discoveries of Newton respecting the Inflection of Light were first published in his Optics in 1704, yet there is reason to think that they were made at a much earlier period. Sir Isaac, indeed, informs us, in his preface to that great work, that the third book, which contains these discoveries, “was put together out of scattered papers;” and he adds at the end of his observations, that “he designed to repeat most of them with more care and exactness, and to make some new ones for determining the manner how the rays of light are bent in their passage by bodies, for making the fringes of colours with the dark lines between them. But I was then interrupted, and cannot now think of taking these things into consideration.” On the 18th March, 1674, Dr. Hooke had read a valuable memoir on the phenomena of diffraction; and, as Sir Isaac makes no allusion whatever to this work, it is the more probable that his “scattered papers” had been written previous to the communication of Dr. Hooke’s experiments.

The phenomena of the inflection of light were first discovered by Francis Maria Grimaldi, a learned Jesuit, who has described them in a posthumous work published in 1665, two years after his death.29

Having admitted a beam of the sun’s light through a small pin-hole in a piece of lead or card into a dark chamber, he found that the light diverged from this aperture in the form of a cone, and that the shadows of all bodies placed in this light were not only larger than might have been expected, but were surrounded with three coloured fringes, the nearest being the widest, and the most remote the narrowest. In strong light he discovered analogous fringes within the shadows of bodies, which increased in number with the breadth of the body, and became more distinct when the shadow was received obliquely and at a greater distance. When two small apertures or pin-holes were placed so near each other that the cones of light formed by each of them intersected one another, Grimaldi observed, that a spot common to the circumference of each, or, which is the same thing, illuminated by rays from each cone, was darker than the same spot when illuminated by either of the cones separately; and he announces this remarkable fact in the following paradoxical proposition, “that a body actually illuminated may become more dark by adding a light to that which it already receives.”

Without knowing what had been done by the Italian philosopher, our countryman, Dr. Robert Hooke, had been diligently occupied with the same subject. In 1672, he communicated his first observations to the Royal Society, and he then spoke of his paper as “containing the discovery of a new property of light not mentioned by any optical writers before him.” In his paper of 1674, already mentioned, and which is no doubt the one to which he alludes, he has not only described the leading phenomena of the inflection, or the deflection of light, as he calls it, but he has distinctly announced the doctrine of interference, which has performed so great a part in the subsequent history of optics.30

Such was the state of the subject when Newton directed to it his powers of acute and accurate observation. His attention was turned only to the enlargement of the shadow, and to the three fringes which surrounded it; and he begins his observations by ascribing the discovery of these facts to Grimaldi. After taking exact measures of the diameter of the shadow of a human hair, and of the breadth of the fringes at different distances behind it, he discovered the remarkable fact that these diameters and breadths were not proportional to the distances from the hair at which they were measured. In order to explain these phenomena, Newton supposed that the rays which passed by the edge of the hair are deflected or turned aside from it, as if by a repulsive force, the nearest rays suffering the greatest, and those more remote a less degree of deflection.

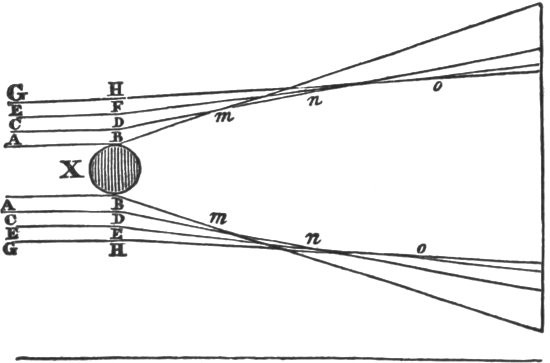
Fig. 10.

Thus, if X, fig. 10, represents a section of the hair, and AB, CD, EF, GH, &c. rays passing at different distances from X, the ray AB will be more deflected than CD, and will cross it at m, the ray CD will for the same reason cross EF at n, and EF will cross GH at o. Hence the curve or caustic formed by the intersections m, n, o, &c. will be convex outward, its curvature diminishing as it recedes from the vertex. As none of the passing light can possibly enter within this curve, it will form the boundary of the shadow of X.

The explanation given by Sir Isaac of the coloured fringes is less precise, and can be inferred only from the two following queries.

1. “Do not the rays which differ in refrangibility differ also in flexibility, and are they not, by these different inflections separated from one another, so as after separation to make the colours in the three fringes above described? And after what manner are they inflected to make those fringes?

2. “Are not the rays of light in passing by the edges and sides of bodies bent several times backwards and forwards with a motion like that of an eel? And do not the three fringes of light above mentioned arise from three such bendings?”

The idea thus indistinctly thrown out in the preceding queries has been ingeniously interpreted by Mr. Herschel in the manner represented in fig. 11, where SS are two rays passing by the edge of the body MN. These rays are supposed to undergo several bendings, as at a, b, c, and the particles of light are thrown off at one or other of the points of contrary flexure, according to the state of their fits or other circumstances. Those that are thrown outwards in the direction aA, bB, cC, dD, will produce as many caustics by their intersections as there are deflected rays; and each caustic, when received on a screen at a distance, will depict on it the brightest part or maximum of a fringe.

Fig. 11.

In this unsatisfactory state was the subject of the inflection of light left by Sir Isaac. His inquiries were interrupted, and never again renewed; and though he himself found that the phenomena were the same, “whether the hair was encompassed with air or with any other pellucid substance,” yet this important result does not seem to have shaken his conviction, that the phenomena had their origin in the action of bodies upon light.

During two sets of experiments which I made on the inflection of light, the first in 1798, and the second in 1812 and 1813, I was desirous of examining the influence of density and refractive power over the fringes produced by inflection. I compared the fringes formed by gold-leaf with those formed by masses of gold,—and those produced by films which gave the colours of thin plates with those formed by masses of the same substance. I examined the influence of platinum, diamond, and cork in inflecting light, the effect of non-reflecting grooves and spaces in polished metals, and of cylinders of glass immersed in a mixture of oil of cassia and oil of olives of the same refractive power; and, as the fringes had the same magnitude and character under all these circumstances, I concluded that they were not produced by any force inherent in the bodies themselves, but arose from a property of the light itself, which always showed itself when light was stopped in its progress.

Dr. Thomas Young, who had supported with great ingenuity and force of argument the undulatory theory of light, as maintained by Hooke and Huygens, was the first who gave a plausible explanation of the inflection of light. By interposing a small screen at B, fig. 10, and intercepting the rays that passed near the hair X, he was surprised to find that all the fringes within the shadow disappeared. The same effect took place when the screen intercepted the rays on the other side; and hence he concluded, that the rays on each side of the hair were necessary to the production of the inner fringes, and that the fringes were produced by the interference of the rays that passed on one side of the hair with those that passed on the other side. In order to account for the coloured fringes without the shadow, Dr. Young conceived that the rays which pass near the edge of the hair interfere with others, which he supposes may be reflected after falling very obliquely upon its edge,—a supposition which, if correct, would certainly produce fringes very similar to those actually observed.

In pursuing these researches so successfully begun by Dr. Young, M. Fresnel had the good fortune to explain all the phenomena of inflection by means of the undulatory doctrine combined with the principle of interference. In place of transmitting the light through a small aperture, he caused it to diverge from the focus of a deep convex lens, and instead of receiving the shadow and its fringes upon a smooth white surface, as was done by Newton, he viewed them directly with his eye through a lens placed behind the shadow; and by means of a microscope he was able to measure the dimensions of the fringes with the greatest exactness. By this mode of observation he made the remarkable discovery, that the inflection of the light depended on the distance of the inflecting body from the aperture or from the focus of divergence;31 the fringes being observed to dilate as the body approached that focus, and to contract as it receded from it, their relative distances from each other, and from the margin of the shadow continuing invariable. In attempting to account for the formation of the exterior fringes, M. Fresnel found it necessary to reject the supposition of Dr. Young, that they were owing to light reflected from the edge of the body. He not only ascertained that the real place of the fringe was the 17/100th of a millimetre different from what it should be on that supposition, but he found that the fringes preserved the same intensity of light, whether the inflecting body had a round or a sharp edge, and even when the edge was such as not to afford sufficient light for their production. From this difficulty the undulatory theory speedily released him, and he was led by its indications to consider the exterior fringes, as produced by an infinite number of elementary waves of light emanating from a primitive wave when partly interrupted by an opaque body.

The various phenomena of inflection, which had so long resisted every effort to generalize them, having thus received so beautiful and satisfactory an explanation from the undulatory doctrine, they must of course be regarded as affording to that doctrine the most powerful support, while the Newtonian hypothesis of the materiality of light is proportionally thrown into the shade. It is impossible, indeed, even for national partiality to consider the views of Newton as furnishing any explanation of the facts discovered by Fresnel; and, as no attempt has been made by the small though able phalanx of his disciples to stay the decision with which, on this count at least, the doctrine of emission has been threatened, we shall venture to suggest some principles by which the refractory phenomena may perhaps be yet brought within the pale of the Newtonian theory.

That the particles of light, like those of heat, are endowed with a repulsive force which prevents them from accumulating when in a state of condensation, or when they are detained by the absorptive action of opaque bodies, will be readily admitted. By this power a beam of light radiating from a luminous point has, in every azimuth, the same degree of intensity at the same distance from its centre of divergence; but if we intercept a portion of such a beam by an opaque body, the repulsive force of the light which formerly occupied its shadow is withdrawn, and consequently the rays which pass near the body will be repelled into the shadow, and will form, by their interference with those similarly repelled on the other side, the interior fringes, which are parallel to the edges of the body. The rays which pass at a greater distance will in like manner be bent towards the body, but with less force, and, interfering with those rays which retain their primitive direction, from the state of their fits or the position of their poles, they will form the exterior fringes. When the inflecting body is placed near the point of divergence, the greater proximity of the rays will produce a greater repulsive force, and consequently a greater inflection of the passing light; while the removal of the body from the point of divergence will be accompanied with an increased distance of the particles, an inferior repulsive force, and a feebler inflection. As the phenomena of inflection, considered under this aspect, arise from a property of the light itself, it follows that they will remain invariable, whatever be the nature or density of the body, or the form of the edge which acts upon the passing rays.

CHAPTER IX.

Miscellaneous Optical Researches of Newton—His Experiments on Refraction—His Conjecture respecting the Inflammability of the Diamond—His Law of Double Refraction—His Observations on the Polarization of Light—Newton’s Theory of Light—His “Optics.”

Before concluding our account of Newton’s optical discoveries, it is necessary to notice some of his minor researches, which, though of inferior importance in the science of light, have either exercised an influence over the progress of discovery, or been associated with the history of other branches of knowledge.

One of the most curious of these inquiries related to the connexion between the refractive powers and the chymical composition of bodies. Having measured the refractive powers and the densities of twenty-two substances, he found that the forces which reflect and refract light are very nearly proportional to the densities of the same bodies. In this law, however, he noticed a remarkable exception in the case of unctuous and sulphureous bodies, such as camphire, olive oil, linseed oil, spirit of turpentine, and diamond, which have their refractive powers two or three times greater in respect of their densities than the other substances in the table, while among themselves their refractive powers are proportional to their densities, without any considerable variation. Hence he concluded that diamond “is an unctuous substance coagulated,”—a sagacious prediction, which has been verified in the discoveries of modern chymistry. The connexion between a high degree of inflammability and a great refracting force has been still more strongly established by the high refractive power which I detected in phosphorus, and which was discovered in hydrogen by MM. Biot and Arago.

There is no part of the optical labours of Newton which is less satisfactory than that which relates to the double refraction of light. In 1690, Huygens, published his admirable treatise on light, in which he has given the law of double refraction in calcareous spar, as deduced from his theory of light, and as confirmed by direct experiment. Viewing it probably as a theoretical deduction, Newton seems to have regarded it as incorrect, and though he has given Huygens the credit of describing the phenomena more exactly than Bartholinus, yet, without assigning any reason, he rejected the law of the Dutch philosopher, and substituted another in its place. These observations of our author form the subject of the twenty-fifth and twenty-sixth queries at the end of his Optics, which was published fourteen years after the appearance of Huygens’s work. The law adopted by Newton is not accompanied with any of the experiments from which it was deduced; and though he has given it without expressing any doubt of its accuracy, it is, nevertheless, entirely incompatible with observation, and has been rejected by all succeeding philosophers.

In his speculations respecting the successive disappearance and reappearance of two of the four images which are formed when a luminous object is viewed through two rhombs of calcareous spar, one of which is made to revolve upon the other, Newton has been more successful. He concluded from these phenomena that every ray of light has two opposite sides originally endued with the property on which the unusual refraction depends, and other two opposite sides not endued with that property; and he suggested it as a subject for future inquiry, whether there are not more properties of light by which the sides of the rays differ, and are distinguished from one another. This is the first occasion on which the idea of a polarity in the rays of light has been suggested.32

From the various optical inquiries in which Newton was engaged, he was strongly impressed with the belief that light consists of small material particles emitted from shining substances, and that these particles could be again recombined into solid matter, so that “gross bodies and light were convertible into one another.” He conceived also that the particles of solid bodies and of light exerted a mutual action upon each other, the former being agitated and heated by the latter, and the latter being attracted and repelled by the former, with forces depending on the inertia of the luminous particles. These forces he regarded as insensible at all measurable distances, and he conceived that the distances between the particles of bodies were very small when compared with the extent of their sphere of attraction and repulsion.

With the exception of Hooke, Huygens, and Euler, almost all the contemporaries and successors of Newton maintained the doctrine of the materiality of light. It was first successfully assailed by Dr. Thomas Young, and since that time it has been shaken to its foundation by those great discoveries which have illustrated the commencement of the present century. The undulatory theory, which has thus triumphed in its turn, is still subject to grave difficulties, and we fear another century must elapse before a final decision can be pronounced on this long-agitated question.

The most important of the optical discoveries of Newton, of which we have given a general history, were communicated to the Royal Society in detached papers; but the disputes in which they had involved their author made him hesitate about the publication of his other discoveries. Although he had drawn up a connected view of his labours under the title of “Opticks, or a Treatise on the Reflexions, Refractions, Inflexions, and Colours of Light,” yet he resolved not to publish this work during the life of Hooke, by whose rival jealousy his tranquillity had been so frequently interrupted. Hooke, however, died in 1702, and the Optics of Newton appeared in English in 1704. Dr. Samuel Clark proposed a Latin edition of it, which appeared in 1706, and he was generously presented by Sir Isaac with 500l. (or 100l. for each of his five children), as a token of the approbation and gratitude of the author. Both the English and the Latin editions have been frequently reprinted both in England and on the Continent,33 and there perhaps never was a work of profound science so widely circulated.

CHAPTER X.

Astronomical Discoveries of Newton—Necessity of combined Exertion to the Completion of great Discoveries—Sketch of the History of Astronomy previous to the Time of Newton—Copernicus, 1473–1543—Tycho Brahe, 1546–1601—Kepler, 1571–1631—Galileo, 1564–1642.

From the optical labours of Newton we now proceed to the history of his astronomical discoveries—those transcendent deductions of human reason by which he has secured to himself an immortal name, and vindicated the intellectual dignity of his species. Pre-eminent as his triumphs have been, it would be unjust to affirm that they were achieved by his single arm. The torch of many a preceding age had thrown its light into the strongholds of the material universe, and the grasp of many a powerful hand had pulled down the most impregnable of its defences. An alliance, indeed, of many kindred spirits had been long struggling in this great cause, and Newton was but the leader of their mighty phalanx,—the director of their combined genius,—the general who won the victory, and therefore wears its laurels.

The history of science presents us with no example of an individual mind throwing itself far in advance of its contemporaries. It is only in the career of crime and ambition that reckless man takes the start of his species, and, uncurbed by moral and religious restraint, erects an unholy dynasty upon the ruins of ancient and venerable institutions. The achievements of intellectual power, though often begun by one mind and completed by another, have ever been the results of combined exertions. Slow in their growth, they gradually approximate to a more perfect condition:—the variety in the phenomena of nature call forth a variety of intellectual gifts;—the powers of analysis and combination are applied to the humbler labours of observation and experiment, and in the ordeal of rival inquiry truth is finally purified from error. How different is it with those systems which the imagination rears,—those theories of wild import which are directed against the consciences and hopes of man. The fatal upas-tree distils its poison in the spring as well as the autumn of its growth, but the fruit which sustains life must have its bud prepared before the approach of winter, its blossom expanded in the spring, and its juices elaborated by the light and heat of the summer and the autumnal sun.

In the century which preceded the birth of Newton the science of astronomy advanced with the most rapid steps. Emerging from the darkness of the middle ages, the human mind seemed to rejoice in its new-born strength, and to apply itself with elastic vigour to unfold the mechanism of the heavens. The labours of Hipparchus and Ptolemy had indeed furnished many important epochs and supplied many valuable data; but the cumbrous appendages of cycles and epicycles with which they explained the stations and retrogradations of the planets, and the vulgar prejudices which a false interpretation of Scripture had excited against a belief in the motion of the earth, rendered it difficult even for great minds to escape from the trammels of authority, and appeal to the simplicity of nature.

The sovereign of Castile, the generous and noble-minded Alphonso, had long before proscribed the rude expedients of his predecessors; and when he declared that if the heavens were thus constituted, he could have given the Deity good advice, he must not only have felt the absurdity of the prevailing system, but must have obtained some foresight of a more simple arrangement. But neither he nor the astronomers whom he so liberally protected seem to have established a better system, and it was left to Copernicus to enjoy the dignity of being the restorer of astronomy.

This great man, a native of Thorn in Prussia, following his father’s profession, began his career as a doctor of medicine, but an accidental attendance on the mathematical lectures of Brudzevius excited a love for astronomy, which became the leading passion of his life. Quitting a profession uncongenial to such pursuits, he went to Bologna to study astronomy under Dominic Maria; and after having enjoyed the friendship and instruction of that able philosopher, he established himself at Rome in the humble situation of a teacher of mathematics. Here he made numerous astronomical observations which served him as the basis of future researches; but an event soon occurred which, though it interrupted for a while his important studies, placed him in a situation for pursuing them with new zeal. The death of one of the canons enabled his uncle, who was Bishop of Ermeland, to appoint him to a canonry in the chapter of Frauenburg, where, in a house situated on the brow of a mountain, he continued, in peaceful seclusion, to carry on his astronomical observations. During his residence at Rome his talents had been so well appreciated, that the Bishop of Fossombrona, who presided over the council for reforming the calendar, solicited the aid of Copernicus in this desirable undertaking. At first he entered warmly into the views of the council, and charged himself with the determination of the length of the year and of the month, and of the other motions of the sun and moon that seemed to be required; but he found the task too irksome, and probably felt that it would interfere with those interesting discoveries which had already begun to dawn upon his mind.

Copernicus is said to have commenced his inquiries by an historical examination of the opinions of ancient authors on the system of the universe; but it is more likely that he sought for the authority of their great names to countenance his peculiar views, and that he was more desirous to present his own theory as one that he had received, rather than as one which he had invented. His mind had been long imbued with the idea that simplicity and harmony should characterize the arrangements of the planetary system, and, in the complication and disorder which reigned in the hypothesis of Ptolemy, he saw insuperable objections to its being regarded as a representation of nature. In the opinions of the Egyptian sages, in those of Pythagoras, Philolaus, Aristarchus, and Nicetas, he recognised his own earliest conviction that the earth was not the centre of the universe; but he appears to have considered it as still possible that our globe might perform some function in the system more important than that of the other planets; and his attention was much occupied with the speculation of Martianus Capella, who placed the sun between Mars and the moon, and made Mercury and Venus revolve round him as a centre; and with the system of Apollonius Pergæus, who made all the planets revolve round the sun, while the sun and moon were carried round the earth in the centre of the universe. The examination, however, of these hypotheses gradually dispelled the difficulties with which the subject was beset; and after the labours of more than thirty years, he was permitted to see the true system of the heavens. The sun he considered as immoveable in the centre of the system, while the earth revolved between the orbits of Venus and Mars, and produced by its rotation about its axis all the diurnal phenomena of the celestial sphere. The precession of the equinoxes was thus referred to a slight motion of the earth’s axis, and the stations and retrogradations of the planets were the necessary consequence of their own motions combined with that of the earth about the sun. These remarkable views were supported by numerous astronomical observations; and in 1530 Copernicus brought to a close his immortal work on the Revolutions of the Heavenly Bodies.

But while we admire the genius which triumphed over so many difficulties, we cannot fail to commend the extraordinary prudence with which he ushered his new system into the world. Aware of the prejudices, and even of the hostility with which such a system would be received, he resolved neither to startle the one nor provoke the other. He allowed his opinions to circulate in the slow current of personal communication. The points of opposition which they presented to established doctrines were gradually worn down, and they insinuated themselves into reception among the ecclesiastical circles by the very reluctance of their author to bring them into notice. In the year 1534, Cardinal Schonberg, Bishop of Capua, and Gyse, Bishop of Culm, exerted all their influence to induce Copernicus to lay his system before the world; but he resisted their solicitations; and it was not till 1539 that an accidental circumstance contributed to alter his resolution. George Rheticus, professor of mathematics at Wirtemberg, having heard of the labours of Copernicus, resigned his chair, and repaired to Frauenberg to make himself master of his discoveries. This zealous disciple prevailed upon his master to permit the publication of his system; and they seem to have arranged a plan for giving it to the world without alarming the vigilance of the church, or startling the prejudices of individuals. Under the disguise of a student of mathematics, Rheticus published in 1540 an account of the manuscript volume of Copernicus. This pamphlet was received without any disapprobation, and its author was encouraged to reprint it at Basle, in 1541, with his own name. The success of these publications, and the flattering manner in which the new astronomy was received by several able writers, induced Copernicus to place his MSS. in the hands of Rheticus. It was accordingly printed at the expense of Cardinal Schonberg, and appeared at Nuremberg in 1543. Its illustrious author, however, did not live to peruse it. A complete copy was handed to him in his last moments, and he saw and touched it a few hours before his death. This great work was dedicated to the Holy Pontiff, in order, as Copernicus himself says, that the authority of the head of the church might silence the calumnies of individuals who had attacked his views by arguments drawn from religion. Thus introduced, the Copernican system met with no ecclesiastical opposition, and gradually made its way in spite of the ignorance and prejudices of the age.

Among the astronomers who provided the materials of the Newtonian philosophy the name of Tycho Brahe merits a conspicuous place. Descended from an ancient Swedish family, he was born at Knudstorp, in Norway, in 1546, three years after the death of Copernicus. The great eclipse of the sun which happened on the 26th August, 1560, while he was at the University of Copenhagen, attracted his notice: and when he found that all its phenomena had been accurately predicted, he was seized with the most irresistible passion to acquire the knowledge of a science so infallible in its results. Destined for the profession of the law, his friends discouraged the pursuit which now engrossed his thoughts; and such were the reproaches and even persecutions to which he was exposed, that he quitted his country with the design of travelling through Germany. At the very commencement of his journey, however, an event occurred in which the impetuosity of his temper had nearly cost him his life. At a wedding-feast in Rostock, a questionable point in geometry involved him in a dispute with a Danish nobleman of the same temperament with himself; and the two mathematicians resolved to settle the difference by the sword. Tycho, however, seems to have been second in the conflict, for he lost the greater part of his nose, and was obliged to supply its place by a substitute of gold and silver, which a cement of glue attached to his face. During his stay at Augsburg he inspired the burgomaster of the city, Peter Hainzell, with a love of astronomy. This public-spirited citizen erected an excellent observatory at his own expense, and here Tycho began that distinguished career which has placed him in the first rank of practical astronomers.

Upon his return to Copenhagen in 1570, he was received with every mark of respect. The king invited him to court, and persons of all ranks harassed him with their attentions. At Herritzvold, near his native place, the house of his maternal uncle afforded him a retreat from the gayeties of the capital, and he was there offered every accommodation for the prosecution of his astronomical studies. Here, however, the passion of love and the pursuits of alchymy distracted his thoughts; but though the peasant girl of whom he was enamoured was of easier attainment than the philosopher’s stone, the marriage produced an open quarrel with his relations, which it required the interference of the king to allay. In the tranquillity of domestic happiness, Tycho resumed his study of the heavens, and in 1572 he enjoyed the singular good fortune of observing, through all its variations, the new star in Cassiopeia, which appeared with such extraordinary splendour as to be visible in the daytime, and which gradually disappeared in the following year.

Dissatisfied with his residence in Denmark, Tycho resolved to settle in some distant country; and having gone as far as Venice in search of a suitable residence, he at last fixed upon Basle, in Switzerland. The King of Denmark, however, had learned his intention from the Prince of Hesse; and when Tycho returned to Copenhagen to remove his family and his instruments, his sovereign announced to him his resolution to detain him in his kingdom. He presented him with the canonry of Roschild, with an income of 2000 crowns per annum. To this he added a pension of 1000 crowns; and he promised to give him the island of Huen, with a complete observatory erected under his own eye. This generous offer was instantly accepted. The celebrated observatory of Uraniburg was established at the expense of about 20,000l.; and in this magnificent retreat Tycho continued for twenty-one years to enrich astronomy with the most valuable observations. Admiring disciples crowded to this sanctuary of the sciences to acquire the knowledge of the heavens; and kings34 and princes felt themselves honoured by becoming the guests of the great astronomer of the age.

One of the principal discoveries of Tycho was that of the inequality of the moon’s motion, called the variation. He detected, also, the annual equation which affects the place of her apogee and nodes, and he determined the greatest and the least inclination of the lunar orbit. His observations on the planets were numerous and precise, and have formed the data of the present generalizations in astronomy. Though thus skilful in the observation of phenomena, his mind was but little suited to investigate their cause, and it was probably owing to this defect that he rejected the system of Copernicus. The vanity of giving his own name to another system was not likely to actuate a mind such as his, and it was more probable that he was led to adopt the immobility of the earth, and to make the sun, with all his attendant planets, circulate round it, from the great difficulty which still presented itself by comparing the apparent diameter of the stars with the annual parallax of the earth’s orbit.

The death of Frederick in 1588 proved a severe calamity to Tycho, and to the science which he cultivated. During the first years of the minority of Christian IV. the regency continued the royal patronage to the observatory of Uraniburg; and in 1592 the young king paid a visit of some days to Tycho, and left him a gold chain in token of his favour. The astronomer, however, had made himself enemies at court, and the envy of his high reputation had probably added fresh malignity to the irritation of personal feelings. Under the ministry of Wolchendorf, a name for ever odious to science, Tycho’s pension was stopped;—he was in 1597 deprived of the canonry of Roschild, and was thus forced, with his wife and children, to seek an asylum in a foreign land. His friend, Henry Rantzau, of Wansbeck, under whose roof he found a hospitable shelter, was fortunately acquainted with the emperor Rodolph II., who, to his love of science, added a passion for alchymy and astrology. The reputation of Tycho having already reached the imperial ear, the recommendation of Rantzau was scarcely necessary to ensure him his warmest friendship. Invited by the emperor, he repaired in 1599 to Prague, where he met with the kindest reception. A pension of three thousand crowns was immediately settled upon him, and a commodious observatory erected for his use in the vicinity of that city. Here the exiled astronomer renewed with delight his interrupted labours, and the gratitude which he cherished for the royal favour increased the satisfaction which he felt in having so unexpectedly found a resting-place for approaching age. These prospects of better days were enhanced by the good fortune of receiving two such men as Kepler and Longomontanus for his pupils; but the fallacy of human anticipation was here, as in so many other cases, strikingly displayed. Tycho was not aware of the inroads which both his labours and his disappointments had made upon his constitution. Though surrounded with affectionate friends and admiring disciples, he was still an exile in a foreign land. Though his country had been base in its ingratitude, it was yet the land which he loved,—the scene of his earliest affection,—the theatre of his scientific glory. These feelings continually preyed upon his mind, and his unsettled spirit was ever hovering among his native mountains. In this condition he was attacked with a disease of the most painful kind, and though the paroxysms of its agonies had lengthened intermissions, yet he saw that death was approaching. He implored his pupils to persevere in their scientific labours. He conversed with Kepler on some of the profoundest points of astronomy, and with these secular occupations he mingled frequent acts of piety and devotion. In this happy condition he expired without pain at the age of fifty-five, the unquestionable victim of the councils of Christian IV.

Notwithstanding the accessions which astronomy had received from the labours of Copernicus and Tycho, no progress was yet made in developing the general laws of the system, and scarcely an idea had been formed of the power by which the planets were retained in their orbits. The labours of assiduous observers had supplied the materials for this purpose, and Kepler arose to lay the foundations of physical astronomy.

John Kepler was born at Wiel, in Wirtemberg, in 1571. He was educated for the church, and discharged even some of the clerical functions; but his devotion to science withdrew him from the study of theology. Having received mathematical instruction from the celebrated Mæstlinus, he had made such progress in the science, that he was invited in 1594 to fill the mathematical chair of Gratz in Styria. Endowed with a fertile imagination, his mind was ever intent upon subtle and ingenious speculations. In the year 1596 he published his peculiar views in a work on the Harmonies and Analogies of Nature. In this singular production, he attempts to solve what he calls the great cosmographical mystery of the admirable proportion of the planetary orbits; and by means of the six regular geometrical solids,35 he endeavours to assign a reason why there are six planets, and why the dimensions of their orbits and the time of their periodical revolutions were such as Copernicus had found them. If a cube, for example, were inserted in a sphere, of which Saturn’s orbit was one of the great circles, it would, he supposed, touch by its six planes the lesser sphere of Jupiter; and, in like manner, he proposes to determine, by the aid of the other geometrical solids, the magnitude of the spheres of the other planets. A copy of this work was presented by its author to Tycho Brahe, who had been too long versed in the severe realities of observation to attach any value to such wild theories. He advised his young friend “first to lay a solid foundation for his views by actual observation, and then, by ascending from these, to strive to reach the causes of things;” and there is reason to think that, by the aid of the whole Baconian philosophy, thus compressed by anticipation into a single sentence, he abandoned for a while his visionary inquiries.

In the year 1598 Kepler suffered persecution for his religious principles, and was compelled to quit Gratz; but though he was recalled by the States of Styria, he felt his situation insecure, and accepted of a pressing invitation from Tycho to settle at Prague, and assist him in his calculations. Having arrived in Bohemia in 1600, he was introduced by his friends to the Emperor Rodolph, from whom he ever afterward received the kindest attention. On the death of Tycho in 1601, he was appointed mathematician to the emperor,—a situation in which he was continued during the successive reigns of Matthias and Ferdinand; but what was of more importance to science, he was put in possession of the valuable collection of Tycho’s observations. These observations were remarkably numerous; and as the orbit of Mars was more oval than that of any of the other planets, they were peculiarly suitable for determining its real form. The notions of harmony and symmetry in the construction of the solar system, which had filled the mind of Kepler, necessarily led him to believe that the planets revolved with a uniform motion in circular orbits. So firm, indeed, was this conviction, that he made numerous attempts to represent the observations of Tycho by this hypothesis. The deviations were too great to be ascribed to errors of observation; and in trying various other curves, he was led to the discovery that Mars revolved round the sun in an elliptical orbit, in one of the foci of which the sun itself was placed. The same observations enabled him to determine the dimensions of the planet’s orbit, and by comparing together the times in which Mars passed over different portions of its orbit, he found that they were to one another as the areas described by the lines drawn from the centre of the planet to the centre of the sun, or, in more technical terms, that the radius vector describes equal areas in equal times. These two remarkable discoveries, the first that were ever made in physical astronomy, were extended to all the other planets of the system, and were communicated to the world in 1609, in his “Commentaries on the Motions of the Planet Mars, as deduced from the observations of Tycho Brahe.”

Although our author was conducted to these great laws by the patient examination of well-established facts, his imagination was ever hurrying him among the wilds of conjecture. Convinced that the mean distances of the planets from the sun bore to one another some mysterious relation, he not only compared them with the regular geometrical solids, but also with the intervals of musical tones; an idea which the ancient Pythagoreans had suggested, and which had been adopted by Archimedes himself. All these comparisons were fruitless; and Kepler was about to abandon an inquiry of about seventeen years’ duration, when, on the 8th March, 1618, he conceived the idea of comparing the powers of the different members which express the planetary distances, in place of the numbers themselves. He compared the squares and the cubes of the distances with the same powers of the periodic times; nay, he tried even the squares of the times with the cubes of the distances; but his hurry and impatience led him into an error of calculation, and he rejected this law as having no existence in nature! On the 15th May, his mind again reverted to the same notion, and upon making the calculations anew, and free from error, he discovered the great law, that the squares of the periodic times of any two planets are to one another as the cubes of their distances from the sun. Enchanted with this unexpected result, he could scarcely trust his calculations; and, to use his own language, he at first believed that he was dreaming, and had taken for granted the very truth of which he was in search. This brilliant discovery was published in 1619, in his “Harmony of the World;” a work dedicated to James VI. of Scotland. Thus were established what have been called the three laws of Kepler,—the motion of the planets in elliptical orbits,—the proportionality between the areas described and their times of description,—and the relations between the squares of the periodic times and the cubes of the distances.

The relation of the movements of the planets to the sun, as the general centre of all their orbits, could not fail to suggest to Kepler that some power resided in that luminary by which these various motions were produced; and he went so far as to conjecture that this power diminishes as the square of the distance of the body on which it was exerted; but he immediately rejects this law, and prefers that of the simple distances. In his work on Mars, he speaks of gravity as a mutual and corporeal affection between similar bodies. He maintained that the tides were occasioned by the moon’s attraction, and that the irregularities of the lunar motions, as detected by Tycho, were owing to the joint actions of the sun and the earth; but the relation between gravity, as exhibited on the earth’s surface, and as conducting the planets in their orbits, required more patience of thought than he could command, and was accordingly left for the exercise of higher powers.

The misery in which Kepler lived forms a painful contrast with the services which he performed to science. The pension on which he subsisted was always in arrears, and though the three emperors whose reigns he adorned directed their ministers to be more punctual in its payment, the disobedience of their commands was a source of continued vexation to Kepler. When he retired to Sagan, in Silesia, to spend in retirement the remainder of his days, his pecuniary difficulties became still more harassing. Necessity at last compelled him to apply personally for the arrears which were due; and he accordingly set out in 1630 for Ratisbon; but in consequence of the great fatigue which so long a journey on horseback produced, he was seized with a fever, which carried him off on the 30th November, 1630, in the 59th year of his age.

While Kepler was thus laying the foundation of physical astronomy, Galileo was busily employed in extending the boundaries of the solar system. This distinguished philosopher was born at Pisa in 1564. He was the son of a Florentine nobleman, and was educated for the medical profession; but a passion for geometry took possession of his mind, and called forth all his powers. Without the aid of a master, he studied the writings of Euclid and of Archimedes; and such were his acquirements, that he was appointed by the Grand-duke of Tuscany to the mathematical chair of Pisa in the twenty-fifth year of his age. His opposition to the Aristotelian philosophy gained him many enemies, and at the end of three years he quitted Pisa, and accepted of an invitation to the professorship of mathematics at Padua. Here he continued for eighteen years adorning the university by his name, and diffusing around him a taste for the physical sciences. With the exception of some contrivances of inferior importance, Galileo had distinguished himself by no discovery till he had reached the forty-fifth year of his age. In the year 1609, the same year in which Kepler published his celebrated commentary on Mars, Galileo paid a visit to Venice, where he heard, in the course of conversation, that a Dutchman of the name of Jansens had constructed and presented to Prince Maurice an instrument through which he saw distant objects magnified and rendered more distinct, as if they had been brought nearer to the observer. This report was credited by some and disbelieved by others; but, in the course of a few days, Galileo received a letter from James Badovere at Paris, which placed beyond a doubt the existence of such an instrument. The idea instantly filled his mind as one of the utmost importance to science; and so thoroughly was he acquainted with the properties of lenses, that he not only discovered the principle of its construction, but was able to complete a telescope for his own use. Into one end of a leaden tube he fitted a spectacle-glass plane on one side and convex on the other, and in the other end he placed another spectacle-glass concave on one side and plane on the other. He then applied his eye to the concave glass, and saw objects “pretty large and pretty near him.” They appeared three times nearer, and nine times larger in surface, than to the naked eye. He soon after made another, which represented objects above sixty times larger; and, sparing neither labour nor expense, he finally constructed an instrument so excellent, as “to show things almost a thousand times larger, and above thirty times nearer to the naked eye.”

There is, perhaps, no invention that science has presented to man so extraordinary in its nature, and so boundless in its influence, as that of the telescope. To the uninstructed mind, the power of seeing an object a thousand miles distant, as large and nearly as distinct as if it were brought within a mile of the observer, must seem almost miraculous; and to the philosopher, even, who thoroughly comprehends the principles upon which it acts, it must ever appear one of the most elegant applications of science. To have been the first astronomer in whose hands such a gift was placed was a preference to which Galileo owed much of his future reputation.

No sooner had he completed his telescope than he applied it to the heavens, and on the 7th January, 1618, the first day of its use, he saw round Jupiter three bright little stars lying in a line parallel to the ecliptic, two to the east, and one to the west of the planet. Regarding them as ordinary stars, he never thought of estimating their distances. On the following day, when he accidentally directed his telescope to Jupiter, he was surprised to see the three stars to the west of the planet. To produce this effect it was requisite that the motion of Jupiter should be direct, though, according to calculation, it was actually retrograde. In this dilemma he waited with impatience for the evening of the 9th, but unfortunately the sky was covered with clouds. On the 10th he saw only two stars to the east—a circumstance which he was no longer able to explain by the motion of Jupiter. He was therefore compelled to ascribe the change to the stars themselves; and upon repeating his observations on the 11th, he no longer doubted that he had discovered three planets revolving round Jupiter. On the 13th January he for the first time saw the fourth satellite.36

This discovery, though of the utmost importance in itself, derived an additional value from the light which it threw on the true system of the universe. While the earth was the only planet enlightened by a moon, it might naturally be supposed that it alone was habitable, and was therefore entitled to the pre-eminence of occupying the centre of the system; but the discovery of four moons round a much larger planet deprived this argument of its force, and created a new analogy between the earth and the other planets. When Kepler received the “Sidereal Messenger,” the work in which Galileo announced his discovery in 1610, he perused it with the deepest interest; and while it confirmed and extended his substantial discoveries, it dispelled at the same time some of those harmonic dreams which still hovered among his thoughts. In the “Dissertation” which he published on the discovery of Galileo, he expresses his hope that satellites will be discovered round Saturn and Mars,—he conjectures that Jupiter has a motion of rotation about his axis,—and states his surprise, that, after what had been written on the subject of telescopes by Baptista Porta, they had not been earlier introduced into observatories.

In continuing his observations, Galileo applied his telescope to Venus, and in 1610 he discovered the phases of that planet, which exhibited to him the various forms of the waxing and the waning moon. This fact established beyond a doubt that the planet revolved round the sun, and thus gave an additional blow to the Ptolemaic system. In his observations on the sun, Galileo discovered his spots, and deduced from them the rotation of the central luminary. He observed that the body of Saturn had handles attached to it; but he was unable to detect the form of its ring, or render visible its minute satellites. On the surface of the moon he discovered her mountains and valleys, and determined the curious fact of her libration, in virtue of which parts of the margin of her disk occasionally appear and disappear. In the Milky Way he descried numerous minute stars which the unassisted eye was unable to perceive; and as the largest fixed stars, in place of being magnified by the telescope, became actually minute brilliant points, he inferred their immense distance as rendered necessary by the Copernican hypothesis. All his discoveries, indeed, furnished fresh arguments in favour of the new system; and the order of the planets and their relation to a central sun may now be considered as established by incontrovertible evidence.

While Galileo was occupied with these noble pursuits at Pisa, to which he had been recalled in 1611, his generous patron, Cosmo II. Grand-duke of Tuscany, invited him to Florence, that he might pursue with uninterrupted leisure his astronomical observations, and carry on his correspondence with the German astronomers. His fame had now resounded through all Europe;—the strongholds of prejudice and ignorance were unbarred;—and the most obstinate adherents of ancient systems acknowledged the meridian power of the day-star of science. Galileo was ambitious of propagating the great truths which he contributed so powerfully to establish. He never doubted that they would received with gratitude by all,—by the philosopher as the consummation of the greatest efforts of human genius,—and by the Christian as the most transcendent displays of Almighty power. But he had mistaken the disposition of his species, and the character of the age. That same system of the heavens which had been discovered by the humble ecclesiastic of Frauenberg, which had been patronised by the kindness of a bishop, and published at the expense of a cardinal, and which the pope himself had sanctioned by the warmest reception, was, after the lapse of a hundred years, doomed to the most violent opposition, as subversive of the doctrines of the Christian faith. On no former occasion has the human mind exhibited such a fatal relapse into intolerance. The age itself had improved in liberality;—the persecuted doctrines themselves had become more deserving of reception;—the light of the Reformed faith had driven the Catholics from some of their most obnoxious positions;—and yet, under all these circumstances, the church of Rome unfurled her banner of persecution against the pride of Italy, against the ornament of his species, and against truths immutable and eternal.

In consequence of complaints laid before the Holy Inquisition, Galileo was summoned to appear at Rome in 1615, to answer for the heretical opinions which he had promulgated. He was charged with “maintaining as true the false doctrine held by many, that the sun was immoveable in the centre of the world, and that the earth revolved with a diurnal motion;—with having certain disciples to whom he taught the same doctrine;—with keeping up a correspondence on the subject with several German mathematicians;—with having published letters on the solar spots, in which he explained the same doctrine as true;—and with having glossed over with a false interpretation the passages of Scripture which were urged against it.” The consideration of these charges came before a meeting of the Inquisition, which assembled on the 25th February, 1616; and the court, declaring their disposition to deal gently with the prisoner, pronounced the following decree:—“That Cardinal Bellarmine should enjoin Galileo to renounce entirely the above-recited false opinions; that, on his refusal to do so, he should be commanded by the commissary of the Inquisition to abandon the said doctrine, and to cease to teach and defend it; and that, if he did not obey this command, he should be thrown into prison.” On the 26th of February Galileo appeared before Cardinal Bellarmine, and, after receiving from him a gentle admonition, he was commanded by the commissary, in the presence of a notary and witnesses, to desist altogether from his erroneous opinions; and it was declared to be unlawful for him in future to teach them in any way whatever, either orally or in his writings. To these commands Galileo promised obedience, and was dismissed from the Inquisition.

The mildness of this sentence was no doubt partly owing to the influence of the Grand-duke of Tuscany, and other persons of rank and influence at the papal court, who took a deep interest in the issue of the trial. Dreading, however, that so slight a punishment might not have the effect of putting down the obnoxious doctrines, the Inquisition issued a decree denouncing the new opinions as false and contrary to the sacred writings, and prohibiting the sale of every book in which they should be maintained.

Thus liberated from his persecutors, Galileo returned to Florence, where he pursued his studies with his wonted diligence and ardour. The recantation of his astronomical opinions was so formal and unreserved, that ordinary prudence, if not a sense of personal honour, should have restrained him from unnecessarily bringing them before the world. No anathema was pronounced against his scientific discoveries; no interdict was laid upon the free exercise of his genius. He was prohibited merely from teaching a doctrine which the church of Rome considered to be injurious to its faith. We might have expected, therefore, that a philosopher so conspicuous in the eyes of the world would have respected the prejudices, however base, of an institution whose decrees formed part of the law of the land, and which possessed the power of life and death within the limits of its jurisdiction. Galileo, however, thought otherwise. A sense of degradation37 seems to have urged him to retaliate, and before six years had elapsed, he began to compose his “Cosmical System, or Dialogues on the two greatest Systems of the World, the Ptolemean and the Copernican,” the concealed object of which is to establish the opinions which he had promised to abandon. In this work the subject is discussed by three speakers, Sagredo, Salviatus, and Simplicius, a peripatetic philosopher, who defends the system of Ptolemy with much skill against the overwhelming arguments of the rival disputants. Galileo hoped to escape notice by this indirect mode of propagating the new system, and he obtained permission to publish his work, which appeared at Florence in 1632.

The Inquisition did not, as might have been expected, immediately summon Galileo to their presence. Nearly a year elapsed before they gave any indication of their design; and, according to their own statement, they did not even take the subject under consideration till they saw that the obnoxious tenets were every day gaining ground, in consequence of the publication of the Dialogues. They then submitted the work to a careful examination, and having found it to be a direct violation of the injunction which had been formerly intimated to its author, they again cited him before their tribunal in 1633. The venerable sage, now in his seventieth year, was thus compelled to repair to Rome, and when he arrived he was committed to the apartments of the Fiscal of the Inquisition. The unchangeable friendship, however, of the Grand-duke of Tuscany obtained a remission of this severity, and Galileo was allowed to reside at the house of the Tuscan ambassador during the two months which the trial occupied. When brought before the Inquisition, and examined upon oath, he acknowledged that the Dialogues were written by himself, and that he obtained permission to publish them without notifying to the person who gave it that he had been prohibited from holding, defending, or teaching the heretical opinions. He confessed also that the Dialogues were composed in such a manner, that the arguments in favour of the Copernican system, though given as partly false, were yet managed in such a manner that they were more likely to confirm than overturn its doctrines; but that this error, which was not intentional, arose from the natural desire of making an ingenious defence of false propositions, and of opinions that had the semblance of probability.

After receiving these confessions and excuses, the Inquisition allowed Galileo a proper time for giving in his defence; but this seems to have consisted solely in bringing forward the certificate of Cardinal Bellarmine already mentioned, which made no allusion to the promise under which Galileo had come never to defend, nor teach in any way whatever, the Copernican doctrines. The court held this defence to be an aggravation of the crime rather than an excuse for it, and proceeded to pronounce a sentence which will be ever memorable in the history of the human mind.

Invoking the name of our Saviour, they declare, that Galileo had made himself liable to the suspicion of heresy, by believing the doctrine, contrary to Scripture, that the sun was the centre of the earth’s orbit, and did not move from east to west; and by defending as probable the opinion that the earth moved, and was not the centre of the world; and that he had thus incurred all the censures and penalties which were enacted by the church against such offences;—but that he should be absolved from these penalties, provided he sincerely abjured and cursed all the errors and heresies contained in the formula of the church, which should be submitted to him. That so grave and pernicious a crime should not pass altogether unpunished, that he might become more cautious in future, and might be an example to others to abstain from such offences, they decreed that his Dialogues should be prohibited by a formal edict,—that he should be condemned to the prison of the Inquisition during pleasure,—and that, during the three following years, he should recite once a week the seven penitential psalms.

This sentence was subscribed by seven cardinals; and on the 22d June, 1633, Galileo signed an abjuration humiliating to himself and degrading to philosophy. At the age of seventy, on his bended knees, and with his right hand resting on the Holy Evangelists, did this patriarch of science avow his present and his past belief in all the dogmas of the Romish Church, abandon as false and heretical the doctrine of the earth’s motion and of the sun’s immobility, and pledge himself to denounce to the Inquisition any other person who was even suspected of heresy. He abjured, cursed, and detested those eternal and immutable truths which the Almighty had permitted him to be the first to establish. What a mortifying picture of moral depravity and intellectual weakness! If the unholy zeal of the assembly of cardinals has been branded with infamy, what must we think of the venerable sage whose gray hairs were entwined with the chaplet of immortality, quailing under the fear of man, and sacrificing the convictions of his conscience and the deductions of his reason at the altar of a base superstition? Had Galileo but added the courage of the martyr to the wisdom of the sage,—had he carried the glance of his indignant eye round the circle of his judges,—had he lifted his hands to heaven, and called the living God to witness the truth and immutability of his opinions, the bigotry of his enemies would have been disarmed, and science would have enjoyed a memorable triumph.

The great truths of the Copernican system, instead of being considered as heretical, had been actually adopted by many pious members of the Catholic church, and even some of its dignitaries did not scruple to defend it openly. Previous to the first persecution of Galileo in 1615, a Neapolitan nobleman, Vincenzio Caraffa, a person equally distinguished by his piety and birth, had solicited Paul Anthony Foscarinus, a learned Carmelite monk, to illustrate and defend the new system of the universe. With this request the ecclesiastic speedily complied; and in the pamphlet which he completed on the 6th January, 1615, he defends the Copernican system with much boldness and ingenuity; he reconciles the various passages of Scripture with the new doctrine, and he expresses the hope that such an attempt, now made for the first time, will prove agreeable to philosophers, but particularly to those very learned men, Galileo Galilei, John Kepler, and all the members of the Lyncean Academy, who, he believes, entertain the same opinion. This remarkable production, written from the convent of the Carmelites at Naples, is dedicated to the very Reverend Sebastian Fantoni, general of the order of Carmelites, and was published at Florence, with the sanction of the ecclesiastical authorities, in 1630; three years before the second persecution of Galileo.

It would be interesting to know the state of public feeling in Italy when Galileo was doomed to the prisons of the Inquisition. No appeal seems to have been made against so cruel a sentence; and neither in remonstrance nor in derision does an individual voice seem to have been raised. The master spirits of the age looked with sullen indifference on the persecution of exalted genius; and Galileo lay in chains, deserted and unpitied. This unrebuked triumph of his enemies was perhaps favourable to the object of their vengeance. Resistance might have heightened the rigour of a sentence, which submission seems to have alleviated. The interference of some eminent individuals of Rome, among whom we have no doubt that the Grand-duke of Tuscany was the most influential, induced Pope Urban VIII., not only to shorten the period, but to soften the rigour of Galileo’s imprisonment. From the dungeon of the Inquisition, where he had remained only four days, he was transported to the ambassador’s palace in the Garden de Medici at Rome; and when his health had begun to suffer, he was permitted to leave the metropolis; and would have been allowed to return to Florence, but as the plague raged in that city, he was sent, in July, 1633, to the archiepiscopal palace of Sienna, the residence of the Archbishop Piccolimini, where he carried on and completed his valuable investigations respecting the resistance of solids. Here he continued five months, when, in consequence of the disappearance of the plague at Florence, he was allowed to retire to his villa at Bellosguardo, and afterward to that of Arcetri in the vicinity of Florence.

Though Galileo was now, to a certain degree, liberated from the power of man, yet the afflicting dispensations of Providence began to fall thickly around him. No sooner had he returned to Arcetri, than his favourite daughter, Maria, was seized with a dangerous illness, which soon terminated in her death. He was himself attacked with hernia, palpitation of the heart, loss of appetite, and the most oppressive melancholy; and though he solicited permission to repair to Florence for medical assistance, yet this deed of mercy was denied him. In 1638, however, the pope permitted him to pay a visit to Florence, and his friend, Father Castelli, was allowed to visit him in the company of an officer of the Inquisition. But this indulgence was soon withdrawn, and at the end of a few months he was remanded to Arcetri. The sight of his right eye had begun to fail in 1636, from an opacity of the cornea. In 1637 his left eye was attacked with the same complaint; so that in a few months he was affected with total and incurable blindness. Before this calamity had supervened, he had noticed the curious phenomenon of the moon’s libration, in consequence of which, parts of her visible disk that are exposed to view at one time are withdrawn at another. He succeeded in explaining two of the causes of this curious phenomenon, viz. the different distances of the observer from the line joining the centre of the earth and the moon, which produces the diurnal libration, and the unequal motion of the moon in her orbit, which produces the libration in longitude. It was left, however, to Hevelius to discover the libration in latitude, which arises from the inclination of her axis being a little less than a right angle to the ecliptic; and to Lagrange to discover the spheroidal libration, or that which arises from the action of the earth upon the lunar spheroid.

The sorrows with which Galileo was now beset, seemed to have disarmed the severity of the Inquisition. He was freely permitted to enjoy the society of his friends, who now thronged around him to express their respect and their sympathy. The Grand-duke of Tuscany was his frequent visiter, and Gassendi, Deodati, and our countryman Milton went to Italy for the purpose of visiting him. He entertained his friends with the warmest hospitality, and though simple and abstemious in his diet, yet he was fond of good wine, and seems even in his last days to have paid particular attention to the excellence of his cellar.

Although Galileo had nearly lost his hearing as well as his sight, yet his intellectual faculties were unimpaired; and while his mind was occupied in considering the force of percussion, he was seized with fever and palpitation of the heart, which, after two months’ illness, terminated his life on the 8th of January, 1642.

Among the predecessors of Newton in astronomical research we must not omit the names of Bouillaud (Bullialdus), Borelli, and Dr. Hooke. Ismael Bouillaud, a native of Laon in France, and the author of several valuable astronomical works, has derived more reputation from a single sentence in his Astronomica Philolaica, published in 1645, than from all the rest of his labours. He was not a believer in the doctrine of attraction, which, as we have already seen, had been broached by Copernicus, and discovered by Kepler; but in speaking of that power as the cause of the planetary motions, he remarks, “that if attraction existed, it would decrease as the square of the distance.” The influence of gravity was still more distinctly developed by Borelli, a Neapolitan philosopher, who published in 1666 a work on Jupiter’s satellites.38 In this work he maintains, that all the planets perform their motions round the sun according to a general law; that the satellites of Jupiter and of Saturn move round their primary planets in the same manner as the moon does round the earth, and that they all revolve round the sun, which is the only source of any virtue, and that this virtue attaches them, and unites them so that they cannot recede from their centre of action.39

Our countryman Dr. Robert Hooke seems to have devoted much of his attention to the cause of the planetary motions. On the 21st March, 1666, he read to the Royal Society an account of a series of experiments for determining if bodies experience any variation in their weight at different distances from the centre of the earth. His experiments, as Hooke himself saw, were by no means satisfactory, and hence he was led to the ingenious idea of measuring the force of gravity by observing, at different altitudes, the rate of a pendulum clock. About two months afterward, he exhibited to the Society an approximate representation of the forces which retain the planets in their orbits, in the paths described by a circular pendulum impelled with different degrees of force; but though this experiment illustrated the production of a curvilineal motion, by combining a tangential force with a central power of attraction, yet it was only an illustration, and could not lead to the true cause of the planetary motions. At a later period, however, viz. in 1674, Hooke resumed the subject in a dissertation entitled “An Attempt to prove the Motion of the Earth from Observation,” which contains the following remarkable observations upon gravity:—

“I shall hereafter explain a system of the world differing in many particulars from any yet known, answering in all things to the common rules of mechanical motions. This depends upon three suppositions:—first, that all celestial bodies whatsoever have an attraction or gravitating power towards their own centres, whereby they attract, not only their own parts, and keep them from flying from them, as we may observe the earth to do, but that they also do attract all the other celestial bodies that are within the sphere of their activity, and consequently, that not only the sun and moon have an influence upon the body and motion of the earth, and the earth upon them, but that Mercury, Venus, Mars, Jupiter, and Saturn, also, by their attractive powers, have a considerable influence upon its motion, as in the same manner the corresponding attractive power of the earth hath a considerable influence upon every one of their motions also. The second supposition is this, that all bodies whatsoever that are put into a direct and simple motion will so continue to move forward in a straight line, till they are, by some other effectual powers, deflected, and sent into a motion describing a circle, ellipsis, or some other more compounded curve line. The third supposition is, that those attractive powers are so much the more powerful in operating by how much the nearer the body wrought upon is to their own centres. Now, what these several degrees are I have not yet experimentally verified; but it is a notion which, if fully prosecuted, as it ought to be, will mightily assist the astronomers to reduce all the celestial motions to a certain rule, which I doubt will never be done without it. He that understands the nature of the circular pendulum and circular motion will easily understand the whole of this principle, and will know where to find directions in nature for the true stating thereof. This I only hint at present to such as have ability and opportunity of prosecuting this inquiry, and are not wanting of industry for observing and calculating, wishing heartily such may be found, having myself many other things in hand, which I would first complete, and therefore cannot so well attend it. But this I do not promise the undertaker, that he will find all the great motions of the world to be influenced by this principle, and that the true understanding thereof will be the true perfection of astronomy.”

This passage, which has been considered as a remarkable one by the philosophers of every country, has, we think, been misapprehended by M. Delambre, when he asserts that every thing which it contains “is to be found expressly in Kepler.”40

CHAPTER XI.

The first Idea of Gravity occurs to Newton in 1666—His first Speculations upon it—Interrupted by his Optical Experiments—He resumes the Subject in consequence of a Discussion with Dr. Hooke—He discovers the true Law of Gravity and the Cause of the Planetary Motions—Dr. Halley urges him to publish his Principia—His Principles of Natural Philosophy—Proceedings of the Royal Society on this Subject—The Principia appears in 1687—General Account of it, and of the Discoveries it contains—They meet with great Opposition, owing to the Prevalence of the Cartesian System—Account of the Reception and Progress of the Newtonian Philosophy in foreign Countries—Account of its Progress and Establishment in England.

Such is a brief sketch of the labours and lives of those illustrious men who prepared the science of astronomy for the application of Newton’s genius. Copernicus had determined the arrangement and general movements of the planetary bodies: Kepler had proved that they moved in elliptical orbits; that their radii vectores described arcs proportional to the times; and that their periodic times were related to their distances. Galileo had added to the universe a whole system of secondary planets; and several astronomers had distinctly referred the motion of the heavenly bodies to the power of attraction.

In the year 1666, when the plague had driven Newton from Cambridge, he was sitting alone in the garden at Woolsthorpe, and reflecting on the nature of gravity,—that remarkable power which causes all bodies to descend towards the centre of the earth. As this power is not found to suffer any sensible diminution at the greatest distance from the earth’s centre to which we can reach, being as powerful at the tops of the highest mountains as at the bottom of the deepest mines, he conceived it highly probable, that it must extend much farther than was usually supposed. No sooner had this happy conjecture occurred to his mind, than he considered what would be the effect of its extending as far as the moon. That her motion must be influenced by such a power he did not for a moment doubt; and a little reflection convinced him that it might be sufficient for retaining that luminary in her orbit round the earth. Though the force of gravity suffers no sensible diminution at those small distances from the earth’s centre at which we can place ourselves, yet he thought it very possible, that, at the distance of the moon, it might differ much in strength from what it is on the earth. In order to form some estimate of the degree of its diminution, he considered that, if the moon be retained in her orbit by the force of gravity, the primary planets must also be carried round the sun by the same power; and by comparing the periods of the different planets with their distances from the sun, he found, that if they were retained in their orbits by any power like gravity, its force must decrease in the duplicate proportion,41 or as the squares of their distances from the sun. In drawing this conclusion, he supposed the planets to move in orbits perfectly circular, and having the sun in their centre. Having thus obtained the law of the force by which the planets were drawn to the sun, his next object was to ascertain if such a force, emanating from the earth and directed to the moon, was sufficient, when diminished in the duplicate ratio of the distance, to retain her in her orbit. In performing this calculation, it was necessary to compare the space through which heavy bodies fall in a second at a given distance from the centre of the earth, viz. at its surface, with the space through which the moon, as it were, falls to the earth in a second of time while revolving in a circular orbit. Being at a distance from books when he made this computation, he adopted the common estimate of the earth’s diameter then in use among geographers and navigators, and supposed that each degree of latitude contained sixty English miles. In this way he found that the force which retains the moon in her orbit, as deduced from the force which occasions the fall of heavy bodies to the earth’s surface, was one-sixth greater than that which is actually observed in her circular orbit. This difference threw a doubt upon all his speculations; but, unwilling to abandon what seemed to be otherwise so plausible, he endeavoured to account for the difference of the two forces, by supposing that some other cause42 must have been united with the force of gravity in producing so great a velocity of the moon in her circular orbit. As this new cause, however, was beyond the reach of observation, he discontinued all further inquiries into the subject, and concealed from his friends the speculations in which he had been employed.

After his return to Cambridge in 1666, his attention was occupied with those optical discoveries of which we have given an account in a preceding chapter; but he had no sooner brought them to a close than his mind reverted to the great subject of the planetary motions. Upon the death of Oldenburg in August, 1678, Dr. Hooke was appointed secretary to the Royal Society; and as this learned body had requested the opinion of Newton about a system of physical astronomy, he addressed a letter to Dr. Hooke on the 28th November, 1679. In this letter he proposed a direct experiment for verifying the motion of the earth, viz. by observing whether or not bodies that fall from a considerable height descend in a vertical direction, for if the earth were at rest the body would describe exactly a vertical line, whereas if it revolved round its axis, the falling body must deviate from the vertical line towards the east. The Royal Society attached great value to the idea thus casually suggested; and Dr. Hooke was appointed to put it to the test of experiment. Being thus led to consider the subject more attentively, he wrote to Newton, that wherever the direction of gravity was oblique to the axis on which the earth revolved, that is, in every part of the earth except the equator, falling bodies should approach to the equator, and the deviation from the vertical, in place of being exactly to the east, as Newton maintained, should be to the south-east of the point from which the body began to move. Newton acknowledged that this conclusion was correct in theory, and Dr. Hooke is said to have given an experimental demonstration of it before the Royal Society in December, 1679.43 Newton had erroneously concluded that the path of the falling body would be a spiral; but Dr. Hooke, on the same occasion on which he made the preceding experiment, read a paper to the Society, in which he proved that the path of the body would be an eccentric ellipse in vacuo, and an ellipti-spiral, if the body moved in a resisting medium.44

This correction of Newton’s error, and the discovery that a projectile would move in an elliptical orbit when under the influence of a force varying in the inverse ratio of the square of the distance, led Newton, as he himself informs us in his letter to Halley,45 to discover “the theorem by which he afterward examined the ellipsis,” and to demonstrate the celebrated proposition, that a planet acted upon by an attractive force varying inversely as the squares of the distances will describe an elliptical orbit, in one of whose foci the attractive force resides.

But though Newton had thus discovered the true cause of all the celestial motions, he did not yet possess any evidence that such a force actually resided in the sun and planets. The failure of his former attempt to identify the law of falling bodies at the earth’s surface with that which guided the moon in her orbit threw a doubt over all his speculations, and prevented him from giving any account of them to the public.

An accident, however, of a very interesting nature induced him to resume his former inquiries, and enabled him to bring them to a close. In June, 1682, when he was attending a meeting of the Royal Society of London, the measurement of a degree of the meridian, executed by M. Picard in 1679, became the subject of conversation. Newton took a memorandum of the result obtained by the French astronomer, and having deduced from it the diameter of the earth, he immediately resumed his calculation of 1665, and began to repeat it with these new data. In the progress of the calculation he saw that the result which he had formerly expected was likely to be produced, and he was thrown into such a state of nervous irritability that he was unable to carry on the calculation. In this state of mind he intrusted it to one of his friends, and he had the high satisfaction of finding his former views amply realized. The force of gravity which regulated the fall of bodies at the earth’s surface, when diminished as the square of the moon’s distance from the earth, was found to be almost exactly equal to the centrifugal force of the moon as deduced from her observed distance and velocity.

The influence of such a result upon such a mind may be more easily conceived than described. The whole material universe was spread out before him;—the sun with all his attending planets;—the planets with all their satellites;—the comets wheeling in every direction in their eccentric orbits;—and the systems of the fixed stars stretching to the remotest limits of space. All the varied and complicated movements of the heavens, in short, must have been at once presented to his mind, as the necessary result of that law which he had established in reference to the earth and the moon.

After extending this law to the other bodies of the system, he composed a series of propositions on the motion of the primary planets about the sun, which were sent to London about the end of 1683, and were soon afterward communicated to the Royal Society.46

About this period other philosophers had been occupied with the same subject. Sir Christopher Wren had many years before endeavoured to explain the planetary motions “by the composition of a descent towards the sun, and an impressed motion; but he at length gave it over, not finding the means of doing it.” In January, 1683–4, Dr. Halley had concluded, from Kepler’s Law of the Periods and Distances, that the centripetal force decreased in the reciprocal proportion of the squares of the distances, and having one day met Sir Christopher Wren and Dr. Hooke, the latter affirmed that he had demonstrated upon that principle all the laws of the celestial motions. Dr. Halley confessed that his attempts were unsuccessful, and Sir Christopher, in order to encourage the inquiry, offered to present a book of forty shillings’ value to either of the two philosophers who should, in the space of two months, bring him a convincing demonstration of it. Hooke persisted in the declaration that he possessed the method, but avowed it to be his intention to conceal it for some time. He promised, however, to show it to Sir Christopher; but there is every reason to believe that this promise was never fulfilled.

In August, 1684, Dr. Halley went to Cambridge for the express purpose of consulting Newton on this interesting subject. Newton assured him that he had brought this demonstration to perfection, and promised him a copy of it. This copy was received in November by the doctor, who made a second visit to Cambridge, in order to induce its author to have it inserted in the register book of the society. On the 10th of December, Dr. Halley announced to the society, that he had seen at Cambridge Mr. Newton’s treatise De Motu Corporum, which he had promised to send to the society to be entered upon their register; and Dr. Halley was desired to unite with Mr. Paget, master of the mathematical school in Christ’s Hospital, in reminding Mr. Newton of his promise “for securing the invention to himself till such time as he can be at leisure to publish it.” On the 25th February Mr. Aston, the secretary, communicated a letter from Mr. Newton, in which he expressed his willingness “to enter in the register his notions about motion, and his intentions to fit them suddenly for the press.” The progress of his work was, however, interrupted by a visit of five or six weeks which he made in Lincolnshire; but he proceeded with such diligence on his return, that he was able to transmit the manuscript to London before the end of April. This manuscript, entitled Philosophiæ Naturalis Principia Mathematica, and dedicated to the society, was presented by Dr. Vincent on the 28th April, 1686, when Sir John Hoskins, the vice-president, and the particular friend of Dr. Hooke, was in the chair. Dr. Vincent passed a just encomium on the novelty and dignity of the subject; and another member added, that “Mr. Newton had carried the thing so far, that there was no more to be added.” To these remarks the vice-president replied, that the method “was so much the more to be prized as it was both invented and perfected at the same time.” Dr. Hooke took offence at these remarks, and blamed Sir John for not having mentioned “what he had discovered to him;” but the vice-president did not seem to recollect any such communication, and the consequence of this discussion was, that “these two, who till then were the most inseparable cronies, have since scarcely seen one another, and are utterly fallen out.” After the breaking up of the meeting, the society adjourned to the coffee-house, where Dr. Hooke stated that he not only had made the same discovery, but had given the first hint of it to Newton.

An account of these proceedings was communicated to Newton through two different channels. In a letter dated May 22d, Dr. Halley wrote to him “that Mr. Hooke has some pretensions upon the invention of the rule of the decrease of gravity being reciprocally as the squares of the distances from the centre. He says you had the notion from him, though he owns the demonstration of the curves generated thereby to be wholly your own. How much of this is so you know best, as likewise what you have to do in this matter. Only Mr. Hooke seems to expect you would make some mention of him in the preface, which it is possible you may see reason to prefix.”

This communication from Dr. Halley induced our author, on the 20th June, to address a long letter to him, in which he gives a minute and able refutation of Hooke’s claims; but before this letter was despatched, another correspondent, who had received his information from one of the members that were present, informed Newton “that Hooke made a great stir, pretending that he had all from him, and desiring they would see that he had justice done him.” This fresh charge seems to have ruffled the tranquillity of Newton; and he accordingly added an angry and satirical postscript, in which he treats Hooke with little ceremony, and goes so far as to conjecture that Hooke might have acquired his knowledge of the law from a letter of his own to Huygens, directed to Oldenburg, and dated January 14th, 1672–3. “My letter to Hugenius was directed to Mr. Oldenburg, who used to keep the originals. His papers came into Mr. Hooke’s possession. Mr. Hooke, knowing my hand, might have the curiosity to look into that letter, and there take the notion of comparing the forces of the planets arising from their circular motion; and so what he wrote to me afterward about the rate of gravity might be nothing but the fruit of my own garden.”

In replying to this letter, Dr. Halley assured him that Hooke’s “manner of claiming the discovery had been represented to him in worse colours than it ought, and that he neither made public application to the society for justice, nor pretended that you had all from him.” The effect of this assurance was to make Newton regret that he had written the angry postscript to his letter; and in replying to Halley on the 14th July, 1686, he not only expresses his regret, but recounts the different new ideas which he had acquired from Hooke’s correspondence, and suggests it as the best method “of compromising the present dispute,” to add a scholium, in which Wren, Hooke, and Halley are acknowledged to have independently deduced the law of gravity from the second law of Kepler.47

At the meeting of the 28th April, at which the manuscript of the Principia was presented to the Royal Society, it was agreed that the printing of it should be referred to the council; that a letter of thanks should be written to its author; and at a meeting of the council on the 19th May, it was resolved that the MSS. should be printed at the society’s expense, and that Dr. Halley should superintend it while going through the press. These resolutions were communicated by Dr. Halley in a letter dated the 22d May; and in Newton’s reply on the 20th June already mentioned, he makes the following observations: “The proof you sent me I like very well. I designed the whole to consist of three books; the second was finished last summer, being short, and only wants transcribing, and drawing the cuts fairly. Some new propositions I have since thought on, which I can as well let alone. The third wants the theory of comets. In autumn last I spent two months in calculation to no purpose for want of a good method, which made me afterward return to the first book, and enlarge it with diverse propositions, some relating to comets, others to other things found out last winter. The third I now design to suppress. Philosophy is such an impertinently litigious lady, that a man had as good be engaged in lawsuits as have to do with her. I found it so formerly, and now I can no sooner come near her again but she gives me warning. The first two books without the third will not so well bear the title of Philosophiæ Naturalis Principia Mathematica; and therefore I had altered it to this, De Motu Corporum Libri duo. But after second thoughts I retain the former title. It will help the sale of the book, which I ought not to diminish now ’tis yours.”

In replying to this letter on the 29th June, Dr. Halley regrets that our author’s tranquillity should have been thus disturbed by envious rivals; and implores him in the name of the society not to suppress the third book. “I must again beg you,” says he, “not to let your resentments run so high as to deprive us of your third book, wherein your applications of your mathematical doctrine to the theory of comets, and several curious experiments, which, as I guess by what you write ought to compose it, will undoubtedly render it acceptable to those who will call themselves philosophers without mathematics, which are much the greater number.”

To these solicitations Newton seems to have readily yielded. His second book was sent to the society, and presented on the 2d March, 1686–7. The third book was also transmitted, and presented on the 6th April, and the whole work was completed and published in the month of May, 1687.

Such is a brief account of the publication of a work which is memorable, not only in the annals of one science or of one country, but which will form an epoch in the history of the world, and will ever be regarded as the brightest page in the records of human reason. We shall endeavour to convey to the reader some idea of its contents, and of the brilliant discoveries which it disseminated over Europe.

The Principia consists of three books. The first and second, which occupy three-fourths of the work, are entitled, On the Motion of Bodies; and the third bears the title, On the System of the World. The first two books contain the mathematical principles of philosophy, namely, the laws and conditions of motions and forces; and they are illustrated with several philosophical scholia, which treat of some of the most general and best established points in philosophy, such as the density and resistance of bodies, spaces void of matter, and the motion of sound and light. The object of the third book is to deduce from these principles the constitution of the system of the world; and this book has been drawn up in as popular a style as possible, in order that it may be generally read.

The great discovery which characterizes the Principia is that of the principle of universal gravitation, as deduced from the motion of the moon, and from the three great facts or laws discovered by Kepler. This principle is, that every particle of matter is attracted by, or gravitates to, every other particle of matter, with a force inversely proportional to the squares of their distances. From the first law of Kepler, namely, the proportionality of the areas to the times of their description, Newton inferred that the force which kept the planet in its orbit was always directed to the sun; and from the second law of Kepler, that every planet moves in an ellipse with the sun in one of its foci, he drew the still more general inference, that the force by which the planet moves round that focus varies inversely as the square of its distance from the focus. As this law was true in the motion of satellites round their primary planets, Newton deduced the equality of gravity in all the heavenly bodies towards the sun, upon the supposition that they are equally distant from its centre; and in the case of terrestrial bodies, he succeeded in verifying this truth by numerous and accurate experiments.

By taking a more general view of the subject, Newton demonstrated that a conic section was the only curve in which a body could move when acted upon by a force varying inversely as the square of the distance; and he established the conditions depending on the velocity and the primitive position of the body, which were requisite to make it describe a circular, an elliptical, a parabolic, or a hyperbolic orbit.

Notwithstanding the generality and importance of these results, it still remained to be determined whether the force resided in the centres of the planets, or belonged to each individual particle of which they were composed. Newton removed this uncertainty by demonstrating, that if a spherical body acts upon a distant body with a force varying as the distance of this body from the centre of the sphere, the same effect will be produced as if each of its particles acted upon the distant body according to the same law. And hence it follows that the spheres, whether they are of uniform density, or consist of concentric layers, with densities varying according to any law whatever, will act upon each other in the same manner as if their force resided in their centres alone. But as the bodies of the solar system are very nearly spherical, they will all act upon one another, and upon bodies placed on their surface, as if they were so many centres of attraction; and therefore we obtain the law of gravity which subsists between spherical bodies, namely, that one sphere will act upon another with a force directly proportional to the quantity of matter, and inversely as the square of the distance between the centres of the spheres. From the equality of action and reaction, to which no exception can be found, Newton concluded that the sun gravitated to the planets, and the planets to their satellites; and the earth itself to the stone which falls upon its surface; and, consequently, that the two mutually gravitating bodies approached to one another with velocities inversely proportional to their quantities of matter.

Having established this universal law, Newton was enabled, not only to determine the weight which the same body would have at the surface of the sun and the planets, but even to calculate the quantity of matter in the sun, and in all the planets that had satellites, and even to determine the density or specific gravity of the matter of which they were composed. In this way he found that the weight of the same body would be twenty-three times greater at the surface of the sun than at the surface of the earth, and that the density of the earth was four times greater than that of the sun, the planets increasing in density as they receded from the centre of the system.

If the peculiar genius of Newton has been displayed in his investigation of the law of universal gravitation, it shines with no less lustre in the patience and sagacity with which he traced the consequences of this fertile principle.

The discovery of the spheroidal form of Jupiter by Cassini had probably directed the attention of Newton to the determination of its cause, and consequently to the investigation of the true figure of the earth. The spherical form of the planets have been ascribed by Copernicus to the gravity or natural appetency of their parts; but upon considering the earth as a body revolving upon its axis, Newton quickly saw that the figure arising from the mutual attraction of its parts must be modified by another force arising from its rotation. When a body revolves upon an axis, the velocity of rotation increases from the poles, where it is nothing, to the equator, where it is a maximum. In consequence of this velocity the bodies on the earth’s surface have a tendency to fly off from it, and this tendency increases with the velocity. Hence arises a centrifugal force which acts in combination with a force of gravity, and which Newton found to be the 289th part of the force of gravity at the equator, and decreasing, as the cosine of the latitude, from the equator to the poles. The great predominance of gravity over the centrifugal force prevents the latter from carrying off any bodies from the earth’s surface, but the weight of all bodies is diminished by the centrifugal force, so that the weight of any body is greater at the poles than it is at the equator. If we now suppose the waters at the pole to communicate with those at the equator by means of a canal, one branch of which goes from the pole to the centre of the earth, and the other from the centre of the earth to the equator, then the polar branch of the canal will be heavier than the equatorial branch, in consequence of its weight not being diminished by the centrifugal force, and, therefore, in order that the two columns may be in equilibrio, the equatorial one must be lengthened. Newton found that the length of the polar must be to that of the equatorial canal as 229 to 230, or that the earth’s polar radius must be seventeen miles less than its equatorial radius; that is, that the figure of the earth is an oblate spheroid, formed by the revolution of an ellipse round its lesser axis. Hence it follows, that the intensity of gravity at any point of the earth’s surface is in the inverse ratio of the distance of that point from the centre, and, consequently, that it diminishes from the equator to the poles,—a result which he confirmed by the fact, that clocks required to have their pendulums shortened in order to beat true time when carried from Europe towards the equator.

The next subject to which Newton applied the principle of gravity was the tides of the ocean. The philosophers of all ages have recognised the connexion between the phenomena of the tides and the position of the moon. The College of Jesuits at Coimbra, and subsequently Antonio de Dominis and Kepler, distinctly referred the tides to the attraction of the waters of the earth by the moon, but so imperfect was the explanation which was thus given of the phenomena, that Galileo ridiculed the idea of lunar attraction, and substituted for it a fallacious explanation of his own. That the moon is the principal cause of the tides is obvious from the well-known fact, that it is high water at any given place about the time when she is in the meridian of that place; and that the sun performs a secondary part in their production may be proved from the circumstance, that the highest tides take place when the sun, the moon, and the earth are in the same straight line, that is, when the force of the sun conspires with that of the moon, and that the lowest tides take place when the lines drawn from the sun and moon to the earth are at right angles to each other, that is, when the force of the sun acts in opposition to that of the moon. The most perplexing phenomenon in the tides of the ocean, and one which is still a stumbling-block to persons slightly acquainted with the theory of attraction, is the existence of high water on the side of the earth opposite to the moon, as well as on the side next the moon. To maintain that the attraction of the moon at the same instant draws the waters of the ocean towards herself, and also draws them from the earth in an opposite direction, seems at first sight paradoxical; but the difficulty vanishes when we consider the earth, or rather the centre of the earth, and the water on each side of it as three distinct bodies placed at different distances from the moon, and consequently attracted with forces inversely proportional to the squares of their distances. The water nearest the moon will be much more powerfully attracted than the centre of the earth, and the centre of the earth more powerfully than the water farthest from the moon. The consequence of this must be, that the waters nearest the moon will be drawn away from the centre of the earth, and will consequently rise from their level, while the centre of the earth will be drawn away from the waters opposite the moon, which will, as it were, be left behind, and consequently be in the same situation as if they were raised from the earth in a direction opposite to that in which they are attracted by the moon. Hence the effect of the moon’s action upon the earth is to draw its fluid parts into the form of an oblong spheroid, the axis of which passes through the moon. As the action of the sun will produce the very same effect, though in a smaller degree, the tide at any place will depend on the relative position of these two spheroids, and will be always equal either to the sum or to the difference of the effects of the two luminaries. At the time of new and full moon the two spheroids will have their axes coincident, and the height of the tide, which will then be a spring one, will be equal to the sum of the elevations produced in each spheroid considered separately, while at the first and third quarters the axes of the spheroids will be at right angles to each other, and the height of the tide, which will then be a neap one, will be equal to the difference of the elevations produced in each separate spheroid. By comparing the spring and neap tides, Newton found that the force with which the sun acted upon the waters of the earth was to that with which the sun acted upon them as 4.48 to 1;—that the force of the moon produced a tide of 8.63 feet;—that of the sun one of 1.93 feet;—and both of them combined, one of 10½ French feet,—a result which in the open sea does not deviate much from observation. Having thus ascertained the force of the moon on the waters of our globe, he found that the quantity of matter in the moon was to that in the earth as 1 to 40, and the density of the moon to that of the earth as 11 to 9.

The motions of the moon, so much within the reach of our own observation, presented a fine field for the application of the theory of universal gravitation. The irregularities exhibited in the lunar motions had been known in the time of Hipparchus and Ptolemy. Tycho had discovered the great inequality called the variation, amounting to 37′, and depending on the alternate acceleration and retardation of the moon in every quarter of a revolution, and he had also ascertained the existence of the annual equation. Of these two inequalities Newton gave a most satisfactory explanation. The action of the sun upon the moon may be always resolved into two, one acting in the direction of the line joining the moon and earth, and consequently tending to increase or diminish the moon’s gravity to the earth, and the other in a direction at right angles to this, and consequently tending to accelerate or retard the motion in her orbit. Now, it was found by Newton that this last force was reduced to nothing, or vanished at the syzigies or quadratures, so that at these four points the moon described areas proportional to the times. The instant, however, that the moon quits these positions, the force under consideration, which we may call the tangential force, begins, and it reaches its maximum in the four octants. The force, therefore, compounded of these two elements of the solar force, or the diagonal of the parallelogram which they form, is no longer directed to the earth’s centre, but deviates from it at a maximum about 30 minutes, and therefore affects the angular motion of the moon, the motion being accelerated in passing from the quadratures to the syzigies, and retarded in passing from the syzigies to the quadratures. Hence the velocity is in its mean state in the octants, a maximum in the syzigies, and a minimum in the quadratures.

Upon considering the influence of the solar force in diminishing or increasing the moon’s gravity to the earth, Newton saw that her distance and her periodic time must from this cause be subject to change, and in this way he accounted for the annual equation observed by Tycho. By the application of similar principles, he explained the cause of the motion of the apsides, or of the greater axis of the moon’s orbit, which has an angular progressive motion of 3° 4′ nearly in the course of one lunation; and he showed that the retrogradation of the nodes, amounting to 3′ 10″ daily, arose from one of the elements of the solar force being exerted in the plane of the ecliptic, and not in the plane of the moon’s orbit, the effect of which was to draw the moon down to the plane of the ecliptic, and thus cause the line of the nodes, or the intersection of these two planes, to move in a direction opposite to that of the moon. The lunar theory thus blocked out by Newton, required for its completion the labours of another century. The imperfections of the fluxionary calculus prevented him from explaining the other inequalities of the moon’s motions, and it was reserved to Euler, D’Alembert, Clairaut, Mayer, and Laplace to bring the lunar tables to a high degree of perfection, and to enable the navigator to determine his longitude at sea with a degree of precision which the most sanguine astronomer could scarcely have anticipated.

By the consideration of the retrograde motion of the moon’s nodes, Newton was led to discover the cause of the remarkable phenomenon of the precession of the equinoctial points, which moved 50″ annually, and completed the circuit of the heavens in 25,920 years. Kepler had declared himself incapable of assigning any cause for this motion, and we do not believe that any other astronomer ever made the attempt. From the spheroidal form of the earth, it may be regarded as a sphere with a spheroidal ring surrounding its equator, one-half of the ring being above the plane of the ecliptic and the other half below it. Considering this excess of matter as a system of satellites adhering to the earth’s surface, Newton saw that the combined actions of the sun and moon upon these satellites tended to produce a retrogradation in the nodes of the circles which they described in their diurnal rotation, and that the sum of all the tendencies being communicated to the whole mass of the planet, ought to produce a slow retrogradation of the equinoctial points. The effect produced by the motion of the sun he found to be 40″, and that produced by the action of the moon 10″.

Although there could be little doubt that the comets were retained in their orbits by the same laws which regulated the motions of the planets, yet it was difficult to put this opinion to the test of observation. The visibility of comets only in a small part of their orbits rendered it difficult to ascertain their distance and periodic times, and as their periods were probably of great length, it was impossible to correct approximate results by repeated observation. Newton, however, removed this difficulty, by showing how to determine the orbit of a comet, namely, the form and position of the orbit and the periodic time, by three observations. By applying this method to the comet of 1680, he calculated the elements of its orbit, and from the agreement of the computed places with those which were observed, he justly inferred that the motions of comets were regulated by the same laws as those of the planetary bodies. This result was one of great importance; for as the comets enter our system in every possible direction, and at all angles with the ecliptic, and as a great part of their orbits extend far beyond the limits of the solar system, it demonstrated the existence of gravity in spaces far removed beyond the planet, and proved that the law of the inverse ratio of the squares of the distance was true in every possible direction, and at very remote distances from the centre of our system.48

Such is a brief view of the leading discoveries which the Principia first announced to the world. The grandeur of the subjects of which it treats, the beautiful simplicity of the system which it unfolds, the clear and concise reasoning by which that system is explained, and the irresistible evidence by which it is supported might have ensured it the warmest admiration of contemporary mathematicians, and the most welcome reception in all the schools of philosophy throughout Europe. This, however, is not the way in which great truths are generally received. Though the astronomical discoveries of Newton were not assailed by the class of ignorant pretenders who attacked his optical writings, yet they were every where resisted by the errors and prejudices which had taken a deep hold even of the strongest minds. The philosophy of Descartes was predominant throughout Europe. Appealing to the imagination, and not to the reason of mankind, it was quickly received into popular favour, and the same causes which facilitated its introduction extended its influence, and completed its dominion over the human mind. In explaining all the movements of the heavenly bodies by a system of vortices in a fluid medium diffused through the universe, Descartes had seized upon an analogy of the most alluring and deceitful kind. Those who had seen heavy bodies revolving in the eddies of a whirlpool, or in the gyrations of a vessel of water thrown into a circular motion, had no difficulty in conceiving how the planets might revolve round the sun by analogous movements. The mind instantly grasped at an explanation of so palpable a character, and which required for its development neither the exercise of patient thought nor the aid of mathematical skill. The talent and perspicuity with which the Cartesian system was expounded, and the show of experiments with which it was sustained, contributed powerfully to its adoption, while it derived a still higher sanction from the excellent character and the unaffected piety of its author.

Thus intrenched, as the Cartesian system was, in the strongholds of the human mind, and fortified by its most obstinate prejudices, it was not to be wondered at that the pure and sublime doctrines of the Principia were distrustfully received and perseveringly resisted. The uninstructed mind could not readily admit the idea, that the great masses of the planets were suspended in empty space, and retained in their orbits by an invisible influence residing in the sun; and even those philosophers who had been accustomed to the rigour of true scientific research, and who possessed sufficient mathematical skill for the examination of the Newtonian doctrines, viewed them at first as reviving the occult qualities of the ancient physics, and resisted their introduction with a pertinacity which it is not easy to explain. Prejudiced, no doubt, in favour of his own metaphysical views, Leibnitz himself misapprehended the principles of the Newtonian philosophy, and endeavoured to demonstrate the truths in the Principia by the application of different principles. Huygens, who above all other men was qualified to appreciate the new philosophy, rejected the doctrine of gravitation as existing between the individual particles of matter, and received it only as an attribute of the planetary masses. John Bernouilli, one of the first mathematicians of his age, opposed the philosophy of Newton. Mairan, in the early part of his life, was a strenuous defender of the system of vortices. Cassini and Maraldi were quite ignorant of the Principia, and occupied themselves with the most absurd methods of calculating the orbits of comets long after the Newtonian method had been established on the most impregnable foundation; and even Fontenelle, a man of liberal views and extensive information, continued, throughout the whole of his life, to maintain the doctrines of Descartes.

The Chevalier Louville of Paris had adopted the Newtonian philosophy before 1720. S’Gravesande had introduced it into the Dutch universities at a somewhat earlier period, and Maupertuis, in consequence of a visit which he paid to England in 1728, became a zealous defender of it; but notwithstanding these and some other examples that might be quoted, we must admit the truth of the remark of Voltaire, that though Newton survived the publication of the Principia more than forty years, yet at the time of his death he had not above twenty followers out of England.

With regard to the progress of the Newtonian philosophy in England, some difference of opinion has been entertained. Professor Playfair gives the following account of it. “In the universities of England, though the Aristotelian physics had made an obstinate resistance, they had been supplanted by the Cartesian, which became firmly established about the time when their foundation began to be sapped by the general progress of science, and particularly by the discoveries of Newton. For more than thirty years after the publication of these discoveries, the system of vortices kept its ground; and a translation from the French into Latin of the Physics of Rohault, a work entirely Cartesian, continued at Cambridge to be the text for philosophical instruction. About the year 1718, a new and more elegant translation of the same book was published by Dr. Samuel Clarke, with the addition of notes, in which that profound and ingenious writer explained the views of Newton on the principal objects of discussion, so that the notes contained virtually a refutation of the text; they did so, however, only virtually, all appearance of argument and controversy being carefully avoided. Whether this escaped the notice of the learned doctor or not is uncertain, but the new translation, from its better Latinity, and the name of the editor, was readily admitted to all the academical honours which the old one had enjoyed. Thus the stratagem of Dr. Clarke completely succeeded; the tutor might prelect from the text, but the pupil would sometimes look into the notes; and error is never so sure of being exposed as when the truth is placed close to it, side by side, without any thing to alarm prejudice, or awaken from its lethargy the dread of innovation. Thus, therefore, the Newtonian philosophy first entered the university of Cambridge under the protection of the Cartesian.” To this passage Professor Playfair adds the following as a note:—

“The universities of St. Andrew’s and Edinburgh were, I believe, the first in Britain where the Newtonian philosophy was made the subject of the academical prelections. For this distinction they are indebted to James and David Gregory, the first in some respects the rival, but both the friends of Newton. Whiston bewails, in the anguish of his heart, the difference, in this respect, between those universities and his own. David Gregory taught in Edinburgh for several years prior to 1690, when he removed to Oxford; and Whiston says, ‘He had already caused several of his scholars to keep acts, as we call them, upon several branches of the Newtonian philosophy, while we at Cambridge, poor wretches, were ignominiously studying the fictitious hypotheses of the Cartesians.’49 I do not, however, mean to say, that from this date the Cartesian philosophy was expelled from those universities; the Physics of Rohault were still in use as a text-book,—at least occasionally, to a much later period than this, and a great deal, no doubt, depended on the character of the individual. Professor Keill introduced the Newtonian philosophy in his lectures at Oxford in 1697; but the instructions of the tutors, which constitute the real and efficient system of the university, were not cast in that mould till long afterward.” Adopting the same view of the subject, Mr. Dugald Stewart has stated, “that the philosophy of Newton was publicly taught by David Gregory at Edinburgh, and by his brother, James Gregory, at St. Andrew’s,50 before it was able to supplant the vortices of Descartes in that very university of which Newton was a member. It was in the Scottish universities that the philosophy of Locke, as well as that of Newton, was first adopted as a branch of academical education.”

Anxious as we should have been to have awarded to Scotland the honour of having first adopted the Newtonian philosophy, yet a regard for historical truth compels us to take a different view of the subject. It is well known that Sir Isaac Newton delivered lectures on his own philosophy from the Lucasian chair before the publication of the Principia; and in the very page of Whiston’s life quoted by Professor Playfair, he informs us that he had heard him read such lectures in the public schools, though at that time he did not at all understand them. Newton continued to lecture till 1699, and occasionally, we presume, till 1703, when Whiston became his successor, having been appointed his deputy in 1699. In both of these capacities Whiston delivered in the public schools a course of lectures on astronomy, and a course of physico-mathematical lectures, in which the mathematical philosophy of Newton was explained and demonstrated, and both these courses were published, the one in 1707, and the other in 1710, “for the use of the young men in the university.” In 1707, the celebrated blind mathematician Nicholas Saunderson took up his residence in Christ’s College without being admitted a member of that body. The society not only allotted to him apartments, but gave him the free use of their library. With the concurrence of Whiston he delivered a course of lectures “on the Principia, Optics, and Universal Arithmetic of Newton,” and the popularity of these lectures was so great, that Sir Isaac corresponded on the subject of them with their author; and on the ejection of Whiston from the Lucasian chair in 1711, Saunderson was appointed his successor. In this important office he continued to teach the Newtonian philosophy till the time of his death, which took place in 1739.

But while the Newtonian philosophy was thus regularly taught in Cambridge, after the publication of the Principia, there were not wanting other exertions for accelerating its progress. About 1694, the celebrated Dr. Samuel Clarke, while an under-graduate, defended, in the public schools, a question taken from the Newtonian philosophy; and his translation of Rohault’s Physics, which contains references in the notes to the Principia, and which was published in 1697 (and not in 1718, as stated by Professor Playfair), shows how early the Cartesian system was attacked by the disciples of Newton. The author of the Life of Saunderson informs us, that public exercises or acts founded on every part of the Newtonian system were very common about 1707, and so general were such studies in the university, that the Principia rose to four times its original price.51 One of the most ardent votaries of the Newtonian philosophy was Dr. Laughton, who had been tutor in Clare Hall from 1694, and it is probable that during the whole, or at least a greater part, of his tutorship he had inculcated the same doctrines. In 1709–10, when he was proctor of that college, instead of appointing a moderator, he discharged the office himself, and devoted his most active exertions to the promotion of mathematical knowledge. Previous to this, he had even published a paper of questions on the Newtonian philosophy, which appear to have been used as theses for disputations; and such was his ardour and learning that they powerfully contributed to the popularity of his college. Between 1706 and 1716, the year of his death, the celebrated Roger Cotes, the friend and disciple of Newton, filled the Plumian chair of astronomy and experimental philosophy at Cambridge. During this period he edited the second edition of the Principia, which he enriched with an admirable preface, and thus contributed, by his writings as well as by his lectures, to advance the philosophy of his master. About the same time, the learned Dr. Bentley, who first made known the philosophy of his friend to the readers of general literature, filled the high office of master of Trinity College, and could not fail to have exerted his utmost influence in propagating doctrines which he so greatly admired. Had any opposition been offered to the introduction of the true system of the universe, the talents and influence of these individuals would have immediately suppressed it; but no such opposition seems to have been made; and though there may have been individuals at Cambridge ignorant of mathematical science, who adhered to the system of Descartes, and patronised the study of the Physics of Rohault, yet it is probable that similar persons existed in the universities of Edinburgh and St. Andrew’s; and we cannot regard their adherence to error as disproving the general fact, that the philosophy of Newton was quickly introduced into all the universities of Great Britain.

But while the mathematical principles of the Newtonian system were ably expounded in our seats of learning, its physical truths were generally studied, and were explained and communicated to the public by various lecturers on experimental philosophy. The celebrated Locke, who was incapable of understanding the Principia from his want of mathematical knowledge, inquired of Huygens if all the mathematical propositions in that work were true. When he was assured that he might depend upon their certainty, he took them for granted, and carefully examined the reasonings and corollaries deduced from them. In this manner he acquired a knowledge of the physical truths in the Principia, and became a firm believer in the discoveries which it contained. In the same manner he studied the treatise on Optics, and made himself master of every part of it which was not mathematical.52 From a manuscript of Sir Isaac Newton’s, entitled “A demonstration that the planets, by their gravity towards the sun, may move in ellipses,53 found among the papers of Mr. Locke, and published by Lord King,” it would appear that he himself had been at considerable trouble in explaining to his friend that interesting doctrine. This manuscript is endorsed, “Mr. Newton, March, 1689.” It begins with three hypotheses (the first two being the two laws of motion, and the third the parallelogram of motion), which introduce the proposition of the proportionality of the areas to the times in motions round an immoveable centre of attraction.54 Three lemmas, containing properties of the ellipse, then prepare the reader for the celebrated proposition, that when a body moves in an ellipse,55 the attraction is reciprocally as the square of the distance of the body from the focus to which it is attracted. These propositions are demonstrated in a more popular manner than in the Principia, but there can be no doubt that, even in their present modified form, they were beyond the capacity of Mr. Locke.

Dr. John Keill was the first person who publicly taught natural philosophy by experiments. Desaguliers informs us that this author “laid down very simple propositions, which he proved by experiments, and from these he deduced others more compound, which he still confirmed by experiments, till he had instructed his auditors in the laws of motion, the principles of hydrostatics and optics, and some of the chief propositions of Sir Isaac Newton concerning light and colours. He began these courses in Oxford about the year 1704 or 1705, and in that way introduced the love of the Newtonian philosophy.” When Dr. Keill left the university, Desaguliers began to teach the Newtonian philosophy by experiments. He commenced his lectures at Harthall in Oxford, in 1710, and delivered more than a hundred and twenty courses; and when he went to settle in London in 1713, he informs us that he found “the Newtonian philosophy generally received among persons of all ranks and professions, and even among the ladies by the help of experiments.” Such were the steps by which the Newtonian philosophy was established in Great Britain. From the time of the publication of the Principia, its mathematical doctrines formed a regular part of academical education; and before twenty years had elapsed, its physical truths were communicated to the public in popular lectures illustrated by experiments, and accommodated to the capacities of those who were not versed in mathematical knowledge. The Cartesian system, though it may have lingered for a while in the recesses of our universities, was soon overturned; and long before his death, Newton enjoyed the high satisfaction of seeing his philosophy triumphant in his native land.

CHAPTER XII.

Doctrine of Infinite Quantities—Labours of Pappus—Kepler—Cavaleri—Roberval—Fermat—Wallis—Newton discovers the Binomial Theorem—and the Doctrine of Fluxions in 1666—His Manuscript Work containing this Doctrine communicated to his Friends—His Treatise on Fluxions—His Mathematical Tracts—His Universal Arithmetic—His Methodus Differentialis—His Geometria Analytica—His Solution of the Problems proposed by Bernouilli and Leibnitz—Account of the celebrated Dispute respecting the Invention of Fluxions—Commercium Epistolicum—Report of the Royal Society—General View of the Controversy.

Previous to the time of Newton, the doctrine of infinite quantities had been the subject of profound study. The ancients made the first step in this curious inquiry by a rude though ingenious attempt to determine the area of curves. The method of exhaustions which was used for this purpose consisted in finding a given rectilineal area to which the inscribed and circumscribed polygonal figures continually approached by increasing the number of their sides. This area was obviously the area of the curve, and in the case of the parabola it was found by Archimedes to be two-thirds of the area formed by multiplying the ordinate by the abscissa. Although the synthetical demonstration of the results was perfectly conclusive, yet the method itself was limited and imperfect.

The celebrated Pappus of Alexandria followed Archimedes in the same inquiries; and in his demonstration of the property of the centre of gravity of a plane figure, by which we may determine the solid formed by its revolution, he has shadowed forth the discoveries of later times.

In his curious tract on Stereometry, published in 1615, Kepler made some advances in the doctrine of infinitesimals. Prompted to the task by a dispute with the seller of some casks of wine, he studied the measurement of solids formed by the revolution of a curve round any line whatever. In solving some of the simplest of these problems, he conceived a circle to be formed of an infinite number of triangles having all their vertices in the centre, and their infinitely small bases in the circumference of the circle, and by thus rendering familiar the idea of quantities infinitely great and infinitely small, he gave an impulse to this branch of mathematics. The failure of Kepler, too, in solving some of the more difficult of the problems which he himself proposed roused the attention of geometers, and seems particularly to have attracted the notice of Cavaleri.

This ingenious mathematician was born at Milan in 1598, and was Professor of Geometry at Bologna. In his method of Indivisibles, which was published in 1635, he considered a line as composed of an infinite number of points, a surface of an infinite number of lines, and a solid of an infinite number of surfaces; and he lays it down as an axiom that the infinite sums of such lines and surfaces have the same ratio when compared with the linear or superficial unit, as the surfaces and solids which are to be determined. As it is not true that an infinite number of infinitely small points can make a line, or an infinite number of infinitely small lines a surface, Pascal removed this verbal difficulty by considering a line as composed of an infinite number of infinitely short lines, a surface as composed of an infinite number of infinitely narrow parallelograms, and a solid of an infinite number of infinitely thin solids. But, independent of this correction, the conclusions deduced by Cavaleri are rigorously true, and his method of ascertaining the ratios of areas and solids to one another, and the theorems which he deduced from it may be considered as forming an era in mathematics.

By the application of this method, Roberval and Toricelli showed that the area of the cycloid is three times that of its generating circle, and the former extended the method of Cavaleri to the case where the powers of the terms of the arithmetical progression to be summed were fractional.

In applying the doctrine of infinitely small quantities to determine the tangents of curves, and the maxima and minima of their ordinates, both Roberval and Fermat made a near approach to the invention of fluxions—so near indeed that both Lagrange and Laplace56 have pronounced the latter to be the true inventer of the differential calculus. Roberval supposed the point which describes a curve to be actuated by two motions, by the composition of which it moves in the direction of a tangent; and had he possessed the method of fluxions, he could, in every case, have determined the relative velocities of these motions, which depend on the nature of the curve, and consequently the direction of the tangent which he assumed to be in the diagonal of a parallelogram whose sides had the same ratio as the velocities. But as he was able to determine these velocities only in the conic sections, &c. his ingenious method had but few applications.

The labours of Peter Fermat, a counsellor of the parliament of Toulouse, approached still nearer to the fluxionary calculus. In his method of determining the maxima and minima of the ordinates of curves, he substitutes x + e for the independent variable x in the function which is to become a maximum, and as these two expressions should be equal when e becomes infinitely small or 0, he frees this equation from surds and radicals, and after dividing the whole by e, e is made = 0, and the equation for the maximum is thus obtained. Upon a similar principle he founded his method of drawing tangents to curves. But though the methods thus used by Fermat are in principle the same with those which connect the theory of tangents and of maxima and minima with the analytical method of exhibiting the differential calculus, yet it is a singular example of national partiality to consider the inventer of these methods as the inventer of the method of fluxions.

“One might be led,” says Mr. Herschel, “to suppose by Laplace’s expression that the calculus of finite differences had then already assumed a systematic form, and that Fermat had actually observed the relation between the two calculi, and derived the one from the other. The latter conclusion would scarcely be less correct than the former. No method can justly be regarded as bearing any analogy to the differential calculus which does not lay down a system of rules (no matter on what considerations founded, by what names called, or by what extraneous matter enveloped) by means of which the second term of the development of any function of x + e in powers of e, can be correctly calculated, ‘quæ extendet se,’ to use Newton’s expression, ‘citra ullum molestum calculum in terminis surdis æque ac in integris procedens.’ It would be strange to suppose Fermat or any other in possession of such a method before any single surd quantity had ever been developed in a series. But, in point of fact, his writings present no trace of the kind; and this, though fatal to his claim, is allowed by both the geometers cited. Hear Lagrange’s candid avowal. ‘Il fait disparaitre dans cette equation,’ that of the maximum between x and e, ‘les radicaux et les fractions s’il y en à.’ Laplace, too, declares that ‘il savoit etendre son calcul aux fonctions irrationelles en se debarrassant des irrationalités par l’elevation des radicaux aux puissances.’ This is at once giving up the point in question. It is allowing unequivocally that Fermat in these processes only took a circuitous route to avoid a difficulty which it is one of the most express objects of the differential calculus to face and surmount. The whole claim of the French geometer arises from a confusion (too often made) of the calculus and its applications, the means and the end, under the sweeping head of ‘nouveaux calculs’ on the one hand, and an assertion somewhat too unqualified, advanced in the warmth and generality of a preface, on the other.”57

The discoveries of Fermat were improved and simplified by Hudde, Huygens, and Barrow; and by the publication of the Arithmetic of Infinites by Dr. Wallis, Savilian professor of geometry at Oxford, mathematicians were conducted to the very entrance of a new and untrodden field of discovery. This distinguished author had effected the quadrature of all curves whose ordinates can be expressed by any direct integral powers; and though he had extended his conclusions to the cases where the ordinates are expressed by the inverse or fractional powers, yet he failed in its application. Nicolas Mercator (Kauffman) surmounted the difficulty by which Wallis had been baffled, by the continued division of the numerator by the denominator to infinity, and then applying Wallis’s method to the resulting positive powers. In this way he obtained, in 1667, the first general quadrature of the hyperbola, and, at the same time, gave the regular development of a function in series.

In order to obtain the quadrature of the circle, Dr. Wallis considered that if the equations of the curves of which he had given the quadrature were arranged in a series, beginning with the most simple, these areas would form another series. He saw also that the equation of the circle was intermediate between the first and second terms of the first series, or between the equation of a straight line and that of a parabola, and hence he concluded, that by interpolating a term between the first and second term of the second series, he would obtain the area of the circle. In pursuing this singularly beautiful thought, Dr. Wallis did not succeed in obtaining the indefinite quadrature of the circle, because he did not employ general exponents; but he was led to express the entire area of the circle by a fraction, the numerator and denominator of which are each obtained by the continued multiplication of a certain series of numbers.

Such was the state of this branch of mathematical science, when Newton, at an early age, directed to it the vigour of his mind. At the very beginning of his mathematical studies, when the works of Dr. Wallis fell into his hands, he was led to consider how he could interpolate the general values of the areas in the second series of that mathematician. With this view he investigated the arithmetical law of the coefficients of the series, and obtained a general method of interpolating, not only the series above referred to, but also other series. These were the first steps taken by Newton, and, as he himself informs us, they would have entirely escaped from his memory if he had not, a few weeks before,58 found the notes which he made upon the subject. When he had obtained this method, it occurred to him that the very same process was applicable to the ordinates, and, by following out this idea, he discovered the general method of reducing radical quantities composed of several terms into infinite series, and was thus led to the discovery of the celebrated Binomial Theorem. He now neglected entirely his methods of interpolation, and employed that theorem alone as the easiest and most direct method for the quadratures of curves, and in the solution of many questions which had not even been attempted by the most skilful mathematicians.

After having applied the Binomial theorem to the rectification of curves, and to the determination of the surfaces and contents of solids, and the position of their centres of gravity, he discovered the general principle of deducing the areas of curves from the ordinate, by considering the area as a nascent quantity, increasing by continual fluxion in the proportion of the length of the ordinate, and supposing the abscissa to increase uniformly in proportion to the time. In imitation of Cavalerius, he called the momentary increment of a line a point, though it is not a geometrical point, but an infinitely short line; and the momentary increment of an area or surface he called a line, though it is not a geometrical line, but an infinitely narrow surface. By thus regarding lines as generated by the motion of points, surfaces by the motions of lines, and solids by the motion of surfaces, and by considering that the ordinates, abscissæ, &c. of curves thus formed, vary according to a regular law depending on the equation of the curve, he deduces from this equation the velocities with which these quantities are generated; and by the rules of infinite series he obtains the ultimate value of the quantity required. To the velocities with which every line or quantity is generated, Newton gave the name of Fluxions, and to the lines or quantities themselves that of Fluents. This method constitutes the doctrine of fluxions which Newton had invented previous to 1666, when the breaking out of the plague at Cambridge drove him from that city, and turned his attention to other subjects.

But though Newton had not communicated this great invention to any of his friends, he composed his treatise, entitled Analysis per equationes numero terminorum infinitas, in which the principle of fluxions and its numerous applications are clearly pointed out. In the month of June, 1669, he communicated this work to Dr. Barrow, who mentions it in a letter to Mr. Collins, dated the 20th June, 1669, as the production of a friend of his residing at Cambridge, who possesses a fine genius for such inquiries. On the 31st July, he transmitted the work to Collins; and having received his approbation of it, he informs him that the name of the author of it was Newton, a fellow of his own college, and a young man who had only two years before taken his degree of M.A. Collins took a copy of this treatise, and returned the original to Dr. Barrow; and this copy having been found among Collins’s papers by his friend Mr. William Jones, and compared with the original manuscript borrowed from Newton, it was published with the consent of Newton in 1711, nearly fifty years after it was written.

Though the discoveries contained in this treatise were not at first given to the world, yet they were made generally known to mathematicians by the correspondence of Collins, who communicated them to James Gregory; to MM. Bertet and Vernon in France; to Slusius in Holland; to Borelli in Italy; and to Strode, Townsend, and Oldenburg, in letters dated between 1669 and 1672.

Hitherto the method of fluxions was known only to the friends of Newton and their correspondents; but, in the first edition of the Principia, which appeared in 1687, he published, for the first time, the fundamental principle of the fluxionary calculus, in the second lemma of the second book. No information, however, is here given respecting the algorithm or notation of the calculus; and it was not till 1693–5[?] that it was communicated to the mathematical world in the second volume of Dr. Wallis’s works, which were published in that year. This information was extracted from two letters of Newton written in 1692.

About the year 1672, Newton had undertaken to publish an edition of Kinckhuysen’s Algebra, with notes and additions. He therefore drew up a treatise, entitled, A Method of Fluxions, which he proposed as an introduction to that work; but the fear of being involved in disputes about this new discovery, or perhaps the wish to render it more complete, or to have the sole advantage of employing it in his physical researches, induced him to abandon this design. At a later period of his life he again resolved to give it to the world; but it did not appear till after his death, when it was translated into English, and published in 1736, with a commentary by Mr. John Colson, Professor of Mathematics in Cambridge.59

To the first edition of Newton’s Optics, which appeared in 1704, there were added two mathematical treatises, entitled, Tractatus duo de speciebus et magnitudine figurarum curvilinearum, the one bearing the title of Tractatus de Quadratura Curvarum, and the other Enumeratio linearum tertii ordinis. The first contains an explanation of the doctrine of fluxions, and of its application to the quadrature of curves; and the second a classification of seventy-two curves of the third order, with an account of their properties. The reason for publishing these two tracts in his Optics (in the subsequent editions of which they are omitted) is thus stated in the advertisement:—“In a letter written to M. Leibnitz in the year 1679, and published by Dr. Wallis, I mentioned a method by which I had found some general theorems about squaring curvilinear figures on comparing them with the conic sections, or other the simplest figures with which they might be compared. And some years ago I lent out a manuscript containing such theorems; and having since met with some things copied out of it, I have on this occasion made it public, prefixing to it an introduction, and joining a scholium concerning that method. And I have joined with it another small tract concerning the curvilineal figures of the second kind, which was also written many years ago, and made known to some friends, who have solicited the making it public.”

In the year 1707, Mr. Whiston published the algebraical lectures which Newton had, during nine years, delivered at Cambridge, under the title of Arithmetica Universalis, sive de Compositione et Resolutione Arithmetica Liber. We are not accurately informed how Mr. Whiston obtained possession of this work; but it is stated by one of the editors of the English edition, that “Mr. Whiston thinking it a pity that so noble and useful a work should be doomed to a college confinement, obtained leave to make it public.” It was soon afterward translated into English by Mr. Ralphson; and a second edition of it, with improvements by the author, was published at London in 1712, by Dr. Machin, secretary to the Royal Society. With the view of stimulating mathematicians to write annotations on this admirable work, the celebrated S’Gravesande published a tract, entitled, Specimen Commentarii in Arithmeticam Universalem; and Maclaurin’s Algebra seems to have been drawn up in consequence of this appeal.