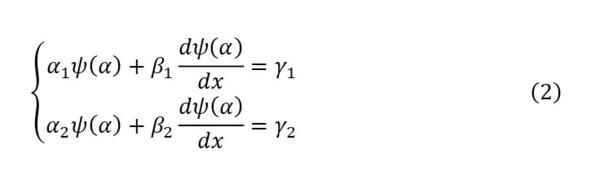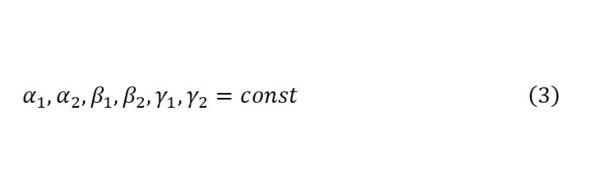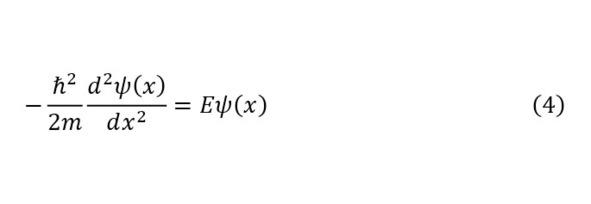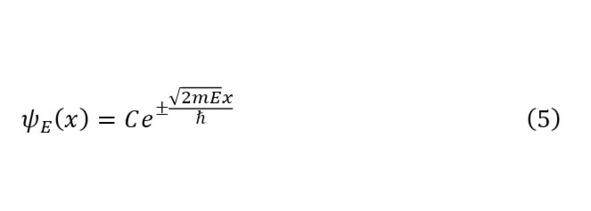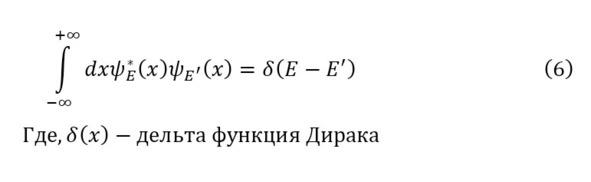QUESTIONS CONCERNING THE SPECTRAL SOLUTION IN A ONE-DIMENSIONAL STATIONARY LINEAR PARTIAL DIFFERENTIAL EQUATION BY ERWIN RUDOLF JOSEF ALEXANDER SCHRODINGER
UDC 150.145
Nasriddinov Otadavlat Usubzhonovich
Senior Lecturer of the Department of «Natural Sciences» of the Faculty of Computer Engineering of the Ferghana branch of the Tashkent University of Information Technologies
Ferghana Branch of Tashkent University of Information Technologies, Ferghana, Uzbekistan
Annotation. The impossibility of intuitive understanding of the most diverse spectrum of quantum phenomena reduces to the need to use all physical and mathematical methods before all empirical and experimental actions. One of the most popular and important in this vein is a linear partial differential equation describing the change in space and time of the pure state, given by the wave function, in Hamiltonian quantum systems for photonic phenomena expressed in a stationary state.
Keywords: Schrodinger equation, stationary state, spectral problems, quantization, differential equation, physical and mathematical calculation and modeling.
Аннотация. Невозможность интуитивного понимания самого различного спектра квантовых явлений сводит к необходимости использования перед всеми эмпирическими и экспериментальными действиями всех физико-математических методов. Одним из самым популярным и важных в данном ключе является линейное дифференциальное уравнение в частных производных, описывающее изменение в пространстве и во времени чистого состояния, задаваемое волновой функцией, в гамильтоновых квантовых системах для фотонных явлений выражаемое в стационарном состоянии.
Ключевые слова: уравнение Шрёдингера, стационарное состояние, спектральные задачи, квантование, дифференциальное уравнение, физико-математическое вычисление и моделирование.
Before presenting the question itself, it is worth noting the representation of the one-dimensional stationary Schrodinger equation itself, which is a linear ordinary differential equation of the second order (1), which is also used to solve problems of the spectral plan in wave modeling of photonic phenomena.
In order to solve such an approach, it is necessary to introduce boundary conditions (2), depending on the formulation of which it is possible to determine a general description of the situation and at the same time pay attention to the statement of indicators (3).
Of course, one could try to determine a general solution, but, unfortunately, this is simply impossible and it is necessary to introduce certain boundary conditions that are reduced from certain conditions. A striking example of such states is the solution for a free particle, which is essentially a plane wave. And if we take the potential equation for a free particle, including when taking the corpuscular form of photons, we can get equation (4).
One of the partial solutions is the function (5), derived through a direct solution of a second-order differential equation.
In (4), the constant E can take almost all values above zero, it is from here that we can conclude that the values belong to a continuous spectrum. Moreover, to determine its boundaries, it is necessary to use the integral equation (6), from which the resulting constant C from (5) is obtained.
Hence the value (7) is obtained.