Я. И. Перельман «Занимательная физика», издательство П. П. Сойкина, 1916г.

Предисловие

Эта книга представляет собой самостоятельный сборник, не являющийся продолжением первой книги «Занимательной физики»; она названа «второю» лишь потому, что написана позднее первой. Успех первого сборника побудил автора обработать остальной накопившийся у него материал, и таким образом составилась эта вторая – или, вернее, другая – книга, охватывающая те же отделы школьной физики.

Настоящая книга «Занимательной физики», как и первая, предназначается для чтения, а не для изучения. Ее цель – не столько сообщить читателю новые знания, сколько помочь ему «узнать то, что он знает», т. е. углубить и оживить уже имеющиеся у него основные сведения по физике, научить сознательно распоряжаться ими и побудить к разностороннему их применению. Достигается это, как и в первом сборнике, рассмотрением пестрого ряда головоломок, замысловатых вопросов, занимательных задач, забавных парадоксов, неожиданных сопоставлений из области физики, относящихся к кругу повседневных явлений или почерпаемых из популярных произведений общей и научно-фантастической беллетристики. Материалом последнего рода составитель пользовался особенно широко, считая его наиболее соответствующим целям сборника: привлечены отрывки из общеизвестных романов Жюля Верна, Уэллса, Курда Лассвица и др. Фантастические опыты, помимо их заманчивости, могут играть немаловажную роль при преподавании в качестве живых иллюстраций; они находили себе место даже в школьных учебниках. «Цель их – пишет наш известный педагог В. Л. Розенберг[1] – освободить ум от оков привычки и выяснить одну из сторон явления, понимание которого затемняется обычными условиями, вторгающимися в ум учащегося независимо от его воли, вследствие привычки».

Составитель старался, насколько умел, придавать изложению внешне интересную форму, сообщать привлекательность предмету, не останавливаясь иногда и перед тем, чтобы черпать интерес со стороны. Он руководствовался тою психологическою аксиомою, что интерес к предмету повышает внимание, внимание облегчает понимание и, следовательно, способствует более сознательному усвоению.

Вопреки обычаю, установившемуся для подобного рода сборников, в «Занимательной физике» весьма мало места отводится описанию забавных и эффектных физических опытов. У нас имеется уже достаточно сборников подобных опытов из области физики; кроме того, образовательное значение такого рода материала не всегда бесспорно. Не говоря уже о том, что опыты обычно удаются лишь наиболее предприимчивым и терпеливым читателям, оставляя у других чувство разочарования и досады по поводу испорченных вещей, – центр внимания невольно переносится при этом на работу рук, а не на деятельность ума; в результате нередко создается почва для насаждения непродуманного, чисто формального отношения к физическому объяснению. Между тем, главная цель «Занимательной физики» – возбудить деятельность научного воображения, приучить читателя мыслить в духе физической науки и создать в его памяти многочисленные ассоциации физических знаний с самыми разнородными явлениями жизни, со всем тем, с чем он обычно входит в соприкосновение.

Для оживления интереса к физическим вычислениям в некоторые задачи этого сборника введены числовые данные (чего в первой книге автор избегал).

В общем, настоящий сборник по подбору материала предназначается для несколько более подготовленного читателя, нежели первая книга «Занимательной физики», – хотя различие в этом отношении между обеими книгами настолько незначительно, что их можно читать в любой последовательности и независимо одну от другой[2]. Я. П.

Глава первая

Законы движения

Самый дешевый способ путешествовать

Остроумный французский писатель XVII века Сирано де Бержерак в своем сатирическом «Путешествии на Луну» рассказывает, между прочим, о таком удивительном случае, будто бы произошедшем с ним самим. Занимаясь однажды физическими опытами, он вдруг каким-то непостижимым образом был поднят вместе со своими склянками высоко на воздух. Когда же через несколько часов ему удалось, наконец, спуститься вновь на землю, то, к изумлению своему, очутился он уже не в родной Франции и даже не в Европе, а – В Америке, в Канаде!

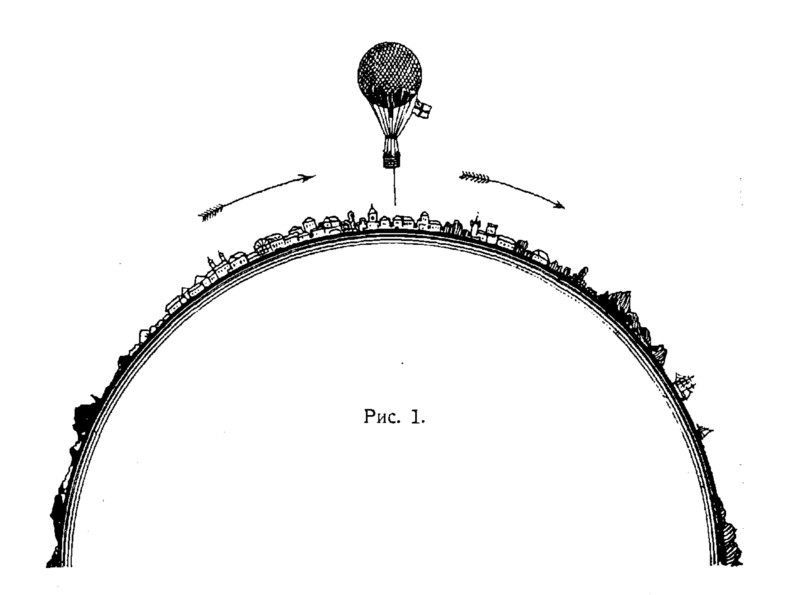
Рис. 1. Могут ли пассажиры аэростата видеть, как под ними вращается земной шар?

(Художнику пришлось пренебречь на этом рисунке точным соблюдением масштаба. Если бы он пожелал изобразить Землю сообразно с размерами аэростата, ему понадобился бы лист бумаги в десять верст шириной.)

Такой неожиданный перелет через Атлантический океан французский писатель объясняет тем, что, пока невольный путешественник был отделен от земной поверхности, наша планета продолжала по-прежнему вращаться с запада на восток; вот почему, когда он вновь опустился, под ногами его, вместо Франции, очутился уже материк Америки…

Вот видите, какой дешевый и простой способ путешествовать! Стоит только подняться над землей и продержаться в воздухе хотя бы несколько минут, чтобы опуститься уже в другом месте, далеко на запад от первого. Вместо того чтобы предпринимать долгие и утомительные путешествия через материки и океаны, можно неподвижно висеть над землей и выжидать, пока земной шар сам услужливо подставит путнику место назначения.

Жаль только, что этот удивительный способ – не более чем фантазия… Дело в том, что, поднявшись в воздух, мы, в сущности, вовсе еще не отделяемся от земного шара: мы остаемся связанными с газообразной оболочкой нашей планеты, висим в ее атмосфере, которая тоже участвует в обращении Земли вокруг оси; воздух вращается вместе с Землей, увлекая с собой все, что в нем находится – облака, воздушные шары, аэропланы, всех летящих птиц, насекомых и т. д.

Если бы воздух не участвовал во вращении земного шара, то, стоя на земле, мы постоянно чувствовали бы сильнейший ветер, по сравнению с которым самый страшный ураган должен считаться нежным дуновением. Ведь совершенно безразлично: мы ли стоим на месте, а воздух движется мимо нас, или же, наоборот, – воздух неподвижен, а мы перемещаемся в нем: в обоих случаях мы ощущаем одинаково сильный ветер. Автомобилист, мчащийся со скоростью 80 верст[3] в час, чувствует сильнейший ветер даже в совершенно тихую погоду.

Но если бы даже мы могли подняться вверх, за пределы атмосферы, или если бы Земля не была окружена воздухом – нам все равно не удалось бы воспользоваться тем дешевым способом путешествовать, о котором фантазировал французский поэт. В самом деле, отделяясь от поверхности вращающейся Земли, мы продолжаем по инерции двигаться с прежнею скоростью, т. е. с тою же, с какой перемещается под нами Земля. И когда снова опускаемся вниз, мы оказываемся в том же самом пункте, от которого раньше отделились – подобно тому, как, подпрыгнув в вагоне движущегося поезда, мы опускаемся на прежнее место.

«Земля, остановись!»

У современного английского романиста Герберта Уэллса есть фантастический рассказ о том, как творил чудеса некий конторский писец. Весьма недалекий и малообразованный молодой человек оказался, сверх ожидания, обладателем удивительного дара: стоило ему высказать какое-нибудь пожелание – и оно немедленно же исполнялось. Однако столь заманчивый дар не принес ни его обладателю, ни другим людям ничего, кроме неприятностей. Для нас особенно поучителен конец этой истории.

После чересчур затянувшейся ночной попойки писец-чудодей, опасаясь явиться домой на рассвете, вздумал воспользоваться своим даром, чтобы продлить ночь. Как это сделать? Надо приказать светилам неба приостановить свой бег. Писец не сразу решился на такой необычайный подвиг, и когда его приятель посоветовал ему остановить Луну, он, внимательно поглядев на нее, сказал в раздумье:

– Мне кажется, она слишком далека для этого…

– Но почему же не попробовать? – настаивал Мейдиг (так звали приятеля). – Она, конечно, не остановится, вы только прекратите вращение Земли. Течение времени остановится. Надеюсь, это никому не повредит!

– Гм! – сказал Фотерингей (писец). – Хорошо, попробую. Ну…

Застегнувшись на все пуговицы, он стал в повелительную позу, простер руки над миром и торжественно произнес:

– Земля, остановись! Перестань вращаться!

Не успел он договорить этих слов, как приятели уже летали в пространстве вниз головою со скоростью несколько дюжин[4] миль[5] в минуту.

Несмотря на это, он продолжал думать, так как мысль иногда почти не требует времени. Меньше чем в секунду он успел и подумать, и высказать про себя следующее пожелание:

– Что бы ни случилось, пусть я буду жив и невредим!

Нельзя не признать, что желание это было высказано как раз вовремя, поскольку костюм Фотерингея, вследствие трения о воздух, начал уже загораться. Еще несколько секунд, – и он упал на какую-то свежевзрытую землю, а вокруг него, не принося ему никакого вреда, неслись громадные камни, обломки зданий, металлические предметы разного рода; между прочим, летела какая-то несчастная корова, разбившаяся при ударе о землю. Шум кругом стоял страшный. Ни прежде, ни после того Фотерингей не слыхивал ничего подобного. Ветер дул с такой силою, что он не мог бы даже приподнять своей головы, чтобы оглянуться вокруг. Да, признаться, он об этом и не думал, – до такой степени ошеломило его все происшедшее.

– Господи! – воскликнул он прерывающимся голосом. – Что такое случилось? Буря, что ли? Ведь ночь была так тиха! Это все Мейдиг виноват. И зачем я его послушался! Где-то он теперь? Должно быть, я что-нибудь не так сделал!

Осмотревшись, насколько позволял ему ветер и развевавшиеся фалды пиджака, он продолжал:

– На небе-то, кажется, все в порядке. Вот и Луна. Стои́т по-прежнему прямо над головой. Ну, а все остальное… где же город? Где дома и улицы? Откуда, наконец, взялся ветер? Я не приказывал быть ветру.

Фотерингей попробовал встать на ноги, но это оказалось совершенно невозможным, и потому он проследовал вперед на четвереньках, придерживаясь за камни и выступы почвы. Идти, впрочем, было решительно некуда, так как, насколько можно было видеть из-под фалд пиджака, закинутых ветром на голову пресмыкающегося чудодея, все кругом представляло собою одну общую картину разрушения.

– Что-то такое во вселенной серьезно попортилось, – подумал Фотерингей, – а что именно – Бог знает.

Рис. 2. Что случилось бы, если бы Земля внезапно перестала вращаться вокруг своей оси.

Действительно, попортилось. Ни домов, ни деревьев, ни каких-либо живых существ – ничего не было видно. Одни только бесформенные развалины да разнородные обломки валялись кругом, едва видные от целого урагана пыли, несомой ветром. Гром и молния при совершенно ясном небе довершали картину, представившуюся виновнику всей этой катавасии.

Сам этот виновник не понимал, конечно, в чем дело. А объяснялось всё очень просто. Остановив Землю сразу, Фотерингей не подумал о центробежной силе, а между тем она при внезапной остановке кругового движения неминуемо должна была сбросить с поверхности Земли все, на ней находящееся. Таким образом, дома, люди, деревья, животные – вообще все, что только не было неразрывно связано с главной массой земного шара, полетело по касательной к его поверхности со скоростью, превышающей ту, которой обладает ядро, только что вылетевшее из жерла пушки. А затем все это вновь попадало на землю, разбиваясь вдребезги.

Фотерингей не знал, в чем дело, но он тотчас же понял, что чудо, им совершенное, оказывается не особенно удачным; а потому им сразу овладело глубокое отвращение ко всяким чудесам, и он дал себе слово не творить их больше. Но прежде всего нужно было поправить каким-нибудь образом ту беду, которую он наделал. А беда эта оказывалась немалой. К довершению своего ужаса, Фотерингей видел, что она даже увеличивается. В самом деле: буря все свирепела, облака пыли совсем закрыли Луну и вдали слышен был шум приближающейся воды; Фотерингей видел даже, при свете молнии, целую водяную стену, со страшной скоростью надвигавшуюся к тому месту, на котором он лежал.

– Мейдиг! Мейдиг! – вскричал он. – Где вы?

Но не получая никакого ответа и видя, что приходится действовать на свой страх и на свою ответственность, не посоветовавшись с опытными людьми, он стал решительным.

– Стой! – вскричал он, обращаясь к воде. – Ни шагу далее!

Затем повторил то же распоряжение грому, молнии и ветру.

Все затихло.

– Постойте немножко, – сказал Фотерингей, – дайте мне собраться с мыслями… Что же мне теперь делать?

Присев на корточки, мистер Фотерингей задумался.

– Как бы это опять не наделать какой-нибудь кутерьмы, – подумал он и затем сказал: – да… во-первых, когда исполнится все, что я сейчас прикажу, пусть я потеряю способность творить чудеса и буду таким же, как все обыкновенные люди. Не люблю чудес. Это слишком опасная игрушка. А во-вторых, пусть все будет по-старому: тот же город, те же люди, такие же дома, и я сам такой же, каким был тогда. Довольно чудить, не хочу больше!..

Письмо с воздушного шара

Вы находитесь в корзине аэростата, который быстро несется над землей. Внизу – знакомые места. Сейчас вы пролетите над усадьбой приятеля: «Хорошо бы послать ему весточку» – мелькает у вас в уме. Быстро набрасываете вы несколько слов на листке записной книжки, привязываете свою записку к камню и, выждав момент, когда знакомый сад оказывается как раз под вашими ногами, роняете камень.

Вы в полной уверенности, конечно, что камень упадет прямо в сад. Но, оказывается, он падает вовсе не туда…

Почему же? Ведь сад расположен прямо под корзиной аэростата?

Вот оттого-то камень и не падает в сад. Следя за его падением с корзины аэростата, вы увидите странное явление: камень опускается вниз, но в то же время продолжает оставаться под аэростатом, словно скользя по привязанной к нему невидимой веревке. И когда камень достигнет земли, он будет находиться далеко впереди того пункта, который вы себе наметили. Здесь проявляется тот же закон инерции, который мешает нам воспользоваться соблазнительным советом дешево путешествовать по способу Сирано де Бержерака. Пока камень был в корзине аэростата, он вместе с нею несся в пространстве с некоторою скоростью. Вы уронили его, – но, отделившись от аэростата и падая вниз, камень все же не утрачивает своей первоначальной скорости, а, падая, продолжает в то же время совершать движение в воздухе в прежнем направлении. Оба движения, отвесное и горизонтальное, складываются – и в результате камень летит вниз по кривой линии, оставаясь все время под аэростатом (если только, конечно, сам аэростат внезапно не изменит своего направления или скорости полета). Камень летит совершенно так же, как горизонтально брошенное тело, – например, пуля, вылетевшая из горизонтально поставленного ружья: под влиянием горизонтального толчка и притяжения Земли оно описывает дугообразный путь, упирающийся в землю.

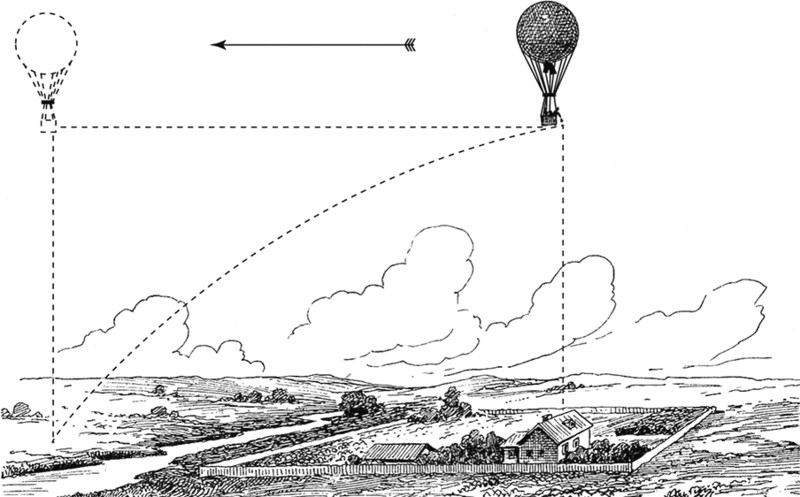
Рис. 3. Если уронить с летящего аэростата камень, то он падает не отвесно вниз, а по кривой линии, все время оставаясь под воздушным шаром.

Безостановочная железная дорога

Когда вы стои́те на неподвижной платформе и мимо нее проносится курьерский поезд, то вскочить в вагон на ходу, конечно, мудрено. Но представьте, что платформа под вами также движется, при том с такою же скоростью и в ту же сторону, как и поезд. Трудно ли вам будет тогда войти в вагон?

Нисколько: вы войдете так же спокойно, как если бы вагон стоял неподвижно. В самом деле: раз и вы и поезд движетесь в одну сторону с одинаковой скоростью, то по отношению к вам поезд находится в полном покое.

Правда, колеса его вращаются, но вам будет казаться, что они вертятся на одном месте.

Следовательно, вполне мыслимо устроить так, чтобы поезд, проходя мимо станций, принимал и высаживал пассажиров на полном ходу, не останавливаясь.

Приспособления такого рода нередко устраиваются на выставках, чтобы дать публике возможность быстро и удобно осматривать их достопримечательности, раскинутые на обширном пространстве. Так, на международной архитектурной выставке в Лейпциге осенью 1913 года крайние пункты выставочной площади были, словно бесконечной лентой, соединены железной дорогой; при этом пассажиры могли в любой момент и в любом месте входить в вагоны и выходить из них на полном ходу поезда.

Схема этого любопытного устройства видна на прилагаемых рисунках. На рис. 4 буквами А и В отмечены крайние станции. На каждой станции помещается круглая неподвижная платформа, окруженная большим вращающимся кольцеобразным диском. Вокруг вращающихся дисков обеих станций проходит канат, к которому прицеплены вагоны. Теперь проследите, что происходит при вращении платформы. Вагоны обегают вокруг платформ с такою же скоростью, с какою вращаются внешние края платформ; следовательно, пассажиры без малейшего опасения могут переходить с платформ в вагоны или, наоборот, покидать поезд. Выйдя из вагона, пассажир идет к центру круга, пока не дойдет до неподвижной платформы; а здесь перейти с внутреннего края подвижного диска на неподвижный уже нетрудно, так как при малом радиусе круга весьма мала и скорость вращения[6]. Достигнув внутренней, неподвижной платформы, пассажиру остается лишь перебраться по мостику на землю вне железной дороги (рис. 5).

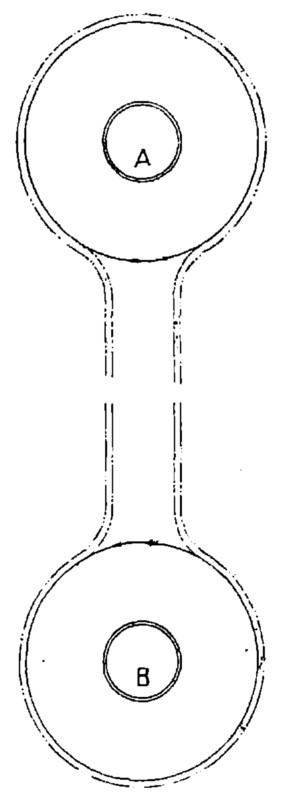
Рис. 4. Как была устроена «безостановочная» железная дорога на Лейпцигской выставке. Дорога обозначена пунктиром. А и В – вокзалы.

Рис. 4 и 5 поясняют сказанное. Размеры кругов и скорость их вращения выбраны были так, что внешние края их пробегали две сажени[7] в секунду (около 16 верст в час), внутренний же край двигался со скоростью всего полусажени в секунду; при такой скорости – вернее сказать, при такой медленности – можно было, разумеется, вполне безопасно переходить на платформу.

Отсутствие частых остановок дает огромный выигрыш во времени и затратах силы. Во всяком трамвае большая часть времени и чуть не ²/₃ всей энергии тратится на постепенное ускорение движения при отходе со станции, а также на замедление и торможение при остановках.

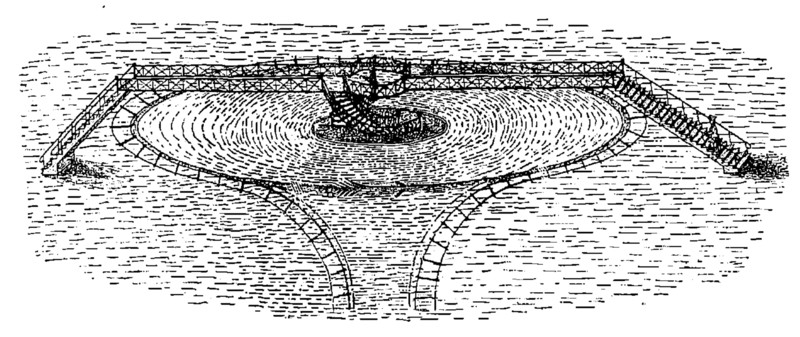
Рис. 5. Вокзал безостановочной железной дороги.

Через круглую, вечно вращающуюся платформу перекинута галерея, по которой пассажиры спокойно переходят из внутреннего, неподвижного круга на землю вне дороги.

На станциях железных дорог можно было бы обойтись даже без специальных подвижных платформ, чтобы принимать и высаживать пассажиров на полном ходу поезда. Вообразите, что мимо обыкновенной неподвижной станции проносится курьерский поезд; мы хотим, чтобы он, не останавливаясь, принял здесь новых пассажиров. Пусть же эти пассажиры займут пока места в другом поезде, стоящем на запасном параллельном пути, и пусть этот поезд начнет двигаться вперед, стремясь развить ту же скорость, что и курьерский. Необходимо устроить так, чтобы, когда оба поезда будут идти рядом, скорости их сравнялись. В этот момент оба поезда будут словно неподвижны один относительно другого: достаточно перекинуть мостки, которые соединяли бы вагоны соседних поездов, – и пассажиры «временного» поезда могут спокойно перейти в курьерский. Остановки на станциях сделаются, как видите, излишними.

Такова теория. Осуществление этого проекта на практике, вероятно, очень хлопотливо; потому-то ничего подобного нигде пока не устраивалось.

Улицы будущего

Не осуществлено на практике еще и другое приспособление, основанное на том же законе относительного движения: так называемые «движущиеся тротуары».

Вот чертеж такого устройства (рис. 6). Вы видите пять замкнутых полос-тротуаров, движущихся посредством особого механизма, одна внутри другой, с различной скоростью. Самая крайняя полоса ползет довольно медленно – со скоростью всего 5 верст в час; это скорость обыкновенного пешехода, и, понятно, вступить на такую медленно ползущую полосу не трудно даже ребенку или старику. Рядом с ней, внутри, бежит вторая полоса, со скоростью 10 верст в час. Вскочить на нее прямо с неподвижной улицы было бы очень опасно, но зато перейти на нее с первой полосы – ничего не стоит. В самом деле, по отношению к этой первой полосе, ползущей со скоростью 5 верст, вторая, бегущая с 10-верстной быстротой, делает ведь только 5 верст; значит, перейти с первой на вторую столь же легко, как перейти с земли на первую. Далее, третья полоса движется уже с 15-верстной скоростью, – но перейти на нее со второй полосы, конечно, нетрудно. Так же легко перейти с третьей полосы на следующую, четвертую, бегущую с 20-верстной скоростью, и, наконец, с нее на пятую, мчащуюся со скоростью 25 верст в час. Эта пятая полоса доставляет пассажира до того пункта, который ему нужен; здесь, спокойно переходя обратно с полосы на полосу, он высаживается на неподвижную землю.

Рис. 6. Движущиеся тротуары.

Такую непрерывно движущуюся улицу-поезд предполагалось устроить в Нью-Йорке, в подземном туннеле. Эта железная дорога представляла бы собой непрерывную круговую ленту с устроенными на ней сиденьями для пассажиров; лента движется, согласно проекту, со скоростью 21 версты в час. К ней примыкают еще три вспомогательные ленты, облегчающие переход с неподвижной почвы на ленту-поезд. Скорости их – 16, 10½ и 5 верст в час. Пассажиру, желающему сесть в поезд, нетрудно вступить с неподвижного пола на первую ленту (держась за один из ее вертикальных стержней); так же легко перейти с нее на вторую ленту, затем на третью, и, наконец, сесть в поезд.

Рис. 7. Движущаяся улица-поезд под землей. Перед тем как попасть с неподвижной платформы в поезд, пассажиры проходят через три полосы, движущиеся вперед, каждая немного быстрее предыдущей.

Непостижимый закон

Ни один из законов механики не вызывает, вероятно, столько недоумений, как знаменитый «третий закон Ньютона» – закон равенства действия и противодействия. Все его знают, умеют даже, когда нужно, правильно применять его – и все-таки мало кто верит в его истинность. Может быть, вы имели счастье, читатель, сразу понять его, – но что касается меня, то, должен сознаться, я постиг его много лет спустя после моего первого с ним знакомства. Я расспрашивал разных лиц, имеющих более или менее близкое отношение к механике, и убедился, что большинство из них готовы признать правильность этого закона лишь с довольно существенными оговорками. Охотно допускают, что он верен для тел неподвижных, но не понимают, как можно применять его к взаимодействию движущихся тел…

«Действие, – гласит этот закон, – всегда равно и противоположно противодействию». Это значит, что когда, например, лошадь тянет телегу, то телега тянет лошадь назад с точно такою же силою, с какою лошадь тянет телегу вперед. Но если так, то выходит, что телега должна оставаться на месте; почему же она все-таки движется? Почему лошадь увлекает телегу, а не телега увлекает лошадь назад? Ведь они тянут друг друга с одинаковой силой… И почему эти силы не уничтожаются взаимно, если они равны?

Эти недоумения разрешаются довольно просто. Силы не уничтожают друг друга потому, что приложены к разным телам: одна – к телеге, другая – к лошади. Силы эти равны, да, – но разве одинаковые силы всегда производят одинаковые действия? Разве равные силы сообщают всем телам равные скорости? Разве действие силы на тело не зависит также и от самого тела, – от величины того сопротивления, которое тело оказывает силе?

Если подумаете об этом, вам сразу станет понятно, почему лошадь все же увлекает телегу, хотя телега тянет ее обратно с такою же силою. Сила, действующая на телегу, и сила, действующая на лошадь, равны; но так как телегу гораздо легче заставить катиться, чем волочить назад идущую лошадь, то вполне понятно, что телега катится в сторону лошади, а не лошадь притягивается к телеге. Поясним на числовом примере. Пусть лошадь тянет телегу с силою 20 пудов[8]; следовательно, и телега тянет к себе лошадь с силою 20 пудов. Для того, чтобы сообщить телеге некоторую скорость, сила в 20 пудов достаточна; но она далеко не достаточна, чтобы сообщить обратную скорость лошади, которая уже привела себя в движение по направлению вперед. Натягивая постромки и отталкиваясь ногами от земли, лошадь, в общем, развивает силу не в 20 пудов, а бóльшую – пудов в 30, скажем. Часть этой силы – 10 пудов – сообщает самой лошади движение вперед, а остальная часть, 20 пудов, преодолевает сопротивление телеги и приводит ее в движение. Закон равенства действия и противодействия здесь не нарушается: сила в 20 пудов, приложенная к телеге, вызывает равную противодействующую силу со стороны телеги, а сила в 10 пудов, с которой лошадь отталкивается от земли, вызывает равное противодействие со стороны земли.

Даже падение тел строго подчиняется закону равенства действия и противодействия. Яблоко падает на землю оттого, что его притягивает земной шар. Но с точно такою же силою и яблоко притягивает к себе нашу планету. Строго говоря, яблоко и Земля падают друг на друга, но скорость этого падения различна для яблока и для Земли. Одна и та же сила взаимного притяжения сообщает яблоку ускорение в 5 сажень, а земному шару – во столько раз меньше, во сколько раз масса Земли превышает массу яблока. Конечно, масса земного шара в неимоверное число раз больше массы яблока, и потому Земля получает перемещение настолько ничтожное, что практически его можно считать равным нулю. Оттого-то мы и утверждаем, что яблоко падает на землю, вместо того, чтобы говорить: «яблоко и Земля падают друг на друга».

Отчего погиб Святогор-богатырь?

Вы помните былину о Святогоре-богатыре, который вздумал поднять Землю? Архимед, если верить преданию, тоже намеревался, не будучи богатырем, совершить такой подвиг и искал лишь точки опоры для своего рычага. Позднее мы побеседуем о том, какой непредвиденный сюрприз ожидал бы гениального математика, если бы ему была дана эта желанная точка опоры. Но Святогор был силен и без рычага. Он мечтал лишь о том, чтобы было за что ухватиться, к чему приложить свои богатырские руки. Случай представился: богатырь нашел на земле «сумочку переметную», в которой сосредоточена была «вся тяга земная». Ухватившись за нее, Святогор стал тянуть вверх изо всей силы. Но сумочка не поддалась – зато сам Святогор по колено в землю увяз. «Тут ему было и кончание».

Если бы Святогору был известен закон равенства действия и противодействия, он сообразил бы, что его богатырская сила, приложенная к Земле, вызовет равную, а, следовательно, столь же колоссальную противодействующую силу, которая может втянуть его самого в землю.

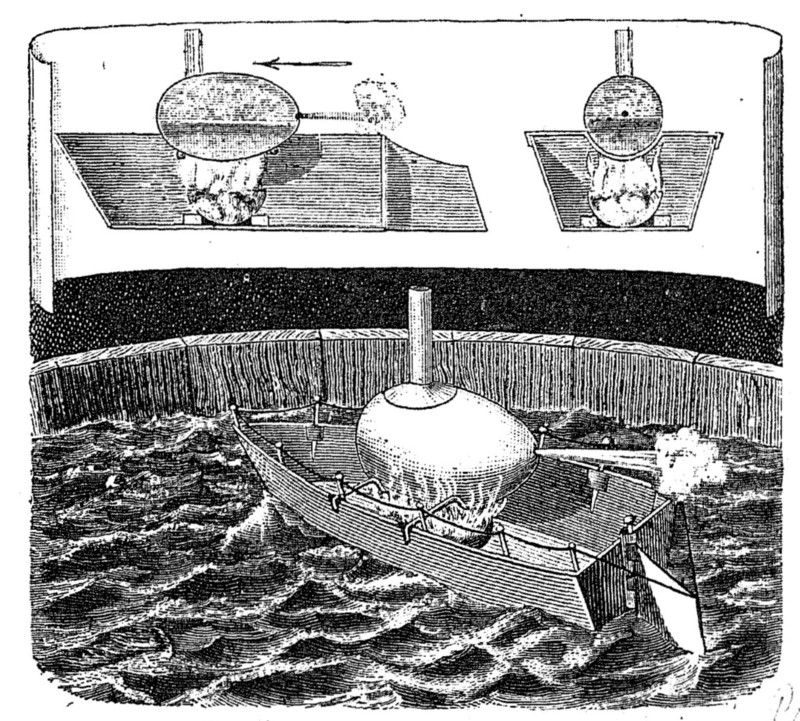
Рис. 8. Игрушечный пароходик из пустого яйца и бумаги, наглядно доказывающий, что «действие равно противодействию». В яйцо наливают воды, и этот миниатюрный паровой котел подогревается горением намоченной в спирте ваты.

Когда из отверстия в яйце начинает бить струя пара, весь пароходик, силою возвратного толчка, движется в противоположном направлении.

Во всяком случае, из былины видно, что народная наблюдательность давно подметила противодействие, оказываемое Землей, когда на нее опираются. Народ бессознательно применял закон равенства действия и противодействия за тысячелетия до того, как Ньютон впервые сформулировал его в своей бессмертной книге «Математические основы натуральной философии» (т. е. физики).

Можно ли двигаться, ни на что не опираясь?

Когда человек ходит, он отталкивается ногами от земли или от пола; все знают, что по очень гладкому полу, от которого нога не может оттолкнуться, ходить нельзя. Паровоз при движении отталкивается колесами от рельсов: если рельсы смазать маслом, паровоз останется на месте. Пароход лопастями своего винта отталкивается от воды. Аэроплан отталкивается от воздуха также при помощи винта – пропеллера. Словом, в какой бы стихии ни двигался предмет, он опирается на нее при своем перемещении. Но может ли тело двигаться, не имея никакой опоры вне себя?

Казалось бы, такое движение невозможно, и стремиться к нему все равно, что желать поднять самого себя за волосы. Но это только кажется: именно такое будто бы невозможное движение часто происходит на наших глазах. Правда, тело не может привести себя целиком в движение одними лишь внутренними силами, но оно может заставить некоторую часть своей массы двигаться в одну сторону, остальную же – в другую, противоположную. Сколько раз видели вы летящую ракету, – а задумывались ли над вопросом: почему она летит? Между тем, в ракете мы имеем прекрасный пример того рода движения, которое сейчас нас интересует.

Почему взлетает ракета?

Даже среди людей науки приходится нередко слышать превратное объяснение полета ракеты: она летит, мол, потому, что своими газами (которые образуются при горении пороха внутри нее) она отталкивается от воздуха. Однако, если пустить ракету в безвоздушном пространстве, она полетит нисколько не хуже, пожалуй, даже лучше, чем в воздухе. Истинная причина движения ракеты состоит в том, что, когда пороховые газы стремительно вытекают из нее вниз, сама трубка ракеты, по закону равенства действия и противодействия, отталкивается вверх. Здесь, в сущности, происходит то же, что и при выстреле из пушки: ядро летит вперед, а сама пушка отталкивается назад. Вспомните «отдачу» ружья и всякого вообще огнестрельного оружия! Если бы пушка висела в воздухе, ни на что не опираясь, она после выстрела двигалась бы назад с некоторой скоростью, которая во столько же раз меньше скорости ядра, во сколько раз ядро легче самой пушки. Когда 12-дюймовая[9] пушка, установленная в башне современного дредноута[10], извергает из своего жерла 30-пудовое ядро со скоростью 400 саженей в секунду, – все огромное судно, весящее более миллиона пудов, отталкивается назад со скоростью одного дюйма в секунду. Основываясь на том же правиле механики, герои романа Жюля Верна «Вверх дном» задумали «выпрямить» земную ось выстрелом из колоссальной пушки. Ракета – та же пушка, только извергает она не ядра, а пороховые газы.

По той же причине вертится и так называемое «китайское колесо»: при горении пороха в трубках, прикрепленных к колесу, газы вытекают в одну сторону, сами же трубки (а с ними и колесо) получают обратное движение.

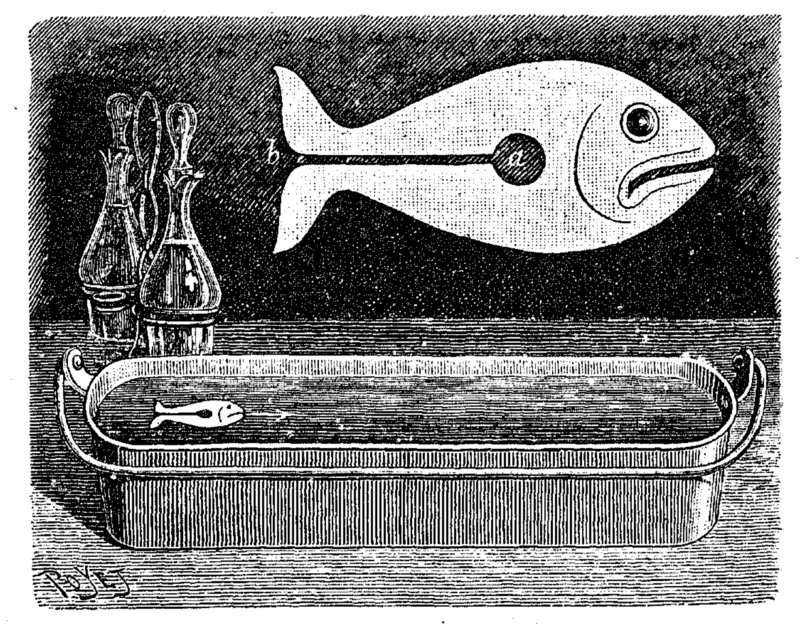
Рис. 9. Плавающая рыбка, вырезанная из визитной карточки. Это маленькое изобретение Тома Тита основано на законе противодействия: если в вырезанный кружок а капнуть масла, то, свободно растекаясь по воде вдоль канала от а к b, масляная пленка будет оказывать давление в обратную сторону и заставит рыбку двигаться в направлении ее головы.

Есть множество игрушек, основанных на этом начале. Игрушечный пароход (Рис. 8.), изобретенный остроумным Томом Титом, движется потому, что пар, вытекая в одну сторону, толкает весь пароход в обратную. Если в прорезь картонной рыбки, положенной на воду (см. рис. 9), капнуть масла, она поплывет в направлении, обратном тому, по которому растекается масляная пленка. Наконец, мы знаем, что самая древняя в мире паровая машина, изобретенная Героном Александрийским еще в III век до Р. X., была устроена по тому же принципу: пар из котла αβ (рис. 10) поступал по трубке εζη в шар, вращающийся на горизонтальной оси; вытекая затем из коленчато-изогнутых трубок, пар толкал эти трубки в обратном направлении, – и шар начинал вращаться. К сожалению, Геронова паровая турбина в древности оставалась только любопытной игрушкой, не более, так как дешевизна труда живых двигателей – рабов – никого не понуждала к практическому использованию мертвых машин.

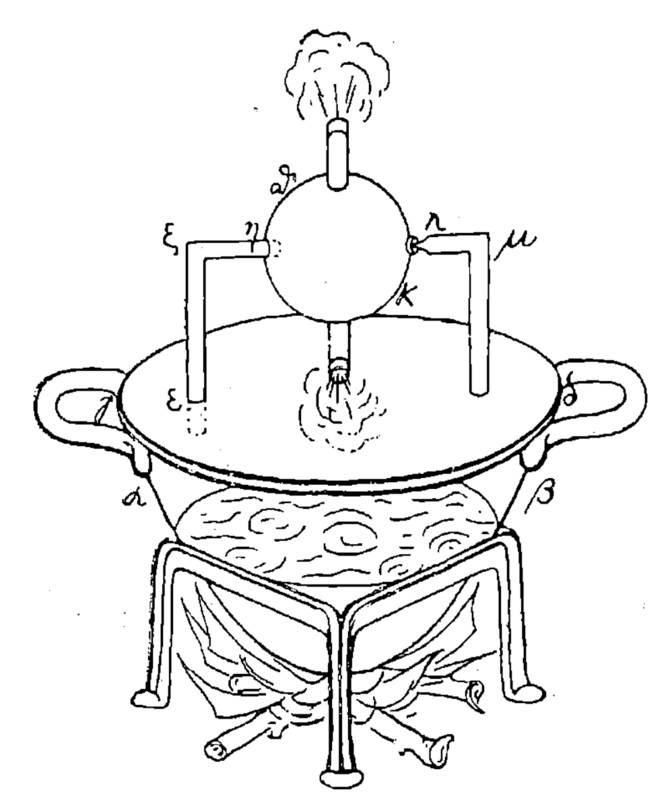
Рис. 10. Самая древняя в мире паровая машина (турбина), изобретенная Героном Александрийским в III веке до Р. X.

Как движется каракатица?

Вероятно, вам странно будет слышать, что существует множество живых существ, для которых мнимое «вытаскивание самого себя за волосы» является весьма обычным способом перемещения.

Каракатица и вообще большинство головоногих моллюсков движутся в воде таким образом: они набирают воду в жаберную полость через боковую щель и особую воронку впереди тела и затем энергично выбрасывают струю воды через упомянутую воронку; при этом они получают обратный толчок, достаточный для того, чтобы довольно быстро плавать задней стороной тела вперед. Каракатица может, впрочем, направить трубку воронки вбок или назад и, энергично выдавливая из нее воду, двигаться в любом направлении.

На том же основано и движение медузы: сокращением мускулов она выталкивает из-под своего колоколообразного тела воду, получая толчок в обратном направлении. Сходным приемом пользуются при движении сальпы, личинки стрекоз и многие другие водные животные. А мы еще сомневались, можно ли так двигаться!

Рис. 11. Как передвигается в воде каракатица. С силою выбрасывая из своего тела набранную воду, животное получает толчок, который и относит его назад.

К звездам на ракете

Что может быть заманчивее, чем покинуть наш земной шар и путешествовать по необъятной вселенной, перелетать с планеты на планету, со звезды на звезду? Сколько фантастических романов написано на эту тему! Кто только не увлекал нас в воображаемое путешествие по небесным светилам! Вольтер в «Микромегасе», Жюль Верн в «Путешествии на Луну» и «Гектор Сервадак», Уэллс в «Первых людях на Луне» и множество их подражателей совершали воображаемые путешествия на небесные светила, – конечно, в мечтах. В действительности же мы – увы! – остаемся пленниками земного шара[11].

Неужели же нет возможности осуществить эту давнишнюю мечту человечества? Неужели все остроумные проекты, с такой заманчивой правдоподобностью изображенные в романах, на самом деле неисполнимы? В дальнейшем мы еще будем беседовать о фантастических проектах межпланетных путешествий; теперь же познакомимся с единственным серьезным проектом подобных путешествий, предложенным русским ученым К. Э. Циолковским.

Можно ли долететь до Луны на аэроплане? Конечно, нет: аэропланы и дирижабли движутся только потому, что опираются о воздух, отталкиваются от него, – а между Землей и Луной воздуха нет. В межпланетном пространстве вообще нет никакой материальной среды, на которую мог бы опереться «межпланетный дирижабль». Значит, надо придумать такой снаряд, который мог бы двигаться, ни на что не опираясь.

Мы уже знакомы с подобным снарядом в виде игрушки – это ракета. Так отчего бы не устроить огромную ракету, с особым помещением для людей, съестных продуктов, запасов воздуха и всем прочим? Вообразите, что люди в этой ракете везут с собой большой запас взрывчатых веществ и, подобно каракатице, могут направлять истечение газов в любою сторону. Вы получите настоящий управляемый небесный корабль, на котором можно плыть в беспредельном океане мирового пространства, полететь на Луну, на планеты, к звездам… Пассажиры могут посредством ряда отдельных мелких взрывов увеличивать скорость этого межпланетного дирижабля с необходимой постепенностью, чтобы возрастание скорости было безвредно для них. При желании спуститься на какую-нибудь планету они могут постепенно уменьшить скорость снаряда и тем ослабить силу падения. Наконец, пассажиры могут таким же путем возвратиться и обратно на Землю. Для всего этого надо только захватить с собой достаточный запас взрывчатых веществ.

«Зачем же дело стало? – спросите вы. – Почему же никто не сооружает такой гигантской ракеты и не отправляется исследовать глубины межзвездных пространств?»

Остановка в том, что мы пока не имеем достаточно сильного взрывчатого вещества. Чтобы сообщить исполинской ракете скорость, потребную для преодоления силы тяжести, нужно взрывчатое вещество силою в 10–15 раз больше, чем у пироксилина[12]. Такого вещества мы еще не знаем; не имеем мы и достаточно крепких материалов для «небесной ракеты».

Но то, что невозможно сегодня, может осуществиться завтра. Человечество уже было однажды в подобном положении: когда найден был принцип летания по способу парения, для сооружения аэроплана не хватало лишь достаточно сильного двигателя и достаточно прочных материалов. Прошло 15 лет, – и что же? Аэропланы высоко реют в воздухе, перелетая через горы и моря; мы присутствовали уже и при воздушной войне… Так отчего не допустить, что когда-нибудь люди полетят к звездам в огромном ракетообразном снаряде?

Глава вторая

Силы. Работа. Трение

Задача о лебеде, раке и щуке

История о том, как «лебедь, рак да щука везти с поклажей воз взялись» – известна, конечно, всем. Но пробовали ли вы проверять этот рассказ на основании законов механики? Результат проверки получается, сверх ожидания, вовсе не похожий на вывод баснописца.

Будем рассуждать так, словно перед нами обыкновенная задача на сложение нескольких сил, действующих под углом одна к другой. Направление сил определено в басне:

…Лебедь рвется в облака,

Рак пятится назад, а щука тянет в воду.

Это значит, что одна сила, тяга лебедя (А), направлена вверх; другая, тяга щуки (В) – вбок; третья, тяга рака (С) – назад. Не забудем, что существует еще четвертая сила, вес воза, которая направлена отвесно вниз. Крылов утверждает, что «воз и ныне там», – другими словами, что равнодействующая всех четырех сил в данном случае равна нулю.

Так ли это?

Посмотрим. Лебедь, рвущийся к облакам, не только не мешает работе рака и щуки, но даже помогает им: тяга лебедя, направленная против силы тяжести, облегчает вес воза, а может быть, даже и вполне уравновешивает его – ведь груз невелик («поклажа бы для них казалась и легка»). Остаются всего две силы: тяга рака и тяга щуки. О направлении этих сил говорится, что «рак пятится назад, а щука тянет в воду». Само собою разумеется, что вода находилась не впереди воза, а сбоку (не потопить же воз собрались крыловские труженики!). Но если силы рака и щуки направлены под углом одна к другой, то равнодействующая их никак не может равняться нулю.

Рис. 13. Задача о лебеде, раке и щуке, решенная по правилам механики. – Равнодействующая D должна сдвинуть воз с места.

Поступая по правилам механики, строим на обеих силах В и С параллелограмм; диагональ его D дает направление и величину искомой равнодействующей. Ясно, что эта равнодействующая сила должна сдвинуть воз с места, тем более что вес воза вполне или частью уничтожается тягою лебедя (трением мы здесь, ради простоты, пренебрегаем). Другой вопрос – в какую сторону сдвинется воз: вперед, назад или в бок; это зависит от соотношения сил и от величины угла между ними.

Во всяком случае, как видите, Крылов едва ли мог с уверенностью утверждать, что «возу все нет ходу», что «воз и ныне там».

Вопреки Крылову

Мы только что видели, что житейское правило Крылова: «когда в товарищах согласья нет, на лад их дело не пойдет» – не применимо в механике. Силы могут быть направлены не в одну сторону и, несмотря на это, давать известный результат.

Мало кто знает, что даже усердные труженики-муравьи, которых тот же Крылов восхваляет, как образцовых работников, трудятся совместно именно по осмеянному баснописцем рецепту. И все же дело у них, в общем, идет на лад. Выручает опять-таки закон сложения сил. Если вы станете внимательно следить за муравьями во время работы, то очень скоро убедитесь, что разумное сотрудничество их – только кажущееся; на деле же каждый муравей работает сам для себя, вовсе не думая помогать товарищу.

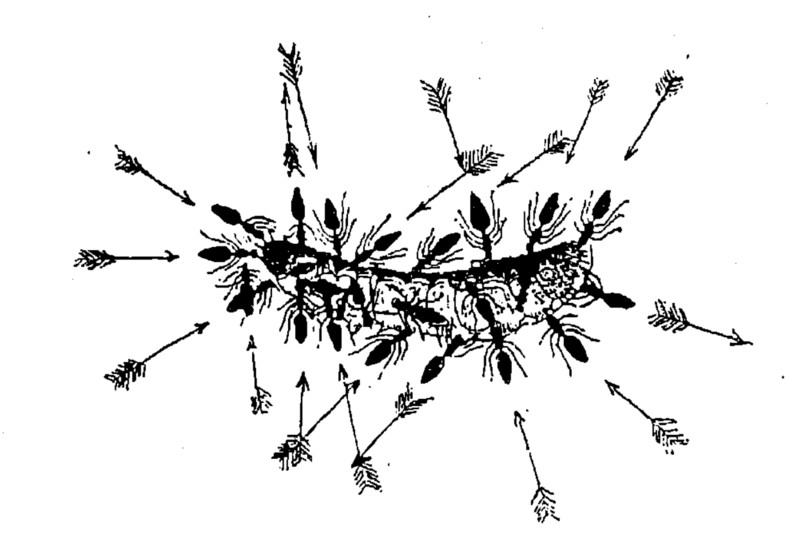
Рис. 14. Каждый муравей тянет ношу в свою сторону. – Стрелки показывают направление тяги.

Вот как описывает работу муравьев один исследователь[13]:

«Если крупную добычу тащит десяток муравьев по ровному месту, то все действуют одинаково, и получается видимость сотрудничества. 

Но вот добыча, например гусеница, зацепилась за какое-либо препятствие, за стебель травы, за камешек. Дальше вперед тащить нельзя, надо обогнуть. И тут с ясностью обнаруживается, что каждый муравей, по-своему и ни с кем из «товарищей» не сообразуясь, старается справиться с препятствием (см. рис. 14 и 15). Один тащит направо, другой – налево; один толкает вперед, другой, рядом с ним стоящий, тянет назад. Переходят с места на место, хватаются за гусеницу в другом месте, и каждый толкает или тянет по-своему. Когда случится, что силы работающих сложатся так, что в одну сторону будут двигать гусеницу 4 муравья, а в другую – 6, то гусеница, в конце концов, и двинется именно в сторону этих 6-ти, несмотря на противодействие 4-х».

Приведем еще поучительный пример, наглядно иллюстрирующий это мнимое сотрудничество муравьев. На рис. 16 изображен прямоугольный кусочек сыра, за который ухватилось 25 муравьев. Сыр медленно подвигался в направлении, указанном стрелкою, и можно было думать, что передняя шеренга муравьев тянет ношу к себе, задняя – толкает ее вперед, боковые же муравьи помогают и тем и другим. Однако это совершенно не так, в чем нетрудно убедиться: отделите ножом всю заднюю шеренгу – и ноша поползет гораздо быстрее. Ясно, что эти 11 муравьев тянули назад, а не вперед: каждый из них старался повернуть ношу так, чтобы, пятясь назад, волочить ее к гнезду. Значит, задние муравьи не только не помогали передним волочить ношу, но усердно мешали им, парализуя их усилия. Для того, чтобы волочить этот кусочек сыра, достаточно было бы усилий всего четырех муравьев, но несогласованность действий и взаимные помехи приводят к тому, что его едва тащат 25 муравьев!

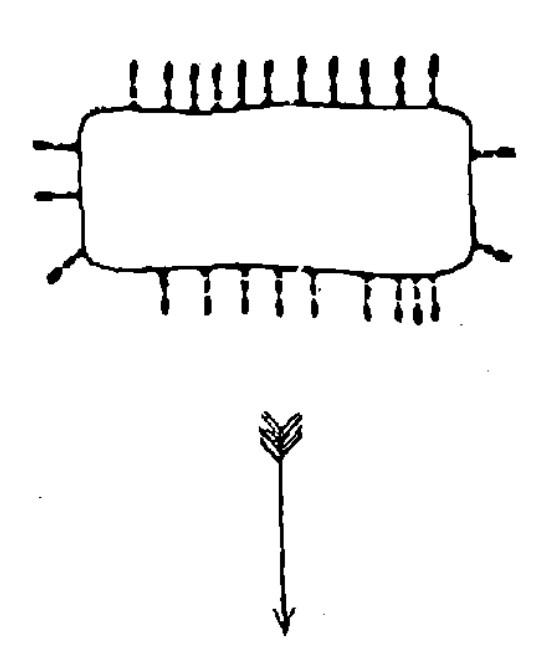
Рис. 16. Муравьи стараются притащить кусок сыра к муравейнику, расположенному в направлении стрелки.

Легко ли сломать яичную скорлупу?

Если вы думаете, что яичная скорлупа очень хрупкая и нежная вещь, то попробуйте раздавить яйцо между ладонями, напирая на его острые концы. Вам удастся это далеко не так легко, как вы воображаете: нужно немалое усилие, чтобы сломить скорлупу при подобных условиях.

Столь необычайная крепость яичной скорлупы зависит исключительно от его выпуклой формы и объясняется совершенно так же, как и прочность всякого рода сводов и арок.

На прилагаемом чертеже (рис. 17) изображен разрез небольшого каменного свода над окном. Груз S (т. е. вес вышележащих частей кладки), напирающий на клинообразный средний камень свода, давит вниз с силою, которая обозначена на чертеже стрелкой А. Но сдвинуться вниз камень не может, вследствие своей суживающейся формы, – и он давит на соседние камни. Другими словами, сила А разлагается, по правилу параллелограмма, на две боковые силы, обозначенные стрелками С и В; силы эти уничтожаются сопротивлением прилегающих камней, в свою очередь зажатых между соседними. Таким образом, сила, давящая на свод снаружи, не может его разрушить. Зато сравнительно легко разрушить его силой, действующей изнутри. Это и понятно, так как клинообразная форма камней, мешающая им опускаться, нисколько не мешает им подниматься.

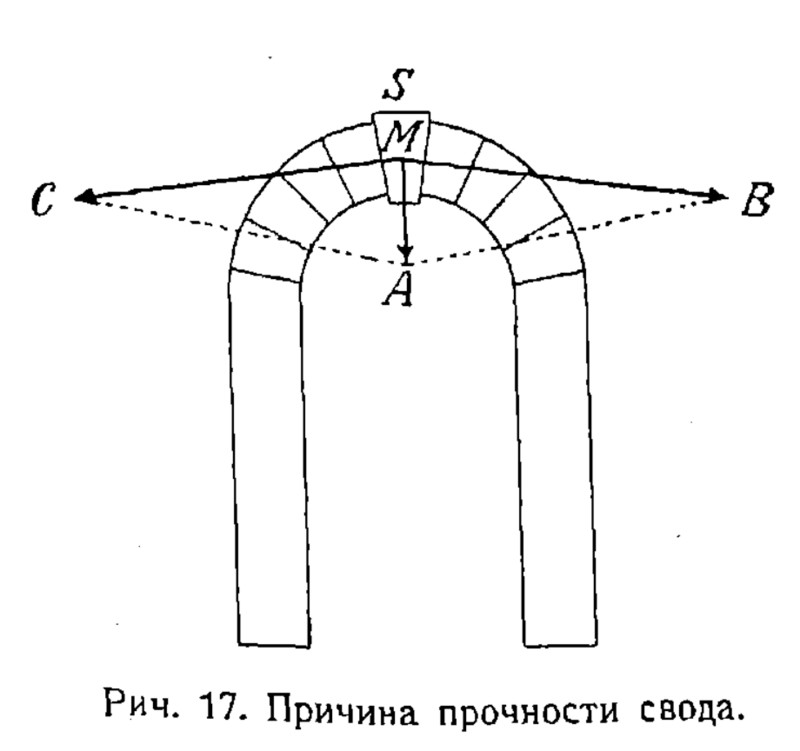
Рис. 17. Причина прочности свода.

Скорлупа яйца есть тот же свод, только сплошной, а не составленный из отдельных частей. При давлении снаружи он разрушается далеко не так легко, как можно бы ожидать от такого хрупкого материала. Теория доказывает, что наибольшее сопротивление давлению оказывает свод не строго полушаровидный, а именно такой формы, как выпуклость на остром конце яйца. Можно поставить ножки довольно тяжелого стола на четыре сырых яйца, и последние не раздавятся. (Для устойчивости яиц и увеличения площади давления надо снабдить яйца гипсовыми расширениями на концах; гипс легко пристает к известковой скорлупе.)

Теперь вы понимаете, почему наседке не приходится опасаться сломить скорлупу яиц тяжестью своего тела. И в то же время, слабый птенчик, желая выйти из своей природной темницы, без труда пробивает скорлупу клювиком: тонкий известковый свод не может противостоять давлению изнутри.

С легкостью разламывая скорлупу яйца боковым ударом, мы и не подозреваем, как прочна она, когда сила действует на нее при естественных условиях, и какой надежной броней природа защитила развивающееся в ней живое существо.

Загадочная, почти чудесная прочность электрических лампочек, казалось бы столь нежных и хрупких, объясняется совершенно так же, как и прочность яичной скорлупы. Их необыкновенная крепость станет еще поразительнее, если вспомним, что они почти абсолютно пусты, и давлению внешнего воздуха ничто не противодействует изнутри; между тем, на пористую стенку куриного яйца атмосферное давление, конечно, не оказывает никакого влияния. А величина давления воздуха на электрическую лампочку весьма не мала. Шарообразная лампочка, поперечником, например, в 20 сантиметров, имеет поверхность в 1 260 см². На каждый сантиметр, как известно, воздух давит с силою 1 килограмма: эта дает на всю лампочку давление 1 260 килограммов, или 75 пудов! Вот какое огромное давление непрерывно выдерживает тонкая стеклянная пленка электрической лампочки! Достаточно четвертой части этого давления, чтобы, действуя изнутри, разнести лампочку вдребезги.

На парусах против ветра

Для всякого не моряка представляется непостижимым, как могут парусные суда идти «против ветра». Правда, моряк скажет вам, что прямо против ветра на парусах идти нельзя, а можно двигаться под очень острым углом к направлению ветра. Но угол этот так мал (12°), что представляется, пожалуй, одинаково непонятным – плыть ли прямо против ветра, или под углом к нему в 12°.

Для теории это, однако, небезразлично, и мы сейчас объясним, каким образом можно силою ветра идти навстречу ему под небольшим углом. Сначала рассмотрим, как вообще действует ветер на парус, т. е. куда он толкает парус, когда дует на него в каком-либо направлении. Если вы не моряк, то, вероятно, думаете, что ветер всегда толкает парус в ту сторону, куда дует. Но это не так: куда бы ни дул ветер, он толкает парус перпендикулярно к его плоскости. В самом деле: пусть ветер дует в направлении, указанном стрелками на рис. 18; линия АВ обозначает парус. Так как ветер напирает равномерно на всю поверхность паруса, то мы можем заменить давление ветра силой R, приложенной к середине паруса. Эту силу мы разложим на две: силу Q, перпендикулярную к парусу, и силу Р, направленную вдоль него. Последняя сила будет скользить по парусу, не толкая его, так как трение ветра о полотно очень незначительно. Остается только сила Q, которая толкает парус в перпендикулярном к нему направлении.

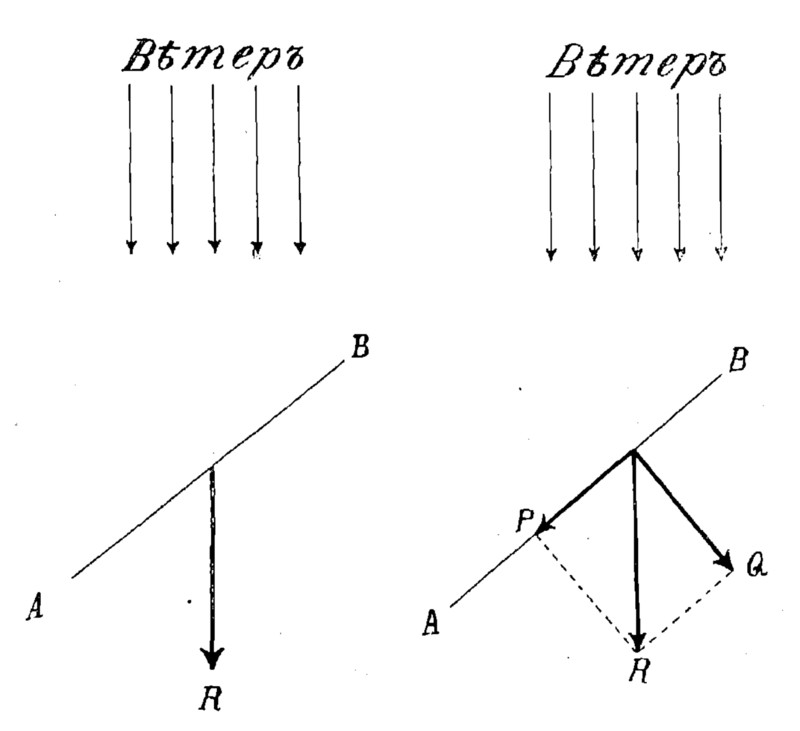
Рис. 18. Почему ветер всегда толкает парус под прямым углом к его плоскости.

Итак, под каким бы углом к парусу ни дул ветер, он во вся́ком случае напирает под прямым углом к парусу.

Зная это, мы уже без труда поймем, как может парусное судно идти под очень острым углом навстречу ветру. Пусть линия KK (рис. 19) изображает килевую линию судна. Ветер дует под острым углом к этой линии в направлении, указанном рядом стрелок. Линия АВ изображает парус; его помещают так, чтобы плоскость его делила пополам угол между направлением киля и направлением ветра. Проследите на рис. 19 за разложением сил. Напор ветра на парус мы изображаем силой Q, которая, как мы знаем, должна быть перпендикулярна к парусу. Силу эту разложим на две: силу R, перпендикулярную к килю, и силу S, направленную вперед, вдоль килевой линии судна. Так как движение судна в направлении R вызывает сильное сопротивление воды (киль в парусных судах делается очень глубоким), то сила R почти полностью уничтожается; остается одна лишь сила S, которая, как видите, направлена вперед, а следовательно, подвигает судно под углом, как бы навстречу ветру.

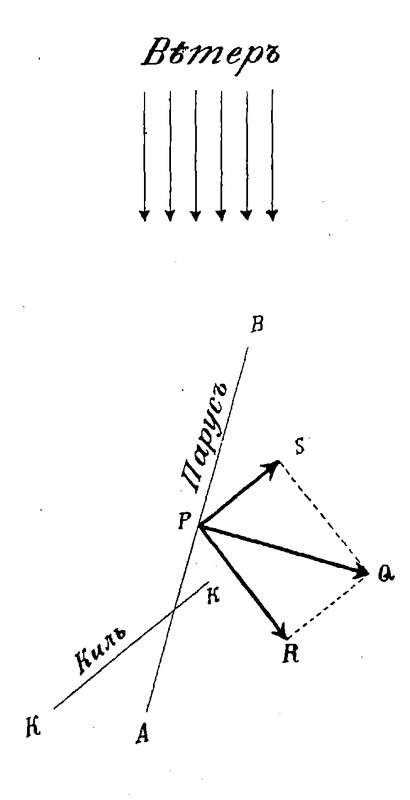
Рис. 19. Разложение сил, объясняющее, почему возможно идти на парусах против ветра.

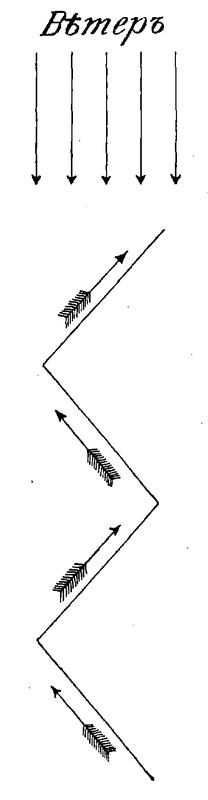
Рис. 20. «Лавирование» парусного судна.

Моряки заметили, что наименьшая величина угла ВРS, под которым можно идти против ветра, равна 11–12 градусам. Из чертежа видно, что скорость такого движения против ветра очень невелика (в сравнении с силою ветра), так как при этом используется лишь часть полного напора ветра на паруса. Но как бы то ни было, идти против ветра можно. Обыкновенно это движение выполняется зигзагами, как показывает рис. 20. На языке моряков такое движение судна называется «лавированием».

Мог ли Архимед поднять Землю?

«Дайте мне точку опоры – и я подниму всю Землю», – сказал, если верить преданию, Архимед, когда открыл закон рычага. И действительно, нет такой тяжести, которую нельзя было бы поднять самой слабой силой, если воспользоваться рычагом: стоит только приложить эту силу к очень длинному плечу рычага, а короткое плечо заставить действовать на груз. Поэтому может показаться, что Архимед был вполне прав в своем смелом утверждении: напирая на чрезвычайно длинное плечо рычага, он мог бы силою своих рук поднять тяжесть, равную весу всего земного шара.

Но если бы великий механик древности знал, как огромен вес земного шара, он, вероятно, воздержался бы от своего горделивого восклицания. Вообразим на мгновение, что ему дана та точка опоры, которую он так тщетно искал; вообразим далее, что он изготовил рычаг нужной длины. Знаете ли, сколько времени понадобилось бы ему, чтобы поднять земной шар хотя бы на один дюйм? Десять биллионов лет! Сто тысяч миллионов веков!..

В самом деле, Земля весит круглым числом – 365.000.000.000.000.000.000.000 пудов.

Рис. 21. Архимед поднимает Землю. (Из старинного сочинения по механике.)

Если человек может прямо поднять только пять пудов, то чтобы поднять Землю, ему понадобится приложить свои руки к длинному плечу рычага, которое больше короткого в 73.000.000.000.000.000.000.000 раз!

Простой расчет убедит вас, что пока конец короткого плеча поднимется на 1 дюйм, другой конец опишет во вселенной огромную дугу в 1.740.000.000.000.000.000 верст!

Вот какой невообразимо длинный путь должна была бы пройти рука Архимеда, чтобы поднять земной шар только на один дюйм. Сколько же времени понадобилось бы ему для совершения этого подвига? Считайте, что он способен в секунду поднять пятипудовую гирю на одну сажень; тогда, чтобы пройти путь в 1.740.000 биллионов верст и тем поднять нашу планету на один дюйм, ему понадобилось бы не менее десяти биллионов лет!

Следовательно, если бы даже Архимед налегал на рычаг целый миллион лет, он не поднял бы Землю даже на толщину волоса. И если бы рука Архимеда пробегала этот путь с самой большой скоростью, какую только мы наблюдаем в природе, именно – со скоростью света (280.000 верст в секунду), то и тогда понадобилось бы полтораста тысяч лет, чтобы поднять Землю на один дюйм! За всю свою жизнь Архимед даже при такой фантастически быстрой работе не успел бы поднять земной шар на сотую долю толщины волоса…

И никакие ухищрения гениального ученого не помогли бы ему сократить этот срок. «Золотое правило механики» гласит, что на всякой машине выигрыш в силе неизбежно сопровождается соответствующей потерей в скорости, т. е. во времени.

Жюль-верновский силач и – формула Эйлера

Вы помните у Жюля Верна силача-атлета Матифу? «Великолепная голова, пропорциональная исполинскому росту; грудь, похожая на кузнечный мех; ноги, как хорошие бревна; руки – настоящие подъемные краны, с кулаками, похожими на молоты»… Вероятно, из всех подвигов этого силача, описанных в романе «Матиас Сандорф», вам более других памятен поразительный случай со спуском судна «Trabocolo», когда гигант Матифу силою своих могучих рук задержал спуск целого корабля.

Вот как рассказывает романист об этом подвиге:

«Судно, освобожденное уже от подпорок, которые поддерживали его по бокам, было готово к спуску. Хотя оно имело не более 50 тонн водоизмещения, но представляло значительную массу, вследствие чего нужно было принять все необходимые предосторожности. Все уже было готово и приспособлено для спуска, ожидали только сигнала. Достаточно было отнять швартов[14], чтобы судно начало скользить вниз. Уже с полдюжины плотников возилось под килем судна, стараясь приподнять его, покачнуть и направить его путь к морю. Среди всеобщей тишины зрители с живым любопытством следили за операцией. В этот момент, обогнув береговой выступ, который прикрывает с юга порт Гравозу, появилась увеселительная яхта. Чтобы войти в порт, яхта должна была пройти перед верфью, где подготовлялся спуск «Trabocolo», и как только она подала сигнал, пришлось, во избежание всяких случайностей, задержать спуск, чтобы снова приняться за дело после прохода яхты в канал. Если бы суда, – одно, стоявшее поперек, другое, подвигающееся с большой быстротой, – столкнулись, яхта погибла бы.

Рабочие перестали стучать молотками, а один из них, который должен был отнять швартов, получил приказание подождать. Все взоры были устремлены на грациозное судно, белые паруса которого казались позолоченными в косых лучах солнца. Скоро яхта очутилась как раз против верфи, где замерла тысячная толпа любопытных. Вдруг раздался крик ужаса: «Trabocolo» закачалось и пришло в движение в тот самый момент, когда яхта повернулась к ней штирбортом[15]! Оба судна готовы были столкнуться; не было ни времени, ни возможности помешать этому столкновению. В ответ на испуганные крики зрителей раздался крик экипажа яхты. Тем временем «Trabocolо» быстро скользило вниз по наклону… Белый дымок, появившийся вследствие трения, закрутился перед его передней частью, тогда как корма погрузилась уже в воду бухты (судно спускалось кормой вперед).

Вдруг появляется человек, схватывает швартов, висящий у передней части «Trabocolo», и старается удержать его, пригнувшись к земле. В одну минуту он наматывает швартов на вбитую в землю железную тумбу и, рискуя быть раздавленным, держит с нечеловеческой силой в руках канат в продолжение 10 секунд. Наконец, швартов обрывается. Но этих 10 секунд было достаточно: «Trabocolo», погрузившись в воду, только слегка задело яхту и пронеслось вперед.

Яхта была спасена. Что касается человека, которому никто не успел даже прийти на помощь – так быстро и неожиданно все это произошло, – то это был Матифу».

* * *

Легко представляю себе, как изумился бы талантливый автор «Матиаса Сандорфа», если бы ему сказали, что для совершения подобного подвига не нужно вовсе быть великаном и обладать, как Матифу, «силою тигра»: каждый находчивый человек, при самой обыкновенной силе мышц, мог бы без труда сделать то же самое!

Механика учит, что при скольжении каната, обвитого на тумбе, трение возрастает в сильнейшей степени. Чем большее число раз навить канат, тем трение больше; правило возрастания трения таково, что с увеличением числа завитков в арифметической прогрессии трение растет в геометрической прогрессии. Поэтому даже слабый ребенок, держа за свободный конец каната, 3–4 раза навитого на неподвижный вал, может уравновесить огромную тяжесть. Подростки, служащие на речных пароходных пристанях, именно этим приемом останавливают подходящие к пристаням пароходы с сотней пассажиров. Помогает им здесь не феноменальная сила их рук, а изученная знаменитым Эйлером зависимость величины трения от числа оборотов веревки вокруг столба.

Для тех из читателей, которых не пугает сжатый язык алгебраических выражений, приводим здесь эту поучительную формулу Эйлера:

F = fе^kα.

Здесь F – та сила, против которой направлено наше усилие f. Буквой e обозначено основание натуральных логарифмов, которое равно 2,718…; k – коэффициент трения между канатом и тумбой. Буквой α обозначен «угол навивания», т. е. отношение длины дуги, охваченной веревкой, к радиусу этой дуги.

Попробуем применить эту формулу к тому случаю, который описан у Жюля Верна. Результат получится поразительный. Силой F в данном случае является сила тяги судна, скользящего по доку. Вес судна нам известен: 50 тонн, т. е. 3000 пудов. Пусть наклон дока ¹/₁₀; тогда на канат действовал не полный вес судна, а ¹/₁₀ его, т. е. 300 пудов. Итак, F=300 пудов.

Далее, величину k – коэффициента трения каната о железную тумбу – будем считать равной ¹/₃. Величину α легко определим, если примем, что Матифу обвил канат вокруг тумбы всего три раза. Тогда:

α = 3×2πr/r = 6π.

Подставив все эти значения в приведенную выше формулу Эйлера, получим уравнение:

300 = f·2,718^{6π 1/3} = f·2,718^2π.

Неизвестное f (т. е. величину необходимого усилия) можно определить из этого уравнения, прибегнув к помощи логарифмов:

lg300 = lg f + 2π lg2,718;

откуда:

f = 0,6 пуда = 24 фунта[16].

Итак, великану Матифу, чтобы совершить свой подвиг, достаточно было тянуть канат с силою всего 24 фунтов!

Не думайте, что эта цифра – 24 фунта – только теоретическая и что на самом деле потребуется гораздо большее усилие. Напротив, у нас получился результат даже чересчур значительный: при пеньковой[17] веревке и деревянной свае усилие потребуется до смешного ничтожное. Лишь бы веревка была достаточно крепка и могла выдержать натяжение, – тогда даже ребенок, благодаря формуле Эйлера, мог бы, навив веревку 3–4 раза, не только повторить подвиг жюль-верновского исполина, но и превзойти его.