Оглавление

Часть первая для школьников 12+

Предисловие

Посвящается нашим детям и внукам

Могут ли обычные школьники сделать научное открытие? Какой должна быть современная школа? Кого, чему и как учить? — ответы на эти вопросы имеют важное значение.

Сократите в микрорайоне или посёлке школу — и сразу получите рост преступности, причём не только подростковой. Выходит, что без воспитания подрастающего поколения нет будущего. Сейчас в мире происходит борьба за умы и души молодых людей через Интернет и мобильные устройства. Забыть собственную историю и достижения, засорить мозги людей мусором, «подсадить на иглу» развлекательных информационных потоков, оболванить, заставить купить ненужное, но престижное, сузить выбор до мнений непоколебимых экспертов и «авторитетов», набравших миллионы «лайков» — вот задача наших «Западных друзей».

Наше общество становится очень жёстким и консервативным в выражении свободы собственного мнения: всё заранее уже решено, выбор уже сделан на уровне подсознания. В качестве компенсации предоставляется лишь свобода в изощрённых пороках: переплюнь всех, опереди и шокируй даже ценой риска для жизни.

Вызов, который сделан в этой книге, показывает на одном конкретном примере, как этому можно и нужно противостоять. Автор поставил задачу развеять господствующие мифы о научном превосходстве стран большого Запада, о научной этике, о беспристрастности и просветительской миссии по всей Земле. Проще говоря, есть «правильные народы», обучающие отсталые, «неправильные народы» — и таков порядок вещей. На деле оказывается совсем не так.

Просто формулируемая Великая теорема Ферма и её наглядное доказательство, понятное всем, кто имеет лишь школьную подготовку, стала своего рода тестом на несостоятельность этих мифов. История для адептов Большого Запада вышла совсем не красивая и даже комичная.

Но пройдёт ещё не мало времени, прежде, чем простое доказательство Великой теоремы Ферма, будет признано миллиардами обычных людей — слишком силён поток дезинформации из разряда оболванивания потребителя.

Но даже, если эта книга заставит думать самостоятельно всего несколько человек и будет стимулировать их во всём следовать собственному выбору, уважать свой народ и свою историю, то автор будет считать свою задачу исполненной.

России. Новосибирск. Сургут. 2020 — 2021 г.

История Великой теоремы

Великая Теорема Ферма была сформулирована Пьером де Ферма в 1637 г., она гласит, что уравнение:

aⁿ + bⁿ = cⁿ не имеет решений в целых, кроме нулевых значений, при n> 2

Когда n = 2, мы имеем дело с привычной теоремой Пифагора, при этом существует бесконечное число решений уравнения в целых числах — Пифагоровы тройки. Примеры Пифагоровых троек известны:

(3, 4, 5); (5, 12, 13); (15, 8, 17) и др.

Со времён Евклида был найден целый ряд способов генерации Пифагоровых троек. Из школьного куса математики легко понять, что Пифагоровы тройки имеют наглядную интерпретацию в терминах геометрии рациональных точек на единичной окружности. Эйлер в 1770 году доказал теорему (1) для случая n=3, Дирихле и Лежандр в 1825 — для n=5, Ламе — для n=7. Куммер показал, что теорема верна для всех простых n, меньших 100.

В сентябре 1994 года профессор Принстонского университета Эндрю Уайлс доказал Великую теорему, для всех n, но это доказательство, насчитывающее свыше ста сорока страниц, понятных лишь профильным специалистам в теории чисел, нельзя уместить на полях перевода «Арифметики» Диофанта, «если бы они были немного шире», по выражению самого Пьера де Ферма, утверждавшего, что он «нашёл поистине чудесное доказательство, но поля здесь слишком узки, чтобы вместить его».

Необычайная красота и лаконичность формулировки Великой теоремы Ферма заставляют искать наглядное решение. Итак, для n ≥ 3 Пифагоровых троек найти ещё никому не удалось. Почему?

Глава 1 Необычная встреча

— Итак, Матвей, за что Вы его так сильно ударили? — обратился профессор Борщов со своей обычной доброй улыбкой. За столом в комнате примирения сидели подравшиеся одноклассники: Матвей Строев и Сергей Тагильцев.

— Я его не ударил, а бросил через бедро… с подсечкой — чуть смущёно ответил Матвей, — но я не ожидал, что он упадёт так неудачно.

— Так за что? — уже строже переспросил Борщов.

— Ну он оскорбил меня… он назвал меня китайцем — Матвей посмотрел на Сергея с сожалением.

— А это было действительно так? — обратился Борщов к Сергею.

— Да, мы спорили о музыке, о Рей Чарльзе, ну о том самом слепом пианисте из США и мы… то есть я, неожиданно перешли на личности — Сергей потупился и замолчал. — ну словом, я больно и неудачно упал от его приёма. Я уже не обижаюсь на Матвея.

— Я тоже, — слегка улыбнувшись сказал Матвей.

Борщов облеченно откинулся на стуле и резюмировал:

— Таким образом инцидент исчерпан?

— Да, можно считать исчерпанным, — ответили разом Матвей и Сергей, оба они уже посматривали на дверь комнаты.

— Можно мне выразить Вам свои пожелание на будущее? — остановил их жестом Борщов.

— Да, — последовал общий ответ мальчиков.

— Нужно уметь контролировать свои эмоции. Ответ должен быть соразмерен. Лучше ограничиться шуткой, без применения физической силы, потому что даже ненароком можно покалечить человека и всю жизнь потом каяться. — Борщов посмотрел на Матвея. — А словом можно и убить… это я к тому, что есть такие обидные слова которые вспыхивают как порох, — Борщов уже смотрел в сторону Сергея. — пожар легче предупредить, чем потушить. Словом, каждый из Вас извлёк из этого ЧП свой урок. Надеюсь, что обид не осталось?

— Да, мы теперь вместе будем ходить заниматься борьбой — ответил Сергей с улыбкой.

— Вот и отлично! — облегченно подытожил Борщов. — Я не буду рекомендовать на педагогическом совете прекратить дело примирением. И ещё минутку, коллеги, распишитесь в этом журнале… здесь и вот здесь.

Матвей и Сергей стремительно проследовали на второй завтрак, который начинался после второй пары занятий аккуратно в 12:20 в фойе школы.

— Выходит что, Гангрена всё таки подала на меня докладную с рекомендацией об отчислении из школы? — Матвей, изобразил на ходу рукой полет самолёта обратно домой к родителям.

— Скорее всего, — пожав плечами быстро ответил Сергей. И оба одноклассника продиффундировали через толпу к столам, где были расставлены стаканы с чаем и булочками.

Гангреной одноклассники называли между собой классного руководителя и одновременно преподавателя математики девятого-четвертого класса физико-математической школы-интерната, где обучались школьники девятых — одиннадцатых классов, победители олимпиад по физике, математике, химии. Поскольку классов было много, вместо буквенного обозначения А, Б, В, Г использовались цифры: 9¹, 9², 9³, … 10¹, 10² … вплоть до тринадцатого-четырнадцатого.

Матвей был призером олимпиады по физике увлечённым трудоголиком и одновременно страшным разгильдяем, как его метко охарактеризовала Генриетта Григорьевна или просто Гангрена. Она упрекала Матвея в «индифферентном отношением к общественной жизни в классе», несвоевременной сдаче зачётов и лабораторных работ, в нарушении режима самоподготовки, как например игра с одноклассниками в карты на расстеленном на полу одеяле — Ведь мы прежде чисто вымыли пол! — оправдывался Матвей, просто захотелось немного вспомнить о доме!… — Но разве этот аргумент имел хоть какое-нибудь значение для Гангрены? Именно в период обострения воспитательной работы Гангрена обнаружила на столе Матвея тетрадь с торчащей стопкой листов. Вынув их для приведения тетради в приличествующий вид, Гангрена пробежала по диагонали записи Матвея и громко рассмеялась: А он ещё увлекается такими бессмыслицами! Ещё один горе-математик пытается штурмовать Великую теорему Ферма! За этим последовало наставление о необходимости прилежной учёбы. Но Матвей не сдавался, он пошёл на принцип и заявил, что скорее бросит физматшколу, чем откажется от поиска краткого доказательства Великой теоремы Ферма! Ну-ну, мы это ещё посмотрим, … математик — последовал ехидный ответ Гангрены. Так было заключено это кабальное для Матвея пари. Как это ни удивительно, но близкие друзья поддержали выбор Матвея, хотя и считали его пари чистым безумством.

Профессор Борщов преподавал в физико-математической школе, вызывал уважение ребят, потому что умел надёжно хранить их секреты, никогда не выступал с менторских позиций, и даже если ему приходила в голову мысль дать кому- то совет, он делал это только с разрешения собеседника. Школьников профессор называл уважительно на «Вы», как себе равных, и никогда им не «тыкал». Одновременно ребята не чувствовали дистанции, что называется generation gap (конфликта поколений) с профессором в два с половиной раза более старшего возраста, чем любой из них. В его кабинете было уютно и уже стояла маленькая новогодняя ёлка в преддверии праздника. Примирительная процедура произошла как раз в накануне зимней сессии школьников. Борщов проводил время от времени такие школьные медиации, «чтобы не потерять форму», как любил объяснять он коллегам.

Картины прошедшей примирительной процедуры прокручивались в голове Матвея вместе с целым роем мыслей. Как чувствует себя сейчас его старший брат Денис после неудачного падения с подоконника второго этажа студенческого общежития? Воображение Матвея снова воспроизводит сюжет о том, как его старший брат, откликаясь на просьбу однокурсницы открыть захлопнувшуюся дверь, решается перелезть через окно соседней комнаты с тем, чтобы открыть форточку и затем дверь, с этим коварным английским замком изнутри. Но нога соскальзывает с подоконника, вернее, сам подоконник неожиданно съезжает куда-то вбок, и Денис, не рассчитав усилий, падает вниз. В результате — перелом суставов ног, тазобедренного сустава. Нужна срочная дорогостоящая операция. Затем появляются из ниоткуда три этих вложенных в другу в друга кубика и один и тот же сверлящий вопрос: почему в плоскости Пифагоровы тройки существуют, а уже начиная с трёхмерного случая — нет? Мысленно Матвей снова рассекает куб на шесть равных пирамид. Он ищет взором что-то напоминающее эту картину на орнаменте красивого деревянного панно в коридоре школы. Но тут ход его мыслей перебивает Татьяна.

— Ну и чем всё закончилось? — озабоченно спросила она тихим голосом.

Вместе с шестнадцатилетним Матвеем в школе обучалась Татьяна, ученица одиннадцатого-седьмого класса. Они познакомились полгода назад на занятиях по ликбезу — ликвидации безграмотности по русскому языку.

— Пока получил отсрочку от смертного приговора, — отшутился Матвей, — но думаю, что Гангрена ещё повоюет на педсовете.

— Ну и флаг ей в руки! — улыбнулась Татьяна. — А как твой брат?

— Да пока по-прежнему. Не лучше и не хуже. Нужна операция и деньги. Большие деньги. — лицо Матвея стало опять серьёзным.

— Мне кажется, что ты взваливаешь на себя непосильную ношу как взрослый — Татьяна жестом показала, не прекословь и продолжила. — Проблему денег должны помочь решать родители, они взрослые, а не ты. Ты ещё ребёнок.

— Не говори мне так! — горячо возразил Матвей. Я сумею ему помочь! А вот родители не смогут! И далее более спокойно. — если бы это произошло через два года, когда они закроют ипотеку и выкупят квартиру, хотя лучше не произошло бы и совсем…

Большая перемена продолжалась и ребята увидели в коридоре Александра Николаевич Борщова, который объяснял что-то директору. Наконец оба кивнули, посмотрели на Матвея, улыбнулись и пошли по своим делам.

— Александр Николаевич! — Татьяна окликнула профессора, — нам снова нужна Ваша помощь. Борщов остановился и удивленно посмотрел на Татьяну и подталкиваемого ею Матвея.

— ?

— Можно поговорить пять минут в Вашем кабинете.

— Можно, конечно, — и профессор пригласил ребят войти. — Только не больше десяти минут.

Татьяна быстро и точно изложила Борщову суть дела: что Матвей отчаянно пытается решить Великую теорему Ферма в надежде получить премию, чтобы помочь сделать дорогостоящую операцию брату (керамический протез), что такое напряжение ума для подростка опасно, что денежные проблемы должны помочь решить взрослые, что таким способом денег не заработаешь и так далее.

Матвей смущённо молчал и думал, вот он сейчас решит, что я «заливаю», что этой теоремы я никогда не докажу и за нарушение общих правил (мало того, что бросил на асфальт одноклассника, но и получил двойки по генетике) я «отправлюсь к маме и папе домой», точно как в песне из школьного капустника.

Странно, но профессор Борщов даже не улыбался. Неужели поверил в меня? А может сейчас рассмеётся и скажет, ну старик ты даёшь! Но профессор Борщов покачал головой и задумчиво проговорил:

— Не хотел бы я заключать такое пари,. — он протер очки о собственный свитер. — Шансы выиграть меньше, чем упасть за борт тихоокеанского лайнера и остаться в живых. Профессор коротко рассказал о пассажире, который бессонной ночью вышел покурить, загляделся на звёзды и по ошибке шагнул за борт. Долгих одиннадцать часов он плавал в воде, прежде, чем на лайнере заметили пропажу пассажира, развернулись назад и самое невероятное — нашли человека в Океане!

— А нельзя ли было «заключить пари» на какую-нибудь более простую теорему, например очередное геометрическое доказательство теоремы Пифагора? — улыбаясь спросил Борщов ….

— Александр Николаевич, — вступила в разговор Татьяна Кузнецова, теперь это уже поздно. Если Матвей пойдёт на попятную, то Гангрена всё равно добьется его отчисления, вернее сделает так, что Матвей сам захочет «чтобы его ушли», то есть «уволили по собственному желанию». Мы так хотим этого не допустить, и готовы разыграть свой шанс, даже если счастливый билет — лишь один на миллион.

— Да, как мне это напоминает мир взрослых, — с сожалением задумчиво заметил Борщов, — и чем я могу Вам помочь? Ведь если я стану заниматься подсказками, то Ваш спор или пари будет считаться нечестным. Вместе с тем, если Вы, Татьяна, признаетесь Генриетте Григорьевне, что помогали Матвею, потому что Теорема очень трудная, сотни и сотни маститых математиков, как говорится, «обломали себе зубы» в поисках решения, то я уверен, что даже самые консервативные преподаватели поддержат Матвея. Если не ошибаюсь, в в 1994 году профессор математики Эндрю Уайлс отыскал доказательство на 140—150 страниц. Вы представляете теперь, насколько это сложно?

— А что если Пьер де Ферма был прав, утверждая, что существует простоте краткое решение, о котором он упоминал на полях Арифметики Диофанта? — уверенно возразил Матвей.

— Если он не хвастал, то нам остаётся лишь включить творческое воображение и воссоздать это поистине чудесное решение! — продолжила Татьяна. Она увлекалась книгами по психологии, самопознанию и часто читала популярную литературу о лидерстве.

— Хорошо, сказал Борщов. Я помогу Вам но не в роли преподавателя, а скорее в качестве фасилитатора, то есть, создающего общие условия научного поиска, но решение, если оно существует, будет только Вашим решением. Если Вы его не найдёте, то бескомпромиссно выполните требования Генриетты Григорьевны, какими бы «драконовскими» они Вам не представлялись, и при этом, как говорится, без слёз и соплей, то есть не будете давить на жалость. Идёт? — профессор Борщов замолчал и пристально посмотрел на Матвея с Татьяной.

Сейчас его взгляд был суровым, как с доски Наша ревизионная комиссия: те же усы, та же полированная лысина (не хватает лишь нагана для полного комплекта так, на всякий случай! Шутили университетские студенты и физматшкольники). При этом эта революционная внешность совсем не вязалась с мягким негромким голосом Борщова, его робостью, с которой он всякий раз входил в аудиторию, тщательно перепроверяя, не ошибся ли он дверью.

— Идёт, ответили ребята.

— Мы знаем, в каком направлении искать, сказал Матвей. Если Пьер де Ферма упомянул о сильном озарении, посетившем его, то скорее всего, решение может быть в виде рисунка, чертежа с минимальным количеством формул, как в Олимпиадной задаче. Просто раньше математики искали доказательство не в том направлении.

Борщов многозначительно кивнул и указал на часы. Ребята поспешно удались.

Не меняя общности, можно считать что справедливо неравенство для нашей тройки чисел a <b, где b, в свою очередь, меньше числа с, стоящего в правой части уравнения теоремы Ферма.

Слагаемые a, b не могут быть равными, в силу иррациональности числа √2, которое невозможно представить в виде дроби, состоящей из не имеющих общих делителей числителя и знаменателя p и q.

Врезка. Числа древние, но вечно юные

Числа натуральные, целые, рациональные, иррациональные и трансцендентальные.

Напомним, что в начальных классах школы на уроках арифметики изучаются натуральные числа: 1,2,3,4,5…, которые используются, например для счёта предметов. Говорят, что такие числа образуют бесконечное множество N. Оно обозначается фигурными скобками N = {1,2,3,4,5 ….}. Каким бы большим не было натуральное число n, всегда найдётся число на единицу больше n+1. Конечно, это математическое упрощение, физики установили, что даже Вселенная имеет конечные размеры, определяемое как скорость света с = 3*10⁸ м/с умножить на 15 млрд лет. (Любознательные могут рассчитать размер Вселенной в метрах, для чего удобно принять во внимание, что в году примерно π *10⁷ секунд). Оказалось, что для вычислений очень удобно работать с целыми числами, где наряду с положительными имеются также ноль и отрицательные числа. Кольцо целых чисел Z =… -3, -2, -1,0,1,2,3 … с операциями слоения вычитания и умножения. Но и целых чисел не достаточно было для решения задач аграрной индустрии, архитектуры, торговли и мануфактуры, промышленности: именно эти отрасли знаний стимулировали развитие математики. Ещё в Древней Греции были открыты рациональные, иррациональные и трансцендентные числа, впоследствии математики дали им строгое определение.

Рациональное числа представляются в виде дроби p/q. Можно сократить числитель и знаменатель до взаимно простых чисел, разделив их на НОД — наибольший общий делитель. Например, вместо 4/6 писать 2/3. Целую часть можно записать рядом с дробной как-то: 3/2 =1 ½.

Если читать умеет делить числа в столбик, то сможет дробное представление числа привести к десятичному виду, как например 2/3 = 0,6666666666…, рано или поздно в этом ряду появится повторение одной или последовательности цифр или одной и той же цифры. Это происходит потому, что остаток от деления чисел всегда делится на одно и то же делимое. Рано или поздно варианты разных остатков будут исчерпаны и начнётся циклическое повторением (математики вводят понятие сравнение чисел по модулю, принцип Дирихле, а можно просто поэкспериментировать самостоятельно и убедиться!)

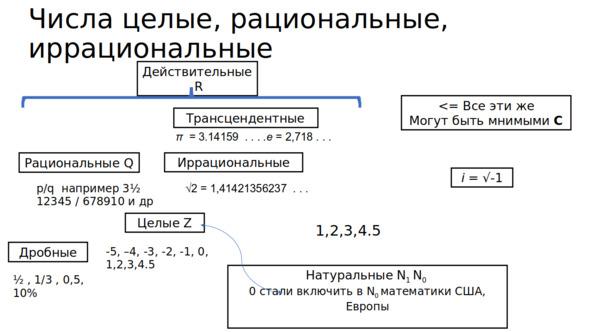
Вместе с тем, наряду с рациональными существуют иррациональные числа, они не могут быть представлены в виде десятичной дроби с повторяющейся последовательностью чисел, как например, √2= 1.41…. является иррациональным числом. Допустим обратное, которое представимо в виде дроби, состоящей из не имеющих общих делителей числителя и знаменателя p и q. Рассмотрим внимательнее уравнение 2q² = p² Его левая часть делится на два, значит правая часть делится уже на четыре, поскольку p можно разложить на простые числа, как то: 2,3,5,7,11,13,17 …. делящиеся только на себя и на единицу. Набор сомножителей в правой части будет повторяться дважды для p², отсюда свойство делимости на четыре. Но тогда в этом уравнении и q будет делиться на два. Смело сократив левую часть на общий делитель два в итоге получим что числа p и q, вопреки сделанному допущению, имеют в качестве общего делителя двойку и её степени. А это означает, что исходное предложение относительно числителя и знаменателя оказалось ошибочным: оба они четные, делятся на два, но мы исходно предполагали, что p, q не имеют общих делителей, которые заранее сократили. Значит √2 не представляется в виде дроби, аналогичные рассуждения применимы для корня из двух степени n.

Трансцендентное число не может быть корнем алгебраического выражения, например число π = 3.14158 или число Эйлера е = 2.718. Вместе с тем трансцендентные числа играют важную роль не только в геометрии, но при описании динамических процессов в физике, экономике, социологии.

Целые, рациональные, иррациональные и трансцендентные числа образуют вместе множество действительных чисел R можно сопоставить каждому числу точку на оси абсцисс Х и радиус вектор из начала координат до этой точки, при этом длина этого вектора будет равна модулю числа |х|. Для случая плоскости R², мы будем иметь дело с парами чисел: (x, y) и радиус вектором из начала координат до точки на плоскости. Для трехмерного пространства R³ понадобится задавать координаты его точек уже тройками чисел (x, y, z) а для многомерного пространства Rⁿ координаты любой точки по осям описываются радиус-вектором (x₁, x₂,…x_n).

Интересно заметить, что целые числа можно сосчитать, а именно: сопоставить каждому целому числу натуральное число — его модуль. Отрицательные числа можно считать парами вместе с положительными (это напоминает работу проводника на два вагона). Такое множество, хотя и бесконечно, является счётным. Несложные рассуждения позволяют сделать вывод, что является счётным множество рациональных числе p/q. Представим себе огромный (бесконечный) кинозал, где номер ряда — это числитель, а номер места — знаменатель. Так например в первом ряду расположены слева направо (или с Запада на Восток) зрительские места с дробями 1/1, 1/2, 1/3, 1/4 и т. д. Во втором — 2/1, 2/2, 2/3, 2/4 и т. д. Предположим, что все места размещены в зале с соблюдением социальной дистанции, так что контролёр может свободно перемещаться как по рядам, так насквозь любого ряда.

Если безбилетник сидит на месте p в ряду q, то проводник — робот, следующий из вершины 1/1 всё равно его обнаружит, если будет придерживаться несложного алгоритма. Итак, контролёр входит в зрительский зал с Северо-Запада, как раз в месте размещения 1/1.

Контролёр делает один шаг на Восток к месту 1/2;

далее шагает в Юго-Западном направлении к месту 2/1;

после этого делает ещё один шаг на Юг к месту 3/1;

затем совершает два шага в Северо-Восточном направлении к местам 2/2 и 1/3;

после чего совершает один шаг на Восток к 1/4;

потом три шага в Юго-Западном направлении, проверяя места 2/3, 3/2, 4/1…

И таким образом контролёр последовательно исследует зрительский зал, дрейфуя как челнок, то в Юго-Западном, то в Северно-Восточном направлениях, охватывая контролируемую территорию всё расширяющимся на один шаг с каждым обходом треугольником, вершина которого размещается в Северо-Западной части зала.

Вместе с тем, действительные числа сосчитать невозможно это множество образует континуум. Между двумя близкими рациональными числами всегда найдётся сколько угодно много других иррациональных чисел. Например, в треугольнике средняя линяя равномощна основанию. Это следует понимать так, что каждой точке на средней линии треугольника соответствует точка на его основании, и наоборот.

Основные математические знания

Трёх и n- мерная система координат

Представим себе, что Вы управляете дроном. Пульт управления необычен. Он имеет кнопочки, задающие движения:

Дрон может двигаться:

на Север, на Юг,

на Запад

на Восток

Вниз

Вверх

Сам дрон имеет гирокомпас и отлично ориентируется в пространстве, ожидая Ваших команд.

Допустим, Вам требуется доставить пакет с вакциной от корнавируса на 10-ый этаж и аккуратно подать его в окно. Вы находитесь в начале координат, а пункт назначения — 10 м на Восток, 10 м. на Север, и 20 м. вверх. Эти координаты можно задать так:

Пункт назначения точка P = (10, 10, 20) в координатных осях

При этом подразумевается, что мысленно мы используем оси:

Запад -Восток — ось Х

Юг- Север — ось Y

Низ-Верх — ось Z

А теперь, допустим, Вы производите запуск с балкона небоскрёба.

Если бы окно находилось по отношению к Вам на 20 м. западнее, на 5 м. южнее и на 15 м. ниже Вашего балкона, то координаты точки P = (-10, -5, -15)

Это так называемая Декартова система координат по имени математика и философа Рене Декарта. Наглядный двумерный случай Декартовой системы координат — это шахматная доска, это плоская карта местности. Каждая точка однозначно определяется двумя координатами.

Как бы Вы объяснили двумерному существу?

Как бы Вы объяснили двумерному существу третье измерение — высоту? Предположим, что в совершенно плоском мире Вы ведёте диалог с философом, имеющим богатое творческое воображение, Вы принялись бы объяснять, как можно повернуть ботинок, больше напоминающий в этом случае стельку от обуви, в третьем измерении и сделать из правого ботинка левый и наоборот.

Точно так же трёхмерный ботинок можно разверзнуть в четырехмерном пространстве и сделать правый левым, а левый — правым.

====== Знаете ли Вы что такое Флатландия? ======

«Флатла́ндия» (англ. «Flatland: A Romance of Many Dimensions») — роман Эдвина Э. Эбботта, который вышел в свет в 1884 году. Этот научно-фантастический роман считается полезным для людей, изучающих, например, понятия о других пространственных измерениях или гиперпространствах. Как литературное произведение роман ценится из-за сатиры на социальную иерархию викторианского общества. Айзек Азимов в предисловии к одной из многих публикаций романа написал, что это «лучшее введение в способ восприятия измерений, которое может быть найдено».

По этой книге было снято несколько фильмов, в том числе одноимённый художественный фильм 2007 года, в России известный как Плоский Мир.

=======================================================

Итак, в многомерном пространстве координаты любой точки P задаются относительно начала координат выражением: P = (x₁, x₂, … x_n), а вектор соединяющий начало координат — точку (0, 0,0 … 0) и точку P именуется радиус вектором например A, B, C его компоненты — это координаты по осям: x1, x2, … xn

интересно заметить, что как в двумерном, трёхмерном пространстве, так и многомерном пространстве радиус векторы можно складывать — вычитать покомпонентно:

A + B = (a₁ + b₁, a₂ + b₂ …. a_n + b_n)

Так например, в физике происходит сложение перемещений, скоростей либо сил.

А что будет при умножении векторов? Да, такая операция возможна. Познакомимся со скалярным произведением двух векторов, которое происходит также по каждой компоненте отдельно, а результат — число образуемое путем сложения результатов таких произведений:

A * B = a₁ * b₁ + a₂ * b₂ + …. + a_n * b_n

Попробуем умножить вектор a = (1,1,1) на самого себя

(1,1,1) * (1,1,1) = 1*1 +1 *1 +1 * 1 = 3 или квадрат модуля вектора обозначаемого как |a|². Не принято говорить длина вектора — принято говорить модуль вектора. Легко вычислить, что в n -мерном кубе с ребром a длина наибольшей диагонали равна a * √n в самом деле в квадрате это a * √2 а для случая куба a * √3.

В чём же состоит смысл скалярного произведения?

Например, в физике вектор силы умножить на вектор пройденного путем есть совершенная над телом работа. Если эти вектора со-направлены, то результат будет максимальный, если перпендикулярны, — то нулевой (санки нельзя ускорить, если Вы прикладываете силу поперёк их движения).

======================================================

Глава 2 Удивительный мир симметрии

Вечером на ручных часах Татьяны раздалось бип-бип-бип и появилось сообщение:

Предл. Встрет. завтра 12:00 в «Собачьих бутербродах» у М. Г@ // Борщ. Ок?

Татьяна ответила ОК! и сразу увидела результат голосования других ребят: Матвея и Артура, младшего одиннадцатилетнего брата Татьяны, — все они были согласны. Матвей был самым юным участником творческой группы, представителем той самой целевой группы, для которой необходимо отыскать доказательство. Если ты сможешь объяснить всё это одиннадцатилетнему школьнику, то будь уверен, сможешь объяснить миллиардам других людей с обычной школьной подготовкой! — убеждала она Матвея. И Матвей хорошо подумав, получив еще раз заверения от сохранении строжайшей конфиденциальности от Татьяны, согласился.

Кафе быстрого питания было расположено прямо у выхода метро, напротив университета в этом месте обычно любил назначать встречи Борщов, сопровождая это словами: конечно пища там лишь условно съедобная, но зато место удобное и обстановка уютная, подходящая для диалога.

Он пунктуально пришел на встречу за десять минут до начала и, заняв пустой столик у окна, принялся читать только что изданную коллективную монографию, где наряду с прочими работами была и его: «Социологические методы идентификации судебной коррупции». За окном бурлила предновогодняя жизнь, под аккомпанемент лёгкого пушистого снега и солнышка (вот уже настоящий предновогодний подарок! — отметил про себя Борщов), прохожие и автомобили мелькали в окне, а их полупрозрачные отражения — в самом кафе. Методично раздавался голос кассиров на выдаче:

— Номер восемьдесят пять, один Американо и чизбургер, номер сто четырнадцатый салат из крабов, номер сто одиннадцать: картошка фри…

И вот дружная компания снова собралась за одним столом: Матвей небрежно стаскивал с себя куртку, запорошенную снегом, Татьяна элегантно сняла красивое пальто, которое так эффектно подчёркивало её фигуру. Артур уже сидел в строгом деловом костюмчике, — прямо таки аккуратно причесанный примерны отличник со школьной фотографии.

Матвей заказал кофе, Татьяна и Артур — мороженое, Борщов — чай, который сразу