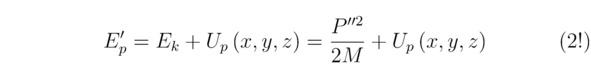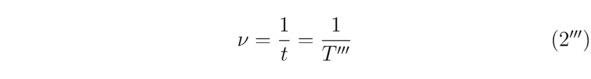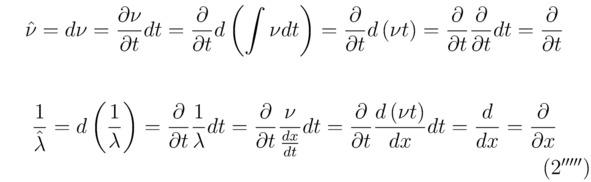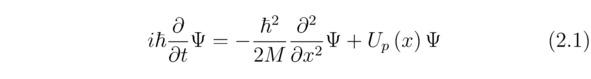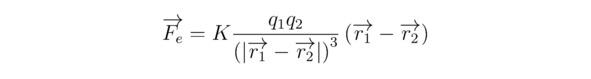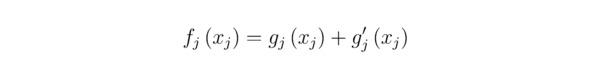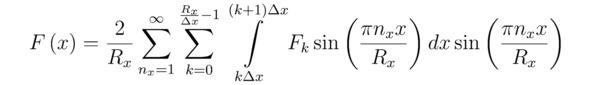2. О фундаментальных законах физики
Во второй главе этой монографии будут рассмотрены 2 концепции, с помощью которых можно сформулировать те или иные предназначенные для описания окружающей нас действительности физические законы. Очевидно, что первая доктрина направлена на исследование дифференциальных соотношений, позволяющих по меньшей мере обобщить почти все материальные явления и процессы, а вторая связана с определением корреляций в заранее известном наборе функций f1 (x1), f2 (x2),…,fN`` (xN``). Последние могут быть найдены в результате экстраполяции округлённых до рациональных значений, относящихся непосредственно к частным аналитическим решениям тех или иных вырожденных дифференциальных уравнений, или получены опытным путём. К слову сказать, достоверность абсолютно любого численного метода, который опирается на анализ экспериментальных данных, изначально просто нельзя не поставить под сомнение. Впрочем, применяя эмпирический подход на практике, в подавляющем большинстве случаев несложно будет обосновать теоретически как минимум не самую малую долю от всех наблюдаемых в линейных или хотя бы в линеаризованных физических системах фундаментальных взаимодействий. Итак, начнём этот раздел с вывода одномерного стационарного линейного уравнения Шрёдингера. Кстати говоря, методика, ориентированная на поиск зависимостей между математическими величинами Ψ, Up (x), M и ħ, присутствующими в указанном дифференциальном уравнении, базируется на человеческой интуиции. Примечательно, что перечисленные мною тезисы в дальнейшем могут помочь исследователям разобраться в самой сути каждого из представленных на Ваш суд научных открытий.
2.1 Вывод уравнения Шрёдингера
В 1924 году французский физик Луи де Бройль выдвинул смелую гипотезу, согласно которой корпускулярно-волновому дуализму приписывается универсальный характер. Исходя из предположения де Бройля, важно констатировать, что всякая материальная частица обладает волновыми свойствами, причём соотношения (2`), (2``), (2```) и (2````), связывающие между собой волновые и корпускулярные характеристики, например, единичного фермиона, остаются точно такими же, как и в случае электромагнитного излучения веществом. Действительно, полную энергию Ep` и импульс P`` абсолютно любой элементарной частицы возможно выразить через частоту излучения ν и через длину волны де Бройля λ соответственно, тогда:
здесь h` — постоянная Планка; k`=2π/λ; ħ=h`/ (2π).
Далее сформулируем закон сохранения энергии для волны де Бройля. Безоговорочно, искомая величина Ep` представляет собой сумму 2-х энергий (кинетической Ek и потенциальной Up (x,y,z)), следовательно:
Вместе с тем
Разумеется, длину волны де Бройля λ удобно выразить через скорость υ (υ=dx/dt), тогда:
Беспрекословно, вывод того или иного линейного нестационарного уравнения Шрёдингера надо производить в трёхмерном аналитическом пространстве C3, но для упрощения расчётов мы будем использовать полярную систему координат. В довершении всего, переходя от действительных чисел к комплексным λ -> -2πiλ и ν -> -ν/ (2πi) (знаки перед исследуемыми переменными -2πiλ и -ν/ (2πi) выбраны отрицательными, поскольку в противном случае (при λ -> 2πiλ, а также при ν -> ν/ (2πi)) формула (2.1) просто-напросто потеряет смысл, если в неё подставить алгебраическую величину Ψ=∑nt=-∞∞∑nx=-∞∞C (nt, nx) e2iπ (ntt/Rt+nxx/Rx), так как в конечном счёте в любой ситуации должно соблюдаться равенство (2!)), перепишем составленный для волны де Бройля закон сохранения энергии в следующем виде:
где M — масса электрона (в дальнейшем лептона или фермиона); T``` — период волны де Бройля; t — время; x — координата; Cn — амплитуда колебаний; ω` — угловая частота; Up (x) — потенциальная энергия.
К тому же
В итоге, ссылаясь на математические преобразования, разобранные выше, найдём тождество:
После чего нам потребуется внести новую величину Ψ под каждый из знаков частных производных ∂/∂t и ∂2/∂x2, тогда:
Так вот, полученное выражение (2.1) называется одномерным нестационарным линейным уравнением Шрёдингера. Теперь, опираясь на отыщенные прежде формулы (2``), (2`````) и (2.1), определим оператор импульса P``, следовательно:
2.2 Эмпирический метод
Обычно с изучением школьной программы почему-то не принято ставить под сомнение справедливость основных положений, позволяющих осуществить вывод фундаментальных законов физики. В этом параграфе мы обобщим сведения о том, как соотносятся между собой некоторая физическая величина F и математически несвязанные выражения f1 (x1),…,fN`` (xN``). Отталкиваясь от постулата о наличии корреляций между искомым параметром F и неравномерно распределёнными вдоль соответствующих осей x1,…,xN`` функциями f1 (x1),…,fN`` (xN``), заданные соотношения f1 (x1),…,fN`` (xN``) надлежит перемножать друг с другом только в том случае, когда последние окажутся независимыми. Иначе говоря, приращение некоторого заранее известного аналитического решения fj (xj), составленного для того или иного вырожденного дифференциального уравнения, по факту будет происходить без взаимного влияния одних действительных значений fj (min (xj)),…,fj (max (xj)) на другие множители f1 (x1),…,fo (xo),…,fN`` (xN``) (o≠j). Итак, запишем тождество (2*) для нахождения алгебраического произведения Пj=1N``fj (xj) γj. Бесспорно, подобранные коэффициенты γ1,…,γN`` будут численно равны вещественным константам (+1 или -1), представляющим из себя степени показательных функций f1 (x1) γ1,…,fN`` (xN``) γN``, тогда:

здесь N`` — общее количество независимых величин f1 (x1),…,fN`` (xN``).
Совершенно ясно, что наглядным примером применения эмпирического подхода на практике является закон Кулона, полученный для силы электростатического взаимодействия 2-х заряженных частиц Fe. Таким образом, следующие выражения (f1 (x1), f2 и f3 (x3)) могут быть сгруппированы друг с другом как несвязанные между собой параметры: f1 (x1) — произведение 2-х взятых по модулю электрических зарядов |q1||q2|; f2 — поправочная постоянная K; f3 (x3) — квадрат расстояния (|r1-r2|) 2 между 2-мя имеющимися в нашем распоряжении материальными частицами, где r1 и r2 — соответственно построенные из начала координат (0,0,0) в точки с зарядами q1 и q2 радиус-векторы.
Хорошо известно, что сила Кулона Fe прямо пропорциональна искомым множителям f1 (x1) и f2 (γ1=γ2=1), но обратно пропорциональна математическому соотношению f3 (x3) (γ3=-1). Наконец, запишем сформулированный для 2-х одно- или разноимённых зарядов q1 и q2 закон Кулона, следовательно:
Помимо этого
Если найденные величины gj (xj) и gj` (xj) окажутся взаимно зависимыми, то справедливым будет равенство:
Кстати говоря, подобранные функции gj (xj) и gj` (xj) могут задаваться более сложным образом, нежели упомянутые ранее степенные выражения f1 (x1) γ1, f2γ2, f3 (x3) γ3. Порой с помощью эмпирического метода нельзя описать тот или иной закон природы, тогда для реализации намеченных целей соискатели обычно составляют либо линейные, либо нелинейные дифференциальные уравнения (ДУ). Разрешить нелинейные ДУ в частных производных иногда бывает затруднительно, поскольку абсолютно все современные персональные компьютеры имеют недостаточно высокую производительность. В подобных случаях исследователи используют суперкомпьютеры. В дальнейшем мы сконцентрируемся на проблеме поиска общего аналитического решения того или иного вырожденного ДУ с частными производными.