автордың кітабын онлайн тегін оқу Отличная квантовая механика
Все права защищены. Данная электронная книга предназначена исключительно для частного использования в личных (некоммерческих) целях. Электронная книга, ее части, фрагменты и элементы, включая текст, изображения и иное, не подлежат копированию и любому другому использованию без разрешения правообладателя. В частности, запрещено такое использование, в результате которого электронная книга, ее часть, фрагмент или элемент станут доступными ограниченному или неопределенному кругу лиц, в том числе посредством сети интернет, независимо от того, будет предоставляться доступ за плату или безвозмездно.
Копирование, воспроизведение и иное использование электронной книги, ее частей, фрагментов и элементов, выходящее за пределы частного использования в личных (некоммерческих) целях, без согласия правообладателя является незаконным и влечет уголовную, административную и гражданскую ответственность.
Предисловие
Почему я написал эту книгу?
Впервые строгое определение квантовой механики (КМ) предложили Вернер Гейзенберг и Эрвин Шрёдингер почти век назад. С тех пор эта область науки претерпела громадные изменения. Направленная изначально на объяснение атомных спектров, сегодня квантовая механика является одной из основ почти всех разделов физики. Соответственно, КМ — неотъемлемая часть программы обучения любого студента-физика: какую бы специализацию ни избрали выпускники после окончания вуза, квантовая механика им почти наверняка потребуется в дальнейшей работе.
В то же время методы обучения студентов квантовой механике с годами почти не меняются. Мы начинаем с понятия волновой функции и пишем сначала стационарное, а затем временнóе уравнение Шрёдингера в координатном представлении. Мы определяем энергетические спектры и соответствующие им волновые функции в простых потенциальных ямах и рассматриваем эволюцию волновых пакетов, связанную с потенциальными барьерами. Наконец, мы вводим оператор момента импульса и вычисляем спектр атома водорода. Последние три четверти века именно так, с небольшими вариациями, выглядела программа первого семестра вузовского курса квантовой механики.
У этой традиции множество положительных сторон. Она работает с физической системой, с которой студент уже разобрался в курсе классической физики и которую ему нетрудно себе представить. Она позволяет увидеть различия между поведением классической и квантовой частицы и привлекает внимание к некоторым фундаментальным явлениям, характерным для квантового мира: туннелированию, квантованию и принципу неопределенности. Она снабжает студента инструментами для решения экспериментально значимых задач, с которыми невозможно справиться классическими методами: рассчитав в аудитории спектр водорода, студент отправляется в лабораторию и измеряет его!
Однако такой подход неидеален. Он дает студенту алгоритм для анализа конкретной физической системы, но не раскрывает внутреннего устройства квантовой физики и ее концептуальной логики. Мы знакомим студентов с многочисленными фактами и преподаем вычислительные подходы, связанные с волновыми функциями, операторами и измерениями, но не выстраиваем жесткой логической связи между ними и не объясняем, какие из этих фактов являются постулатами, а какие — их следствиями и в какой именно логической последовательности эти следствия выводятся.
В результате студент — по крайней мере думающий студент — основательно запутывается. Почему достаточно всего лишь поставить над буквами крышечки, чтобы превратить классическую формулу в квантовую? Почему действие оператора импульса на волновую функцию эквивалентно взятию производной? Почему мы никогда не встречаем собственных состояний импульса (и кошек Шрёдингера) в практической реальности? Почему атомы, которые мы наблюдаем, переходят между энергетическими собственными состояниями, а не какими-нибудь другими? Как проективное измерение связано с измерением наблюдаемого оператора? Почему одни состояния описываются волновыми функциями, а другие — столбцами чисел? Если все состояния имеют норму 1, то как мы нормируем волны де Бройля? Если наблюдаемые представляют собой матрицы, то как выглядит матрица импульса?
На вершине всего этого — самый подлый вопрос. Если рассматривать квантовую физику как более общую теорию, чем физика классическая, то почему нужно обращаться к классическим представлениям, чтобы разобраться в концепции измерения? Почему это самое измерение, в отличие от всех прочих физических процессов, не описывается унитарной эволюцией? Если квантовые системы действительно в какой-то момент измерения становятся классическими, то в какой же именно момент это происходит?
Основополагающий образ мышления, который мы стараемся привить нашим студентам за годы обучения физике, можно сформулировать так: «Подвергай все сомнению!» В курсах квантовой физики наше послание студентам звучит, кажется, с точностью до наоборот: «Заткнись и считай!»[1]
Поскольку я тоже когда-то был студентом и изучал квантовую механику, то со временем нашел ответы на эти вопросы, но во многих случаях это произошло через много лет после получения ученой степени. Когда же я пытался задавать подобные вопросы, будучи студентом, вокруг не было никого, кто мог бы не то что ответить мне на них, но хотя бы помочь правильно сформулировать.
Моя задача при написании этой книги состояла в том, чтобы изменить сложившуюся ситуацию. Я попытался выстроить ясную логическую структуру, в которой осталось бы как можно меньше дыр, которая позволила бы читателю по логической цепочке отследить любое заявление назад, до самых основ… Которая не оставила бы вопросов без ответов.
Итак, в определенном смысле я написал эту книгу для себя. Но не для сегодняшнего себя, а для того, каким я был в 18 лет. Такую книгу, которую я счастлив был бы на третьем курсе иметь в своей библиотеке и которая избавила бы меня от многолетних мучительных поисков истины.
Естественно спросить: «Насколько реалистична такая цель? Некоторые из поставленных выше вопросов представляются достаточно сложными. Может быть, без научной степени в них и не разобраться?»
Я дам двойной ответ. Во-первых, с педагогической точки зрения: механика с ее гильбертовым пространством бесконечной размерности едва ли оптимальна для иллюстрации квантовых принципов. Во многих приведенных выше вопросах можно разобраться, если использовать вместо механической более простую физическую систему; чуть позже я расскажу об этом подробнее. Во-вторых, бóльшую часть нестыковок и парадоксов вполне реально устранить, если правильно ввести понятие запутанности. Это понятие лежит в основе двух важных взаимосвязанных концепций: измерения фон Неймана и декогеренции. Первая из них обеспечивает способ избежать превращения измерения в некое исключительное явление в мире квантовой физики и таким образом устраняет логическую бутылку Клейна, характерную для копенгагенской интерпретации. Вторая описывает происходящие естественным образом «самопроизвольные» измерения, благодаря которым квантовый мир предстает перед макроскопическим и наблюдателями вроде нас в том виде, который мы знаем под именем «классическая физика».
Эти концепции не слишком сложны. Математически они намного проще многих элементов традиционного квантового курса, таких как уже упоминавшийся атом водорода или теория рассеяния. Главная трудность в понимании запутанности — не недостаток у студента необходимых математических навыков; она связана скорее с его воображением. Чтобы стать хорошим физиком, необходимо эту способность у себя развить; как говорил Эйнштейн, воображение на самом деле важнее знаний.
Квантовая механика или квантовая оптика?
Название нашей дисциплины — квантовая механика — подразумевает, что мы изучаем применение квантовых принципов к законам движения. На самом же деле рамки квантовой теории не ограничены механикой; она применима во всех областях физики. Если наша цель состоит в том, чтобы изучить общие принципы квантовой физики, то разумно ли выбирать именно механику в качестве физической системы для иллюстрации этих принципов?
Если мы задумаемся над этим вопросом всерьез, то вынуждены будем дать отрицательный ответ. Использование механики — в основном дань традиции, поскольку именно в механике исторически имело место первое успешное применение квантовых принципов в их современной форме. Но если говорить об обучении, то объяснение базовых квантовых принципов на примере механики — весьма неудачный подход. Гильбертово пространство, связанное с этой системой, имеет бесконечную размерность; более того, базис имеет мощность континуума. Студенту приходится иметь дело с незнакомым, чрезвычайно сложным и не всегда строгим математическим аппаратом, включающим в себя обобщенные функции, преобразование Фурье и функциональный анализ. В результате вместо того, чтобы сосредоточить усилия студентов на понимании физических концепций, мы заставляем их сражаться с математикой, а это зачастую ведет к путанице средств и целей. Трудно ожидать от подобного опыта сколько-нибудь глубокого понимания. Студент попросту не увидит за деревьями леса.
Если мы поставим перед собой выбор физической системы для иллюстрирования квантовой физики, нам следует взять ту, у которой гильбертово пространство обладает наименьшей нетривиальной размерностью, а именно — равной двум. Имеется множество таких систем, которые в настоящее время изучаются в контексте квантовых информационных технологий в качестве квантовых бит. Среди подобных систем выделяется одна как наиболее тщательно исследованная и интуитивно понятная: поляризация фотона. Как правило, студент, приступающий к изучению квантовой физики, успел уже освоить оптическую волновую поляризацию. Векторы поляризации Джонса напрямую транслируются в векторы состояния фотонной поляризации, а матрицы, описывающие трансформацию этих векторов различными волновыми пластинками, превращаются в операторы. Принимая во внимание дискретную природу фотона, несложно обосновать постулат квантового измерения из классической картины измерения поляризации. Таким образом, основные квантовые принципы выводятся из классической поляризационной оптики (и студенческого лабораторного опыта обращения с ней) самым простым и естественным образом.
Фотонная поляризация оказывается полезной и позже, когда мы переходим к изучению запутанности. Огромное количество экспериментов по проверке принципиальных моментов в квантовой информатике было проделано с использованием именно данного объекта в качестве носителя квантового бита. Некоторые из этих экспериментов — в частности, по квантовой криптографии, телепортации и нелокальности — относятся непосредственно к концепциям, описанным в книге. Иллюстрируя теоретический материал данными экспериментов из актуальнейших на сегодняшний день исследовательских тем, эта книга сразу, с самого начала, вводит студентов в самое сердце квантовой физики. А что может придать изучению академической дисциплины больший интерес, чем свежие результаты из исследовательских лабораторий?
Раз уж мы заговорили о лабораториях, замечу, что опыт студентов не должен ограничиваться чтением материалов об экспериментах, проведенных кем-то другим. Огромное преимущество поляризационного кубита как иллюстрирующей системы состоит в том, что он позволяет усилить курс лабораторным компонентом. Почти весь материал главы 1 иллюстрируется классическим экспериментом с поляризацией, для которого требуются лазер, несколько поляризационных пластинок, поляризующий светоделитель и два детектора. Материал по запутанности можно подать наглядно при помощи серии лабораторных работ по удаленному приготовлению состояния, однофотонной интерференции и нелокальности Белла. Организовать такие эксперименты силами среднестатистической кафедры физики сложнее, но вполне по силам, о чем свидетельствует опыт множества колледжей по всему миру, в том числе и моего родного Университета Калгари. Дополнительные подробности на предмет возможных образовательных лабораторных работ можно найти на сайте книги.
Связь между квантовой физикой и квантовой оптикой в этой книге не ограничена использованием фотона для иллюстрации основных концепций соответствующей дисциплины. Она проявляется также в многочисленных примерах из оптики, обильно рассыпанных по всей книге, и в выборе предметов для более углубленного изучения (подробное описание гармонического осциллятора, представления Гейзенберга, сжатия, матриц плотности, двухуровневых систем, квантовой томографии). Эти предметы будут особенно полезны тем, кто интересуется квантовой информатикой в целом и квантовой оптикой в частности.
Структура курса
Книга содержит материал, который можно преподать студентам в рамках двухсеместрового курса квантовой механики. В главе 1 вводятся главные принципы и постулаты КМ, которые иллюстрируются кубитом поляризации фотона. Читатель, возможно, захочет изучать эту главу параллельно с приложением A, в котором разобраны основы линейной алгебры, необходимые в КМ, как показано в таблице ниже.
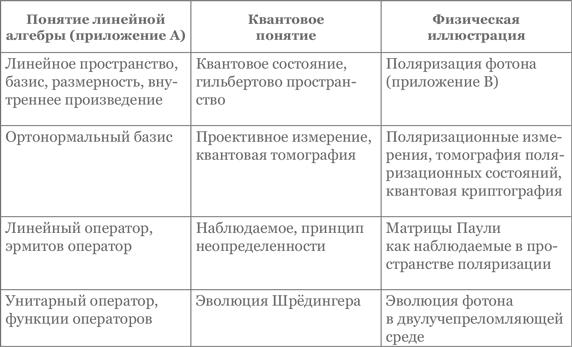
Глава 2 целиком посвящена запутанности, ее следствиям и приложениям. Сначала я ввожу пространство тензорных произведений математически, затем рассказываю о частичных квантовых измерениях, удаленном приготовлении состояния и парадоксе нелокальности (в формах Белла и Гринбергера — Хорна — Цайлингера), иллюстрируя теорию экспериментами с запутанными фотонами. Нелокальность, пожалуй, главный парадокс квантовой механики, и после него естественно обсудить механизм квантовых измерений, их естественный аналог (декогеренцию) и интерпретации квантовой механики. В разд. 2.4 мы выясняем, когда и почему квантовая система становится классической в ходе измерения и почему мы не встречаем гуляющих по городу кошек Шрёдингера. После этого я весьма подробно рассматриваю приложения запутанности, такие как квантовые вычисления, телепортация и повторители. При преподавании этого материала имеет смысл предложить двум или трем студентам сделать презентации по свежим исследованиям в данной области.
Главы 3 и 4 представляют собой в некоторой степени реверанс в сторону «общепринятой» вузовской квантовой механики частицы в потенциальном поле. Там нам придется иметь дело с гильбертовым пространством, базисом которого является континуум, поэтому глава 3 сопровождается кратким курсом по дельта-функциям Дирака и преобразованию Фурье (приложение Г). Я надеюсь, что после того, как студенты уже усвоят базовые положения КМ, они смогут воспринимать технические особенности гильбертовых пространств с непрерывными переменными, не теряя из виду физические принципы. Вводя системы с непрерывными переменными я объясню, как и почему при этом изменяются правила нормирования. Затем я приведу обычные примеры потенциальных ям, потенциальных барьеров, туннелирования и гармонического осциллятора. На этом, как мне представляется, должна завершиться программа первого семестра курса.
Далее в главе 3 объясняется представление Гейзенберга и то, как оно согласуется с представлением Шрёдингера; все это иллюстрируется многочисленными примерами, связанными с физикой гармонического осциллятора (и продемонстрированными в квантово-оптических экспериментах): смещением, фазовым сдвигом, а также одно- и двумодовым сжатием. С помощью последнего я показываю первоначальный вариант парадокса Эйнштейна — Подольского — Розена.
В главе 4 я рассматриваю трехмерное геометрическое пространство (как тензорное произведение трех одномерных пространств) и рассказываю про момент импульса, спин и, наконец, атом водорода. Затем обсуждается поведение спина в магнитном поле и магнитный резонанс, а также дается понятие о спиновом эхе и спектроскопии Рамзея.
В главе 5 мы вновь обращаемся к фундаментальным принципам квантовой механики, представив их на этот раз на языке операторов плотности, который имеет важнейшее значение во всех приложениях квантовой физики. Чтобы продемонстрировать полезность этого языка, я даю с его помощью строгое описание декогеренции и релаксации при ядерном магнитном резонансе. Затем я затрагиваю важные для современной квантовой информатики темы: обобщенные измерения, а также томографию квантового состояния, процесса и детектора.
Как пользоваться этой книгой (послание студенту)
Бóльшую часть своей сознательной жизни я был вовлечен в процесс образования — сначала как школьник и студент, а затем как преподаватель и профессор. Этот опыт помог мне понять простую истину: почти невозможно изучить что бы то ни было, пассивно слушая лектора или читая книгу. Обучение требует активного участия студента. В случае теоретической физики это означает, что ты должен выводить формулы сам, а не наблюдать, как это проделывает кто-то другой на доске или в учебнике.
Помня об этом, я попытался написать этот текст, руководствуясь сократовским принципом: ученик приходит к истине, отвечая на вопросы учителя. Я лично познакомился с данным методом в старших классах. Мне повезло учиться в одной из лучших школ России с естественно-научным уклоном, где практиковался уникальный подход к обучению математике. Вместо объяснений нам давали листочки, состоявшие исключительно из определений, аксиом и задач. Справившись с задачами, мы обсуждали наше решение с преподавателем, который должен был убедиться, что мы верно поняли предложенный материал.
Эта книга устроена аналогичным образом. Вы наверняка заметите, что в ней необычно много упражнений. Некоторые из них представляют собой концептуальные теоремы; другие вставлены просто для практики; многие выступают в обеих ролях. Идея в том, что, выполнив их одно за другим, вы сами построите квантовую механику — с моей минимальной помощью. Соответственно, пропускать упражнения не рекомендуется. Пропуск упражнения равнозначен пропуску страницы-другой в традиционном учебнике: вы не сможете понять последующий материал.
Почти все упражнения имеют решения, которые приведены на сайте книги[2]. Однако прошу не заглядывать туда до тех пор, пока вы хотя бы не попытаетесь выполнить упражнение самостоятельно. Даже при условии, что вам не удастся самому получить результат, вы поймете, на каком этапе ваше решение застопорилось, — и тогда готовое решение поможет вам, дав ответ на заранее сформулированный вопрос. Таким образом, семя упадет на уже удобренную почву.
Однако, даже если у вас есть собственное решение, я рекомендую вам все же заглянуть в мое. Таким образом вы получите представление об ошибках, которые вы (или я), возможно, сделали, или, скажем, об альтернативном подходе к решению той же задачи.
Упражнения, которые я считаю более сложными, помечены звездочкой*. Здесь есть тонкость. Дело в том, что многие из них содержат утверждения, важные для изучения последующего материала. Поэтому, хотя допустимо отложить выполнение этих упражнений (или подробный разбор их решений) на потом, вам следует по крайней мере разобраться в утверждениях, которые в них содержатся.
Некоторые из упражнений (они помечены символом параграфа §) даны без решений. Как правило, это происходит в тех случаях, когда я считаю задачу относительно простой; тогда я обычно привожу ответ сразу после упражнения. Очень редко встречаются упражнения, помеченные и звездочкой, и символом параграфа. Такие «упражнения», по сути, представляют собой независимые исследовательские проекты, которыми вам, возможно, захочется заняться в свободное время.
Какими знаниями вам, по моему мнению, следует уже обладать, прежде чем открывать эту книгу?
- Я исхожу из того, что вы накомы с тригонометрией (знаете, например, как представить cos (α + β) или cos α cos β в виде суммы).
- Вы умеете работать с комплексными числами, имеете представление о понятиях сопряженности, комплексной фазы и комплексной экспоненты (к примеру, можете упростить |1 + eiϕ|2).
- У вас есть общее представление о теории вероятностей. Здесь вам может помочь приложение Б, где содержатся некоторые основы этой области знания.
- То же относится к физике поляризации оптической волны: в приложении В кратко изложена необходимая информация, но его нельзя считать хорошей заменой соответствующего учебника.
- У вас есть навыки дифференциального исчисления и решения обыкновенных дифференциальных уравнений, которые необходимы при изучении всех частей книги, особенно главы 3 (квантовая физика систем с непрерывными переменными); это требование распространяется на анализ функций многих переменных (якобиан и т.п.) для главы 4. По дифференциальному исчислению нет специального приложения, но в приложении Г говорится о дельта-функции Дирака, а также о прямом и обратном преобразованиях Фурье, так что предварительные знания по математической физике не требуются.
- Первостепенное значение в квантовой физике играет линейная алгебра, включающая в себя понятия линейных пространств, базиса, размерности, скалярного произведения, ортонормального базиса, линейных операторов и матриц, спектральную теорему, функции операторов и т.п. Все это изложено в приложении A. Однако базовые методы работы с матрицами, такие как их перемножение, нахождение собственных векторов и собственных значений, не рассматриваются в этом приложении и должны быть знакомы вам до начала изучения данного курса.
Подробнее об этом лозунге, ошибочно приписываемом Фейнману, см. в разд. 2.4.
Во втором томе русского издания. — Прим. ред.
ПРЕДИСЛОВИЕ К РУССКОязычному ИЗДАНИЮ
Название этой книги — «Отличная квантовая механика» — отражает не только ее качество и даже не оценку, которую вы, возможно, получите на экзамене, изучив ее. Главное, что книга отличается от тех учебников квантовой физики, к которым мы привыкли. Вместо разбора волновых функций и потенциальных ям (с чего стартуют все курсы, начиная от Ландау и Лифшица) в этой книге речь пойдет о концептуально более простых и в то же время более сутевых и интересных вещах: пространстве состояний, сущности измерений, запутанности и нелокальности. Об этом я подробно рассказываю выше в предисловии к англоязычному изданию. Здесь же я хочу поговорить о другом.
«Дай бог побольше разных стран, не потеряв своей, однако». По мерке этих слов Евгения Евтушенко, я счастливый человек. Покинув Родину в двадцать лет, я обрел ее вновь в сорок, когда начал регулярно приезжать в Россию по делам, связанным с созданием Российского квантового центра и последующей научной работой в нем. Это возвращение подарило мне неугасающий душевный подъем, новую ступень для личностного роста и новый плацдарм для научных идей. Помимо этого, я смог увидеть и критически оценить — с высоты собственного преподавательского опыта — разницу в методах обучения физике в России и за рубежом.
У российско-советской школы немало заслуг перед мировой культурой — как в науке и технике, так и «в области балета». Одним из ее важнейших преимуществ является, как мне кажется, глубина рассмотрения материала, желание дойти до самой сути явления. Но у этой медали есть и оборотная сторона. Очевидно, что любая учеба — тяжелый, мучительный труд. No pain, no gain. Однако в западной системе образования имеет место сознательное стремление помочь студенту в этом труде, минимизировать его мучения посредством множества примеров и иллюстраций (и порой, к сожалению, излишне поверхностного изложения). Вероятно, это следствие рыночной экономики в сфере образовательных услуг: если студенту станет слишком трудно, он просто купит другой учебник или уйдет в другой университет. В советской же школе подобные стремления со стороны преподавателей почти полностью отсутствуют. Более того, зачастую имеется подспудное убеждение, что чем болезненнее студенту дается гранит науки, тем ему больше пользы, тем лучше он выучится. Это хорошо показано в фильме «Легенда № 17» на примере хоккея — но и в физике за примером далеко ходить не надо: достаточно открыть того же Ландафшица.
В своей книге я попытался взять лучшее из обеих школ. С одной стороны — постарался дойти до сути, дать ответы на все возможные вопросы, как бы сложны они ни были. С другой — «разжевать» материал, проиллюстрировать его в достаточной степени, сделать как можно меньше количество мест, где можно застопориться. Удалось ли мне это — судить вам.
Я хотел бы поблагодарить творцов русского перевода этой книги. Это в первую очередь директор по развитию Российского квантового центра Анна Шангина и генеральный директор Центра Руслан Юнусов, которые инициировали издание русской версии и его финансирование. Также благодарю руководителя проекта со стороны издательства Анну Тарасову — не только за пот и нервы, с которыми связана подготовка к печати любой книги, но и за внимание к моим авторским прихотям. Огромное спасибо редактору Анастасии Ростоцкой, проведшей со мной много вечеров на телефоне для совместного оттачивания формулировок. Удивительным образом Анастасия, не будучи профессиональным физиком, сумела найти ряд опечаток, которые я допустил в формулах (!) в английском оригинале. В чтении корректур решений к упражнениям оказали неоценимую помощь мои студенты и аспиранты: Дима Белобородов, Артем Иванов, Арсен Кужамуратов, Катя Сажина, Демид Сычев, Егор Тиунов, Саша Уланов и Митя Чермошенцев.
Несмотря на всю эту помощь, основная ответственность за опечатки и ошибки, которые могли остаться в переводе, лежит на мне. Я старался максимально тщательно вычитать его текст и гранки книги, но почти наверняка что-то упустил. Прошу сообщать мне о замеченных проблемах по электронной почте; адрес легко найти в интернете.
Вы без сомнения заметите, что всем главам предшествуют эпиграфы. Для них я использовал строки песен Михаила Щербакова. С его поэзией я познакомился больше двадцати лет назад и во многом благодаря ему сохранил живую связь с русским языком, которая совсем не помешала мне при подготовке этого текста. Включая эти эпиграфы в книгу, я хочу поделиться с вами своей любовью к творчеству этого автора, которая в моей душе не менее сильна, чем любовь к квантáм, пусть и безответна — ибо в квантовую физику я могу внести хотя бы какой-то вклад.
Оксфорд,
27 июня 2019 г.
Предисловие Российского Квантового Центра
Как много людей сталкивается в своей повседневной жизни со словосочетаниями «квантовая физика» или «квантовая механика». А сколько из них действительно понимают всю глубину, которая скрывается за этими понятиями? Думаю, ответ очевиден: немного (по крайней мере, меньше, чем хотелось бы). Квантовая механика является одной из самых сложных областей физики, которую приходится изучать студентам в технических вузах. В дополнение к далеко не самому простому математическому аппарату сложность этой дисциплины заключается в высокой степени абстракции рассматриваемых в ее рамках явлений. К тому же постулаты квантовой механики зачастую противоречат «здравому смыслу», что также не способствует быстрому освоению предмета. В результате существенная часть материала часто остается непонятой студентами, что значительно уменьшает их желание заниматься квантовой физикой в дальнейшем. В своем учебнике «Отличная квантовая механика» наш коллега и замечательный ученый Александр Львовский сделал вполне успешную попытку исправить сложившуюся ситуацию и, не теряя глубины изложения, объяснил многие сложные вещи простым языком, тем самым делая обучение живее и интереснее. На мой взгляд, Александр проделал титаническую работу по переосмыслению и структурированию одной из самых тяжелых областей физики, и я надеюсь, что эта книга вдохновит еще не одно поколение студентов на изучение столь сложной, многогранной, но при этом невероятно красивой науки — квантовой механики.
Руслан Юнусов,
генеральный директор Российского квантового центра
Благодарности
Мне потребовалось 13 лет, чтобы написать эту книгу, — я начал ее в январе 2005 г., а закончил в декабре 2017 г. Дату окончания работы над книгой запоминают часто, поскольку это, как правило, срок, заданный издателем (в моем случае срок сдачи переносился много раз на протяжении нескольких лет). Причина того, что я помню также дату начала, вот в чем: она соответствует семестру, когда я приступил к преподаванию вводного курса квантовой механики в Университете Калгари. Я тогда только-только пополнил ряды профессоров университета и, строго говоря, еще не должен был заниматься преподаванием. Однако, когда заведующий кафедрой Барт Хикс однажды подошел ко мне и мило спросил «Алекс, не хотели бы вы начать преподавание чуть раньше? Я слышал, ваши интересы связаны с квантáми, а у нас как раз есть место в расписании», я (наивный, романтично настроенный профессор-новичок) ответил «да». Вот тогда и появился первый рукописный конспект.
Но подлинная история плода начинается с корней. А поскольку эта книга во многом посвящена именно корням, имеет смысл следовать данному принципу и в этом разделе. Я могу проследить корни до 1962 г., когда мои родители Исай и Татьяна всего за несколько месяцев до того, как познакомились друг с другом в Москве, посмотрели «Девять дней одного года» — советский фильм о физиках, ставший в то время культовым. (Кстати говоря, вам тоже стоит посмотреть его, если будет возможность. Его несложно найти в онлайн-варианте с английскими субтитрами; он наверняка доставит вам удовольствие. И, между прочим, этот фильм проповедует вполне правильные ценности.) Культовость «Девяти дней…» быстро поблекла, но не для моих родителей. Так что моя будущая профессия была выбрана за 11 лет до моего рождения. Единственное, о чем не могли договориться родители, так это стоит ли мне стать академиком (в Советском Союзе это было аналогично статусу члена Королевского общества) или лауреатом Нобелевской премии. Мой дед примирил их, указав, что одно не мешает другому.
К счастью, мои природные наклонности не противоречили амбициям родителей — если не по величине, то по крайней мере по направлению. (Я иногда спрашиваю себя, кем мог бы стать, если бы был воспитан в другой семье. Мне кажется, либо автомехаником, либо программистом. Так что физик-экспериментатор представляется неплохим компромиссом.) Поэтому через несколько лет я оказался учащимся знаменитой московской школы № 57 (у школ в Советском Союзе были номера, а не названия) с углубленным преподаванием математики и физики. Именно там я на себе испытал сократовский принцип преподавания, о котором говорил в предисловии и на котором основана моя книга. Метод этот придумал московский учитель Николай Николаевич Константинов, но в нашем классе преподавал — и, соответственно, познакомил меня с данным методом — Борис Михайлович Давидович. Сюжет первых двух разделов приложения A и некоторые упражнения оттуда взяты прямо из моих школьных архивов.
Затем институт. Профессором, который открыл для меня квантовую физику и увлек ею, был Юрий Михайлович Белоусов. Он искусно сочетал строгость «старой школы» Льва Ландау и Евгения Лифшица с ярким, глубоким и страстным стилем преподавания: «Что такое состояние? Неопределяемое понятие! Как в геометрии: вы же не определяете, что такое точка или прямая, правда? Так же и с состоянием. Каково ваше состояние? Вы пьяный? Трезвый? Усталый? Вот вам состояние. Множество состояний называется пространством состояний. Опять же — почему нет? Но затем мы говорим, что это пространство линейно. А вот это уже претензия…»
Тем не менее, как тоже говорилось выше, не все мои вопросы получили ответы (и даже были правильно заданы) в институте, и мне пришлось долго искать их самостоятельно, уже после выпуска. В этом поиске меня поддерживали многие блестящие ученые. Назову лишь некоторых: Ален Аспе, Конрад Банашек, Мауро д’Ариано, Хауке Хансен, Петер Марцлин, Филипп Гранжье, Миклош Гуиласси, Пол Квят, Миша Лукин, Юджин Ползик, Майк Реймер, Барри Сандерс, Кристоф Симон, Эфраим Стейнберг, Иан Уолмсли, Син Вэй и Антон Цайлингер. Два имени я должен упомянуть отдельно: моего институтского научного руководителя Анатолия Викторовича Масалова, который познакомил меня с исследовательской деятельностью, и научного руководителя моей диссертации Свена Хартмана, или мистера Фотонное Эхо. Свен научил меня не только многому из физики, но и искусству писать научные тексты. Если в этой книге есть какой-то стиль, то благодаря ему.
Хотя мне трудно назвать одного-единственного человека, который оказал бы наибольшее влияние на формирование моих представлений о квантовой физике, я могу точно назвать период своей жизни, когда я достиг наибольшего прогресса. Я тогда работал постдоком в Университете Констанца, в институте, который возглавлял доктор Юрген Млынек. Этот институт в те годы был настоящей Меккой для квантовых физиков, там бывали лучшие умы, занимающиеся этой сферой науки. Иногда мне удавалось урвать несколько минут из их плотного расписания, чтобы обсудить с ними волновавшие меня вопросы, включая фундаментальные для квантовой физики (если только мне удавалось набраться храбрости и преодолеть страх показаться глупым или невежественным).
Теперь я хотел бы вновь вернуться к тому моменту, когда приступил к преподаванию Квантовой Механики I в Калгари и составил свои первые заметки. Впоследствии они переписывались и дополнялись десятки раз. Возможно, поворотным пунктом в превращении заметок в книгу стало добавление в них решений к упражнениям. Первоначально их там не было; я просто излагал решения устно на лекциях (я до сих пор не понимаю, как те студенты умудрялись сдавать экзамены). Но затем у меня состоялось два важных разговора. Во-первых, я поговорил с профессором Массачусетского технологического института Джеффом Шапиро, научившим меня многому в квантовой оптике во время наших (увы, кратких) встреч. Я сообщил Джеффу об идее превратить свои лекционные записи в книгу и о сократовском методе. Джефф серьезно посмотрел на меня и спросил: «Но ведь у задач будут и решения… Правда?» А во-вторых, почти чудесным образом, примерно в то же время, ко мне подошли два моих студента, Джефф Кэмпбелл и Даллас Хоффман. «С решениями ваши заметки станут намного лучше. Мы подумали, может быть, нам стоило бы написать некоторые из них?» И они сделали это — многие решения для упражнений из глав 1, 2 и приложения A принадлежат им, и я очень благодарен этим ребятам.
На самом деле поддержка студентов была чрезвычайно важна на всех этапах создания этого труда. Начиная с 2005 г. я преподавал Квантовую Механику I шесть раз примерно 200 студентам, и многие из них внесли в книгу важный вклад. Вот их имена: Рассел Бейт, Данте Бенчивенга, Трэвис Брэннан, Артур Бери-Джоунз, Авик Чандра, Хосе да Коста, Иш Дханд, Стефан Донса, Марк Жирар, Крис Хили, Катаня Кунтц, Кимберли Оуэн, Адарш Прасад, Мэтью Ричардс, Стивен Роговски, Мэттью Таунли-Смит, Раджу Валивартхи. Помощь студентов состояла не только в построении решений; они постоянно искали ошибки и задавали многочисленные вопросы, которые позволяли мне увидеть, какие части текста недостаточно понятны и требуют пояснений. Опять же, я не смогу назвать всех, кто мне помогал, поэтому должен попросить прощения у тех, кого не упомянул.
Поскольку вдохновением для создания данного метода обучения во многом послужил мой собственный опыт в старшей школе, я всегда хотел опробовать его в той же обстановке. Мне это удалось в 2013 г., когда я взял академический отпуск в своем университете, чтобы помочь в создании Российского квантового центра в Москве. Я организовал кружок по квантовой физике для московских школьников. Вместе с командой преподавателей-энтузиастов во главе с Алексеем Федоровым мы еженедельно встречались с учащимися, чтобы выслушать, как они решили задачи из конспекта (решений мы им не давали), исправить их ошибки, объяснить тонкости и — что не менее важно — обсудить сам конспект. Отзывы, полученные в ходе этих дискуссий, сыграли важную роль в формировании настоящего текста, а несколько участников кружка, включая Алексея, теперь стали профессиональными учеными, занимающимися исследованиями квантовых технологий на постоянной основе.
Я хотел бы поблагодарить Стефана Лайла за тщательную вычитку книги и множество разумных замечаний.
Но самую свою горячую благодарность я выражаю своей жене Бхавии Равал. Сейчас, когда я пишу эти строки, она в пути — едет забирать нашу дочку Софи от дедушки. Это лишь одна из многих сотен ситуаций, в которых мне следовало бы, по идее, быть с семьей, а не прятаться за монитором, выводя на экране странные закорючки. Но теперь даже бесконечное терпение Бхавии, кажется, истощается. Вчера мы по ее совету посмотрели фильм «Париж подождет», в котором жена одного парня, который слишком много работает, позволяет соблазнить себя его коллеге-французу. Дорогая, намек понят. Париж больше не может ждать. И это последнее предложение, которое я добавляю в книгу!
Калгари, 10 декабря 2017 г.
Учебное пособие
Квантовые постулаты
А дальше — стоп.
А дальше, извини, стена.
1.1. Предмет квантовой механики
Пожалуй, первое, что нужно понять о квантовой механике, — это то, что к механике она имеет такое же отношение, как, скажем, к электродинамике, оптике, физике конденсированного состояния или высоких энергий. Квантовая механика, по существу, не описывает какой-то конкретный класс физических явлений; скорее, она обеспечивает универсальную теоретическую основу, которую можно использовать во всех областях физики, — так операционная система компьютера обеспечивает базу, на которой могут исполняться другие приложения. Употребление термина «квантовая механика» сложилось исторически, поскольку впервые квантовую основу удалось успешно применить при исследовании механического движения электронов в атоме. Более удачными терминами были бы «квантовая физика» или «квантовая теория».
Так что предмет квантовой механики (квантовой физики) глобален: она охватывает все физические явления во Вселенной. Однако применять квантовый подход имеет смысл только в случае очень маленьких (микроскопических) физических систем. Поведение более крупных систем очень хорошо аппроксимируется законами классической физики, намного более простыми и интуитивно понятными, по крайней мере для существ, эволюция которых проходила именно на этом масштабе величин.
Проиллюстрируем это примером. Вы, вероятно, слышали о принципе неопределенности Гейзенберга: ∆p∆x ≳ ℏ/2. То есть координату и импульс частицы невозможно измерить точно и одновременно: произведение неопределенностей составляет по крайней мере ℏ/2 ≈ 5 × 10−35 кг∙м2/с. Чтобы макроскопический объект с массой порядка килограмма достиг предела неопределенности, потребовалось бы измерить и координату объекта с точностью порядка ~ 10–17 м и скорость с точностью ~ 10–17 м/с. Это, разумеется, нереально, так что для всех практических целей мы можем просто забыть о принципе неопределенности и рассматривать координату и импульс как точные величины. Но для электрона массой ~ 10–30 кг произведение неопределенностей координаты и скорости составит около 5 × 10–5 м2/с, что вполне укладывается в экспериментально доступную точность измерений и должно приниматься во внимание.
Таким образом, предсказания квантовой теории отличаются от классических только для относительно простых, микроскопических объектов. Это объясняет, почему квантовая механика была открыта лишь в начале XX в. До того времени мы (сами представляющие собой макроскопические тела) имели дело исключительно с макроскопическими предметами. Но стоило нам изобрести инструменты, позволяющие достаточно глубоко проникать в микроскопический мир, как сразу же проявились квантовые явления.
Это пример принципа соответствия — философской максимы, согласно которой любая новая, более современная теория должна воспроизводить результаты более старых, устоявшихся теорий в тех областях, где эти теории были проверены. Вот еще один пример для иллюстрации этого принципа. Пока мы имели дело только с объектами, движущимися намного медленнее света, для описания окружающего нас мира достаточно было ньютоновой механики. Но стоило нам получить возможность наблюдать тела, которые движутся быстро (например, Земля вокруг Солнца в эксперименте Майкельсона — Морли), мы начали замечать несоответствия и вынуждены были разработать теорию относительности. Эта теория заметно отличается от ньютоновой механики — но тем не менее согласуется с ней в предельном случае низких скоростей. Было бы неразумно использовать специальную теорию относительности для описания, например, трансмиссии трактора, потому что классическое приближение в данном случае и вполне достаточное, и многократно более простое в применении. Аналогичным образом использование квантовой физики для описания макроскопических явлений в большинстве случаев было бы переусложненным и ненужным.
В классической физике мы имеем дело с величинами: скоростью полета камня 10 м/с, силой протекающего по электрическому контуру тока 0,2 А и т.д. Даже если мы не знаем точного значения какой-то физической величины, мы можем работать над улучшением нашей теории и эксперимента, чтобы предсказать и измерить эту величину со все более высокой точностью. Иными словами, классический мир бесконечно познаваем. В квантовой физике ситуация иная: некоторые знания (например, одновременные значения координаты и импульса) могут быть «священными»: их в принципе невозможно получить. И эту ситуацию уже нельзя описывать в терминах одних только величин. Вместо этого мы должны использовать концепцию квантового состояния физической системы. Как мы увидим, эта концепция содержит в себе границу между знанием, которое можно получить, и знанием, которое получить невозможно. Мы можем узнать точно, в каком состоянии находится система, но каждое состояние связано с фундаментальными ограничениями на точность, с которой физические величины могут быть определены.
Поскольку квантовая механика играет уже упомянутую роль общей основы, мы изучаем ее с известной степенью математической строгости. Я буду вводить определения и аксиомы, потом описывать явления, которые из них проистекают, а затем иллюстрировать эти явления примерами из разных областей физики, преимущественно из оптики.
Основной математический инструмент квантовой механики — линейная алгебра. В приложении A приводятся концепции этой дисциплины, важные для квантовой физики. Так что, если вы знакомы с линейной алгеброй и свободно себя в ней чувствуете, переходите сразу к следующему разделу. В противном случае я рекомендовал бы вам, прежде чем двигаться дальше, изучить первые четыре раздела приложения A.
1.2. Постулат гильбертова пространства
Я сначала сформулирую этот постулат[3], а затем объясню его смысл более подробно.
a) Возможные состояния физической системы образуют гильбертово пространство над полем комплексных чисел.
b) Несовместимые квантовые состояния соответствуют ортогональным векторам.
c) Все векторы, представляющие физические квантовые состояния, нормированы.
Данный постулат содержит два понятия, которые мы еще не определили: квантовое состояние и физическая система. Понятия эти настолько фундаментальны, что строгое определение им дать трудно[4]. Поэтому я проиллюстрирую их интуитивно, на примерах.
Физическая система — это объект или даже одна либо несколько степеней свободы объекта, которые можно изучать независимо от остальных степеней свободы и других объектов. Например, если наш объект — атом, то квантовая механика может изучать его движение как целого (одна физическая система), а может исследовать движение его электронов вокруг ядра (другая физическая система). Но если мы хотим изучать образование из двух атомов молекулы, то нам следует учитывать, что динамические состояния обоих атомов и электронов в них влияют друг на друга, поэтому мы должны рассматривать все эти степени свободы как единую физическую систему. Если же речь идет о самой молекуле, то квантовая механика может изучать движение ее центра масс (одна физическая система), вращательное движение (другая физическая система), колебания ее атомов (третья система) или квантовые состояния ее электронов (четвертая система) и т.д.
Чтобы разобраться в понятии состояния, рассмотрим следующую физическую систему: массивную частицу, которая может двигаться вдоль координатной оси x. С одной стороны, возможно определить ее квантовое состояние, сказав, что «координата частицы — в точности x = 5 м». Это допустимое определение; мы будем обозначать такое состояние как |x = 5 м⟩. Еще одно допустимое состояние можно обозначить как |x = 3 м⟩. Эти состояния ортогональны (⟨x = 5 м| x = 3 м⟩ = 0), потому что «несовместимы»: если достоверно известно, что координата частицы равна 5 м, она не может быть обнаружена в состоянии x = 3 м. Еще один пример допустимого квантового состояния, в котором частица может находиться, — это «движется со скоростью 푣 = 4 м/с». Поскольку в таком состоянии импульс частицы известен точно, ее координата остается полностью неопределенной — т.е. данная частица может быть с некоторой вероятностью обнаружена в точке x = 5 м. Следовательно, скалярное произведение ⟨x = 5 м| 푣 = 4 м/с⟩ не равно нулю; эти состояния не являются несовместимыми.
Данный постулат гласит также, что если |x = 5 м⟩ и |x = 3 м⟩ — допустимые квантовые состояния, то состояние
Являются ли суперпозиции состояний математической абстракцией или они каким-то образом отражаются в физическом поведении системы? Верно, конечно же, второе. Как мы вскоре увидим, если подвергнуть, например, кошку в состояниях
Напрашивается еще один вопрос. Мы не видим состояний суперпозиции в повседневной жизни — хотя они полностью совместимы с канонами квантовой механики. Почему? Как мы узнаем из следующей главы, дело в том, что суперпозиции макроскопически различных состояний чрезвычайно хрупки и быстро переходят в один из своих компонентов — в случае кошки Шрёдингера та быстро становится либо живой, либо мертвой. В микроскопическом мире, однако, состояния суперпозиции относительно устойчивы и нужны для физического описания системы. Необходимость иметь дело с объектами, само существование которых вступает в противоречие с нашим повседневным опытом, — одна из причин того, почему квантовая механика так сложна для понимания.
Упражнение 1.1. Чему равен нормирующий множитель 풩 состояния кошки Шрёдингера |ψ⟩ = 풩 [2|жива⟩ + i|мертва⟩], гарантирующий, что |ψ⟩ — физическая система?
Упражнение 1.2. Какова размерность гильбертова пространства, связанного с одной кинетической степенью свободы массивной частицы?
Подсказка: если вам кажется, что ответ очевиден, загляните в решение.
1.3. Поляризация фотона
Мы начнем изучение квантовой механики с одной из простейших физических систем: поляризации фотона[6]. Размерность гильбертова пространства этой системы равна всего лишь двум, но этого вполне достаточно, чтобы показать, насколько поразительным может быть мир квантовой механики.
Предположим, что мы в состоянии выделить единичную частицу света — фотон — из поляризованной волны. Фотон — микроскопический объект, поэтому рассматривать его следует в рамках квантовой механики. Начнем с того, что определим связанное с ним гильбертово пространство. Для начала отметим, что горизонтально поляризованное состояние фотона, которое мы обозначим |H⟩, несовместимо с его вертикально поляризованным состоянием |V⟩: фотон |H⟩ невозможно обнаружить в состоянии |V⟩. То есть если мы приготовим горизонтально поляризованный фотон и прогоним его через поляризующий светоделитель (PBS, polarizing beam splitter) — оптический элемент, описанный в разд. В.2, то данный фотон во всех случаях будет проходить насквозь, а отражаться не будет никогда. Это означает, что состояния |H⟩ и |V⟩ ортогональны.
Мы постулируем, что световая волна, электрическое поле которой задано в виде функции координаты и времени [см. (В.2)]
(с действительными AH,V и ϕH,V), состоит из фотонов в состоянии[7]
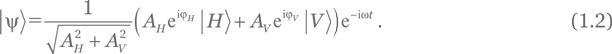
Отступление 1.1. Открытие фотона
В 1900 г. Макс Планк объяснил экспериментально наблюдаемый спектр излучения абсолютно черного тела, введя понятие кванта света, который мы сегодня знаем как фотон[8]. Он обнаружил, что хорошее совпадение теории и эксперимента можно получить, если считать, что энергия фотона пропорциональна частоте ω световой волны. Коэффициент пропорциональности ℏ = 1,05457148 × 10−34 получил название постоянной Планка.

В 1905 г. Альберт Эйнштейн еще раз подтвердил обоснованность формулы Планка
E = ℏω,
воспользовавшись ей для количественного объяснения экспериментальных результатов по фотоэлектрическому эффекту (более подробно см. отступление 4.6[9]. Позже, в 1916 г., Эйнштейн сделал вывод, что, поскольку из классической электродинамики[10] известно, что электромагнитный волновой пакет, несущий энергию E, несет также импульс p = E/c, это же соотношение должно выполняться и для фотонов. По формуле Планка он нашел[11] p = ℏω/c. Выразив частоту волны через ее длину, он получил ω = 2πc/λ, а затем записал
p = 2πℏ/λ.

Артур Холли Комптон в 1923 г. использовал результаты Эйнштейна для теоретического объяснения собственных экспериментов, в которых он исследовал рассеяние рентгеновских лучей на свободных электронах[12]. Рассматривая фотоны рентгеновского излучения как частицы высоких энергий, он применил законы сохранения энергии и импульса к столкновению между фотоном и электроном, чтобы рассчитать энергию рассеянных фотонов в зависимости от угла рассеяния. Затем он соотнес эту энергию с длиной волны — и получил теоретическое описание для своих экспериментальных данных. Увиденное им превосходное совпадение тех и других стало служить наглядным доказательством существования фотона.
Интересно отметить, что термина «фотон» в то время не существовало. Его ввел в 1926 г. специалист по физической химии Гильберт Льюис[13].
Например, если AH = AV и ϕH = ϕV = 0, то соответствующая классическая волна выглядит как
Из этого следует, что состояния |H⟩ и |V⟩ образуют в гильбертовом пространстве поляризационных состояний фотона ортонормальный базис — т.е. пространство двумерно. Действительно, прежде всего эти состояния ортогональны и потому линейно независимы (упр. A.17). Кроме того, любая поляризованная классическая волна может быть записана в виде (1.1), так что любое поляризационное состояние фотона тоже может быть записано аналогично (1.2), т.е. как линейная комбинация состояний |H⟩ и |V⟩. Мы будем называть базис {|H⟩,|V⟩} каноническим базисом нашего гильбертова пространства.
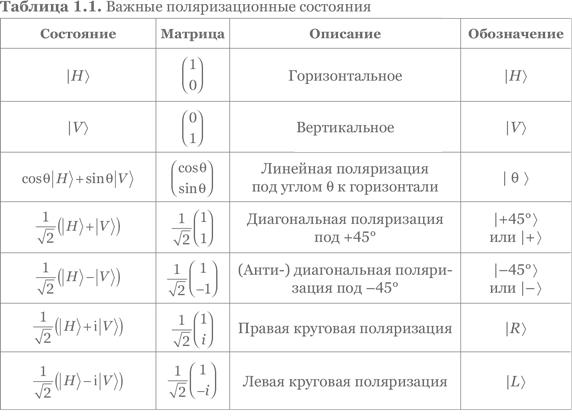
Упражнение 1.3. Покажите, что:
a) поляризационные состояния ±45° образуют ортонормальный базис;
b) правое и левое круговые поляризационные состояния образуют ортонормальный базис.
Упражнение 1.4. Разложите |H⟩ и |V⟩ по базисам {|+⟩,|–⟩} и {|R⟩,|L⟩}.
Упражнение 1.5. Разложите |a⟩ = |+30°⟩ и |b⟩ = |–30°⟩ по базисам {|H⟩,|V⟩}, {|+⟩,|–⟩} и {|R⟩,|L⟩}. Найдите скалярное произведение ⟨a|b⟩ во всех трех базисах, используя операцию перемножения матриц. Одинаковые ли получились результаты?
Здесь есть сложный момент, который следует прояснить. Множество углов поляризации линейно поляризованных фотонов — континуум. Но в случае одномерного движения частицы, о котором говорилось в предыдущем разделе, множество позиционных состояний — также континуум. Почему же мы говорим, что одно из этих гильбертовых пространств имеет размерность два, а другое — бесконечность?
Разница в том, что линейно поляризованные состояния могут быть записаны в виде (1.2), т.е. в виде суперпозиции других линейно поляризованных состояний. Если мы поместим поляризующий светоделитель (разд. В.2), пропускающий только горизонтально поляризованные фотоны, на пути диагонально поляризованной волны, часть ее пройдет сквозь светоделитель. Это означает, что диагонально поляризованный фотон может быть обнаружен в горизонтальном поляризационном состоянии.
Состояния же, связанные с разными положениями в пространстве, напротив, все ортогональны: частицу, приготовленную в состоянии |x = 3 м⟩, невозможно обнаружить в точке x = 4 м. Также невозможно записать позиционное состояние в виде суперпозиции других позиционных состояний. Это значит, что соответствующее гильбертово пространство должно иметь намного более широкий базис, чем гильбертово пространство поляризационных состояний.
Для классической волны (1.1) сдвиг фаз одновременно горизонтального и вертикального компонентов на равную величину (т.е. ϕH → ϕH + ϕ0, ϕV → ϕV + ϕ0, что эквивалентно умножению правой части на
Аналогичное правило применимо и к квантовым состояниям. Умножение вектора состояния на eiϕ не меняет физической природы состояния. К примеру, |V⟩, i|V⟩ и –|V⟩ представляют один и тот же физический объект, как и, скажем,
Мы называем комплексную величину eiϕ с действительным ϕ фазовым множителем. Умножение квантового состояния на фазовый множитель называется применением фазового сдвига на ϕ. Соответственно мы говорим, что применение фазового сдвига к квантовому состоянию не меняет его физических свойств. Как мы увидим в следующем разделе, это правило оказывается весьма общим: оно выполняется для всех физических систем, не только для электромагнитных волн. Разумеется, фазовый сдвиг должен быть глобальной природы (overall phase shift): если мы применим его только к части состояния, это состояние изменится. Например, если мы применим фазовый сдвиг на π/2 к вертикальному компоненту поляризованного под +45° фотона,
Поляризация фотона — это реализация квантового бита (кубита). Данный термин используется для обозначения любой физической системы, гильбертово пространство которой двумерно, в контексте рассмотрения этой системы как носителя информации. Кубит — базовая единица квантовой информации, по аналогии с битом — единицей информации в классических компьютерах. В противоположность последнему квантовый бит может находиться не только в одном из двух базовых состояний, но и в их суперпозиции. Это открывает для нас множество новых технологических возможностей, которые мы будем обсуждать на протяжении всей книги.
1.4. Квантовые измерения
1.4.1. Постулат об измерениях
Второй постулат относится к квантовым измерениям, т.е. к экспериментам, цель которых — получить информацию о квантовом состоянии некоторой системы. В классической, макроскопической физике измерения больше вопрос технологии, чем фундаментальной науки. Дело в том, что там мы можем точно измерить состояние и эволюцию системы, не потревожив ее. Так, футбольный мяч не полетит разными способами в зависимости от того, пуст стадион или заполнен до отказа восторженными болельщиками, — следовательно, нам не нужно знать, каким методом фиксируют траекторию мяча, чтобы изучить законы его движения.
В квантовом мире ситуация выглядит иначе: мы велики, а те объекты, которые мы хотим измерить, малы. Поэтому любое измерение, скорее всего, изменит квантовое состояние нашей системы. В более общем плане можно сказать, что квантовые измерения — это события, при которых состояние микроскопического квантового объекта влияет на состояние макроскопического прибора. Таким образом, измерение пересекает границу между квантовым и классическим царствами физики. А как мы знаем, законы, управляющие ими, сильно различаются между собой. Чтобы получить цельную картину мира, нам необходимо понять, когда и как происходит переход между этими двумя «юрисдикциями».
Далее, явления, при которых квантовое состояние чего-то микроскопического влияет на что-то макроскопическое, не ограничены стенами лабораторий. К ним относятся самые разные события — от термодинамических фазовых переходов и лазерной генерации до ураганов, рождения черных дыр и, возможно, рождения самой Вселенной. Физика подобных явлений аналогична физике квантовых измерений. Из этого следует, что разобраться в этой физике необходимо для понимания природы окружающего нас мира.
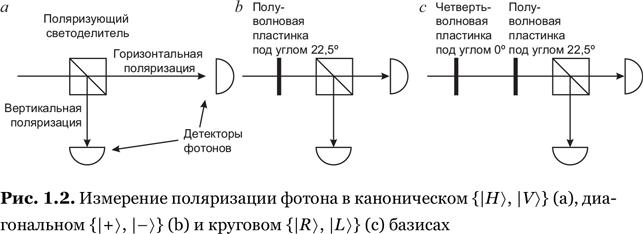
Основные принципы постулата об измерениях можно вывести интуитивно. Предположим, что фотон в состоянии (1.2) попадает в поляризующий светоделитель (PBS) — оптический элемент, который пропускает горизонтально поляризованный свет, но отражает вертикально поляризованный (рис. 1.2 a). Что произойдет с этим фотоном? Если бы мы имели дело с классической волной (1.1), то сказали бы, что она разделится: часть ее пройдет сквозь PBS, а остальное отразится. Доли энергии, попадающие в прямой и отраженный каналы, были бы пропорциональны
Мы подошли к очевидному противоречию. Мы знаем, с одной стороны, что классическая волна, состоящая из фотонов, делится на части. С другой — что каждый отдельный фотон неделим. Как могут два этих требования выполняться одновременно?
Представляется, что единственный способ разрешить данный парадокс состоит в том, чтобы постулировать, что результат в таком случае будет случайным: фотон пройдет через PBS с вероятностью
Как мы знаем, часть классической волны, проходящая через PBS, является горизонтально поляризованной, т.е. все фотоны, из которых состоит эта волна, находятся в состоянии |H⟩. Аналогично все фотоны отраженной волны находятся в состоянии |V⟩. Но тогда это же должно быть верно и в случае, когда фотоны попадают в PBS по одному. Фотон будет не только случайным образом выбирать свой путь, но также и, вполне в духе Оруэлла, изменять свое состояние, чтобы соответствовать выбранному пути. После PBS состояние фотона в прямом канале станет |H⟩, а в отраженном — |V⟩. Если мы поместим серию дополнительных PBS на пути фотона, прошедшего через первый светоделитель, то фотон пройдет также и через все эти PBS — никаких случайностей больше не будет.
Процесс, который я только что описал, представляет собой измерение состояния поляризации фотона. Чтобы его завершить, поместим по детектору одиночных фотонов (отступление 1.2) в оба выходящих канала PBS. Из этих двух детекторов один сработает («щелкнет» на квантовом жаргоне), снабдив нас информацией о характере поляризации фотона (рис. 1.2 a).
Описанный измерительный прибор предназначен для того, чтобы различать горизонтальную и вертикальную поляризации. Существуют и другие схемы. Например, наклонив PBS на 45°, мы заставим его пропускать состояние |+⟩ и отражать |–⟩, так что, если мы направим на такой PBS фотон в произвольном состоянии |ψ⟩, он пройдет или отразится с вероятностями pr+ = |⟨+|ψ⟩|2 и pr_ = |⟨-|ψ⟩|2 соответственно. Вообще, мы можем сконструировать измерительный прибор, различающий любые два состояния поляризации, при условии что эти состояния ортогональны друг другу.
Теперь мы готовы сформулировать наш постулат.
Отступление 1.2. Как обнаружить фотон?
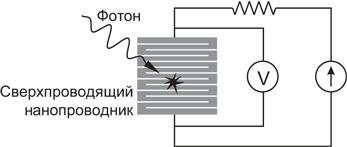
Детектор фотонов представляет собой устройство, которое преобразует фотон в «щелчок» (click) — макроскопический импульс электрического тока или напряжения. Изготовить столь чувствительное устройство — непростая техническая задача. На рисунке схематично изображен один из современных способов выполнения этой задачи: сверхпроводящий детектор единичных фотонов.
Чувствительным элементом детектора является охлажденный до сверхпроводящего состояния нанопроводник, по которому течет небольшой постоянный ток. Нанопроводник настолько тонок, что при поглощении даже одного фотона он нагревается достаточно, чтобы стать резистивным на части длины. Ток, в соответствии с законом Джоуля — Ленца, начинает нагревать этот участок проводника, еще сильнее разрушая сверхпроводимость вокруг него. Развивается лавинообразный процесс, так что весь нанопроводник на какое-то время становится резистивным. Это сопротивление и дает на концах нанопроводника импульс напряжения, который несложно зарегистрировать.
У такого детектора есть несколько недостатков, типичных для реальных фотонных устройств. Во-первых, это недискриминирующий детектор: на пучок из множества фотонов он реагирует точно таким же импульсом, что и на одиночный фотон. Происходит это потому, что нанопроводник, сколько бы фотонов он ни поглотил, целиком теряет сверхпроводимость и приобретает одинаковое сопротивление (замечу, что в последнее время научились делать и дискриминирующие детекторы, использующие эту технологию). Во-вторых, фотон, попадающий на детектор, может отразиться — и тогда никакого щелчка не будет. Вероятность того, что на прилет одиночного фотона детектор отреагирует щелчком, известна как квантовая эффективность (quantum efficiency) детектора. В некоторых современных модификациях этот параметр превосходит 99%. И в-третьих, детектор может выдать щелчок даже в отсутствие фотона. Частота таких темновых событий (dark counts) — еще одна важная техническая характеристика прибора.
Постулат об измерениях. Всякий идеальный измерительный прибор связан с некоторым ортонормальным базисом {|푣i⟩}. После измерения прибор случайным образом, с вероятностью
pri = |⟨푣i|ψ⟩|2, (1.3)
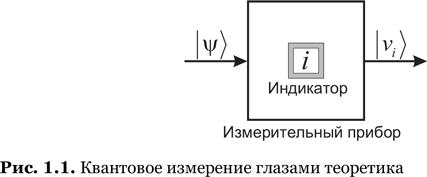
где |ψ⟩ — начальное состояние системы, укажет на одно из состояний |푣i⟩. Система при этом, если не разрушится, перейдет в состояние |푣i⟩ (спроецируется на него) (рис. 1.1).
Квантовое измерение, протекающее в соответствии с приведенным выше постулатом, называется проективным измерением. Проекция измеренного состояния на один из элементов базиса именуется также коллапсом квантового состояния. Уравнение (1.3) — это правило Борна.
Вероятностное поведение квантовых объектов вызывало множество споров в те времена, когда квантовая механика только зарождалась. Дело в том, что к концу XIX в. общепринятым считался принцип детерминизма: физики уверенно полагали, что, если бы начальные условия заданной квантовой системы были известны с достаточной точностью, ее развитие можно было бы предсказать сколь угодно хорошо. Квантовая физика разрушила данное фундаментальное убеждение, и многим физикам оказалось чрезвычайно трудно это принять. Например, Альберт Эйнштейн сделал по данному поводу свое знаменитое заявление, что «Бог не играет в кости», и предложил блестящий Gedankenexperiment[15], показывающий, что постулаты квантовой механики противоречат здравому смыслу. Мы разберем этот мысленный эксперимент в следующей главе и увидим, как квантовую случайность можно объяснить тем, что сами наблюдатели тоже являются квантовыми объектами, но не могут экспериментально убедиться в своей квантовой природе. Давайте, однако, пока примем квантовую случайность как постулат, который подтверждается большим объемом экспериментальных данных.
Упражнение 1.6. Покажите математически, что для состояния |ψ⟩ сумма вероятностей регистрации (1.3) для всех элементов базиса составляет ⟨ψ|ψ⟩, т.е. равна единице, если состояние физическое.
Упражнение 1.7. Покажите, что применение общего фазового множителя к квантовому состоянию не меняет вероятностей результатов его измерения — в согласии с тем фактом, что фаза никак не влияет на физику состояния, о чем говорилось в предыдущем разделе.
1.4.2. Измерения поляризации
Выше мы говорили о возможности повернуть PBS и изменить в результате этого прибор на рис. 1.2a так, что он будет измерять поляризацию в неканоническом, линейно поляризованном базисе. Однако фотон, отраженный PBS, не станет распространяться в горизонтальном направлении, а это неудобно при проведении практического лабораторного эксперимента (отступление 1.3). Поэтому большинство экспериментаторов пользуется оптическим элементом, известным как волновая пластинка[16], который переводит поляризованные состояния фотона одно в другое. Вот несколько примеров.
Упражнение 1.8. Покажите, что:
a) устройство на рис. 1.2b выполняет измерение поляризации фотона в диагональном (|±45º⟩) базисе;
b) устройство на рис. 1.2c выполняет это же измерение в круговом ( {|R⟩,|L⟩}) базисе.
Подсказка: когда устройство, описанное в постулате об измерениях, измеряет одно из своих собственных базисных состояний |푣i⟩, то результат измерения укажет на это состояние с вероятностью 1. Верно и обратное: если это устройство способно строго различить некий конкретный ортонормальный набор состояний, то мы можем сделать вывод, что этот набор является измерительным базисом данного устройства. Следовательно, чтобы выполнить это упражнение, достаточно показать, что базисные состояния [т.е. |±45º⟩ в варианте a) и |R⟩, |L⟩ в варианте b)] после PBS дадут щелчки на разных фотонных детекторах.
Отступление 1.3. Оптический стол

На этой фотографии вы видите типичный квантово-оптический эксперимент. Он выполняется на оптическом столе — массивной металлической плите, на которую устанавливаются различные оптические элементы, такие как линзы, зеркала, лазеры, кристаллы и детекторы. Лучи, как правило, проходят горизонтально, на одном уровне по всей длине стола.
Упражнение 1.9.§ Каждое из состояний |H⟩, |V⟩, |+⟩, |–⟩, |R⟩, |L⟩ измеряется в
a) каноническом,
b) диагональном,
c) круговом базисах.
Найдите вероятности возможных результатов для каждого случая.
Ответ: для каждого состояния, когда измерение производится в базисе, к которому принадлежит это состояние, вероятности составляют 0 и 1. Если же состояние не принадлежит к измерительному базису, то вероятность обоих результатов равняется
Упражнение 1.10. Предложите схему для квантового измерения в базисе
Упражнение 1.11. Предложите схему для квантового измерения в базисе {|R⟩, |L⟩}, в которой использовалась бы только одна волновая пластинка.
Упражнение 1.12. Рассмотрим фотон, который находится в состоянии не суперпозиции, а случайной статистической смеси, или ансамбля[17] (statistical mixture/ensemble): либо |H⟩ с вероятностью 1/2, либо |V⟩ с вероятностью 1/2. Поляризация этого фотона измеряется в:
a) каноническом,
b) диагональном,
c) круговом базисах.
Найдите вероятности возможных результатов для каждого случая.
Упражнение 1.13. Фотон приготовлен с линейной поляризацией 30º к горизонтали. Найдите вероятность каждого результата, если его поляризация измеряется в:
a) каноническом,
b) диагональном и
c) круговом базисах.
Упражнение 1.14. Фотон в состоянии
Это упражнение, так же как и упр. 1.7, еще раз демонстрирует важную разницу между фазовым множителем, примененным к части квантового состояния или к квантовому состоянию целиком. В первом случае добавочная фаза влияет на измеряемые свойства объекта, во втором — нет.
Хотя одиночное измерение дает нам некоторую информацию о начальном состоянии квантовой системы, информация эта очень ограничена. Предположим, например, что мы измерили фотон в каноническом базисе и обнаружили, что он прошел через PBS. Можем ли мы из этого сделать вывод, что первоначальный фотон находился в состоянии |H⟩? Нет, не можем. Он мог находиться в любом состоянии ψH |H⟩ + ψV |V⟩; коль скоро ψH ≠ 0, существует некоторая вероятность получения щелчка в пропускающем канале. Поэтому единственное, что мы узнаем из данного измерения, — это то, что фотон не был вертикально поляризован.
Теперь предположим, что мы провели одно и то же измерение неоднократно, каждый раз приготавливая наш фотон в одинаковом состоянии[18]. Теперь мы знаем намного больше! Мы знаем, сколько щелчков получено нами от «горизонтального» детектора, а сколько — от «вертикального», т.е. у нас появилась статистика измерений. По этим данным мы можем рассчитать, с некоторой ошибкой, prH = |ψH|2 и prV = |ψV|2, т.е. узнать кое-что об абсолютных величинах компонентов состояния. Но и ψH, и ψV — комплексные числа, и их аргументы (углы на комплексной плоскости) по-прежнему неизвестны. К примеру, если мы наблюдаем prH = prV = 1/2, то состояние |ψ⟩ может быть или |R⟩, или |L⟩, или |+⟩, или |–⟩, или еще каким-нибудь из множества вариантов. Что нам с этим делать?
Как видно из следующего упражнения, надлежит провести дополнительные серии измерений в других базисах. Полученная статистика даст новые уравнения, которые можно решить и найти ψH и ψV с точностью до неопределенности, связанной с общим фазовым множителем.
Упражнение 1.15. Предположим, что множественные измерения поляризации фотонов, идентично приготовленных в состоянии |ψ⟩, проводятся в каноническом, диагональном и круговом базисах и при этом определяются все шесть соответствующих вероятностей (prH, prV, pr+, pr — , prR, prL). Покажите, что этой информации достаточно, чтобы полностью определить |ψ⟩ и выразить его разложение в каноническом базисе через prH, pr+ и prR. Приведите пример, показывающий, что измерений только в каноническом и диагональном базисах для этого было бы недостаточно, — т.е. найдите два различных состояния, которые дадут одинаковые prH и pr+.
Метод получения полной информации о квантовом состоянии путем проведения серий измерений в нескольких разных базисах на множестве идентичных копий измеряемого состояния называется томографией квантового состояния (quantum state tomography). Его можно обобщить на другие квантовые системы, включая системы более высокой размерности. Мы подробнее поговорим о квантовой томографии в конце основного текста (разд. 5.7).
Упражнение 1.16. Предположим, вам дан единственный экземпляр квантовой системы, находящейся в одном из двух неортогональных состояний |a⟩ и |b⟩. Вам известно, что это за состояния, но вы не знаете, в каком именно из них находится система.
a) Покажите, что невозможно построить устройство, которое всегда достоверно определяло бы состояние системы.
b) * Покажите, что можно сконструировать измерительное устройство, которое будет выдавать, с некоторой вероятностью, результаты трех типов: «определенно |a⟩», «определенно |b⟩» и «не уверен», причем результаты первых двух типов всегда будут верными.
Подсказка: попробуйте использовать неполяризующий светоделитель — оптический элемент, который случайным образом либо пропускает, либо отражает фотон вне зависимости от его поляризации.
1.5. Квантовая интерференция и дополнительность
Рассмотрим эксперимент, показанный на рис. 1.3. Единичный фотон, находившийся первоначально в диагонально поляризованном состоянии
Линия задержки вводит разницу между оптической длиной пути вертикального и горизонтального компонентов. Если длина этой линии равна l, то вертикальный компонент получит сдвиг фазы на ϕ = kl по отношению к горизонтальному, где k = 2π/λ есть волновое число. В результате фотон, выходя из интерферометра, будет в состоянии
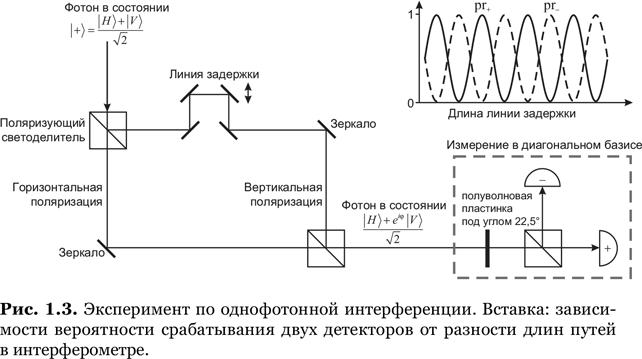
Мы изучили измерение этого состояния в упр. 1.14 и выяснили, что вероятности срабатывания детекторов «+» и «–» составляют
Что в этом выводе поистине замечательно (и, разумеется, целиком и полностью подтверждено экспериментально), так это то, что интерференционные полосы порождает один-единственный фотон. Это решительно противоречит нашим интуитивным представлениям. Действительно, в классическом эксперименте интерференция возникает потому, что две волны, проходящие по двум путям интерферометра, получают разные фазы и затем складываются когерентно на фотодетекторах. Но в нашем эксперименте присутствует всего один фотон! Фотон — неделимая элементарная частица света, поэтому он не может расщепиться[21] в интерферометре и породить две волны, необходимые для образования интерференционных полос. Он должен двигаться в одиночестве либо по верхнему, либо по нижнему пути интерферометра — но не по двум путям одновременно.
Эти разумные и интуитивно понятные доводы противоречат и нашим расчетам, и экспериментальным наблюдениям. Как можно это объяснить?
Фотон, попадающий в интерферометр, находится в суперпозиции состояний вертикальной и горизонтальной поляризации. После первого PBS он по-прежнему находится в состоянии суперпозиции — но теперь это также суперпозиция верхнего и нижнего путей интерферометра. После воссоединения путей она вновь превращается в суперпозицию состояний поляризации — но уже с фазовым сдвигом у одного из ее компонентов. Именно эти два компонента суперпозиции играют здесь роль двух волн из классического эксперимента и интерферируют друг с другом. Так проявляется корпускулярно-волновой дуализм (wave-particle duality) квантовых частиц[22].
Получается, что в определенном смысле фотон все-таки расщепляется между двумя каналами интерферометра. Однако такое волноподобное поведение возможно только в том случае, если компоненты остаются в состоянии суперпозиции. Чтобы это проиллюстрировать, предположим, что в обоих каналах интерферометра мы размещаем детекторы, способные регистрировать фотоны, не разрушая их. Всякий раз, когда какой-нибудь фотон попадает в интерферометр, один из этих детекторов срабатывает и показывает нам, по верхнему или по нижнему пути прошел фотон. Таким способом, как сказали бы отцы-основатели квантовой механики, мы получаем о фотоне информацию Welcher Weg[23].
Получение информации Welcher Weg означает измерение положения фотона. В предыдущем разделе мы узнали, что такое измерение схлопывает состояние суперпозиции и превращает его, в зависимости от результата, либо в фотон, находящийся на верхнем, либо в фотон, находящийся на нижнем пути интерферометра. Глядя на детектор Welcher Weg, наблюдатель может точно сказать, в каком состоянии — горизонтальном или вертикальном — фотон выйдет из интерферометра. Так или иначе, последующее измерение этого фотона в диагональном базисе выдаст тот или другой результат с вероятностью 1/2 независимо от разности хода. Таким образом измерение Welcher Weg разрушает волновые свойства фотона и заставляет его вести себя как частица.
Отступление 1.4. Квантовая инспекция военной техники
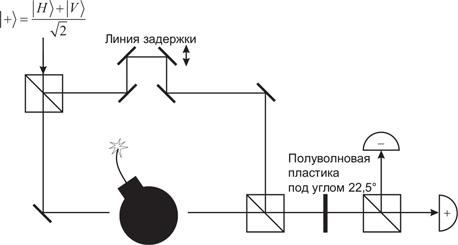
Вот любопытный парадокс, связанный с экспериментом по однофотонной интерференции, обсуждающийся в разд. 1.5[24]. Пусть имеется бомба, оборудованная датчиком фотонов и настроенная так, что взорвется, даже если датчик провзаимодействует с одним-единственным фотоном. Можем ли мы обнаружить присутствие бомбы в одном из каналов нашего интерферометра, не подорвав ее при этом?
Установим линию задержки в нашем однофотонном интерферометре (рис. 1.3) так, чтобы иметь ϕ = 0. Тогда если бомбы нет, то каждый попадающий в интерферометр фотон будет выходить из него поляризованным под углом +45° и вызывать срабатывание детектора «+». Детектор «–» в таком случае не будет срабатывать никогда.
Если же бомба есть, как показано на рисунке выше, она может взорваться или не взорваться в зависимости от того, каким путем проследует фотон. В этом смысле бомба проводит измерение типа Welcher Weg. Соответственно, фотон будет вести себя как частица, которая проходит случайным образом либо по верхнему, либо по нижнему маршруту интерферометра. Если он пойдет по нижнему маршруту, бомба взорвется. Но, если он пойдет поверху, бомба останется нетронутой, а фотон выйдет из интерферометра в состоянии вертикальной поляризации. При измерении в диагональном базисе он с равной вероятностью будет вызывать срабатывание каждого из двух детекторов.
Следовательно, если бомба имеется, у нас будет ненулевая вероятность услышать щелчок в детекторе «–». Более того, этот детектор может сработать только при наличии бомбы. Если он сработает, мы будем точно знать, что бомба в интерферометре есть — не потревожив ее при этом!
Вышеописанное устройство нельзя считать идеальным инструментом по инспекции вооружений, поскольку оно не гарантирует ни однозначного результата, ни того, что бомба все-таки не взорвется (см. упр. 1.17). Однако если поместить бомбу не в интерферометр Маха — Цендера, а в высокодобротный интерферометр Фабри — Перо, то можно получить эффективность, близкую к 100%. В этом случае фотон с высокой вероятностью пройдет через интерферометр при отсутствии в нем бомбы, но отразится, если бомба в нем есть.
Конечно, дело обстоит именно так даже в том случае, если наблюдатель не смотрит на детекторы Welcher Weg. Тогда фотон находится в смешанном состоянии — он движется либо по верхнему, либо по нижнему пути интерферометра с вероятностью 1/2, — но уже не в состоянии суперпозиции. То есть вместо ситуации упр. 1.14 мы оказываемся в ситуации упр. 1.12. Состояние фотона утратило свою квантовую когерентность — четко определенное соотношение фаз между членами суперпозиции. А такой фотон больше не может демонстрировать интерференцию.
Этот мысленный эксперимент демонстрирует квантовую дополнительность (complementarity) — общий принцип квантовой физики, гласящий, что объекты могут обладать дополнительными свойствами, которые невозможно наблюдать или измерять одновременно. Мы можем получить либо информацию Welcher Weg, либо интерференцию, но не то и другое вместе.
Упражнение 1.17. В условиях, описанных в отступлении 1.4, чему равны вероятности:
a) обнаружения бомбы без ее взрыва;
b) взрыва бомбы;
c) получения результата, не свидетельствующего однозначно о наличии бомбы?
1.6. Квантовая криптография
Теперь мы можем обсудить первое в этом курсе практическое приложение квантовой физики. Это приложение — криптография, обмен тайными сообщениями по незащищенным каналам.
Искусство тайнописи, известное с древности, сегодня представляет собой крупную отрасль индустрии телекоммуникаций, защищающую информационную безопасность отдельных лиц, предприятий и правительственных учреждений. В отступлении 1.5 описаны классические подходы к криптографии. В одном предложении ее содержание заключается в том, что в рамках классической физики мы вынуждены выбирать между надежным, но дорогим одноключевым шифрованием и дешевым, но не полностью безопасным шифрованием с открытым ключом.
Отступление 1.5. Классическая криптография
Криптографический обмен данными осуществить легко, если у обеих сторон, которые мы традиционно называем Алисой и Бобом, есть заранее оговоренный тайный набор данных (последовательность нулей и единиц), известный как секретный ключ, или одноразовый шифровальный блокнот (one-time pad). Тогда криптографический протокол может выглядеть следующим образом. Алиса берет фрагмент секретного ключа такой же длины (т.е. с тем же числом битов), что и послание, которое она хочет передать Бобу. Затем она применяет операцию XOR (исключающее ИЛИ, или побитное сложение по модулю 2) к каждому биту своего сообщения и соответствующему биту своего секретного ключа.

Таким способом Алиса приготавливает зашифрованное сообщение, которое можно безопасно передавать по незащищенному каналу, поскольку его нельзя расшифровать без доступа к секретному ключу. Боб, со своей стороны, может расшифровать полученное сообщение без труда. Для этого он применяет операцию XOR к его каждому биту и соответствующему биту секретного ключа.

Этот протокол, известный как одноключевое, или классическое, шифрование, очень надежен и прост; он используется уже сотни лет. Проблема в том, что создать общий набор случайной информации, секретной для всех остальных, Алисе и Бобу достаточно непросто. Как правило, единственный надежный способ сделать это — послать курьера с чемоданом, полным случайных данных. Это, разумеется, очень дорого. Поэтому одноключевая криптография используется только для наиболее секретной правительственной и коммерческой связи.
Для других приложений, таких как онлайн-шопинг, используется семейство протоколов, известных как шифрование с открытым ключом (public-key cryptography). Не вдаваясь в детали, скажу, что эти протоколы основаны на существовании «односторонних» функций, которые легко вычислить, но очень трудно инвертировать. Например, перемножение двух простых чисел, состоящих из нескольких десятков цифр каждое, на современном компьютере занимает пару-тройку микросекунд, но разложение числа аналогичной длины на простые множители займет месяцы, а то и годы. Протоколы шифрования с открытым ключом при помощи односторонних функций обеспечивают надежную связь между участниками, у которых не было возможности обменяться секретными ключами.
Протоколы с открытым ключом удобны и недороги, но не обеспечивают абсолютной секретности на фундаментальном уровне. Доступные нам вычислительные мощности удваиваются чуть ли не ежегодно, так что расчет, на который в настоящее время требуются годы, через несколько лет, возможно, будет занимать всего несколько часов. Более того, квантовые компьютеры (разд. 2.5) потенциально способны взламывать сообщения, зашифрованные по протоколам с открытым ключом, почти мгновенно.
Квантовая механика предлагает нам решение проблемы, с которым и волки будут сыты, и овцы целы. С одной стороны, оно обеспечивает информационную безопасность с гарантией на уровне фундаментальных законов природы. С другой, это решение не требует обязательного предварительного обмена большим объемом случайной информации между сторонами.
1.6.1. Протокол BB84
Квантовая криптография, или, точнее, квантовое распределение ключа (quantum key distribution), основана на свойстве измерений изменять квантовое состояние, к которому они применяются. Идея в том, что отправляющая сторона (Алиса) высылает секретные данные принимающей стороне (Бобу) посредством единичных фотонов, в квантовых состояниях которых зашифрованы передаваемые данные. Всякий, кто попытается «подслушать» передачу, либо разрушит, либо изменит эти фотоны, выдав таким образом свое вмешательство.
Самый известный квантовый протокол шифрования называется «BB84» в честь его изобретателей Чарльза Беннета и Жиля Брассара[25]. При его применении Алиса и Боб выполняют следующие операции.
1. Алиса случайно выбирает значение бита, 0 или 1, которое следует передать.
2. Алиса случайно выбирает базис шифрования — канонический или диагональный.
3. Алиса генерирует фотон и шифрует свой бит в поляризации этого фотона:
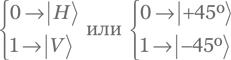
После этого она отправляет фотон Бобу.
4. Боб случайно выбирает базис измерения — канонический или диагональный.
5. Боб измеряет полученный фотон в выбранном базисе:
- если он выбирает тот же базис, что и Алиса, то в результате измерения он получит то самое значение бита, которое отправила Алиса;
- если он выбирает другой базис, то получит случайное значение бита.
Эта процедура повторяется много раз. Конечно, и Алиса, и Боб должны тщательно все записывать: какие базисы использовали, какие состояния отправили или измерили, а также точное время, в которое фотоны были отправлены или получены. После того как окажутся собраны многие тысячи таких записей, Алиса и Боб сообщают друг другу (по классическому незащищенному каналу), какие базисы были выбраны для каждого фотона, но не конкретные значения отправленных или измеренных ими битов. Боб также сообщает Алисе о тех случаях, когда фотон ему измерить не удалось — если, например, тот был поглощен где-то в линии передачи (для этого нужно, конечно, чтобы время передач Алисы было точно известно Бобу, но эту информацию засекречивать не нужно). После обмена информацией Алиса и Боб отбрасывают данные по тем событиям, где были использованы разные базисы или фотон был потерян.
Теперь у Алисы и Боба имеется строка идентичных битов, которые они могут использовать как одноразовый блокнот в классическом протоколе. Чтобы понять, почему эта строка будет гарантированно секретной, предположим, что «шпион» (eavesdropper, Ева) перерезает линию передачи, перехватывает фотоны Алисы, измеряет их поляризацию и затем отправляет Бобу то, что измерила (рис. 1.4). Сможет ли она получить копию секретного ключа?
Ответ отрицательный. Проблема Евы в том, что согласно постулату об измерениях она должна измерять в конкретном базисе и не знает, какой базис выбрать. Какой бы базис она ни выбирала, все равно будут такие случаи, что Алиса и Боб работают в одном базисе, а Ева — в другом. Но в этом случае измерение Евы изменит состояние фотона и Боб, возможно, получит значение бита, не равное тому, которое отправила ему Алиса. Секретные ключи, записанные Алисой и Бобом, в конечном итоге окажутся разными, и это станет для них свидетельством возможного перехвата.
Предположим, например, что и Алиса, и Боб работают в каноническом базисе, а Ева — в диагональном. Алиса отправляет горизонтально поляризованный фотон, в котором зашифрован бит 0. Но Ева пользуется диагональным базисом, поэтому она увидит |+⟩ или |–⟩ с равной вероятностью. Если после перехвата она отошлет Бобу фотон в том состоянии, которое она задетектировала, Боб (измеряющий в каноническом базисе) с равной вероятностью увидит |H⟩ или |V⟩. Если это окажется |V⟩, Боб запишет значение бита, отличное от того, которое отправила ему Алиса.
Чтобы проверить, не следит ли кто-нибудь за их перепиской, Алисе и Бобу нужно будет обменяться по незащищенному каналу частью секретной битовой строки, полученной ими обоими. Если ошибок в ней нет (или очень мало), они могут использовать остальную часть строки в качестве одноразового блокнота.
Упражнение 1.18. Предположим, Ева перехватывает фотоны Алисы и измеряет их либо в каноническом, либо в диагональном базисе (базис она выбирает случайным образом). Затем она кодирует измеренный бит в том же базисе и посылает его Бобу. Какова средняя доля битов создаваемого ими секретного ключа, которая получится разной?
Ответ: 25%.
Это упражнение показывает, что если Алиса и Боб видят в получаемом ими секретном ключе определенную долю неидентичных битов, то они не могут больше быть уверены, что их сообщения не перехватываются. Однако значение доли ошибок, полученное в упр. 1.18, относится только к случаю одной конкретной стратегии перехвата (атаки) со стороны Евы. Выбрав более хитроумную атаку, Ева может получить копию секретного ключа, оставив при этом в записях Алисы и Боба даже более низкую долю ошибок.
Так насколько низкой должна быть доля ошибок у Алисы и Боба, чтобы они могли уверенно полагаться на безопасность своей связи? Доказано[26], что граница проходит примерно по 11%. Какую бы стратегию ни выбрала Ева, если частота ошибок ниже этой величины, Алиса и Боб смогут, воспользовавшись процедурой усиления секретности (privacy amplification), «отфильтровать» для себя совершенно надежный и полностью идентичный секретный ключ из частично несовпадающей битовой строки, полученной посредством квантового протокола.
Упражнение 1.19. Как уже говорилось, значительная доля фотонов, отправленных Алисой, до Боба не доходит. Но Алиса и Боб не знают, были ли на самом деле эти фотоны потеряны из-за поглощения на линии или их «украл» перехватчик. Влияет ли это соображение на безопасность передачи ключа?
1.6.2. Практические вопросы квантовой криптографии
Квантовая криптография — не фантастика. Описанный выше протокол вполне реализуем современными техническими средствами. Мало того, существуют коммерческие квантово-криптографические серверы, которые можно подключать к коммерческим оптоволоконным линиям связи, где они будут реализовывать протокол BB84. Многие крупные города уже обзавелись своими квантовыми коммуникационными сетями. Квантовое шифрование использовалось для связи во время выборов в Федеральное собрание Швейцарии в 2007 г. и чемпионата мира по футболу 2010 г. в Южной Африке. Существуют такие сети и в Москве, Петербурге, Казани. За время, прошедшее с момента публикации этой книги, наверняка появились новые примеры.
Тем не менее мы пока не наблюдаем повсеместной замены классических криптографических протоколов квантовым распределением ключей. Что мешает? Существует ли здесь какое-то техническое препятствие или проблема в психологической инерции?
К сожалению, в этой области действительно имеются нерешенные практические вопросы, главный из которых — потери в линиях связи. Потери эти подчиняются закону Бугера — Ламберта — Бера (Beer’s law): n (L) = n0e–βL, где n (L) — число непоглощенных фотонов на расстоянии L от Алисы, а β — коэффициент поглощения. Лучшие волокна, используемые в системах связи на сегодняшний день, дают потери около 5% на километр. Кажется, что это немного; тем не менее при передаче по небезопасной линии связи до Боба дойдет лишь крохотная часть фотонов; остальные будут утрачены.
Упражнение 1.20. Алиса отправляет фотон Бобу, который находится от нее на расстоянии 300 км, по оптоволоконной линии. Каждый километр волокна поглощает 5% энергии света, распространяющегося по нему.
a) Найдите коэффициент потерь β этого волокна.
Подсказка: ответ 0,05 км−1 близок к верному, но не совсем точен.
b) Какая доля фотонов, отправленных Алисой, дойдет до Боба?
Помимо потерь существует еще проблема, связанная с темновым счетом (см. отступление 1.2). Может случиться так, что, например, фотон |H⟩, отправленный Алисой, будет потерян и в это же время детектор Боба в канале вертикальной поляризации даст ложное срабатывание. Тогда Боб интерпретирует это срабатывание как фотон |V⟩, полученный от Алисы, и сделает соответствующую запись. В результате Алиса и Боб увидят ошибку и, возможно, потеряют уверенность в безопасности связи.
Если линия передачи не слишком длинна, до Боба будет доходить достаточно фотонов, чтобы доля ошибок, связанных с темновым счетом, была невелика. Но доля дошедших фотонов с увеличением расстояния экспоненциально падает, тогда как частота темновых срабатываний остается постоянной. Так что в какой-то момент надежная передача данных станет попросту невозможной.
Этот эффект показан на рис. 1.5. Когда длина линии связи невелика, частота получения надежных битов (secure bit rate), отфильтрованных Алисой и Бобом (пунктирные линии), равна частоте получения фотонов Бобом (сплошные линии), умноженной на некоторый постоянный коэффициент. Но когда частота их получения снижается настолько, что доля ошибок, связанных с темновым счетом, становится значимой, число надежных битов начинает падать быстрее, а протокол усиления секретности становится все менее эффективным. Когда число фотонов, доходящих до Боба, падает ниже некоторого критического уровня, соответствующего доле ошибок в 11%, передача перестает быть надежной.
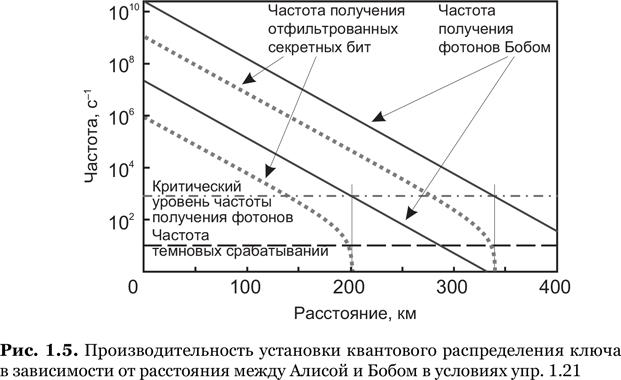
Упражнение 1.21. Полагая, что у Алисы есть идеальный источник единичных фотонов, постройте примерный график количества фотонов, получаемых Бобом, а также количества отфильтрованных битов секретного ключа в секунду в зависимости от расстояния передачи. На основании этого оцените максимальное возможное расстояние безопасной связи при следующих параметрах:
- потери фотонов в оптоволоконной линии: β = 0,05 км–1;
- частота эмиссии фотонов источником Алисы: n0 = 2 × 107 и 2 × 1010 фотонов в секунду;
- квантовая эффективность фотонных детекторов: η = 0,1;
- частота темновых срабатываний, синхронизированных с фотонами Алисы[27], в каждом из детекторов Боба: 푓d = 10 с–1.
Ответ: см. рис. 1.5.
Дальность защищенной квантовой связи можно улучшить, повысив производительность источника фотонов на стороне Алисы или снизив частоту темновых срабатываний детектора. Однако это не приведет к принципиальному улучшению ситуации: экспоненциальная природа закона Бугера — Ламберта — Бера в любом случае ограничивает квантовую связь расстояниями, не превышающими несколько сотен километров. В условиях упр. 1.21 повышение производительности источника на три порядка позволит увеличить дистанцию всего в 1,7 раза (рис. 1.5).
Чтобы преодолеть этот предел — и создать «квантовый интернет», который пересек бы океаны и со временем покрыл бы своей сетью всю планету, — нам потребуется принципиально иная технология. Про эту технологию, известную как квантовый повторитель, речь пойдет в конце главы 2.
1.7. Операторы в квантовой механике
Теперь мы переходим к обсуждению линейных операторов, представляющих собой ключевой элемент квантовой физики[28]. Они играют двоякую роль. Прежде всего операторы описывают эволюцию: с течением времени квантовые состояния изменяются, и это изменение математически выражается операторами. Второе, несколько менее очевидное, приложение линейных операторов состоит в формальном описании квантовых измерений. В этом разделе мы начнем с первой их роли.
Упражнение 1.22. Найдите матрицу оператора |+⟩⟨–| в каноническом базисе и базисе {|R⟩, |L⟩}.
Упражнение 1.23. Найдите в каноническом базисе матрицу линейного оператора Â, отображающего
a) |H⟩ на |R⟩ и |V⟩ на 2|H⟩;
b) |+⟩ на |R⟩ и |–⟩ на |H⟩.
Примером физической операции, которую можно связать с квантовым оператором, может служить волновая пластинка, изменяющая состояние поляризации фотона. Чтобы рассчитать этот оператор, мы должны принять некоторое соглашение. Как сказано в разд. В.3, волновая пластинка изменяет относительную фазу необыкновенной (параллельной оптической оси) и обыкновенной (перпендикулярной оптической оси) поляризаций на угол ∆ϕ, который равен π для полуволновой пластинки и π/2 для четвертьволновой. Кроме того, она вводит общий сдвиг фазы для всей волны.
Эти оптические фазовые сдвиги в применении к единичному фотону превращаются в квантовые фазовые сдвиги. Общим фазовым сдвигом, одинаковым для всех компонентов поляризации, можно пренебречь (см. разд. 1.3). Мы, однако, должны договориться, как с ним обращаться в наших выкладках. Будем считать, что волновая пластинка не дает фазового сдвига на обыкновенный компонент поляризации, тогда как необыкновенный ее компонент претерпевает фазовый сдвиг ∆ϕ. Иными словами, волновая пластинка с оптической осью, ориентированной под углом θ к горизонтали, производит следующие преобразования:

Упражнение 1.24. Найдите в каноническом базисе матрицы операторов, связанных с полуволновой и четвертьволновой пластинками с оптической осью, ориентированной под углом α к горизонтали, при помощи следующего пошагового алгоритма:
a) Напишите оператор Â∆ϕ, связанный с преобразованием (1.4), в виде уравнения (A.25).
b) Выразите каждый бра- и кет-вектор в ответе пункта a) в матричной форме в каноническом базисе и вычислите матрицу результирующего оператора.
c) Подставьте значения ∆ϕ для полуволновой и четвертьволновой пластинок.
Ответ:
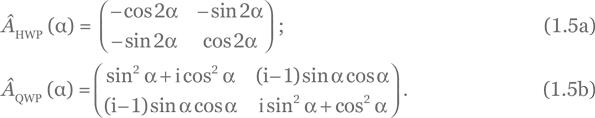
Упражнение 1.25. Пользуясь результатом предыдущего упражнения, убедитесь в верности следующих утверждений:
a) при применении к фотону, линейно поляризованному под углом θ, полуволновая пластинка с оптической осью, ориентированной под углом α, дает фотон, линейно поляризованный под углом 2α – θ, в соответствии с рис. В.4;
b) четвертьволновая пластинка с оптической осью, ориентированной горизонтально или вертикально, превращает фотон с круговой поляризацией в фотон с поляризацией под ±45° и наоборот в соответствии с упр. В.9.
Отступление 1.6. Как получить фотон?
Вот самый очевидный, но неверный ответ на этот вопрос: использовать ослабленный сигнал лазера. Предположим, у нас есть импульсный лазер со средней мощностью P и частотой повторения импульсов R. Тогда каждый импульс лазера содержит n = P/Rℏω фотонов, где ω — частота излучения лазера. Поэтому можно, казалось бы, разместить на пути лазерного луча ослабитель (темное стекло), который уменьшал бы его мощность в n раз, так чтобы каждый импульс содержал ровно один фотон.
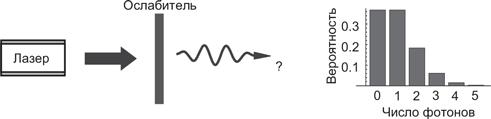
Эти рассуждения ошибочны, поскольку не учитывают, что реальное число фотонов в импульсах, проходящих через ослабитель, будет стохастическим в соответствии с распределением Пуассона (см. разд. Б.3). Хотя в среднем, возможно, действительно получится один фотон на импульс, это не означает, что каждый импульс будет содержать ровно один фотон. Иногда фотонов в импульсе вообще не окажется, иногда там будет один фотон, иногда два или больше.
Несмотря на это возражение, в некоторых случаях ослабленный лазер служит полезной заменой настоящего источника фотонов. В частности, в практической квантовой криптографии лазер ослабляется до чрезвычайно низкого уровня, так чтобы вероятность того, что каждый импульс содержит хотя бы один фотон, стала весьма малой. Тогда вероятность содержания в импульсе более одного фотона пренебрежимо мала, и безопасность связи не страдает.
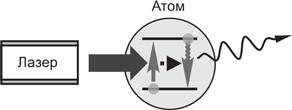
Чтобы гарантировать генерацию единичного фотона «по требованию», нужны более хитроумные схемы. Например, единичный двухуровневый атом, будучи возбужденным, автоматически вернется в основное состояние, излучив при этом ровно один фотон. Практическая реализация такого источника, однако, представляет серьезные трудности. Во-первых, необходимо поймать единичный атом и неподвижно удерживать его в ходе всего эксперимента. Во-вторых, фотон будет излучен в случайном направлении. Чтобы заставить атом излучать в каком-то конкретном направлении, физики иногда окружают его резонатором Фабри — Перо. Этот метод развился в целое научное направление, называемое квантовой электродинамикой в резонаторе.
Чтобы обойти необходимость в захвате атома, эксперименты проводят с твердотельными атомоподобными источниками, такими как единичные дефекты кристаллической решетки или квантовые точки. Идея та же: взять объект, в котором возможен только один квант возбуждения с определенной энергией. Пока я пишу эту книгу, подобные эксперименты стремительно развиваются в сторону большей эффективности и лучшей воспроизводимости получаемых фотонов.
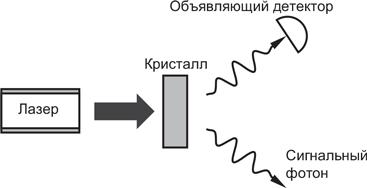
Многие физики используют мощный альтернативный подход к приготовлению единичных фотонов — спонтанное параметрическое рассеяние (spontaneous parametric down-conversion). Это нелинейный квантово-оптический процесс, который происходит, когда сильный лазерный луч проходит сквозь кристалл с нелинейными оптическими свойствами. Каждый фотон луча может при этом спонтанно расщепиться на два менее энергичных фотона. Данное событие имеет очень низкую вероятность. Однако у него есть фундаментальное свойство: в нем каждый раз рождается именно пара фотонов. Так что если мы зарегистрируем один из этих фотонов, то будем знать наверняка, что появилась также и его копия, — и можем с ней экспериментировать.
Такое устройство называется источником объявленных одиночных фотонов (heralded single photon source), потому что обнаружение одного фотона «объявляет» о присутствии второго. Этот источник не способен производить фотоны «по требованию»; он только сигнализирует о появлении спонтанно испущенного фотона, не разрушая его. Поэтому его применение в квантовых технологиях ограничено. Однако, поскольку у нас пока нет надежного способа приготовления единичных фотонов по заказу, источники объявленных фотонов широко используются в экспериментальных квантово-оптических исследованиях.
Упражнение 1.26. Операторы Паули[29] определяются как

или в матричной записи
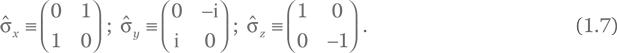
Предложите реализацию этих операторов средствами волновых пластинок.
Подсказка: найдите состояния, на которые операторы Паули отображают |H⟩ и |V⟩, затем используйте упр. 1.24.
Упражнение 1.27. Матрица оператора Адамара Ĥ в каноническом базисе равна:
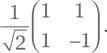
a) Выразите этот оператор в нотации Дирака.
b) На какие состояния Ĥ отображает |H⟩ и |V⟩?
c) Как можно реализовать этот оператор с помощью волновых пластинок?
1.8. Проекционные операторы и ненормированные состояния
Ранее мы постулировали, что физические квантовые состояния имеют норму 1. Давайте теперь расширим это соглашение. Норма вектора состояния |a⟩ может быть меньше единицы; это означает, что состояние |a⟩ существует не точно, а с вероятностью, равной квадрату его нормы:
pra = ║ |a⟩ ║2 = ⟨a|a⟩. (1.8)
Такие состояния называют ненормированными.
Рассмотрим проективное измерение состояния |ψ⟩ в базисе {|푣i⟩}. Каноническая формулировка постулата об измерениях гласит, что измерение превращает |ψ⟩ в одно из |푣i⟩ с вероятностью (1.3). Воспользовавшись расширенным соглашением, мы можем сказать, что это измерение превращает |ψ⟩ в набор ненормированных состояний
Это можно записать иначе:
где мы ввели проекционный оператор (projection operator или projector):
Например, неразрушающее измерение состояния
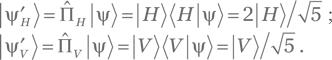
Состояние
Интерпретировать измерения на языке проекционных операторов часто оказывается удобным, как мы увидим позже.
Упражнение 1.28. Найдите матрицу проекционного оператора, связанного с базисным состоянием |푣2⟩ в базисе {|푣i⟩} для гильбертова пространства размерности N = 4.
1.9. Квантовые наблюдаемые
1.9.1. Наблюдаемые операторы
Постулат квантовой физики об измерениях, определенный нами в разд. 1.4, гласит, что квантовое измерение выполняется в ортонормальном базисе, а результат этого измерения есть случайный элемент этого базиса. Сделаем еще шаг вперед и свяжем с каждым элементом |푣i⟩ базиса действительное число 푣i. Тогда вместо «результатом измерения является состояние |푣i⟩» мы будем говорить «результатом измерения является величина 푣i».
Для некоторых измерений такая связь естественна. Например, состояние с определенным положением, такое как |xi⟩ = |x = 3 м⟩, естественным образом связано со значением координаты частицы (xi = 3 м). Для других измерений, вроде измерения поляризации фотона, естественной связи между элементами базиса и числами не существует, но такую связь можно ввести искусственно. К примеру, если мы измеряем в каноническом базисе, то можем связать число 1 с состоянием |H⟩, а число –1 с состоянием |V⟩.
Информацию о базисе измерения и связанных с ним величинах удобно выразить, скажем, в виде оператора:
Этот оператор называется наблюдаемым оператором, или просто наблюдаемым (observable). Как мы знаем (разд. A.8), элементы |푣i⟩ базиса измерений (собственного базиса наблюдаемого) представляют собой собственные состояния, или собственные векторы наблюдаемого, а соответствующие им величины 푣i являются его собственными значениями. Воспользовавшись (1.12), можно ввести наблюдаемый оператор для почти любого измерения или измеряемой величины: положения, импульса, момента импульса, энергии и т.п. Как мы увидим в ближайших разделах, наблюдаемые операторы в квантовой физике имеют первостепенное значение.
Из этого общего утверждения есть одно важное исключение. Время в квантовой физике никогда не рассматривается как оператор. Не существует ни собственных состояний времени, ни квантов времени. Время — это просто непрерывная переменная.
Упражнение 1.29. Найдите наблюдаемые, связанные с базисами {|H⟩, |V⟩}, {|+⟩, |–⟩} и {|R⟩, |L⟩} (т.е. с измерительными приборами на рис. 1.2) и собственными значениями ±1 (соответственно) в нотации Дирака. Найдите матрицы этих операторов в базисе {|H⟩, |V⟩}.
Ответ: операторы Паули (1.6):
|H⟩⟨H|–|V⟩⟨V| = σz; (1.13a)
|+⟩⟨+|–|–⟩⟨–| = σx; (1.13b)
|R⟩⟨R|–|L⟩⟨L| = σy. (1.13c)
Итак, мы увидели обе роли операторов в квантовой механике: это преобразования квантовых состояний и описания измерительных приборов. Естественно спросить, схожи ли физические реализации одних и тех же операторов в разных ролях. Пример выше показывает, что это не так. Измерительные приборы, реализующие оператор Паули, показаны на рис. 1.2. При этом операторы Паули как средства преобразования состояния реализованы в упр. 1.26. Видно, что конфигурации в том и другом случаях совершенно различны.
Упражнение 1.30. Покажите, что:
a) операторы, соответствующие физическим наблюдаемым (1.12), являются эрмитовыми;
b) любой эрмитов оператор может быть связан с некоторым физическим наблюдаемым, т.е. его можно выразить в виде (1.12) с действительными собственными значениями и собственными состояниями, образующими ортонормированный базис.
Упражнение 1.31. Выполните спектральное разложение матриц Паули (1.7) с использованием методов линейной алгебры. Проверьте соответствие вашего результата определению, данному в упр. 1.29.
Мы видим, что каждое измерение может быть связано с некоторым эрмитовым оператором и каждый эрмитов оператор может быть связан с некоторым измерением. Более того, наблюдаемый оператор содержит в компактной форме полную информацию о базисе измерения и связанных с ним собственных значениях. Если дается эрмитова матрица наблюдаемого оператора, мы можем извлечь из нее эту информацию посредством спектрального разложения[30].
1.9.2. Среднее значение и неопределенность наблюдаемого
Предположим, мы измеряем наблюдаемое
Упражнение 1.32. Наблюдаемое
a) Покажите, что математическое ожидание этого измерения равно
Выражение в правой части этого уравнения называется также квантовым средним значением наблюдаемого
b) Покажите, что дисперсия величины

и что эта дисперсия может быть вычислена по формуле:
Как и в теории вероятностей, неопределенность квантовой величины равна квадратному корню из его дисперсии.
Странное понятие наблюдаемого оператора, введенное в предыдущем подразделе, оказывается весьма полезным. Оно не только несет в себе полную информацию об измерении, но и обеспечивает простой способ вычисления статистических свойств этого измерения в применении к заданному состоянию. Решим простой пример.
Упражнение 1.33§. Вычислите среднее значение, дисперсию и неопределенность наблюдаемого
Чтобы интерпретировать приведенный ответ, вспомним, что наблюдаемое
Это хороший пример перехода между классическими и квантовыми измерениями. Квантовые измерения имеют вероятностный характер: в данном случае каждый фотон будет случайным образом пропущен или отражен. В классической же физике все имеет детерминистский характер: если мы направим поляризованную под 45º классическую волну на PBS, она расщепится ровно пополам, безо всякой неопределенности. Принцип соответствия требует, чтобы квантовое поведение в макроскопическом пределе становилось классическим. Этот переход от квантового к классическому поведению можно проследить в следующем упражнении.
Упражнение 1.34. Группа из N поляризованных под +45º фотонов направляется в PBS. Вычислите среднее значение и неопределенность разности N_ между числом пропущенных и отраженных фотонов.
Подсказка: воспользуйтесь упр. Б.5.
Ответ: среднее равно нулю, неопределенность равна
На первый взгляд это может показаться странным: по мере того как наш эксперимент становится более макроскопическим, неопределенность в нем не снижается, а, напротив, повышается. Как это согласуется с классической физикой? Дело в том, что здесь имеет значение не абсолютная неопределенность, а относительная, т.е.
Например, если N = 104, то статистическое отклонение равно
1.9.3. Принцип неопределенности
Упражнение 1.35. Покажите, что наблюдаемое
Упражнение 1.36. Рассмотрим два эрмитовых оператора
Подсказка: доказательство будет проще, если предположить, что один из операторов не имеет вырожденных собственных значений.
Последнее упражнение показывает, что любые два коммутирующих наблюдаемых могут быть измерены одновременно. То есть можно построить устройство, выполняющее измерения в ортонормальном базисе, который можно связать одновременно с обоими этими наблюдаемыми.
Коммутирующие наблюдаемые «совместимы»: существует собственный базис Â, такой, что если система приготовлена в одном из его элементов |푣i⟩, то она останется в этом состоянии при измерении наблюдаемого
Упражнение 1.37. Покажите, что для любых эрмитовых операторов

где квантовое среднее вычисляется в произвольном состоянии |ψ⟩.
Упражнение 1.38. Покажите, что для любых двух эрмитовых операторов Â,
Подсказка: введите |a⟩ = Â|ψ⟩ и
Упражнение 1.39. Докажите принцип неопределенности Гейзенберга (Heisenberg uncertainty principle): для эрмитовых Â,
считая для простоты, что ⟨A⟩ = ⟨B⟩ = 0. (1.22)
Упражнение 1.40. Повторите доказательство без предположения (1.22). Остался бы принцип неопределенности (1.21) в силе, если бы правая часть уравнения равнялась
Упражнение 1.41. Покажите, что если

Упражнение 1.42. Для

Принцип неопределенности Гейзенберга — одно из важнейших следствий квантовой физики и одно из главных ее отличий от физики классической. В те времена, когда квантовая механика только зарождалась, этот принцип был одной из самых противоречивых идей. Как и постулат об измерениях, принцип неопределенности прямо противоречил детерминистской картине мира, принятой тогда в классической физике. Согласно этой картине, любая неопределенность, полученная в ходе измерений, являлась следствием несовершенства измерительной техники, и путем усовершенствования этой техники ее можно было снижать до бесконечности. В рамках квантовой механики это не так: если создать устройство, способное точно измерить одно наблюдаемое в каком-то конкретном состоянии системы, то эта установка, какой бы замечательной она ни была, обязательно покажет плохой результат при измерении другого наблюдаемого.
Особенно интересен случай из упр. 1.41. Если коммутатор двух наблюдаемых пропорционален единичному оператору, то произведение их неопределенностей имеет нижнюю границу для всех состояний. Пример такой пары — координата и импульс, которые мы будем изучать в главе 3. Их коммутатор равен iℏ, из чего следует, что произведение неопределенностей для любого состояния не может быть меньше
1.10. Квантовая эволюция
Наша цель в этом разделе — выяснить, как меняются (эволюционируют) квантовые состояния со временем: при заданном начальном состоянии |ψ(0)⟩ физической системы нам нужно определить ее состояние |ψ(t)⟩ в произвольный момент времени. В классической физике полный набор уравнений движения можно получить из гамильтониана (полной энергии) системы. В гамильтониане заключена вся информация о зависящем от времени поведении системы, для любого ее начального состояния. Как мы увидим, это верно и для квантовой физики.
Правила квантовой эволюции невозможно вывести из тех постулатов, которые мы изучали до сих пор. Поэтому применим здесь ту же тактику, которую использовали при выработке постулата об измерениях. Сначала проведем интуитивные физические рассуждения об эволюции конкретной физической системы — фотона. Затем обобщим их на остальные системы и придадим им строгий вид.
Посмотрим еще раз на уравнение (1.2). Эволюция состояния фотона здесь заключена в общем фазовом множителе e−iωt.
До сих пор мы не обращали на него внимания, потому что, согласно нашим рассуждениям, он никак не влияет на физические свойства состояния. Но теперь давайте рассмотрим этот множитель подробнее.
Вспомнив, что энергия фотона равна E = ℏω, мы можем записать (1.24) в виде
где индекс E напоминает нам, что мы имеем дело с состоянием определенной энергии (в данном случае с фотоном определенной частоты).
Следующий наш шаг заключается в привлечении гипотезы де Бройля; согласно ей, не только фотоны, но и все свободно движущиеся частицы могут быть связаны с волнами, пространственно-временное поведение которых описывается множителем
Поговорим об этом операторе подробнее. Поскольку он соответствует некоторому физическому наблюдаемому, он эрмитов и потому допускает спектральное разложение
где собственные состояния с определенной энергией {|Ej⟩} образуют базис, в котором может быть разложено любое произвольное состояние:
Каждый компонент данного разложения меняется во времени согласно (1.25). Поскольку эта эволюция линейна, мы можем записать:
Мы постулируем, что это уравнение универсально и применимо к эволюции всех квантовых состояний.
Упражнение 1.43. Пусть начальное состояние некоторой системы есть суперпозиция двух энергетических собственных состояний
Мы видим, что в то время как для энергетических собственных состояний (например, в случае состояний поляризации фотона определенной частоты) квантовая эволюция соразмеряется с нефизичным фазовым множителем, другие состояния все же меняют со временем свои физические свойства.
Поскольку энергетические собственные состояния физически не меняются, их называют стационарными. Еще один пример стационарных состояний — атом в рамках модели Бора. Согласно этой модели, если электрон находится на «орбитали», соответствующей определенной величине энергии, то он может оставаться на ней в течение долгого времени.
Уравнение (1.28) можно использовать для вычисления эволюции квантового состояния непосредственно. Однако иногда практичнее бывает представить эволюцию в более компактном виде оператора эволюции, отображающего любое начальное состояние на его изменившийся вариант:
Получим оператор эволюции в явном виде.
Упражнение 1.44. Пользуясь уравнениями (1.27) и (1.28):
a) получите матрицу оператора эволюции в собственном базисе гамильтониана;
b) покажите, что[34]
Убедитесь, что этот оператор является унитарным.
Унитарность оператора эволюции неудивительна. Данный оператор должен отображать одно физическое состояние на другое физическое состояние, а это означает, что он должен сохранять норму.
Упражнение 1.45§. Убедитесь, что операторы преобразования (1.5), задаваемые волновыми пластинками, унитарные.
Как мы знаем (упр. A.82), все унитарные операторы обратимы и оператор, обратный унитарному, также является унитарным. У этого есть одно глубокое следствие. Если мы знаем оператор эволюции и состояние, которое является результатом этой эволюции, то мы можем воспроизвести начальное состояние, применив оператор, обратный оператору эволюции, к конечному состоянию.
Уравнение (1.30) показывает нам в явном виде, как применять эту инверсию. Замена Ĥ на -Ĥ в (1.30) эквивалентна замене t на –t, т.е. она обращает эволюцию вспять во времени, в конечном итоге приводя систему к ее начальному состоянию. Это явление, известное как обратимость времени (time reversibility) в квантовой механике, имеет множество интересных приложений, например спиновое эхо (подразд. 4.7.4).
В ходе эволюции замкнутой квантовой системы никогда не теряется никакая информация. На языке статистической физики это означает, что энтропия физической системы не увеличивается в ходе ее эволюции.
Упражнение 1.46. Для любого состояния |ψ(t)⟩ покажите, что
Уравнение (1.31) называется уравнением Шрёдингера. Это еще один способ описать закон эволюции квантовой системы, причем исторически этот способ был первым.
Наша следующая задача — попрактиковаться в нахождении временнóй эволюции квантовых состояний. Физическая система, которую мы использовали до сих пор, — поляризация фотона — не слишком подходит для этой цели, поскольку энергия фотона равна ℏω вне зависимости от его поляризации. Однако для тренировки (пока мы не познакомимся с другими физическими системами с невырожденным энергетическим спектром) будем предполагать, что при определенных условиях энергия фотона может стать зависимой от поляризации, и посмотрим, как меняется эта поляризация.
Предположим, нам дано начальное состояние |(0)⟩ системы и ее гамильтониан Ĥ и нужно предсказать состояние этой системы |ψ(t)⟩ в произвольный момент времени. Для этой цели мы можем воспользоваться тремя методами:
I. Разложить |ψ(0)⟩ в энергетический собственный базис в соответствии с уравнением (1.27), а затем применять простое уравнение эволюции (1.28) к каждому элементу базиса, чтобы найти |ψ(t)⟩.
II. Вычислить оператор эволюции из (1.30) с помощью приемов, освоенных в разд. A.11, а затем применить этот оператор к начальному состоянию в соответствии с (1.29).
III. Решить задачу Коши, состоящую из дифференциального уравнения Шрёдингера (1.31) и начального состояния |ψ (0)⟩. В этом подходе уравнение Шрёдингера можно записать в матричной форме
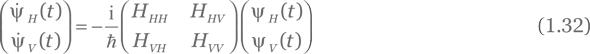
и решить как систему из двух дифференциальных уравнений для пары функций (ψH(t), ψV(t)).
Упражнение 1.47. Напишите уравнение Шрёдингера для следующих гамильтонианов:
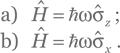
Для каждого случая найдите состояние поляризации фотона в момент t, если его начальное состояние равно либо |ψ(0)⟩ = |H⟩, либо |ψ(0)⟩ = |±45º⟩, с использованием каждого из трех перечисленных выше методов. Выразите ответ в каноническом базисе.
Упражнение 1.48. Найдите величины t в упр. 1.47, для которых действие оператора эволюции эквивалентно действию полуволновой и четвертьволновой пластинок на угле 0º для части (a) и 45º для части (b) соответственно.
Мы видим, что эволюция фотонов, исследованная в упр. 1.47, эквивалентна тому, что происходит в двулучепреломляющих материалах. Однако физика происходящего не совсем аналогична. В двулучепреломляющих материалах собственные состояния оператора эволюции накапливают разные фазы из-за разных коэффициентов преломления для обыкновенной и необыкновенной поляризации (приложение В). В эволюции же гамильтониана сдвиг фазы объясняется разными энергиями энергетических собственных состояний.
1.11. Задачи
Задача 1.1. Найдите коммутатор
Задача 1.2. Два состояния раскладываются в круговом базисе в соответствии с
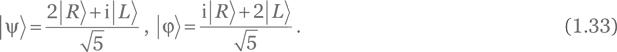
a) Покажите, что эти состояния образуют ортонормальный базис.
b) Найдите разложения этих состояний в каноническом базисе с использованием двух методов:
- выразив |R⟩ и |L⟩ в каноническом базисе и подставив в (1.33);
- найдя матричные формы состояний |ψ⟩, |ϕ⟩, |H⟩ и |V⟩ в круговом базисе и использовав скалярное произведение.
c) Убедитесь, что состояния |ψ⟩ и |ϕ⟩ образуют ортонормальное множество, воспользовавшись скалярным произведением в каноническом базисе.
d) Разложите состояния |H⟩, |V⟩, |R⟩, |L⟩,
e) Состояния |H⟩, |V⟩, |R⟩, |L⟩,
Задача 1.3. Повторите упр. 1.12 для фотона, который находится в случайном статистически смешанном состоянии, описываемом следующим ансамблем:
a) либо |+⟩ с вероятностью 1/2, либо |–⟩ с вероятностью 1/2;
b) либо |R⟩ с вероятностью 1/2, либо |L⟩ с вероятностью 1/2.
Задача 1.4. Рассмотрите модифицированный протокол BB84, в котором Алиса посылает, а Боб анализирует фотон в поляризационном базисе, выбранном случайно, с равной вероятностью для каждого варианта из следующих трех: (0º, 90º), (30º, 120º), (60º, 150º). Найдите долю битовых ошибок, которые увидят Алиса и Боб в случае прямолинейной атаки, в которой Ева перехватывает фотон, измеряет его в одном из трех приведенных выше базисов (выбранном случайно и равновероятно) и отправляет Бобу то, что измерила. Потерь в линии нет, все оборудование идеально.
Задача 1.5. Рассмотрим оператор Â, выполняющий следующее преобразование:

a) Как состояние вертикальной поляризации преобразуется оператором Â?[35]
b) Напишите матрицу Â в каноническом базисе.
c) Выразите Â в нотации Дирака через внешнее произведение состояний |H⟩ и |V⟩.
d) Используя тот факт, что для любого линейного оператора  (λ|a⟩ + µ|b⟩) = λÂ|a⟩ + µ  |b⟩, определите, как  действует на состояния с круговой поляризацией.
e) Пользуясь предыдущим результатом, найдите матрицу Â в базисе круговой поляризации.
f) Найдите матрицу Â в каноническом базисе по его матрице в круговом базисе при помощи разложения (А.26) единичного оператора. Согласуется ли ваш результат с результатом пункта b)?
g) Является ли Â эрмитовым? Если нет, то каков оператор, сопряженный с ним?
Задача 1.6. Выполните упр. 1.24 с использованием альтернативного метода.
a) Напишите матрицу оператора волновой пластинки в базисе {|α⟩, |90º + α⟩}
b) Переведите эту матрицу в канонический базис при помощи разложения (A.26) единичного оператора.
Задача 1.7. Используя уравнение (1.5), покажите, что
Задача 1.8. Используя перемножение матриц, покажите, что четвертьволновая пластинка, ориентированная под любым углом, при применении к состоянию круговой поляризации дает состояние линейной поляризации.
Задача 1.9. Найдите базис измерения, связанный с устройством, которое состоит из:
a) полуволновой пластинки,
b) четвертьволновой пластинки
с оптической осью, ориентированной под углом α, за которой следует поляризующий светоделитель и два детектора фотонов.
Задача 1.10. Оператор Â имеет в каноническом базисе следующую матрицу:
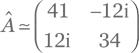
a) Представьте этот оператор в виде Â = 푣1|푣1⟩⟨푣1| + 푣2|v2⟩⟨푣2|, где {|v1⟩, |푣2⟩} — ортонормальный базис. Найдите 푣1, 푣2, а также матрицы |푣1⟩ и |푣2⟩ в каноническом базисе.
b) Напишите матрицы внешних произведений |푣1,2⟩⟨푣1,2| в каноническом базисе и убедитесь явно, что Â = 푣1|푣1⟩⟨푣1| + 푣2|푣2⟩⟨푣2|.
c) Наблюдаемое Â измеряется в состоянии круговой поляризации |R⟩. Каковы вероятности возможных результатов?
d) Вычислите математическое ожидание результата измерения:
- используя определение математического ожидания из теории вероятностей;
- используя выражение для квантового среднего.
Убедитесь, что результаты одинаковы.
e) Вычислите дисперсию наблюдаемого Â в состоянии |R⟩.
Задача 1.11. Рассмотрите устройство для измерения поляризации фотона, имеющее следующие свойства:
- всякий раз, когда фотон, линейно поляризованный под углом q, попадает в устройство, индикатор устройства показывает «2»;
- всякий раз, когда фотон, линейно поляризованный под углом π/2 + q, попадает в устройство, индикатор устройства показывает «3».
a) Найдите собственные значения и собственные состояния оператора Â, связанные с наблюдаемым, измеренным этим устройством.
b) Найдите матрицы оператора Â в его собственном базисе и базисе {|H⟩, |V⟩}.
c) Найдите вероятность каждого результата измерения для фотона, линейно поляризованного под некоторым углом ϕ.
d) Найдите среднее и дисперсию этого измерения.
Задача 1.12. Напишите принцип неопределенности для наблюдаемых
Задача 1.13. Измерения наблюдаемого Â в состоянии |H⟩ дают результаты 0 либо 1, каждый с вероятностью 1/2. Измерения наблюдаемого
Задача 1.14. Найдите
Задача 1.15. Атом описывается в некотором базисе {|푣1⟩, |푣2⟩} гамильтонианом
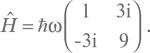
a) Найдите собственные состояния и собственные значения энергии.
b) Энергия этого атома измеряется в состоянии
Найдите вероятности обнаружения каждого собственного значения энергии, а также среднего арифметического и дисперсии этого измерения.
c) Первоначально этот атом находится в состоянии |푣1⟩. Найдите его состояние |ψ (t)⟩ в произвольный момент времени t. Сколько пройдет времени, прежде чем атом вновь окажется в состоянии |푣1⟩ (с точностью до фазового множителя)?
Задача 1.16. Предположим, что оператор (1.5a), связанный с полуволновой пластинкой под углом α, соответствует эволюции под некоторым гамильтонианом в течение времени t0.
a) Найдите матрицу этого гамильтониана в каноническом базисе.
b) Убедитесь, что эволюция за время t0/2 породит оператор четвертьволновой пластинки (1.5b).
c) Для гамильтониана, найденного в пункте a), и α = 30º решите дифференциальное уравнение Шрёдингера (1.31) для начального состояния |H⟩. Согласуется ли результат для t = t0 с тем, что можно было бы ожидать от физики преобразования поляризации?
Задача 1.17. Квантовая система может быть обнаружена в одном из трех ортогональных состояний |a⟩, |b⟩, |c⟩. Эти три состояния образуют ортонормальный базис.  представляет собой оператор, который циклически переставляет эти состояния, т.е. Â|a⟩ = ℏω|b⟩, Â|b⟩ = ℏω|c⟩, Â|c⟩ = ℏω|a⟩, (где ω действительно). Гамильтониан равен Ĥ =  + †.
a) Найдите собственные значения и собственные состояния энергии системы.
b) Найдите эволюцию системы, первоначально находившейся в состоянии |c⟩.
Задача 1.18. Атом имеет два энергетических собственных состояния |푣1⟩, |푣2⟩ с собственными значениями 0 и 3ℏω соответственно, где w > 0.
a) Напишите матрицу соответствующего гамильтониана Ĥ0.
b) В момент времени t = 0 включается поле, которое делает гамильтониан равным
c) В момент времени t = 0 атом находится в состоянии |푣1⟩. Найдите все значения времени t, в которые вероятность обнаружения атома в состоянии |푣2⟩ максимальна.
Это состояние иногда называют кошкой Шрёдингера в честь одного из отцов-основателей квантовой физики Эрвина Шрёдингера. На самом деле Шрёдингер говорил о более сложном объекте, см. отступление 2.5.
Как в геометрии, которая представляет собой чрезвычайно строгую науку, несмотря на то что первичные понятия в ней, такие как точка, прямая и плоскость, не определены.
Может показаться удивительным, что уравнение (1.2) не несет никакой информации о координате фотона по оси z. Причина в том, что этот фотон, будучи квантовой частицей, размазан в пространстве и времени. К факторам, влияющим на степень размазанности, относятся, в частности, характеристики источника, а также «объем квантования», выбранный для теоретического анализа. В случае лазерного луча длина фотона ограничивается длиной когерентности лазера, которая может составлять не один километр. В данной книге мы, как правило, будем считать, что фотоны размазаны на расстояние, намного превышающее размер любого прибора, и потому могут рассматриваться как бесконечно большие.
Если вы не знакомы с понятием поляризации электромагнитной волны, то теперь самое время прочесть первые два раздела приложения В.
Общепринятых постулатов квантовой механики не существует. Если вы скажете «Это следует из второго закона Ньютона», вас поймут, но утверждения «Это следует из первого постулата квантовой механики» никто не поймет. Вместо этого следует сказать, к примеру, «Это следует из линейности квантового гильбертова пространства».
A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt, Annalen der Physik 17, 132 (1905).
M. Planck, Über das Gesetz der Energieverteilung im Normalspectrum, Annalen der Physik 4, 553 (1901).
В данном случае общая фаза в правой части уравнения (1.35) имеет значение. Дело в том, что нас интересует не только преобразование самого состояния |+⟩, но и вся линейная операция, определенная этим преобразованием. Чтобы увидеть действие этой общей фазы, вы можете попытаться решить часть a) , заменив (1.35) на |+⟩ → |+⟩.
О функциях операторов см. разд. A.11.
Даже если  не коммутируют, это не означает, что измерение наблюдаемого
не коммутируют, это не означает, что измерение наблюдаемого  в собственном состоянии наблюдаемого Â всегда дает случайный результат.
в собственном состоянии наблюдаемого Â всегда дает случайный результат.
Это не означает, однако, что любое собственное состояние наблюдаемого Â даст определенный результат при измерении  Если у Â есть вырожденные собственные величины, его собственный базис не является единственным (см. разд. A.8), так что не каждый собственный вектор оператора Â гарантированно является также собственным вектором
Если у Â есть вырожденные собственные величины, его собственный базис не является единственным (см. разд. A.8), так что не каждый собственный вектор оператора Â гарантированно является также собственным вектором  состояние |+⟩ является собственным состоянием Â, но не
состояние |+⟩ является собственным состоянием Â, но не  так что наблюдаемое
так что наблюдаемое  при измерении в этом состоянии будет проявлять неопределенность, несмотря на то что
при измерении в этом состоянии будет проявлять неопределенность, несмотря на то что 
Чтобы узнать о коммутаторах, загляните в разд. A.9.
Важное исключение здесь — случай, когда матрица имеет вырожденные собственные величины. В этом случае решение для собственного базиса не единственно. Пример см. в упр. A.68.
C.H. Bennett, G. Brassard, “Quantum Cryptography: Public Key Distribution and Coin Tossing”, Int. Conf. on Computers, Systems and Signal Processing, Bangalore, India (IEEE, New York, 1984), p. 175.
A. C. Elitzur, L. Vaidman, Quantum mechanical interaction-free measurements, Foundations of Physics 23, 987 (1993).
«Который путь» (нем.).
Именно поэтому, вероятно, популярные книги по квантовой механике любят описывать состояния суперпозиции как состояния, в которых «объект находится в двух разных местах в одно и то же время».
Значение индексов x, y и z прояснится в главе 4, когда мы будем изучать квантование момента импульса.
Более полное введение в линейные операторы и матрицы можно найти в разд. A.5 и A.6.
На самом деле частота темновых срабатываний может быть выше. Но, поскольку Боб знает точные моменты передачи фотонов Алисой, на частоту ошибки будут влиять только те темновые события, которые произойдут синхронно с щелчками, ожидаемыми от фотонов Алисы.
P.W. Shor and J. Preskill, Simple Proof of Security of the BB84 Quantum Key Distribution Protocol, Physical Review Letters 85, 441 (2000).
Позже мы увидим, что на самом деле фотон может расщепиться на два фотона с меньшей энергией при нелинейном оптическом явлении, известном как параметрическое рассеяние. Однако этот довольно экзотический эффект возникает с низкой вероятностью и только в особых условиях. Наш интерферометр не содержит нелинейных оптических элементов, так что параметрическое рассеяние здесь ни при чем.
Считаем, что линия задержки много короче, чем длина светового импульса, так что изменение задержки не влияет на видность интерференции.
Обсуждение договоренностей, принятых для состояний с круговой (циркулярной), поляризацией, см. в сноске 141.
G. N. Lewis, The conservation of photons, Nature 118, 874 (1926).
A. H. Compton, A Quantum Theory of the Scattering of X-Rays by Light Elements, Physical Review 21 483 (1923).
Выражение для импульса фотона можно получить также следующим образом. Воспользовавшись знаменитым уравнением Эйнштейна E = mc2 и формулой Планка, мы можем рассчитать массу фотона M = ℏω/c2. Фотон движется со скоростью света, следовательно, его импульс равен p = Mc = ℏω/c.
Хотя мы не знаем, каково это состояние, мы можем многократно приготавливать фотон в одном и том же состоянии путем сохранения постоянных условий эксперимента.
Такие смешанные состояния не являются элементами квантового гильбертова пространства. Подробнее об этом см. подразд. 2.2.4.
Сейчас подходящий момент, чтобы прочитать в приложении разд. В.3.
«Мысленный эксперимент» (нем.).
Конкретнее, интерферометр Маха — Цендера.
Это явление выражается, в частности, в эффекте давления света, который экспериментально наблюдал Петр Лебедев в 1900 г.
Запутанность
И лишь тогда, а вовсе не до того, не загодя, не вначале
2.1. Пространство тензорных произведений
2.1.1. Тензорное произведение состояний и запутанные состояния
Рассмотрим две физические системы, разделенные в пространстве и/или во времени, но взаимодействующие между собой или по крайней мере взаимодействовавшие в прошлом. Чтобы исследовать состояния, возникающие после такого взаимодействия, работать с каждой системой в отдельности недостаточно. С ними надлежит иметь дело как с единым гильбертовым пространством, объединяющим гильбертовы пространства, связанные с отдельными системами.
Предположим, например, что у Алисы на Венере имеется[36] горизонтально поляризованный фотон |H⟩, а у Боба на Марсе — фотон в состоянии |V⟩. Тогда мы говорим, что совместное состояние фотонов Алисы и Боба описывается выражением
|H⟩A ⊗ |V⟩B ≡ |H⟩|V⟩ ≡ |HV⟩. (2.1)
Такие совместные состояния называются тензорными произведениями[37].
Однако совместное гильбертово пространство содержит не только тензорные произведения. Так, поскольку оно включает в себя состояния |HV⟩ и |VH⟩ и является линейным, то должно также содержать состояние, к примеру,
Мы видим, что объединение двух гильбертовых пространств порождает совершенно новый класс состояний, который дает начало новой физике — физике нелокальных квантовых явлений. Это основная тема настоящей главы. Некоторые из таких явлений не только немыслимы с точки зрения классической физики, но и выглядят противоречащими фундаментальному здравому смыслу.
Прежде чем мы начнем изучать эту новую физику, нам придется заточить карандаши и обновить наш теоретический аппарат, чтобы его можно было применять к таким составным пространствам. Мы будем все рассуждения проводить для двусоставных (bipartite) пространств, но они могут быть расширены прямолинейным образом на системы с тремя и более частями.
Пространство тензорных произведений (мы также будем применять термин «составное пространство») 핍A ⊗ 핍B гильбертовых пространств 핍A и 핍B есть гильбертово пространство, состоящее из элементов |a⟩ ⊗ |b⟩ (где |a⟩ ∈ 핍A и |b⟩ ∈ 핍B) и их линейных комбинаций. Вот правила, которым подчиняются операции в этом пространстве:
1. Умножение на число:
λ (|a⟩ ⊗ |b⟩) = (λ|a⟩) ⊗ |b⟩ = |a⟩ ⊗ (λ|b⟩). (2.2)
2. Распределительный закон:
(|a1⟩ + |a2⟩) ⊗ |b⟩ = |a1⟩ ⊗ |b⟩ + |a2⟩ ⊗ |b⟩; (2.3a)
|a⟩ ⊗ (|b1⟩ + |b2⟩) = |a⟩ ⊗ |b1⟩ + |a⟩ ⊗ |b2⟩. (2.3b)
3. Скалярное произведение двух состояний |a⟩ ⊗ |b⟩ и |a'⟩ ⊗ |b'⟩ в 핍A ⊗ 핍B задается формулой
⟨ab| a'b'⟩ = ⟨a| a'⟩⟨b| b'⟩. (2.4)
Элементы 핍A ⊗ 핍B, которые могут быть представлены в виде тензорного произведения |a⟩ ⊗ |b⟩, называют разделимыми, или сепарабельными (separable). Остальные запутаны.
Упражнение 2.1. Для любых двух векторов |a⟩ ∈ 핍A и |b⟩ ∈ 핍B покажите, что
Упражнение 2.2. Если заданы ортонормальные базисы
Ответ: множество тензорных произведений {|푣i⟩ ⊗ |ωj⟩} есть ортонормальный базис. Размерность составного пространства есть произведение NM размерностей его компонентов.
Например, гильбертово пространство, представляющее поляризации двух фотонов, четырехмерно. Канонический ортонормальный базис в этом пространстве таков: {|HH⟩, |HV⟩, |VH⟩, |VV⟩}.
Упражнение 2.3. Найдите разложение в каноническом базисе для состояния, в котором Алиса имеет фотон, поляризованный под 30°, а фотон Боба находится в состоянии правой круговой поляризации. Напишите матричное представление для этого состояния. Разделимое оно или запутанное?
Упражнение 2.4. Найдите скалярное произведение ⟨Π|Ω⟩, где:
a) |Π⟩ = 5 |HH⟩ + 6i |R — ⟩ и |Ω⟩ = 2 |+L⟩ + 3 |RR⟩;
b) |Π⟩ = i (2 |H⟩ + i |V⟩) ⊗ |R⟩ и |Ω⟩ = (2i |H⟩ — 3i |V⟩) ⊗ |+⟩.
Упражнение 2.5§. Образуют ли множества
a) {|+ +⟩, |– +⟩, |+ –⟩, |– –⟩},
b) {|RR⟩, |RL⟩, |LR⟩, |LL⟩},
c) {|H — ⟩, |H+⟩, |V — ⟩, |V+⟩},
d) {|H — ⟩, |H+⟩, |VR⟩, |VL⟩},
e) {|H — ⟩, |HH⟩, |VR⟩, |VL⟩}
базисы в двухфотонном гильбертовом пространстве? Ортонормальны ли эти базисы?
Ответ: все пять множеств образуют базисы; все они, кроме последнего, ортонормальны.
Упражнение 2.6. Покажите, что белловские состояния

запутаны.
Упражнение 2.7. Покажите, что эти четыре белловских состояния образуют ортонормальный базис.
Упражнение 2.8. Перепишите белловские состояния (2.5) в диагональном базисе.
Упражнение 2.9. Пусть |θ⟩ — состояние линейной поляризации под углом θ к горизонтали. Покажите, что для любого θ состояние
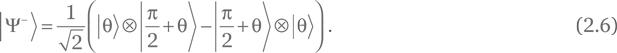
Это означает, что состояние |Ψ–⟩ изотропно, т.е. остается неизменным вне зависимости от того, какое направление мы определим как горизонтальное (при условии что оно перпендикулярно направлению движения фотонов, разумеется). Этим свойством из всех белловских состояний обладает только |Ψ–⟩.
2.1.2. Измерения в составных пространствах
Постулат о квантовых измерениях применим к тензорным произведениям гильбертовых пространств в обычном режиме. Базис измерения может состоять как из разделимых, так и из запутанных состояний. Если базис построен в виде тензорного произведения базисов в 핍A и 핍B, как в упр. 2.2, то Алисе и Бобу нужно просто провести измерения в этих базисах в своих гильбертовых пространствах (рис. 2.1).
Отступление 2.1. Как создать запутанное состояние?
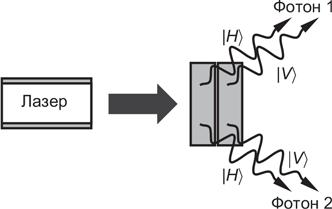
Рассмотрим параметрическое рассеяние (отступление 1.6) на последовательности двух нелинейных кристаллов, как показано на рисунке[38]. Кристаллы построены таким образом, что первый из них выдает только пары горизонтально поляризованных фотонов |H⟩ ⊗ |H⟩, а второй — только пары вертикально поляризованных |V⟩ ⊗ |V⟩. Вероятность появления пары мала в обоих кристаллах. Тогда любая пара, если она есть, может находиться либо в состоянии |HH⟩, либо в состоянии |VV⟩. Поскольку расстояние между кристаллами постоянно, постоянна и оптическая фаза между этими двумя парами. Так что состояние двух фотонов, выданных кристаллами, есть
|HH⟩ + eiϕ|VV⟩.
Выбирая величину ϕ, можно получить любое из белловских состояний |Φ+⟩ или |Φ—⟩. Чтобы превратить эти состояния в |Ψ+⟩ или |Ψ—⟩, достаточно поместить в один из выходных каналов полуволновую пластинку.
Упражнение 2.10. Для двух фотонов, приготовленных в состоянии
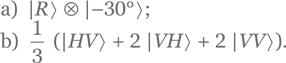
Считаем, что измерение выполняется в некотором ортонормальном базисе, в который входит интересующее нас состояние.
Упражнение 2.11. Алиса и Боб имеют общее состояние
a) Найдите вероятности всех результатов, если Алиса и Боб измерят |Ψ⟩ в (1) каноническом и (2) диагональном {|+ +⟩, |+ –⟩, |– +⟩, |– –⟩} базисах.
b) Алиса и Боб имеют общую единственную копию одного из белловских состояний, |Ψ–⟩ или |Ψ+⟩, но не знают, какого именно. Могут ли они выяснить это при помощи измерений в каноническом базисе? А в диагональном?
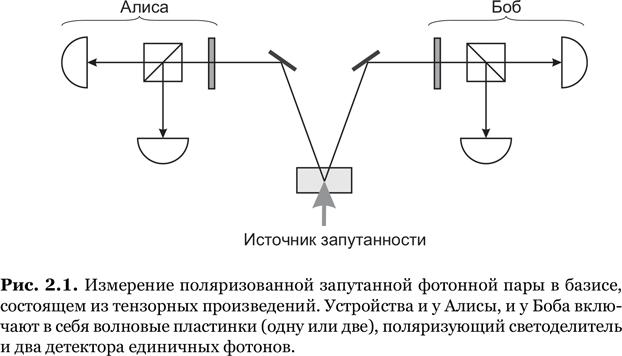
Важный вывод, который мы можем сделать из этого упражнения, состоит в том, что, хотя запутанные состояния могут возникать только при взаимодействии двух физических систем, их измерение (например, с целью отличить одно от другого) не требует не только взаимодействия, но даже проекции на запутанные состояния. Более того, можно провести полную квантовую томографию квантового состояния в составном гильбертовом пространстве при помощи измерений в базисах, содержащих только разделимые состояния. Мы покажем это строго в конце основного текста (упр. 5.78).
Упражнение 2.12*. Предложите процедуру выполнения измерения в базисе {|H– ⟩, |H+⟩, |VR⟩, |VL⟩}.
Подсказка: считайте, что Алиса и Боб связаны классическим каналом связи.
2.1.3. Тензорное произведение операторов
Расширим понятие тензорного произведения на операторы. Это расширение относительно прямолинейно: в операторе
Тензорное произведение оператора Â, который действует на 핍A, и оператора
Упражнение 2.13. Выразите матрицу тензорного произведения оператора
Ответ: для каждого элемента матрицы[39]
Упражнение 2.14. Найдите математическое ожидание и неопределенность оператора
Упражнение 2.15§. Предположим, что |푣⟩ и |ω⟩ — собственные состояния операторов
Упражнение 2.16. Покажите, что для операторов
Упражнение 2.17§. Покажите, что тензорное произведение операторов не может сделать запутанное состояние из разделимого.
Упражнение 2.18. Для двух операторов внешнего произведения
Понятие о тензорном произведении операторов красиво иллюстрируется таким значительным результатом, как теорема о запрете клонирования (no-cloning theorem)[40]. Предположим, у нас имеется два объекта, представленные идентичными гильбертовыми пространствами 핍A и 핍B, причем объект, представленный 핍A, находится в некотором произвольном квантовом состоянии |a⟩. Квантовое клонирование — гипотетическая операция, которая создавала бы копию |a⟩ в 핍B, сохраняя при этом оригинал в 핍A. Иными словами, она соответствует некоторому оператору на 핍A ⊗ 핍B, такому, что для любого |a⟩ ∈ 핍A и некоторого |0⟩ ∈ 핍B
|a⟩ ⊗ |0⟩ → |a⟩ ⊗ |a⟩. (2.10)
Упражнение 2.19. Покажите, что квантовое клонирование в том виде, как оно определено выше, невозможно.
Подсказка: воспользуйтесь тем фактом, что любая физически возможная эволюция в квантовой механике описывается линейным оператором.
Сопряженное пространство тензорного произведения определяется аналогично тому, как мы определили прямое, т.е. для любого состояния тензорного произведения |a⟩ ⊗ |b⟩[41]
сопр (|a⟩ ⊗ |b⟩) ≡ сопр (|a⟩) ⊗ сопр (|b⟩) ≡ A⟨a| ⊗B⟨b| ≡ ⟨ab|. (2.11)
Упражнение 2.20. Покажите, что для
Упражнение 2.21. Покажите, что:
a) тензорное произведение двух эрмитовых операторов эрмитово;
b) тензорное произведение двух унитарных операторов унитарно.
2.1.4. Локальные операторы
Операторы тензорного произведения вида
Упражнение 2.22. Покажите, что локальный унитарный оператор не может сделать разделимое состояние запутанным, и наоборот.
Упражнение 2.23. Предположим, что |a⟩ — собственное состояние оператора Â на гильбертовом пространстве Алисы с собственным значением a. Покажите, что для любого вектора |b⟩ в гильбертовом пространстве Боба вектор |ab⟩ есть собственное состояние локального оператора
Упражнение 2.24. Пусть
a) Приведите пример такой ситуации.
b) Покажите, что всякий раз, когда Алиса измеряет Â, а Боб —
Подсказка: воспользуйтесь упр. A.66.
Упражнение 2.25. Предположим, Алиса и Боб располагают белловским состоянием |Ψ–⟩. Алиса производит локально над своим кубитом операцию, соответствующую одному из трех операторов Паули. Покажите, что:
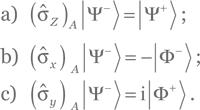
Данный результат имеет интересное приложение в квантовом протоколе связи, известном как квантовое сверхплотное кодирование (quantum superdense coding, см. отступление 2.2).
Отступление 2.2. Граница Холево и квантовое сверхплотное кодирование
Предположим, что Алиса и Боб связаны неким каналом связи (например, оптоволоконным). Алиса хочет послать Бобу классическое сообщение из n бит, зашифровав информацию в некотором наборе квантовых частиц, каждая из которых несет в себе кубит[42]. Сможет ли она достичь своей цели, использовав меньше, чем n квантовых частиц?
Простое рассуждение показывает, что на этот вопрос следует ответить отрицательно. В самом деле, n кубитов соответствуют 2n-мерной квантовой системе (упр. 2.2). Как бы Алиса ни кодировала свои биты в кубитах, Боб при измерении этой системы сможет получить не более 2n возможных результатов, так что полное количество различных сообщений, которые можно зашифровать в n кубитов, равно 2n. Емкость n бит классической информации точно такая же. Это ограничение — пример так называемой границы Холево в квантовой информатике.
Однако если у Алиса и Боба есть заранее приготовленные общие запутанные кубиты, то границу Холево можно обойти при помощи протокола, известного как квантовое сверхплотное кодирование. Предположим, Алиса хочет послать Бобу два бита классической информации. Протокол тогда выглядит следующим образом:
- Алиса и Боб заранее готовят общее состояние |Ψ — ⟩ из двух кубитов (к примеру, фотонов).
- В зависимости от значения своих двух битов Алиса производит над своим кубитом операцию превращая таким образом общее запутанное состояние в одно из четырех белловских состояний, как в упр. 2.25. Реализовать это можно при помощи волновых пластинок (см. упр. 1.26).
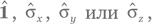
- Алиса отправляет свой кубит Бобу.
- Теперь у Боба два кубита. Он измеряет их в базисе Белла и получает одно из четырех состояний, что соответствует двум классическим битам.
Таким способом Алиса может передать два бита классической информации, переслав всего один кубит.
Упражнение 2.26. Предположим, что гамильтониан в 핍A ⊗ 핍B задается суммой
Ĥ = ĤA + ĤB
гамильтонианов, которые представляют собой локальные операторы в своих пространствах-компонентах. Покажите, что:
a) если начальное состояние в 핍A ⊗ 핍B есть тензорное произведение
|ψ (0)⟩ = |ψA (0)⟩ ⊗ |ψB (0)⟩,
то в ходе шрёдингеровой эволюции это состояние остается тензорным произведением
|ψ (t)⟩ = |ψA (t)⟩ ⊗ |ψB (t)⟩,
где каждое |ψA,B (t)⟩ есть решение уравнения Шрёдингера для соответствующего гамильтониана ĤA,B;
b) если некоторые |ψA⟩ и |ψB⟩ являются собственными состояниями своих гамильтонианов с энергиями EA и EB соответственно, то состояние |Ψ⟩ = |ψA⟩ ⊗ |ψB⟩ в 핍A ⊗ 핍B есть собственное состояние полного гамильтониана Ĥ с энергией E = EA + EB;
c) * любое собственное состояние гамильтониана, соответствующего энергии E, может быть записано как линейная комбинация произведений вида |ψA⟩ ⊗ |ψB⟩, где |ψA,B⟩ — собственные состояния гамильтониана для отдельных гильбертовых пространств, ĤA,B |ψA,B⟩ = EA,B |ψA,B⟩, с E = EA + EB.
2.2. Локальные измерения запутанных состояний
Как мы видели в последнем упражнении, расширение постулата об измерениях на двусоставные системы достаточно прямолинейно, если два наблюдателя производят измерения на своих гильбертовых пространствах одновременно. Однако, поскольку эти два наблюдателя независимы, может оказаться, что только один из них (например, Алиса) производит измерение, тогда как другой (Боб) этого не делает. Мы называем это локальным измерением.
2.2.1. Удаленное приготовление состояния
Предположим, что Алиса измеряет состояние
Такая корреляция сама по себе не так уж удивительна. Даже в обычной жизни мы можем представить себе игру, в которой Алисе дается одна туфля из пары, а Бобу — вторая. Каждая туфля упакована в непрозрачную коробку, так что их «ориентацию» увидеть нельзя. Затем Алиса летит к Венере, а Боб — к Марсу, где они открывают свои коробки. Предположим, Алиса обнаруживает в своей коробке левую туфлю. При этом она мгновенно узнает, что у Боба в коробке лежит правая туфля, хотя того при этом отделяют от нее миллионы километров.
Но свойства квантовых суперпозиций идут дальше этой простой картины. Помимо поляризационных корреляций в них существует определенное фазовое соотношение (когерентность), которое обозначается знаком «минус» между |HV⟩ и |VH⟩. Этим состояние
Упражнение 2.27. Предположим, что Алиса и Боб располагают состоянием |Ψ–⟩. Алиса измеряет свою часть состояния в базисе {|θ, |π/2 + θ⟩}. Покажите, что:
a) если Алиса обнаруживает |θ⟩, то состояние Боба становится |π/2 +θ⟩;
b) если Алиса обнаруживает |π/2 +θ⟩, то состояние Боба становится |θ⟩;
c) каждый из этих результатов наблюдается с вероятностью 1/2.
Подсказка: используйте свойство изотропности состояния |Ψ–⟩ (упр. 2.9).
Это поистине замечательный результат. Выбрав угол наклона базиса измерения q, Алиса может удаленно приготовить произвольное состояние линейной поляризации (с точностью до ±90º) в локации Боба. Так происходит несмотря на то, что Алиса и Боб находятся, возможно, в миллионах километров друг от друга и не имеют возможности общаться между собой. Более того, все происходит мгновенно, т.е. быстрее скорости света!
На первый взгляд, такое удаленное приготовление состояния (remote state preparation) откровенно противоречит специальной теории относительности и, мало того, принципу причинности (causality), который правит всей известной нам физикой и следует из самого что ни на есть фундаментального здравого смысла. Как можно менять что-то мгновенно на огромном расстоянии от себя, да еще при отсутствии какой-либо возможности взаимодействовать с той локацией?
Наверное, каждый прилежный студент-физик в этот момент первым делом спросит, был ли данный вывод проверен экспериментально. Ответ положительный. Чтобы провести этот эксперимент, исследователь многократно подготавливает состояние |Ψ–⟩ и проводит измерение Алисы, все время в одном и том же базисе. Каждый раз, когда Алиса обнаруживает, скажем, |θ⟩, экспериментатор измеряет поляризацию фотона Боба. По статистике этих измерений он может восстановить искомое состояние при помощи квантовой томографии (см. упр. 1.15) со сколь угодно высокой точностью.
За последнюю четверть века физики исследовали самые разные варианты эффекта удаленного приготовления состояния. Некоторые из экспериментов были организованы так, что лаборатории Алисы и Боба разделялись несколькими километрами, а измерения происходили гарантированно в пределах пространственноподобного интервала, чтобы исключить даже теоретическую возможность для Алисы повлиять на состояние Боба посредством каких бы то ни было известных в природе взаимодействий. Все эти эксперименты недвусмысленно подтверждают верность квантовых предсказаний.
Но как же примирить полученные данные с причинностью? Чтобы ответить на данный вопрос, дадим сначала формальное описание локального измерения.
2.2.2. Частичное скалярное произведение
Предположим, что Алиса и Боб располагают некоторым запутанным состоянием и что Алиса проводит локальное измерение своей части этого состояния в некотором базисе. Каковы вероятности возможных результатов и какое состояние будет удаленно подготовлено в локации Боба в случае каждого результата? Прежде чем ответить на этот вопрос в общем случае, рассмотрим пример. Пусть общее состояние
и предположим, что Алиса проводит измерение в диагональном базисе.
Упражнение 2.28. Перепишите состояние (2.12), выразив векторы состояния, соответствующие фотону Алисы, в диагональном базисе.
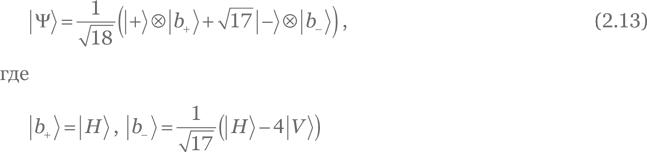
суть нормированные векторы в гильбертовом пространстве Боба.
Поскольку векторы |+⟩ и |–⟩ ортогональны, ортогональны также |+⟩ ⊗ |b+⟩ и |–⟩ ⊗ |b–⟩ в соответствии с уравнением (2.4). Это означает, что мы можем построить в 핍A ⊗ 핍B ортонормальный базис, содержащий упомянутые состояния в качестве элементов. Если мы измерим |Ψ⟩ в этом базисе, то получим |+⟩ ⊗ |b+⟩ с вероятностью
Мы видим, что для ответа на вопрос, поставленный в начале этого подраздела, достаточно переписать начальное запутанное состояние в виде линейной комбинации таких тензорных произведений, в каждом из которых компонент Алисы представляет собой элемент ее измерительного базиса. Проведем то же рассуждение в более общем виде.
Предположим, начальное состояние
где {|푣i⟩} — ортонормальный базис, в котором Алиса будет проводить свое измерение, а {|ωj⟩} — некоторый ортонормальный базис в гильбертовом пространстве Боба. Перепишем это в виде:
где

есть нормирующий множитель, такой что ║|bi⟩║ = 1 для любого i (в сумме (2.15) мы опускаем слагаемые с
Таким образом, мы выразили состояние, которое предстоит измерить, в виде суммы ортогональных компонентов |푣i⟩ ⊗ |bi⟩. Амплитуды этих компонентов равны 1/퓝i, так что вероятность, с которой Алиса увидит соответствующий |푣i⟩, равна prA,i = 1/퓝i2. Всякий раз, когда это происходит, система Боба принимает соответствующее состояние |bi⟩.
Упражнение 2.29. Для физического состояния |Ψ⟩ покажите, что в (2.15)
Упражнение 2.30. Для состояния |Ψ⟩ = 퓝 (|RV⟩ + |H+⟩):
a) найдите множитель 퓝 такой, при котором |Ψ⟩ нормировано;
b) представьте это состояние в виде (2.15), где {|푣i⟩} — канонический базис;
c) найдите вероятности возможных результатов при проведении Алисой локального измерения в каноническом базисе и напишите удаленно приготовленное состояние фотона Боба для каждого из результатов Алисы.
Мы разработали метод предсказания результатов локальных измерений на запутанном состоянии. Этот метод функционален, но несколько неуклюж, так что мы сейчас введем понятие, которое позволит нам существенно упростить процедуру.
Частичное скалярное произведение (partial inner/scalar product) локального состояния |a⟩ в гильбертовом пространстве 핍A и двусоставного состояния

Определение для частичного скалярного произведения |Ψ⟩ и локального состояния в пространстве 핍B дается аналогично.
Упражнение 2.31. Для |ψ⟩ = 2|H⟩ + i|핍⟩ найдите B⟨ψ|Ω⟩ и ⟨Π|ψ⟩A, где |Ω⟩ = 2|HH⟩ + 3|H핍⟩ + 4|핍H⟩, |Π⟩ = (2 |H⟩ + i|핍⟩) ⊗ (i|H⟩ — |핍⟩), а индексы A и B на состоянии |ψ⟩ указывают, что оно локализовано в пространстве Алисы или Боба соответственно.
Упражнение 2.32. Покажите, что для любого разделимого состояния |ab⟩ ∈ 핍A ⊗ 핍B и любого состояния |a'⟩ ∈ 핍A
⟨a' | ab⟩ = ⟨a' | a⟩ |b⟩. (2.18)
Упражнение 2.33. Предположим, что |Ψ⟩ — состояние в пространстве тензорных произведений, а |a⟩ и |b⟩ — состояния в пространствах Алисы и Боба соответственно. Покажите, что
⟨a | (⟨b|Ψ⟩) = ⟨b | (⟨a|Ψ⟩) = ⟨ab|Ψ⟩. (2.19)
Упражнение 2.34. Покажите, что для любых двух ортонормальных базисов {|푣i⟩} ⊗ {|ωj⟩} и {|v'i⟩} ⊗ {|ω'j⟩} в 핍A ⊗ 핍B локального состояния |a⟩ ∈ 핍A и двусоставного состояния
частичное скалярное произведение ⟨a| Ψ⟩ не зависит от выбора базиса, т.е.
Упражнение 2.35. Покажите, что в уравнении (2.15):
a) |bi⟩ = 퓝i ⟨푣i|Ψ⟩;
b) ║ ⟨푣i|Ψ⟩ ║ = 1/퓝i.
Последнее упражнение предлагает прямолинейный способ вычислить разложение (2.15) для заданного состояния и базиса измерения Алисы и, следовательно, вычислить также результаты локальных измерений. И в самом деле, частичное скалярное произведение дает не только состояние |bi⟩, которое будет приготовлено удаленно в локации Боба, но и вероятность каждого результата
Мы можем рассматривать этот результат как обобщение постулата квантовой физики об измерениях на локальные измерения. Резюмируем его. Локальное измерение Алисы на двусоставном состоянии |Ψ⟩ в базисе {|푣i⟩} вызовет коллапс |Ψ⟩ на одно из случайно выбранных состояний 퓝i |푣i⟩ ⊗ ⟨푣i|Ψ⟩ с вероятностью
prA,i = ⟨Ψ|푣i⟩ ⟨푣i|Ψ⟩. (2.22)
Это можно переформулировать на языке проекционных операторов (разд. 1.8): измерение Алисы превращает состояние |Ψ⟩ в множество ненормированных состояний
После локального измерения запутанное двусоставное состояние коллапсирует в разделимое состояние. Если Алиса разрушит в процессе измерения свою систему, то результирующее состояние 퓝i ⟨푣i|Ψ⟩ будет локализовано у Боба.
Упражнение 2.36. Выполните упр. 2.30 c) с использованием частичных скалярных произведений.
Упражнение 2.37. Для каждого белловского состояния покажите, что локальное измерение Алисы в любом ортонормальном базисе выдаст тот или иной результат с вероятностью 1/2.
Упражнение 2.38§. Предположим, Алиса измеряет
в базисе круговой поляризации. На какое состояние проецируется фотон Боба для каждого из результатов Алисы?
Упражнение 2.39. Предположим, что Алиса и Боб располагают состоянием |Ψ–⟩. Алиса хочет удаленно приготовить в локации Боба некоторую линейную суперпозицию α|H⟩ + β|V⟩, где α и β произвольны, но |α|2 + |β|2 = 1 (т.е. результирующее состояние нормировано). В каком базисе ей следует измерять? Какова вероятность успеха?
2.2.3. Локальные измерения и причинность
Вернемся теперь к нашему недавнему обсуждению того, противоречит ли эффект удаленного приготовления принципу причинности. Тот факт, что измерение Алисы влияет на состояние фотона Боба, сам по себе не содержит такого противоречия, ибо квантовое состояние — понятие вполне абстрактное. Вопрос, которым нам следует задаться, звучит так: изменятся ли физические свойства фотона Боба — т.е. его поведение при измерениях — после измерения Алисы?
Налицо искушение дать положительный ответ. И в самом деле, до измерения состояние Боба было частью полностью изотропного двусоставного состояния; после измерения это уже состояние с определенным углом поляризации — т.е. с кардинально другими физическими свойствами.
Однако при таком ответе упускается один важный момент. Локальное измерение Алисы не всегда приготавливает одно и то же состояние в локации Боба: иногда это |θ⟩, а иногда |π/2 + θ⟩. Чтобы узнать, какое именно возникло состояние, Бобу нужно принять от Алисы классическое сообщение о результате, полученном ею при измерении. До этого момента Боб знает лишь, что у него имеется одно из двух возможных состояний — и благодаря этой неопределенности измеряемые свойства фотона Боба остаются полностью идентичными тем, что были до измерения. Прежде чем доказать это утверждение строго, рассмотрим пример.
Упражнение 2.40. В условиях упр. 2.27 Боб измеряет поляризацию своего фотона в каноническом базисе после измерения Алисы. Какова вероятность каждого результата при условии, что Боб не знает результата измерения Алисы?
Ответ: prБоб,H = prБоб,V = 1/2 независимо от базиса, который использовала Алиса.
Упражнение 2.41. Алиса и Боб выполняют измерения на своих частях двусоставного состояния |Ψ⟩ в базисах {|푣i⟩} и {|ωj⟩} соответственно. Эти измерения могут проходить по трем альтернативным сценариям:
1. Алиса и Боб выполняют свои измерения одновременно, так что к проективному измерению состояния |Ψ⟩ в базисе {|푣i⟩ ⊗ |ωj⟩} применим оригинальный постулат об измерениях.
2. Алиса выполняет свое измерение первой, а затем Боб измеряет удаленно приготовленное состояние.
3. Боб выполняет свое измерение первым, а затем Алиса измеряет удаленно приготовленное состояние.
Покажите, что вероятность ситуации, в которой Алиса обнаружит |푣i⟩, а Боб — |ωj⟩, одинакова для каждого из этих сценариев: prij = |⟨푣iωj | Ψ⟩|2.
Упражнение 2.42. Проверьте утверждение из предыдущего упражнения на примере состояния |Ψ⟩ из упр. 2.30 и измерений, проведенных обеими сторонами в канонических базисах:
a) Найдите вероятности prHH, prHV, prVH и prVV для случая, когда Алиса и Боб производят свои измерения одновременно.
b) Считая, что Алиса производит свое измерение первой, найдите вероятности и удаленно приготовленные состояния фотона Боба для каждого из ее результатов. Затем предположите, что Боб измеряет каждое из этих удаленно приготовленных состояний и определите соответствующие вероятности. Используйте эту информацию, чтобы оценить prHH, prHV, prVH и prVV, и убедитесь, что они получились такими же, как в пункте a).
c) § Повторите пункт b) для случая, когда Боб производит свое измерение первым.
Упражнение 2.43. Для каждого из сценариев упр. 2.41 покажите, что для Боба суммарная вероятность увидеть состояние |ωj⟩ составляет ║⟨ωj | Ψ⟩║2.
Приведенные результаты означают, что без знания результата измерения Алисы физические свойства фотона Боба не меняются, так что Боб не может извлечь вообще никакой информации о действиях Алисы. Хотя мгновенное удаленное приготовление состояния предсказывается теорией и подтверждается экспериментом, оно не может быть использовано для сверхсветовой бесконтактной связи. Квантовая механика наводит нас на противоположную мысль, утверждая, что состояние Боба после измерения Алисы зависит от условий измерения. Но квантовое состояние — это чисто теоретический конструкт, его невозможно непосредственно наблюдать в эксперименте. Мы можем получить информацию о состоянии только косвенным путем, из статистики, полученной в многочисленных измерениях.
Так, может быть, от всех этих парадоксов получится уйти, вообще отказавшись от концепции квантового состояния и придумав другую теорию, которая столь же хорошо объясняла бы экспериментальные результаты, но не содержала бы теоретических концепций, противоречащих здравому смыслу? Ответ на этот вопрос мы найдем в разд. 2.3. А пока давайте обсудим еще один парадокс, который позволяет взглянуть на проблему под еще более острым углом. Рассмотрим следующий сценарий:
1. Алиса и Боб имеют множество общих копий состояния |Ψ–⟩.
2. Над каждой копией сначала Боб производит измерение в каноническом, диагональном или круговом базисе (он выбирает случайным образом). Затем Алиса измеряет свой фотон в базисе {|θ⟩, |π/2 + θ⟩} и сообщает результат Бобу.
3. После того как все измерения завершены, Боб восстанавливает квантовое состояние своего фотона по данным, которые он записал с использованием метода квантовой томографии (упр. 1.15), принимая «задним числом» во внимание (постселектируя) только те события, в которых Алиса измерила |θ⟩.
Если бы измерения Боба происходили после измерений Алисы, то он благодаря явлен
...