автордың кітабын онлайн тегін оқу Живая математика. Занимательная алгебра


Серийное оформление В. Пожидаева
Оформление обложки В. Пожидаева-мл.
Иллюстрации Н. Максимова и Ю. Скалдина
Перельман Я.
Живая математика ; Занимательная алгебра / Яков Перельман. — СПб. : Азбука, Издательство АЗБУКА, 2025. — (Азбука-классика. Non-Fiction).
ISBN 978-5-389-31290-6
12+
Почему декабрь называется декабрем, что означает «десятый», хотя на самом деле это двенадцатый месяц? Как вычислить, сколько в среднем растет вóлос на голове человека, прежде чем выпасть? Действительно ли мы умеем считать, или нам это только кажется? Ответы на эти и многие другие вопросы читатель найдет в увлекательной книге Я. Перельмана «Живая математика», где автор собрал разнообразные математические головоломки и загадки, придав им форму любопытных коротких рассказов. В настоящее издание также вошла работа «Занимательная алгебра», цель которой «воспитать в читателе вкус к занятию алгеброй» и предложить ему «разнообразные задачки с необычными сюжетами, подстрекающими любопытство, занимательные экскурсии в область истории математики, неожиданные применения алгебры к практической жизни».
© Оформление.
ООО «Издательство АЗБУКА», 2023
Издательство Азбука®

Предисловие [1]
Для чтения этой книги достаточна весьма скромная математическая подготовка: знание правил арифметики и элементарные сведения из геометрии. Лишь незначительная часть задач требует уменья составлять и решать простейшие уравнения. Тем не менее содержание книги весьма разнообразно: от пестрого подбора головоломок и замысловатых трюков математической гимнастики до полезных практических примеров счета и измерения. Составитель заботился о свежести включаемого материала и избегал повторения того, что входит в другие сборники того же автора («Фокусы и развлечения», «Занимательные задачи»). Читатель найдет здесь сотню головоломок, не включенных в прежние книги, причем некоторые из задач, например крокетные, вообще никогда не публиковались. Глава седьмая — «Рассказы о числах-великанах» — представляет собой переработку брошюры автора, пополненной четырьмя новыми рассказами.
[1] Текст книги «Живая математика» печатается по изданию: Перельман Я. И. Живая математика. М.; Л. : Государственное издательство технико-теоретической литературы, 1949. Иллюстрации Ю. Д. Скалдина. — Примеч. ред.

Глава первая
Завтрак с головоломками
— Есть предложение, товарищи, не расходиться, — сказал после завтрака один из собравшихся за столом дома отдыха. — Так как в дождь гулять никто не пойдет, а перестанет дождик, видно, не скоро, то давайте, проведем здесь время за головоломками. Пусть каждый по очереди придумает или припомнит какую-нибудь головоломку. Вы же, профессор, явитесь нашим верховным судьей.
— Если головоломки будут с алгеброй или с геометрией, то я должна отказаться, — заявила молодая женщина.
— И я тоже — присоединился кто-то.
— Нет-нет, участвовать должны все! А мы попросим присутствующих не привлекать ни алгебры, ни геометрии, разве только самые начатки. Возражений не имеется?
— Тогда я согласна и готова первая предложить головоломку.
— Прекрасно, просим! — донеслось с разных сторон. — Начинайте.
1. В коммунальной кухне. — Головоломка моя зародилась в обстановке коммунальной квартиры. Задача, так сказать, бытовая. Жилица — назову ее для удобства Тройкиной — положила в общую плиту 3 полена своих дров, жилица Пятеркина — 5 полен, жилец Бестопливный, у которого, как вы догадываетесь, не было своих дров, получил от обеих гражданок разрешение сварить обед на общем огне. В возмещение расходов он уплатил соседкам 8 рублей. Как должны они поделить между собой эту плату?
— Пополам, — поспешил заявить кто-то. Бестопливный пользовался их огнем в равной мере.
— Ну нет, — возразил другой, — надо принять в соображение, как участвовали в этом огне дровяные вложения гражданок. Кто дал 3 полена, должен получить 3 рубля; кто дал 5 поленьев — получает 5 рублей. Вот это будет справедливый дележ.
— Товарищи, — взял слово тот, кто затеял игру и считался теперь председателем собрания. — Окончательные решения головоломок давайте пока не объявлять. Пусть каждый еще подумает над ними. Правильные ответы судья огласит нам за ужином. Теперь следующий. Очередь за вами, товарищ пионер!
2. Работа школьных кружков. — В нашей школе, — начал пионер, — имеется 5 кружков: политкружок, военный, фотографический, шахматный и хоровой. Политкружок занимается через день, военный — через 2 дня на 3-й, фотографический — каждый 4-й день, шахматный — каждый 5-й день, и хоровой — каждый 6-й день. Первого января собрались в школе все 5 кружков, а затем занятия велись в назначенные по плану дни, без отступлений от расписания. Вопрос состоит в том, сколько в первом квартале было еще вечеров, когда собирались в школе все 5 кружков.
— А год был простой или високосный? — осведомились у пионера.
— Простой.
— Значит, первый квартал — январь, февраль, март — надо считать за 90 дней?
— Очевидно.
— Позвольте к вопросу вашей головоломки присоединить еще один, — сказал профессор. — А именно: сколько в том же квартале года было таких вечеров, когда кружковых занятий в школе вовсе не происходило?
— Ага, понимаю! — раздался возглас. — Задача с подвохом. Ни одного дня не будет больше с 5 кружками и ни одного дня без всяких кружков. Это уж ясно!
— Почему? — спросил председатель.
— Объяснить не могу, но чувствую, что отгадчика хотят поймать впросак.
— Ну, это не довод. Вечером выяснится, правильно ли ваше предчувствие. За вами очередь, товарищ!
3. Кто больше? — Двое считали в течение часа всех, кто проходил мимо них на тротуаре. Один стоял у ворот дома, другой прохаживался взад и вперед по тротуару. Кто насчитал больше прохожих?
— Идя, больше насчитаешь, ясное дело, — донеслось с другого конца стола.
— Ответ узнаем за ужином, — объявил председатель. — Следующий!
4. Дед и внук. — То, о чем, я скажу, происходило в 1932 году. Мне было тогда ровно столько лет, сколько выражают последние две цифры года моего рождения. Когда я об этом соотношении рассказал деду, он удивил меня заявлением, что с его возрастом выходит то же самое. Мне это показалось невозможным...
— Разумеется, невозможно, — вставил чей-то голос.
— Представьте, что вполне возможно. Дед доказал мне это. Сколько же лет было каждому из нас?
5. Железнодорожные билеты. — Я — железнодорожная кассирша, продаю билеты, — начала следующая участница игры. — Многим это кажется очень простым делом. Не подозревают, с каким большим числом билетов приходится иметь дело кассиру даже маленькой станции. Ведь необходимо, чтобы пассажиры могли получить билеты от данной станции до любой другой на той же дороге, притом в обоих направлениях. Я служу на дороге с 25 станциями. Сколько же, по-вашему, различных образцов билетов заготовлено железной дорогой для всех ее касс?
— Ваша очередь, товарищ летчик, — провозгласил председатель.
6. Полет дирижабля. — Из Ленинграда вылетел прямо на север дирижабль. Пролетев в северном направлении 500 км, он повернул на восток. Пролетев в эту сторону 500 км, дирижабль сделал новый поворот — на юг — и прошел в южном направлении 500 км. Затем он повернул на запад и, пролетев 500 км, опустился на землю. Спрашивается: где расположено место спуска дирижабля относительно Ленинграда — к западу, к востоку, к северу или к югу?
— На простака рассчитываете, — сказал кто-то: — 500 шагов вперед, 500 вправо, 500 назад да 500 влево — куда придем? Откуда вышли, туда и придем!
Рис. 1. «500 шагов вперед, 500 вправо, 500 назад…»
— Итак, где по-вашему спустился дирижабль?
— На том же ленинградском аэродроме, откуда поднялся. Не так разве?
— Именно не так.
— В таком случае я ничего не понимаю!
— В самом деле, здесь что-то неладно, — вступил в разговор сосед. — Разве дирижабль спустился не в Ленинграде?.. Нельзя ли повторить задачу?
Летчик охотно исполнил просьбу. Его внимательно выслушали и с недоумением переглянулись.
— Ладно, — объявил председатель. — До ужина успеем подумать об этой задаче, а сейчас будем продолжать.
7. Тень. — Позвольте мне, — сказал очередной загадчик, — взять сюжетом головоломки тот же дирижабль. Что длиннее: дирижабль или его полная тень?
— В этом и вся головоломка?
— Вся.
— Тень, конечно, длиннее дирижабля: ведь лучи солнца расходятся веером, — последовало сразу решение.

Рис. 2. Расходящиеся лучи от спрятанного за облаком солнца
— Я бы сказал, — возразил кто-то, — что, напротив, лучи солнца параллельны; тень и дирижабль одной длины.
— Что вы! Разве не случалось вам видеть расходящиеся лучи от спрятанного за облаком солнца? Тогда можно воочию убедиться, как сильно расходятся солнечные лучи. Тень дирижабля должна быть значительно больше дирижабля, как тень облака больше самого облака.
— Почему же обычно принимают, что лучи солнца параллельны? Моряки, астрономы — все так считают...
Председатель не дал спору разгореться и предоставил слово следующему загадчику.
8. Задача со спичками. Очередной оратор высыпал на стол все спички из коробка и стал распределять их в три кучки.
— Костер собираетесь раскладывать? — шутили слушатели.
— Головоломка, — объяснил загадчик, — будет со спичками. Вот их три неравные кучки. Во всех вместе 48 штук. Сколько в каждой, я вам не сообщаю. Зато отметьте следующее: если из первой кучи я переложу во вторую столько спичек, сколько в этой второй куче имелось; затем из второй в третью переложу столько, сколько в этой третьей перед тем будет находиться; и, наконец, из третьей переложу в первую столько спичек, сколько в этой первой куче будет тогда иметься, — если, говорю, все это проделать, то число спичек во всех кучках станет одинаковым. Сколько же было в каждой кучке первоначально?
9. Коварный пень. — Головоломка эта, — начал сосед последнего загадчика, — напоминает задачу, которую давно как-то задал мне деревенский математик. Это был целый рассказ, довольно забавный. Повстречал крестьянин в лесу незнакомого старика. Разговорились. Старик внимательно оглядел крестьянина и сказал:
— Известен мне в леску этом пенечек один удивительный. Очень в нужде помогает.
— Как помогает? Вылечивает?
— Лечить не лечит, а деньги удваивает. Положишь под него кошель с деньгами, досчитаешь до ста — и готово: деньги, какие были в кошельке, удвоились. Такое свойство имеет. Замечательный пень!
— Вот бы мне испробовать, — мечтательно сказал крестьянин.
— Это можно. Отчего же? Заплатить только надо.
— Кому платить? И много ли?
— Тому платить, кто дорогу укажет. Мне, значит. А много ли, о том особый разговор.
Стали торговаться. Узнав, что у крестьянина в кошельке денег мало, старик согласился получать после каждого удвоения по 1 руб. 20 коп. На том и порешили.
Старик повел крестьянина вглубь леса, долго бродил с ним и наконец разыскал в кустах старый, покрытый мхом еловый пень. Взяв из рук крестьянина кошелек, он засунул его между корнями пня. Досчитали до ста. Старик снова стал шарить и возиться у основания пня, наконец извлек оттуда кошелек и подал крестьянину.
Заглянул крестьянин в кошелек, и что же? — деньги в самом деле удвоились! Отсчитал из них старику обещанные 1 руб. 20 коп. и попросил засунуть кошелек вторично под чудодейственный пень.
Снова досчитали до ста, снова старик стал возиться в кустах у пня, и снова совершилось диво: деньги в кошельке удвоились. Старик вторично получил из кошелька обусловленные 1 руб. 20 коп.
В третий раз спрятали кошель под пень. Деньги удвоились и на этот раз. Но когда крестьянин уплатил старику обещанное вознаграждение, в кошельке не осталось больше ни одной копейки. Бедняга потерял на этой комбинации все свои деньги. Удваивать дальше было уже нечего, и крестьянин уныло побрел из лесу.
Секрет волшебного удвоения денег вам, конечно, ясен: старик недаром, отыскивая кошелек, мешкал в зарослях у пня. Но можете ли вы ответить на другой вопрос: сколько было у крестьянина денег до злополучных опытов с коварным пнем?
10. Задача о декабре. — Я, товарищи, языковед, от всякой математики далек, — начал пожилой человек, которому пришел черед задавать головоломку. — Не ждите от меня поэтому математической задачи. Могу только предложить вопрос из знакомой мне области. Разрешите задать календарную головоломку?
— Просим!
— Двенадцатый месяц называется у нас «декабрь». А вы знаете, что собственно значит «декабрь»? Слово это происходит от греческого слова «дека» — десять, отсюда также слова «декалитр» — десять литров, «декада» — десять дней и др. Выходит, что месяц декабрь носит название «десятый». Чем объяснить такое несоответствие?
— Ну теперь осталась только одна головоломка, — произнес председатель.
11. Арифметический фокус. — Мне приходится выступать последним. Для разнообразия покажу вам арифметический фокус и попрошу раскрыть его секрет. Пусть кто-нибудь из вас, хотя бы вы, товарищ председатель, напишет на бумажке, тайно от меня, любое трехзначное число.
— Могут быть и нули в этом числе?
— Не ставлю никаких ограничений. Любое трехзначное число, какое пожелаете.
— Написал. Что теперь?
— Припишите к нему это же число еще раз. У вас получится, конечно, шестизначное число.
— Есть. Шестизначное число.
— Передайте бумажку соседу, что сидит подальше от меня. А он пусть разделит это шестизначное число на семь.
— Легко сказать: разделить на семь! Может и не разделится.
— Не беспокойтесь, поделится без остатка.
— Числа не знаете, а уверены, что поделится.
— Сначала разделите, потом будем говорить.
— На ваше счастье разделилось.
— Результат вручите своему соседу, не сообщая мне. Он разделит его на одиннадцать.
— Думаете, опять повезет — разделится?
— Делите, остатка не получится.
— В самом деле без остатка! Теперь что?
— Передайте результат дальше. Разделим его... ну, скажем, на тринадцать.
— Нехорошо выбрали. Без остатка на тринадцать мало чисел делится... Ан нет, разделилось нацело. Везет же вам!
— Дайте мне бумажку с результатом; только сложите ее, чтобы я не видел числа.
Не развертывая листка бумаги, «фокусник» вручил его председателю:
— Извольте получить задуманное вами число. Правильно?
— Совершенно верно! — с удивлением ответил тот, взглянув на бумажку. — Именно это я и задумал... теперь, так как список ораторов исчерпан, позвольте закрыть наше собрание, благо и дождь успел пройти. Разгадки всех головоломок будут оглашены сегодня же, после ужина. Записки с решениями можете подавать мне.
Решения головоломок 1–11
1. Нельзя считать, как многие делают, что 8 рублей уплачено за 8 поленьев, по 1 рублю за полено. Деньги эти уплачены только за третью часть от 8 поленьев, потому что огнем пользовались трое в одинаковой мере. Отсюда следует, что все 8 поленьев оценены были в 8 × 3, т. е. в 24 руб., и цена одного полена — 3 рубля.
Теперь легко сообразить, сколько причитается каждому. Пятеркиной за ее 5 поленьев следует 15 рублей; но она сама воспользовалась плитой на 8 рублей; значит, ей остается дополучить еще 15 — 8, т. е. 7 рублей. Тройкина за 3 свои полена должна получить 9 рублей, а если вычесть 8 рублей, причитающихся с нее за пользование плитой, то следовать ей будет всего только 9–8, т. е. 1 рубль.
Итак, при правильном дележе Пятеркина должна получить 7 рублей, Тройкина — 1 рубль.
2. На первый вопрос — через сколько дней в школе соберутся одновременно все 5 кружков — мы легко ответим, если сумеем разыскать наименьшее из всех чисел, которое делится без остатка на 2, на 3, на 4, на 5 и на 6. Нетрудно сообразить, что число это 60. Значит, на 61-й день соберется снова 5 кружков: политический — через 30 двухдневных промежутков, военный — через 20 трехдневных, фотокружок — через 15 четырехдневных, шахматный — через 12 пятидневок и хоровой — через 10 шестидневок. Раньше чем через 60 дней такого вечера не будет. Следующий подобный же вечер будет еще через 60 дней, т. е. уже во втором квартале.
Итак, в течение первого квартала окажется только один вечер, когда в клубе снова соберутся для занятий все 5 кружков.
Хлопотливее найти ответ на второй вопрос задачи: сколько будет вечеров, свободных от кружковых занятий? Чтобы разыскать такие дни, надо выписать по порядку все числа от 1 до 90 и зачеркнуть в этом ряду дни работы политкружка, т. е. числа 1, 3, 5, 7, 9 и т. д. Потом зачеркнуть дни работы военного кружка: 4, 7, 10-й и т. д.
После того как зачеркнем затем дни занятий фотокружка шахматного и хорового, у нас останутся незачеркнутыми те дни первого квартала, когда ни один кружок не работал.
Кто проделает эту работу, тот убедится, что вечеров, свободных от занятий, в течение первого квартала будет довольно много: 24. В январе их 8, а именно: 2, 8, 12, 14, 18, 20, 24 и 30-го. В феврале насчитывается 7 таких дней, в марте — 9.
3. Оба насчитали одинаковое число прохожих. Хотя тот, кто стоял у ворот, считал проходивших в обе стороны, зато тот, кто ходил, видел вдвое больше встречных людей.
4. С первого взгляда может действительно показаться, что задача неправильно составлена: выходит как будто, что внук и дед одного возраста. Однако требование задачи, как сейчас увидим, легко удовлетворяется.
Внук, очевидно, родился в XX столетии. Первые две цифры года его рождения, следовательно, 19: таково число сотен. Число, выражаемое остальными цифрами, будучи сложено с самим собой, должно составить 32. Значит, это число 16: год рождения внука — 1916, и ему в 1932 году было 16 лет.
Дед его родился, конечно, в XIX столетии; первые две цифры года его рождения 18. Удвоенное число, выражаемое остальными цифрами, должно составить 132. Значит, само это число равно половине 132, т. е. 66. Дед родился в 1866 году, и ему в 1932 году было 66 лет.
Таким образом, и внуку и деду в 1932 году было столько лет, сколько выражают последние две цифры годов их рождения.
5. На каждой из 25 станций пассажиры могут требовать билет до любой станции, т. е. на 24 пункта. Значит, разных билетов надо напечатать 25 × 24 = 600 образцов.
6. Задача эта никакого противоречия не содержит. Не следует думать, что дирижабль летел по контуру квадрата: надо принять в расчет шарообразную форму Земли. Дело в том, что меридианы к северу сближаются; поэтому, пройдя 500 км по параллельному кругу, расположенному на 500 км севернее широты Ленинграда, дирижабль отошел к востоку на большее число градусов, чем пролетел потом в обратном направлении, очутившись снова на широте Ленинграда. В результате дирижабль, закончив полет, оказался восточнее Ленинграда.
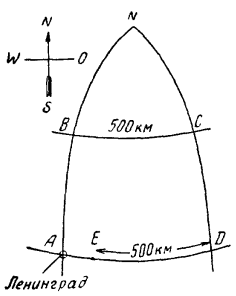
Рис. 3. Как летел дирижабль
На сколько именно? Это можно рассчитать. На рис. 3 вы видите маршрут дирижабля: ABCDE. Точка N — северный полюс; в этой точке сходятся меридианы АВ и DC. Дирижабль пролетел сначала 500 км на север, т. е. по меридиану AN. Так как длина градуса меридиана 111 км, то дуга меридиана в 500 км содержит 500 : 111 = 4,5°. Ленинград лежит на 60-й параллели; значит, точка В находится на 60° + 4,5° = 64,5°. Затем дирижабль летел к востоку, т. е. по параллели ВС, и прошел по ней 500 км. Длину одного градуса на этой параллели можно вычислить (или узнать из таблиц); она равна 48 км. Отсюда легко определить, сколько градусов пролетел дирижабль на восток: 500 : 48 = 10,4°. Далее воздушный корабль летел в южном направлении, т. е. по меридиану CD, и, пройдя 500 км, должен был очутиться снова на параллели Ленинграда. Теперь путь лежит на запад, т. е. по AD; 500 км этого пути явно короче расстояния AD. В расстоянии AD заключается столько же градусов, сколько и в ВС, т. е. 10,4°. Но длина 1° на ширине 60° равна 55,5 км. Следовательно, между А и D расстояние равно 55,5 × 10,4 = 577 км. Мы видим, что дирижабль не мог спуститься в Ленинграде; он не долетел до него 77 км, т. е. спустился на Ладожском озере.
7. Беседовавшие об этой задаче допустили ряд ошибок. Неверно, что лучи солнца, падающие на земной шар, заметно расходятся. Земля так мала по сравнению с расстоянием ее от солнца, что солнечные лучи, падающие на какую-либо часть ее поверхности, расходятся на неуловимо малый угол: практически лучи эти можно считать параллельными. То, что мы видим иногда (при так называемом «иззаоблачном сиянии», рис. 2) лучи солнца, расходящиеся веером, — не более как следствие перспективы.
В перспективе параллельные линии представляются сходящимися; вспомните вид уходящих вдаль рельсов (рис. 4) или вид длинной аллеи.
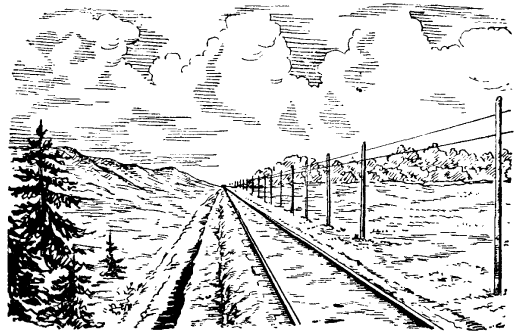
Рис. 4. Рельcы, уходящие вдаль
Однако из того, что лучи солнца падают на землю параллельным пучком, вовсе не следует, что полная тень дирижабля равна по длине самому дирижаблю. Взглянув на рис. 5, вы поймете, что полная тень дирижабля в пространстве суживается по направлению к земле и что, следовательно, тень, отбрасываемая им на земную поверхность, должна быть короче самого дирижабля: CD меньше, чем АВ.
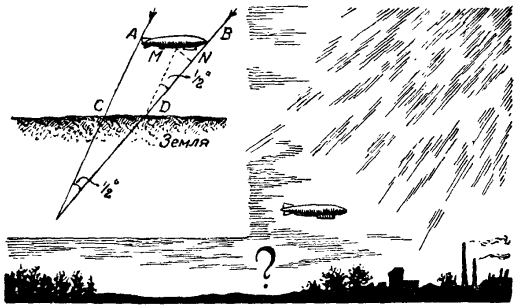
Рис. 5. Как падает тень от дирижабля
Если знать высоту полета дирижабля, то можно вычислить и то, как велика эта разница. Пусть дирижабль летит на высоте 1000 м над земной поверхностью. Угол, составляемый прямыми АС и BD между собой, равен тому углу, под которым усматривается солнце с земли; угол этот известен: около 1/2°. С другой стороны, известно, что всякий предмет, видимый под углом в 1/2°, удален от глаза на 115 своих поперечников. Значит, отрезок MN (этот отрезок усматривается с земной поверхности под углом в 1/2°) должен составлять 115-ю долю от АС. Величина АС больше отвесного расстояния от А до земной поверхности. Если угол между направлением солнечных лучей и земной поверхностью равен 45°, то АС (при высоте дирижабля 1000 м) составляет около 1400 м, и, следовательно, отрезок MN равен
Но избыток длины дирижабля над длиною тени, т. е. отрезок MB, больше MN, а именно больше в 1,4 раза, потому что угол MBD почти точно равен 45°. Следовательно, MB равно 12 × 1,4; это дает почти 17 м.
Все сказанное относится к полной тени дирижабля — черной и резкой — и не имеет отношения к так называемой полутени, слабой и размытой.
Расчет наш показывает, между прочим, что будь на месте дирижабля небольшой воздушный шар, диаметром меньше 17 м, он не отбрасывал бы вовсе полной тени; видна была бы только его смутная полутень.
8. Задачу решают с конца. Будем исходить из того, что после всех перекладываний число спичек в кучках сделалось одинаковым. Так как от этих перекладываний общее число спичек не изменилось, осталось прежнее (48), то в каждой кучке к концу всех перекладываний оказалось 16 штук.
Итак, имеем в самом конце:

Непосредственно перед этим в 1-ю кучку было прибавлено столько спичек, сколько в ней имелось; иначе говоря, число спичек в ней было удвоено. Значит, до последнего перекладывания в 1-й кучке было не 16, а только 8 спичек. В кучке же 3-й, из которой 8 спичек было взято, имелось перед тем 16 + 8 = 24 спички.
Теперь у нас такое распределение спичек по кучкам:

Далее: мы знаем, что перед этим из 2-й кучки было переложено в 3-ю столько спичек, сколько имелось в 3-й кучке. Значит, 24 — это удвоенное число спичек, бывших в 3-й кучке до этого перекладывания. Отсюда узнаем распределение спичек после первого перекладывания:
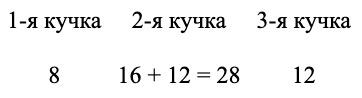
Легко сообразить, что раньше первого перекладывания (т. е. до того как из 1-й кучки переложено было во 2-ю столько спичек, сколько в этой 2-й имелось) распределение спичек было таково:

Таковы первоначальные числа спичек в кучках.
9. Эту головоломку также проще решить с конца. Мы знаем, что после третьего удвоения в кошельке оказалось 1 руб. 20 коп. (деньги эти получил старик в последний раз). Сколько же было до этого удвоения? Конечно, 60 коп. Остались эти 60 коп. после уплаты старику вторых 1 руб. 20 коп., а до уплаты было в кошельке 1 руб. 20 коп. + 60 коп. = 1 руб. 80 коп.
Далее: 1 руб. 80 коп. оказались в кошельке после второго удвоения; до того было всего 90 коп., оставшихся после уплаты старику первых 1 руб. 20 коп. Отсюда узнаем, что до уплаты находилось в кошельке 90 коп. + 1 руб. 20 коп. = 2 руб. 10 коп. Столько денег имелось в кошельке после первого удвоения; раньше же было вдвое меньше — 1 руб. 5 коп. Это и есть те деньги, с которыми крестьянин приступил к своим неудачным финансовым операциям.
Проверим ответ:

10. Наш календарь ведет свое начало от календаря древних римлян. Римляне же (до Юлия Цезаря) считали началом года не 1 января, а 1 марта. Декабрь тогда был, следовательно, десятый месяц. С перенесением начала года на 1 января названия месяцев изменены не были. Отсюда и произошло то несоответствие между названием и порядковым номером, которое существует теперь для ряда месяцев (см. таблицу ниже).
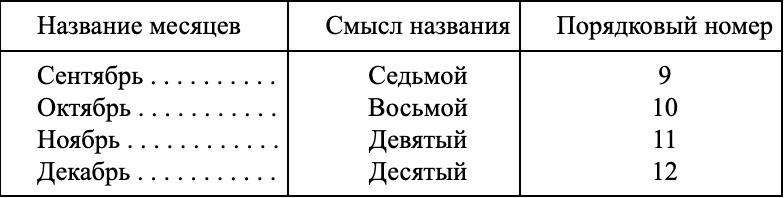
11. Проследим за тем, что проделано было с задуманным числом. Прежде всего к нему приписали взятое трехзначное число еще раз. Это то же самое, что приписать три нуля и прибавить затем первоначальное число; например:
872 872 = 872 000 + 872.
Теперь ясно, чтó собственно проделано было с числом: его увеличили в 1000 раз и, кроме того, прибавили его самого; короче сказать — умножили число на 1001.
Что же сделано было потом с этим произведением? Его разделили последовательно на 7, на 11 и на 13. В конечном итоге, значит, разделили его на 7 × 11 × 13, т. е. на 1001.
Итак, задуманное число сначала умножили на 1001, потом разделили на 1001. Надо ли удивляться, что в результате получилось то же самое число?
* * *
Прежде чем закончить главу о головоломках в доме отдыха, расскажу еще о двух арифметических фокусах, которыми вы можете занять досуг ваших товарищей. Первый состоит в отгадывании чисел, а второй — в отгадывании владельцев вещей.
Это — старые, быть может даже и известные вам, фокусы, но едва ли все знают, на чем они основаны. А без знания теоретической основы фокуса нельзя сознательно и уверенно его выполнять. Обоснование первого фокуса потребует от нас весьма скромной и ничуть не утомительной экскурсии в область начальной алгебры.
12. Зачеркнутая цифра. Пусть товарищ ваш задумает какое-нибудь многозначное число, например 847. Предложите ему найти сумму цифр этого числа (8 + 4 + + 7 = 19) и отнять ее от задуманного числа. У загадчика окажется:
847 – 19 = 828.
В том числе, которое получится, пусть он зачеркнет одну цифру — безразлично какую — и сообщит вам все остальные. Вы немедленно называете ему зачеркнутую цифру, хотя не знаете задуманного числа и не видели, что с ним проделывалось.
Как можете вы это выполнить и в чем разгадка фокуса?
Выполняется это очень просто: подыскивается такая цифра, которая вместе с суммой вам сообщенных цифр составила бы ближайшее число, делящееся на 9 без остатка. Если, например, в числе 828 была зачеркнута первая цифра (8) и вам сообщены цифры 2 и 8, то, сложив 2 + 8, вы соображаете, что до ближайшего числа, делящегося на 9, т. е. до 18, не хватает 8. Это и есть зачеркнутая цифра.
Почему так получается? Потому что если от какого-либо числа отнять сумму его цифр, то должно остаться число, делящееся на 9, — иначе говоря, такое, сумма цифр которого делится на 9. В самом деле, пусть в задуманном числе цифра сотен — а, цифра десятков — b и цифра единиц — с. Значит, всего в этом числе содержится единиц
100а +10b + с.
Отнимаем от этого числа сумму его цифр а + b + с. Получим
100а + 10b + с – (а + b + с) = 99а + 9b = 9(11а + b).
Но 9 (11а + b), конечно, делится на 9; значит, при вычитании из числа суммы его цифр всегда должно получиться число, делящееся на 9 без остатка.
При выполнении фокуса может случиться, что сумма сообщенных вам цифр сама делится на 9 (например, 4 и 5). Это показывает, что зачеркнутая цифра есть либо 0, либо 9. Так вы и должны ответить: 0 или 9.
Вот видоизменение того же фокуса: вместо того чтобы из задуманного числа вычитать сумму его цифр, можно вычесть число, полученное из данного какой-либо перестановкой его цифр. Например, из числа 8247 можно вычесть 2748 (если получается число, большее задуманного, то вычитают меньшее из большего). Дальше поступают, как раньше сказано: 8247 – 2748 = 5499; если зачеркнута цифра 4, то, зная цифры 5, 9, 9, вы соображаете, что ближайшее к 5 + 9 + 9, т. е. 23, число, делящееся на 9, есть 27. Значит, зачеркнутая цифра 27 – 23 = 4.
13. Кто что взял? Для выполнения этого остроумного фокуса необходимо приготовить три какие-нибудь мелкие вещицы, удобно помещающиеся в кармане, например карандаш, ключ и перочинный ножик. Кроме того, поставьте на стол тарелку с 24 орехами; за неимением орехов годятся шашки, кости домино, спички и т. п.
Троим товарищам вы предлагаете во время вашего отсутствия из комнаты спрятать в карман карандаш, ключ или ножик, кто какую вещь хочет. Вы беретесь отгадать, в чьем кармане какая вещь.
Процедура отгадывания проводится так. Возвратившись в комнату после того, как вещи спрятаны по карманам товарищей, вы начинаете с того, что вручаете им на сохранение орехи из тарелки. Первому даете один орех, второму — два, третьему — три. Затем снова удаляетесь из комнаты, оставив товарищам следующую инструкцию. Каждый должен взять себе из тарелки еще орехов, а именно: обладатель карандаша берет столько орехов, сколько ему было вручено; обладатель ключа берет вдвое больше того числа орехов, какое ему было вручено; обладатель ножа берет вчетверо больше того числа орехов, какое ему было вручено.
Прочие орехи остаются на тарелке.
Когда все это проделано и вам дан сигнал возвратиться, вы, входя в комнату, бросаете взгляд на тарелку и объявляете, у кого в кармане какая вещь.
Фокус тем более озадачивает, что выполняется без участия тайного сообщника, подающего вам незаметные сигналы. В нем нет никакого обмана: он целиком основан на арифметическом расчете. Вы разыскиваете обладателя каждой вещи единственно лишь по числу оставшихся орехов. Остается их на тарелке немного — от 1 до 7, и счесть их можно одним взглядом.
Как же, однако, узнать по остатку орехов, кто взял какую вещь?
Очень просто: каждому случаю распределения вещей между товарищами отвечает иное число остающихся орехов. Мы сейчас в этом убедимся.
Пусть имена ваших товарищей Владимир, Георгий, Константин; обозначим их начальными буквами: В, Г, К. Вещи также обозначим буквами: карандаш — а, ключ — b, нож — с. Как могут три вещи распределиться между тремя обладателями? На 6 ладов:

Других случаев, очевидно, быть не может; наша таблица систематически исчерпывает все комбинации.
Посмотрим теперь, какие остатки отвечают каждому из этих 6 случаев:

Вы видите что остаток орехов всякий раз получается иной. Поэтому зная остаток, вы легко устанавливаете, каково распределение вещей между вашими товарищами. Вы снова — в третий раз — удаляетесь из комнаты и заглядываете там в свою записную книжку, где записана сейчас воспроизведенная таблица (собственно, нужны вам только первая и последняя графы); запомнить ее наизусть трудно, да и нет надобности. Таблица скажет вам, в чьем кармане какая вещь. Если, например, на тарелке осталось 5 орехов, то это означает (случай b, с, а), что
ключ — у Владимира;
нож — у Георгия;
карандаш — у Константина.
Чтобы фокус удался, вы должны твердо помнить, сколько орехов вы дали каждому товарищу (раздавайте орехи поэтому всегда по алфавиту, как и было сделано в нашем случае).

Глава вторая
Математика в играх
Домино
14. Цепь из 28 костей. Почему 28 костей домино можно выложить с соблюдением правил игры в одну непрерывную цепь?
15. Начало и конец цепи. Когда 28 костей домино выложены в цепь, на одном ее конце оказалось 5 очков.
Сколько очков на другом конце?
16. Фокус с домино. Ваш товарищ берет одну из костей домино и предлагает вам из остальных 27 составить непрерывную цепь, утверждая, что это всегда возможно, какая бы кость ни была взята. Сам же он удаляется в соседнюю комнату, чтобы не видеть вашей цепи!
Вы приступаете к работе и убеждаетесь, что товарищ ваш прав: 27 костей выложились в одну цепь. Еще удивительнее то, что товарищ, оставаясь в соседней комнате и не видя вашей цепи, объявляет оттуда, какие числа очков на ее концах.
Как может он это знать? И почему он уверен, что из всяких 27 костей домино составится непрерывная цепь?
17. Рамка. Рис. 6 изображает квадратную рамку, выложенную из костей домино с соблюдением правил игры. Стороны рамки равны по длине, но не одинаковы по сумме очков: верхний и левый ряды заключают по 44 очка, остальные же два ряда — 59 и 32.
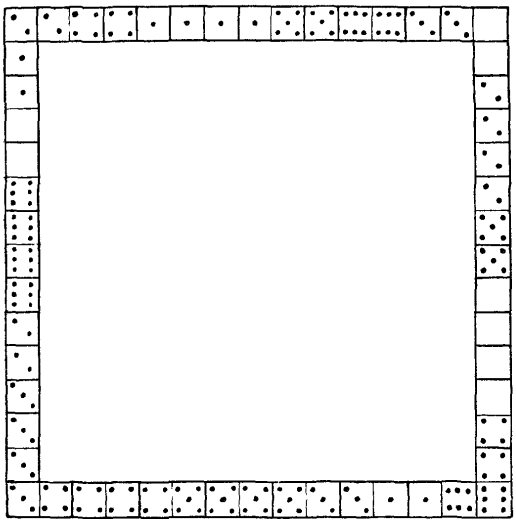
Рис. 6. Рамка из домино
Можете ли вы выложить такую квадратную рамку, все стороны которой заключали бы одинаковую сумму очков — именно 44?
18. Семь квадратов. Четыре кости домино можно выбрать так, чтобы из них составился квадратик с равной суммой очков на каждой стороне. Образчик вы видите на рис. 7: сложив очки на каждой стороне квадратика, во всех случаях получите 11.
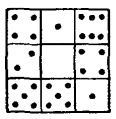
Рис. 7
Можете ли вы из полного набора домино составить одновременно cемь таких квадратов? Не требуется, чтобы сумма очков на одной стороне получалась у всех квадратов одна и та же; надо лишь, чтобы каждый квадрат имел на своих четырех сторонах одинаковую сумму очков.
19. Магические квадраты из домино. На рис. 8 показан квадрат из 18 косточек домино, замечательный тем, что сумма очков любого его ряда — продольного, поперечного или диагонального — одна и та же: 13. Подобные квадраты издавна называются магическими.

Рис. 8. Магический квадрат из домино
Вам предлагается составить несколько таких же 18-косточковых магических квадратов, но с другой суммой очков в ряду. 13 — наименьшая сумма в рядах магического квадрата, составленного из 18 костей. Наибольшая сумма — 23.
20. Прогрессия из домино. Вы видите на рис. 9 шесть косточек домино, выложенных по правилам игры и отличающихся тем, что число очков на косточках (на двух половинах каждой косточки) возрастает на 1: начинаясь с 4, ряд состоит из следующих чисел очков:
4; 5; 6; 7; 8; 9.
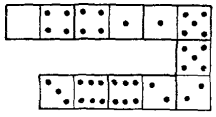
Рис. 9. Прогрессия из домино
Такой ряд чисел, которые возрастают (или убывают) на одну и ту же величину, называется арифметической прогрессией. В нашем ряду каждое число больше предыдущего на 1; но в прогрессии может быть и любая другая «разность».
Задача состоит в том, чтобы составить еще несколько 6-косточковых прогрессий.
Игра в 15
Общеизвестная коробочка с 15 нумерованными квадратными шашками имеет любопытную историю, о которой мало кто из игроков подозревает. Расскажем о ней словами немецкого исследователя игр, математика В. Аренса.

Рис. 10. Игра в 15
«Около полувека назад — в конце 70-х годов — вынырнула в Соединенных Штатах игра в „15“; она быстро распространилась и, благодаря несчетному числу усердных игроков, которых она заполонила, превратилась в настоящее общественное бедствие.
То же наблюдалось по эту сторону океана, в Европе. Здесь можно было даже в конках видеть в руках пассажиров коробочки с 15 шашками. В конторах и магазинах хозяева приходили в отчаяние от увлечения своих служащих и вынуждены были воспретить им игру в часы занятий и торговли. Содержатели увеселительных заведений ловко использовали эту манию и устраивали большие игорные турниры.
В Париже игра эта нашла себе приют под открытым небом, на бульварах, и быстро распространилась из столицы по всей провинции. „Не было такого уединенного сельского домика, где не гнездился бы этот паук, подстерегая жертву, готовую запутаться в его сетях“, — писал один французский автор.
В 1880 году игорная лихорадка достигла, по-видимому, своей высшей точки. Но вскоре после этого тиран был повержен и побежден оружием математики. Математическая теория игры обнаружила, что из многочисленных задач, которые могут быть предложены, разрешима только половина; другая не разрешима никакими ухищрениями».
Познакомим читателя с начатками теории этой игры. В полном виде она очень сложна и тесно примыкает к одному из отделов высшей алгебры («теории определителей»). Мы ограничимся лишь некоторыми соображениями, изложенными В. Аренсом.
«Задача игры состоит обыкновенно в том, чтобы посредством последовательных передвижений, допускаемых наличием свободного поля, перевести любое начальное расположение 15 шашек в нормальное, т. е. в такое, при котором шашки идут в порядке своих чисел: в верхнем левом углу 1, направо — 2, затем 3, потом в верхнем правом углу 4; в следующем ряду слева направо: 5, 6, 7, 8 и т. д. Такое нормальное конечное расположение мы даем здесь на рис. 11.
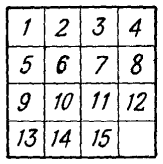
Рис. 11. Нормальное расположение шашек (положение I)
Вообразите теперь расположение, при котором 15 шашек размещены в пестром беспорядке. Рядом передвижений всегда можно привести шашку 1 на место, занимаемое ею на рисунке.
Точно так же возможно, не трогая шашки 1, привести шашку 2 на соседнее место вправо. Затем, не трогая шашек 1 и 2, можно поместить шашки 3 и 4 на их нормальные места: если они случайно не находятся в двух последних вертикальных рядах, то легко привести их в эту область и затем рядом передвижений достичь желаемого результата. Теперь верхняя строка 1, 2, 3, 4 приведена в порядок, и при дальнейших манипуляциях с шашками мы трогать этого ряда не будем. Таким же путем стараемся мы привести в порядок и вторую строку: 5, 6, 7, 8; легко убедиться, что это всегда достижимо. Далее, на пространстве двух последних рядов необходимо привести в нормальное положение шашки 9 и 13; это тоже всегда возможно. Из всех приведенных в порядок шашек 1, 2, 3, 4, 5, 6, 7, 8, 9 и 13 в дальнейшем ни одной не перемещают; остается небольшой участок в шесть полей, в котором одно свободно, а пять остальных заняты шашками 10, 11, 12, 14, 15 в произвольном порядке. В пределах этого шестиместного участка всегда можно привести на нормальные места шашки 10, 11, 12. Когда это достигнуто, то в последнем ряду шашки 14 и 15 окажутся размещенными либо в нормальном порядке, либо в обратном (рис. 12). Таким путем, который читатели легко могут проверить на деле, мы приходим к следующему результату.
Любое начальное положение может быть приведено к расположению либо рис. 11 (положение I), либо рис. 12 (положение II).
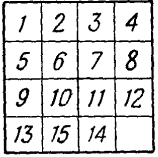
Рис. 12. Неразрешимый случай (положение II)
Если некоторое расположение, которое для краткости обозначим буквой S, может быть преобразовано в положение I, то, очевидно, возможно и обратное — перевести положение I в положение S. Ведь все ходы шашек обратимы: если, например, в схеме 1 мы можем шашку 12 поместить на свободное поле, то можно ход этот тотчас взять обратно противоположными движениями.
Итак, мы имеем две серии расположений таких, что положения одной серии могут быть переведены в нормальное I, а другой серии — в положение II. И наоборот, из нормального расположения можно получить любое положение первой серии, а из расположения II — любое положение второй серии. Наконец, два любых расположения, принадлежащих к одной и той же серии, могут быть переводимы друг в друга.
Нельзя ли идти дальше и объединить эти два расположения — I и II? Можно строго доказать (не станем входить в подробности), что положения эти не превращаются одно в другое никаким числом ходов. Поэтому все огромное число размещений шашек распадается на две разобщенные серии: 1) на те, которые могут быть переведены в нормальное I: это — положения разрешимые, 2) на те, которые могут быть переведены в положение II и, следовательно, ни при каких обстоятельствах не переводятся в нормальное расположение: это — положения, за разрешение которых назначались огромные премии.
Как узнать, принадлежит ли заданное расположение к первой или ко второй серии? Пример разъяснит это.
Рассмотрим расположение, представленное на рис. 13.
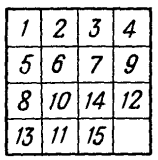
Рис. 13. Шашки не приведены в порядок
Первый ряд шашек в порядке, как и второй, за исключением последней шашки (9). Эта шашка занимает место, которое в нормальном расположении принадлежит 8. Шашка 9 стоит, значит, ранее шашки 8: такое упреждение нормального порядка называют «беспорядком». О шашке 9 мы скажем: здесь имеет место 1 беспорядок. Рассматривая дальнейшие шашки, обнаруживаем «упреждение» для шашки 14; она поставлена на три места (шашек 12, 13, 11) ранее своего нормального положения; здесь у нас 3 беспорядка (14 ранее 12; 14 ранее 13; 14 ранее 11). Всего мы насчитали уже 1 + 3 = 4 беспорядка. Далее, шашка 12 помещена ранее шашки 11, и точно так же шашка 13 ранее шашки 11. Это дает еще 2 беспорядка. Итого имеем 6 беспорядков. Подобным образом для каждого расположения устанавливают общее число беспорядков, освободив предварительно последнее место в правом нижнем углу. Если общее число беспорядков, как в рассмотренном случае, четное, то заданное расположение может быть приведено к нормальному конечному; другими словами, оно принадлежит к разрешимым. Если же число беспорядков нечетное, то расположение принадлежит ко второй серии, т. е. к неразрешимым (нуль беспорядков принимается за четное число их).
«Благодаря ясности, внесенной в эту игру математикой, прежняя лихорадочная страстность в увлечении сейчас совершенно немыслима. Математика создала исчерпывающую теорию игры, теорию, не оставляющую ни одного сомнительного пункта. Исход игры зависит не от каких-либо случайностей, не от находчивости, как в других играх, а от чисто математических факторов, предопределяющих его с безусловной достоверностью».
Обратимся теперь к головоломкам в этой области.
Вот несколько разрешимых задач.
21. Первая задача. Исходя из расположения, показанного на рис. 11, привести шашки в правильный порядок, но со свободным полем в левом верхнем углу (рис. 14).
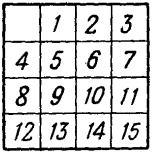
Рис. 14. К первой задаче
22. Вторая задача. Исходя из расположения рис. 11, поверните коробку на четверть оборота и передвигайте шашки до тех пор, пока они не примут расположения рис. 15.
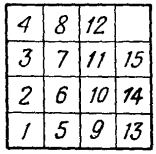
Рис. 15. Ко второй задаче
23. Третья задача. Передвигая шашки согласно правилам игры, превратите коробку в «магический квадрат», а именно разместите шашки так, чтобы сумма чисел была во всех направлениях равна 30.
Крокет
Крокетным игрокам предлагаю следующие пять задач.
24. Пройти ворота или крокировать? Крокетные ворота имеют прямоугольную форму. Ширина их вдвое больше диаметра шара. При таких условиях, что легче: свободно, не задевая проволоки, пройти с наилучшей позиции ворота или с такого же расстояния крокировать шар?
25. Шар и столбик. Толщина крокетного столбика внизу — 6 см. Диаметр шара — 10 см. Во сколько раз попасть в шар легче, чем с такого же расстояния заколоться?
26. Пройти ворота или заколоться? Шар вдвое ýже прямоугольных ворот и вдвое шире столбика. Что легче: свободно пройти ворота с наилучшей позиции или с такого же расстояния заколоться?
27. Пройти мышеловку или крокировать? Ширина прямоугольных ворот втрое больше диаметра шара. Что легче: свободно пройти с наилучшей позиции мышеловку или с такого же расстояния крокировать шар?
28. Непроходимая мышеловка. При каком соотношении между шириной прямоугольных ворот и диаметром шара пройти мышеловку становится невозможным?
Решения головоломок 14–28
14. Для упрощения задачи отложим пока в сторону все 7 двойных косточек: 0–0, 1–1, 2–2 и т. д. Останется 21 косточка, на которых каждое число очков повторяется 6 раз. Например, 4 очка имеется (на одном поле) на следующих 6 косточках:
4–0; 4–1; 4–2; 4–3; 4–5; 4–6.
Итак, каждое число очков повторяется, мы видим, четное число раз. Ясно, что косточки такого набора можно приставлять одну к другой равными числами очков до исчерпания всего набора. А когда это сделано, когда наша 21 косточка вытянута в непрерывную цепь, тогда между стыками 0–0, 1–1, 2–2 и т. д. вдвигаем отложенные 7 двойняшек. После этого все 28 косточек домино оказываются вытянутыми, с соблюдением правил игры, в одну цепь.
15. Легко показать, что цепь из 28 костей домино должна кончаться тем же числам очков, каким она начинается. В самом деле: если бы было не так, то числа очков, оказавшиеся на концах цепи, повторялись бы нечетное число раз (внутри цепи числа очков лежат ведь парами); мы знаем, однако, что в полном наборе костей домино каждое число очков повторяется 8 раз, т. е. четное число раз. Следовательно, сделанное нами допущение о неодинаковом числе очков на концах цепи — неправильно: числа очков должны быть одинаковы. (Такого рода рассуждения, как это, в математике называются доказательствами от противного.)
Между прочим, из сейчас доказанного свойства цепи вытекает следующее любопытное следствие: цепь из 28 косточек всегда можно сомкнуть концами и получить кольцо. Полный набор костей домино может быть выложен, с соблюдением правил игры, не только в цепь со свободными концами, но также и в замкнутое кольцо.
Читателя может заинтересовать вопрос: сколькими различными способами выполняется такая цепь или кольцо? Не входя в утомительные подробности расчета, скажем здесь, что число различных способов составления 28-косточковой цепи (или кольца) огромно: свыше 7 триллионов. Вот точное число:
7 959 229 931 520
(оно представляет собой произведение следующих множителей: 213 × 38 × 5 × 7 × 4231).
16. Решение этой головоломки вытекает из сейчас сказанного. 28 косточек домино, мы знаем, всегда выкладываются в сомкнутое кольцо; следовательно, если из этого кольца вынуть одну косточку, то
1) остальные 27 косточек составят непрерывную цепь с разомкнутыми концами;
2) концевые числа очков этой цепи будут те, которые имеются на вынутой косточке.
Спрятав одну кость домино, мы можем поэтому заранее сказать, какие числа очков будут на концах цепи, составленной из прочих костей.
17. Сумма очков всех сторон искомого квадрата должна равняться 44 × 4 = 176, т. е. на 8 больше, чем сумма очков на косточках полного набора домино (168). Происходит это, конечно, оттого, что числа очков, занимающих вершины квадрата, считаются дважды. Сказанным определяется, какова должна быть сумма очков на вершинах квадрата: 8. Это несколько облегчает поиски требуемого расположения, хотя нахождение его все же довольно хлопотливо. Решение показано на рис. 16.
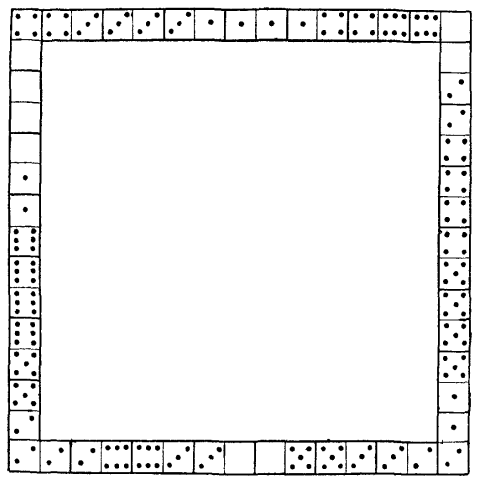
Рис. 16
18. Приводим два решения этой задачи из числа многих возможных. В первом решении (рис. 17) имеем:
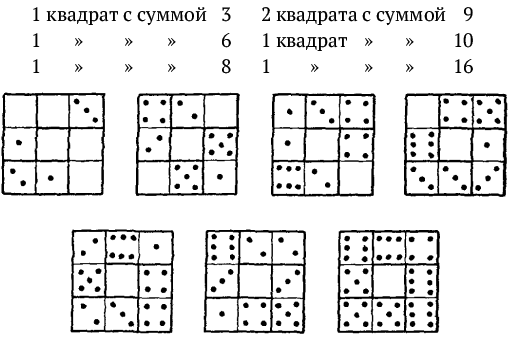
Рис. 17
Во втором решении (рис. 18):
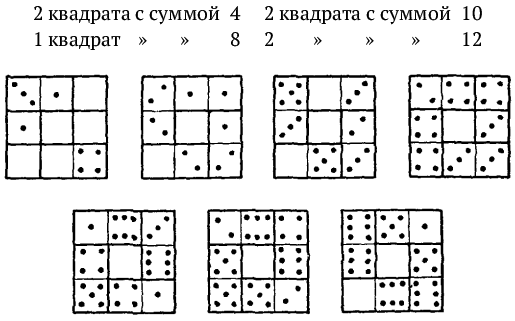
Рис. 18
19. На рис. 19 дан образчик магического квадрата с суммой очков в ряду 18.

Рис. 19
20. Вот в виде примера две прогрессии с разностью 2:
a) 0–0; 0–2; 0–4; 0–6; 4–4 (или 3–5); 5–5 (или 4–6).
b) 0–1; 0–3 (или 1–2); 0–5 (или 2–3); 1–6 (или 3–4); 3–6 (или 4–5); 5–6.
Всех 6-косточковых прогрессий можно составить 23. Начальные косточки их следующие:
а) для прогрессий с разностью 1:
0 — 0 1 — 1 2 — 1
0 — 1 2 — 0 3 — 0
1 — 0 0 — 3 0 — 4
0 — 2 1 — 2 1 — 3
2 — 2 3 — 2
3 — 1 2 — 4
1 — 4 3 — 6
2 — 3 3 — 4
b) для прогрессий с разностью 2:
0 — 0; 0 — 2; 0 — 1.
21. Расположение задачи может быть получено из начального положения следующими 44 ходами:

22. Расположение задачи достигается следующими 39 ходами:

23. Магический квадрат с суммой 30 получается после ряда ходов:

Занимаясь головоломками, относящимися к домино и к игре в 15, мы оставались в пределах арифметики. Переходя к головоломкам на крокетной площадке, мы вступаем отчасти в область геометрии.
24. Даже опытный игрок скажет, вероятно, что при указанных условиях пройти ворота легче, чем крокировать: ведь ворота вдвое шире шара. Однако такое представление ошибочно: ворота, конечно, шире, нежели шар, но свободный проход для шара через ворота вдвое ýже, чем мишень для крокировки.
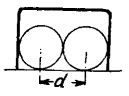
Рис. 20
Взгляните на рис. 20, и сказанное станет вам ясно. Центр шара не должен приближаться к проволоке ворот меньше чем на величину радиуса, иначе шар заденет проволоку. Значит, для центра шара останется мишень на два радиуса меньше ширины ворот. Легко видеть, что в условиях нашей задачи ширина мишени при прохождении ворот с наилучшей позиции равна диаметру шара.
Посмотрим теперь, как велика ширина мишени для центра движущегося шара при крокировке. Очевидно, что, если центр крокирующего приблизится к центру крокируемого меньше чем на радиус шара, удар обеспечен. Значит, ширина мишени в этом случае, как видно из рис. 21, равна двум диаметрам шара.
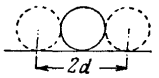
Рис. 21
Итак, вопреки мнению игроков, при данных условиях вдвое легче попасть в шар, нежели свободно пройти ворота с самой лучшей позиции.
25. После сейчас сказанного эта задача не требует долгих разъяснений. Легко видеть (рис. 22), что ширина цели при крокировке равна двум диаметрам шара, т. е. 20 см; ширина же мишени при нацеливании в столбик равна сумме диаметра шара и столбика, т. е. 16 см (рис. 23). Значит, крокировать легче, чем заколоться в
всего на 25%. Игроки же обычно сильно преувеличивают шансы крокировки по сравнению с попаданием в столбик.
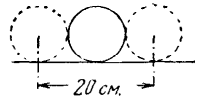
Рис. 22
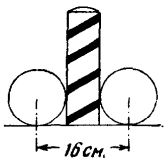
Рис. 23
26. Иной игрок рассудит так: раз ворота вдвое шире, чем шар, а столбик вдвое ýже шара, то для свободного прохода ворот мишень вчетверо шире, чем для попадания в столбик. Наученный предыдущими задачами, читатель наш подобной ошибки не сделает. Он сообразит, что для прицела в столбик мишень в 11/2 раза шире, чем для прохода ворот с наилучшей позиции. Это ясно из рассмотрения рис. 24 и 25.
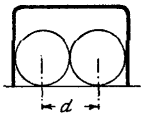
Рис. 24
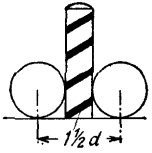
Рис. 25
(Если бы ворота были не прямоугольные, а выгнутые дугой, проход для шара был бы еще ýже— как легко сообразить из рассмотрения рис. 26.)
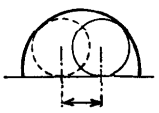
Рис. 26
27. Из рис. 27 и 28 видно, что промежуток а, остающийся для прохода центра шара, довольно тесен при указанных в задаче условиях. Знакомые с геометрией знают, что сторона (AВ) квадрата меньше его диагонали (АС) в 1,4 раза. Если ширина ворот 3d (где — d диаметр шара), то АВ равно
3d : l,4 = 2,1d.
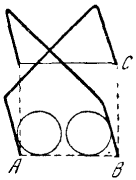
Рис. 27
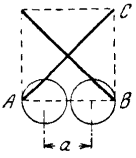
Рис. 28
Промежуток же а, который является мишенью для центра шара, проходящего мышеловку с наилучшей позиции, — еще ýже. Он на целый диаметр меньше и равен
2,1d – d = 1,1d.
Между тем мишень для центра крокирующего шара равна, мы знаем, 2d. Следовательно, крокировать почти вдвое легче при данных условиях, чем пройти мышеловку.
28. Мышеловка становится совершенно непроходимой в том случае, когда ширина ворот превышает диаметр шара менее чем в 1,4 раза. Это вытекает из объяснения, данного в предыдущей задаче. Если ворота дугообразные, условия прохождения еще ухудшаются.
