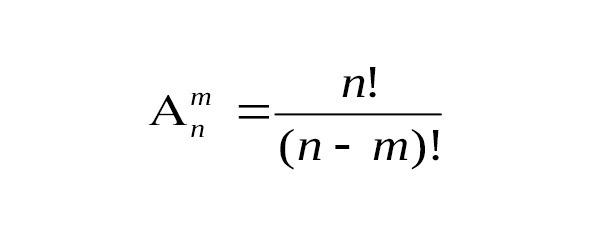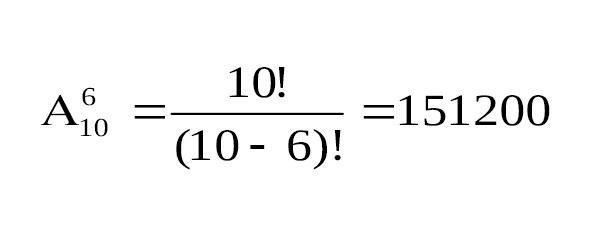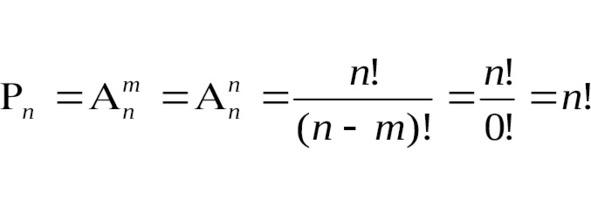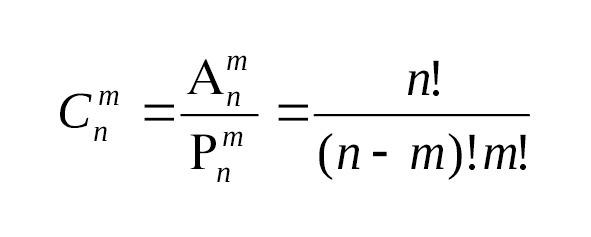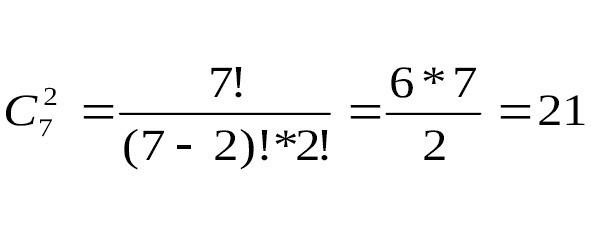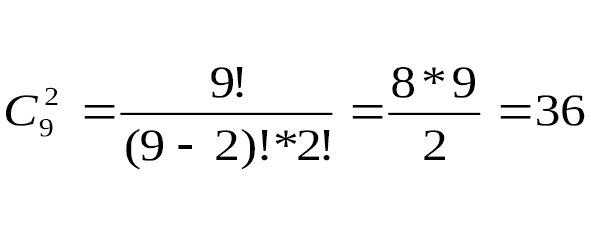1. Основные формулы комбинаторики
Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения [1,6].
1.1.Правило суммы
Если конечные множества не пересекаются, то число элементов X U {или} Y равно сумме числа элементов множества X и числа элементов множества Y.
То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.
Примеры задач
№1
Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение: X=17, Y=13
По правилу суммы X U Y=17+13=30 тем.
Ответ: 30 способов.
№2
Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи?
Решение: всего 6+10=16 вариантов.
Ответ: 16 способов.
1.2.Правило произведения
Если элемент X можно выбрать k способами, а элемент Y — m способами, то пару (X,Y) можно выбрать k*m способами.
То есть, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.
Примеры задач
№1
Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.
№2
Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X — не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.
Очень часто для наглядного решения таких задач применяются круги Эйлера.
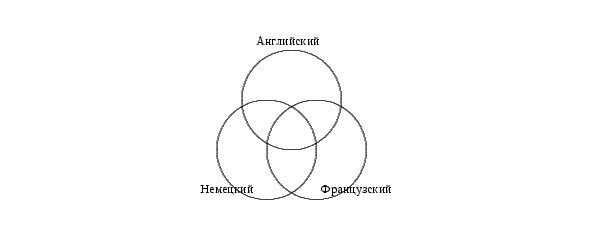
Пример 1. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?
Решение: Выразим условие этой задачи графически (см. рис.1). Обозначим кругом тех, кто знает английский, другим кругом — тех, кто знает французский, и третьим кругом — тех, кто знают немецкий.
Рис.1.
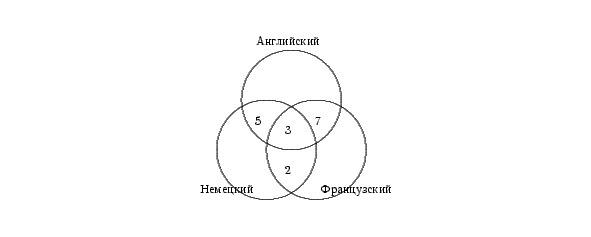
Рис.2.
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10—3 = 7 человек.
Аналогично получаем, что только английским и немецким владеют 8—3 = 5 человек, а немецким и французским 5—3 = 2 туриста. Вносим эти данные в соответствующие части рисунка 2.
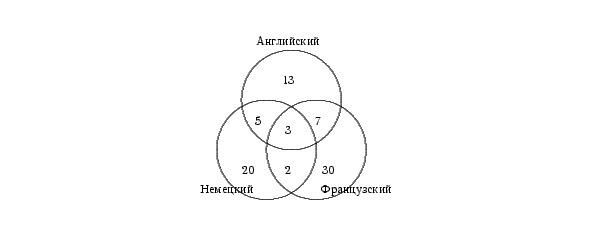
Определим теперь, сколько человек владеют только одним, из перечисленных языков. Немецкий знают 30 человек, но 5 +3 +2 = 10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским — 30 человек (см. рис.3).
Рис.3.
По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.
Ответ: 20 человек не владеют ни одним из данных языков.
1.3. Размещения без повторений
Пример1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?
Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.
Если X-множество, состоящие из n элементов, m≤n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество А, содержащее m элементов из m элементов.
Количество всех размещений из n элементов по m обозначают (см. рис.4):
Рис.4.
Где n! — n-факториал (factorial анг. сомножитель) произведение чисел натурального ряда от 1 до какого либо числа n. n!=1*2*3*…*n. 0!=1.
Значит, ответ на выше поставленную задачу будет следующим (см. рис.5):
Рис.5.
1.4. Перестановки без повторений
В случае n=m (см. размещения без повторений) А из n элементов по m называется перестановкой множества x.
Количество всех перестановок из n элементов обозначают Pn.
Pn=n!
Действительно при n=m (см. формулу на рисунке 6):
Рис.6.
Пример 2. Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?
Таким образом, количество вариантов при сочетании будет меньше числа вариантов размещений.
Число сочетаний из n элементов по m обозначается (см. рис.7).
Рис.7.
Решение:
Найдем количество всех перестановок из этих цифр: P6=6!=720.
Ответ: 720.
Пример 3.
«Проказница Мартышка, Осел, Козел, Да косолапый Мишка
Затеяли играть квартет…
Стой, братцы стой! — Кричит Мартышка, — погодите!
Как музыке идти? Ведь вы не так сидите…
И так, и э так пересаживались — опять музыка на лад не идет.
Тут пуще прежнего пошли у них раздоры.
И споры, Кому и как сидеть…»
Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько?
Решение
Здесь речь идет о перестановке из четырех элементов,
Значит, возможно, P4=4!=24 варианта перестановок.
Ответ: 24.
1.5. Сочетания без повторений
Сочетанием без повторений называется такое размещение, при котором порядок следования элементов не имеет значения [2]
Всякое множество X состоящее из m элементов, называется сочетанием из n элементов по m.
Таким образом, количество вариантов при сочетании будет меньше числа вариантов размещений.
Число сочетаний из n элементов по m обозначается (см.рис.7).
Рис.7.
Формула для числа сочетаний из n элементов по m показана рис.8.
Рис.8.
Пример 1. У одного человека 7 книг по математике, а у второго — 9. Сколькими способами они могут обменять друг у друга две книги на две книги.
Решение:
Так как порядок следования книг не имеет значения, то выбор 2 книг — сочетание.
Первый человек может выбрать 2 книги способами (как это показано на рис.9).
Второй человек может выбрать 2 книги способами (как это показано на рис.10).
Значит всего по правилу произведения возможно 21*36=756 вариантов.
Ответ: 756 вариантов.
Рис.9.
Рис.10.