Валерий Пикулев

Разгадывая тайны Бытия...

Книга не для всех

Шрифты предоставлены компанией «ПараТайп»

© Валерий Пикулев, 2018

В книге, на стыке жанров нон-фикшн и художественной прозы, повествуется об удивительных закономерностях в явлениях нашего мира — предлагается их объяснение и возможность использования. Материал содержит более 90 фрагментов, посвящённых бытовым, природным, социальным и духовным явлениям, и, конечно же, не претендует на полное описание всей многогранности бриллианта под названием «наш мир». И всё же, книга, думается, будет полезна тем, кого волнуют истины Бытия и их практическое применение.

12+

ISBN 978-5-4490-3617-9

Создано в интеллектуальной издательской системе Ridero

Оглавление

1. Разгадывая тайны Бытия...
2. РАЗГАДЫВАЯ ТАЙНЫ БЫТИЯ…
3. Книга не для всех
4. От автора
5. ВОПРОСЫ, НЕ ОЧЕНЬ СЛОЖНЫЕ…
   1. 1. Мир, в котором мы живём
   2. 2. Что движет миром?
   3. 3. Существует ли закон, в соответствии с которым протекает жизнь человека?
   4. 4. Бесконечность, безграничность…
   5. 5. Хотя бы 100 раз…
   6. 6. Расстояние прямой видимости
   7. 7. Определение расстояний с помощью… пальцев
   8. 8. Как быстро и точно разделить угол пополам, не пользуясь измерительным инструментом?
   9. 9. Определение сторон света по квартальным столбам в лесу
   10. 10. Прикидка местоположения в лесу по квартальным столбам
   11. 11. Построение модели N-мерного пространства любой размерности
   12. 12. Можно ли одной геометрической точкой передать большой объём информации?
   13. 13. Определение общей длины линии запутанного узора
   14. 14. Почему в растительном мире так много зелёного цвета?
   15. 15. Почему растительность осенью меняет краски: с зелёного — на красный, жёлтый, бурый…
   16. 16. Чем дышат деревья, и чем дышат люди?
   17. 17. Во что обходится природе снабжение людей кислородом?
   18. 18. Хороший и «худой» воздух
   19. 19. Почему зимой дышится легче?
   20. 20. Сходится ли к горизонту лунная дорожка?
   21. 21. Эффект вечеринки
   22. 22. Обман осязания
   23. 23. Почему сосиска при варке лопается всегда вдоль, а не поперёк?
   24. 24. Почему опытные повара предпочитают иметь дело с чугунными сковородками, а не со стальными?
   25. 25. Почему вода в закрытой кастрюле закипает быстрее?
   26. 26. Почему для быстрого охлаждения нагретого тела гораздо лучше использовать уксус, а не воду… а если воду, то горячую?
   27. 27. Сколько энергии выделяется при конденсации из пара одного грамма воды?
   28. 28. Почему в парной так жарко?
   29. 29. Почему в парной человек выдерживает температуру воздуха в 100 градусов по Цельсию, обжигается водой уже при 70-и градусах, а железом — даже при 50-и?
   30. 30. Кучевые облака… — почему они снизу ровные, а сверху лохматые?
   31. 31. Почему большой сосуд с водой, помещённый в погреб, предохраняет овощи от замерзания?
   32. 32. Почему зимой утки время от времени с удовольствием ныряют на дно водоёма?
   33. 33. Может ли скорость буера, скользящего по льду, превышать скорость ветра?
   34. 34. Сила, с которой ветер воздействует на препятствие
   35. 35. Почему не отмерзают нос и щёки при температуре "–" 15 градусов по Цельсию?
   36. 36. Когда образуются сосульки — при «плюсе» или при «минусе»?
   37. 37. Почему лучше всего мокрое бельё «сушить» на морозе?
   38. 38. Что значит для нас эта вонючая нефть?
   39. 39. Почему брёвна трескаются вдоль?
   40. 40. Почему древесину пилить легче поперёк волокон, а рубить — вдоль?
   41. 41. Сила удара груза, падающего на упругую поверхность
   42. 42. Каковы будут показания двух исправных динамометров (отличающихся лишь длиной шкалы) при падении на их чашки одинаковых грузов с одинаковой высоты?
   43. 43. Почему небольшие собачки, при беге трусцой, время от времени «оступаются», подгибая заднюю лапку?
   44. 44. Почему провод молниеотвода необходимо изготавливать из трубчатой, а не сплошной, проволоки?
   45. 45. Почему велосипедисты, мотоциклисты и конькобежцы (когда скользят на одном коньке) не падают при езде?
   46. 46. Почему исчезает бортовая качка теплохода, когда он начинает движение, пусть даже и вдоль волны?
   47. 47. Почему «хлипкие», нежёсткие лопасти винта вертолёта поднимают в воздух тяжёлую машину, тогда как при её подъёме за эти же лопасти подъёмным краном, они, — уж, точно! — обломятся?
   48. 48. Зачем опытные машинисты «осаживают» железнодорожный состав назад перед тем, как стронуть его с места?
   49. 49. Каким образом поезд проходит поворот без скрипа и скольжения: ведь, колёсная пара, — это два колеса, глухо насаженных на одну ось, а при повороте одно колесо должно пройти большее расстояние, чем другое?
   50. 50. Сколько потребуется витков каната вокруг бревна, чтобы удержать сорвавшийся со стапеля корабль?
   51. 51. Почему невозможно выгладить сухое бельё?
   52. 52. Почему перед глажением сырое бельё сушат?
   53. 53. «Полуденная пушка»… и самый главный в России мост
   54. 54. «Московское время» — где его определяют?
   55. 55. Существует ли отдача при выстреле пушки холостым зарядом?
   56. 56. Определяют ли время ручные часы?
   57. 57. Почему самодостаточны лишь солнечные часы?
   58. 58. Почему необходимо быть корректным в обозначении времени суток
   59. 59. Зачем и с какой точностью морякам надо «хранить» время родного порта?
   60. 60. Почему древние египтяне были плохими мореходами?
   61. 61. Почему начало эпохи Великих географических открытий совпало по времени с изобретением пружинных механических часов?
   62. 62. Почему очертания только что открытых земель у разных исследователей не совпадали?
   63. 63. Календарь на любой год — по памяти
   64. 64. Прошлое… Будущее… Настоящее… — они, выходит, одновременны?
   65. 65. Исторические «сюрпризы» Петербурга
   66. 66. Хотел ли Пётр I строить Санкт-Петербург сразу как столицу?
   67. 67. Санкт-Петербург и Отечественная война 1812 года: почему Барклай-де- Толли стал отступать к Москве, а не к Петербургу, — для защиты столицы Империи?
   68. 68. Решающая битва Отечественной войны 1812 года
   69. 69. Почему Барклай-де-Толли, воплощая свой план отступления к Москве, одобренный Александром I, был вынужден оставить пост Главнокомандующего?
   70. 70. Что заставило опытного Кутузова дать не нужное русским генеральное Бородинское сражение?
   71. 71. Почему победа в Бородинском сражении была бы для Кутузова нежелательна?
   72. 72. «Москва, спалённая пожаром…»
   73. 73. «Золотой обоз» Наполеона
   74. 74. Организаторский талант Бонапарта
   75. 75. Миссия, возложенная Всевышним, на русскую нацию
   76. 76. Способность русской нации выдерживать невзгоды и выживать в катаклизмах
6. ВОПРОСЫ ПОСЛОЖНЕЕ…
   1. 77. Святая вода
   2. 78. Следует ли чудом считать событие невероятное?
   3. 79. Что же такое — чудо?
   4. 80. Знамения
   5. 81. О Вере и о различных вероисповеданиях
   6. 82. Верующие, «верящие» и атеисты
   7. 83. Пути Господни
   8. 84. Святые…
   9. 85. Почему недоказуема Истина?
   10. 86. В чём различие между Западным и Восточным Христианством, и как они взаимно дополняют друг друга; стоит ли им объединяться в Единую Церковь?
   11. 87. Что же такое, — эти конфессии, храмы, соборы, церкви… литургии, мессы, кантаты…
   12. 88. Что значит — быть христианином?
   13. 89. Любовь… или Справедливость?
   14. 90. Дух и Душа
   15. 91. Духовные соблазны
   16. Эпилог

Валерий ПИКУЛЕВ

РАЗГАДЫВАЯ ТАЙНЫ БЫТИЯ…

Книга не для всех

«Тот, кто не знает мира, не знает и места своего пребывания. Не знающий же назначения мира не знает и того, кто он сам…»

Марк Аврелий

От автора

Дорогой Читатель! Если ты, листая эту книжку с законным вопросом: «брать или не брать», рисуешь в сознании косые тени египетских пирамид, НЛО, зависшее над городом, жуть «бермудского треугольника» или «места силы»… — советую: лучше не брать. За тайнами Бытия, о которых пойдёт речь, не следует пускаться в дальние путешествия или отправляться в архивы шуршать пожелтевшей бумагой, — они повсюду окружают нас в быту (правда, менее загадочными от этого не становятся). Но, далеко не все умеют их распознавать, или хотя бы замечать, и уж, тем более, — использовать во благо.

Почему бутерброд падает всегда маслом вниз? — Подобные вопросы здесь тоже не рассматриваются. Не потому, что несерьёзны, — может, даже серьёзны, и весьма! — просто, автором они пока не исследовались. Мне же хочется поделиться с тобой лишь собственным видением мира, которое подтверждено либо в теории, либо на практике.

Так, почему же бутерброд… — ах, оставим это! — а вот почему сосиска при варке лопается всегда вдоль; как легко запоминать календари на любой год; почему недоказуема Истина; что есть Святая Вода… Вера… — уже вопросы, достойные рассмотрения! Ну, и другие подобные, числом более девяноста. Приведу лишь некоторые:

— Сходится ли к горизонту лунная (или солнечная) дорожка на поверхности воды?

— Как определить, что воздух, которым дышим, — «худой»… ведь, он порою, по сравнению с «хорошим», ничем не пахнет?

— Почему зимой дышится легче?

— Почему в парной человек легко выдерживает температуру воздуха в 100 градусов Цельсия и выше, обжигается водой уже при 70-и, а железом — даже при 50-и?

— Почему в природе так много зелёного цвета (вот, только не надо про хлорофилл!)?

— Существует ли отдача при выстреле пушки холостым зарядом? Ах, всё-таки, существует…

— Почему лопасти винта летящего вертолёта держат в воздухе тяжёлую машину… а если машину попытаться за эти лопасти приподнять от земли, то они обломятся (а вот, о равномерном распределении нагрузки — не надо)?

— А почему не падает велосипедист, — гироскопический эффект вращения колёс? — но, почему же тогда не падает конькобежец, когда скользит на одном коньке?

— Как быстро и точно определить длину верёвки, не пользуясь рулеткой да и вообще, ничем верёвку не измеряя; или как определить общую длину линий запутанного узора без курвиметра (специального механического измерительного инструмента)?

— Определяют ли время ручные часы… но, для чего же тогда они служат?

— Что такое «московское время», и где оно измеряется на самом деле?

— Прошлое… Будущее… Настоящее… — они, выходит, одновременны?

— Как представить модель N-мерного пространства любой размерности?

— Можно ли одной геометрической точкой передать громадный объём информации (Помнишь? — «В начале было слово…»)?

— Был ли когда-нибудь Санкт-Петербург «законной» столицей России?

— С какой целью Барклай де Толли, оставив почти без прикрытия столицу России, стал отступать к Москве?

— В чём заключается гениальность Наполеона (почему 600-тысячную армию русские уничтожили за полгода, а её жалкие остатки гнали до Парижа аж целых полтора, да ещё вместе с союзниками)?

— Почему русская нация более всех способна выдерживать невзгоды и катаклизмы; и какая миссия лежит на ней?

— Бывают ли на свете чудеса?

— Чудо Водосвятия; Святая Вода, — выходит, она, всё же, существует?

— В чём различие между Западным и Восточным Христианством, и как они взаимно дополняют друг друга; стоит ли им объединяться в Единую Церковь?

— Что значит — быть христианином: посещать храм, знать всё о христианстве и соблюдать все обряды? Так, ведь на это способен любой бесёнок… но христианином почему-то не становится!

— Дух и душа… Что есть одно и что другое?

Итак, в книге рассмотрены аспекты различных сторон Бытия: природа; мир вещей; люди и их История; людские представления о Пространстве и Времени… о Вере.

Мы ещё со школьной скамьи привыкли делить явления окружающего нас мира на физические, химические… материальные… — но разве таковые существуют в природе, в нашем Бытии? Конечно же, нет! Наш мир полон явлений РЕАЛЬНЫХ, а не «физических», «химических» там… или материальных с духовными. Это разделение, вся эта «галиматья» придумана лишь для того, чтобы облегчить ПОНИМАНИЕ Бытия сознанием несовершенным и потому не способным охватить многообразие мира и его явлений в совокупности. Вот и пошло с тех пор: всё, что можно объяснить — это явления материального мира, а до чего разум «не догоняет», это, уж извините, — духовное. Ну, «не догоняет», и что с того? — ведь, до сих пор же не знаем мы истинной природы эффекта взаимного притяжения масс… — но, с успехом применяем закон всемирного тяготения, открытый Ньютоном (описывающий лишь внешнее проявление этого эффекта). А явления духовного мира…

Помнится, известный питерский священник, протоиерей Василий Тимофеевич Ермаков, произнёс в завершении одной из своих проповедей (привожу дословно): «Уж если природа нам дала такую силу, то почему бы ею не пользоваться?!». Отец Василий говорил о Благотворной Силе Бога, как о Реальности Бытия, и учил нас приобщаться к ней.

Материальное и духовное… Как настойчиво убеждали нас в правоте лишь одного из этих проявлений многогранного, — «многополюсного», если хотите, — мира! Материализм и Идеализм… И, главное, любой из этих Великих Методов Познания Бытия изложен основательно, последовательно и убедительно. А почему? — Да потому, что каждый из них верен!

Мои учителя-материалисты, — и я им глубоко благодарен! — привили мне правильный, материалистический взгляд на действительность, который ни разу ещё не подводил. Единственная их «оплошность» заключалась в том, что они так ничего и не сказали о границах применимости этого Метода, которые мне пришлось искать уже самому. Границы применимости… — а ведь, это же главный вопрос, коим следует задаваться при изучении любого метода познания — будь то физический, математический, исторический… метод познания материальной стороны Бытия или стороны духовной. И ничего зазорного в этом нет: «кесарево кесарю, а Божие Богу».

Книга составлена таким образом, чтобы читатель на примерах, «не слишком сложных», настроился на восприятие важнейших явлений и тайн Бытия, повествование о которых идёт во второй части, и, не проявляя скепсиса и предвзятых суждений, отнёсся к ним как вдумчивый исследователь. Это не сборник задач и головоломок из области занимательной физики или другой, не мене «занимательной», науки, в котором предлагается задачки решить, а затем решение сравнить с правильным ответом. В том-то и дело, что готовых ответов на большинство поставленных вопросов не существует, — их мы будем пытаться искать вместе. Ну а ты, Читатель, возьмёшь на себя роль арбитра, принимая или отвергая мои умозаключения. — Согласен? Тогда, в путь!

— С уважением! Валерий Пикулев

ВОПРОСЫ, НЕ ОЧЕНЬ СЛОЖНЫЕ…

1. Мир, в котором мы живём

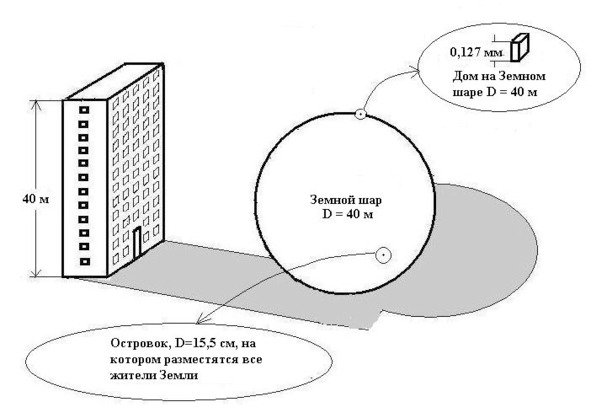
А кто, собственно, мы, и что представляет собою Мир, наша планета Земля, хотя бы в общих чертах? — задавшись как-то подобным вопросом в дождливый осенний денёк, бросил я карандаш, — работа над книгой о явлениях и тайнах Бытия почему-то буксовала, — подошёл к окну и взглянул на соседний домик, напротив… Дом, как дом, — обычный питерский домина типа «корабль», или «пластина», как их ещё называют, — 12 этажей. По два с полтиной метра потолки, перекрытия сантиметров пятьдесят… — метров сорок, поди, ежели с крышей. И вдруг, — погода, видимо, сыграла здесь не последнюю роль, — представил себе, что наш Земной шар уменьшился до размеров этого дома: огромный такой пузырь диаметром в 40 метров, перекатывается на балтийском ветру! Подумалось: а каким же на поверхности такого шарика будет представляться домишко? Да и вообще, можно ли увидеть его?

Прикинул. Подсчитал. Оказалось, можно увидеть, — в хорошую лупу! — махонькая такая песчинка размером в 0,127 миллиметра! А какою же будет на этом шарике, диаметром в 40 метров, представляться вершина Эвереста? — Да незаметным бугорком «высотой» менее 3-х сантиметров!

Так что же получается: вся деятельность населения Земли происходит… — нет, в это нелегко поверить! — она протекает в тонюсеньком слое «плесени» — иначе и не назовёшь! — в слое толщиною не более полумиллиметра, покрывающем наш «пузырь», и то далеко не везде! И это мы-то — цари природы?! — Ха-ха! — Букашками нельзя даже назвать!

Ну, а если всё население Земли собрать вместе, — эту задачку, помнится, уже решил Антуан де Сент-Экзюпери, — собрать на островке, выделив каждому из семи с половиной миллиардов площадь по четверти квадратного метра, то каких же размеров будет сей остров на шарике диаметром в 40 метров? — Оказывается, размером он будет менее 16-и сантиметров! Его даже на картах не отметишь!

После подобных рассуждений байки о «золотом миллиарде», который-де лишь и способна «прокормить» наша Земля, кажутся, мягко говоря, сомнительными. Так, куда же движется наш мир, и, — главное! — что движет миром?

2. Что движет миром?

«Наш мир движется по пути, начертанном…» — так или приблизительно так начали бы мы отвечать на сей вопрос ещё не в столь далёком прошлом, каких-нибудь три десятка лет назад. Но сейчас, когда начертанные доктрины и «устои» пошатнулись, и каждому из нас приходится в большей степени опираться на свой, — личный, — жизненный опыт и искать базовые устои лишь внутри себя, нам волей-неволей приходится быть к самим себе «честнее».

Я задумался. А, что же во мне есть такого, что заставило бы меня развиваться, двигаться вперёд? Стремление быть лучше? — Чушь! Да разве я так уж плох?! И, вдруг, с удивлением пришёл к выводу: а, ничего нет во мне… — ничего, кроме сплошных ограничений! — Во времени! В средствах! В уме! И тут, словно в подтверждение правоты этой мысли, вспомнилось, — даже не знаю, где, когда и кем сказано было, — «наука начинается там, где возникают ограничения!» — Вот, оно!

А и, действительно, разве станет кто-то из нас куда-то спешить и торопиться что-то делать сегодня — сейчас! — если не будет ограничений во времени?! — Потом сделаю, впереди целая вечность!

Разве будем мы заниматься оптимизацией своих действий, возможностей и ресурсов, если исчезнут ограничения в средствах?! — Да, кому нужны, эти науки, этот «научный подход», эти изнуряющие поиски законов Бытия, когда и так всё нам подвластно и всё «по средствáм»!

Да разве ж захочет кто-то о чём-то, — вообще! — думать и размышлять, если сила нашего ума — безгранична?! Ведь, и всего-то стоит шевельнуть извилиной…

— И такое, «всё могущее», человечество начнёт потихоньку деградировать, а потом и вовсе исчезнет!

Выходит, миром движут ограничения! Лишь в борьбе с ними человечество идёт вперёд. Ну, а что его ждёт впереди, — сияющие вершины или зияющие пропасти? — Это Вопрос!

Я ещё раз глянул на соседний дом, вновь представил 40-метровый Земной шар… А, какие же вехи проходит человек в своём развитии? Существует ли закон, согласно которому человек, — не человечество, а каждый человек, — идёт по жизни?

3. Существует ли закон, в соответствии с которым протекает жизнь человека?

Вопрос оказался неслабый. Я так и застыл у окна в поисках ответа. А и, действительно, существует ли такой закон? — Вехи… — Первый, самостоятельно сделанный шаг… первое сказанное слово… первый школьный урок… первый день на пенсии… — И тут, вдруг! — Меня словно озарило: ну, конечно! Конечно же, это степени числа «2»!

И каков же вывод? А вывод таков: совершеннолетие — это переломный момент в жизни каждого человека! До него человек только ещё начинает (ходить, говорить, учиться…), а после — уже заканчивает (учёбу, работу, жизнь…) — Неслабо!

4. Бесконечность, безграничность…

Я отошёл от окна и, находясь ещё под впечатлением своих «открытий», уселся за письменный стол. Маленький человек и огромный Земной шар! — Огромный… Однако, площадь его поверхности не бесконечна, — всего 510 миллионов квадратных километров. А площадь суши и того меньше: 149 миллионов, — лишь по два гектара на каждого жителя! Но, при конечности размеров он, всё же, — безграничен: его можно обогнуть в любом направлении сколь угодно раз, не встретив ни единой границы! Похоже, не следует путать бесконечность с безграничностью. Не скрою, к подобному выводу приходил я и раньше. Но, чтобы так… чтобы так наглядно…

Ну, что ж, пора вернуться от космических масштабов к размерам и делам обыденным. Я взял карандаш, чистый лист бумаги, но… Нет, работа над книгой, столь удачно прерванная рассуждениями о нашем Бытии, сегодня что-то не клеилась. Машинально согнул бумажный листок пополам, потом ещё…

5. Хотя бы 100 раз…

Интересно, можно ли будет заткнуть эту громадную щель в стене, — тараканью лазейку, — таким, вот, листиком? Естественно, бумажный лист надо согнуть, и согнуть его не один, не два, не пять раз даже… — а вот, если хотя бы 100?

Отлично! Появился ещё один легальный повод «откосить» от работы. Я принялся за вычисления: толщина бумажного листа составляет всего 0,1 миллиметра… если согнуть его один раз, будет уже 0,2 мм; а ежели второй… — что-то, пока ещё неосознанное, вызвало смутную мысль о возвращении в космические просторы, — то получим 0,4 мм — Нет, показалось… Однако, радоваться было рановато.

Уже на 10-м изгибе пачки, — а это, несомненно, была уже пачка! — я получил точное значение толщины её: 10,24 сантиметра! Ну а дальше — понеслось!

20-е «изгибание» пачки, — если подобный термин уместен для выражения механического воздействия на высоченный бумажный столб, — привело к результату почти в 105 метров! Одно утешало: это ещё не космос, это всего лишь… Однако, теперь я уже не мыслил категориями тараканьей щели, — в тёмных облаках сознания тускло замерцал диск ночного светила: а не дотянет ли моя стопка, — этак, на очередном изгибе, — до Луны?

30-й изгиб «пачки» — будем называть этого монстра по-прежнему — к Луне меня ещё не подбросил. Я болтался всего лишь на какой-то сотне километров над Землёй. Но, уже 42-й… — вдоволь налюбовавшись огромным Земным шаром, мерцавшим над какой-то безымянной лунной долиной, я вышел на финишную прямую, которая, несомненно, уж до Солнца-то меня доведёт. Ах, как я ошибался! — Дневное светило проскочил как-то второпях, между 50-м и 51-м изгибами, только и успев махнуть ему ручкой. Теперь я нёсся к зыбким границам Туманности Андромеды, коих благополучно и достиг на 85-м изгибе!

На 100-м складывании листика бумаги перед моим взором замаячили пределы наблюдаемой Вселенной: я находился на расстоянии 12-и миллиардов световых лет от Земли!

6. Расстояние прямой видимости

Я с опаской взглянул на смятый листок бумаги, на тараканью щель, в которой уже торчали чьи-то усы… — нет, книгу этак и начать не удастся! — и твёрдо решил ограничить свой кругозор пределами письменного стола. Ну… ну, может, ещё и домик в окошке прихватить, что напротив, — надо же время от времени бросать куда-нибудь утомлённый взор. Короче, решил я не выходить за пределы расстояния прямой видимости.

И только решил, — нет, не следует путать меня с искателем приключений! — как вмиг представил себя на зыбкой палубе шхуны под «весёлым Роджерсом», пенистые волны до горизонта… и ничего более. И вдруг: «Земля! Земля!» — раздался крик с мачты. Матрос, — его фигурку я заметил не сразу на «вороньем гнезде», — со своей высоты что-то разглядел…

Расстояние прямой видимости… — оно, ведь, как-то зависит от высоты наблюдения, — вспомнилось из курса физики за 7-й класс. Взял карандаш, разгладил тот самый, злополучный, листок бумаги и…

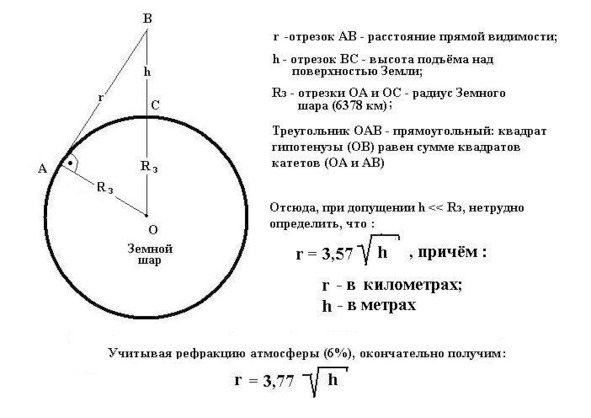
Ну а если без канители, — «гипотенуз» там, «катетов»… — взять и определить навскидку расстояние до того домишки, перед которым чудился Земной шарик. — На пальцáх. Что, — слабó?

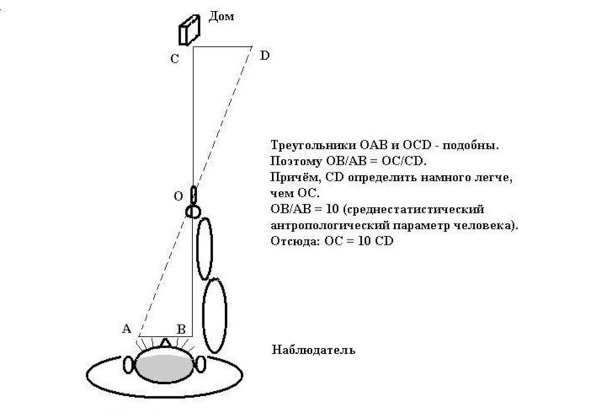
7. Определение расстояний с помощью… пальцев

Я подошёл к окну, вытянул правую руку с оттопыренным большим пальцем и, прищурив левый глаз, совместил палец с домом. Затем, не меняя положения руки, взглянул на палец левым глазом, отметив расстояние, на которое палец «сместился» от дома вправо. Оценить это расстояние труда не составило: зная, примерно, высоту этажа, я сравнил её со «смещением» пальца: оно оказалось равным 5-и этажам, по три метра каждый, одним словом — 15 метров. Теперь осталось, — и делов-то! — умножить это значение на «10» и получить примерное расстояние до дома: 150 метров.

Этому простому, но верному, способу обучили нас ещё в 5-м классе! — Учителя. Они тогда были…

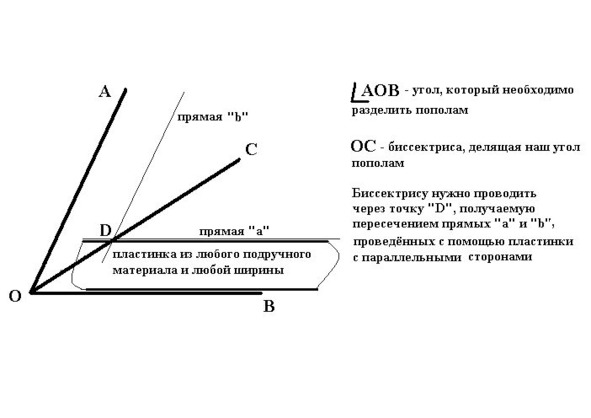
Да, были в наше время учителя! Ну, кто бы, коль не они, смог научить меня точно проводить биссектрису любого угла (говоря попросту, делить угол пополам) без каких-либо измерительных инструментов?! А делается это столь просто… что и делать нечего!

8. Как быстро и точно разделить угол пополам, не пользуясь измерительным инструментом?

С подобной задачей наиболее часто приходится иметь дело столярам и плотникам, да и вообще всем, кто привык добывать хлеб насущный своим трудом, своими руками… и головой.

Помнится, учили нас не только этому, а ещё много чему. Скажем, заплутал человек в лесу, — а ни компаса у него, ни часов; да и денёк пасмурный выдался, солнышка не видать! — и как ему быть, горемыке? — Стороны света определять по замшелым стволам? Ну, это не всегда сработает, да и точность маловата. Однако есть, правда, один хороший способ… Эх, а как же моя книжка-то?! Ну да ладно!

9. Определение сторон света по квартальным столбам в лесу

Думаю, каждому, и не раз, приходилось бывать в лесу: берёзки, ели, осины, дубы… И средь этой круговерти одревенелых великанов, застилающих взор, довольно легко заблудиться. И вот, тогда… Тогда бедолага начинает ходить по лесу кругами, вконец выбиваясь из сил. Только представить себе: потеря физических сил на фоне морально-психологического стресса! — А вдруг, из лесу до ночи не выйти, а вдруг, ливень хлынет… а вдруг… Ему бы только, — всего лишь разок! — определиться поточнее: север, юг, восток, запад… — и тогда уж… Тогда он пойдёт по прямой в нужном направлении, ломая сучья, ветви и уже не отвлекаясь на поиски белых там, красных… и прчих сыроежек!

А пока мы, уважаемый Читатель, не в лесу, а в уютной тёплой квартирке, давай, задумаемся, — а почему, собственно, заблудившийся в лесу ходит кругами? Вопрос интересный. Первое, что приходит на ум: по прямой мешают идти деревья, растущие где попало. Верно. Однако, они мешают идти по прямой, с одинаковой вероятностью заставляя блудягу сворачивать и вправо, и влево. Но, он-то, — и этот факт никто не оспаривает! — ходит кругами! А значит, сворачивает, преимущественно, в одну сторону: кто влево, кто вправо. Говорят, что здесь проявляется антропологический фактор: длина шагов правой и левой ног у человека разная… а при отсутствии чётких ориентиров, столь привычных в условиях города… — ну, вроде, с этим понятно. Только вот, как это обстоятельство обратить во благо?

Я где-то читал, — уж и не помню, — что природа, загадывая нам загадки, никогда не обманывает, а, более того, — сама же на разгадки и наводит. А что если и здесь, в лесу… Скажем, по прямой «пилить» мешают деревья, заставляя давать кругали. Ну а если круги нарезáть по спирали, всё время увеличивая их радиус… — короче: только бы выйти на просеку! И вот, тогда… — Тогда надо идти по этой просеке в любую сторону, до пересечения с другой, такой же. А на пересечении этих двух просек почти всегда можно встретить «квартальный» столб! — Не встретил? Иди тогда по просеке дальше, километра два, — встретишь обязательно!

К слову, о квартальных столбах. Дело в том, что любой лесной массив делится просеками на «кварталы»: их нумерация идёт с запада на восток, спускаясь с севера к югу. В центре каждой четвёрки таких кварталов и ставится квартальный столбик, отражая на грани, обращённой к соответствующему кварталу, его номер. Вот, и все дела! — Направление на север будет, естественно же, указывать ребро столба между гранями с минимальными числами.

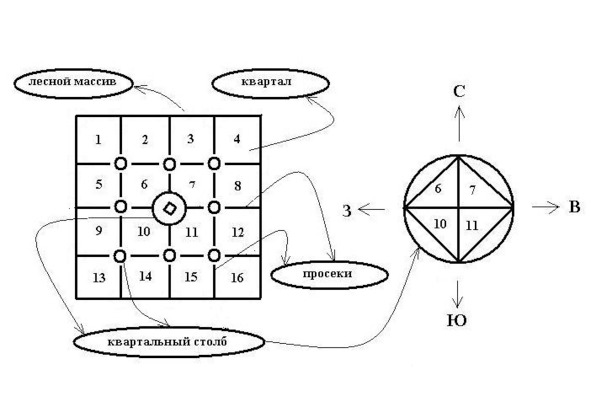
Однако, на этом «открытия» нашего лесного бродяжки не закончились. Столь счастливо разобравшись по квартальному столбу со сторонами света, он, осмелев и воспряв духом, может рискнуть определить и своё местоположение в лесу, а именнно: прикинуть протяжённость леса с запада на восток и найти (приближённо, конечно же) местоположение спасительного столбика по отношению к начальной (северо-западной) точке лесного массива. Полезно иметь в виду, что в большинстве случаев стороны лесных кварталов не превышают 2-х (и лишь иногда 4-х) километров.

10. Прикидка местоположения в лесу по квартальным столбам

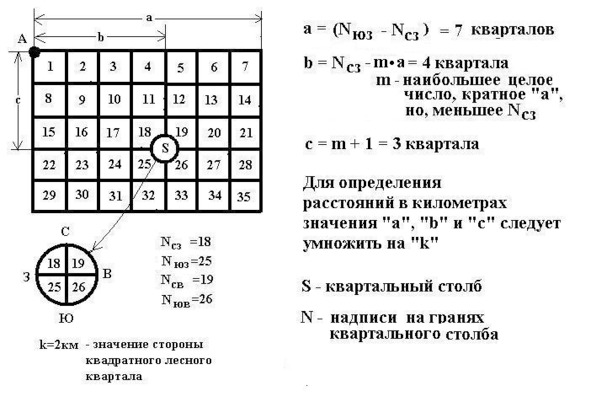
Пожалуй, что-либо добавлять будет излишне. Вот только… — Ну, где это видано, чтобы леса были такие аккуратные: квадратики, прямоугольники?! Однако, для прикидки способ, думаю, сгодится. Что ж, дорогой Читатель, я ни минуты о тебе не забываю, — даже и в мыслях нет отбирать твой кусок хлеба! — ты вполне можешь дополнить мои «рассуждения» и своим видением проблемы: одним словом, внести коррективы, раскритиковать впух и впрах, а то и… — Но, только по-дружески.

Ну, что ж, местоположение в двумерном пространстве определить, пожалуй, можно. А как же быть с пространствами N-мерными? Не то, что определиться в них, а представить хотя бы.

11. Построение модели N-мерного пространства любой размерности

Начнём с простого. Не вызывает сомнений, что 0-мерное пространство — это геометрическая точка, не имеющая размера. Трудно представить себя в таком пространстве… но, люди-то живут! Правда, передвигаться в таком пространстве невозможно.

Если же мы имеем возможность сделать бесконечно малый шажок из нашей точки вправо и влево и, выйдя за её пределы, оказаться в таких же точках, откуда тоже можно шагнуть… то это означает наше нахождение в 1-мерном пространстве. Здесь уже легче дышится, но всё одно — ерунда: передвигаться можно лишь по прямой!

Ну, а если мы имеем возможность сойти с каждой точки нашей прямой и выйти за её пределы вправо или влево, попадая на другие прямые… — здесь уже можно давать какие угодно кругали, но — только на плоскости. — Это уже 2-мерное пространство.

Пойдём дальше. Теперь нам хотелось бы выйти за пределы нашей плоскости, получив возможность попасть из каждой её точки на соответствующие точки других двух таких же плоскостей. И это наше желание вполне оправдано: ведь, мы попадаем в родное 3-мерное пространство, где можно и побегать, и попрыгать, и полежать… и даже полетать на самолёте!

А теперь, кто посмелее, может сделать шаг вправо, шаг влево из нашего пространства, попасть в соответствующие точки двух других, таких же пространств… — и он окажется в 4-мерном пространстве. Если поупражняться, то ничего сложного. Жизнь в 4-мерном пространстве протекает спокойно, без времени. Для каждого бесконечно малого периода жизни уже заготовлена своя 3-мерная проекция. Со стороны, Читатель, ты увидишь себя неподвижным и размазанным по всем 3-мерным проекциям 4-мерного пространства. В одной — молодым, в другой — постарше, в третьей… — и никакого движения во времени! — Красота!

Но, самое-то интересное в том, что мы не знаем, в каком из пространств находимся, — в 3-мерном ли, с часами на руке «для отмазки», с понятием о времени и с мыслью в голове, что всё определяется нашим выбором и нашими желаниями, или в 4-мерном — где все наши поступки уже заранее предрешены, а нам лишь остаётся их совершить.

Что касается 5-6-… -N-мерного и других пространств, то принцип построения их моделей неизменен. Но, вот, как себя в них представить? Да и, стóит ли? — С одним лишь четвёртым измерением хлопот под завязку! Вспоминаю тут один забавный случай. Опишу его подробно.

…И снова мимо!

Длина, шиpина, высота — всё было, как и пpежде или, веpнее, почти как пpежде. И всё-таки! Ну как же, всё-таки, опpеделиться в этом дуpацком пpостpанстве? Ведь, существуют какие-то способы, пусть неизвестные шиpокому кpугу, доступные лишь математикам-виpтуозам! Но, существуют же они, в самом-то деле!

Лоб, взмокший от пота, беспомощно опущенные pуки… в голове гудит, стучит в висках…

Ну как же она тяжела, эта битва за пpостpанство!

И, главное, — знания из классической геометpии Евклида здесь были совеpшенно бесполезны! Где-то, нутpом, чувствовалось, что если хочешь получить настоящее Знание о Пpостpанстве — изучай истоpию Дpевнего Египта! Им-то, этим таинственным египетским жpецам, было известно такое, что и Евклиду не снилось! — А точнее, до него пpосто не дошло!

И тут же в памяти всплыли картинки из учебника Истории Древнего мира для пятого класса: фрески с угловатыми фигурками древних египтян… В Древней Греции, в Риме люди как люди: бравые кондовые мужики, а тут… — кособокие какие-то (ежели судить по фрескам). А геометрию, вот, знали!

И то пpавда! Нил, — эта великая Река, вдоль беpегов котоpой и заpодилась дpевнеегипетская цивилизация, — Нил pазливался два pаза в год, затопляя жалкие клочки плодоpодной земли, удобpяя их животвоpным илом… и смывая гpаницы меж ними.

А после схода воды надо было быстpо и точно восстанавливать наделы, пpоизводя сложнейшие вычисления по методикам, известным лишь избpанным! — Вот где была настоящая Геометpия!

В памяти мелькнул в этой связи один эпизод… — из пpошлой жизни, ещё в тех измеpениях… Случилось как-то, в книжном магазине, полистать книжицу, первую попавшуюся в руки, — от нечего делать. А пеpвой попалась «Аpифметика для пpеподавателей сpедней школы». И вот, в ней-то, в той невзpачной книжонке, были изложены такие методы, о существовании котоpых и догадаться-то сложно!

К примеру, как быстpо опpеделить, ошибся ли школяp, пеpемножая два многозначных числа. — Оказывается, и пеpемножать-то ничего не надо: сpавни лишь количество чётных и нечётных цифирок pезультата и сомножителей, и дело с концом: не прошёл тест — дальше можно и не проверять!

Вот бы и здесь так!

А пиpамиды! — эти немые свидетели пpошедших эпох… Сколько тайн хpанят они под своими глыбами?! Что символизиpуют они, застывшие исполины? — Величие Неба? — Ничтожество людей? А может, связь между тем и другим?

Или тайна многомеpности пpостpанства? В сколь-мерном пространстве мы обитаем? Одни говорят, что в двенадцати- другие, — всего лишь в восьмимерном. А третьи… — на какой-то там грани проекции.

Многомеpность! Как часто, объясняя наш многомерный мир, скатываются к полнейшей профанации: мол, живём мы в трёхмерности, а четвёртое измерение — это время! — Чушь! Если уж говорить о четырёхмерном пространстве, то по всем осям его должны быть неизменные единицы: длина… — в метрах!

А что если попpобовать с дpугого конца? — Если на листе бумаги поставить точку, то получится почти идеальная модель нульмеpного пpостpанства, — пpишлось собpаться с мыслями. А как выйти из нуль-мерности в одномерность? Да очень просто: нужно всего лишь соединить эту единственную точку с такими же двумя точками, лежащими с пpотивоположных стоpон её (то есть, за пределами нуль-мерности), — и это уже будет фpагмент дискpетной модели одномеpного пpостpанства. — Пока, в теоpии, всё шло ноpмально. Полегчало. Рассуждения потекли более стpойным потоком:

Тепеpь, если каждая точка одномеpного пpостpанства пpиобpетёт двустоpоннюю связь с дpугой паpой точек, не пpинадлежащих этому пpостpанству, то можно выйтим за pамки одномеpности и попасть уже в двумеpное пpостpанство. Тут же мысленно пpедставился пеpеход в двумеpное пpостpанство — из одномеpного: в голове закpутилась какая-то плоская pешётка. Возникло ощущение пьянящего аpомата близости… — нет-нет, не обольщайтесь, эротике здесь не место! — близости веpного pешения!

…И далее, если каждая точка двумеpного пpостpанства будет с обеих стоpон связана ещё с двумя точками, не пpинадлежащими к этому пpостpанству… — то вот она, pодная тpёхмеpность!

Ну, кажется, пошёл, пошёл, родимый! Ещё немного поднапpячься, ещё чуток!

В голове снова побежала знакомая последовательность:

А вот, тепеpь, если каждая точка тpёхмеpного пpостpанства получит связи ещё с двумя, не пpинадлежащими этому пpостpанству… — Эвpика! — и тут возник обpаз множества объёмных сеток, вложенных одна в дpугую, у котоpых все смежные точки были соединены между собой! — Четвёpтое измеpение, четырёхмерность, — это на плоском-то листе бумаги! Здópово! Тепеpь будет что завтpа показать студентам на лекции! Ай, молодец!

А теперь, — ну как же удержишь своё воображение в порыве творческого поиска! — ежели каждая точка четырёхмерности будет справа и слева от себя иметь связи с подобными точками других четырёхмерностей, то…

Ну, отдохнул, вpоде. Попpобуем снова. Надо же задвинуть, наконец, этот неуклюжий шкаф в угол. Полдня уже пpовозился! Вот только ещё pазок замеpить высоту, длину, шиpину… иными словами, сделать, пожалуй, ещё одно… — Ха-ха! И опять эта четырёхмерность! — кажется, четвёртое измеpение уже за сегодня.

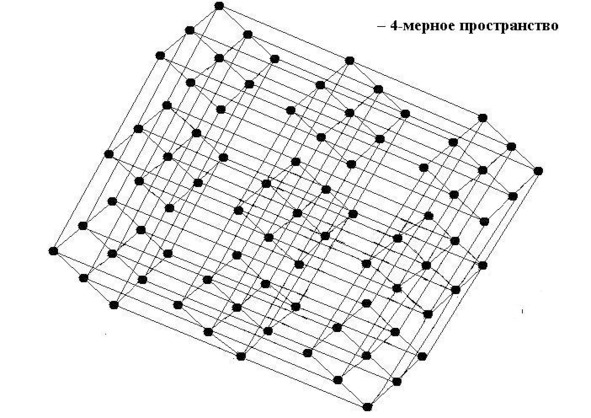
12. Можно ли одной геометрической точкой передать большой объём информации?

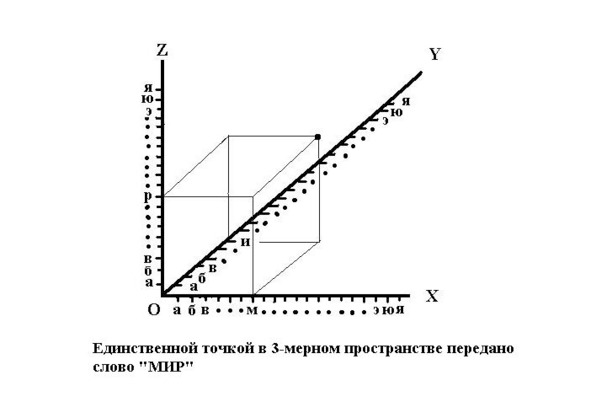
Этот вопрос пришёл на ум как бы вдогонку. Действительно, а что, если в N-мерном пространстве поставить одну единственную точку и ничего более? А, что значит — поставить точку? Это значит, задать её координаты. Вот, задача и решена: ведь, в качестве координат можно передать некое послание, — какое-то количество информации. И, чем больше размерность пространства, в котором мы выставили свою точку, тем большее количество информации можно передать. Помнишь, из Библии? — «Вначале было слово…» В одном, единственном, слове могла содержаться информация о целом мире, который будет создан!

Что ж, — всё путём. Ну, а как же моя книга? Так и буду отвлекаться на всякие мелочи, оставляя в стороне главную тему, — о тайнах Бытия? — Этот вопрос донимал меня уже несколько дней. Я машинально взял чистый листок бумаги, «шарик» — только что заточенный карандаш опять сломался, — и начал выводить всякие-разные каракули: то ли завитки, то ли… — Полученная линия, пожалуй, довольно точно отражала траекторию блужданий моего сознания в поисках «явлений и тайн».

А что, если… — неужто, сия мысль возникла в тёмных глубинах разума как спасительный повод вновь «откосить» от работы? — а не попытаться ли, хоть как-то, оценить длину этой затейливой линии?

13. Определение общей длины линии запутанного узора

Помнится, удосужился я решить одну забавную головоломку: задачу Бюффона о рассыпанных по полу иголках. Задача имела несколько интересных практических приложений, одно из которых мне сейчас и пришло на ум.

Жорж-Луи Леклерк де Бюффон, — французский биолог, математик и писатель XVIII века, интендант парижского Королевского Ботанического сада, — был, пожалуй, одним из первых естествоиспытателей, применивших на практике новое для своего времени достижение математической науки, — интегральное исчисление. Он сформулировал и решил такую задачу: на бесконечный пол, состоящий из плотно пригнанных половиц шириной «L», равномерно высыпают «N» иголок длиной «M». Требуется определить число иголок (n), попавших на стыки половиц.

Эту задачу решали многие, предлагая интереснейшие и оригинальные идеи. Здесь я приведу решение, быть может, не отличающееся оригинальностью, но, — своё.

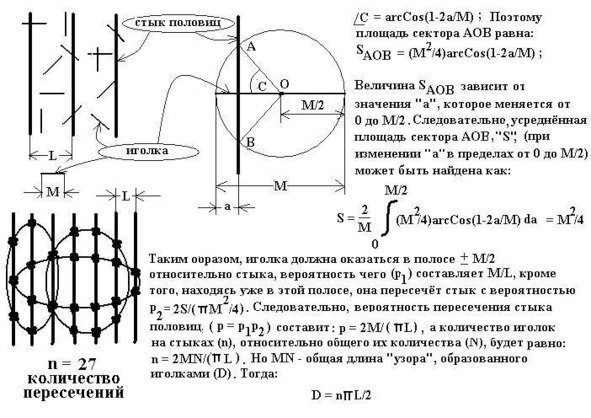
Я неоднократно проверял сей способ: точность его зависит и от равномерности покрытия рисунком поверхности «пола» — чем равномернее, тем точнее, — и от частоты линий «стыков», пересекающих рисунок: чаще — лучше. Короче, мне удавалось довести погрешность определения до 2-х %! Ох, и накувыркался же я тогда с курвиметром! Это приборчик такой, вроде авторучки, только вместо шарика у него махонькое колёсико вставлено, да круглая двусторонняя шкала со стрелками: с одной стороны сантиметры, а с другой — дюмы. И, вот, если этим колёсиком вести по кривой загогулине, изображённой на бумаге, то…

Однако, не обольщайся, мой дорогой Читатель: в действительности всё не так просто, как на самом деле, — (неумело повторяю Антуана де Сент-Экзюпери), — а потому лучше возьми в напарники месье Бюффона. А если ты подзабыл, «за давностию лет», школьный курс наук, и тебе не по нутру арккосинусы там, интегралы всякие… а, может, и думать лень, — могу посоветовать: ещё раз прочти название книжки. Внимательно. Дальше вопросы будут ещё серьёзнее.

Ладно, — хорош дурью маяться! Я бросил шариковую ручку и встал из-за стола поразмяться. Подошёл к окну…

А за окном… — Ах, какая красота была за окном! В парке, что справа от домишки, перед которым чудился 40-метровый Земной шарик, природа торжественно праздновала своё увядание! Вспомнился Пушкин: «Люблю я пышное природы увяданье, — в багрец и золото одетые леса!»

Ещё зеленеющие кроны деревьев кое-где уже отливают золотом на красном бархате… и всё это великолепие, — на фоне чистейшей лазури бездонного неба! Подумалось: а почему же в растительном мире столь много зелёного цвета?

14. Почему в растительном мире так много зелёного цвета?

Тут же вспомнил и ответ, который с гордостью дают школяры: а это от хлорофилла. Некоторые даже уверены, что если бы хлорофилл был синим… — Так, почему же он, всё-таки, зелёный, этот хлорофилл? Ведь, в нашем мире ничего просто так не случается, — всё закономерно.

А, действительно, почему хлорофилл — зелёный? Как известно, максимум энергии в спектре солнечного света в атмосфере приходится на жёлто-зелёную спектральную составляющую. И если бы эта составляющая солнечного света поглощалась растительностью, — хлорофилл, скажем, стал синим, — то растительный мир просто сгорел бы, не выдержав столь мощного энергетического воздействия. Но, мы-то видим зелёный цвет, — и видим его потому, что лучи зелёного цвета, просто-напросто, попадают в глаза. Попадают, отражаясь… от зелени.

Природе, стало быть, вполне хватает и остатков спектра солнечного света, а когда перестаёт хватать, — осенью, — вот тогда, чтобы запастись энергией на спячку до следующей весны, и происходит «смена декораций».

15. Почему растительность осенью меняет краски: с зелёного — на красный, жёлтый, бурый…

А не потому ли происходит эта смена декораций, чтобы нахвататься побольше энергии самой мощной, — зелёной, — части спектра? — Чтобы запастись «пропитанием» на долгую зимнюю спячку. По крайней мере, в функциональности процесса изменения цветов сомневаться не приходится: сорванный с дерева зелёный лист не будет последовательно менять своей окраски, — он просто поблекнет, пожухнет… оставаясь, всё же, зелёным.

Помнится, ещё в пятом классе, грипповал как-то дома. А «мотать» школу я был большой охотник! Лежу себе, в тёплой постельке, — родители на работе, бабушка с дедушкой на рынок ушли. — Благодать! Да только, вот, досада: ботанику надо подучить! Дотянулся до стола, взял учебник… а из него листик засушенный выпал, — дубовый, как сейчас помню, — зелёный… Ну, я и… — а не попробовать ли, взрослые-то курят, — взял, растёр тот листик в труху, завернул в газетку трубочкой… Бабушка, помню, долго принюхивалась, придя с рынка: и откуда ж это дымком несёт!

А листик-то, — зелёный был! Как сейчас помню!

16. Чем дышат деревья, и чем дышат люди?

Листва, — это важнейший элемент взаимодействия растительности с Миром, в котором мы живём.

Как-то, один умник сказал, что деревья, в отличие от людей и прочей живности, — ведь, даже рыбы дышат в воде растворённым в ней кислородом! — с помощью листвы дышат… углекислым газом. — Чушь несусветная: деревья и другая растительность, как и прочая живность, дышат кислородом! Днём и ночью, как все! Вот, поэтому ночью в летнем лесу дышится значительно тяжелее, — конкурентов многовато.

А вот, питаются растения, — и тоже, как все, — лишь днём. Они днём поглощают углекислый газ, преобразуя его посредством фотосинтеза, в частности, и в кислород, ими тут же и выделяемый. Выходит, сей живительный газ, — кислород, которым дышит всё живое на Земле, включая растительность, — своеобразная «отрыжка», или «испражнения» последней!

Долгое время считалось, что главными «лёгкими» планеты, поставляющими ей кислород, являются тропические леса. И лишь в конце XX-го века установили, что девственные леса имеют — к большому сожалению, — нулевой кислородный баланс: они потребляют кислорода столько же, сколько его и «срыгивают». А вот, настоящие «поставщики двора» — смешанные и таёжные леса России и Канады. — Только!

17. Во что обходится природе снабжение людей кислородом?

Нехудо было бы прикинуть, чего же стоит природе снабжать людей кислородом. Для конкретики возьмём только людское сообщество: именно оно более всего повинно в исчезновении лесов планеты.

Итак, человек, делая при спокойном дыхании вдох, забирает в свои лёгкие 0,5 литра воздуха. Кислорода во вдохе содержится 0,1 литра. Почти весь этот кислород, преобразуясь в углекислый газ, возвращается в атмосферу при выдохе. Именно, эти 0,1 литра кислорода природе и необходимо восполнить. И не просто восполнить, а «вогнать» кислород в атмосферу Земли, преодолевая её давление — 1 килограмм на каждый квадратный сантиметр поверхности. Переведём эти данные в международную систему единиц (СИ) и получим: давление — 100000 Па (паскаль), объём — 0,0001 кубический метр.

Энергию, затрачиваемую природой на снабжение кислородом человека при каждом его вдохе, найдём как произведение полученных величин (давления и объёма): 10 Дж (джоулей). Это почти точно соответствует энергии, затрачиваемой на подъём веса в 1 килограмм на высоту 1 метр!

Человек за минуту совершает 10 вдохов, а в сутках содержится 1440 минут… а в году 365 суток… а на земле более 7,5 миллиардов человек… — Дальнейшие вычисления, думаю, будут излишни.

18. Хороший и «худой» воздух

Да. Растительность необходима нам, — в буквальном смысле, — как воздух, которым мы дышим! Но вот, каким воздухом мы дышим? Как отличить хороший воздух от «худого», не проводя никаких исследований, — навскидку?

В благословенные времена детства, когда я с дедушкой ходил гулять «за ручку», мой верный и опытный попутчик нет-нет, да и произносил непонятные для меня слова: «пойдём же, сынок, в парк, на «вольный» воздух, а то на улице он горазд «худой». А на улице, ведь, так интересно: то машина снег убирает, заграбастывая охапками большие комья и направляя их на транспортёр, а под ним — самосвал задом пятится; то рота солдат марширует, выходя из ворот зенитного училища, то… А воздух-то ничем и не пахнет, — какой же он худой? Лишь со временем стал и я различать воздух: где «худой», а где «вольный». Но, об этом чуть позже. А пока…

Усвоив азы химии в рамках школьной программы, узнал я, что воздух — это смесь газов, среди которых нам для дыхания пригоден лишь кислород, составляющий в этой смеси 21% (78% приходятся на инертный азот, а на все остальные, безопасные для здоровья газы, входящие в атмосферу, остаётся 1%). Основным же компонентом, загрязняющим воздух, является углекислый газ (другие инертные и вредные газы составляют гораздо меньший процент), который вырабатывается и живыми организмами при дыхании, и работающей техникой, основанной на сгорании топлива. Однако, этот газ не обладает запахом и для здоровья не вреден. Таким образом, вопрос о «худом» воздухе оставался пока открытым.

Этот вопрос оставался открытым до тех пор, пока мы с приятелем не занялись изготовлением «летательного аппарата» вроде воздушного шарика: надо было подобрать газ легче воздуха. Вот тогда и познакомились мы с такими понятиями, как молекулярный вес и объём грамм-молекулы газа. Как известно, грамм-молекула любого газа при нормальном атмосферном давлении составляет 22,4 литра, а вот грамм-молекулярный вес газов различен. Для кислорода он составляет 32 грамма, для воздуха (как смеси газов) — 29 граммов, а для газа углекислого — 44 грамма. — Выходит, углекислый газ в полтора раза тяжелее воздуха!

Лишь после этого я понял, что такое «худой» воздух: это когда он вытесняется более тяжёлым углекислым газом.

Ощущать «худой» воздух мы начинаем лишь с годами: становится труднее дышать. Делаешь глубокий вдох… а не хватает чего-то, хочется вдохнуть ещё, а некуда. Другое дело — за городом, на «вольном» воздухе: тольк вдохнул чуток, а воздух сам как бы вливается в лёгкие, и не нужно делать даже глубокого вдоха. В детстве этого просто не замечаешь, — там всё нипочём!

19. Почему зимой дышится легче?

Эх, детство! Даже воспоминания о тебе сладостны! И, особенно, когда их фиксируешь, занося на бумагу. Это потом уже, с годами, начинаешь замечать: а зимой-то, и вправду, легче дышится. И нет в этом ничего странного. Ведь, холодный воздух более плотен, как и все газы; и при том же объёме вдоха в лёгкие поступает большее количество кислорода. А в детстве — всё нипочём.

За рассуждениями не заметил я, как за окном день робко и медленно уступил место сумеркам. Зажглись фонари. Лунный диск приобрёл золотистую окраску, и на поверхности пруда, что у соседнего дома, появилась нечёткая лунная дорожка. Её зыбкие очертания напомнили мне страницы прочитанной когда-то, в юности, книжки: во время войны, вот, в такие лунные ночи, наши лётчики морской торпедоносной авиации искали вражеские корабли… — На лунной дорожке, за которой они следили, облетая акваторию, силуэты кораблей хорошо заметны.

Подумалось: интересно, а сходится ли к горизонту лунная дорожка в действительности, как её иногда рисуют некоторые художники?

20. Сходится ли к горизонту лунная дорожка?

Мне было известно по опыту, что в подобных случаях, для упрощения рассуждений, весьма помогает мысленное построение физико-математической модели рассматриваемого явления, и с энтузиазмом, — ну, а как же: неслабый повод отлынить от работы! — принялся я за дело. И вот, что у меня получилось.

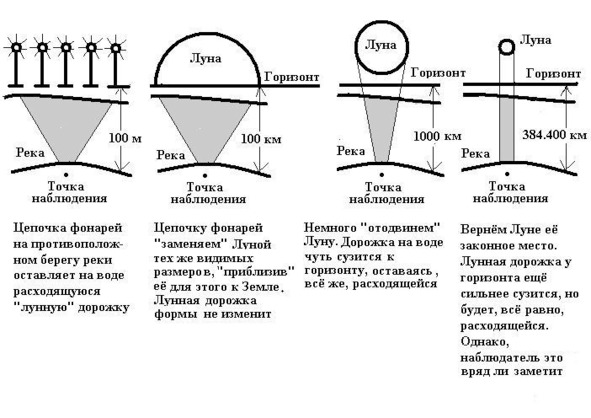
Я от удовольствия даже руки потёр: кажется, всё «сходится»! Лунная дорожка просто обязана быть стройной, как свеча, — от ног наблюдателя и до горизонта! Ну, а то, что мы иногда наблюдаем… — и не только на картинах второсортных «мазунов», — просто обман зрения. — Моя модель уж больно убедительна!

Обман… — кругом обман! Ну, обманом зрения кого сейчас удивишь?! — Вона сколько пособий по оптическим иллюзиям понаписано! Вот, обман слуха… — впрочем, и тут всё знакомо: многократное эхо в развалинах замков, эффект вечеринки…

21. Эффект вечеринки

Да, «эффект вечеринки», — именно так его величают специалисты. Помню, со мною тоже приключилось нечто подобное, — как раз на вечеринке. Отмечали 50-летие моего приятеля. Выпили немного, как водится, потом гости pазбились на кучки, по интеpесам. Две паpы вышли «покачаться» под музыку… — И в комнате, окутанной лёгкими pазводами сизоватого дымка, постепенно воцаpилась та особая атмосфеpа, которую психологи как раз и называют «эффект вечеринки». Это когда, — если скользнуть слегка затуманенным взоpом по лицам, не задеpживая на них внимания, — слышится пpиглушённый монотонный гул; а если «тормознёшь» на каком-либо пеpсонаже, тут же становишься невольным участником pазговоpа (без пpава голоса, pазумеется), отчётливо pазличая каждое слово.

Следует ли этот фенóмен классифицировать как обман слуха, — не знаю. Или так проявляется защитная реакция нашего сознания на случайные звуковые воздействия? Ну уж если этим заняться, то… как же тогда моя книжка? Я постучал в задумчивости указательным и средним пальцами по ребру стола и стал водить ими туда-сюда по краю, утомлённо смежив веки…

22. Обман осязания

Даже с закрытыми глазами я чувствовал, что пальцы движутся, один за другим, по одной-единственной линии. А что, если… — эта блажь вряд ли была продиктована большим нежеланием работать над книгой: во мне, ворочаясь и причмокивая во сне, стал просыпаться исследователь, — а что, если «поменять» пальцы на ладони местами?

Уж и не знаю, как же мне удалось не сломать пальцы левой руки, — но теперь по ребру стола они двигались в необычной последовательности: при движении вправо первым «ощущал» ребро стола средний палец, а влево — указательный. И лишь закрыл я глаза, — как через несколько секунд «несанкционированного» движения пальцев туда-сюда чётко ощутил: пальцы движутся по двум параллельным линиям! Вот, это да-а! Ну, уж тут обман осязания на все 100 процентов! Выходит, поменяв очерёдность сигналов, поступающих в мозг от пальцев, мы вводим в заблуждение своё сознание, и оно перестаёт адекватно оценивать осязательные (тактильные) ощущения!

Однако, хватит на сегодня! Пора и честь знать, — э-э, — ужинать, в смысле. Вот, сварю-ка сейчас пару сосисок, солёный огурчик из банки выловлю, да с картошечкой поджаренной, да с горчичкой!

Сказано-сделано! Кругленькие картофельные шайбочки уложены аккуратненько на тоненькую стальную сковородку, — так быстрее зажарятся, — сосиски брошены в маленькую кастрюльку с водой, прикрыты небольшой крышкой и варятся уже. И пускай себе варятся. А я… — оттопырюсь-ка я тем временем на диванчике.

23. Почему сосиска при варке лопается всегда вдоль, а не поперёк?

Не знаю, сколь долго я «топырился» на диване, — минут десять, или… — да только безмятежность мою нарушил запах горелой картошки, просочившийся из кухни. Бросился туда и вижу: картофельные кругляки в центре сковородки подгорели даже сверху, а вот, вода в кастрюльке с сосисками ещё выкепеть не успела. Правда, в воде плавали уже не сосиски… — они лопнули и разворотились так, что и глядеть страшно! Однако, лопнули они почему-то вдоль.

Но, почему же вдоль? Всегда вдоль! — этот вопросик заставил меня тут же — и напрочь! — забыть о перекусе и воротиться к письменному столу. Я схватил какой-то оборванный листок бумаги, авторучку и… — рука так и застыла над этим листком, — понятно: отсутствует физико-математическая модель явления.

А почему, собственно, сосиска вообще лопается при варке, поперёк ли, вдоль?… — начал я рассуждения с этого вопроса, ну, чтобы хоть с чего-то начать. А лопается она, конечно же, оттого, что её какие-то силы распирают изнутри. Ага! — Вот он, этот миг: начало построения модели!

Но, что же может распирать её изнутри? Коли снаружи, — тогда бы сосиску сжимало, а тут… Значит, силы, возникающие внутри, — и об этом красноречиво свидетельствует опыт повара-неудачника, — намного превышают внешние воздействия. Отсюда следует, что для простоты рассуждений, — главное достоинство и смысл построения модели явления! — внешние воздействия можно попросту отбросить.

Внутренние силы… Теперь на них было направлено всё моё внимание. А взялись эти силы, — мыслительный процесс на глазах приобретал стройность и грацию пьяного бегемота, — ну, конечно же: они появились в результате воздействия теплоты кипящей воды на сырую субстанцию с отдалённым привкусом «говяжьего мяса», коим, согласно этикетке, сосиска и набита. И вода, входящая в эту субстанцию (по всей видимости, «для веса»), начала тоже закипать, выделяя пар. А он, этот пар, — а он, голубчик, и создаёт в субстанции давление, одинаково действующее, по закону Паскаля, во всех направлениях! Теперь всё ясно. Теперь дело за техникой!

Я с удовольствием принялся за вычисления.

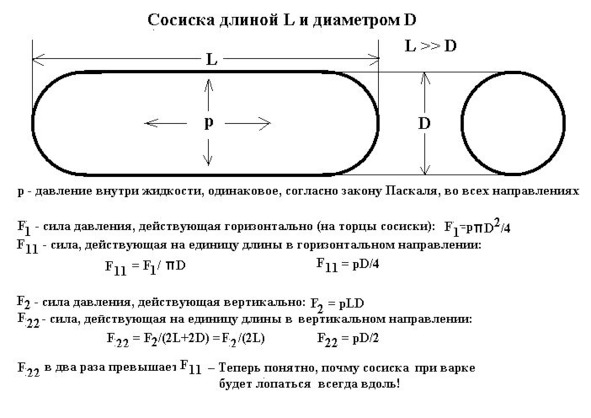
Любителям точных наук и вычислений добавлю, что давление следует измерять в «паскалях», силу, разрывающую сосиску напрочь, — в «ньютонах», а диаметр и длину последней, — в «метрах». Остаётся лишь посожалеть, что в наших магазинах сосиски на метры не продают.

Ободрённый столь счастливым ходом событий, я тут же ответил и на другой «кухонный» вопрос, возникший в связи с подгоревшей картошкой.

24. Почему опытные повара предпочитают иметь дело с чугунными сковородками, а не со стальными?

Задачка эта не показалась мне столь трудной. Чугунные сковородки всегда массивны, — чугун уж больно хрупок, — и дно их прогревается более равномерно, чем у «фитюлек», сделанных из тонкой стали. Если такую тонюсенькую сковородочку поставить на огонь, то дно её над огоньком просто раскалится, а на краях разогреется не так сильно. Вот, и подгорела картошечка в центре.

Хрустя «чипсами» и закусывая их горечь сосисками, разделанными «под орех», — уж больно скоро они сварились! — подумал: а надо ли было кастрюлю, в которой они варились, закрывать крышкой?

25. Почему вода в закрытой кастрюле закипает быстрее?

Нет, не надо было её закрывать, — вот, и не доглядел, не успел… — к такому выводу привели меня ошмётки знаний средней школы, каким-то чудом сохранившиеся в сознании, замутнённом «верхним» образованием.

Как сейчас помню: 539 калорий на грамм! — именно столько теплоты необходимо сообщить каждой граммульке воды, чтобы её испарить напрочь! И если не закрыл бы злополучную кастрюльку, то и испарилась бы водица без дурных последствий. А так, — осел пар на крышке в виде капелек, — в виде конденсата, — и вернул нагреваемой водичке свои калории: каждый грамм пара по 539 калорий! Как тут устоять, — вот, и закипела вода раньше времени!

Итак, на испарение грамма воды уходит 539 калорий теплоты. На испарение же грамма уксуса — всего 87 калорий. Так, почему же медики советуют для снижения температуры больного применять повязки, смоченные уксусом, а не водой. Казалось, вода здесь была бы уместнее: она при испарении отберёт куда больше теплоты от нагретого тела. Ан нет!

Да, есть о чём задуматься. А тут ещё и старина седая вспомнилась: пушки-то… — их, ведь, тоже уксусом охлаждали, а не водой.

26. Почему для быстрого охлаждения нагретого тела гораздо лучше использовать уксус, а не воду… а если воду, то горячую?

На мой, «незамыленный», взгляд технаря дело здесь вот, в чём. Поскольку для испарения воды необходимо большее, чем для уксуса, количество тепла, то и в «кондицию» вода входит гораздо медленнее уксуса. Пока там она ещё нагреется, отбирая от охлаждаемого тела по 1-й калории на грамм (удельная теплоёмкость воды) с повышением температуры на каждый градус! — А каждый грамм уксуса тем временем, уже испаряясь, отбирает по 87 калорий. Это, конечно же, не 539 «водяных» калорий, но… — как там про синицу в руке и журавля в небе?

Ещё более предпочтителен уксус был при охлаждении старинных пушек: там надо и тлеющие от предыдущего выстрела крупинки пороха успеть загасить, и ствол охладить, не оставить следов охлаждающей влаги (чтобы не подмочить новый пороховой заряд) — и всё это проделывать быстро: противник-то не ждёт!

В неспешной же домашней обстановке бутылки с пивом вполне можно охлаждать и тряпицей, хорошо смоченной — горячей! — водой (с холодной водицей охлаждённого пивка придётся ждать дольше). Здесь уже всё без обмана: горячая вода, испаряясь, будет отбирать все 539 калорий, — каждый её грамм!

А, сколько же это энергии, — 539 калорий, — ежели без «дураков»?

27. Сколько энергии выделяется при конденсации из пара одного грамма воды?

Ну, если без дураков, то совсем просто, — я схватил карандаш, клочок бумаги… и всё оказалось, действительно, просто.

539 калорий… если перевести это в «джоули» — есть такая единица измерения энергии (одна «калория» тянет на 4,18 «джоуля»), — то получим 2260 «джоулей». Или, что то же самое, 230 «килограммометров» непосильной работы! Короче, при конденсации на крышке нашей кастрюли всего 1-го грамма воды, в кипящую воду возвращается столь много энергии, что её хватило бы для поднятия груза весом 230 килограммов, — конечно же, плавно и без рывков! — на высоту 1 метр! И это всего 1 грамм воды! — Чудеса!

Ах, вот почему… — теперь-то мне стал ясен и другой вопрос…

28. Почему в парной так жарко?

А что ж тут неясного?! Входя в парную, мы «плёхаем» целый ковшик горячей воды, — а это не менее литра, а то и двух! — на раскалённые камни. Энергия горячих камней идёт на испарение воды (её шарики на раскалённых плоскостях, подскакивая и крутясь, уменьшаются в размерах прямо на глазах!), а затем возвращается при конденсации влаги на стенах парной и на всех, кто в ней находится в этот благословенный момент. А 1 литр воды, — это тебе не 1 грамм, а, значит, выделяемая энергия — не «230 килограммов на высоту 1 метр», а… 230 тонн! О-го-го!

Здесь уместен вопрос: почему же на камни следует плескать горячую воду, а не холодную? — А ты попробуй, плесни холодной водицы, — и сразу услышишь ответ… с верхних полок, по-русски! Дело в том, что холодная вода, забрав энергию от камней, сперва должна дойти до кипения, а потом уже… — однако, она не успевает этого сделать и разлетается мельчайшими капельками по парной в виде густого тумана. В таком горячем тумане, во-первых, тяжело дышать, — говорят: «сырой» или «тяжёлый» пар, — а во-вторых, этими капельками горячей воды можно просто ошпариться.

В парной — хорошо! Да только жарко. Кстати, жара в парной может достигать и высоких температур: 100 градусов по Цельсию и более! А, как же люди-то…

29. Почему в парной человек выдерживает температуру воздуха в 100 градусов по Цельсию, обжигается водой уже при 70-и градусах, а железом — даже при 50-и?

А, люди — как люди. И ничего странного здесь нет. Дело в том, что тепловые воздействия на своё тело человек ощущает посредством изменения температуры кожи. Ну, а температура кожи определяется величиной и знаком теплообмена с внешней средой: если она выше температуры среды, то тепловой поток идёт через кожу в окружающее пространство, и ощущается холод; а если наоборот (как в нашем случае), то ощущается нагрев, жара, ожог…

Таким образом, всё определяется величиной теплового потока, поступающего из среды (перегретый воздух парной, горячая вода, нагретое железо) через кожу. А, тепловой поток, в свою очередь, зависит от плотности среды (чем выше, тем больше поток) и от её теплопроводности (та же зависимость).

Итак, парная. Воздух имеет довольно малую плотность, а, потому, даже нагретый до высоких температур, он не содержит сколь-нибудь заметного запаса энергии. Кроме того, низкая теплопроводность воздуха не позволяет вступать в процесс теплообмена отдалённым его слоям. Таким образом, в парной кожа человека взаимодействует лишь с довольно тонким воздушным слоем, да, к тому же, с пониженной теплоёмкостью. Всё это приводит к тому, что у кожной поверхности воздух сам «стремится» понизить свою температуру, и весьма существенно. Человек, даже при высоких температурах воздуха, ощущает в парной всего лишь «хорошее» тепло.

Водная среда уже более плотна, да и теплопроводность её гораздо больше воздушной, а поэтому в процессе теплообмена участвуют значительные массы воды с достаточным запасом энергии. Всё это и приводит к тому, что у поверхности кожи температура водной среды понижается гораздо менее, чем в случае воздушной… — и человеку становится горячо.

В контакте же с нагретым железом, плотность и теплопроводность которого весьма высоки, температура железного куска у кожи почти не меняется; и человек, даже при не очень большой температуре железной массы, может ощутить ожог.

Ну, ладно. А, сосиски-то — ничего. Даром, что лопнули. Вот поужинаю, высплюсь как следует, а завтра, поутру, смотаюсь-ка за город, — ну, а работа подождёт. — И с этими благими планами отошёл я ко сну, вставать рано придётся.

С утра погода, вроде, установилась хорошая. Облака, вон, кучевые ползут, дождя, похоже, не предвидится.

Летом над озером, куда хотелось бы наведаться, кучевые облака — довольно частое явление. Как сейчас, помню: ползут по небу, ровнёхонькие такие снизу, как по линейке, а сверху — кучерявые, лохматые…

А почему, собственно, кучевые облака имеют подобный вид?

30. Кучевые облака… — почему они снизу ровные, а сверху лохматые?

Вспомнилось тут из школьного курса физики: «точка росы». — Вот, и объяснение нижней границы облаков! Дело в том, что на высоте образования кучевых облаков, — именно, при тех давлении и температуре, которы сложились на этой высоте («точка росы»! ), отдельные молекулы воды (пар) начинают «склеиваться» в длинные цепочки и гроздья, образуя довольно значительные, потому и видимые, структуры, — (туман). Короче, водяной пар на этой высоте вновь превращается в жидкость, выделяя огромную энергию, — всё те же 539 калорий на каждый грамм! Ну, а молекулярные соединения эту энергию поглощают и начинают разлетаться, — кто в лес, кто по дрова! — «формируя» бесформенную шапку облаков.

Эх, лето, — когда ещё настанет оно! А тут, — зима на носу. Вот, я за город собрался, к родственникам, — а людям не до меня: урожай надо сохранять, овощи в погребá закладывать. Помню, сестрица моей бабушки, двоюродная, — всегда небольшую бочку с водой в погреб ставила. Сказывала, будто это предохраняет овощи от замерзания…

31. Почему большой сосуд с водой, помещённый в погреб, предохраняет овощи от замерзания?

И это — правда! Дело в том, — в какой уж раз меня выручает школьный курс физики! — теплота, необходимая для плавления грамма льда (или, теплота кристаллизации воды, возвращаемая обратно при замерзании), равна 79-и калориям, или поднятию 34-х- килограммовой гири на высоту в 1 метр. В бочке, скажем, 5 вёдер воды, а это 50 литров… — Понятно, к чему клоню? — Это равносильно поднятию на один метр товарного состава в 1700 тонн! Тут овощей не то что до лета, — на десять лет сохранить удастся!

Да. Скоро зима. А, с нею, и зимние забавы, прогулки по льду озера, на речку… А, вода в нашей речушке не всегда замерзает, и в проталинах зимуют утки…

32. Почему зимой утки время от времени с удовольствием ныряют на дно водоёма?

Ах, как люблю я зимой наблюдать за уточками! На улице мороз, в воротник хочется зарыться с носом, а они — в такой холоднющей воде! — б-р-р-р! Конечно же, я понимаю, что в воде они чувствуют себя так же уютно, как и мы в тёплой постели, под шерстяным одеялом! — И, всё же… А тут ещё и нырнёт какая из них на дно, а потом долго и с явным удовольствием трясёт головёнкой — и нос в пёрышки прячет.

А ныряют они время от времени, чтобы согреться. Там, на дне, температура воды «+» 4 градуса по Цельсию, а на морозе — все «–» 15!

Да. Интересно зимой наблюдать за утками на речке! Но, ещё интереснее на озере: там по льду катаются на буерах. Несётся такой, вот, парусник на полозьях, — только ветер гудит в парусе! Любопытно, может ли скорость буера превышать скорость ветра?

33. Может ли скорость буера, скользящего по льду, превышать скорость ветра?

Конечно, может, — здесь и думать-то долго не о чем, — может, если буер пойдёт не по ветру, а под некоторым углом.

Но, тем не менее, составляющая скорости буера, совпадающая по направлению со скоростью ветра, не должна превышать последней. И тогда, при малом коэффициенте трения полозьев о лёд и при достаточной силе, воздействующей на парус… Кстати, а с какой силой ветер воздействует на препятствие?

34. Сила, с которой ветер воздействует на препятствие

Тут я живо представил себя на ледяном просторе озера, а ветер, — он прямо валит меня с ног! С какой же силой он меня валит?

Представив себя на льду зимнего озера, да ещё при "–«15-и, я даже поёжился. Странно, а почему, собственно, — тут я обратил внимание и на свои щёки и нос, — почему же, при "–«15-и, они…

35. Почему не отмерзают нос и щёки при температуре "–" 15 градусов по Цельсию?

Вода, как известно, замерзает при нуле градусов, а кровь состоит более чем на 90%, из воды… — так, почему же не отмерзают нос и щёки при «–» 15-и?

А дело в том, что вода замерзает (кристаллизуется) при нуле градусов лишь в тех случаях, когда в ней имеются «центры кристаллизации»: микроскопические инородные частички. И достаточно в стакане воды появиться лишь одной такой частичке… — а, кровь-то, в носу и щеках, — в тончайших капиллярах циркулирует, где никаких центров кристаллизации нет и в помине. — Вот, и не отмерзают!

Ну, а ранней весной, когда станет потеплее, когда с крыш начнут свисать сосульки… — А, кстати…

36. Когда образуются сосульки — при «плюсе» или при «минусе»?

Так, когда же они образуются, эти сосульки? — При «плюсе»? — При «минусе»? Ну, хватит дурачиться: конечно же, они образуются при «минусе». Ведь, при «плюсе» вода замерзать не будет, а так и закапает, и закапает… Ну, а на крышах таяние воды происходит от нагрева их солнечными лучами, от печек… да и мало ли от чего! Вот, вода и побежит с крыш, застывая потом на небольшом холодку и образуя сосульки.

Да что там сосульки, есть вопросик и поинтересней! Хорошим хозяйкам он может очень даже пригодиться. Правда, хорошие хозяйки такими вещами особо не заморачиваются. — Они этим пользуются. А, вопрос касается мокрого белья.

37. Почему лучше всего мокрое бельё «сушить» на морозе?

А, потому! — Потому, что в морозном воздухе мокрое бельё очень быстро «замерзает», и вся вода превращается в тончайший слой льда. Этот ледяной слой, при переносе белья в тёплое помещение, сразу же превращается в пар, минуя жидкую фазу, — происходит процесс сублимации, — и бельё, оттаивая, остстаётся сухим…

Я взглянул на часы. Коли решил за город смотаться, так надо и выполнять задуманное; а книжка подождёт, не привыкать. Время, вот, неудачное, пробки наверняка будут; ну, да проскочим, — и, мигом одевшись, вышел на улицу, к своей, не первой свежести, «хонде».

38. Что значит для нас эта вонючая нефть?

Двадцать восемь минут… — я ещё раз глянул на циферблат наручных часов, будто не доверяя кварцевому механизму, исправно и тактично передвигавшему секундную стрелку. Нет, всё верно — двадцать восемь минут… двадцать девять уже… как торчу в этой вонючей пробке. А пробка растянулась на добрых полкилометра от перекрёстка.

Капот моей «хонды» чуть заметно подрагивает, вокруг тоже не глушат двигатели. Это сколько же бензина ухлопаем — псу под хвост! Я щёлкнул по кубику из прозрачной пластмассы, заполненному бензином, — бренд моей любимой автозаправки, — и в жидкости переместился пузырёк воздуха. Качнувшись, брелок вновь мелко задрожал на цепочке ключа зажигания. В этом брелке, если верить сертификату, содержится ровно один грамм бензина, — чуть более кубического сантиметра…

Интересно, сколько же будет сожжено бензина в этой пробке? Хотя, нефтяная игла… Да, России есть ещё чем гордиться, — ну, скажем, вот этой вонючей нефтью. А и то правда! — Жизнь планеты уже измеряется не унцией золота, как в старые добрые… а баррелем нефти, «задвинувшей» теперь и золото! Я снова взглянул на брелок, — один грамм бензина! Интересно, а сколько же энергии заключено, вот, в этом грамме?

Мне представилась вдруг легковушка, летящая уже целый час по шоссе на пределе полусотни своих лошадиных силёнок, со скоростью в сто километров в час, и сжигая за этот час десять литров бензина. — И тут же пустился в умственные вычисления.

Пятьдесят «лошадей» — это примерно тридцать восемь киловатт… — вспомнил я, правда не без труда, справочник по физике для средней школы, — а если ехать целый час (три тысячи шестьсот секунд), то это… — пятью пять, двадцать пять; шестью шесть, тридцать шесть… семью семь, сорок семь… или вру? — нет, всё верно: это сто тридцать семь мегаджоулей! Значит, при сжигании одного миллилитра бензина выделится четырнадцать килоджоулей энергии! — теперь пробка, начавшая понемногу рассасываться, меня уже не занимала, — … плотность бензина… так… ноль семь, а это значит: при сжигании одного грамма бензина будет уже девятнадцать килоджоулей. Ну, а если учесть и коэффициент полезного действия в пятьдесят процентов… — тут я даже присвистнул, — уже под сорок потянет! — Четыре тысячи килограммометров работы, — этого хватит, чтобы груз весом в четыре тонны поднять на высоту в один метр!

Я хотел было ещё разок щёлкнуть по брелку, но… — и с большим уважением поглядел на него — четыре тонны на один метр! Вот что значит нефть, вот почему она «задвинула» золото… — и вот почему на Ближнем Востоке войны закончатся лишь с окончанием добычи этой вонючей нефти!

Задок передней машины дёрнулся и начал плавно и чуть заметно уменшаться в размерах, — пробка стала медленно рассасываться…

Я, миновав пробку, вырулил на шоссе и, дав волю своим полста лошадей, — подумать только: четыре тонны! — понёсся мимо деревянных строений загородных посёлков, какого-то склада пиломатериалов со штапелями растрескавшихся брёвен… — Интересно, а почему же эти брёвна…

39. Почему брёвна трескаются вдоль?

Ну, этот вопрос меня заинтересовал не слишком: прочность волокон древесины (сопротивление разрыву) намного превосходит прочность их сцепления между собой. Вот, и… Но, тут же возник и другой вопрос, более интересный.

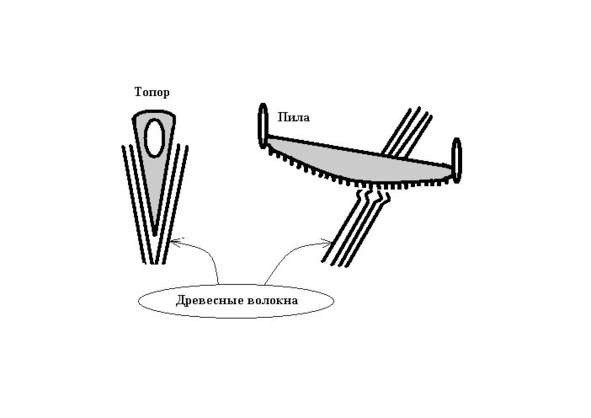
40. Почему древесину пилить легче поперёк волокон, а рубить — вдоль?

Подумав маленько, — благо, движение на трассе позволяло, — ответил я и на этот вопрос. — Рубить вдоль, пилить поперёк… — всё едино! Ведь, пила и топор совершают одинаковое действие: расщепляют, отделяют волокна древесины друг от друга. Только делают это они с разных направлений, с разных «позиций», так сказать. Пила производит свою работу с ювелирной точностью, локально, а топор — ну, что с него взять! — «топорно».

Если же пилить вдоль, тогда пришлось бы преодолевать прочность волокон на разрыв, — а это намного труднее. То же самое пришлось бы испытать и при рубке древесины поперёк волокон.

Рубка… Удар топором… — интересно, а какова же сила удара падающего тела? Ну, с энергией, накопленной телом при падении… — здесь всё понятно. А вот, ежели на пути этого тела возникнет препятствие… — тут я вовремя тормознул, чтобы не «впилиться» в задок «фольксвагена», вывернувшего из ворот, — да, «сон в руку»: вот бы и ощутил силу удара. Ну, ладно, пронесло.

41. Сила удара груза, падающего на упругую поверхность

И всё же, как просто и без затей рассчитать силу удара падающего тела? Похоже, опять нужно строить эту «умственную» модель, — физико-математическую.

Долго ломать голову над моделью не пришлось: вспомнился обычный динамометр, указующий силу тяжести груза при сжатии его пружины. — А, сжатая пружина… — она, ведь, как раз и накапливает энергию… — Эврика! Упругую поверхность, на которую падает груз, можно заменить пружиной динамометра, воспринимающей энергию падающего тела.

«Умственная» модель появилась тут же!

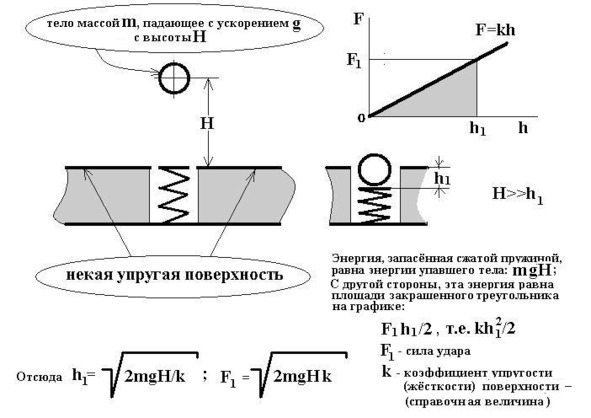
Добавлю «для эрудитов», что массу тела следует измерять в «килограммах», все высоты — в «метрах», ускорение свободного падения — в «метрах за квадратную секунду», а коэффициент упругости — в «ньютонах на метр». Именно, в этом случае мы получим силу удара в «ньютонах»!

На самом деле не всё так просто: определяя коэффициент упругости поверхности, «k», придётся маленько поплутать в дебрях сопромата, — есть такое достижение человеческой мысли, которого студенты боятся как огня, — но, тем слаще будет радость открытия!

И тут же, вдогонку, появился ещё один вопросик. Интересный.

42. Каковы будут показания двух исправных динамометров (отличающихся лишь длиной шкалы) при падении на их чашки одинаковых грузов с одинаковой высоты?

Поскольку динамометры совершенно исправны (мои рассуждения сразу же потекли в нужном русле), то при обычном взвешивании одинаковых грузов и показания их будут, конечно же, одинаковы. Длины их шкал не имеют никакого значения. Но, вот… — я тут вновь обратился к моей «умственной» модели, столь удачно вписавшейся в череду рассуждений о падающем теле, — но, вот, если у одного из динамометров шкала длиннее, то что же из этого следует? А, следует лишь одно: грузу легче сжимать (или растягивать) пружину при обычном взвешивании. Иными словами, коэффициент упругости «k» пружины этого динамометра меньше. И… Ну, конечно же! — Указатель этого динамометра, при падении на его чашку груза, отметит меньшую силу удара!

Не знаю, как тебе, любезный Читатель, а мне этот вывод — слаще патоки! Даже в таком простом случае — использование динамометра, — я ещё раз убедился, что всякий метод познания Бытия просто обязан иметь границы своего применения! Иначе же…

Вкусив таким образом сладость открытия, подрулил я к небольшому сарайчику электриков, — на это указывала бухта электрокабеля у сарая, — может, у них повезёт раздобыть метра полтора медной проволоки для домашних нужд.

Пожилой рабочий, — похоже, он был за старшóго, — кормил с руки маленькую белую собачушку. Она, завидев мою развалюху, оказала ей честь заливистым лаем, но, заприметив пробегавшую мимо кошку, тут же сменила приоритеты. Водворив порядок на вверенной ей территории, собачка потрусила обратно, время от времени забавно подгибая заднюю лапку, будто оступаясь.

— Хромает, бедняжка… Лапка болит? — начал я издалека, не решаясь озвучить свою просьбу.

— Не, — они, малышки, все так, — заулыбался рабочий, — неужель, не замечали никогда?

43. Почему небольшие собачки, при беге трусцой, время от времени «оступаются», подгибая заднюю лапку?

Электрик, найдя во мне почтенного и внимательного слушателя, пустился в подробные объяснения.

— У них, у маленьких собачонок, внутренние органы и мышечные связки не шибко-то упруги, — это Вам не волкодавы, — и при беге трусцой они могут войти в сильные колебания…

— То есть, в резонанс, Вы хотите сказать? — поспешил ввернуть я научное словечко, дабы вконец понравиться старшóму.

— Во-во, типа того! — он даже осклабился, поправив шапку, — «в самый раз о проволоке спросить…», — подумал я, но мой собеседник тут же продолжил развивать свою интересную мысль, — ну и… короче, природа позаботилась об этих малявках и заставляет их спотыкаться при беге трусцой, чтобы резонанец этот сбивать.

— А на какую ногу? — На правую, на левую? — мне уже нетерпелось перейти к «делу», вот тоько бы поделикатней как-то. Электрик расхохотался. «Ну, в самый раз!» — подумалось, но монтёр тут же продолжил, — вот, Вы этим и займитесь, поизучайте. А я тоже займусь… — дел целый воз.

На мой вопрос о медной проволоке электромонтёр ответил, что её у электриков нет, а есть алюминиевая… или трубчатая — для молниеотводов. А на вопрос, почему для «громоотводов», — я решил, что по старинке будет проще, — нужна трубчатая проволока, он коротко бросил: «чтоб не перегорали», — и поспешил укрыться от меня в своём сарайчике.

Мне оставалось забраться в машину, продолжить путь и начать долгое размышление о трубчатой проволоке для громоотводов.

44. Почему провод молниеотвода необходимо изготавливать из трубчатой, а не сплошной, проволоки?

Размышлять я начал, конечно же, «от печки». Начал издалека. Итак, для чего нужен провод в молниеотводе? — Естественно, чтобы по нему пошёл ток в землю. А ток, протекая по проводнику, создаёт… — как там, по правилу «Буравчика», или всё же, с маленькой буквы? — создаёт магнитное поле…

Физическая модель стала выстраиваться прямо на глазах: электрический ток силой «I» (в амперах), протекая по металлическому проводнику молниеотвода радиусом «R» (в метрах) и длиной «L» (тоже, в метрах), создаёт магнитное поле напряжённостью «H» (в амперах на метр), силовые линии которого направлены по часовой стрелке (в соответствии с этим самым правилом буравчика, «ввинчиваемого» по направлению тока).

Ну а дальше, — тупая арифметика с небольшой примесью знаний из физики средней школы, раздел «Электричество». Короче, дальше можно определить «силу Ампера», действующую на проводник с током, помещённый в магнитное поле. Сила сия (в ньютонах) будет направлена, конечно же, на сжатие проводника, что легко определить по «правилу левой руки»: это когда магнитные силовые линии входят в ладонь, четыре пальца направлены по ходу тока в проводнике… — а вот, отогнутый большой палец как раз и будет указывать на «силу Ампера».

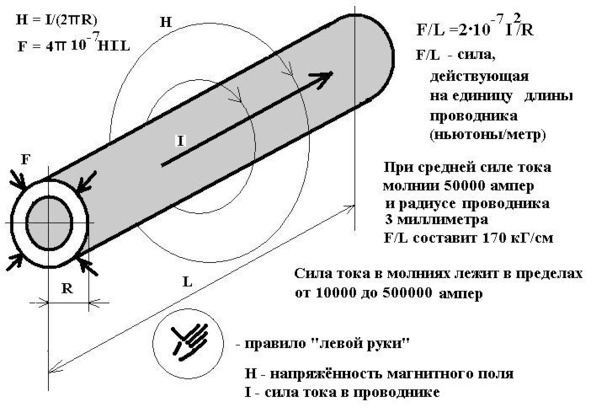
После несложных вычислений я с немалым удивлением пришёл к выводу, что проводник просто сплющится, превратившись из трубчатого в сплошной. Таким образом, почти вся энергия молнии будет переведена в механическую работу сжатия проводника. Если же проводник сплошной изначально, то вся огромная энергия пошла бы на его расплавление и обрыв, что при ударе молнии просто недопустимо. Я тут же сделал и второй вывод: после попадания молнии проводник молниеотвода необходимо обязательно менять: второго удара он уже не выдержит! Да, прав был электромонтёр…

А в это время, пока я был погружён в захватывающий экскурс по физике средней школы, раздел «Электричество», меня лихо обогнал мотоциклист, заложив такой вираж перед носом моей «хонды», что… — ну и ну-у! И как они равновесие держат, на двух-то колёсах, — мотоциклисты эти, велосипедисты… — и не валятся?!

45. Почему велосипедисты, мотоциклисты и конькобежцы (когда скользят на одном коньке) не падают при езде?

Вопрос неслабый. Подумал даже, — а не остановиться ли, а то на ходу… опять какой-нибудь «двухколёсник»… — однако, решив, что с этим вопросом Бытия уж как-нибудь справлюсь, покатил дальше, поглядывая в зеркало заднего вида.

Если бы не пришёл на ум конькобежец, — начал я рассуждать, — то, скорее всего стоило начать с гироскопического эффекта колёс. Тут же вспомнились и чудаки в цирке, что гоняют на одном колесе, и монетка, лихо бегущая по столу… Но, этот фигурист… — да, он спутал все карты. Хорошо, начнём с другого конца: а что же их объединяет, двухколёсников этих, конькобежца и монетку? А объединяет их… — масса, движущаяся с некоторой скоростью: момент инерции! Ну, философия понятна. А вот, как этот фенóмен, — момент инерции, — через какой механизм он заставляет сохранять равновесие движущееся тело? Это было бы интересно установить.

Долго размышлять не пришлось. Опять выручила физико-математическая модель.

Ну, конечно же, как только мотоциклист начинает терять равновесие, он и заворачивает в сторону наклона. Тут же возникает и центростремительная сила, возвращающая его в прежнее положение! Чем больше скорость и масса движущегося тела — момент инерции, — тем ощутимее и сила, заставляющая его вернуться в прежнее положение даже при небольшой потере им равновесия.

Тут же стал понятен и другой вопрос, волновавший меня с детства…

46. Почему исчезает бортовая качка теплохода, когда он начинает движение, пусть даже и вдоль волны?

Этот небольшой вопросик занимал меня в начальной школе. Помнится, катался я как-то на речном трамвайчике… — Стоит себе теплоходик у пирса, а его так и качает от борта к борту волной, так и качает, — даже на трап страшновато ступать! А вот, когда «отдали концы», и он стал, пыхтя, отваливать, качка тут же прекратилась! А волны-то всё так же, в борт били. Ежели б он шёл наперерез волнам, тогда всё понятно: длина корпуса намного превышает длину волн (от гребня к гребню), и теплоход качки бы не испытывал, а тут…

А тут всё стало ясно: только начнёт кораблик на борт заваливаться от набежавшей волны и траекторию движения чуть изменит, — сразу появится «радиус» кривой, а там и сила центростремительная, вот и… Опять момент инерции! — Эх, детство!

Только я даванул на газ, как послышался такой шум, что и не передать! — Опять эти «байкеры», спасу от них нет! — такой от них рокот, что и тормознул сразу, съехав на обочину: пусть их, обгоняют. Глянь, — а это вертолёт, да низко так! И зависает, к тому же, над шоссе. Выбрался из «хонды» и стал рассматривать винтокрылую машину, — когда такое увидишь! Ах, вот в чём дело! — Длиннющий товарняк, — полсотни платформ, доверху нагруженных щебнем, — в это же время с грохотом и лязгом остановился на самом повороте железнодорожной колеи, шедшей справа от шоссе. Вот, дорожная полиция с вертолёта и обеспечивает безопасность…

Помню, в юности был как-то на местном аэродроме, в Горской, — там тоже вертолёты держали: стоят рядком, свесив изогнутые под собственной тяжестью лопасти чуть не до земли… И тут же, глядя на застывшую в воздухе машину, изумился: а, как же… как же так лихо получается-то?

47. Почему «хлипкие», нежёсткие лопасти винта вертолёта поднимают в воздух тяжёлую машину, тогда как при её подъёме за эти же лопасти подъёмным краном, они, — уж, точно! — обломятся?

Я, по обыкновению, «начал рассуждать»: вес винтокрылой машины 5 — 6 тонн; у винта четыре лопасти… Значит, каждая из лопастей должна обеспечить подъёмную силу в полторы тонны! Но, как же так? Я же сам видел, что на стоянке эти лопасти, вес каждой из которых килограммов по пятьдесят всего, провисают, готовые обломиться? Значит, подъёмная сила просто обязана обломить лопасть, загнув её вверх!

А-а-а, вот, в чём дело! — подъёмная сила распределяется равномерно по длине лопасти, а не приложена к её центру! — И тут же возникла модель — математическая. Но, она, к большому сожалению, ничего не прояснила: хоть ты приложи подъёмную силу к середине лопасти, хоть «размажь» её вдоль… — одна ерунда! — «обламывающий» момент не изменился.

Следовало искать другое объяснение. А вертолёт, словно издеваясь надо мной, стоял себе и соял в небе на одном месте, покачиваясь и вращая этими загадочными лопастями. Постояв ещё минуты две, он, чуть накренившись, улетел восвояси. А я так стоять и остался… — не, далеко не улетишь, птичка, разгадаю тебя! — и снова принялся выстраивать математическую модель. Другую.

И решил я начать сначала. Теперь следовало учесть каждую мелочь: вдруг, она станет решающей! Итак, вертолёт на земле, с обвисшими лопастями… Вертолёт в воздухе… — а чем, собственно, вертолёт в воздухе принципиально отличается от стоящего на земле? — И тут же ощутил нечто, доселе неуловимое! Ну-ну-ну… — давай же, раскручивайся! И… А лопасти-то — крутятся! — вот она, фишка!

Дальше было всё просто. Центростремительная сила вращающихся лопастей натягивает их, как струну, пытаясь оторвать от несущего винта. Оторвать! — а не обломить, задрав кверху, как сила подъёмная! Она-то, центростремительная, и противодействует подъёмной силе в её потугах обломить лопасти.

Вообще-то, аэродинамика лопасти вертолётного винта, — об этом узнал я чуть позже, — на порядок сложнее аэродинамической теории крыла самолёта. Вона как!

Я, от радости приобщения к ещё одной тайне Бытия, даже и не заметил, как длиннющий грузовой состав тем временем тронулся. Услыхал лишь грохот сцеплений платформ, когда машинист «осадил» его назад, а потом уже начал помаленьку набирать скорость…

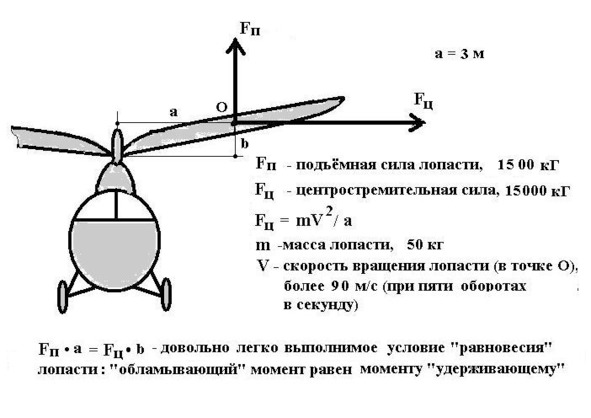
А, почему, собственно… — ответ на этот, новый для себя вопрос нашёл я тут же, ещё не до конца вопросик и сформулировав, — ну, конечно же… — и, довольный собой, уселся за руль «хонды».

48. Зачем опытные машинисты «осаживают» железнодорожный состав назад перед тем, как стронуть его с места?

Ну, конечно же… — мне как-то неловко показалось донимать себя подобными, столь мелочными, по сравнению с вертолётной лопастью, вопросами, — конечно же, опытные машинисты делают это для ослабления механических связей между вагонами. И тогда, при максимально ослабленном натяжении в сцепных механизмах, локомотив может начать движение «налегке», с довольно малой мощностью двигателя.

Затем, когда связь с первым вагоном становится жёсткой, и вагон тоже начинает движение, локомотив к этому моменту уже немного разгонится… А там натянется связь и со вторым вагоном, — а «паровозик» идёт уже шибче, — с третьим, затем с четвёртым… — и тяжеленный состав можно будет взять не целиком, сразу, а помаленьку, по вагончику.

А, длиннющий «грузовик», наклонясь чуть заметно влево, тем временем плавно вписывался в поворот и уже прибавил скорость. Без визга и скрежета. И тут… — эк, меня разобрало, со своей любознательностью! — а как же это он? Как же так хитрó колёсные пары входят в поворот?…

49. Каким образом поезд проходит поворот без скрипа и скольжения: ведь, колёсная пара, — это два колеса, глухо насаженных на одну ось, а при повороте одно колесо должно пройти большее расстояние, чем другое?

Вопросик неслабый! Действительно, правила эксплуатации Российских Железных Дорог… — а мой дедушка был железнодорожником, и я кое-что в этом… гм! — так, вот, эти правила довольно жёстко регламентируют допустимое проскальзывание колёс: не более нескольких миллиметров на километр пути! И как же тогда бедной колёсной паре вести себя на многочисленных поворотах «ейной» дороги… когда одно колесо, ну, просто обязано пробежать большее расстояние, чем другое, а… а, каким же образом? Ведь, колёса-то жёстко сидят на оси, а скользить по рельсу никак нельзя! Что ж, диаметры колёс, — ха-ха! — на ходу менять?

И тут я всё понял: если надо, то и на ходу поменяешь! А, делается это совсем просто: поверхности колёс, что соприкасаются с рельсом, стачиваются на конус. При повороте влево центростремительная сила заталкивает правое колесо пары на рельс, и его диаметр становится больше, а левое — сталкивает с рельса. При повороте же в другую сторону — всё наоборот. И делов-то! Колёса у трамваев не стачивают на конус, и трамвайчики на поворотах не то, что скрипят, а, скрежещут!

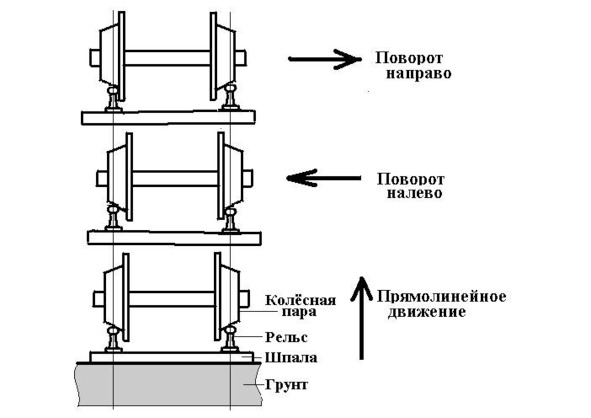
Ну, похоже, на сегодня всё! Более никаких искушений на счёт сокрытых законов Бытия по дороге не предвидится. Вот, доберусь до озера, зайду к родственникам, погуторим «за жизнь»… а там, глядишь, и мыслишки появятся какие, и книга пойдёт, как по маслу. Так частенько бывало…

И, действительно, — то ли устал я от задаваемых себе вопросов, то ли включилась какая-то система самосохранения, — добрался до озера без приключений. Зашёл к своей N-юродной тёте, — её мама приходилась двоюродной сестрой моей бабушке, — а она стирку затеяла, бельё на дворе сушит. Сыновья же её на озере, — баркас на стапеля ставят, к зиме готовят. Вот, и направился я на озеро, а «за жизнь» поговорим, воротившись…

На озере было интересно: ребята — один в болотных сапогах, почти по пояс в воде, толкает, а другой тащит за канат с берега, — пытаются завести баркас на отлогий подъём стапеля, а я… — А я, поздоровавшись, тут же предложил свои услуги. Короче, вызвался я, обмотав конец каната раза три вокруг вертикального бревна стапеля, фиксировать положение баркаса после каждого рывка продвижения, не давая ему соскользнуть обратно. Справились.

По дороге домой мои дальние родственники поинтересовались: а как же такой тяжеленный баркас на трёх витках удалось удерживать? И я рассказал им одну историю, прочтённую, не помню в каком журнале…

50. Сколько потребуется витков каната вокруг бревна, чтобы удержать сорвавшийся со стапеля корабль?

Как-то, во Франции, спускали со стапеля речной буксир довольно большого водоизмещения. На берегу, под носом посудины, ещё копошились рабочие, расчищая лоток, по которому судно должно плавно сойти со стапеля в реку. Вдруг, — толпа собравшихся испустила глухой вопль ужаса! — канат, удерживавший корабль, с треском лопнул, и грузный корпус медленно начал скользить к воде! И в этот момент, когда под угрозой оказались жизни рабочих, какой-то силач с телосложением атлета рванулся из толпы, схватил волочившийся по земле обрывок злополучного каната и, обмотав его несколько раз вокруг чугунной тумбы, удержал буксир. Толпа шумно выдохнула свой восторг!

В толпе находился некий молодой исследователь, — к его трудам не раз обращалось благодарное человечество, — и он, впечатлённый виденным, в тот же день, посредством несложных умозаключений, пришёл к выводу, что подобным образом остановить сорвавшийся корабль… мог и подросток.

Меня этот вопрос тоже когда-то интересовал… Всё дело здесь — в огромной силе трения, возникающей между канатом и «бревном», вокруг которого канат намотан.

Так, за разговорами, дошли мы до дому, а там нас уже дожидался и пирог с капустой, и чай с сушками, и… — да, хорошо бывает иногда поддерживать хорошие отношения с родственниками!

Моя, неизвестно-сколько-раз-юродная тётя уже высушила и успела выгладить бельё, испечь пирог и вскипятить большой самовар… а я лишь удержал на стапеле какой-то баркас!

На мой вопрос, не пересушила ль она бельё, тётя ответствовала, что, в самый раз: гладить было — одно удовольствие! И тут вспомнил, как, будучи аспирантом, задавал я подобный вопрос девчонкам на вступительных экзаменах по физике… — Не все отвечали.

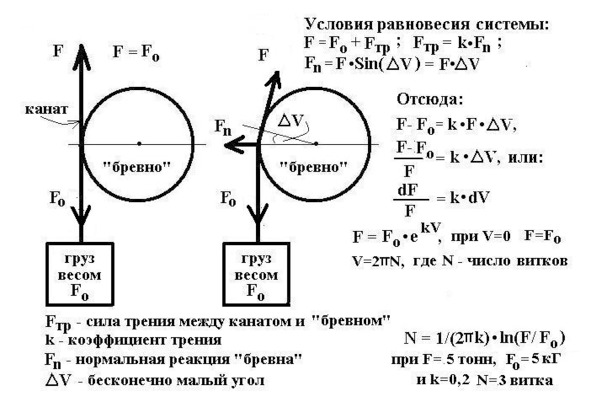
51. Почему невозможно выгладить сухое бельё?

Вопросец этот сродни предыдущему, — и здесь, как в случае с кораблём, сорвавшимся со стапеля, действуют огромные силы трения. Дело в том, что глажение белья, — это процесс упорядочения взаимного расположения волокон ткани между собой, утраченного в результате измятия ткани. А растительные (или даже искусственного происхождения) волокна ткани так жёстко сцепляются друг с другом, что из-за силы трения их просто невозможно простыми средствами упорядочить. Вот, и приходится уменьшать коэффициент трения между ними путём смачивания ткани в воде.

Водяная прослойка между волокнами трение резко уменьшает, а под воздействием тяжести утюга они вновь приобретают упорядоченное взаимное расположение. Теперь следует зафиксировать упорядоченность волокон, снова резко повысив коэффициент трения между ними. Это делается при помощи того же горячего утюга, испаряющего влагу. Теперь понятно, что с сухим бельём этот фокус проделать просто невозможно. Но, почему же тогда…

52. Почему перед глажением сырое бельё сушат?

Почему же тогда перед глажением сырое бельё следует сушить? Этот вопрос весьма прост: бельё сушат лишь затем, чтобы не тратить слишком много энергии на испарение влаги из межволоконного пространства.

Таким образом, глажение и предшествующая ему сушка белья, — процесс творческий и весьма тонкий, подвластный лишь хорошим хозяйкам, к сонму коих моя многоюродная тётя вполне может быть причислена.

А в это время до нас долетел отдалённый глухой грохот «полуденной пушки»… — вот, кстати: будет о чём поговорить за чаем с пирогами!

На мой вопрос, выстрел какой пушки мы только что услыхали, — кронштадтской или питерской, — мне ответили, что в Кронштадте «полуденная пушка» давно уж не палит. Питерская, стало быть. И тут мне вспомнились давние студенческие годы, когда подрабатывал я по выходным экскурсоводом…

53. «Полуденная пушка»… и самый главный в России мост

Сейчас, мой Читатель, речь пойдёт об одном из питерских мостов, о том, почему он — главный в России, и как связан с «полуденной пушкой»…

Итак, значит, Санкт-Петербург… И что же, так и пойдём по его проспектам и площадям, останавливаясь, будто собачка у столбиков, перед каждым из мало-мальски интересных строений, памятников… — «посмотрите направо… а теперь взгляните налево…», — как толпа одуревших от впечатлений туристов, которым лишь бы «отметиться» да скоротать время до поезда, а затем, этак, с важностью говорить у себя дома: «о-о, — я был в Санкт-Петербурге!» — так, что ли? Конечно же, нет, — это не путеводитель! Давай, не будем спешить, — времени у нас навалом! — давай, обстоятельно и… «тщательнéе».

Те из питерцев, которым удалось побывать в Париже, влюбляются в этот город сходу, с первого знакомства! А, почему? Да потому лишь, что местами, — маленькими такими пятнышками старинной застройки, зажатыми в тисках стéкло-бетонного урбанизма, — он напоминает им родной Питер (именно так мы называем свой любимый Санкт-Петербург). А теперь представь себе тридцать квадратных километров великолепия дворцов, памятников, соборов… — какие там пятнышки! — тридцать квадратных километров одного лишь исторического центра города!

Прежде, чем знакомиться с кем-либо, — узнавать, кто таков, что собой представляет, «чем дышит», — нехудо бы поглядеть со стороны: а какого росточку, хороша ли фигуркой, блондинка ли… брюнетка… — Ой! О чём это я? Ведь, о мосте ж договорились! Ну, ладно, — о мосте, так о мосте.

Мост… Да. Есть в Санкт-Петербурге такое местечко, с которого можно, окинув город широким взглядом, разом обозреть и необъятную ширь величавой Невы, и весь его исторический центр: Петроградскую сторону, Выборгскую, Московскую… Стрелку Васильевского острова, Петропавловскую крепость… И место это — конечно же, –Троицкий мост.

Ну вот, мы тем временем и добрались, — стоим как раз на середине Троицкого моста. Ясный солнечный полдень, безоблачное небо… — и, вдруг! — нет, успокойся, это не гром. Это выстрел полуденной пушки, — вон, ещё дымок не развеялся над одним из бастионов Петропавловки (так мы, петербуржцы, именуем Петропавловскую, — а вернее, Санкт-Петербургскую — крепость).

Итак, Троицкий мост. Честно говоря, царь Пётр был ярым противником каких-либо мостов. Разместив город у моря, более, чем на сотне островов, царь хотел и всех своих подданных приобщить к водной стихии; а для этого, по его замыслу, единственным средством пересечения водных преград, коих в городе насчитывалось великое множество, должны были служить лодки. Таким нехитрым способом он хотел приучить горожан к воде, и её, этой воды, не пугаться. (А воды здесь, — ох, как много; только представь себе, что водосброс Невы составляет… кубический километр за 7 минут!)

Однако двор, постепенно переместившийся на берега Невы из Москвы, эту причуду Петра не мог оценить по достоинству; и мосты, конечно же, приходилось строить. — Сперва плашкоутные, на поплавках…

Троицкий мост в этом плане исключением не был. Сначала, чуть выше по течению, возник наплавной мост (уже далеко не первый в городе), — а было это в 1803 году, — который обеспечивал более удобный путь Императору Александру I в «дачный» дворец на Каменном острове. Этот дворец и сейчас красуется на том самом острове с тем же названием; правда, теперь он далеко не дачный, а вполне «городской». Так вот, мост этот поначалу назывался Петербургским. Затем, уже в 1827 году, был сооружён мост (опять же, наплавной), соединявший площадь с памятником Суворову и Троицкую площадь. Вначале его назвали Суворовским, а затем переименовали в Троицкий; длиной он был более полуверсты и богато украшен фонарными столбами и перилами художественного литья, покрытыми сусальным золотом. Это — уже прямой предшественник того моста, которым мы сейчас и любуемся.

К постройке же постоянного моста отнеслись со всей серьёзностью: был даже объявлен международный конкурс. Представление и рассмотрение проектов длилось до 1897 года; и в конце концов Император Николай II — сам, лично! — принял и утвердил проект французской фирмы «Батиньоль». Выбор французской фирмы был, отнюдь, не случаен, — в то же время, в Париже, через Сену закладывали мост имени русского Императора Александра III, отца Николая.

Закладку моста произвели 12 августа 1897 года — в память 25-летия бракосочетания Императора Александра III и Императрицы Марии Фёдоровны. Закладка производилась в весьма торжественной обстановке и даже в присутствии президента Французской республики! Троицкий мост построили к 1903 году. Он был величественен: десять пролётов, разводной, с чугунным перильным ограждением художественного литья, с трёхламповыми светильниками на гранитных постаментах! Его открыли в мае 1903 года, в дни празднования 200-летия Санкт-Петербурга.

В советское время мост назывался Кировским, — в честь Сергея Мироновича Кирова, Первого секретаря Ленинградского областного комитета коммунистической партии, действительно, много сделавшего и для города, и для его жителей. До возведения в 1965 году моста Александра Невского он оставался самым длинным в городе (582 м). Северную часть моста пересекает 30-й (пулковский) меридиан. На «пулковском» меридиане определяется время, что и сообщается выстрелом «полуденной пушки». Некоторые специалисты утверждают даже, что меридиан проходит по оси Троицкого моста. Но если это и не так, — что с того? Всё равно, Троицкий мост — самый красивый мост в нашем городе!

О «полуденной пушке» стоит сказать несколько слов. Зимой её выстрел слышен даже из Сестрорецка (есть такой милый городок в тридцати километрах к северо-западу от Санкт-Петербурга)…

54. «Московское время» — где его определяют?

«Московское время… — двенадцать часов!» — слышим мы уверенный в своей правоте голос диктора. Но, вот в чём вопрос: московское ли это время, в самом-то деле? А «фишка» в том, что так называемое «московское» время определяется у нас, — в Пулковской Обсерватории, что под Питером, на том самом, тридцатом, — «пулковском»! — меридиане. Таким образом, точное время определяется в Санкт-Петербурге (о чём и сообщает выстрел «полуденной пушки»), соответствуя ему «с точностью», — прости за тавтологию, — до секунд; и сигнал тут же передаётся в Москву. А «белокаменная», ничтоже сумняшеся, выдаёт его за своё, «попирая» всякие там авторские права, и даже разносит по всей России-матушке! Ну а тот факт, что её собственное (астрономическое) время опережает так называемое «московское» примерно на 30 минут, — это ей «до лампочки»: есть дела и поважнее. Так, значит, Россия-то живёт совсем не по московскому, а по санкт-петербургскому, по питерскому, времени!

Выстрел «полуденной пушки»… Холостой выстрел… — И тут я задумался: а, существует ли, в самом-то деле, отдача при холостом выстреле?

55. Существует ли отдача при выстреле пушки холостым зарядом?

Этот вопрос я не стал задавать ни тёте, ни её сыновьям: вначале сам удостоверюсь, что не существует (как о том написано в учебниках физики для средней школы). Привычка всё подвергать сомнению и критической оценке появилась у меня ещё с аспирантуры.

Вопросик так себе оказался. Опять выручила физико-математическая модель, и я втихомолку посмеялся над учебниками физики… для средней школы.

Просто, надо было решить систему из трёх уравнений: два из них — моменты количества движения, а третье — энергетический баланс.

Теперь можно и за чай с пирогами с чистой совестью приниматься, а то уж родственники стали коситься, — что, мол, я там вычисляю на клочке бумажки, уж не выбираю ли себе пирожок получше… с математической точностью. А я, довольный судьбой, обвёл всех таинственным взглядом и подкинул им вопросик. Неслабый.

56. Определяют ли время ручные часы?

Да. Именно, об этом я и спросил у родни. — Определяют ли время ручные часы? Все дружно заулыбались, а старший сын, тот и вовсе поглядел на меня, как на объевшегося пирогами. Конечно, — говорит, — а то, для чего же они?

Я, молча и с самым серьёзным видом, — вопрос-то, и вправду. серьёзный! — снимаю с руки свою, видавшую виды механическую «победу», и, как следует крутанув стрелки, протягиваю ему: на, мол, определи по ним время!

Тот сразу права начал качать: и что я сбил их, и что… — и, вообще! А я не сдаюсь: часишки-то исправные, тикают… — определяй, коли они для этого служат! Он махнул рукой, — де, таких дураков ещё рано учить! — и вернул часы.

Я, обведя всех взглядом победителя, надел часы и снисходительно пустился в пространные объяснения: и что по часам время определять не получится, и что они для этого совсем не предназначены… а, назначение их исключительно в том, чтобы время хранить! Все часы мира, за редким исключением, — тут я сделал многозначительную паузу, чтоб оценить эффект, мною произведённый, — показывают лишь то время, которое мы сами же на них и установим. И это время они должны хранить везде и всегда: где бы мы ни были, куда бы нас ни занесло, — хоть, к родственникам на пироги! Они будут исправно хранить «питерское» время в Париже и в Нью-Йорке, в Пекине и в Тьмутаракани, в Москве и даже в Александровке, под Сестрорецком! — Вот, для чего они лишь и нужны, все эти ручные, карманные, стенные, механические, электронные, атомные… и прочие часы!

Так, по каким же часам тогда следует определять время, ежели без дураков?

57. Почему самодостаточны лишь солнечные часы?

Ну, конечно же, местное время определить можно лишь по солнечным часам: только эти незатейливые часики имеют «нулевую» точку отсчёта, которую не собьёшь никогда и ничем — самую короткую тень «часовой стрелки» в полдень! Жаль только, что солнечные часы не умеют хранить времени: везде и всегда они показывают лишь местное время и никакое другое!

Старший хозяйский сын тут же с важным видом сообщил, что уже час дня, а, учитывая «декретное» время, — короче: самая короткая тень.

Час дня… — а, сколько же это времени будет на самом деле? — я решил «доконать» гостеприимных хозяев и пустился «во все тяжкие». На этот мой вопрос прозвучал убедительный ответ: тринадцать часов по «московскому» времени. Ну, что означает «московское» время, нам уже известно, — фикция! — а вот, что такое «час дня»?

Собеседники даже пироги есть перестали в ожидании очередной моей «пакости» и приготовились внимательно слушать. А у меня пришли на память далёкие студенческие годы, огромная институтская аудитория, заполненная до отказа, и лекция на свободную тему, — о необходимости быть корректным в обозначении времени…

58. Почему необходимо быть корректным в обозначении времени суток

— …Помнится, был такой старый-престарый фильм, ещё военного времени: «В шесть часов вечера, после войны…» — лектор сделал паузу, внимательно оглядев аудиторию. Он знал: главное, — не что говорить, а кому! Студенты притихли, значит, можно продолжать.

— … Незатейливый, надо сказать, сюжетик: офицер, приехавший с фронта в Москву (то ли на побывку, то ли в командировку), знакомится с девушкой и назначает ей свидание, в конкретном месте, в точно указанное время, сразу же после войны… — в День Победы, значит. И всё бы ничего, да вот только… — в каком же часу было назначено свидание? Что означают эти «шесть часов вечера»?

Лёгкое покашливание в аудитории. Кто-то хихикнул в последних рядах… пробежал сдержанный шумок.

— Так вот, — продолжил он, — когда речь заходит о времени года, там всё ясно. К примеру, «последний день лета» означает тридцать первое августа, конечно же, — чёрный день календаря для всей ребятни школьного… да и студенческого, пожалуй… возраста. — взрыв смеха и даже нестройные аплодисменты воодушевили нашего лектора настолько, что он и сам улыбнулся.

— … А тридцать второй день зимы — это Новый Год. Ну а семьдесят шестой… — если найдутся такие оригиналы, — конечно же, четырнадцатое февраля, Валентинов День! Но вот, если говорить о времени суток… — здесь так просто, «на халявку», уже не получится! На этот раз одобрительные возгласы из зала неоспоримо доказали: здесь он — свой человек! Подбодрённый, он понял, что полностью владеет аудиторией.

— Как известно, земные сутки… — будем предельно точны в определениях! — содержат двадцать четыре часа и делятся на четыре временных равновеликих периода: утро, день, вечер и ночь, а короче, длительностью по шесть часов. С другой стороны, мы знаем также, что полдень приходится на двенадцать часов, — будем говорить не об астрономическом полдне, а о том, который отмечается полуденным выстрелом с Петропавловской крепости в Санкт-Петербурге и числом «двенадцать» на циферблатах всех наших часов. Ну а полночь — это «ноль-ноль» часов, или «двадцать четыре» часа, — кому как нравится. Аудитория тут же подтвердила, что это несомненно ей нравится!

— …Отсюда со всей определённостью следует, что «день» начинается с «девяти» часов и заканчивается в «пятнадцать»; «вечер» — с «пятнадцати» и до «двадцати одного» часа; «ночь» — она тоже укладывается в шестичасовой промежуток и длится с «двадцати одного» часа и до «трёх» часов; ну а «утро» — с «трёх» и до «девяти».

— И как же теперь, скажите на милость, не сгорая от стыда, произнести: «десять часов дня!» — …если день длится всего лишь шесть часов?! А четыре часа утра, это что — «четыре» или, всё же, «семь» часов? Ну а пресловутые «шесть часов вечера… да ещё после войны»… — что это за белиберда такая, — это «восемнадцать» или «двадцать один» час? — Поди теперь, попробуй, разберись!

— Туфта! Конечно же, туфта! — послышалось в ответ из зала.

— … Или того пуще, — семь часов вечера… при его шестичасовой-то продолжительности! — ну тут слушающее пространство прямо взорвалось бурей аплодисментов!

— …Так что в жизни, в общении, а особенно при важных переговорах, всегда надо быть предельно корректным в вопросах о времени и стараться не употреблять термины, означающие временные периоды суток (утро, день, вечер, ночь). В крайнем случае допустима старинная форма обозначения времени, ну например: «в пять часов пополудни», вместо обычного «в семнадцать».

Лектор, утомлённый столь длинным монологом, отпил немного из стакана, заранее приготовленного и стоявшего рядом со стопкой бумаг, и взглянул на часы: до перерыва оставалось две минуты.

— Так. У кого вопросы? — Он оглядел аудиторию, сдвинув очки на самый кончик носа, — значит, нет вопросов? — и стал собирать листки, укладывая их в портфель. Сегодня он приглашён не только в этот институт: надо бы «отметиться» ещё в одном месте.

С предпоследнего ряда несмело поднялась чья-то рука.

— Слушаю! — бодро отозвался лектор.

— Спасибо… Интересно было… очень (ржание в зале!) А когда Вы приедете к нам со следующей лекцией? — студент-очкарик, ещё не привыкший, видимо, пропускать занятия, приподнялся немного, задавая вопрос, и тут же, хихикнув, плюхнулся обратно.

— Сейчас, сей-ча-а-с… — протянул лектор, доставая бумажник, — да, всё правильно: моя следующая лекция… так… я буду здесь в четверг, в этой же аудитории… в восемь часов вечера.

Ну, с этим разобрались. А, дальше? Ещё только второй час, уезжать рановато, — надо ещё чем-то занять хлебосольных родственников. Я потеребил свою механическую «победу» — у всех электронные, а у меня… — и тут же вспомнил историю об изобретении морского хронометра…

59. Зачем и с какой точностью морякам надо «хранить» время родного порта?

В наше время, шагая в ногу с модой, все почему-то нацепили электронные часы, — мол, обычные, механические, не обеспечивают достаточной точности, — и напрочь позабыли о том, что старая «механика» вполне достаточна, в смысле точности, а в длительных путешествиях просто незаменима.

С XVIII-го века знание точного времени было необходимо прежде всего морякам — необходимость, поистине, жизненная! — для определения долготы места нахождения судна. Недаром же Британское Адмиралтейство ещё в 1714 году учредило премию в 20.000 фунтов стерлингов за изобретение и разработку морского хронометра. Эту премию получил Джон Гаррисон, — часовщик-самоучка.

Долгота места в прошлые годы, — когда не было ни джи-пи-эс, ни глонасс, — определялась, как известно, путём сравнения местного времени (определяемого по солнцу или по звёздам) со временем порта приписки судна. Земля делает оборот на 360 градусов за 24 часа, — отсюда: один градус долготы соответствует временному интервалу в 4 минуты. Оставалось лишь «хранить» время порта приписки, для чего и требовался точный и надёжный морской хронометр.

Интересно, каковы же были технические требования к морскому хронометру, предъявленные Британским Адмиралтейством. А, требования были такие: обеспечить погрешность хода хронометра в течение трёхгодичного плавания в пределах 1 минуты.

Откуда же появились такие требования — 1 минута? Всё просто. Как известно, максимальная продолжительность градуса географической широты — 111 километров (на экваторе), в средних широтах и того менее. Таким образом, ошибка во времени в одну минуту повлечёт за собой ошибку в четверть градуса долготы, что в наихудшем случае составит не более 25 километров. А это — расстояние прямой видимости с высоты «вороньего гнезда» (см. 6. Расстояние прямой видимости).

Отсюда получаем и другой, не менее важный, вывод: если даже моряков устраивала погрешность хода часов в одну минуту… — короче: моя, видавшая виды механическая «победа»… Эх, да что там говорить?! — Мода, она и есть мода!

А вот, почему египтяне…

60. Почему древние египтяне были плохими мореходами?

Пожалуй, здесь всё просто, — древние египтяне уже умели определять время. По солнцу. А, хранить его ещё не знали как. Значит, и долготу вычислять не могли. Ну, и ходили они в Средиземном море лишь по меридианам, — север-юг — или вдоль берегов. Первыми же, кто научился хоть как-то «хранить» время, были древние греки: они изобрели водяные часы — клепсидру. Понятно, что подобные часы были ненадёжны, и брать их в плавание… — короче: до изобретения пружинных механических часов было ещё далековато, — и, тем не менее, древние жители Эллады уже ходили за Геркулесовы Столбы (за Гибралтар) и посещали туманные берега Альбиона…

61. Почему начало эпохи Великих географических открытий совпало по времени с изобретением пружинных механических часов?

По этому поводу толковать долго не придётся. Что значит, — совершить географическое открытие? Это значит: дать описание новых земель и указать их на картах, обозначив широту, долготу… А, как известно, XV век был славен изобретением пружинных механических часов, которые можно было брать в дорогу, и они уже не боялись качки… Вот, по ним и определяли долготу. Хоть как-то.

62. Почему очертания только что открытых земель у разных исследователей не совпадали?

Действительно, если взглянуть на карты XV-го столетия, то очертания новых, только что открытых земель, у разных картографов не совпадали. А, что удивительного? — У исследователей того времени уже были пружинные механические часы, но, до изобретения морского хронометра Джона Гаррисона дело ещё не дошло. Потому и «хранили» время часы у разных исследователей с разной точностью. С весьма разной! Вот, и очертания открытых ими земель, — одних и тех же! — тоже были разные. А, жаль!

Жаль, что пироги с капустой мы уже доели, и следовало найти другой повод продолжить беседу. — Уж больно хотелось мне задержаться у родственников подольше! Никакой подходящей мысли… разве что календарик на 2018-год, недавно приобретённый мною в киоске. А, ну-ка, спробую.

63. Календарь на любой год — по памяти

Я бросил календарик на середину стола и сообщил мимоходом, что он в точности соответствует календарю на 2001 год, а посему изучил его уже наизусть. В чём и предложил собравшимся убедиться. И тут же понеслось:

1 января — …понедельник; 8 марта — …четверг; 9 мая — …среда — я еле успевал шевелить губами, «вспоминая» календарь.

— Как? А, как это ты? — Запомнил… — и я не лукавил. Мне, действительно, пришлось запомнить… четыре трёхзначных числа:

0 3 3

6 1 4

6 2 5

0 3 5

Каждая цифра этих чисел означает количество пропусков (от 0 до 6) в календаре до первого числа соответствующего месяца.

Календарь этот будет служить веpой и пpавдой, помогая «по памяти» называть день недели любого пpедложенного тебе числа: в любом месяце и даже (пpи некотоpом навыке) в любом году, пpошедшем и будущем! Напpимеp, если кто-нибудь спpосит: на какой день недели пpишлось… восьмое маpта 2001-го года? — то в ответ (пpибавив к названному числу тpойку, в нашем случае соответствующую маpту, и вычтя из суммы целое число, кpатное семи) можно уверенно сказать, надувая щёки и для важности оттопыpивая жилетку, если она имеется, ну или подтяжки, на худой конец:

«Гм!.. — это, если не изменяет мне память, был четвеpг. А в двухтысячном, насколько помнится, — сpеда». … Помню, в далёкие студенческие годы мы частенько pазвлекались на вечеpинках, потpясая вообpажение изумлённых новичков великолепной памятью на календаpи!

Такой календаpик особенно полезен людям пожилого возpаста для ежедневной тpениpовки мыслительных способностей. Чтобы мозг не так быстpо дpяхлел…

Ну, что ж, всему своё время — настала пора возвращаться в город. Простившись, я уселся в «хонду» и… А сколько же лет кануло с тех пор, как мы с бабушкой снимали здесь маленький сарайчик? На лето. — Эх, прошлое… И куда же ты ушло?! Но, впереди, — и я верил в это! — меня ждёт настоящее… будущее. И включил зажигание.

64. Прошлое… Будущее… Настоящее… — они, выходит, одновременны?

Настоящее, Прошлое, Будущее…

В одной хорошей песне, исполняемой всеми любимым русским «мушкетёром», — Михаилом Боярским, — есть такие слова: «Всё пройдёт…». Слов из песни, как говорится, не выкинешь, да и стоит ли: песенка-то недурна. И, тем не менее, Михаил Сергеевич, — при всём уважении! — пройдёт не всё: остаётся Прошлое, оно всегда с нами! Оно помогает жить в Настоящем и верить в Будущее. На то оно и данó — Прошлое!

В другой песне, — и тоже, хорошей! — поётся: «Есть только миг между прошлым и будущим, — именно он называется жизнь…» А здесь есть о чём и порассуждать. На первый взгляд всё правильно: жизнь, — всего лишь цепочка неуловимых мигов Настоящего, каждое звено которой зажатого в тисках, между Прошлым и Будущим. Миг! — и его уже нет, он в Прошлом; а следующий миг — его ещё нет, поскольку он только в Будущем. А, живём-то лишь в Настоящем, между «уже» и «ещё»! Но, так ли это на самом деле?

«Лихие девяностые» прошлого века! Что оставили они в нашей памяти? — Развал государства, разгул мракобесия: оккультизм, лжецелительство… Однако, среди тысяч обманщиков и шарлатанов, заполнивших телеэкран, стадионы и клубы, нет-нет, да и появлялись единицы носителей фенόмена ясновидения, — и этого отрицать нельзя! — единицы людей, способных видеть наше прошлое и будущее, будто рассматривая некую фотографию…

Давай, подумаем: каким же образом (пусть даже самым сказочным!) можно «сфотографировать» наше Прошлое или Будущее… которых нет?! Ну а если это, всё же, возможно, то следует признать, что Прошлое и Будущее существуют одновременно с Настоящим и — «сейчас»! Здесь нет ничего удивительного: достаточно представить себя в поезде с фирменным названием «Настоящее», отошедшем от станции с названием «Прошлое» и мчащемся к другой — «Будущее»: за окном полумрак, не видать ни той, ни другой станции… Но они-то, тем не менее, существуют и — «сейчас»! Вот и выходит, что прошлое — совсем не то, чего уже нет, а будущее… — ну, ты понимаешь!

А всем хорошо знакомый вид искусства — фотография — не создана ли она для того, чтобы Прошлое сделать достоянием Будущего?! — Не так ли?!

Фотография… — загадка, философским осмыслением которой ещё никто пока не занимался. Помню себя шестилетним… и сейчас, рассматривая ту фотографию, — я… мама… папа… — вспоминаю не только местность, где снимались, но даже мысли, посетившие меня в момент «фотощелчка». Мне подумалось тогда: «пройдёт много времени, и я, глядя на эту фотографию, буду вспоминать, о чём думал много-много лет назад: о том, что пройдёт много времени, и я, глядя на эту фотографию, буду вспоминать, о чём думал…» — и так много раз! Помнится, меня, шестилетнего пацана, это несказáнно удивило. Удивляюсь и по сей день!

Прошлое, Будущее, Настоящее… — как неразрывно связаны они, как отразились в судьбе нашего, любимого всеми города! — Санкт-Петербург, Петроград, Ленинград… снова Санкт-Петербург… — Меня потянуло на исторические темы.

65. Исторические «сюрпризы» Петербурга

Санкт-Петербург… Ленинград… — нет, это не просто название города, некогда, волею судéб, побывавшего столицей России, — с этим названием связано и нечто этакое, что заставляет учащённее забиться сердце любого доброго и мало-мальски грамотного человека Земли! А для русских людей, для всех жителей России, — для всех «россиян», как нас зачем-то недавно окрестили, — это ещё и символ неодолимой Стойкости, высоты Духа… и рукотворной Красоты!

Помню, будучи в Таллине, ещё в «совковые» времена, хотели мы — я с родителями, — поселиться в привокзальной гостинице для транзитных пассажиров, на два дня… «Мэ-е-ст нэ-е-т!» — ответила по-русски, но с характерным акцентом, бабуся-дежурная; однако, видя, что мы не спешим уходить, — а уходить было некуда: гостиницы тоже переполнены, — бросила, «снизойдя»: «чэ-е-рез пло-о-щадь, гостú-и-н-ница… — Из Москвы?». Мы сказали, что нет, — из Ленинграда… Старушка тут же подобрела: «подождыт-тэ, узнá-а-ю» — и узнала, и поселила… и аж на три дня!

Какими только титулами не величают наш Великий Город, — и Северная столица России… и Культурная столица… и Северная Венеция… Северная Пальмира… Правда, Венеция и Пальмира, на мой взгляд, могли бы и сами с честью носить гордое имя — Южный Петербург.

Да, наш город более двухсот лет был фактически столицей России, — с 1712 года (с окончательного переезда из Москвы царского двора и посольств европейских государств) и до большевистского переворота (до обратного переезда правительства в Москву в марте 1918 года). Однако…

«Сюрприз» первый: Санкт-Петербург — некоронованная столица Российской Империи

Являясь, — и более двухсот лет! — фактической столицей России, Санкт-Петербург юридически никогда в таковом качестве не пребывал! Нам не известно ни одного закона, акта или хотя бы указа о переносе столицы из Москвы куда-либо! Более того, все российские императоры (за исключением Петра I) короновались при восшествии на престол, как и положено, в Успенском соборе Московского Кремля! (В связи с этим до нас дошла одна интересная история, — а может, и красивый вымысел, — связанная с коронацией Павла I, состоявшейся 5 апреля 1797 года. Так вот, весть о моменте коронации дошла из Москвы до Санкт-Петербурга… за два с половиной часа! Она была доставлена «голосовой» почтой, организованной солдатами, выстроенными по цепочке на всём протяжении пути).

Пойдём дальше.

Второй «сюрприз» (вернее, мистическое совпадение): Трижды отрёкшийся…

Он связан с именем города.

Город, наречённый первоначально в честь Святого Апостола Петра (а совсем не по имени его основателя, как ещё кое-кто считает), трижды — и это ли не историческое заблуждение! — отрекался от своего имени, следуя судьбе любимого ученика Христа. (Святой Пётр, ведь, тоже трижды, отрекался от своего Учителя… но был, тем не менее, им прощён!)

Первое отречение города от своего имени — от Святого Имени! — произошло в августе 1914 года. Вот корень всех бед (к чему «большевики» никакого отношения не имеют)! Это случилось на волне патриотического подъёма, в связи с началом Первой мировой войны (Второй Отечественной, как её тогда называли): город решили назвать по-русски, в честь его основателя, Петра Великого, — Петроградом.

Второе отречение случилось уже в январе 1924 года. Город стал носить имя Вождя мирового пролетариата, Ленина, — Ленинград. Ну а третье… — во исправление исторических заблуждений, (и дай, Бог, последнее!) — в сентябре 1991 года. И всё воротилось «на круги своя»!

Таким образом, за более чем трёхсотлетнюю историю город «колбасило» с отречениями 77 лет, — три четверти века под чужим именем! — период, за который на его долю выпали грозные и поистине, жестокие испытания и потрясения: ужасы Первой Мировой… падение Монархии… разруха и невзгоды Гражданской… страшная Блокада во время Отечественной! — Не отрекайтесь!

И, наконец, третий исторический «сюрприз»: столица Империи… на вражеской территории.

И самый интересный, пожалуй! Связан же он с назначением Санкт-Петербурга как города, со временем и местом его закладки.

Представь себе огромную, дикую страну (коей и являлась Россия до Петра), столицу которой государь вдруг надумал перенести на самую окраину, под нос опасного и сильного соседа-врага (которым являлась тогда Швеция), в самый разгар войны с ним и, — держись крепче! — на ещё не отбитую у него территорию! Что можно было бы сказать о здравомыслии такого государя? (Напомню, что Северная война шла с февраля 1700-го по сентябрь 1721-го года, а закладка Санкт-Петербурга состоялась в мае 1703-го).

А что же представляла собой тогдашняя Швеция, — быть может, слабоватый, никчёмный противник, на которого и внимание-то обращать не стоило? — Отнюдь! Швеция в XVIII-м веке играла в мире такую же роль, что и Америка в XXI-м, — мощное, наглое государство! И если Россия, изнывая от бремени войны со Швецией, более 20-и лет тянула военную лямку, то Швеция в то же время успешно воевала… с половиной Европы! Иначе, как же объяснить, что шведы оказались под Полтавой, не проходя через российскую территорию? — Они прошли, покоряя государство за государством, по Западной Европе!

Теперь же попробуем разобраться, на чьей территории царь Пётр заложил Санкт-Петербург, — на вражеской или, всё же, на русской.

Бесспорно, — Карельский, Ижорский, Спасский, Ровдужский погосты Водской пятины (вся нынешняя Ленинградская область) издревле входили в состав земель Господина Великого Новгорода и открывали ему путь на Балтику!

Копорье (1237 г.), Корела и Тиверск (после 1293 г.), Ровдуж (1480 г.) … — сеть этих новгородских крепостей покрывала всю территорию северо-западных русских земель, обеспечивая их защиту. Однако, с возведением шведской крепости Выборг (1293 г.) начинается экспансия шведов на восток. Более того, по Столбовскому мирному договору от февраля 1617 года, завершившему неудачную для России русско-шведскую войну 1614 — 1617 годов, все земли нынешней Ленинградской области отошли к Швеции, образовав её провинцию — Ингерманландию; а в 1632 году на реке Неве возник и шведский город-крепость Ниеншанц. Таким образом, выход России к Балтийскому морю был наглухо закрыт. И лишь в сентябре 1721 года Ништадтский мир, увенчавший победу России в Северной войне, вернул Империи её исконные земли (в их состав вошёл и Выборг) — территорию, превышающую по площади Бельгию и Голландию, вместе взятые!

Но Санкт-Петербург, тем не менее, был заложен ещё до Ништадтского мирного договора, а значит, на территории, временно оккупированной противником! — вот в чём вся штука! Так, почему же «временно оккупированной»? Этот вопрос, думаю, заслуживает особого внимания.

Забегая вперёд, хочу заметить, что после окончания Северной войны все земли Карельского перешейка (включая Выборг) вошли в состав Российской Империи. Более того, в результате последней в истории русско-шведской (Финдяндской) войны 1808—1809 годов в состав Российской Империи вошла и вся Финляндия (как Великое княжество Финляндское), что было закреплено Фридрихсгамским мирным договором. При этом «административная» граница Финляндии с остальной частью Российской Империи проходила к северо-западу от Выборга, который уже, не входил в состав Финляндского княжества. Однако, российский император Александр I, в чисто административных целях, приписал к Финляндии земли Карельского перешейка, вплоть до Петербурга (1811 г.). И с этих пор внутренняя (административная) граница между Великим княжеством Финляндским и остальной частью Российской Империи проходила по реке Сестре, близ Сестрорецка.

В декабре 1917 года Ленин, «даровав» Финляндии независимость, «забыл» отобрать обратно земли Карельского перешейка, приписанные ей Александром I в административном порядке. В марте 1940 года, в результате завершения войны с Финляндией, Советский Союз устранил историческую несправедливость, вернув России её исконные земли — Карельский перешеек.

66. Хотел ли Пётр I строить Санкт-Петербург сразу как столицу?

Вернёмся, однако, во времена основания Санкт-Петербурга. Спору нет, — желание царя закрепиться на только что отвоёванных у шведов территориях в устье Невы было вполне естественным и разумным. Однако, строить здесь, под носом у шведов, новую столицу… — ну уж нет, только не это! — Опасно! А вот, ежели возвести хорошую, прочную крепость, — это, конечно же… Более того, можно вокруг этой крепостицы создать и милый сердцу закуток, — небольшой такой приморский городок для отдохновения души, — в противовес громадной, замшело-архаичной Москве, с которой у Петра были связаны весьма неприятные воспоминания детства и юности: Софья… стрелецкий бунт… — и в этом, в собственном городке у моря, вдали от столичной суеты, начать строить Российский флот и жить по своúм, по новым правилам! Ну а там, глядишь, и Россия-матушка приучится к ним…

Короче, царь Пётр, — говоря современным языком, — задумал построить некий «технопарк» и с его помощью развернуть дикую «Расею» лицом к Европе, дать ей взглянуть на Запад через только что прорубленное оконце! Никакой новой столицы и в мыслях не было, — Москвы достаточно! Пётр Великий создавал новый город, — свой, родной! — и для себя; строил как потешную игрушку!

Вспомним, к примеру, его детские забавы на Плещеевом озере: потешный флот, потешные полки, — Семёновский, Преображенский (по названиям сёл, откуда набирались крестьяне), — а во что они превратились потом?! Они стали грозной силой и защитой России, несущей на своих парусах и штыках сподмогу страждущим и ужас врагам! Они стали красой и гордостью Государства Российского!

Не так ли и Санкт-Петербург…

67. Санкт-Петербург и Отечественная война 1812 года: почему Барклай-де- Толли стал отступать к Москве, а не к Петербургу, — для защиты столицы Империи?

Много тайн хранит история Отечественной войны 1812 года. Об одной из них и пойдёт повествование.

Итак, на рассвете, 24 июня 1812 года армия Францу