Физическая и коллоидная химия. Лабораторный практикум

Учебное пособие

Под общей редакцией профессора С. Л. Белопухова

---

ebooks@prospekt.org

Информация о книге

УДК 541.1(075.8)

ББК 24.5я73

Ф48

Авторы:

Белопухов С. Л. — кандидат химических наук, доктор сельскохозяйственных наук, профессор, заведующий кафедрой физической и органической химии Российского государственного аграрного университета — МСХА имени К. А. Тимирязева, заслуженный изобретатель Российской Федерации, лауреат премии Правительства Российской Федерации в области науки и техники;

Немировская И. Б. — кандидат химических наук, доцент кафедры физической и органической химии Российского государственного аграрного университета — МСХА имени К. А. Тимирязева;

Старых С. Э. — кандидат биологических наук, доцент кафедры физической и органической химии Российского государственного аграрного университета — МСХА имени К. А. Тимирязева;

Семко В. Т. — кандидат технических наук, доцент кафедры физической и органической химии Российского государственного аграрного университета — МСХА имени К. А. Тимирязева;

Шнее Т. В. — кандидат биологических наук, доцент кафедры физической и органической химии Российского государственного аграрного университета — МСХА имени К. А. Тимирязева.

Под общей редакцией кандидата химических наук, доктора сельскохозяйственных наук, профессора С. Л. Белопухова.

В учебном пособии изложены основы термохимии, химической кинетики, электрохимии, свойств растворов электролитов и буферных систем, потенциометрического титрования, электрической проводимости и ее использования для анализа растворов, химии коллоидных систем и высокомолекулярных соединений. В пособии для удобства студентов представлены правила работы в лабораторном практикуме, словарь основных терминов.

УДК 541.1(075.8)

ББК 24.5я73

© Коллектив авторов, 2015

© ООО «Проспект», 2015

1. Термохимия. Закон Гесса.
Определение тепловых эффектов химических реакций, теплотворной способности кормов. Определение энтропии реакции

Область науки, изучающая отношение между теплотой и работой, получила название термодинамики. Термодинамика изучает законы превращения энергии, законы перехода одного вида энергии в другой. Превращения энергии подчиняются первому, второму и третьему началам (законам) термодинамики. Причем если первое начало формирует законы взаимного перехода, то второе и третье определяют направленность превращения энергии.

Первое начало термодинамики представляет собой всеобщий закон природы — закон сохранения энергии, открытый М. В. Ломоносовым в 1758 году. Затем он нашел свое развитие в трудах таких ученых, как Г. И. Гесс, Д. Джоуль, Р. Майер, Г. Гельмгольц. Наиболее общей формулировкой закона сохранения энергии является следующая:

Общая сумма энергии материальной системы остается постоянной независимо от изменений, происходящих в ней.

Математически этот закон выражается уравнением:

ΔЕ = const,

где Е — энергия; Δ — сумма; const (сокращенное constant) — постоянный, неизменный.

Из этого закона следует, что энергия данной системы не исчезает и не появляется вновь, а только переходит из одной формы в другую в строго эквивалентных количествах. Это и есть современная формулировка первого закона термодинамики.

Первое начало термодинамики устанавливает связь между количеством энергии, полученной или выделенной системой в каком-либо процессе в виде теплоты Q, количеством произведенной или полученной работы W и изменением внутренней энергии системы ΔU:

ΔU = W ± Q.

Внутренняя энергия (U) является полной энергией системы и представляет собой сумму потенциальной и кинетической энергий всех составляющих частей системы (молекул, атомов, ионов и пр.), за исключением потенциальной и кинетической энергии самой системы как материального тела. Данное уравнение является математическим выражением первого начала термодинамики.

Энергию системы в виде абсолютной величины нельзя определить. На практике проводят измерение величины изменения энергии.

Работа, которая выполняется системой, может быть:

• механической (например, по изменению внешнего объема),

• электрической (зарядка аккумулятора) или

• химической (синтез полипептида из аминокислот).

Энергия, теплота и работа измеряются в одних единицах.

Единицы энергии, работы и теплоты. Джоуль — единица энергии в системе СИ.

1 Дж = 1 кг·м²·с^-1

= 1 Н·м

= 1 Вт·с

= 1 Кл·В (кулон · вольт)

1 кал = 4,184 Дж

1 ккал = 1000 кал

= 4,184 кДж

Примеры

1. Работа, которую необходимо совершить для поднятия груза массой 1 кг на высоту 1 м, = 9,807 Дж.

2. Свободная энергия гидролиза 1 моля АТР (трифосфат аденозина — один из компонентов аденилатной системы, которая играет важную роль в энергообмене клеток) при рН = 7 составляет 52,2 кДж или 12,48 ккал.

3. Работа, которую необходимо совершить для повышения концентрации веществ в 1000 раз (например, от 10^–6 до 10^–3 М), составляет 17,1 кДж или 4,09 ккал.

4. Энергия некоторых веществ: в 1 г вещества содержится:

• углеводов — 17 кДж;

• глюкозы — 15,7 кДж;

• липидов — 39 кДж;

• белков — 17 кДж.

Если процесс изохорный, т. е. если он совершается при постоянном объеме (V = const), то работа не совершается, поскольку при V = const ΔV = 0 и, следовательно:

W = –P · ΔV = 0.

Знак минус в этом уравнении указывает на то, что система работает против сил внешней среды. В этом случае:

ΔU = Q_v,

где Q_v — количество энергии (Дж/моль или кал/моль), выделенной или поглощенной системой в виде теплоты в ходе процесса при постоянном объеме. Теплота процесса равна изменению внутренней энергии системы и зависит только от конечного и начального состояний системы, т. е.

U₂ — U₁ = ΔU = Q_v.

В реальной жизни часто встречаются изобарные процессы, протекающие при постоянном давлении (Р = const), например, химические реакции, идущие при атмосферном давлении. Изменение внутренней энергии системы в этом случае будет равно

ΔU = U₂ — U₁ = W + Q_p,

где Q_p — количество энергии (Дж/моль или кал/моль), выделенной или поглощенной системой в виде теплоты в ходе процесса при постоянном давлении. Поскольку в ходе процессов, идущих при Р = const, объем системы изменяется, то работа в таких процессах будет равна величине

W = –P(V₂ — V₁).

Отсюда:

U₂ — U₁ = Q_p — P(V₂ — V₁).

В результате тепловой эффект процесса, протекающего при Р = const, будет равен Q_p = U₂ — U₁ + P(V₂ — V₁);

Q_p = (U₂ + PV₂) — (U₁ + PV₁).

Величина (U + PV) обозначается буквой Н и называется энтальпией. Энтальпия, так же как внутренняя энергия, является функцией состояния, т. е. изменение энтальпии (ΔН = H₂ — Н₁) при переходе системы из состояния 1 в состояние 2 при постоянном давлении не зависит от пути перехода, а зависит только от величин энтальпии в конечном (2) и начальном (1) состояниях. Таким образом, тепловой эффект процесса, идущего при постоянном давлении, будет равен:

Q_p = H₂ — Н₁ = ΔН.

Следует отметить, что физико-химический смысл функций «внутренняя энергия» и «энтальпия» одинаков. Термин «внутренняя энергия» используется для энергетической характеристики процессов, идущих при V = const, а «энтальпия» — для процессов, идущих при P = const. При этом для конденсированных систем ΔН = ΔU, для газов ΔН ≠ ΔU.

Первое начало термодинамики дает только энергетическую оценку процессов, протекающих при постоянном объеме или постоянном давлении, но не дает никаких указаний о направлении процесса и предела, до которого изучаемый процесс может идти самопроизвольно. На эти вопросы отвечает второе начало термодинамики посредством новой термодинамической функции, которая называется энтропия и обозначается латинской буквой S.

Наблюдения и опыт показывают, что процессы, происходящие в природе, идут в определенном направлении. Жидкость течет от высокого уровня к более низкому, вещество диффундирует из области большей концентрации к меньшей, теплота переходит от тела с более высокой температурой к телу с менее высокой и т. д. Все эти процессы происходят самопроизвольно. Второе начало термодинамики гласит:

Каждая материальная система сама по себе стремится к состоянию термодинамического равновесия.

Существует другая формулировка 2-го закона термодинамики: энтропия вселенной всегда возрастает.

Таким образом, второй закон термодинамики ограничивает превращение энергии в материальной системе. Клаузиус, подобно Ломоносову, так формулирует второе начало термодинамики: теплота не может сама собой перейти от тела, менее нагретого, к телу, более нагретому.

В современной трактовке второе начало термодинамики звучит таким образом:

Энергия самопроизвольно перемещается от системы с более высоким потенциалом к системе с более низким потенциалом энергии того же вида, до тех пор, пока не наступит термодинамическое равновесие.

Изменение энтропии равно тепловому эффекту процесса, деленному на абсолютную температуру, при которой он происходит, и измеряется в Дж/мольК или кал/мольК.

Для обратимых изотермических реакций изменение энтропии равно

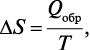
где Q_обр — часть общего количества энергии, выделенной системой в виде тепла.

Таким образом, если ΔS = 0, то процесс обратимый. Данное уравнение является математическим выражением второго начала термодинамики для обратимых процессов, происходящих в изолированной системе.

Для необратимых химических процессов, протекающих в изолированной системе, второе начало термодинамики имеет следующий вид:

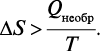
Таким образом, если в изолированной системе протекает самопроизвольный (необратимый) процесс, то ΔS > 0.

Процессы, для которых

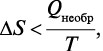
самопроизвольно осуществляться в изолированной системе при постоянной температуре не будут. Энтропия как критерий направленности самопроизвольных (необратимых) процессов может быть использована только для характеристики процессов в изолированных системах.

Физический смысл энтропии сводится к характеристике меры хаоса (беспорядка) в системе. Чем больше изменение энтропии в системе, тем меньше полезной работы может совершить данная система.

Изолированная система является идеальным случаем, т. е. такая система не взаимодействует с окружающей средой ни путем обмена энергией, ни путем обмена веществом. Реальные термодинамические системы являются либо закрытыми (могут обмениваться с окружающей средой энергией), либо открытыми (могут обмениваться с окружающей средой и энергией, и веществом). Для указания на направленность самопроизвольного процесса в таких системах используется другая термодинамическая функция — свободная энергия Гиббса (G).

Термодинамическая функция G = H — TS называется свободной энергией Гиббса, или изобарно-изотермическим потенциалом, или полезной работой. Используется для характеристики системы с точки зрения совершения полезной работы, а также для указания на направленность самопроизвольных процессов, идущих при Р = const и Т = const. В случае самопроизвольных (необратимых) процессов ΔG < 0. Если в результате процесса ΔG увеличивается (ΔG > 0), то такой процесс идет самопроизвольно в обратном направлении. В обратимых процессах в момент достижения равновесия ΔG = 0.

Термохимия — это раздел термодинамики, в котором изучаются химические реакции с точки зрения их тепловых эффектов. Рассмотрим закрытую термодинамическую систему, в которой происходит химическая реакция

аА + bВ = cС + dD.

В начальном состоянии такая система имеет запас внутренней энергии U₁, (а) молей реагента А и (b) молей реагента В. В конечном состоянии, т. е. после прохождения реакции, система будет иметь запас внутренней энергии U₂, (с) молей продукта С и (d) молей продукта D. Тепловым эффектом реакции будет называться количество энергии, которая выделяется либо поглощается в форме тепла при взаимодействии реагентов А и В с образованием продуктов С и D с учетом стехиометрических коэффициентов реакции. В зависимости от условий, в которых будет протекать химическая реакция (либо V = const, либо Р = сonst), тепловым эффектом реакции будет либо Q_v = ΔU, либо Q_p = ΔН.

Чтобы сравнить между собой тепловые эффекты разных реакций, необходимо указать точные условия, при которых они протекают. В термодинамике и термохимии за стандартные условия приняты Р = 1 атм и Т = 298 °К, при этом вещество в этих условиях должно находиться в наиболее устойчивом агрегатном состоянии. Для реакций, проходящих в стандартных условиях, изменение энтальпии обозначается символом ΔН⁰_298K.

Для реакций, протекающих в газовой фазе, было установлено соотношение между Q_p и Q_n:

Q_p = Q_v + ΔnRT.

Это соотношение устанавливает связь между теплотой реакции при постоянном давлении (Q_p или ΔН) и теплотой реакции при постоянном объеме (Q_v или ΔU), является следствием из закона Джоуля. В данном уравнении Δn — разность между числом молей образовавшихся газообразных продуктов и числом молей газообразных реагентов:

Δn = n_{газовых продуктов} — n_{газовых реагентов}.

Для реакций в конденсированных фазах (твердых и жидких), объем которых в ходе реакции практически не изменяется, т. е. Δn = 0, ΔН практически не отличается от ΔU. В этих случаях справедливы равенства

Q_p = Q_v и ΔH = ΔU.

Реакции, в результате которых вещество получается из химических элементов (простых веществ), называются реакциями образования. Изменение энтальпии в ходе таких реакций называется энтальпией образования данного соединения. Не все реакции образования можно реализовать практически. Например, реакция

2С + 3H₂ + ¹/₂O₂ = C₂H₅OH

теоретически является реакцией образования, но практически самопроизвольно не идет. Реакция

С + О₂ = СО₂

тоже является реакцией образования, но, в отличие от первой, она достаточно легко может быть проведена практически.

Стандартной энтальпией образования химического соединения называется изменение энтальпии в ходе реакции образования 1 моля данного соединения из элементов в стандартных условиях и обозначается символом ΔH⁰_f.

В ходе реакций образования тепловой эффект представляет собой именно стандартную энтальпию образования соединений, потому что стандартная энтальпия образования самих химических элементов (или простых веществ) принята равной нулю (ΔH⁰_{f (элементов)} = 0).

Знание стандартных энтальпий образования позволяет рассчитать тепловой эффект любой химической реакции (Q_p = ΔH), не прибегая к экспериментальным измерениям. Из химических элементов можно (а) получить непосредственно продукты. Соответствующее изменение энтальпии этой реакции будет равно ΔH⁰_{f (продуктов)}. Из элементов можно (б) получить реагенты. Эта реакция сопровождается изменением энтальпии ΔH⁰_{f (реагентов)}. Наконец, (в) из реагентов можно получить продукты. Изменение энтальпии в ходе этой реакции будет равно ΔН. Если эти три процесса проходили в стандартных условиях, то термодинамический баланс этих реакций будет равен:

ΔH⁰_298K = ΣΔH⁰_{f 298К (продукты)} — ΣΔH⁰_{f 298К (реагенты)}.

Таким образом, стандартная энтальпия химической реакции равна разности сумм стандартных энтальпий образования всех продуктов и всех реагентов. Так записывается математически закон Гесса.

Если из данных исходных реагентов можно различными путями получить одни и те же конечные продукты, то, независимо от путей получения продуктов, т. е. от вида и количества промежуточных реакций, суммарный тепловой эффект для всех путей будет одним и тем же. Иначе говоря, тепловой эффект химической реакции не зависит от пути перехода «реагенты — продукты», т. е. от промежуточных реакций, а зависит только от вида и состояния продуктов и реагентов. Это положение было постулировано русским ученым Г. И. Гессом в 1840 году и известно как закон Гесса, являющийся основным законом термохимии.

Следствия из закона Гесса:

1. Закон Лавуазье-Лапласа. Тепловой эффект реакции разложения точно равен и противоположен по знаку тепловому эффекту реакции соединения.

Пример:

Са + ¹/₂О₂ = СаО + 634,71 кДж;

СаО = Са + ¹/₂О_2–634,71 кДж;

Q_разл + (–Q_соед) = 0.

2. Если совершаются две реакции, приводящие из различных начальных состояний к одинаковым конечным, то разница между тепловыми эффектами представляет тепловой эффект перехода из одного начального состояния в другое.

Пример:

1) С + О₂ = СО₂ + 409,20 кДж;

2) СО + ¹/₂О₂ = СО₂ + 284,93 кДж.

Вычитая из уравнения (1) уравнение (2), можно вычислить тепловой эффект реакции сжигания углерода до окиси углерода:

С + ¹/₂О₂ = СО + 124,27 кДж.

Таким образом, можно определять тепловые эффекты таких реакций, которые или нереализуемы, или не могут быть проведены чисто и до конца.

3. Если совершаются две реакции, приводящие из одинаковых начальных состояний к различным конечным, то разница между тепловыми эффектами представляет тепловой эффект перехода из одного конечного состояния в другое.

Пример:

С_уголь + О₂ = СО₂ + 409,20 кДж;

С_графит + О₂ = СО₂ + 393,51 кДж.

Таким образом, можно рассчитать тепловой эффект перехода от угля к графиту, который будет равен 409,00–393,51 = = 15,69 кДж/моль.

Энтропия, в отличие от многих других термодинамических функций, имеет точку отсчета. Эта точка отсчета задается 3-м законом термодинамики, который еще называют постулатом Планка: при абсолютном нуле (T = 0 °К) все идеальные кристаллы имеют одинаковую энтропию, равную нулю.

При стремлении температуры к абсолютному нулю не только энтропия стремится к нулю, но и ее производные по всем термодинамическим параметрам. Это означает, что вблизи абсолютного нуля все термодинамические процессы протекают без изменения энтропии.

Биологическое значение

Живые организмы не являются исключением из законов природы. Любой организм, растительный и животный, находится в постоянном обмене энергией и веществом с окружающей средой. Он поглощает разнообразные вещества в виде пищи, ассимилирует и трансформирует их в составные части своего тела, разрушает их в процессе диссимиляции и удаляет их в качестве отработанных продуктов во внешнюю среду. Многочисленными экспериментами была установлена подчиненность этих процессов закону сохранения материи и энергии.

Приведем для иллюстрации опыты Биддера и Шмидта над взрослой кошкой, находящейся в состоянии пищевого равновесия (табл. 1, данные приведены в г/1кг веса животного в сутки).

Сравнение потребляемых и выделяемых веществ свидетельствует о глубоких превращениях пищи в организме. Эти превращения связаны с производством энергии, возникающей в процессе распада пищевых веществ и необходимой организму для производства работы (мышечное сокращение), для синтеза и ассимиляции, для выработки тепла.

Живые организмы также подчинены законам термохимии, в частности закону Гесса. Этот закон имеет огромное значение для физиологии и биохимии. Действительно, окисление пищевых продуктов в организме происходит через серию сложных реакций, однако количество теплоты, выделяемое при этом, сравнимо с количеством теплоты, которое можно получить при непосредственном сжигании этих веществ в колориметрической бомбе (прибор для определения теплоты сгорания).

Таблица 1

Поступления	Общий вес	Н2О	С	Н	N	О	S	Соли
Мясо	44,118	32,957	6,109	0,851	1,390	2,184	0,086	0,441
Вода	27,207	27,207	–	–	–	–	–	–
Кислород	18,632	–	–	–	–	18,632	–	–
ИТОГО	89,957	60,164	6,209	0,851	1,390	20,816	0,086	0,441
Выделения
Моча	53,350	49,817	0,592	0,197	1,380	0,858	0,042	0,409
Кал	0,910	0,718	0,075	0,010	0,002	0,031	0,044	0,032
Н2СО3	20,322	–	5,542	–	–	14,870	–	–
Вода (через легкие и кожу)	15,355	9,569	–	0,644	–	5,152	–	–
Потери азота	0,008	–	–	–	0,008	–	–	–
ИТОГО	89,957	60,164	6,209	0,851	1,390	20,816	0,086	0,441

Закон Гесса дает основание использовать теплоты сгорания пищевых веществ для суждения об энергии окисления в организме. Экспериментальными исследованиями многих ученых были определены теплоты сгорания пищевых веществ в калориметрической бомбе (табл. 2), и они оказались тождественны калорийной ценности при окислении в организме.

Таблица 2

Вещество	Теплота сгорания в организме (ккал)	Теплота сгорания в калориметре (ккал)
Углеводы	4,1	4,1
Жиры	9,3	9,3
Белки	4,1	5,7

Белки в организме окисляются не полностью. В качестве продукта неполного окисления белков выделяется мочевина, чем и обусловливается расхождение теплоты сгорания в организме и калориметре.

Таким образом, приведенные данные неопровержимо свидетельствуют о том, что энергетические процессы в организме подчиняются закону сохранения энергии, как и любые химические реакции вне организма, идут по законам термохимии.

Вопросы для самоконтроля

1. Что изучает термодинамика?

2. Что такое тепловой эффект химической реакции?

3. В каких единицах измеряются тепловые эффекты?

4. Как формулируется первое начало термодинамики? Его математическая запись.

5. Что представляет собой энтальпия, в чем ее физический смысл?

6. Тепловые эффекты при постоянном объеме и постоянном давлении.

7. Как формулируется второе начало термодинамики? Его математическая запись.

8. Изобарно-изотермический потенциал. Свободная энергия Гиббса и Гельмгольца.

9. Что изучает термохимия?

10. Сформулируйте закон Гесса и следствия из закона Гесса. Какова математическая запись закона Гесса?

Экспериментальная часть

При выполнении работы необходимо обращать внимание на знаки «+» или «–», которые характеризуют тепловые эффекты реакций. В термодинамике приняты следующие правила при обозначении обмена энергией между системой и внешней средой. В какой бы форме не происходил обмен энергией, количество энергии, полученное системой, обозначается знаком «+». Количество энергии, отданное системой во внешнюю среду, — знаком «–». В термохимии принято обратное обозначение. Таким образом, в термодинамике и термохимии пользуются обратной системой знаков. Если система отдает энергию во внешнюю среду, в термохимии это обозначается плюсом (экзоэффект, или экзотермические реакции), а в термодинамике — минусом. Если система приобретает энергию из внешней среды, в термохимии будет знак минус (эндоэффект, или эндотермические реакции), а в термодинамике — знак плюс.

Приборы, при помощи которых определяют тепловые эффекты химических реакций, называются калориметрами. В данной работе для экспериментального определения теплового эффекта химической реакции используется калориметр с воздушной изотермической оболочкой. Подобные приборы обеспечивают точность определения тепловых эффектов до ±2% при изменении температуры системы на 0,5° и больше. Поскольку в калориметрах такой конструкции реакция происходит при постоянном (атмосферном) давлении, то измеряемый тепловой эффект будет представлять собой Q_p.

Калориметр состоит из толстостенного сосуда А объемом 2–3 л, в который на корковых пробках устанавливается стеклянный или пластмассовый стакан Б емкостью 500–600 мл. Сосуд А закрывается стеклянной или пластмассовой крышкой с тремя отверстиями: для мешалки М, для термометра Т и для воронки В, через которую вносится реагент (рис. 1).

Рис. 1. Калориметр: А — внешний сосуд; Б — внутренний сосуд, в который заливается реагент; Т — термометр; М — мешалка; В — воронка, через которую всыпается второй реагент

Задание 1. Определение постоянной калориметра

Теплота химической реакции, принимаемая или отдаваемая водяным калориметром, будет изменять температуру воды, находящейся в стакане Б, и температуру других частей прибора, находящихся в воде. В этом случае количество теплоты будет равно

Q = (M₁C₁ + M₂C₂)Δt,

где M₁ — масса воды; С₁ — теплоемкость воды; М₂ и С₂ — усредненные значения масс и теплоемкости для стекла стакана, мешалки и других частей калориметра.

При наполнении стакана Б и неизменности частей, погружаемых в воду, М₁С₁ + М₂C₂ = const = Z, которую называют постоянной калориметра.

Таким образом,

Q = ZΔt,

из чего следует, что при Δt = 1° Q = Z. Иначе говоря, постоянная калориметра — это количество теплоты, необходимое для изменения температуры всех частей калориметра на 1°. Следовательно, до проведения эксперимента по определению теплового эффекта химической реакции Q_p следует прокалибровать прибор (калориметр), т. е. определить постоянную калориметра Z. Этого можно достичь, вводя или отнимая известное количество теплоты (Q_p) в данном калориметре с одновременным точным измерением изменения температуры. Тогда постоянную калориметра можно определить по формуле

Существует несколько способов определения постоянной калориметра. В данной работе постоянная Z устанавливается по теплоте растворения KCl.

В стакан Б калориметра наливают 400 мл дистиллированной воды. Опускают крышку калориметра так, чтобы она плотно соприкасалась с верхней частью сосуда А (рис. 1). Нижняя часть термометра и мешалки при этом должны находиться на расстоянии 1–2 см от дна стакана Б. Включают мотор для вращения мешалки и снимают температуру с точностью до 0,01°, пользуясь при этом лупой. Начинается предварительный период эксперимента, в течение которого записывают показания термометра через каждую минуту. Предварительный период длится 10 минут, время фиксируется по секундомеру.

На 11-й минуте в отверстие крышки калориметра вставляется воронка В, через которую в воду всыпается 7,2 г КСl. В процессе растворения КСl температура начинает резко изменяться. Начинается главный период эксперимента, в течение которого температура фиксируется через каждые полминуты.

После того как температура, достигнув минимума, начнет равномерно повышаться, начинается заключительный период эксперимента, который продолжается 10 минут. В заключительном периоде температура фиксируется через каждую минуту. Данные заносят в табл. 3.

Таблица 3

Определение постоянной калориметра (Z). Масса KCl 7,2 г

Периоды, мин
предварительный		главный		заключительный
время, мин	Т, оС	время, мин	Т, оС	время, мин	Т, оС
0 1 2 3 4 5 6 7 8 9 10		10,5 11 11,5 12 12,5 13 13,5 14 14,5 15		16 17 18 19 20 21 22 23 24 25 26

Полученные данные наносят на миллиметровую бумагу, откладывая по оси абсцисс время в минутах, а по оси ординат — температуру. Через точки предварительного и заключительного периодов проводят прямые линии. Из середины главного периода (точка С, рис. 2) проводят перпендикуляр до пересечения с продолжением прямых предварительного и заключительного периодов (точки М и N рис. 2). Из точек пересечения опускают перпендикуляры на ось ординат. Отсекаемый отрезок на оси ординат (t₁ — t₂) равен Δt.

Рис. 2. Графическое определение Δt для вычисления постоянной калориметра

Тепловой Q_p, как ранее было сказано, вычисляется на 1 моль прореагировавшего вещества, но в данном случае в калориметре находилось g г вещества, а потому

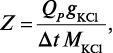
где g — навеска КСl (в граммах); M — молекулярная масса для КСl; Q_p в случае растворения KCl в воде составляет 4440 кал/моль.

Задание 2. Определение теплового эффекта реакции окисления металлического цинка и восстановления ионов меди в водном растворе

Тепловые эффекты реакций измеряются так же, как и постоянная калориметра. Тепловой эффект вычисляется по уравнению

Исследуемая реакция является окислительно-восстановительной, и механизм ее заключается в переносе электронов от металлического цинка к ионам меди согласно уравнению

Cu²⁺ + Zn⁰ = Cu⁰ + Zn²⁺ + Q_p.

Измеряемый тепловой эффект будет равен Q_p = ΔH. Данный процесс необратим, т. к. цинк, переходя в раствор, не восстанавливается, и реакция идет до полного исчезновения ионов меди в растворе с эквивалентной заменой их на ионы цинка.

В стакан Б калориметра наливают 400 мл 0,05 М раствора медного купороса (CuSО₄×5H₂O). Закрывают сосуд А так, чтобы нижние концы термометра и мешалки не доставали дна стакана Б на 1–2 см. Включают мотор мешалки и измеряют температуру, точно следуя тем записям, которые проводились при измерении водяного числа (постоянной калориметра). На 11-й минуте через воронку В в стакан Б высыпают 3 г цинковой пыли.

Данные заносят в табл. 4. По полученным данным строят график изменения температуры и находят Δt (рис. 3).

Таблица 4

Определение теплового эффекта реакции

Периоды, мин
предварительный		главный		заключительный
время, мин	Т, °C	время, мин	Т, °C	время, мин	Т, °C
0 1 2 3 4 5 6 7 8 9 10		10,5 11 11,5 12 12,5 13 13,5 14 14,5 15		16 17 18 19 20 21 22 23 24 25 26

Рис. 3. Графическое определение Δt для вычисления теплового эффекта реакции

Тепловой эффект реакции рассчитывают по уравнению

где g_{CuSO4 5H2O} — количество кристаллогидрата, содержащегося в 400 мл 0,05 М раствора.

Тепловой эффект химической реакции является следствием изменения внутренней энергии реагирующих веществ, и без воздействия внешних сил на условия протекания реакции внутренняя энергия полностью превращается в теплоту. Если эта реакция осуществляется в гальваническом элементе, то часть внутренней энергии будет превращаться в полезную работу. Эта работа будет максимальной, когда химический или физический процесс протекает изотермически и обратимо. Именно этим условиям соответствуют процессы, протекающие в гальванических элементах. Реакция окисления Zn и восстановления Cu²⁺ наблюдается в элементе Даниэля–Якоби:

Cu | Cu²⁺ | KCl | Zn²⁺ | Zn.

Максимальная работа по перенесению заряда равна (Дж×моль^-1)

W = n × F × E,

где n — число переносимых электронов; F — число Фарадея (96 500 Кл); E — электродвижущая сила (1,10 В). Максимальная работа равна, но противоположна по знаку изменению свободной энергии ΔG. Следовательно, ΔG процесса можно рассчитать по уравнению

W = –ΔG.

Свободная энергия является частью энтальпии и связана с ней соотношением ΔG = ΔH — TΔS, где TΔS — связанная энергия. Зная ΔH и ΔG, можно рассчитать энтропию окисления цинка и восстановления ионов меди по уравнению

где Т — температура, при которой проводился эксперимент (температура окончания реакции окисления Zn с точностью до 1°). При расчете ΔS следует свободную энергию (ΔG) и тепловой эффект реакции (ΔH) привести в единую систему измерения величин, т. е. тепловой эффект, рассчитанный в калориях, перевести в джоули (1 калория = 4,18 Дж). Результаты вычислений заносят в табл. 5.

Таблица 5

Результаты вычислений

Опыт	Δt, °C	Z	QP, ккал/моль	ΔG, кДж/моль	ΔS, Дж/моль·К
Определение Z				—	—
Определение QP		—

2. Определение электродных потенциалов и концентрации ионов в растворе методом измерения электродвижущих сил

При известных условиях электрическая энергия может быть получена за счет всех видов энергии: механической, тепловой, световой и т. д. Очень часто электрическую энергию получают за счет химических превращений.

Прибор, в котором в результате химических реакций получается электрическая энергия, т. е. химическая энергия превращается в электрическую энергию, называется гальваническим элементом.

Гальванические элементы нашли широкое применение в качестве источников постоянного тока в промышленности, на транспорте, в военном деле, в лабораторной практике, в медицине и других областях народного хозяйства и науки.

Гальванический элемент состоит из двух или нескольких полуэлементов или электродов. Простейший электрод (первого рода) представляет собой металлическую пластинку, погруженную в раствор, содержащий ионы этого же металла.

Еще в XVIII веке было замечено, что на границе раздела металл–вода (или раствор электролита) возникает разность электрических потенциалов.

По современным представлениям, при погружении металла, например цинка, в воду происходит отрыв ионов от кристаллической решетки металла под влиянием полярных молекул растворителя. В результате перехода катионов металла в раствор металл приобретает некоторый отрицательный заряд за счет оставшихся на нем электронов. Возникающий отрицательный заряд будет во все большей степени препятствовать переходу положительных ионов цинка в раствор. Наконец, растворение металла прекратится вообще, точнее, между пластинкой металла и раствором установится динамическое равновесие — скорость растворения металла станет равной скорости обратного процесса осаждения катионов цинка из раствора на пластинку. Это равновесие, состояние которого определяется природой металла и растворителя, обусловливает появление двойного электрического слоя и определенный скачок потенциала между металлом и растворителем, получивший название электродного потенциала. В случае цинкового электрода протекают две равновесные реакции:

Zn^o — 2e = Zn⁺²;

Zn⁺² + 2e = Zn^o.

У разных металлов вследствие неодинаковой энергии связи атомов в кристаллической решетке и различной способности их катионов к гидратации растворение металла протекает не в одинаковой степени, а следовательно, и равновесные электродные потенциалы, возникающие на границе металл–жидкость, будут различными. Также на величину равновесного потенциала будет оказывать влияние концентрация одноименных с металлической пластинкой ионов.

Это связано с тем, что присутствующие в растворе ионы цинка будут способствовать сдвигу равновесия в сторону увеличения скорости осаждения ионов цинка из раствора на пластинку, тем самым уменьшая отрицательный заряд пластинки. Заряд пластинки будет тем меньше, чем больше концентрация ионов цинка в растворе.

Таким образом, при погружении металлической пластинки в водный раствор, содержащий ионы того же металла, на границе раздела фаз возникает двойной электрический слой, обусловленный конкуренцией двух процессов:

а) растворение металла, характеризуемое работой, затрачиваемой на вырывание протонов из кристаллической решетки металла и перевод их в раствор;

б) осаждение ионов на металлическую пластинку, определяемое работой по разрушению гидратной оболочки ионов и осаждению их на металле.

Если энергия гидратации больше энергии электронно-ионной связи металла, то ионы выходят из металла в раствор, пластинка заряжается отрицательно, а близлежащий слой раствора — положительно.

Если энергия гидратации меньше энергии электронно-ионной связи металла, то ионы осаждаются на пластинке, она заряжается положительно, а близлежащий слой раствора — отрицательно.

Если гальванические цепи составляются из двух качественно различных электродов с различными активностями ионов, то они называются химическими и схематически это записывается следующим образом:

где а₁ и а₂ — активности ионов в растворе; вертикальные черточки представляют границу раздела металл–раствор, причем электрод с большим потенциалом (восстанавливается) записывается справа, а с меньшим (окисляется) — слева.

Электролитический проводник включают для устранения диффузионного потенциала, который возникает на границе электродных электролитов, либо за счет различной подвижности ионов, либо за счет разницы концентраций. При этом электролитический проводник должен удовлетворять следующим требованиям:

• электролит должен быть сильным;

• концентрация электролита должна быть высокой;

• электролитические подвижности ионов должны иметь близкие значения (l_{катиона} = l_аниона);

• электролит не должен образовывать труднорастворимое соединение с электродными растворами.

Примером гальванического элемента может служить медно-цинковый элемент Даниэля-Якоби, состоящий из двух электродов первого рода — медного и цинкового. Электроды представлены медной и цинковой пластинками, погруженными соответственно в растворы сульфата меди и сульфата цинка. Схематически элемент Даниэля-Якоби вглядит так:

Zn | ZnSO₄ || CuSO₄ | Сu.

Если рассматривать цинковый и медный электроды в отдельности, то, как и описывалось выше, на границах металл–раствор в конкретных условиях сформируются равновесные электродные потенциалы. Однако как только соединить два электрода в электрическую цепь при помощи электрического проводника (провод, не путать с электролитическим проводником), в силу более выраженных металлических свойств цинка пластинка последнего будет, растворяясь, окисляться, а ионы меди из раствора будут осаждаться на медной пластинке.

Zn + CuSO₄ = Cu + ZnSO₄,

или

Zn^o + Cu+² = Zn⁺² + Cu^o.

При этом электроны по проводнику будут двигаться от цинковой пластинки к медной, т. е. в цепи возникнет электрический ток.

Таким образом, комплекс протекающих окислительно-восстановительных реакций, представляющий химическую работу по перераспределению зарядов (в нашем случае между металлическими пластинками и растворами каждого электрода), привел к возникновению разности потенциалов между двумя электродами. Данная максимальная разность потенциалов, характеризующая максимальную работу гальванического элемента, называется электродвижущей силой, или ЭДС.

Е = ε₁ — ε₂,

где Е — электродвижущая сила (ЭДС); ε₁ и ε₂ — потенциалы электродов.

В агрохимии, физиологии растений, в почвоведении знание современных методов измерения электродвижущих сил имеет большое значение. Эти методы дают возможность быстро и точно определить кислотность почв и концентрацию водородных ионов в клеточном соке живых организмов. Окислительно-восстановительные и мембранные потенциалы также наиболее надежно определяются измерением электродвижущих сил соответствующих почвенных или физиологических объектов.

Гальванические элементы могут состоять из обратимых или необратимых электродов, соединенных электролитическим проводником. Элемент называется необратимым, если в системе хотя бы один из процессов является необратимым. Обратимый гальванический элемент — это элемент, в котором на границе двойного электрического слоя протекают обратимые окислительно-восстановительные процессы.

Классификация электродов: по своему строению электроды бывают первого и второго рода.

К электродам первого рода относятся электроды, состоящие из металлической пластинки, соприкасающейся с раствором соли того же металла (медный, цинковый, никелевый и др. электроды), или металла с растворенными в нем атомами другого элемента, соприкасающегося с раствором ионов этого элемента (амальгамо-кадмиевый, водородный, кислородный, хлорный и др.). Электродный потенциал электродов первого рода зависит от концентрации катионов в растворе, эти электроды называются электродами, обратимыми по катиону.

В качестве примера электрода первого рода выше уже рассматривался цинковый электрод.

Электродный потенциал электрода первого рода определяется уравнением Нернста:

где ε — электродный потенциал, В; ε⁰ — стандартный (нормальный) электродный потенциал, В; R — универсальная газовая постоянная (8,31 Дж/моль_·К); T — абсолютная температура, °К; F — число Фарадея (96 500 Кл/моль); n — количество переданных электронов; 2,303 — модуль перехода от натурального логарифма к десятичному; a_M^x+ — активность ионов металла в растворе.

Активность ионов связана с концентрацией раствора, и эта связь выражается уравнением

где a_M^x+ — активность; C — молярная концентрация раствора; f_a — коэффициент активности, учитывающий электростатическое взаимодействие ионов в растворе.

Также к электродам первого рода относится водородный электрод. Он относится к группе газовых электродов, которые состоят из инертного проводника, например платиновой пластинки, насыщенного газом, который обменивается ионами с раствором. Происходящие на водородном электроде химические процессы можно изобразить суммарным равенством:

Н₂ ↔ 2Н ↔ 2Н⁺ + 2е.

В результате процессов на границе между платиной и раствором образуется двойной электрический слой и возникает электродный потенциал. Величина его при данной температуре определяется, с одной стороны, активностью водородных ионов в растворе, а с другой — количеством поглощенного платиной водорода, которое пропорционально его давлению.

Платиновая пластинка, насыщенная водородом под давлением 1 атм и погруженная в раствор с активностью ионов водорода, равной единице (1 М раствор серной кислоты), называется нормальным водородным электродом и схематически записывается так:

Pt, H₂ | 2H⁺.

По международному соглашению, потенциал нормального водородного электрода условно принят равным нулю. Нормальный водородный электрод играет роль эталона, потому что с его величиной сопоставляют потенциалы других электродов. Электроды, имеющие устойчивый (известный) потенциал и служащие для определения потенциалов других электродов, называются стандартными электродами, или электродами сравнения. Нормальный водородный электрод является одним из электродов сравнения. Электродный потенциал водородного электрода можно вычислить по формуле:

ε_Н2 = 0.059 lga_Н2.

Таким образом, электродным потенциалом электрода называется ЭДС элемента, составленного из этого электрода (справа) и стандартного водородного электрода (слева).

Водородный электрод может быть использован и как индикаторный электрод. Индикаторным (может быть и первого, и второго рода) называется электрод, который содержит исследуемый раствор и по величине потенциала которого можно рассчитать активность (концентрацию) ионов в растворе, например медный Cu | CuSO₄, цинковый Zn | ZnSO₄, железный Fe | FeCl₃ и др.

Электроды второго рода состоят из металла, покрытого слоем его труднорастворимой соли и погруженного в раствор какой-либо легко растворимой соли с тем же анионом. Эти электроды обратимы относительно аниона, и формула их электродного потенциала записывается так:

Электродами второго рода являются такие электроды, как:

• хлорсеребряный — Ag | AgCl, KCl_{(насыщ. р-р}); ε = 0,203 В;

• каломельный — Hg | Hg₂Cl₂, KCl(_{насыщ. р-р}); ε = 0,25 В.

Электроды второго рода отличаются хорошей воспроизводимостью, постоянством потенциала и легкостью приготовления, поэтому их широко применяют как электроды сравнения. К электродам сравнения относятся также:

• водородный электрод — Pt, H₂ | 2H⁺, ε_H+ = 0 В при а_Н+ = 1 моль/л и

• каломельный — Hg | Hg₂Cl₂, КCl_насыщ, ε_к = 0,25 В.

Однако электроды второго рода могут применяться и в качестве индикаторных электродов. В таком случае их потенциал будет изменяться относительно концентрации измеряемого аниона.

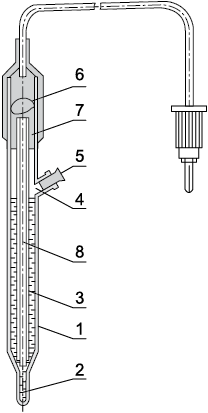
Рис. 4. Хлорсеребряный электрод: 1 — корпус; 2 — асбестовая нить; 3 — раствор KCl; 4 — отверстия для заливки раствора хлористого калия; 5 — резиновая пробка; 6 — серебряная проволока; 7 — хлористое серебро; 8 — асбестовый фитиль

Стандартным (нормальным) электродным потенциалом называется потенциал, возникающий на электроде в нормальных условиях (Р = 101,3 кПа = 1атм; Т = 298 °К) при активности ионов в электродном растворе, равной 1 г-экв/л. Величины нормальных (стандартных) электродных потенциалов находятся экспериментальным путем относительно водородного электрода, причем нормальный потенциал водородного электрода условно принимается равным нулю. Таблица нормальных потенциалов называется рядом напряжений. В табл. 6 приведены стандартные электродные потенциалы некоторых электродов.

Таблица 6

Нормальные потенциалы некоторых электродов при 298 °K (ряд напряжений)

Электрод	Электродный процесс	ε, В
Zn | Zn2+	Zn ⇔ Zn2++ 2e–	–0,76
Fe | Fe2+	Fe ⇔ Fe2+ + 2e–

...