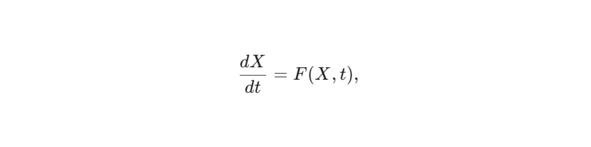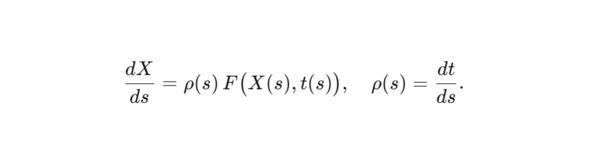Оглавление

ПРЕДИСЛОВИЕ

Сборник объединяет публикации 2025 года, посвящённые исследованию модели «Сфираль» и её применений в смежных областях знания. Материалы представляют системный взгляд на конструкцию, которая опирается на топологию витков, антисимметрию, S-переход и сфиральное время как особую форму параметризации процессов.

В научных статьях формируется согласованная картина, описывающая физические, математические, когнитивные и семантические явления через единый набор структурных принципов. Рассматриваются свойства сфирального времени, связи между локальными и глобальными S-петлями, фазовые последовательности, возникающие в пространствах H₂ и H₃, и фрактальная организация вычислительных процессов. Отдельные разделы посвящены структурным переходам в квантовых системах, геометрии коллапса состояния, механизмам декогеренции и роли антисимметрии в формировании динамических контуров.

В сборнике представлено описание сфиральных закономерностей в биологических системах, включая структуру ДНК, принципы комплементарности и смысловой организации биосистем. Значительная часть материалов обращена к когнитивным механизмам, смысловой структуре мышления, резонансным процессам в сознании и языку как форме отражения топологических связей.

Публикации охватывают как фундаментальные разделы математики и физики, так и модели искусственного интеллекта, где сфиральные схемы проявляют себя в виде фрактальных вычислительных ядер, структур смысловой обработки и когнитивных контуров. В совокупности статьи создают целостное представление о системе, связывающей физическую динамику, структуру информации, процессы восприятия и смысловые трансформации.

Сборник адресован исследователям, работающим в областях фундаментальной физики, математического моделирования, биофизики, когнитивных наук, лингвистики и систем искусственного интеллекта. Представленные материалы ориентированы на междисциплинарный диалог и создают основу для последующего цитирования в публикациях, посвящённых структуре времени, топологическим моделям, квантовым процессам, когнитивным архитектурам и семантическим системам.

ОБЩЕЕ ОПРЕДЕЛЕНИЕ УСТРОЙСТВА «СФИРАЛЬ»

Строгое математико-геометрическое ядро

1. Структурная основа

Сфираль — пространственная система из двух витков, построенных в зеркальной антисимметрии и объединённых S-образной переходной петлёй. Каждый виток имеет собственную ориентацию, собственный локальный знак параметров движения и собственную фазовую развёртку.

Эта конструкция образует единую топологическую форму, в которой витки не повторяют друг друга и не замыкаются в круг, а переходят в иной режим через S-узел.

2. Принцип зеркальной антисимметрии

Антисимметрия задаёт фундаментальную направленность структуры. Витки не являются симметричными отражениями: они формируют сопряжённую пару с инверсией параметров. Переход между витками меняет знак угловой скорости, локальной фазы и ориентации.

Антисимметрия обеспечивает устойчивость связки и алгебраический закон смены полярности, выраженный геометрически.

3. S-петля как зона инверсии

Переходная S-петля — центральный узел конструкции. В ней происходит фазовый поворот на 180°, смена ориентации и перезапись динамических параметров. S-узел формирует режим сопряжения, через который возможен перенос движения, состояния, импульса и фазы между витками.

S-петля — геометрический механизм комплементарности и инверсии.

4. Сопряжённость витков

Оба витка образуют цельную динамическую пару. Каждый виток несёт собственную метрику (радиус, шаг, фазу), а S-узел связывает их в единую топологию с общим параметром эволюции.

Ключевой элемент — не форма витков, а механизм их сопряжения через инверсию.

5. Внутренняя параметризация

Введён параметр s — сфиральное время. Он описывает положение внутри витка и в зоне перехода и заменяет классическое линейное время.

Каждая точка структуры определяется набором функций:

— θ (s) — угловая фаза

— R (s) — радиальная функция витка

— h (s) — вертикальная координата

— ϕ (s) — фазовый угол перехода в S-петле

В динамике производные по s замещают обычные временные производные.

6. Топологическая целостность

Сфираль не является спиралью. Её структура определяется не геометрическим профилем кривой, а связью витков через антисимметрию и инверсию. Эта связь делает систему топологическим объектом, устойчивым к деформациям, масштабированию и фрактальному вложению.

Форма существует как закон свития различий.

7. Универсальность модели

Сфиральная структура описывает:

— физические процессы (фотон, электрон, ядро)

— биологические структуры (ДНК, регуляторные петли)

— вычислительные конструкции (СИН/ФСИН)

— временную динамику (переходы, узлы, ритмы)

— алгебраические системы (неассоциативность, антисимметрия)

Универсальность обеспечивается тем, что модель задаёт механизм перехода и сопряжения, а не форму или материал.

Сводное математически точное определение

Сфираль — это трёхмерная топологическая конструкция, состоящая из двух взаимно комплементарных витков, построенных в зеркальной антисимметрии и сопряжённых через S-образную зону инверсии. Переходная петля обеспечивает поворот на 180° и перенос динамических параметров между витками. Внутренний параметр s задаёт фазу, позицию и направление эволюции внутри структуры. Сфираль функционирует как механизм согласования противоположных режимов, обеспечивая устойчивость, направленность и фрактальную вложенность.

Эталонное определение устройства «Сфираль»

1. Сверхкратко (глоссарий, сноска)

Сфираль — топологически устойчивая пространственная конструкция из двух зеркально антисимметричных витков, сопряжённых S-образной переходной петлёй, через которую осуществляется инверсия и перенос параметров движения между витками.

2. Базовое определение (для введения в книге / статье)

Сфираль — пространственная система из двух взаимно комплементарных витков, построенных в режиме зеркальной антисимметрии и соединённых S-образной переходной петлёй. В S-петле располагается инверсионный узел, в котором происходит поворот на 180°, смена ориентации и переход параметров движения между ветвями.

Эволюция в Сфирали описывается внутренним параметром s (сфиральное время), задающим положение точки на витках и в зоне перехода и допускающим фрактальную вложенность витков и узлов.

3. Технически-развёрнутое определение (для раздела с моделью)

Сфираль — трёхмерная топологическая конструкция, включающая пару витков V₊ и V₋, связанных отношением зеркальной антисимметрии и объединённых S-образной переходной петлёй S.

Каждый виток задаётся набором функций внутреннего параметра s: радиусом R (s), угловой координатой θ (s), высотой h (s) и фазой φ (s). Инверсионный узел в области S реализует поворот на 180^∘ и смену знака ориентированных параметров (фазы, угловой скорости, полярности), за счёт чего возникает комплементарная пара витков. Структура допускает фрактальное вложение витков и S-узлов и задаёт механизм согласования противоположных режимов движения в единой сфере эволюции параметра s.

Развёрнутое математическое ядро модели «Сфираль»

1. Внутренний параметр s (сфиральное время)

Вводится единственный внутренний параметр эволюции s ∈ R, который задаёт положение вдоль структуры Сфирали:

— s <0 — область первого витка V₋;

— s = 0 — зона инверсии (S-петля, узел);

— s> 0 — область второго витка V₊.

Параметр s интерпретируется как сфиральное время: внутренняя «фаза» прохождения системы по структуре, отличная от внешнего времени t.

Связь с внешним временем задаётся функцией

При необходимости динамические уравнения переписываются в виде:

2. Базовая параметризация витка в R³

Для описания одного витка вводятся функции:

— R (s)> 0 — текущий радиус;

— θ (s) — угловая координата;

— h (s) ∈ R — координата вдоль оси «вертикали» (ось свития);

— φ (s) — внутренняя фаза (для динамики, поля, состояния).

Положение точки на эталонном витке задаётся как

Это локальная «несфиральная» заготовка. Сфираль возникает при введении антисимметрии и S-петли.

3. Зеркально антисимметричная пара витков

Два взаимно комплементарных витка V₋ и V₊ строятся как пара пространственных траекторий, связанных оператором зеркальной антисимметрии.

Задаётся линейный оператор отражения M и, при необходимости, вектор сдвига c:

Например, простое отражение относительно плоскости z = 0:

Определение витков:

— первый виток (условно «прошлая ветвь»)

V₋: r₋ (s) = r₀ (s), s ≤ 0;

— второй виток (условно «грядущая ветвь»)

V₊: r₊ (s) = M r₀ (−s) + c, s ≥ 0.

Зеркальная антисимметрия выражается в следующем:

— радиусы совпадают: R₊ (s) = R₋ (−s);

— углы связаны с разворотом:

θ₊ (s) = −θ₋ (−s) + Θ₀,

где Θ₀ — постоянный фазовый сдвиг (обычно π или 0);

— высоты удовлетворяют

h₊ (s) = — h₋ (−s) + h₀.

Векторы скоростей и ориентаций связаны через

Это и есть геометрически строгий вариант фразы «два зеркально антисимметричных витка» с инверсией параметров движения.

4. S-петля как зона инверсии

S-петля — связующая область между ветвями V₋ и V₊. Считаем, что зона перехода занимает интервал

S ∈ [−δ, δ],

где δ> 0 задаёт толщину переходной области.

Вводятся две гладкие весовые функции α (s), β (s) со свойствами:

— α (s) ≈ 1, β (s) ≈ 0 ≈ s ≤ δ;

— α (s) ≈ 0, β (s) ≈ 1 при s ≥ δ;

— α² (s) + β² (s) = 1 для всех s (удобно брать нормированную пару).

Простейший вариант:

α (s) = cos ψ (s), β (s) = sin ψ (s),

где ψ (s) — гладкая монотонная функция, переходящая

из

Положение точки Сфирали на всём диапазоне s:

R (s) = α (s) r₋ (s) + β (s) r₊ (s).

Тогда:

— при s ≤ −δ: α → 1,β → 0, и структура совпадает с первым витком;

— при s ≥ δ: α → 0,β → 1, и структура совпадает со вторым витком;

— при ∣s∣ <δ: траектория проходит через S-петлю — гладкий мост между антисимметричными ветвями.

Инверсионный узел определяется как точка

S = 0, R (0),

где

(или другое симметричное соотношение по выбору модели)

и одновременно меняется знак ориентированных параметров:

Так задаётся строгое математическое содержание фразы «поворот на 180° и переход параметров движения между ветвями».

5. Внутренняя фаза и перенос состояния

Для физической, информационной или вычислительной интерпретации вводится поле состояния

Ψ (s),

которое живёт на Сфирали (волновая функция, спинор, бинарное состояние СИН и т.п.).

Фазовая антисимметрия задаётся условием:

Ψ₊ (s) = A Ψ₋ (−s),

где A — оператор инверсии (например, смена знака, комплексное сопряжение, оператор Парити-Времени и т. п. в зависимости от задачи).

В зоне S-петли состояние интерполируется аналогично геометрии:

Ψ (s) = α (s) Ψ₋ (s) + β (s) Ψ₊ (s), s ∈ [−δ, δ].

Инверсионный узел s = 0 задаёт точку согласования фаз

Φ (s) = arg Ψ (s),

где происходит сфиральный «щелчок» состояния (коллапс, фазовый переход, переключение ветви и т.п.).

6. Фрактальная вложенность Сфирали

Фрактальный характер структуры выражается в возможности построения вложенных Сфиралей оператором масштабирования.

Вводится оператор

F_k: R³ → R³,

F_k (R (s)) = λ_k R (_μks) + d_k,

где:

— λ_k> 0 — масштаб по пространству;

— μ_k> 0 — масштаб по параметру s;

— d_k — сдвиг центра уровня.

Тогда фрактальная Сфираль описывается суммарной структурой:

с весами w_k (например, геометрическая прогрессия).

Так задаётся иерархия уровней:

— k = 0 — базовая Сфираль (ядро);

— k = 1 — Сфираль на уровне подсистемы (подвиток, подканал);

— k ≥ 2 — глубокие уровни вложенности (геномные домены, ядерные уровни, каскады нейронов и т.п.).

7. Перепись динамики через сфиральное время

Любая динамика вида

где X — вектор состояния (координаты, поля, вероятности, параметры нейрона), переписывается через sss как

Если требуется зафиксировать структурное влияние Сфирали, вводится явная зависимость от геометрии R (s) и фазы φ (s):

Далее:

— для свободной частицы r (t) базовое уравнение превращается в геодезическое на сфиральной поверхности;

— для осциллятора возникает осциллятор со структурным демпфированием

— для квантового состояния уравнение Шрёдингера получает множитель ρ (s) и фазовую структуру, что переводит коллапс в переход через S-зону.

8. Итоговое развёрнутое определение

С учётом введённых обозначений удобно сформулировать компактную, но уже математически насыщенную версию:

Сфираль — это трёхмерная топологическая конструкция R (s), s ∈ R, представляющая собой сфиральный путь из двух зеркально антисимметричных витков V₋ и V₊, связанных S-образной переходной петлёй на интервале s ∈ [−δ, δ].

Витки определяются связью

r₊ (s) = M r₋ (−s) + c,

где M — оператор отражения с det M = −1. Переходная петля описывается интерполяцией

R (s) = α (s) r₋ (s) + β (s) r₊ (s), α² (s) + β² (s) = 1.

Внутренний параметр s задаёт сфиральное время и связан с внешним временем t функцией ρ (s) = dt/ds.

Состояние Ψ (s) переносится между витками через оператор A и зону S-петли, что придаёт структуре свойства комплементарности, направленности и фрактальной вложенности.