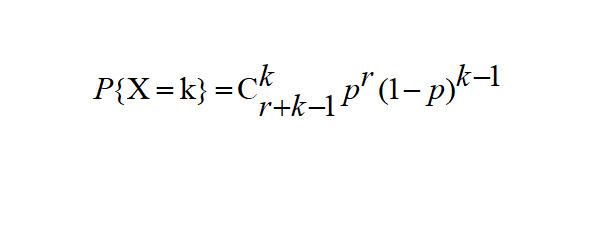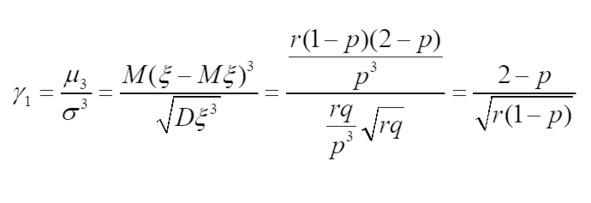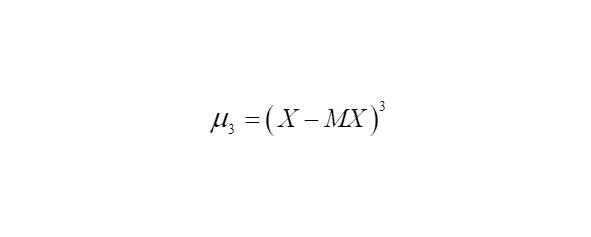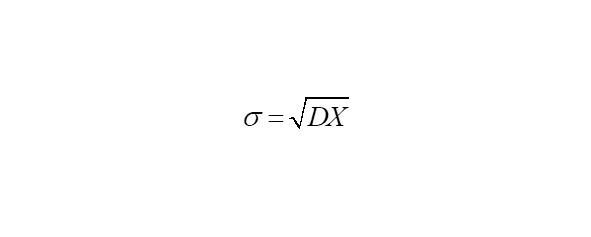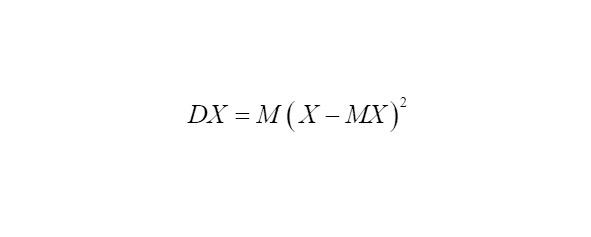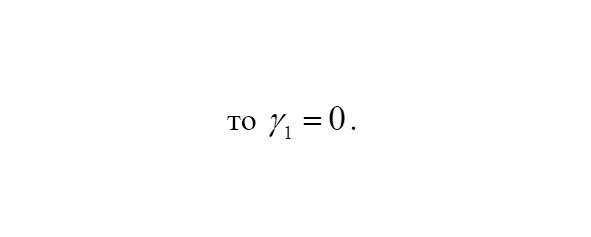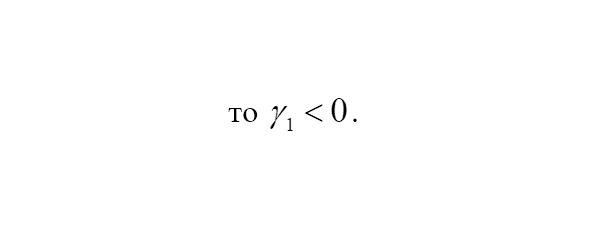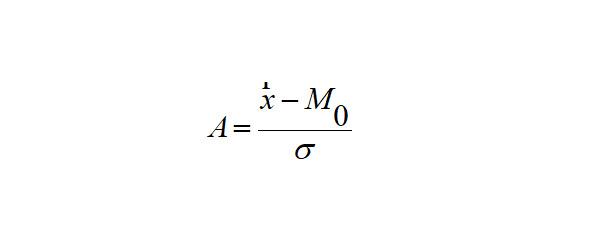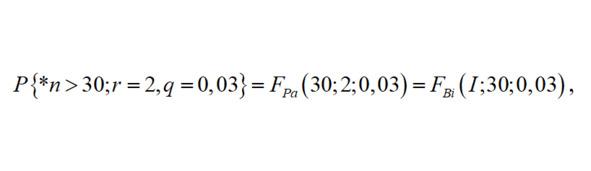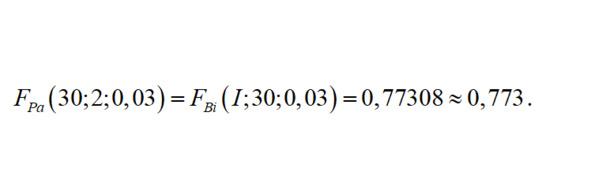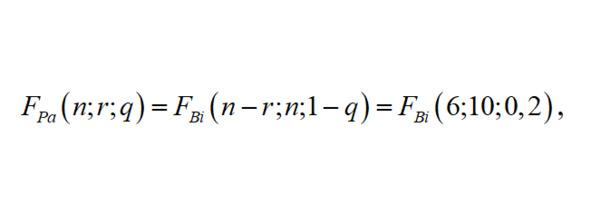ОТРИЦАТЕЛЬНО-БИНОМИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЕГО ПРИМЕНЕНИЕ В ЖИЗНИ
УДК: 530.1
Юсупова Анора Каримовна
Доктор физико-математических наук, профессор
Ферганский государственный университет, 150100, Республика Узбекистан, Ферганская обл., г. Фергана
Аннотация. В работе приведено основные понятие и общая формула отрицательно-биномиального распределение, продемонстрированы формула коэффициент асимметрии и доказательства распределенном на отрицательно-биномиальном распределении. Приведено сферы, где используется отрицательно-биномиальное распределение и примеры решенные с помощью этого распределения.
Ключевые слова: распределение Паскаля, испытание Бернулли, коэффициент асимметрии, центральный момент третьего порядка, среднеквадратичное отклонение, скошенность.
Abstrackt. The work presents the basic concept and general formula of the negative binomial distribution, demonstrates the formula for the skewness coefficient and evidence of distribution on the negative binomial distribution. The areas where the negative binomial distribution is used and examples solved using this distribution are given.
Key words: Pascal distribution, Bernoulli test, asymmetry coefficient, third-order central moment, standard deviation, skewness.
Annotatsiya. ish manfiy binomial taqsimotning asosiy tushunchasi va umumiy formulasini beradi, assimetriya koeffitsienti formulasini va manfiy binomial taqsimot bo’yicha taqsimotni isbotlaydi. Manfiy binomial taqsimot qo’llaniladigan sohalar va bu taqsimot yordamida hal qilingan misollar keltirilgan
Kalit so’zlar: Paskal taqsimoti, Bernulli testi, assimetriya koeffitsienti, uchinchi tartibli markaziy moment, standart og’ish, egrilik.
Введение
Отрицательное биномиальное распределение, также называемое распределением Паскаля — это распределение дискретной случайной величины, равной числу произошедших неудач в последовательности испытаний Бернулли с вероятностью успеха 푝, проводимых до 푟-го успеха.
Испытание Бернулли — это эксперимент с двумя возможными исходами — «успех» или «неудача» — и вероятность успеха одинакова при каждом проведении эксперимента.
Примером испытания Бернулли является подбрасывание монеты. Монета может приземлиться только с двух сторон (мы можем назвать орел «успехом», а решку «неудачей»), а вероятность успеха при каждом броске равна 0,5, если предположить, что монета честная. Если случайная величина Х подчиняется отрицательному биномиальному распределению, то вероятность испытать k неудач, прежде чем испытать r успехов, можно найти по следующей формуле:
КОЭФФИЦИЕТ АСИММЕТРИИ
Коэффициент асимметрии — это числовая характеристика случайной величины, равная отношению центрального момента третьего порядка к кубу среднеквадратического отклонения.
Коэффициент асимметрии характеризует скошенность распределения по отношению к математическому ожиданию. Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания.
Коэффициент асимметрии распределения случайной величины x определяется формулой:
где
— третий центральный момент случайной величины x;
— среднеквадратичное отклонение случайной величины x;
— дисперсия или второй центральный момент случайной величины;
Если плотность распределения симметрична, то
Если левый хвост распределения тяжелее, то
Если правый хвост распределения тяжелее, то
.
На рисунке показаны две кривые распределения: I и II. Кривая I имеет положительную (правостороннюю) асимметрию, а кривая II — отрицательную (левостороннюю).
Кроме вышеописанного коэффициента, для характеристики асимметрии рассчитывают также показатель асимметрии Пирсона:
коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента третьего порядка.
ПРИМЕНЕНИЕ ОТРИЦАТЕЛЬНО-БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Отрицательно биномиальное распределение широко используется в различных областях для моделирования случайных событий. Вот несколько примеров использования отрицательно биномиального распределения:
1. Маркетинг и реклама:
Предположим, что компания запускает рекламную кампанию и хочет оценить вероятность того, что клиент кликнет по рекламе до того, как совершит покупку. Отрицательно-биномиальное распределение может быть использовано для моделирования количества кликов до первой успешной покупки.
2. Производство и качество:
В производственной сфере отрицательно биномиальное распределение может быть применено для оценки количества бракованных изделий до достижения определенного числа рабочих изделий. Это помогает предсказать вероятность производственных сбоев.
3.Медицина и здравоохранение:
В медицинских исследованиях отрицательно-биномиальное распределение может использоваться для анализа количества лечебных процедур, которые пациент должен пройти до достижения определенного уровня выздоровления.
4. Финансы и страхование:
В финансовой сфере отрицательно биномиальное распределение может быть применено для прогнозирования количества страховых случаев до возникновения определенного количества убытков.
5. Техническое обслуживание и ремонт:
В сфере технического обслуживания и ремонта отрицательно биномиальное распределение может быть применено для оценки количества обслуживаний или ремонтов, которые требуются до возникновения определенного количества отказов или поломок.
6. Транспорт и логистика:
В логистике и транспортной отрасли отрицательно биномиальное распределение может использоваться для прогнозирования количества перевозок или доставок, которые могут быть выполнены до возникновения определенного числа задержек или неполадок.
7. Образование и наука:
В образовании и научных исследованиях отрицательно биномиальное распределение может быть применено для анализа количества экспериментов или учебных занятий, которые необходимо провести до достижения определенного уровня понимания или результатов.
8. Социология и психология:
В социологических и психологических исследованиях отрицательно биномиальное распределение может использоваться для моделирования количества повторений определенного поведенческого шаблона или реакции до достижения определенного результата.
Отрицательно биномиальное распределение имеет широкий спектр применений в различных областях и может быть полезным инструментом для анализа случайных событий и вероятностей.
Пример 1. Невосстанавливаемая система, работающая циклически, состоит из трех одинаковых по надежности ЭМ: двух основных и одного резервного, автоматически замещающего любой из отказавших основных ЭМ. Вероятность отказа ЭМ на цикле равна q = 0,03. Определить вероятность того, что система проработает 17 безотказно не менее 30-ти циклов, если резервное устройство не нагружено (не включено) и в этом состоянии не отказывает.
Решение.
Как следует из условия задачи, число циклов до отказа системы, равное числу циклов до второго по порядку отказа ЭМ в системе (r = 2) есть случайная величина *n, распределенная по закону Паскаля. Вероятность безотказной работы системы за 30 циклов равна
если воспользоваться уравнением связи с Биномиальным распределением. Окончательно из Таблицы при n = 30, q = 0,03 и r = 1, получим
Таким образом, примерно в 77 случаях из 100 такая система проработает безотказно не менее 30 циклов.
Пример 2. Спутник сканирует заданную акваторию океана за 4 оборота вокруг Земли. Если на каком-либо витке из-за различных помех происходит искажение текущего результата, то оно обнаруживается, и сканирование, выполненное на этом витке, повторяется заново. Найти вероятность того, что всё сканирование будет завершено не более чем за 10 витков, если вероятность искажения результата на одном витке составляет 0,2.
Решение
Для решения задачи удобно поменять местами события А — искажение результата сканирования на витке — на противоположное, тогда числу r будет соответствовать число успешно завершенных витков с вероятностью неискажения q = 0,8. С учетом этого замечания и связи с биномиальным распределением искомая вероятность решения задачи не более чем за n = 10 витков запишется в виде:
откуда из Таблицы при r = 6, n = 10 и q = 0,2 получим
то есть примерно в одном случае из тысячи в заданных условиях сканирование не завершится за 10 оборотов спутника вокруг Земли.
Заключение
В работе была сформулирована и доказана формула коэффициент асимметрии распределенном на отрицательно-биномиальным распределении. Была приведено примеры и сферы применение этой распределении.
ИСПОЛЬЗОВАННЫЕ ЛИТЕРАТУРЫ
1. Баврин И. И. Теория вероятностей и математическая статистика / И.И.Баврин. — М.: Высш. шк., 2005. — 160 с:
2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике /В. Е. Гмурман. — М., Высш. шк., 2004.- 404 с.
3. Гмурман, Владимир Ефимович. Теория вероятностей и математическая статистика: учебное пособие для вузов /В. Е. Гмурман.-Изд. 12-е, перераб.-М.:Высшая школа,2009.-478с.
4. Гнеденко Б. В. Курс теории вероятностей: Учебник / Б. В. Гнеденко. — Изд. 8-е, испр. и доп. — М.: Едиториал УРСС, 2005. — 448 с.
5. Кремер Н. Ш. Теория вероятностей и математическая статистика: Учебник для вузов / Н. Ш. Кремер. — М.: ЮНИТИ-ДАНА, 2004. — 573 с.
6. Максимов Ю. Д. Вероятностные разделы математики / Ю. Д. Максимов. — Изд.: Иван Федоров, 2001. — 592 с.