Оглавление

Введение

Привет, любители математики и те, кто попал сюда случайно! Представьте себе мир, где древние мудрецы и современные гики объединились ради одной цели — рассказать вам всё о тригонометрии. Да, та самая штука, которая заставляла вас страдать в школе, оказывается, гораздо интереснее, чем кажется!

Здесь мы вспомним всех старых друзей: индийские джья, забытые версинусы и экссекансы, и даже современных ребят типа cas и cis. Каждый из них раскроет вам свои секреты: аналитические описания, графики, и раскраска домена комплексной области (потому что почему бы и нет?).

Но не думайте, что на этом всё закончится. Мы нырнём в глубины гиперболических, параболических и эллиптических тригонометрических функций. Вы слышали о синусах и косинусах лемнискаты и суперэллипса? Нет? А зря!

И, конечно, практическая польза. Навигация, строительство и просто красивые графики — всё это вы найдёте здесь. Мы даже создадим уникальную схему всех древних круговых тригонометрических функций на тригонометрической окружности. Круто, правда?

Так что приготовьтесь к увлекательному путешествию. Эта книга — ваш путеводитель по миру, где математика превращается в магию. Пристегните ремни и поехали!

Очерк истории

Итак, дорогие читатели, приготовьтесь к захватывающему путешествию по волнам синусов и косинусов, и узнайте, как великие умы человечества шаг за шагом раскусывали орех под названием тригонометрия.

Прежде чем нырнуть в тригонометрический зоопарк функций, давайте сначала забросим взгляд на историю возникновения науки об углах. Итак, представьте себе: первым тригонометрическим инструментом был не что иное, как гномон. Да-да, просто столб, воткнутый в землю, который отбрасывал тень. И потом завертелось…

Гномон был как смартфон для древних египтян и вавилонян — простой и эффективный способ отслеживать время и изменения углов. Этот невзрачный столбик показал, что если подойти к углам с умом, можно творить настоящие чудеса. Позже умные ребята начали использовать этот столбик не только для определения времени, но и для того, чтобы предсказывать солнечные и лунные затмения. В общем, столбики стали настоящими предвестниками тригонометрии.

И так началась великая эпопея развития тригонометрии. От древних греков, которые впали в любовную связь с углами, до индийских математиков, которые изобрели свои собственные тригонометрические штучки. Мир не знал покоя. Люди рисовали, вычисляли и доказывали, что тригонометрия — это не просто заумные формулы, а ключ к тайнам Вселенной! И сейчас без этих древних функций, никуда, даже в Квантовой Теории Поля! Но обо всём по порядку. Саму историю становления тригонометрии, как самостоятельной науки, можно разделить на несколько этапов:

Древний Египет и Вавилон: когда тригонометрия была ещё в подгузниках

Начнём с древнего Египта и Вавилона, где задолго до того, как кто-то додумался до интернета, люди уже вовсю играли с углами. Вавилоняне, например, в 2 тысячелетии до н. э. создали первые таблицы синусов. Ну, почти синусов — тогда это были таблицы хорд, но давайте не будем придираться к мелочам.

Эти таблицы можно считать прабабушками современных таблиц синусов. Вавилоняне были настолько крутыми, что их таблицы хорд могли использоваться для решения астрономических задач и предсказания движения небесных тел. Ну, почти как нынешние астрологи, только с реальными математическими вычислениями.

Древняя Греция: когда всё стало серьезно

Перенесёмся в Древнюю Грецию, где тригонометрия нашла своего первого серьёзного гуру — Гиппарха. Этот парень в 2 веке до н. э. не просто забавлялся с углами, он создал первые таблицы хорд для кругов разного радиуса. Да, Гиппарх был настолько зациклен на кругах, что даже по ночам считал углы вместо овец. Но его усилия не пропали даром: его таблицы стали основой для всех последующих тригонометрических исследований.

И тут появляется Птолемей. Нет, не тот фараон, а великий астроном и математик, который в 2 веке н. э. написал «Альмагест» — труд, который можно считать первым тригонометрическим бестселлером. В «Альмагесте» Птолемей объединил знания о хордовых таблицах и сферической тригонометрии, создав своего рода древнегреческий Google Maps для астрономов.

Индия: джья и котиджья — новые тригонометрические магии

Тем временем в Индии всё кипело и бурлило. Ариабхата в 5 веке и Брахмагупта в 7 веке придумали джья и котиджья. Если вы думаете, что это блюда из ресторана, то ошибаетесь — это ранние версии синуса и косинуса. Ариабхата создал таблицы значений джья (синуса) для различных углов, что стало революционным шагом вперёд. Эти ребята не просто изобрели новые функции, но и заложили основу для всех будущих тригонометрических расчётов.

Кроме джья и котиджья, в арсенале индийских математиков был ещё один хитрый инструмент — уктам-джья, аналог ныне уже почти забытого синус-версуса. Эти функции позволяли индийцам решать сложные астрономические задачи с поразительной точностью. В общем, индийская тригонометрия была как айфон своего времени — продвинутая и невероятно полезная.

Исламский мир: эпоха математического ренессанса

Пока Европа спала в Средние века, в исламском мире тригонометрия процветала. Аль-Баттани в 9 веке и Абу-ль-Вафа в 10 веке развили сферическую тригонометрию и добавили новые функции. Эти ребята играли с углами так, как нынешние подростки играют в видеоигры — только с большей пользой для человечества.

Ещё один важный вклад внёс Абу-л-Вафа, который ввёл тангенс и котангенс в сферическую тригонометрию. Это было как найти священный Грааль — теперь астрономы могли делать точные вычисления для навигации и строительства. Астролябия стала их незаменимым гаджетом, с помощью которого они измеряли углы и строили карты звёздного неба.

Средневековая Европа: возвращение тригонометрии

Наконец, Европа проснулась от средневековой спячки. Герхард Меркатор в 16 веке создал таблицы и карты, которые помогли мореплавателям не теряться в океане. Джон Непер в 1614 году изобрёл логарифмы, что существенно упростило тригонометрические расчёты. Представьте, что у вас появился калькулятор после долгих лет вычислений на пальцах — вот такой эффект произвело его изобретение.

Ренессансные учёные, такие как Виет и Клавий, активно работали над улучшением тригонометрических таблиц и методов вычислений. Это позволило Европе выйти на новый уровень в науке и технике, от артиллерии до архитектуры.

Современная эпоха: тригонометрия выходит на новый уровень

И вот мы добрались до современных титанов математики. Леонард Эйлер в 18 веке ввёл современные обозначения, сделав нашу жизнь проще и понятнее. Карл Фридрих Гаусс в 19 веке работал над неевклидовой геометрией и сферической тригонометрией, доводя всё до блеска. С их помощью тригонометрия стала фундаментом для развития физики, инженерии и даже экономики.
С появлением калькуляторов, тригонометрия потеряла часть своего старого шарма — ведь зачем мучиться, когда можно просто нажать на пару кнопок? Из более чем 30 славных функций в наши дни в ходу осталось всего четыре жалкие штучки. Но не печальтесь, математики-сентименталисты, в этой книге мы устроим настоящее тригонометрическое воскрешение! Поднимем все забытые функции из небытия, потому что иногда красота в математике важнее, чем удобство.

Так что, друзья, когда вы в следующий раз будете ломать голову над тригонометрией, вспомните, что за каждым уравнением стоит многовековая история открытий и приключений. Тригонометрия — это не просто формулы, это эволюция человеческой мысли, путь от древних таблиц хорд до современных методов расчёта.

Немного вспомним о полезном

Прежде чем заниматься тригонометрической некромантией, давайте удостоверимся, что вы знакомы с элементарными геометрическими понятиями. Знаете, что такое треугольник (в современном мире это, увы, не шутка), что такое подобные фигуры, углы; помните теорему Пифагора, известную ещё до него в древнем Египте, и какие существуют угловые меры.

Краткий курс для чайников

Угол: Где без него

Угол — это пространство между двумя пересекающимися прямыми. Если провести две прямые и они встретятся, то угол между ними можно измерить в градусах. Углы бывают острые, тупые и прямые, в зависимости от того, насколько круто пересеклись ваши линии.

Градусы: Легенда о 360 кусочках пиццы
Когда-то давно, в Древнем Вавилоне, сидели мудрецы и думали, как бы им порезать круг так, чтобы никто не обиделся. А круг, надо сказать, не простой, а с самыми что ни на есть магическими свойствами. Решили они, что 360 кусочков будет в самый раз. Почему 360? Да просто! Это число делится на кучу других чисел: 2, 3, 4, 5, 6, 8, 9, 10 и так далее. В общем, под это дело можно было закатить любую вечеринку, и каждый получил бы по своему куску пиццы, то есть круга. Вот и получилось, что полный оборот круга — это 360 градусов. Причём, это не просто красивая цифра, а практически волшебная. Ведь тогда ещё не было калькуляторов и компьютеров, так что мудрецы выбрали самое удобное число для своих расчётов. Это позволило легко делить круг на равные части, проводить измерения и строить свои великие Вавилонские башни. Откуда же такие умные головы знали, что 360 — это магическое число? Ну, есть тут один момент. В Вавилоне ещё и астрономы были что надо. Они заметили, что Солнце за год делает один полный оборот по небу. А год, как известно, это 365 дней (ну почти). Но так как мудрецы любили круглые числа, они округлили до 360. Так и родилась градусная мера угла. И вот так, благодаря древним вавилонским гениям, мы теперь меряем углы в градусах. И это настолько прочно вошло в наш обиход, что даже в космос без градусов не полетишь. Ведь с градусами всё понятно: 90 градусов — это прямой угол, 180 — полукруг, 360 — полный круг. Всё просто и логично. И, конечно же, это дало старт для дальнейших тригонометрических подвигов. У нас теперь есть куча формул и вычислений, основанных на градусах. Так что, несмотря на то, что радианы тоже хороши, градусы — это наша древняя, но всё ещё актуальная мера угла. Всё благодаря мудрецам, которые сидели и ломали голову, как порезать круг на равные части. И сделали это так, что мы до сих пор пользуемся их системой.

Треугольник — это такая штука с тремя сторонами и тремя углами. Причем, вы не поверите, углы могут быть разной величины, а стороны разной длины. Самая скучная версия треугольника — это равносторонний, все углы и стороны у него одинаковые, но есть и более интересные экземпляры, такие как разносторонний и равнобедренный.

Подобные треугольники: Братья по пропорциям

Подобные треугольники — это такие треугольники, у которых одинаковые углы и стороны пропорциональны. Представьте, что у вас есть большой треугольник и маленький, но они выглядят как увеличенные или уменьшенные копии друг друга. Стороны таких треугольников относятся как A/a=B/b=C/c=k, где k — логично назвать коэффициентом подобия. Он показывает во сколько раз одна фигура является увеличенной копией другой.

И тут начинается магия. Площади подобных треугольников относятся как квадраты длин соответствующих сторон. То есть, если один треугольник больше другого в два раза по стороне, то его площадь будет больше в четыре раза. Простая математика, ничего сложного.

Таким образом, если у вас есть два треугольника и один из них похож на другого, просто в меньшем масштабе, то они подобные. И это открывает перед вами кучу интересных возможностей, как, например, считать их площади, не утруждаясь долгими вычислениями.

В общем, подобные фигуры — это всегда про увеличенные или уменьшенные копии. Будь то треугольник на листе бумаги или гиперкуб в пятом измерении, всё работает по одним и тем же правилам в пространстве любой размерности. Стороны подобных фигур относятся как первая степень k, площади как вторая, объёмы как третья, гиперобъёмы как четвёртая, ну вы поняли…

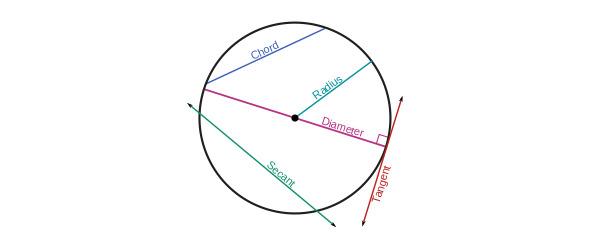
Окружность

Треугольники — это вообще тема отдельная. Их можно нарисовать сколько угодно, с разными углами и сторонами. А вот с окружностями такой номер не пройдёт. Любая окружность всегда подобна другой. То есть, все окружности, что вы нарисуете, будут одинаково хороши. Это знание в древности привело к понятию числа «Пи».

Если разделить длину окружности изображённой в плоском пространстве (это важно!) на диаметр, то мы аккурат получим 3,1415926… Что бы не писать всю эту бесконечную последовательность цифр, её заменили значком π. Ну а что, удобно и красиво!

Теперь, зная про π, можем перейти к измерению дуг и углов в радианах. Радиан — это угол, который вырезает дугу длиной, равной радиусу окружности. То есть, если обхватить окружность с радиусом в 1 метр, то угол в 1 радиан вырежет дугу длиной тоже в 1 метр. Логика здесь простая, как дважды два.

Всё это приводит нас к мысли, что π радиан — это 180 градусов. А значит, полный оборот (или 360 градусов) — это 2π радиан. Ну и делаем из этого кучу полезных выводов. Например, что половина оборота (или 90 градусов) — это π/2 радиана. И так далее. Удобно? Ещё как!

Теперь вы можете измерять углы в радианах, как настоящий математический гуру. Плюс, это знание пригодится для расчётов в тригонометрии. И неважно, занимаетесь ли вы древней геометрией или строите новые гиперпространства — всё это работает одинаково хорошо. Так что давайте нырнём глубже в этот удивительный мир тригонометрии и откроем для себя ещё больше магических чисел и функций!

Радианы удобны в математике и физике, потому что они тесно связаны с длиной дуги и радиусом. А как только начали мерять в радианах, оказалось, что это прямо-таки магическая мера. Всё так красиво и просто в формулах получается. Прямо бальзам на душу любого математика. Обозначаются как рад, и международное: rad; от латинского radius — луч, радиус.

Телесные углы, стерадианы: вечеринка продолжается

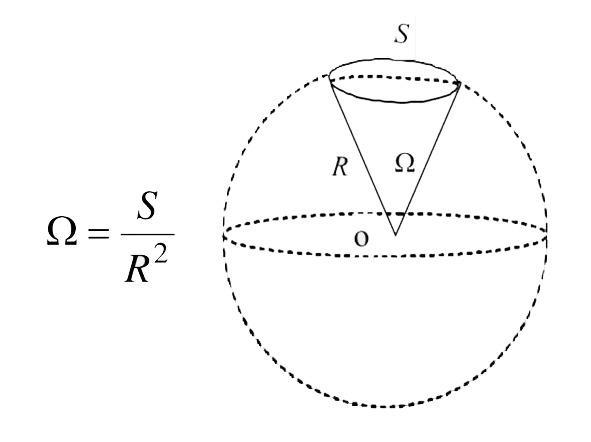
Но время не стояло на месте, и вскоре люди поняли, что мир-то у нас трёхмерный, и начали думать, как бы им померить углы не только на плоскости, но и в объёме. И тут на арену вышли телесные углы и стерадианы — более продвинутая версия углов для измерения в трёхмерном пространстве.

Телесный угол — это такой угол, который вершиной своей упирается в центр сферы, а его «лучи» охватывают часть поверхности этой сферы. Как бы вам это проще объяснить… Представьте, что вы сидите в центре футбольного мяча и светите фонариком. Вот сколько поверхности мяча осветите — это и есть телесный угол.

Теперь к стерадианам. Полный угол вокруг вас в трёхмерном пространстве — это 4π стерадиана (площадь поверхности единичной сферы равна 4π). Если радианами меряют углы на плоскости, то стерадианами — в объёме. Один стерадиан — это такой телесный угол, который отсекает от сферы кусок поверхности, равный квадрату радиуса этой сферы. То есть, если у вас есть шарик радиусом 1 метр, и вы отсекаете кусок поверхности площадью 1 квадратный метр, то это и будет 1 стерадиан. Когда вы смотрите в угол комнаты, то перед вами предстаёт объёмный угол в π/2 стерадиан, что как раз и само просится называться прямым объёмным углом. Плоскость относительно любой своей точки задаёт развёрнутый телесный угол в 2π стерадиан. Круто же?!
Название стерадиан -это смесь древне-греческого στέρεος — твёрдый, объёмный, пространственный, и латыни radius. Обозначается как ср, и в международье как sr. Альтернативой стерадиану является квадратный градус.

Зачем это всё надо? Ну, если вы вдруг решили, что телесные углы и стерадианы — это чисто для гиков-математиков, то глубоко заблуждаетесь. Представьте, что вы астроном, смотрите в телескоп и пытаетесь понять, какой кусок неба охватывает ваше поле зрения. Или вы инженер, занимающийся радиолокацией, и вам нужно точно рассчитать, какой участок пространства покрывает ваш радар. Вот тут-то и приходят на помощь стерадианы. Они делают вашу жизнь проще и точнее.

Так что, хоть на первый взгляд вся эта тригонометрическая магия и кажется сложной, на самом деле это просто разные способы взглянуть на привычные вещи. Градусы, радианы, стерадианы — всё это звенья одной цепи, связывающей плоские и объёмные углы в единую картину. А как только вы это поймёте, мир вокруг станет немного проще и понятнее.

Прямоугольный треугольник: Король тригонометрии

В плоском пространстве у треугольника может быть прямым, только один угол. Если перед вами такой треугольник, то его логично назвать прямоугольным, и это его свойство может значительно упростить вам все расчёты связанные с ним.

Анатомия прямоугольного треугольника проста.

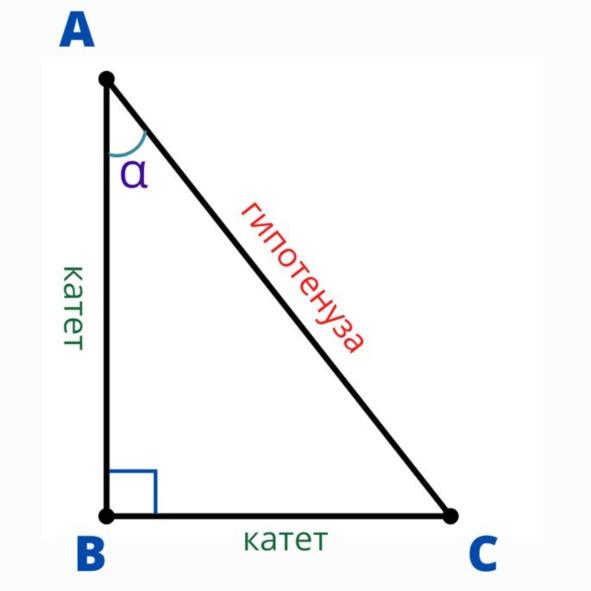
Гипотенуза: Эта самая длинная сторона, напротив прямого угла, является главной звездой шоу. Без неё — никуда.
Катеты: Две стороны, образующие прямой угол. Катеты — это такие скромные труженики, которые всегда в тени гипотенузы, но именно они делают весь тяжёлый подъём.
Прямой угол: Угол в 90 градусов, который делает этот треугольник особенным. Прямой угол — это как VIP-пропуск на любую геометрическую тусовку.