Оглавление

Математика — точная наука. Она с одинаковой точностью отражает законы природы и фантазии физиков. Но физики фантазируют не ради фантазии. Они думают, что открывают законы природы. Поэтому задача официальной науки не запрещать физикам фантазировать, а научиться находить в их фантазиях элементы математики природы.

А. А. Астахов

Удивительно точную мысль по поводу дальнейшего развития физики сформулировал А. П. Смирнов в статье «Осознание знания откровение XXI века». Человечество накопило огромное количество практических, опытных знаний о природе и эмпирически точно установленных закономерностей. Поэтому не нужно искать физические теории в дебрях формально-математических преобразований, чем сегодня увлекается множество современных исследователей. Многие вопросы можно решить, разобравшись с тем, что мы уже знаем достоверно. Этого вполне достаточно для правильных теорий, построенных на основе математики природы.

А. П. Смирнов, А. А. Астахов

«Может быть, мое мнение меня обманывает; поэтому я хочу быть собеседником, а не судьей, исследователем, а не основоположником; я готов учиться у каждого, кто предлагает что-то более правильное и достоверное… Если же читатель увидит, что оснастка моего сочинения равна той, которая имеется у противоположной стороны, тогда он сам взвесит и рассудит, что имеет большее значение: суждение всех просвещенных людей…, всех университетов…, или же частное мнение того или иного человека… Я знаю, в жизни нередко случается, что большая часть побеждает лучшую. Я знаю, что при исследовании истины никогда не лишне добавить свое прилежание к тому, что было сделано прежде».

Эразм Роттердамский

В мире, как он описывается многими науками, отсутствует смысл. Это, однако, означает не то, что мир лишен смысла, а лишь то, что многие науки слепы к нему. Смысл приносится в жертву многими науками.

Виктор Франкл

ВВЕДЕНИЕ

Настоящая работа посвящена анализу физической сущности современных знаний о природе, связанных с движением и взаимодействием материи. Появляющиеся в последнее время в современной науке мнения о первичности вращательного движения, основанные на строении микромира, а также на вращении эфирных вихрей, образующих элементарные частицы вещества несостоятельны. Строение вещества и движение материи это разные вещи. Любое движение первоначально возникает как прямолинейное движение, т.к. в природе не существует криволинейных сил. Это непосредственно следует из законов динамики Ньютона, которые на сегодняшний день считаются незыблемыми. Все попытки некоторых современных авторов внести свои коррективы в законы Ньютона не меняют их физической сущности.

В первом законе Ньютона говорится исключительно о прямолинейном движении. Второй закон Ньютона определяет силу и ускорение, которые возникают вдоль одной общей прямой линии предшествующего равномерного прямолинейного движения взаимодействующих тел. Если предшествующие движения пересекаются под углом, то результирующее движение в любом случае представляет собой результирующую прямую линию. Об этом же говорит и третий закон Ньютона. Попробуйте представить себе силу взаимодействия, которая действует на взаимодействующие тела в противоположных направлениях, но не вдоль одной прямой, а как-либо иначе. Естественно, что это не возможно, т.к. противоположные направления по определению находятся только на одной прямой, но никак не на кривой линии.

Криволинейное движение возникает только при дополнительном силовом воздействии, имеющим иное направление, чем направление текущего активного или так называемого инерционного прямолинейного движения. Криволинейное движение, образующееся за счет множества разнонаправленных прямолинейных взаимодействий, является более сложным движением, чем прямолинейное движение, а, как известно, сложное не может быть элементом простого.

Таким образом, основным элементом механического движения в природе является прямолинейное перемещение в пространстве. Даже если вещество образовано вихрями амеров эфира, то в свободном пространстве между соударениями они, очевидно, движутся прямолинейно.

Вследствие непрерывных разнонаправленных взаимодействий материальных тел между собой, а также с мировой материальной средой прямолинейное движение в чистом виде в природе встречается довольно редко, что дает ложное основание считать основополагающим движением — вращательное движение. Однако в природе так же редко встречается и вращательное движение в чистом виде. Первичность прямолинейного движения непосредственно следует из физического механизма формирования вращательного движения, которое в свою очередь является простейшим базовым элементом любого произвольного криволинейного движения. Вариант такого механизма приведен в настоящей работе.

По некоторым практическим соображениям мы попытались разобраться в физической сущности вращательного движения на уровне физического механизма преобразования движения по направлению и столкнулись с многочисленными противоречиями не только в существующей математической модели вращательного движения во всех его проявлениях, но и с другими проблемами классической физики, связанными с теорией движения в целом. Как выяснилось, в современной физике практически отсутствует описание явлений природы на уровне их физических механизмов.

В большинстве случаев всё сводится лишь к количественному математическому описанию природных закономерностей, в котором нет места физическому, а иногда и элементарному здравому смыслу. За физический смысл природных явлений зачастую выдается лишь краткое словесное описание математических формул. Причем словесное описание даже правильных формул только подтверждает количественную оценку найденной закономерности, но не отражает ее физическую сущность на уровне причинно-следственных связей. Даже популяризаторы науки в основном преподносят широкой аудитории описание природы на уровне её математического отображения в виде условных символов и знаков.

В природе не существует формальных математических правил. Математика это и есть физика, записанная в условных обозначениях: символах и знаках. Однако современный учебный процесс построен так, что в будущих математиках закрепляют знание математических правил в основном на формальном уровне. Во всяком случае, маститые математики практически забывают физическую основу ставших для них привычными стандартных математических операций.

Например, дополнительные множители не нарушают равенство. Однако если речь идёт о физических величинах, в которых этих множителей нет, то такое равенство не является физическим. Тем не менее, некоторые физики от формальной математики, умножая обе части физических формул на одну ту же величину иногда получают новые физические величины, там, где их нет, нарушая главный закон природы — Закон сохранения истины! На формально математических преобразованиях иногда даже строятся новые физические теории, хотя все должно быть наоборот.

В современной теоретической физике спокойно существуют и обсуждаются на самом высоком научном уровне такие понятия, как: «искривление пространства и времени», «кручение пространства», «пространство-время», «вибраторы-струны», «пятые, шестые и энные измерения». Ни один физик на Земле и даже авторы этих понятий не могут объяснить непосвященному человеку и даже специалистам, что это такое, потому что эти понятия не физические. Они получены из формально математических преобразований не физических величин, а предполагаемых допущений — постулатов и из всевозможной замены переменных. Но это уже не наука, а математическая религия.

Найти убедительные аргументы против откровенных глупостей достаточно сложно. Глупость нельзя опровергнуть в принципе, т.к. логика против нее бессильна. Особенно если эта глупость складывалась веками и формально подтверждена правильными математическими формулами. Это касается преобразования направления скорости без преобразования ее величины; однонаправленных линейных ускорений, которые изменяют скорость якобы только своего вида движения без взаимного влияния друг на друга; утверждения о фиктивности силы инерции без знания ее природы и при реальных энергетических затратах на ее преодоление; невозможности изменения импульса замкнутой системы физических тел в мировой материальной среде, в которой в принципе не может существовать замкнутых систем и многого другого.

Альтернатива откровенной глупости вовсе не означает альтернативы законам природы. А вот некоторые представители классической физики делают её альтернативной законам природы. Однако, как это ни парадоксально умные люди бояться идти против общественного мнения, поддерживающего глупость, чтобы самим не прослыть глупцами или альтернативщиками (альтами), как обидно называют официалы всех, кто выступает против откровенных глупостей современной науки. Мало кто отважится сказать, что король голый, если все вокруг утверждают, что он прекрасно и изысканно одет. В результате все вокруг считаются умными людьми, а физика 21 века топчется на месте только потому, что в свите короля нет честного человека, который не боится прослыть «глупцом».

В известной сказке эту роль выполняет младенец, который, может позволить себе говорить то, что он видит и думает и вовсе не потому, что он глуп, а потому, что он еще не научился лгать. В сказке младенца послушали, но в науке этого недостаточно. В науке люди, выступающие в роли таких младенцев, в лучшем случае просто игнорируются «умными» людьми из свиты короля. А в худшем случае на них спускают придворных псов.

Любые математические модели должны отражать только сложную связь давно устоявшихся и проверенных опытом элементарных понятий в физике. Только тогда они будут достаточно точно отражать природные явления. Наверное, современной наукой открыты еще не все элементарные инварианты. Однако возможности существующих классических инвариантов для определения физической сущности всех известных на сегодняшний день явлений природы еще далеко не исчерпаны.

Нарушений законов природы не может быть в принципе. Все, что происходит в природе, происходит только в соответствии с законами природы или не происходит вообще. Нарушения могут быть только в нашем понимании законов природы. Поэтому все, что на первый взгляд не вписывается в классические теории, объясняется только несовершенством существующей теории, а не нарушением законов природы.

В настоящей работе приведены многочисленные примеры, когда не вписывающиеся на первый взгляд в классическую физику явления природы находят у различных авторов вполне приемлемое объяснение, основанное на привычных элементарных понятиях. Например, полный импульс движения включает в себя не только линейный импульс, но и вращение. С учетом полного импульса разрешаются многие вопросы, связанные с кажущимся нарушением закона сохранения импульса в линейных взаимодействиях и многое другое.

Главной задачей настоящей работы является ни в коем случае не пересмотр давно открытых и проверенных опытом природных закономерностей, а придание им физического, а значит и здравого смысла, которого в современной физике хронически не хватает. Конечно же, исходя из истинного физического смысла, возможны некоторые уточнения существующих взглядов. Однако сделанные нами уточнения не выходят за рамки здравого смысла, т.к. они основаны на классических элементарных понятиях и принципах причинности, а не на постулатах, не подтверждающихся экспериментально и изобретаемых только для реализации далеких от реальной действительности математических моделей.

В работе предпринята попытка выявления физического смысла вращательного движения и его динамики, силы и ускорения Кориолиса, полного ускорения сложного движения, явления инерции, определяющего формирование сил взаимодействия, через которые осуществляется перераспределение энергии взаимодействия, а также физического смысла законов Ньютона. Рассмотрены вопросы так называемого безопорного движения. Дана критика некоторых авторов, а также современных ученых, которые очень уж рьяно, но, к сожалению, неумело или недостаточно аргументировано выступают в защиту своих консервативных взглядов.

Читатель может не согласиться с предложенными физическими механизмами, позволяющими разрешить существующие противоречия аналогичных классических моделей природных явлений. Однако мы не претендуем на истину в последней инстанции. Все существующие научные знания это только грубые математические и физические модели природных явлений. Реальная действительность значительно сложнее любых ее моделей, создаваемых наукой.

Мы можем сколь угодно близко подходить к истине, но никогда ее не достигнем, поскольку логика, построенная на элементарных понятиях не способна объяснить сами эти элементарные понятия. Элементарные понятия являются базой нашей логики, а для объяснения базы необходима другая база ещё более элементарных понятий, которой у нас пока нет. Однако другой логики у нас нет. Поэтому самое важное в любой теории это не абсолютная точность во всех её деталях, а её принципиальное соответствие здравому смыслу и проверенным элементарным понятиям. Окончательную оценку любой теории, как всегда, выставит время. Однако если теория не противоречит здравому смыслу, то со временем она никогда полностью не пересматривается, а только уточняется и дополняется.

Конечно же, на бытовом уровне здравый смысл у всех людей разный, поскольку зачастую он отражает законы человеческой психики, не всегда связанной с объективной реальностью. Как говорится правда у всех своя. Однако в науке здравый смысл может быть только один. Он основан на элементарных понятиях, отражающих основные сведения о природе, подтверждающиеся тысячелетним опытом контакта человека с реальной действительностью на доступном ему уровне.

Мы можем не знать всех закономерностей природы и всех причин, происходящих в ней явлений. Однако новые неоткрытые закономерности не могут противоречить тому, что мы уже знаем о ней достоверно, хотя и на уровне элементарных понятий. Это означало бы, что природа противоречит самой себе, чего не может быть в принципе. Непознаваемость природы может быть связана с её бесконечным многообразием, но никак не с отсутствием в ней причинно-следственных связей, которые и определяют и ее, и наш с вами здравый смысл, который основан на образных представлениях.

Природа оперирует не цифрами и не формулами. Она оперирует реальными явлениями и процессами. Так же, как и человек мыслит не цифрами и не формулами, а образами, которые отражают материю во всех её проявлениях в пространстве в нашем сознании. И если математическую модель, какого-либо явления невозможно представить образно, то это вовсе не значит, что природа непознаваема для человека, как, например, говорят в отношении теории относительности Эйнштейна её защитники.

Это означает, что теория, скорее всего, не верна, т.к. она не совместима с образами, отражающими природу, т.е. с самой природой. Поэтому не поддавайтесь на утверждение консервативной части научного сообщества, что вы якобы не умны, раз не способны понять их несостоятельные теории. Они не более умны, чем вы и только прикрываются своими абстрактными математическими формулами, которые без физического обоснования связи этой абстракции с реальной действительностью ничего не значат.

Если отбросить малопонятные для непосвящённого человека термины, то объяснения природных явлений даже у маститых академиков не выходят за рамки обычной детской логики. Попросите академиков объяснить их формулы и представления, облечённые в мудрёные специальные термины, через образные представления, т.е. на пальцах, как говорят в народе, и вы услышите в ответ такой родной и понятный для всех детский лепет, т.к. логика на всех одна и на детей и на маститых академиков.

Причём это в лучшем случае. А в худшем вам просто намекнут, что вы недостаточно умны, что означает, что академики сами не понимают, о чём говорят.

Как говорил сам автор самой непонятной в науке теории Эйнштейн:

«Если не можете объяснить свою мысль пятилетнему ребёнку, значит, Вы сами её плохо понимаете».

И об этом вы тоже прочитаете в настоящей работе.

Ничего позорного и унизительного в ошибках нет. Без ошибок развитие науки не возможно. Но оно невозможно и без признания этих ошибок. Тем не менее, маститые академики, наделавшие эти ошибки и много лет преподающие их студентам и обществу, не хотят их признавать. И руководствуются они в этом вовсе не интересами науки, а собственными низменными интересами. В этих условиях, только накопив критическую массу критических замечаний в обществе, можно стимулировать развитие науки. Поэтому мы обращаемся к вам. Читайте, думайте, анализируйте! И присылайте ваши критические замечания.

И ещё один момент, на который мы хотим обратить внимание читателя. В предлагаемой работе повествование идёт от множественного числа «мы». Это не значит, что нас много. Автор пока практически один. Но выражение «мы» я употребляю по следующим четырем причинам:

Во-первых, когда автор кому-то что-то пытается объяснить, то он приглашает своих слушателей в собеседники, при этом он справедливо полагает, что он уже не один.

Во-вторых, предлагая своё видение вопроса, каждый автор надеется всё-таки приобрести единомышленников и поэтому ведёт повествование и от имени тех, кто с большой долей вероятности в достаточно большой аудитории может его поддерживать. Если же он говорит «я», то он в некотором смысле противопоставляет себя возможным единомышленникам.

В-третьих, говорить от собственного лица, т.е. «якать» не совсем скромно, потому что каким бы новым не было мнение автора, он всегда в значительной степени опирается на опыт, накопленный другими авторами. Ссылки на них, конечно же, этически необходимы. Однако при этом в любом случае даже самое новое видение автора остаётся не совсем его собственным независимым мнением. Ведь даже свои элементарные знания он получает от общества.

И наконец, в-четвёртых, наверное, именно из приведённых выше соображений обращение «мы» общепринято в практике публичных работ.

4. ЯВЛЕНИЕ КОРИОЛИСА — ФИЗИЧЕСКИЙ СМЫСЛ

Густав Гаспар Кориолис (1792—1843 гг.) — французский математик и механик открыл силу инерции, названную впоследствии его именем. Она возникает в неинерциальной вращающейся системе отсчета. Он также вывел ее формулу.

Сила Кориолиса равна удвоенной радиальной скорости (V_р), умноженной на угловую скорость вращения (ω) и умноженную на синус угла между ними, а так же на испытуемую массу (M).

В классической физике описаны два варианта проявления силы и ускорения Кориолиса.

В первом варианте относительная скорость направлена вдоль радиуса вращающейся системы. Здесь действительно проявляется достаточно выраженное явление, которое в классической физике ассоциируют с ускорением Кориолиса. Однако в классической физике за силу и ускорение Кориолиса фактически принимается противо реакция на обычную тангенциальную силу, которая поддерживает угловую скорость переносного вращения. Поддерживающая сила — это либо сила, действующая на движущееся радиально тело со стороны вращающихся масс системы, которые не изменяют своего радиального положения, либо любая внешняя сила, которая поддерживает переносную угловую скорость на постоянном уровне.

В отсутствие поддерживающей силы происходит естественное уменьшение угловой скорости при радиальном движении от центра вращения и естественное увеличение угловой скорости при радиальном движении к центру вращения. Это явление в классической физике называется законом сохранения углового момента, который якобы выполняется в отсутствие тангенциальных сил. Однако в реальной действительности угловой момент сохраняется именно за счёт тангенциальной составляющей радиальной силы. Это и есть основа явления Кориолиса. Поэтому тангенциальную составляющую радиальной силы мы называем истинной силой Кориолиса-Кеплера.

Проявляясь совместно с «обычной» истинной силой Кориолиса, фиктивная сила инерции Кориолиса одновременно противоречит, как физическому смыслу обычных сил, так и фиктивных сил инерции. Поскольку в классической динамике вращательного движения понятие об обычной истинной силе Кориолиса-Кеплера отсутствует, то в классической физике родилась самая странная сила не только из всех сил инерции, но и самая странная из всех обычных сил!!!

Классическая сила Кориолиса — это либо, полу фиктивная обычная сила, либо, полу обычная фиктивная сила. Недаром физики всех народов, начиная со времён Кориолиса, и до сих пор спорят, реальна ли сила Кориолиса или же это только иллюзорная сила инерции.

Поскольку истинная сила Кориолиса-Кеплера в классической модели явления Кориолиса полностью скомпенсирована, то природа этого явления принципиально не может быть раскрыта в классической физике. В частности реальное ускорение и сила Кориолиса за счёт компенсации истинной силы Кориолиса-Кеплера вдвое меньше классического ускорения и силы Кориолиса. При этом классической силе Кориолиса соответствует только общее силовое напряжение, возникающее при противодействии поддерживающей силы и истинной силы Кориолиса-Кеплера.

Во втором варианте относительная скорость направлена перпендикулярно постоянному радиусу вращающейся системы. При этом абсолютная линейная скорость является величиной постоянной. Но это есть не что иное, как равномерное вращательное движение, динамику которого с классической же точки зрения определяет исключительно только центростремительное ускорение. Следовательно, либо никакого ускорения Кориолиса при тангенциальном относительном движении нет, либо классической физике следует пересмотреть свои взгляды, как на явление Кориолиса, так и на классическую модель вращательного движения.

Явление Кориолиса — Кеплера играет очень важную роль в природе. Например, А. И. Андреев в работе «Основы естественной энергетики», Санкт-Петербург, 2004, г. на стр. 181 пишет:

«Поскольку образование и существование вихрей элементарных частиц и гравитации происходит за счёт кориолисовых сил и самовращения, то кориолисово самовращение, именно в этом смысле является основой природы».

В реальной действительности никакого самовращения вихрей за счёт силы Кориолиса нет, и не может быть в принципе. Самовращение есть только в равномерном вращательном движении. Тем не менее, явление Кориолиса — Кеплера заслуживает того, чтобы уделить ему особое внимание при рассмотрении вопросов физики движения, тем более что в классической физике оно не имеет непротиворечивого объяснения.

Рассмотрим эти вопросы подробнее.

4.1. Первый вариант проявления ускорения Кориолиса. Скорость относительного движения направлена вдоль радиуса вращающейся системы

А. Н. Матвеев в работе «Механика и теория относительности», 3-е издание, Москва, «ОНИКС 21 век», «Мир и образование», 2003 г., допущенной в качестве учебника для студентов высших учебных заведений определяет ускорение Кориолиса следующим образом (см. фотокопии ниже).

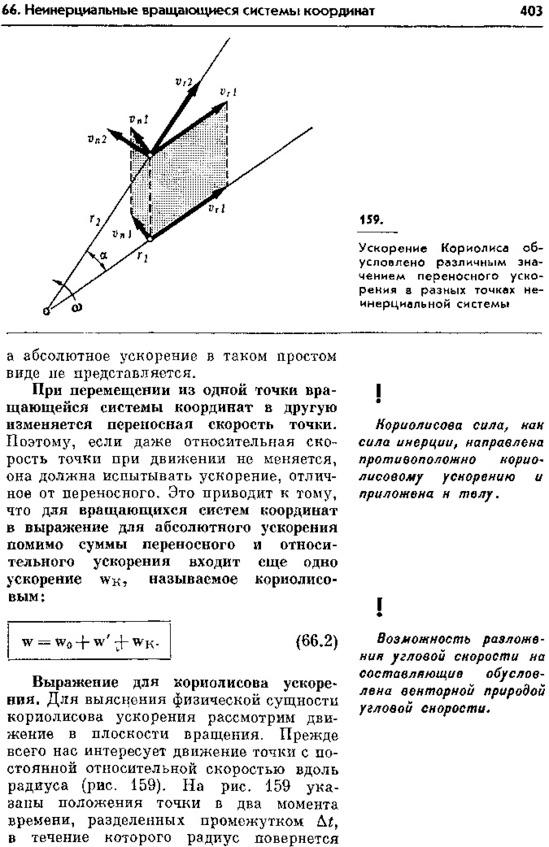
Книга написана в соответствии с программой курса физики для университетов, однако, физики в данном учебнике нисколько не больше, чем во многих других современных учебниках по физике. Форма написания книги больше соответствует справочной литературе по физике, в которой приводятся не столько физические, сколько математические описания физических явлений.

Матвеев пытается выяснить и донести до читателей «физическую сущность кориолисова ускорения», как он сам пишет на странице 403 своей книги. Однако все принципиальные выводы, касающиеся физики явления Кориолиса, подробно не анализируются. Все спорные и противоречивые моменты явления Кориолиса остаются без доказательства и разъяснений. Механизм образования ускорения Кориолиса не раскрыт. Всё представлено на уровне голой математики, за которой не всегда виден физический смысл явлений, хотя в физике все должно быть наоборот.

Ускорение Кориолиса в первом варианте по Матвееву это изменение скорости тела, движущегося радиально внутри вращающейся системы в направлении, перпендикулярном радиусу вращения. Это общепринятое в классической физике определение ускорения Кориолиса.

На стр. 404 Матвеев пишет:

«Скорость вдоль радиуса Vr изменяется за это время (Δt) по направлению, а скорость Vn, перпендикулярная радиусу, изменяется как по направлению, так и по абсолютному значению. Полное изменение составляющей скорости, перпендикулярной радиусу, равно:

ΔVn = Vn₁ — Vn₂ * cos α + Vr * Δα ≈

≈ ω * r₁ — ω * r₂ + Vr * ω Δt = V * Δr + Vr * ω Δt (66.3)

где учтено, что cos α ≈ 1

Следовательно, кориолисово ускорение в пределе при Δt→0 равно:

w_к = ω * Δr / dt + Vr * ω = 2 * Vr * ω (66.4)».

Вообще говоря, поворот вектора переносной скорости происходит под действием переносного центростремительного ускорения, которое проявляется в радиальном направлении и потому не имеет никакого отношения к поворотному ускорению Кориолиса. Поэтому векторы (V_n1) и (V_n2) можно сравнивать по абсолютной величине непосредственно без проецирования (V_n2) на тангенциальное направление с учётом (cos α). Всё намного серьёзнее, чем ненужное в данном случае проецирование и связано с неправильными физическими представлениями классической физики о явлении Кориолиса.

Из выражения (66.4) следует, что ускорение Кориолиса — это изменение абсолютной скорости в направлении перпендикулярном радиусу, которое обеспечивается двумя самостоятельными независимыми ускорениями:

1. Ускорением, характеризующим приращение линейной скорости переносного вращения по абсолютной величине;

2. Ускорением, характеризующим приращение радиальной скорости относительного движения по направлению.

Этим собственно и объясняется «двойка» в ускорении Кориолиса. Но если предположить, что эти две якобы самостоятельные интерпретации ускорения Кориолиса представляют собой одну и ту же физическую величину, достаточную, как для поворота радиально скорости, так и для приращения тангенциальной скорости по величине, то под сомнение подпадает именно её удвоение.

4.1.1. Физический смысл явления Кориолиса определяется Истинной силой Кориолиса-Кеплера из второго закона Кеплера

В соответствии со вторым законом Кеплера, ошибочно называемом в классической лже динамикой вращательного движения законом сохранения не существующей в природе физической величины — момента импульса, линейная и угловая скорость при изменении радиуса изменяется обратно пропорционально первой и второй степени радиуса соответственно. Но как известно единственной причиной изменения скорости (импульса) неизменной массы является только сила. Найдём эту силу Кеплера (см. рисунок ниже).

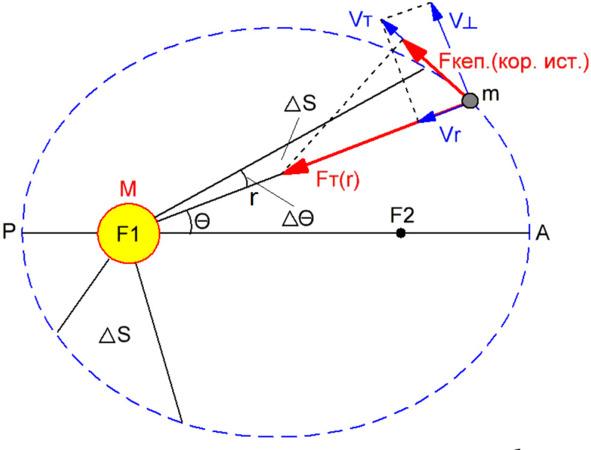
Из рисунка видно, что единственная сила, которая может быть причастна к изменению тангенциальной скорости тела (m) — это проекция силы тяготения на касательную к траектории движения тела, она же радиальная сила (Fт (к)). Это и есть сила Кеплера, она же истинная сила Кориолиса (Fкеп. (кор. ист.). Из формулировки второго закона Кеплера (1609 г.) следует, что радиус-вектор обращающегося тела заметает равные площади за равные промежутки времени (см. рисунок выше). При этом площадь, описываемая радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием r * Δθ и высотой r:

dS = ½ * r² * Δθ

dS / dt = ½ r² * dθ / dt = ½ * r * V_┴ = ½ * ω * r² = const.

А поскольку секторальная скорость (dS / dt) постоянна, то её производная по времени S’t равна нулю:

S« (t) = ½ (r’ (t) * V_┴ + r * V_┴» (t)) = 0

где

r’ (t) = Vr — радиальная скорость

V_┴» (t) = a_{К ист} — ускорение Кориолиса Истинное;

V_┴ = ω * r

Тогда:

Vr * ω * r + r * a_{К ист.} = 0

Сократив на r, получим:

a_{К ист} = — Vr * ω

Тогда Истинная сила Кориолиса равна:

Fк ист = а_{К ист} * m = — Vr * ω * m

Не трудно показать связь второго закона Кеплера с так называемым законом сохранения момента импульса или углового момента классической лже динамики вращательного движения.

L = m * ω * r²

Тогда:

dS / dt = ½ * L / m

Таким образом, угловая скорость при радиальном движении определяется не только чисто геометрическим масштабированием при неизменной линейной скорости с масштабным коэффициентом-радиусом, что совершенно очевидно и без каких-либо выводов, но и за счёт истинной силы Кориолиса-Кеплера, которая физически изменяет линейную скорость на каждом текущем радиусе. При этом истинная сила Кориолиса-Кеплера, тормозящая тело при радиальном движении от центра вращения и разгоняющая его при движении к центру, вдвое меньше классической силы Кориолиса.

По определению сила Кориолиса проявляется только, как противодействие поддерживающей вращение силе, возникающей за счёт инерции вращения базовой системы с неизменным радиусом. Однако поскольку одиночное тело (m) не имеет связи с базовой для него вращающейся системой, которая поддерживала бы его вращение за счёт инерции своей не изменяющей радиус массы, то в рассмотренном случае силы Кориолиса нет.

Как мы уже отмечали в главе (3.4.3) на примере радиального движения от центра вращения в результате ослабления связей с без массовым центром вращения часть энергии связи безвозвратно рассевается в окружающем пространстве. При этом энергия связи, необходимая для установления нового вращения тела на новом радиусе, может быть изъята только из кинетической энергии освобождающегося тела.

Отбор необходимой энергии осуществляется за счёт истинной силы Кориолиса-Кеплера, которая, как отмечалось выше, является тангенциальной проекцией радиальной силы на касательную к спирали. При этом угловая скорость тела уменьшается, как геометрически в результате масштабирования угловой скорости с масштабным коэффициентом-радиусом, так и за счёт непосредственного физического уменьшения линейной скорости силой Кеплера.

При движении к центру вращения этот механизм принципиально сохраняется с той лишь разницей, что необходимая энергия берётся из источника радиального движения. В классическом поворотном движении этим источником может быть либо источник сторонней поддерживающей силы, либо инерция условно массивного центра вращения (базовая вращающаяся система с неизменным радиусом).

Часть поддерживающей вращение силы компенсирует часть истинной силы Кориолиса-Кеплера. Эта равновесная часть поддерживающей силы и истинной силы Кориолиса не причастна к ускорению Кориолиса и к силе реакции на вызывающую его силу, т.к. соответствующие части обоих сил здесь взаимно компенсируются. Дальнейшее восстановление угловой скорости до исходного значения и выше осуществляется только за счёт оставшейся части поддерживающей силы с ускорением Кориолиса.

Как показано выше, истинная сила Кориолиса-Кеплера равна ровно половине классической силы Кориолиса. Следовательно, при неизменной угловой скорости на компенсацию истинной силы Кориолиса-Кеплера уходит ровно половина поддерживающей силы. При этом сила Кориолиса, как реакция на реальное ускорение Кориолиса, т.е. на ответственную за него часть поддерживающей силы, вдвое меньше классической силы Кориолиса, которая на половину определяется статическим равновесием.

Таким образом, классическая сила Кориолиса это либо, полу фиктивная обычная сила, либо полу обычная фиктивная сила.

Если путём компенсации истинной силы Кориолиса-Кеплера поддерживать на неизменном уровне только линейную скорость переносного вращения, то ускорение Кориолиса будет равно нулю. Возникающее при этом движение по спирали осуществляется только с центростремительным ускорением, которое также равно нулю, если речь идёт о вращении на уровне не менее цикла его формирования. На первый взгляд это выглядит парадоксальным. Однако гораздо более парадоксально наличие реального ЦСУ в классической физике.

Равномерное движение по окружности так же, как и равномерное движение по прямой, осуществляется фактически в одном неизменном круговом «направлении», т.к. окружность при этом не изменяет своей постоянной конфигурации. Отклонений от неё, как и в случае движения по прямой — нет, а само движение в целом осуществляется при полном равновесии ЦБ и ЦС сил и постоянной линейной скоростью, т.е. равномерно. При этом постоянный поворот относительно центра вращения объясняется не внешней неуравновешенной силой, а одной из внутренних сил вращательного движения, действующей последней.

Это относится, в том числе и к движению по кругу отдельной материальной точки (тела). Действительно. Возврат на дальний радиус происходит по инерции, т.е. за счёт внутренних сил. Тут вопросов ни у кого не возникает. А для перехода на ближний радиус источник внешней силы сам должен двигаться по кругу неотступно от тела. Для этого ему нужен свой неотступный источник и так далее до бесконечности. Единственный способ избежать этой недостижимой в принципе бесконечности — это диаметрально уравновешенное движение, которое является внутренним движением вращающейся системы без ускорения.

В отсутствие замкнутого диаметрально уравновешенного кругового движения тела, которое осуществляется без ускорения, все внешние воздействия на него не являются центростремительными, а его ускорение не будет соответственно центростремительным. Без цикла формирования вращательного движения (ВД) это будут обычные разрозненные линейные силы и ускорения без какого-либо центра вращения и самого вращения. Это всего лишь абстрактная идеализация или аппроксимация под ВД.

Поскольку активная сила упругости по фазе изменения направления всегда опережает ньютоновскую силу инерции поэлементной поддержки, то, несмотря на отсутствие реального геометрического ускорения во вращательном движении в целом, результирующая сила неизменно отклоняется в сторону центра вращения, формируя общую макро кинематику вращательного движения. Иными словами в случае равновесия двух противодействующих сил, разнесённых по фазе (по времени), движение всегда осуществляется в сторону силы, действующей последней. В этом легко убедиться в простом мысленном эксперименте.

Пусть на тело действуют две равные по величине, но противоположные по направлению силы. При этом в соответствии с первым законом Ньютона тело находится в покое или движется равномерно и прямолинейно. Теперь уберём одну из сил. Тело начнёт движение под действием оставшейся неуравновешенной силы. Но, как только противодействие восстановится, тело вновь остановится или вернётся к предыдущему равномерному и прямолинейному движению. Из этого следует, что состояние движения определяется последней действующей по времени неуравновешенной силой.

Поскольку во вращательном движении последней по времени всегда действует центростремительная сила упругости, то при равенстве центробежных сил инерции и центростремительных сил упругости, разнесённых по фазе, траектория равномерно отклоняется в сторону центра вращения. Этот процесс характеризуется в физике условно-академическим центростремительным ускорением без итогового ускорения. Если оборвать связующее тело, то последней по времени будет сила инерции. При этом вращательное движение вновь преобразуется в прямолинейное движение (см. гл. 3.2.1).

Ну, а если кто то хочет возразить, что ЦБ сила, которая уравновешивает ЦС силу приложена не к самому телу, а к связующему телу, то пусть ответит сам себе на вопрос за счёт чего же тогда поддерживается линейная скорость в направлении от центра вращения, если не за счёт ньютоновской инерции поэлементной поддержки, которая основана именно на реальных силах? И пусть поищет заодно, где у вращающейся массы заканчивается связующее тело и начинается непосредственно само вращающееся тело (см. главу 3.2.).

В классической физике истинная сила Кориолиса-Кеплера отсутствует. Поэтому в расчёте ускорения Кориолиса она ошибочно исходит из приращения движения, соответствующего полной поддерживающей силе, что приводит к удвоению ускорения Кориолиса. Это требует качественной и соответственно количественной коррекции классической версии явления Кориолиса и анализа причин, по которым классическое дифференцирование не видит этой ошибки.

Начнём с прямолинейного движения. На рисунке (4.1.1.1) показаны два отдельных участка прямолинейного равноускоренного движения с координатами (18 м, 21 м) и (21м, 26 м) с секундным интервалом между каждой указанной в скобках парой координат.

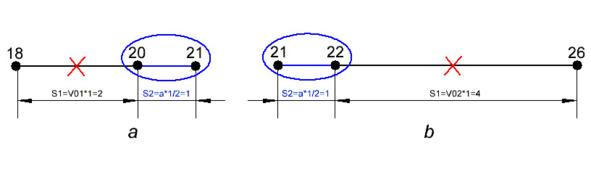
В физике есть известная всем школьная формула пути для равноускоренного движения (S = V₀* t + a * t² / 2), из которой следует, что ускорение равно (a = 2 * (S — V₀ * t) / t²). Как видно, пресловутая двойка не является эксклюзивной исключительно только для явления Кориолиса. Она имеет принципиальное значение для определения ускорения через приращение пути любого равноускоренного движения, т.к. средняя скорость, которая и определяет пройденное расстояние, вдвое меньше мгновенной скорости, достигнутой за счёт ускорения за то же самое время. Однако при определении ускорения через дифференцирование координат эту формулу не используют, т.к. для неё недостаточно одних только координат, нужна ещё и начальная скорость.

Если координаты движения можно легко измерить в любой заданной системе отсчёта, то вычленить начальную скорость в составе переменного движения в двух координатах (18 м, 21 м) или (21м, 26 м), как на рисунке 4.1.1.1 a и b, без дополнительных данных не представляется возможным. Поэтому приращение скорости и ускорения переменного движения определяется в классической физике через дифференцирование разности между парами координат по трёхточечной схеме. В нашем примере это по-прежнему координаты (18 м, 21 м) и (21м, 26 м) с секундным интервалом между каждой парой (см. Рис. 4.1.1.2). Но с учётом общей точки (21 м) мы получаем общую трёхточечную схему для двух смежных участков (18м, 21м, 26м).

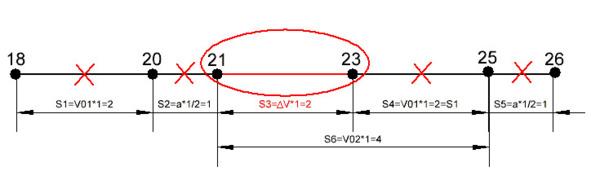
Как показано на рисунке, при вычитании отрезков (26 — 21) минус (21 — 18) расстояние (S1 и S4), пройденное с начальной скоростью (V₀₁), а также расстояние (S2) и (S5), пройденное за счёт ускорения, взаимно уничтожаются. Остаётся только отрезок пути (S3 = ∆V * t), где (∆V) — разность средних скоростей на участках (18 м, 21 м) и (21м, 26 м). Тогда ускорение определяется второй производной приращения по времени (a = d²S3 / dt²) между парами координат (26 — 21) и (21 — 18), равному (S3). Это соответствует школьной формуле пути при равноускоренном движении только без двойки в знаменателе, т.к. сравниваются уже готовые именно средние скорости.

Пресловутая двойка фигурирует и в выводе ЦС ускорения по трёхточечной схеме. Однако это так же, как и в случае с прямолинейным ускоренным движением связано не с удвоением ускорения, а со средней скоростью ускоренного движения. Покажем это на рисунке (4.1.1.3).

Приращение пути за счёт ЦСУ равно:

∆rx = (DL — D”2») — (D”2» — DK) = DL — 2 * D”2» + DK

а = (cos (ωt) * (DL + DK) — 2 * D”2») / t²

Поскольку DL = DK, а угловая скорость (ω) — постоянная, то

|DL — D”2»| = |D”2» — DK|

DL + DК = 2 * D”2»

Тогда:

а = (cos (ωt) — 1) * 2 * D”2») / t²

Как видно, здесь двойка относится вовсе не к удвоению приращения пути за счёт ускорения. Это промежуточный результат связанный с вычислением средней скорости, что становится очевидным при разложении функции (cos (ωt) — 1) в ряд Тейлора:

cos (n) — 1 = — 1 = -n² / 2…

Тогда:

a = — (((ωt) ² / 2) * 2 * D”2») / t² = ω² r

После сокращения (2) и (t²), получаем

a = — = ω² r,

где D”2» = r

На рисунке (4.1.1.3) приведена классическая трёхточечная схема применительно к криволинейному движению. Временной интервал между точками (1, 2, 3), если считать по порядку по ходу движения, как и прежде — одна секунда. Очевидно, что если бы не было радиальной скорости, то все три радиуса-вектора (DK), (D «2»), и (DL) были бы одинаковыми. При этом разница проекций (DK) и (DL) на ось (Y) была бы равна нулю (ВD — DF = 0), что означает отсутствие уско