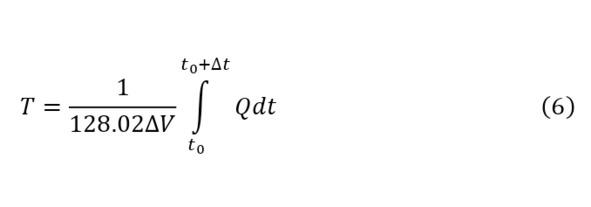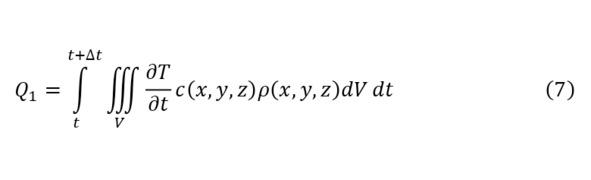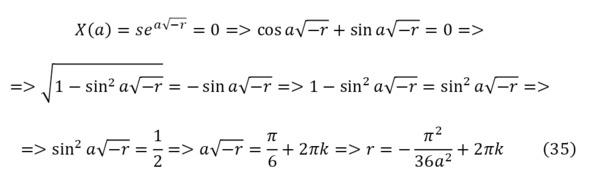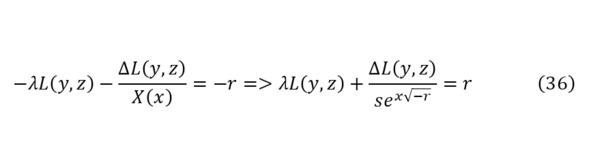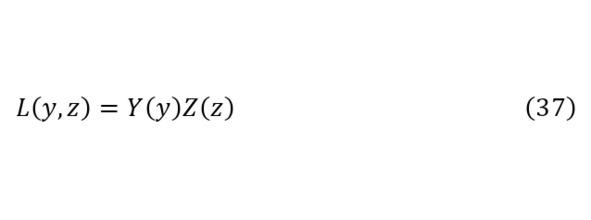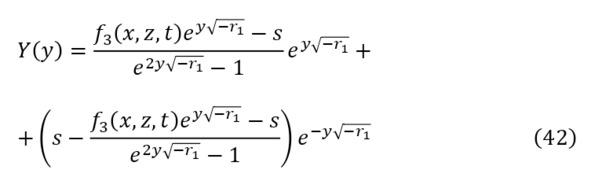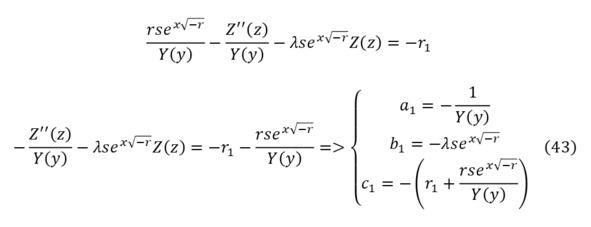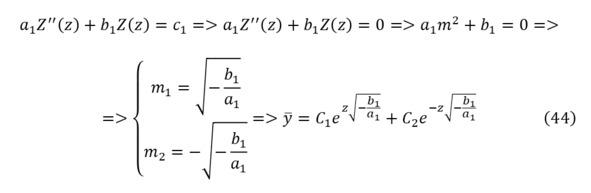АНАЛИЗ ПРОЦЕССА ПЕРЕНОСА ТЕПЛА В ПРОСТРАНСТВЕ
Билолов Иномжон Ўктамович
Отажонов Жамшид Машрабжонович
Исроилов Шаробиддин Махаммадюсуфович
Мавлонова Дилнозахон Шухратжон қизи
Абдурахмонов Султонали Мукарамович
Алиев Ибратжон Хатамович
ФерПИ, 150100, г. Фергана, Ферганская обл., Республика Узбекистан
ФФ ТУИТ, 150100, г. Фергана, Ферганская обл., Республика Узбекистан
НИИ «ФРЯР», Electron Laboratory LLC, 151100, г. Маргилан, Ферганская обл., Республика Узбекистан
Аннотация. В работе теоретически рассмотрены общие принципы переноса тепловой энергии в ограниченном пространстве. Для упрощения задачи задача, определяются в декартовой системе координат. Анализируются зависимость переноса от коэффициентов теплопроводности, теплоёмкости и собственных коэффициентов дифференциальных уравнений в частных производных неоднородного и однородного характера. При моделировании заданы начальные и граничные условия. В решении задачи применён метод множественного разделения переменных. В заключении выводится конечная форма функции явления теплопереноса в ограниченном пространстве от 4 переменных.
Ключевые слова: диффузия, конвенция, абсорбция, теплопроводность, теплоёмкость, поправочные коэффициенты.
Введение
В технологических процессах в основном главную роль играет передача и перенос энергии в зависимости от технологических условий. При анализе и расчёте создаваемых проектов необходимо учесть физические процессы, связанные с энергетическими параметрами на молекулярном уровне. В этих процессах участвуют явления диффузии, конвекции, абсорбции и другие, которые определяются некоторыми свойствами. Каждое явление в отдельности, теоретически обоснована и используется во всех расчётах. Теоретические работы, рассматривающие общий случай, то есть, когда участвуют все эти явления, досконально не рассмотрены.
Достаточно подробно рассмотрен один из случаев расположения термоэлемента под окнами, что обуславливалось тем, что при прохождении более прохладного потока воздуха, такой поток благодаря тому, что прохладный воздух тяжелее тёплого опускается вниз — в сторону нагревательного элемента. Затем увеличивая свою температуру и продолжая своё движение по направлению прохождения он начинает подниматься, а тем временем пребывают новые потоки прохладного воздуха и также поток воздуха, находящийся ближе к потолку, успевает остыть и опуститься к батарее, чтобы вновь продолжить этот цикл. В этом случае, важно заметить, что степень понижения температуры тёплого воздуха у потолка не сводит его температуру к значению поступающего потока, таким образом в помещении удерживается средняя температура.
Ныне активно стали применяться специальные модели нагревательных элементов, которые находятся ближе к потолку, где причина логически не обуславливается согласно вышеописанной модели, однако, известна конструктивная особенность, по сравнению с предыдущей моделью. Существование такой конструкции позволяет рассуждать о том, что возможно нахождение более благоприятных вариантов расположение нагревательных элементов и требует проведение теоретического анализа потока воздуха в помещении. Поэтому теоретическое исследование вышеуказанных вариантов установки нагревательных элементов и элементов потери является актуальным.
Материалы и методы
В исследовании использованы методы анализа полученных данных путём применения изначально алгоритма квантования параметров с последующим выведением отдельных дискретных результирующих последовательностей. Основным использованным методом является аналитический способ анализа физических явлений посредством приведения из общих закономерностей к дифференциальному уравнению в частных производных, с конечным его решением и выведением конечной функции описывающая процесс. Также, среди применённых методов отмечает анализ явления, теоретическое моделирование процесса.
Обсуждение исследования
Для разработки настоящей модели, необходимо ввести некоторые данные. Так, пусть анализируется определённое полностью пустое помещение, с единственным окном. При этом известен объём помещения V, площадь окна So, а также установлено, в что в помещении имеется сухой воздух, состоящий из 78% азота и 22% кислорода, плотность которого равняется (1), коэффициент теплоёмкости (2) и коэффициент теплопроводности (3).
В описанном пространстве имеется единый источник тепла, с известными координатами и величиной энергии. Зная указанные значения в аналитическом виде, можно вычислить теплоёмкость всего воздуха в помещении (4), величину проходящей через произвольную виртуальную плоскость с известной площадью в этом пространстве (5) и температуру в любой точке этого пространства (6), что следует из (4).


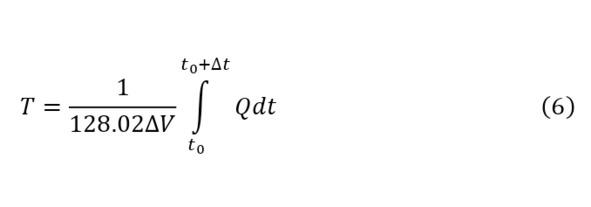
Однако, если обратить внимание в (4—6) получается цикл, для разрешения которого необходимо найти специальную функцию от температуры, зависящая от 4 переменных. Поскольку величина входящей энергии известна, и она равна сумме этих двух температур, принимая, что стены помещения достаточно толстые для изоляции помещения, а также указав, что сумма между температурой входящего потока и температурой, образуемая от вводимой энергии также известна и описывается специальной функцией, то можно принять (9). В функции (9) отдельно не указаны явления диффузии, конвекции, абсорбции, но они учитываются на этапе расчёта каждой из заданных функций. Отметив, что перед переходом к (9), необходимо предварительно переписать (4—5) в (7—8).
В результате выражение упрощается (10).
Принимая, что анализ ведётся в декартовом пространстве без перехода в сферическую или цилиндрическую систему координат, результирующее уравнение описывается в форме дифференциального уравнения в частных производных вида (11), что является уравнением теплопроводности, принимая (12—13).
Для получения уравнения, описывающее исследуемое явление, определяется множество решений уравнения, граничные и начальные условия. Величина температуры в начальный момент времени берётся в качестве нуля и учитывается, что известна скорость её изменения в качестве отдельной функции (14).
Замечается, что начало координат находится в левом нижнем углу помещения напротив стены с окном, при том, что длина помещения равняется a, ширина — b, высота — c, откуда следует (15).
Из приводимых граничных условий можно сделать выводы (16—19), учитывая также, что величину температуры воздуха на уровне пола и потолка можно определить через (17—18), изменение температуры воздуха через окно можно определить через (18).
В решении дифференциального уравнения (11), можно применить метод разделения переменных (21), сделав замену (20) и уже из него изначально превратив настоящее неоднородное уравнение теплопроводности в частных производных второго порядка в однородное (22).
Подстановка значения (22) в (20) получается (23), с дальнейшим преобразованием в (24), где получается первое соотношение равное значению собственной функции.
Далее необходимо перейти к первому решению относительно одной переменной времени, превратив вторую и третью часть соотношения (24) в обыкновенное дифференциальное уравнение (25), имеющее решение в (26).
Дополнительный член в (26) вычисляется при использовании первого начального условия (27).
Собственное значение для времени определяется в данном случае посредством использования второго начального условия из (14) в виде (28).
Продолжение решения задачи, переходит к пространственной форме (29), где выражается вновь представление через разделение переменных (30), откуда можно составить преобразование вида (31), которое превращается в равенство с новым собственным значением, откуда уже можно получить обыкновенное дифференциальное уравнение второго порядка для первой переменной (32).
Далее, решение такого уравнение определяется через нахождение характеристического уравнения, согласно (32) в виде (33), где находиться решение с двумя неизвестными постоянными и собственным значением для обыкновенного дифференциального уравнения первой переменной.
Учитывая вывод для граничных условий, определяется решение уравнения (32) с уже определёнными значениями для постоянных (34).
Остаётся найти собственное значение этого уравнения, для чего применяется (35), после чего полученный результат в (34) подставляется во вторую часть (31) получая (36), как новое дифференциальное уравнение с новым разделением оставшихся переменных (37).
После подстановки, уравнение вновь преобразуется, приходя к новому равенству, где появляется новое собственное значение для второй и третьей переменной (38) и определяя часть уравнения для второй пространственной переменной, можно прийти к обыкновенному дифференциальному уравнению второго порядка, практически идентичный с обыкновенным дифференциальным уравнением второго порядка для случая с первой пространственной переменной, откуда становится очевидным его решение с двумя постоянными неизвестными коэффициентами (39), которые достаточно легко находятся через систему (40) в виде (41).
Легко подставляя полученные значения для констант, организуется конечная форма для функции второй пространственной переменной (42).
Продолжение решения представляется после подстановки решения уравнения (42) для уравнения с третьей пространственной переменной, которая является дифференциальным уравнением второго порядка (43) и для которого вводятся специальные переменные (43).
Поскольку полученное обыкновенное дифференциальное уравнение второго порядка неоднородно, изначально находиться решение для его однородной части, а после вычисляется решение неоднородной части в результате приходя к единому решению (45).
Используя граничные условия также находятся значения для постоянных неизвестных коэффициентов (46), получая значение для первого коэффициента (47) и второго (48), получая конечное значение уравнения для третьей переменной (49).
Откуда легко определить собственные значения для предыдущего и раннего показателя, либо прибегнуть к расчёту посредством изначальных равенств и продемонстрировав конечную форму выражения (50).
Что легче выразить через систему (51).
Поскольку настоящее решение является решением именно однородного 4 мерного дифференциального уравнения в частных производных, для этого уравнения, но с неоднородной формой необходимо применить тот же алгоритм, который применялся в ходе решения частных уравнений пространственных переменных с неоднородными обыкновенными дифференциальными уравнениями второго порядка, а именно добавление к решению определённого члена, который находился бы посредством использования вышеуказанного алгоритма, приводя к конечному решению поставленной задачи (52).
Благодарности
Авторы приносят благодарности за оказание помощи при проведении математических вычислений, решении дифференциальных уравнений д.ф.-м.н., профессору ФерГУ Каримову Ш. Т.
Заключение
Таким образом была получена единая функция, которая описывала бы полноценно, распространение тепла в пространстве в описанной системе с прохождением воздуха, при учёте введения всех необходимых дополнительных вводных функций. При вводе граничных и начальных условий получается результирующая величина температуры в произвольной точке ограниченного пространства.
Использованная литература
1. S. M. Abdurakhmonov, Sh. Sayitov and I. X. Aliyev. Mathematical modeling of soldering iron heating process in automated terminal soldering installations. E3S Web of Conferences 401, 05064 (2023)
2. Mamirjon Turdimatov*, Farrukh Mukhtarov, Sultonali Abdurakhmonov, Umidjon Khudoynazarov and Mastura Muminova. Specialized processors and algorithms for computing standard functions. E3S Web of Conferences 389, 07012 (2023)
3. Sultonali Abdurakhmonov, Shavkatjon Sayitov, Makhmud Mirzajonov, Inomjon Bilolov and Abbos Khaydarov. Research of terminal soldering technology for auto glass heating systems. E3S Web of Conferences 389, 01036 (2023)
4. Simona Olmi, Lucia Valentina Gambuzza, Mattia Frasca. Multilayer control of synchronization and cascading failures in power grids. Chaos, Solitons & Fractals. Volume 180, March 2024, 114412.
5. Przemysław Borys, Paulina Trybek, Beata Dworakowska, Anna Sekrecka-Belniak, Ewa Nurowska, Piotr Bednarczyk, Agata Wawrzkiewicz-Jałowiecka. Selectivity filter conductance, rectification and fluctuations of subdomains — How can this all relate to the value of Hurst exponent in the dwell-times of ion channels states? Chaos, Solitons & Fractals. Volume 180, March 2024, 114492.
6. Yuan Zhang, Jinde Cao, Lixia Liu, Haihong Liu, Zhouhong Li. Complex role of time delay in dynamical coordination of neural progenitor fate decisions mediated by Notch pathway. Chaos, Solitons & Fractals. Volume 180, March 2024, 114479.
7. Willian Cintra, Mirelson M. Freitas, To Fu Ma, Pedro Marín-Rubio. Multivalued dynamics of non-autonomous reaction–diffusion equation with nonlinear advection term. Chaos, Solitons & Fractals. Volume 180, March 2024, 114499. https://doi.org/10.1016/j.chaos.2024.114499
8. Cao Wen, Jinfeng Wang, Yang Liu, Hong Li, Zhichao Fang. Unconditionally optimal time two-mesh mixed finite element algorithm for a nonlinear fourth-order distributed-order time fractional diffusion equation. Physica D: Nonlinear Phenomena. Available online 6 February 2024, 134090.
9. Diana S. Maltseva, Roman O. Popovych. Point-symmetry pseudogroup, Lie reductions and exact solutions of Boiti–Leon–Pempinelli system. Physica D: Nonlinear Phenomena. Available online 5 February 2024, 134081. https://doi.org/10.1016/j.physd.2024.134081
10. Zhongjian Wang, Jack Xin, Zhiwen Zhang. A DeepParticle method for learning and generating aggregation patterns in multi-dimensional Keller–Segel chemotaxis systems. Physica D: Nonlinear Phenomena. Available online 3 February 2024, 134082. https://doi.org/10.1016/j.physd.2024.134082
11. Nang X. Ho, Hung V Vu, Truong V Vu. Migration of a multi-core compound droplet in a ratchet microchannel. European Journal of Mechanics — B/Fluids. Available online 3 February 2024. https://doi.org/10.1016/j.euromechflu.2024.01.016
12. U.S. Mahabaleshwar, A.B. Vishalakshi, Martin Ndi Azese. Corrigendum to «The role of Brinkmann ratio on non-Newtonian fluid flow due to a porous shrinking/stretching sheet with heat transfer» [Eur. J. Mech. B Fluids 92 (2022) 153–165]. European Journal of Mechanics — B/Fluids. Available online 16 January 2024.