Предисловие

Алгоритм — основа computer science и сущность нынешней информационной эпохи. Алгоритмы движут поисковыми системами, которые ежедневно отвечают на миллиарды запросов, и позволяют безопасно передавать данные по всему Интернету. Алгоритмы все чаще оказываются нужны пользователям самых различных областей — от целевой рекламы до онлайн-ценников. Новостные медиа полны обсуждений: что же такое алгоритмы и на что они способны.

Развитие науки, технологии, инженерии и математики (STEM1) дало мощный толчок к непрерывному становлению и модернизации мировой экономики. Однако специалистов, способных формулировать и применять алгоритмы на благо медицины, промышленности и даже государственного управления, просто не хватает. Необходимо, чтобы людей, которые умеют использовать алгоритмы в задачах из собственной области исследования и практики, стало больше.

Для того чтобы разбираться в алгоритмах, не нужно оканчивать четыре курса университета. Увы, большинство книг и материалов в Сети на эту тему рассчитаны именно на студентов: в них делается упор на математические доказательства и основные постулаты компьютерной науки. Справочники содержат пугающее количество самых разнообразных алгоритмов и бесчисленные их варианты для самых изощренных случаев. Слишком часто читатель сдается уже на первой главе такой книги. Это как читать полный английский словарь с целью подправить правописание: лучше бросить сразу. Куда полезнее взять специализированное пособие: в нем будет сто английских слов, в которых чаще всего ошибаются, а также правила, по которым слова составляются (и исключения из них). Вот так же и людям различных профессий и опыта, когда они хотят применять алгоритмы в своей работе, нужно пособие, нацеленное именно на их нужды.

В этой книге в доступной форме описаны алгоритмы, которые сразу же можно применять для улучшения эффективности программ. Все алгоритмы написаны на Python, одном из самых популярных и интуитивно понятном языке программирования, которым пользуются в самых различных сферах — в анализе данных, биоинформатике, промышленности.

Помимо аккуратных описаний самих алгоритмов, в помощь читателю в тексте приведено немало иллюстраций, поясняющих основные идеи. Исходные тексты программ распространяются под свободной лицензией и доступны в репозитории проекта.

Эта книга научит вас основным алгоритмам и структурам данных, принятым в computer science, — с ними ваши программы будут эффективнее. Может помочь при приеме на работу и, несомненно, послужит хорошим началом на пути изучения алгоритмов!

Цви Галиль, почетный декан Технологического института Джорджии, кафедра компьютерных наук им. Фредерика Дж. Стори, Атланта, 2021

---

Введение

Для кого эта книга

Предполагается, что читатель уже имеет практический опыт программирования — например, на Python. Если вы никогда не писали программ, я бы посоветовал сначала выучить какой-нибудь язык программирования, а потом уже браться за чтение. В книге используется Python, потому что он подходит и программистам, и непрограммистам.

Алгоритмы предназначены для решения общих задач, которые постоянно возникают при разработке программного обеспечения. Преподавая на младших курсах, я стараюсь навести мосты между знаниями студентов и понятиями, которые я использую в своих алгоритмах. Большинство учебников содержат тщательные пояснения, но все равно их всегда недостаточно. Частенько студент не может самостоятельно изучить алгоритм, потому что ему не показали, как ориентироваться в материале.

Я опишу цель этой книги одним абзацем и одной иллюстрацией. Начнем мы с нескольких структур данных, которые показывают, как информация представляется примитивными атомарными типами, например 32-разрядными целыми числами или 64-разрядными вещественными. Некоторые алгоритмы, в частности двоичный поиск, работают с такими структурами напрямую. Более сложные алгоритмы, например алгоритмы на графах, используют важные абстрактные типы данных (стек, приоритетная очередь и т.п.), которые мы изучим по ходу изложения. Абстрактный тип подразумевает набор действий над ним, и вот эти действия будут эффективны, только если выбрать подходящую структуру данных для его реализации. Ближе к концу книги мы рассмотрим, как повысить быстродействие различных алгоритмов. Сами алгоритмы мы либо целиком напишем на Python, либо рассмотрим соответствующие сторонние пакеты Python, в которых они эффективно реализованы.

Если вы заглянете в сопутствующие книге исходные тексты программ, то найдете там в каждой главе файл book.py — это программа на Python, которая при запуске воспроизводит на вашем компьютере все схемы из книги (рис. В.1).

Рис. В.1. Сводка по тематическому содержанию книги

В конце каждой главы есть проверочные упражнения, на них вы можете потренироваться применять свежие знания. Очень советую сначала попробовать решить задачи самостоятельно, а потом сравнить с примерами решений в репозитории к книге.

Исходные тексты

Все программы из книги доступны в соответствующем репозитории GitHub: http://github.com/heineman/LearningAlgorithms. Они совместимы с Python 3.4 и выше. Везде, где это было разумно, я старался следовать рекомендациям Python и оформлять системные методы наподобие __str()__ или __len__(). Примеры в книге отформатированы с отступом два пробела — так они лучше помещаются в ширину при печати; в программах репозитория используется стандартный отступ четыре пробела. Изредка в печатных примерах попадаются однострочники, например if j == lo: break.

В программах используются три свободно распространяемые библиотеки Python, которые необходимо скачать и установить самостоятельно2:

• NumPy (https://www.numpy.org) версии 1.19.5;

• SciPy (https://www.scipy.org) версии 1.6.0;

• NetworkX (https://networkx.org) версии 2.5.

NumPy и SciPy — одни из самых популярных свободных библиотек с огромным сообществом. Я их использую, чтобы измерить фактическую производительность алгоритмов. NetworkX — большой сборник эффективных алгоритмов для работы с графами, он нам понадобится в главе 7; там же есть удобная готовая структура данных, реализующая граф. Средства этих библиотек позволят не изобретать очередное колесо, если в этом нет нужды. Если они не установлены, не беда: примеры написаны так, что смогут работать и без них, нужные функции также есть в репозитории.

Время работы примеров в книге замеряется с помощью модуля timeit, который многократно запускает указанный фрагмент программы. Часто для большей аккуратности само измерение делается тоже несколько раз. Из всех замеров выбирается быстрейший, а не средний. Обычно считается, что так лучше измерять производительность: если запустить пример несколько раз, а потом взять среднее время работы, на это среднее повлияет худшее время выполнения, которое может быть большим из-за того, что именно тогда операционная система запускала какие-то еще задачи3.

Если скорость работы алгоритма сильно зависит от свойств обрабатываемых данных (как в примере сортировки вставками из главы 5), о том, что в этом случае измеряется среднее время, будет сказано явно.

В репозитории больше 10 000 строк кода на Python, сценарии для запуска всех тестов и вычисления всех данных для таблиц в книге; можно воспроизвести также большую часть схем и графиков. Исходный текст снабжен, как это принято в Python, строками документации и тестами, причем тестовое покрытие, согласно https://coverage.readthedocs.io, составляет 95 %.

Если у вас возникнут технические вопросы или затруднения в работе примеров, свяжитесь с нами по адресу bookquestions@oreilly.com.

В общем случае все примеры кода из книги вы можете использовать в своих программах и в документации. Вам не нужно обращаться в издательство за разрешением, если вы не собираетесь воспроизводить существенные части программного кода. Если вы разрабатываете программу и используете в ней несколько фрагментов кода из книги, вам не нужно обращаться за разрешением. Но для продажи или распространения примеров из книги вам потребуется разрешение от издательства O’Reilly. Вы можете отвечать на вопросы, цитируя данную книгу или примеры из нее, но для включения существенных объемов программного кода из книги в документацию вашего продукта потребуется разрешение.

Мы рекомендуем, но не требуем добавлять ссылку на первоисточник при цитировании. Под ссылкой на первоисточник мы подразумеваем указание авторов, издательства и ISBN.

За получением разрешения на использование значительных объемов программного кода из книги обращайтесь по адресу permissions@oreilly.com.

Условные обозначения

В книге используются следующие типографические обозначения:

Курсив

Выделяет новые термины, а также все, что автор хотел подчеркнуть.

Шрифт без засечек

Используется для обозначения URL, адресов электронной почты, названий кнопок, клавиш и их сочетаний, элементов интерфейса.

Моноширинный шрифт

Используется для программ в иллюстрациях и для ссылки на фрагменты программ в тексте — например, для переменных, имен функций, типов данных, операторов и ключевых слов.

Полужирный шрифт

В русском переводе обозначает собственные имена алгоритмов и структур данных.

Кошачий лемур сопровождает совет или подсказку. Из всех приматов, включая человека, у кошачьего лемура самое большое суммарное поле зрения — до 280°. В тексте советы позволяют буквально расширить кругозор: в них изложена познавательная информация или описана интересная возможность Python.

Ворона сопровождает теоретические замечания. Большинство зоопсихологов сходятся на том, что вороны — очень умные птицы: они умеют решать сложные задачи и даже пользоваться предметами. В тексте примечание содержит определение термина или разъяснения важного понятия. Прежде чем читать дальше, их надо внимательно изучить.

Скорпион сопровождает предупреждение. Встретив скорпиона в природе, мы осторожно останавливаемся. В книге скорпион предупреждает о том, что надо остановиться и тщательно рассмотреть сложные аспекты, с которыми можно столкнуться при реализации алгоритмов.

Благодарности

Я считаю, что лучшее в computer science — это изучение алгоритмов. Спасибо читателям за то, что дали мне возможность поделиться своими наработками. Спасибо моей жене Дженнифер за то, что поддержала меня в затее с очередной книгой. Спасибо моим сыновьям, Николасу и Александру, за то, что они уже выросли и могут изучать программирование.

Эта книга стала лучше благодаря редакторам O’Reilly — Мелиссе Даффилд, Саре Грей, Бет Келли и Вирджинии Вильсон. Они помогали мне систематизировать общее содержание книги и выстраивать пояснения к нему. Технические рецензенты — Лаура Хелливелл, Чарли Лаверинг, Хелен Скотт, Стенли Силков и Аура Веларде — нашли множество неточностей, улучшили реализацию алгоритмов и дали пояснения к ним. Если остались какие-то недочеты — все они целиком на моей совести.

---

От издательства

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах.

Глава 1. Решение задач

В этой главе

Несколько алгоритмов решения одной и той же вводной задачи.

Как исследовать производительность алгоритма на входных наборах данных размером N.

Как посчитать количество основных действий, выполненных при обработке конкретного набора данных.

Как определить уровень падения производительности при удвоении входных данных.

Как предсказать сложность алгоритма по времени на основании подсчета действий, которые он выполнит на входных данных размером N.

Как предсказать сложность алгоритма по памяти на основании оценки дополнительной памяти, которая потребуется ему для обработки входных данных размером N.

Что ж, начнем!

Что такое алгоритм

Объяснять алгоритм — это как рассказывать сказку. Каждый алгоритм — новый волшебный предмет или неожиданный поступок, которые помогают быстро и легко справиться с казавшейся трудной задачей. В этой главе мы рассмотрим несколько решений нетрудной задачи, а потом разберемся, какой алгоритм эффективнее и почему. Кроме того, поймем, как изучать быстродействие алгоритма независимо от его реализации — хотя непосредственные данные о работе конкретных реализаций у нас тоже будут.

Алгоритм — это пошаговая инструкция решения некоторой задачи, реализованная в виде программы. Программа должна возвращать правильный ответ за предсказуемое время. Изучая алгоритм, мы проверяем и правильность ответа (в том числе на всех допустимых входных данных), и его вычислительную сложность (возможно, есть более эффективные решения задачи).

Давайте посмотрим, как процесс решения и анализа задачи проходит в жизни. Скажем, нам нужно найти наибольшее значение в несортированном списке. На рис. 1.1, слева, приведено три набора данных для нашей задачи4 — каждый набор в виде списка Python. Данные обрабатываются алгоритмом (изображен в виде цилиндра), который должен выдавать правильный ответ; ответы перечислены в правой части. Как реализован алгоритм решения? Как он себя ведет на различных входных наборах? Можно ли предсказать время работы? Как быстро можно найти наибольшее из миллиона чисел?

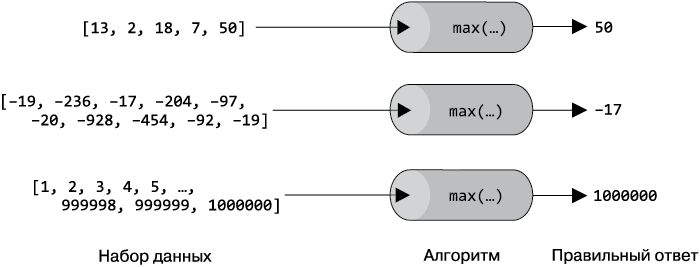
Рис. 1.1. Обработка алгоритмом различных наборов входных данных

Алгоритм и реализующая его программа должны не только давать правильный ответ, но и завершаться за предсказуемое время. Наша задача уже решена — для нее в Python есть функция max(). Правда, аккуратно исследовать эффективность алгоритма, оперируя произвольными входными данными, нельзя. Имеет смысл тщательно подготовить подходящие наборы данных.

Таблица 1.1 показывает время работы функции max() на двух типах входных данных различных размеров: в одних наборах целые числа в списке идут по возрастанию, в других — по убыванию. На разных компьютерах результаты окажутся разными, но всегда можно проверить неизменность двух вещей.

• Время вычисления max() на достаточно длинных возрастающих последо­вательностях всегда больше времени вычисления на таких же, но убывающих.

• Если длина последовательности увеличивается вдесятеро, время вычисления max() на ней тоже увеличивается плюс-минус вдесятеро, как если бы мы каждую проверку делали вручную.

В нашей задаче вычисляется наибольшее значение, а исходная последовательность не меняется. В некоторых других случаях, например в алгоритмах сортировки элементов списка из главы 5, требуется не вычислить новое значение, а изменить сами введенные данные. В нашей книге N обозначает размер набора входных данных.

Таблица 1.1. Запуск функции max() на двух типах наборов входных данных размером N5

N	Восходящая последовательность	Нисходящая последовательность
100	0.001	0.001
1000	0.013	0.013
10 000	0.135	0.125
100 000	1.367	1.276
1 000 000	14.278	13.419

Замечания о времени работы

• Невозможно с уверенностью предсказать время работы алгоритма на наборе, допустим, из 100 000 элементов (обозначим это время T(100 000)). Для разных языков программирования и на разных компьютерах оно будет разным.

• Однако, зная T(10 000), предсказать T(100 000) — время работы на десятикратно больших данных можно, хотя погрешность такого предсказания неизбежна.

Когда придумываешь алгоритм, важнее всего убедиться, что он работает правильно на всех допустимых наборах входных данных. Как сравнивать свойства двух алгоритмов, если они решают одну и ту же задачу? Этим мы по большей части займемся в главе 2. Изучение алгоритма тесно связано с интересными задачами из настоящей жизни, в которых он требуется. Математическая сторона алгоритма может быть непростой, но мы постараемся каждое отвлеченное понятие связать с таким вопросом жизненной практики.

Принято думать, что оценить эффективность алгоритма — значит подсчитать, сколько ему потребовалось вычислительных операций. Но как раз это совсем не просто! Центральный процессор компьютера (CPU) исполняет машинные инструкции — арифметические операции (наподобие сложения и умножения), пересылку данных из памяти в регистры процессора, сравнения и т.п. Современные языки программирования бывают как компилируемые (С или C++), в которых текст программы перед запуском транслируется в машинные инструкции, так и интерпретируемые (Python или Java). Программа на интерпретируемом языке транслируется в промежуточное представление, называемое байт-кодом. Затем программа-интерпретатор, Python например (в свою очередь сам написанный на С и откомпилированный), разбирает и выполняет этот байт-код6. При этом некоторые функции, например min() и max(), встро­ены в Python — они написаны на С, скомпилированы в машинные инструкции и так выполняются.

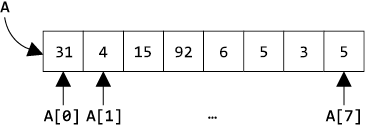
Массив всемогущий Массив — фиксированный набор однотипных значений, занимающий один непрерывный фрагмент оперативной памяти. Это одна из самых старых и самых надежных структур данных. Если значений больше одного — программисты хранят их в массиве. На схеме изображен целочисленный массив из восьми элементов: В массиве A восемь ячеек. Каждая ячейка доступна по номеру, например, A[0] — это 31, а A[7] — 5. В массивах можно хранить и строки, и вообще любые объекты сколь угодно сложного типа. Что следует знать о массивах. Начальный элемент массива A длиной N имеет индекс 0 и обозначается A[0], конечный обозначается A[N-1] и имеет индекс N – 1. Зная номер i элемента в массиве, можно прочитать оттуда элемент Ae[i] или записать на место A[i] новое значение. При этом i — это индекс в диапазоне от 0 до N – 1. Длина массива всегда известна. В Python и Java ее можно задать в процессе работы программы, а в С — только заранее. Чтобы изменить длину массива, необходимо выделить память под новый массив нужной длины и скопировать туда все данные из старого. Просто так размер массива уменьшить или увеличить нельзя. Несмотря на простоту, массивы — очень гибкий и удобный инструмент организации данных. В Python имеется тип данных list, с которым можно смело работать как с массивом, хотя его возможности куда шире: в list можно хранить объекты разных типов одновременно, а размер его может меняться в процессе работы программы.

Посчитать, сколько машинных инструкций выполнилось при работе алгоритма, практически невозможно — современные компьютеры выполняют их миллиардами за секунду! Давайте вместо этого считать, сколько основных действий выполнил алгоритм. Вопрос «Сколько действий?» может означать «Сколько раз сравнивались два элемента массива?» или, к примеру, «Сколько раз вызывалась некоторая функция?». В случае max() нас будет интересовать, сколько раз вызывалась операция сравнения «меньше» (>). Подробнее о правилах подсчета действий мы поговорим в главе 2.

Ну что же, настала пора сорвать покров тайны с алгоритма функции max() и понять, что именно определяет ее поведение.

Поиск наибольшего значения в произвольной последовательности

Рассмотрим проблемную реализацию поиска наибольшего значения произвольной последовательности в примере 1.1. Каждый элемент A сравнивается с my_max, и, если найдено значение больше, my_max обновляется.

Пример 1.1. Проблемная реализация поиска наибольшего значения последовательности

def flawed(A):

  my_max = 0        ❶

  for v in A:       ❷

    if my_max < v:

      my_max = v    ❸

  return my_max

❶ Переменная my_max хранит текущее наибольшее значение. Здесь она инициа­лизируется нулем.

❷ В цикле for определена переменная v, которая на каждом проходе цикла равна очередному элементу A. Оператор if внутри цикла выполняется для каждого такого v.

❸ Переменная my_max обновляется, если v оказалось больше.

Главное в нашем решении — операция сравнения двух выражений (<), которая определяет, меньше ли первое выражение второго. На рис. 1.2 показано, что по мере прохождения переменной v всех значений из A переменная my_max меняется трижды. Функция flawed() определяет наибольшее значение A из шести элементов, вызывая оператор < не более шести раз, по одному разу на каждый элемент. Если в наборе данных будет N элементов, flawed() вызовет < не более N раз.

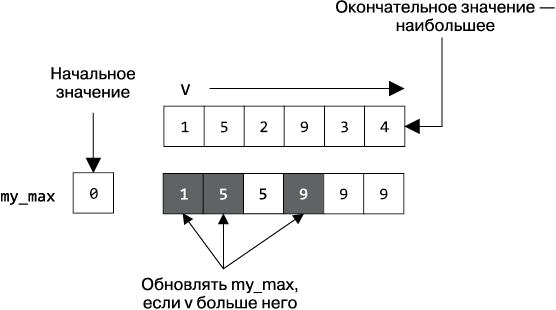
Рис. 1.2. Как работает flawed()

Эта реализация алгоритма содержит ошибку: предполагается, что в A есть хотя бы одно неотрицательное число. Вызов flawed([–5,–3,–11]) вернет 0, что неправильно. Часто вместо нуля пытаются использовать «наименьшее возможное число», примерно так: my_max = float('-inf'). Этот подход также небезупречен, потому что для пустого списка A = [] он вернет -inf, которого там не было. Недочет надо исправить.

Python-выражение range(x,y) вычисляет последовательность целых чисел от x до y (не включая y). Если x больше, чем y, можно задать убывающую последовательность от x до y, не включая y, с помощью range(x,y,–1). Если сделать список из range(1,7), list(range(1,7)) даст [1,2,3,4,5,6]. Соответственно, list(range(5,0,–1)) даст [5,4,3,2,1], а если дополнительно задать шаг — приращение последовательности — list(range(1,10,2)) даст [1,3,5,7,9]: разность между соседними элементами будет равна 2.

Подсчет действий

Первоначальное значение my_max лучше выбрать из элементов A — тогда можно быть уверенными, что вычисленное наибольшее значение будет тоже из A. Работающая на всех входных наборах, кроме пустых, а значит, правильная функция largest() приведена в примере 1.2. Здесь мы выбираем в качестве начального значения my_max начальный элемент A, а затем сравниваем его со всеми остальными: вдруг там найдется побольше?

Пример 1.2. Правильная функция, которая находит наибольшее значение в списке

def largest(A):

  my_max = A[0]                 ❶

  for idx in range(1, len(A)):  ❷

    if my_max < A[idx]:

      my_max = A[idx]           ❸

  return my_max

❶ Сделаем my_max равным начальному элементу списка (он доступен по индексу 0).

❷ Переменная idx принимает целочисленные значения от 1 до len(A)-1 включительно, не достигая len(A).

❸ Если в A по индексу idx стоит большее значение, обновить my_max.

Если передать largest() пустой список — largest([]), в первой же строчке возникнет исключение IndexError, потому что никакого элемента A[0] в списке нет. Встроенная функция max([]) для пустого списка порождает исключение ValueError с пояснением о том, что пустые последовательности не входят в область определения max(). Так программисту проще понять, в чем его ошибка.

В исправленном алгоритме можно уже начинать считать количество действий. Сколько раз вызывалась в нем операция сравнения <? Правильно, N – 1 раз. Значит, мы не только избежали ошибки, но и улучшили производительность алгоритма (по правде говоря, совсем чуть-чуть).

Почему важно считать именно операции сравнения? Это действие, описанное в алгоритме, — сравнить два значения. Другие операторы в программе (например, for или while) выбираются в соответствии с возможностями используемого языка программирования и вполне могут отличаться. Подробнее об этом мы поговорим в следующей главе, а пока продолжим считать сравнения7.

Как оценить эффективность алгоритма по схеме

Допустим, нам предлагают совсем иной алгоритм решения нашей задачи. На каком из них остановиться? Рассмотрим функцию alternate() из примера 1.3. В ней каждое значение из A сравнивается со всеми остальными, и, если выяснится, что оно не меньше, это и есть ответ. Выдаст ли этот алгоритм правильный ответ? И сколько раз в нем выполняется сравнение на входных данных размером N?

Пример 1.3. Другой способ найти наибольшее значение в списке A

def alternate(A):

    for v in A:         ❶

        for x in A:

            if v < x:   ❷

                break

        else:

            return v    ❸

    return None         ❹

❶ Для каждого v из A рассмотрим все x из A и сравним их.

❷ Если v меньше какого-то x, можно больше не сравнивать: это не максимум.

❸ Если мы просмотрели все x, так ни разу и не выполнив break, значит, v — это максимум и его можно уже возвращать.

❹ До этого места выполнение дойдет только при пустом A. В таком случае вернем специальный объект Python — None.

Функция alternate() пытается найти такое значение v из A, чтобы никакое другое значение x из A не оказалось больше него. На этот раз сложно предсказать, сколько потребуется операций сравнения, потому что внутренний цикл по x сразу останавливается, как только выясняется, что x больше v, а внешний — как только v оказывается максимумом. Работа alternate() показана на рис. 1.3.

В данном случае было выполнено 14 сравнений. Впрочем, очевидно, что общее количество действий зависит от того, какие конкретно значения находятся в списке. Что, если бы они шли в другом порядке? Например, так, чтобы для ответа потребовалось как можно меньше действий? Такой набор данных называется лучшим случаем для alternative(). Например, если наибольший из N элементов последовательности стоит в ее начале, количество сравнений в точности равно N. Итак:

• лучший случай — набор данных размером N, на котором алгоритм совершает наименьшее количество действий;

• худший случай — набор данных размером N, требующий наибольшего количества действий.

Рис. 1.3. Как работает alternate()

Попробуем отыскать наихудший вариант входных данных для alternate(), в котором количество проделанных сравнений было бы наибольшим. Очевидно, что максимум должен лежать в конце A, но вдобавок к этому в наихудшем наборе данных все значения в A должны быть упорядочены по возрастанию.

На рис. 1.4 показан наилучший случай, в котором A = [9 5 2 1 3 4], и наихудший случай, в котором A = [1 2 3 4 5 9].

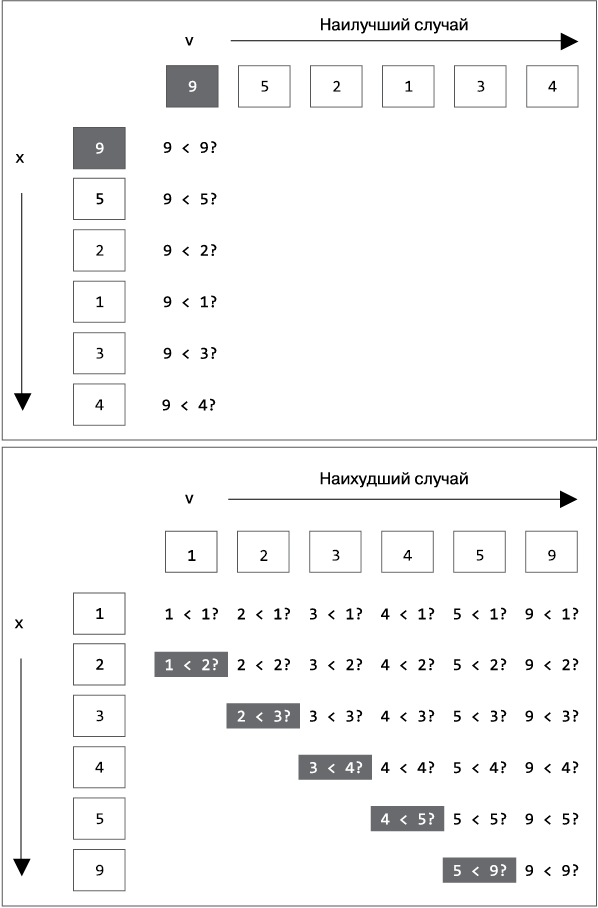
Рис. 1.4. Как работает alternate() в лучшем и худшем случаях

В проиллюстрированном лучшем случае функция делает шесть сравнений >. Если значений всего N, сравнений будет N. В худшем случае подсчет действий слегка сложнее (табл. 1.2). На рис. 1.4 видно, что шесть элементов, упорядоченные по возрастанию, потребовали 26 сравнений. Немного арифметики, и становится понятно, что для N элементов число сравнений будет равно

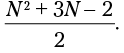
Таблица 1.2. Сравнение работы largest() и alternate() в худших случаях

N	largest() (количество сравнений)	alternate() (количество сравнений)	largest() (время в миллисекундах)	alternate() (время в миллисекундах)
8	7	43	0.001	0.001
16	15	151	0.001	0.003
32	31	559	0.002	0.011
64	63	2143	0.003	0.040
128	127	8383	0.006	0.153
256	255	33 151	0.012	0.599
512	511	131 839	0.026	2.381
1024	1023	525 823	0.053	9.512
2048	2047	2 100 223	0.108	38.161

Пока данных мало, это еще терпимо. Но если удвоить размер набора данных, количество сравнений у alternate() фактически увеличится вчетверо, а largest() останется далеко позади. Последние два столбца табл. 1.2 показывают быстродействие обоих алгоритмов на сотне случайно выбранных наихудших наборов данных размером N. Время работы alternate() тоже увеличивается вчетверо.

Здесь измерялось время, потраченное алгоритмом на обработку набора размером N. Представлены данные о самом быстром (потребовавшем меньше всего времени) решении среди всех попыток. Такой подход лучше обычного вычисления среднего времени по всем однотипным наборам данных, потому что в среднее может закрасться измерение, которое оказалось большим не по вине алгоритма.

В книге будут появляться таблицы с подсчетом количества выполненных действий и затраченного времени наподобие табл. 1.2, где измерялось количество сравнений >. Строки таких таблиц соответствуют различным объемам входных данных. Если просмотреть таблицу сверху вниз, становится понятно, как растут показания в каждом столбце по мере удвоения размера данных.

Подсчет количества сравнений показывает, как работают функции largest() и alternate(). При удвоении N количество сравнений в largest() удваивается, а в alternate() — увеличивается вчетверо. Это поведение вполне стабильно, и несложно предсказать, как оба алгоритма поведут себя на данных большего размера. На рис. 1.5 показано, что количество сравнений в функции alternate() (отмечено по оси Y с левой стороны) довольно точно соответствует ее производительности (затраченное время отмечено по оси Y с правой стороны).

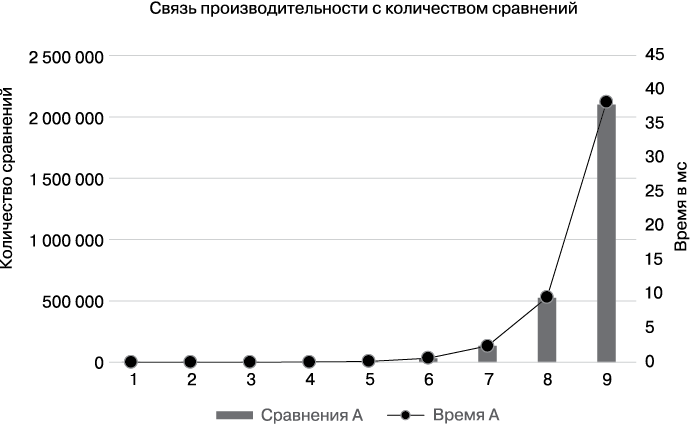
Рис. 1.5. Соотношение количества сравнений и времени работы