Посвящается папе — моему первому учителю математики и информатики.

Предисловие

Я начал работать над этой книгой в 2017 году, будучи техническим директором организации Tachyus, которую я основал. В ней мы разрабатываем программное обеспечение для прогностической аналитики в нефтегазоперерабатывающей промышленности. К тому времени мы закончили работу над нашим основным продуктом — симулятором движения жидкостей, который был создан в том числе с использованием машинного обучения. Этот инструмент позволил нашим клиентам заглянуть в будущее своих нефтяных месторождений и выявить новые возможности экономии на сотни миллионов долларов.

Моя задача как технического директора состояла в масштабировании разработанного программного обеспечения по мере ввода в эксплуатацию в некоторых крупнейших компаниях мира. Трудность была не только в высокой сложности проекта, но и в том, что код был переполнен математическими вычислениями. Примерно в то же время мы начали искать сотрудников на должность, которая называлась «научный инженер-программист», полагая, что нам нужны высококвалифицированные инженеры-программисты, хорошо владеющие математикой, физикой и машинным обучением. В ходе поиска и найма специалистов я понял, что такое сочетание профессиональных навыков встречается редко и пользуется большим спросом. Наши инженеры-программисты тоже осознали это и стремились отточить свои знания математики, чтобы внести вклад в разработку специализированных серверных компонентов, составляющих наш стек. Поскольку в нашей команде уже были специалисты, с энтузиазмом изучающие математику, то в процессе найма я начал задумываться о том, как же из сильного инженера-программиста сделать еще и отличного математика.

К своему разочарованию, я обнаружил, что на рынке нет достойных книг по математике для программистов. Конечно, есть сотни книг и тысячи бесплатных онлайн-статей на такие темы, как линейная алгебра и математический анализ, но не было ничего, что я мог бы дать обычному инженеру-программисту и быть уверенным, что тот освоит необходимое за несколько месяцев. Я говорю это не для того, чтобы принизить инженеров-программистов, я просто отмечаю, что читать книги по математике и разбираться в них — это сложный навык, которому трудно научиться самостоятельно. Для этого сначала нужно понять, какие конкретные темы вам следует изучить (что довольно сложно, особенно если не знать, что в действительности нужно!), прочитать книги по этим темам, а затем подобрать подходящие упражнения и попрактиковаться в применении новых знаний. Иначе можно прочитать учебник от корки до корки, решить все упражнения, предложенные в нем, потратив кучу времени!

В своей книге «Математические алгоритмы для программистов» я надеялся организовать альтернативную возможность. Я считаю, что можно прочитать эту книгу от первого до последнего слова и выполнить все упражнения за разумное время, а затем взяться за работу, уже владея некоторыми ключевыми математическими концепциями.

Как создавалась эта книга

Осенью 2017 года я связался с издательством Manning, рассказал им о своей задумке, и они подтвердили, что были бы заинтересованы в издании такой книги. Это положило начало долгому процессу преобразования моего видения книги в конкретный план, что оказалось намного сложнее, чем я себе представлял, будучи начинающим автором. В издательстве мне задали несколько трудных вопросов по содержимому будущей книги.

• Будет ли кому-то интересна эта тема?

• Не будет ли она чересчур абстрактной?

• Вы действительно сможете вместить семестровую программу преподавания численных методов в одну главу?

Все эти вопросы заставили меня тщательнее оценить достижимость цели. Я расскажу, как мы ответили на некоторые из них, чтобы вы могли понять, как устроена эта книга.

Во-первых, я решил раскрыть в книге один из ключевых приемов — выражение математических идей в коде. Я думаю, что это отличный способ обучения математике, даже если вы не программист по профессии. Когда я учился в старших классах, я научился программировать на графическом калькуляторе TI-84. У меня возникла грандиозная идея написать программы, которые будут делать за меня домашнюю работу по математике и естественным наукам, давая правильный ответ и раскладывая решение по шагам. Как и следовало ожидать, это оказалось намного сложнее, чем просто выполнять домашние задания, зато я получил полезный опыт. В любой задаче, которую я хотел запрограммировать, мне нужно было четко понимать, что имеется на входе и что должно получиться на выходе, а также то, что происходит на каждом шаге решения. В результате я получил надежные знания и рабочую программу, подтверждающую это.

Этим опытом я и постараюсь поделиться с вами в книге. Каждая глава основана на реальном примере программы, для запуска которой нужно правильно собрать воедино все математические компоненты. Сделав это, вы будете уверены, что поняли идею и сможете применить ее снова в будущем. Я включил в текст множество упражнений, чтобы вы могли проверить, что действительно разобрались в математике и представленном программном коде, а также мини-проекты, предлагающие поэкспериментировать.

Еще один вопрос, который я обсуждал с Manning, заключался в выборе языка программирования для примеров. Первоначально я хотел использовать функциональный язык программирования, потому что математика сама является функциональным языком. В конце концов, понятие «функции» возникло в математике задолго до того, как появились компьютеры. В различных областях математики есть функции, которые возвращают другие функции, например интегралы и производные. Однако, если попросить читателей выучить незнакомый язык, такой как LISP, Haskell или F#, одновременно с изучением новых математических понятий, это серьезно усложнит книгу. Поэтому было решено остановиться на Python — популярном и простом в освоении языке с отличными математическими библиотеками. Python также фаворит для пользователей из реального мира — как ученых, так и разработчиков.

Последний важный вопрос, на который мне нужно было ответить, состоял в том, какие именно математические темы я бы включил в книгу, а какие опустил. Это было трудное решение, но по крайней мере мы договорились о названии «Математические алгоритмы для программистов», широта которого давала некоторую гибкость в выборе содержания книги. Вот мой главный критерий: это должны быть «Математические алгоритмы для программистов», а не «Математические алгоритмы для ИТ-специалистов». С учетом этого я мог бы опустить такие темы, как дискретная математика, комбинаторика, графы, логика, нотация «О большое» и т.д., которые изучаются на уроках информатики и в основном используются для изучения программ.

Но даже после того как это решение было принято, на выбор оставался широкий круг математических тем. В конце концов я решил сосредоточиться на линейной алгебре и численных методах. У меня есть определенные педагогические взгляды на эти темы и много хороших примеров визуальных и интерактивных приложений. Вы можете написать большой учебник либо только по линейной алгебре, либо по численным методам и тем самым еще больше сузить круг тем. Я решил, что книга будет основываться на некоторых приложениях в модной нынче области машинного обучения. После принятия этих решений содержание книги стало вырисовываться яснее.

Охватываемые математические идеи

Эта книга охватывает множество математических тем, но основных — несколько. Вот некоторые из них.

• Многомерные пространства. Вы наверняка понимаете, что означают слова «двухмерное пространство» и «трехмерное пространство». Мы с вами живем в трехмерном мире и можем представить двухмерный мир как плоский лист бумаги или экран компьютера. Местоположение в двухмерном пространстве можно описать двумя числами (их часто называют координатами x и y), а местоположение в трехмерном пространстве определяется тремя числами. Мы не можем вообразить 17-мерное пространство, но можем описать его точки списками из 17 чисел. Такие списки чисел называются векторами, а векторная математика помогает прояснить понятие «-мерности».

• Пространства функций. Иногда список чисел может задавать функцию. Например, два числа, такие как a = 5 и b = 13, могут задавать (линейную) функцию вида f(x) = ax + b, и в этом случае функция будет иметь конкретный вид f(x) = 5x + 13. Для каждой точки в двухмерном пространстве с координатами (a, b) существует связанная с ней линейная функция. Таким образом, множество всех линейных функций можно представить как двухмерное пространство.

• Производные и градиенты. Это вычислительные операции, измеряющие скорость изменения функций. Производная говорит о том, как быстро функция f(x) увеличивается или уменьшается с увеличением входного значения x. Функцию в двухмерном пространстве можно представить как f(x, y), и она может увеличиваться или уменьшаться при изменении значений x или y. Если представить пары (x, y) в виде точек в двухмерном пространстве, может возникнуть вопрос: в каком направлении следует двигаться в этом пространстве, чтобы функция f увеличивалась быстрее всего? Ответ на этот вопрос дает градиент.

• Оптимизация функции. Для функции вида f(x) или f(x, y) можно сформулировать еще более широкую версию предыдущего вопроса: какие входные данные дают наибольшее значение функции? Для f(x) ответом будет некоторое значение x, а для f(x, y) — точка в двухмерном пространстве. В случае двухмерного пространства нам может помочь градиент. Если он говорит, что f(x, y) увеличивается в каком-то направлении, то можно найти максимальное значение f(x, y), следуя в этом направлении. Аналогичная стратегия применяется для поиска минимального значения функции.

• Прогнозирование данных с помощью функций. Допустим, вы хотите предсказать число, например цену акции в определенный момент времени. Можете создать функцию p(t), которая принимает время t и выводит цену p. Мерой прогностического качества такой функции является близость к фактическим данным. В этом смысле поиск прогностической функции сводится к минимизации ошибки между вашей функцией и реальными данными. Для этого нужно исследовать пространство функций и найти минимальное значение. Это называется регрессией.

Я думаю, что знание этих математических понятий пригодится каждому, даже тем, кто не интересуется машинным обучением, потому что эти и другие концепции, представленные в книге, имеют множество других применений.

Темы, которые мне скрепя сердце пришлось оставить за рамками книги, — это вероятность и статистика. Вероятность как концепция количественной оценки неопределенности в целом играет важную роль в машинном обучении. Но эта книга и без того получилась довольно объемной, поэтому мне просто не хватило бы ни времени, ни места, чтобы втиснуть хоть сколько-нибудь достойное внимания введение в эти темы. Следите за продолжением книги. Помимо тем, которые я смог охватить на этих страницах, есть еще много интересных и полезных сведений, и я надеюсь, что смогу поделиться ими с вами в будущем.

Благодарности

Я работал над этой книгой около трех лет. За эти годы я получил помощь от многих людей, и поэтому у меня очень длинный список тех, кого я хотел бы поблагодарить.

Прежде всего, я благодарен издательству Manning за помощь в подготовке этой книги. Они поверили, что я, начинающий автор, смогу написать эту большую и сложную книгу, и проявили большое терпение, так как работа над ней не раз отставала от графика. В частности, хочу сказать спасибо Марьян Бейс (Marjan Bace) и Майклу Стивенсу (Michael Stephens) за продвижение проекта и за то, что помогли определить, каким он должен быть. Мой первоначальный редактор-консультант Ричард Уоттенбергер (Richard Wattenbarger) тоже сыграл ключевую роль в создании книги, помогая снова и снова уточнять содержание. Он просмотрел шесть черновых вариантов глав 1 и 2, прежде чем мы решили, как будет структурировано издание.

Большую часть книги я написал в 2019 году под чутким руководством моего второго редактора Дженнифер Стаут (Jennifer Stout), которая довела проект до финишной черты и многому научила меня в области написания технических книг. Научный редактор Крис Ати (Kris Athi) и рецензент Майк Шепард (Mike Shepard) прошли с нами весь путь. Они внимательно вычитали каждое слово и каждую строку кода и исправили бесчисленное количество ошибок. Немалую помощь в работе мне оказала Микаэла Леунг (Michaela Leung), которая проверила всю книгу на предмет грамотности и технической точности. Я также хотел бы поблагодарить маркетинговую команду Manning. Благодаря программе раннего доступа к книгам MEAP (Manning Early Access Program) мы смогли убедиться, что эта книга будет интересна людям. Знание того, что она будет иметь хотя бы скромный коммерческий успех, стало отличным мотиватором на заключительных напряженных этапах ее подготовки к публикации.

Мои нынешние и бывшие коллеги из Tachyus многому научили меня в программировании, и часть их уроков вошли в эту книгу. Я благодарю Джека Фокса (Jack Fox) за то, что он первым заставил меня задуматься о связи между функциональным программированием и математикой, о которой рассказывается в главах 4 и 5. Уилл Смит (Will Smith) учил меня проектированию видеоигр, и у нас состоялось множество содержательных дискуссий о векторной геометрии для отображения трехмерных сцен. Стелиос Кириаку (Stelios Kyriacou) научил меня почти всему, что я знаю об алгоритмах оптимизации, и помог отладить часть кода из книги. Он также познакомил меня с философией, согласно которой «любая задача является задачей оптимизации»— ее обсуждением мы займемся во второй половине книги.

Спасибо всем рецензентам: Адиру Рамджиавану (Adhir Ramjiawan), Анто Аравинту (Anto Aravinth), Кристоферу Хаупту (Christopher Haupt), Клайву Харберу (Clive Harber), Дэну Шейху (Dan Sheikh), Дэвиду Онгу (David Ong), Дэвиду Тримму (David Trimm), Эмануэлю Пиччинелли (Emanuele Piccinelli), Федерико Бертолуччи (Federico Bertolucci), Фрэнсису Буонтемпо (Frances Buontempo), Герману Гонсалесу-Моррису (German Gonzalez-Morris), Джеймсу Ньике (James Nyika), Йенсу Кристиану Б. Медсену (Jens Christian B. Madsen), Йоханнесу ван Неймегену (Johannes Van Nimwegen), Джонни Хопкинсу (Johnny Hopkins), Джошуа Хорвицу (Joshua Horwitz), Хуану Руфесу (Juan Rufes), Кеннету Фрикласу (Kenneth Fricklas), Лоуренсу Джиглио (Laurence Giglio), Натану Мише (Nathan Mische), Филипу Бесту (Philip Best), Река Хорвату (Reka Horvath), Роберту Уолшу (Robert Walsh), Себастьену Портебуа (Sébastien Portebois), Стефано Палуэлло (Stefano Paluello) и Винсенту Жу (Vincent Zhu). Ваши замечания и предложения помогли сделать эту книгу лучше.

Я не эксперт по машинному обучению, поэтому обращался к множеству источников, чтобы убедиться, что представил его точно и правильно. Больше всего на меня повлиял курс Эндрю Ына (Andrew Ng) Machine Learning на Coursera и серия Deep Learning от 3Blue1Brown на YouTube. Это отличные ресурсы, и если вы обращались к ним, то заметите, как они повлияли на подачу сведений в трети книги. Я также должен поблагодарить Дэна Рэтбоуна (Dan Rathbone), чей веб-сайт CarGraph.com был источником данных для многих моих примеров.

Я также хочу сказать спасибо своей супруге Маргарет, астроному, за то что познакомила меня с блокнотами Jupyter. Перенос примеров кода для этой книги в блокноты Jupyter значительно упростил их опробование. Мои родители тоже оказали значительную поддержку, когда я писал книгу: несколько раз случалось так, что я пытался закончить очередную главу во время праздничного визита к ним. Еще они лично гарантировали, что я обязательно продам хотя бы один экземпляр (спасибо, мама!).

Наконец, эта книга посвящена моему папе, который первым показал мне, как реализуется математика в программном коде, обучая меня программированию на APL, когда я учился в пятом классе. Если выйдет второе издание, я мог бы заручиться его помощью, чтобы переписать весь код на Python одной строкой на APL!

Об этой книге

Книга научит вас решать математические задачи с помощью программного кода на языке Python. Математические навыки становятся все более важными для профессиональных разработчиков программного обеспечения, особенно в связи с тем, что компании комплектуют команды, занимающиеся исследованием данных и машинным обучением. Математика играет важнейшую роль и в других областях, таких как разработка игр, компьютерная графика и анимация, обработка изображений и сигналов, система ценообразования и анализ фондового рынка.

Мы начнем с введения в двух- и трехмерную векторную геометрию, векторные пространства, линейные преобразования и матрицы, составляющие основу линейной алгебры. В части II будут представлены численные методы с упором на наиболее полезные для программистов темы: производные, градиенты, метод Эйлера и символьные вычисления. Наконец, в части III все перечисленное ранее собирается вместе, чтобы показать, как работают некоторые важные алгоритмы машинного обучения. К последней главе книги вы будете знать математику на достаточном уровне, чтобы написать собственную нейронную сеть с нуля.

Но имейте в виду, это не учебник! Цель книги — дать адаптированное введение в темы, которые могут показаться пугающими, запутанными или скучными. В каждой главе демонстрируется пример практического применения математической концепции, дополненный упражнениями, которые помогут проверить, как вы поняли материал, а также мини-проектами, которые помогут продолжить исследование.

Кому адресована книга

Издание адресовано всем, кто имеет значительный опыт программирования и хочет освежить свои знания по математике или узнать больше о ее применении в программном обеспечении. Для этого не требуется разбираться в матанализе или линейной алгебре — достаточно знания алгебры и геометрии на уровне средней школы, даже если вы ее давно окончили. Эта книга предназначена для чтения за клавиатурой. Наибольшую пользу от нее вы получите, если будете выполнять представленные в ней примеры и упражнения.

Структура издания

Глава 1 приглашает вас в мир математики. Она охватывает некоторые важные области применения этой науки в программировании, знакомит с темами, которые будут обсуждаться в книге, и объясняет, насколько полезным инструментом может быть программирование для изучающих математику. Далее книга делится на три части.

• Часть I посвящена векторам и линейной алгебре.

• Глава 2 посвящена векторной математике в двухмерном пространстве с упором на использование координат в двухмерной графике. Здесь же рассматриваются некоторые основы тригонометрии.

• Глава 3 дополняет предыдущую обсуждением трехмерных пространств, точки которых имеют три координаты. Здесь будут представлены понятия скалярного и векторного произведений, которые можно применять для измерения углов и отображения трехмерных моделей.

• Глава 4 знакомит с линейными преобразованиями — функциями, принимающими и возвращающими векторы, которые создают определенные геометрические эффекты, такие как поворот или отражение.

• Глава 5 знакомит с матрицами — массивами чисел, которые могут кодировать линейное векторное преобразование.

• Глава 6 обобщает принципы операций с двух- и трехмерными векторами до произвольного числа измерений. Пространства таких векторов называют векторными пространствами. В качестве основного примера в ней используется обработка изображения с помощью векторной математики.

• Глава 7 посвящена наиболее важной вычислительной задаче линейной алгебры — решению систем линейных уравнений. Здесь она задействуется в системе обнаружения столкновений в простой видеоигре.

• Часть II знакомит с численными методами и примерами их применения в физике.

• Глава 8 вводит понятие скорости изменения функции. Она охватывает производные, определяющие скорость изменения функции, и интегралы, позволяющие восстановить функцию по скорости ее изменения.

• В главе 9 рассматривается важный метод приближенного интегрирования, называемый методом Эйлера. Здесь игра, представленная в главе 7, будет дополнена движущимися и ускоряющимися объектами.

• Глава 10 демонстрирует приемы манипулирования алгебраическими выражениями в коде, включая автоматический поиск формулы производной функции. Здесь вы познакомитесь с символьным программированием — подходом к выполнению математических операций в коде, отличным от подходов, используемых в других частях книги.

• Глава 11 расширяет тему вычислительных методов до двух измерений, определяя операцию градиента и показывая пример определения силового поля с ее помощью.

• Глава 12 демонстрирует применение производных для поиска максимальных или минимальных значений функций.

• Глава 13 показывает возможность представления звуковых волн в виде функций и их разложения на суммы других, более простых функций, называемых рядами Фурье. Здесь рассказывается, как реализовать на Python воспроизведение музыкальных нот и аккордов.

• Часть III объединяет приемы из первых двух частей для представления некоторых важных принципов машинного обучения.

• Глава 14 рассказывает, как методом линейной регрессии аппроксимировать двухмерные данные прямой линией. Примером в этой главе служит поиск функции, которая наиболее точно предсказывает цену подержанного автомобиля по его пробегу.

• Глава 15 рассматривает другую задачу машинного обучения — определение модели автомобиля на основе некоторых данных о нем. Выяснение того, какой объект представлен точкой данных, называется классификацией.

• Глава 16 показывает, как спроектировать и реализовать нейронную сеть — особый вид математической функции — и использовать ее для классификации изображений. В этой главе применяется то, что рассматривалось почти во всех предыдущих главах.

Каждая глава должна быть понятна, если вы прочитали и поняли предыдущие главы. Необходимость описания идей в определенном порядке обусловлена тем, что они могут иметь самые разные практические применения. Надеюсь, что разнообразие примеров сделает чтение книги увлекательным занятием и покажет вам широкий спектр практических применений математики.

О примерах кода

В этой книге темы представлены (я надеюсь) в логическом порядке. Концепции, описанные в главе 2, используются как основа в главе 3, на тех, что рассмотрены в главах 2 и 3, базируется глава 4 и т.д. Программный код не всегда пишется по порядку. То есть самые простые концепции в готовой компьютерной программе не всегда находятся в первых строках первого файла исходного кода. Это различие затрудняет представление исходного кода книги в понятной форме.

Я попытался решить эту проблему за счет включения в каждую главу пошагового файла с кодом в виде блокнота Jupyter. Блокнот Jupyter можно считать аналогом записи интерактивного сеанса Python со встроенными визуальными элементами, такими как графики и изображения. Используя блокнот Jupyter, вы вводите какой-то код, выполняете его, а позже переопределяете в ходе сеанса по мере реализации своих идей. Блокнот для каждой главы включает код для каждого раздела и подраздела, который выполняется в том же порядке, что и в книге. Это означает, что вы можете опробовать примеры во время чтения. Вам не нужно добираться до конца главы, где код станет достаточно полным для выполнения. В приложении A показано, как настроить Python и Jupyter, а в приложении Б перечислены некоторые функции Python, полезные для начинающих изучать этот язык.

Эта книга содержит множество примеров исходного кода как в отдельных листингах, так и прямо внутри текста. В обоих случаях исходный код оформлен моноширинным шрифтом, чтобы его легко было отличить от обычного текста.

Кроме того, комментарии, имеющиеся в исходном коде, удалены из листингов, если они описываются в тексте. Многие листинги сопровождаются отдельными описаниями, подчеркивающими наиболее важные понятия. Если в исходном коде в репозитории книги будут обнаружены и исправлены какие-то ошибки, то там же, в репозитории, я добавлю примечания, объясняющие любые отличия от кода, напечатанного в книге.

В некоторых случаях примерами служат целые сценарии на Python, а не ячейки в блокноте Jupyter. Эти сценарии можно запускать в командной строке, например, командой python script.py, или в ячейке блокнота Jupyter командой !python script.py. Я включил ссылки на такие сценарии в некоторые блокноты Jupyter, чтобы в процессе чтения вы могли находить и опробовать соответствующие файлы с исходным кодом.

На протяжении всей книги я неизменно придерживаюсь одного соглашения: примеры выполнения отдельных команд Python начинаются с приглашения к вводу >>>, которое используется также в интерактивной оболочке Python. Я настоятельно рекомендую применять Jupyter вместо интерактивной оболочки Python, но в любом случае строки, начинающиеся с >>>, — это ввод, а остальные строки — вывод. Вот пример блока кода, представляющего вычисление выражения «2 + 2» в интерактивной оболочке Python:

>>> 2 + 2

4

В следующем примере отсутствует последовательность символов >>>, так что этот пример содержит обычный код на Python, а не последовательность ввода и вывода:

def square(x):

    return x * x

В книге приводятся сотни упражнений для закрепления пройденного материала, а также мини-проекты — либо более сложные, либо требующие более творческого подхода, либо знакомящие с новыми понятиями. Большинство упражнений и мини-проектов предлагают решить некоторые математические задачи с использованием кода на Python. Я дал решения почти всех, кроме некоторых мини-проектов, реализация которых не ограничивается временными рамками. Решения приводятся в блокноте Jupyter для соответствующей главы.

Код примеров из этой книги доступен для загрузки на веб-сайте издательства Manning (https://www.manning.com/books/math-for-programmers), а также в репозитории GitHub (https://github.com/orlandpm/math-for-programmers).

От издательства

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах.

Об авторе

Пол Орланд (Paul Orland) — предприниматель, программист и математик-энтузиаст. Поработав инженером-программистом в Microsoft, он основал компанию Tachyus, занимающуюся прогностической аналитикой в сфере оптимизации производства энергии в нефтегазовой отрасли. Как технический директор и основатель Tachyus, Пол руководил разработкой программного обеспечения для машинного обучения и моделирования физических процессов, а позже, как генеральный директор, расширил сферу влияния компании, найдя клиентов на пяти континентах. Пол имеет степень бакалавра по математике, полученную в Йельском университете, и степень магистра по физике, полученную в Вашингтонском университете. Его тотемное животное — лобстер.

Иллюстрация на обложке

На обложку книги помещена иллюстрация, подписанная Femme Laponne — женщина из Лапландии, ныне Сапми, которая включает части северной Норвегии, Швеции, Финляндии и России. Иллюстрация взята из каталога костюмов жителей разных стран, изданного Жаком Грассе де Сен-Совером (Jacques Grasset de Saint-Sauveur; 1757–1810) в 1797 году во Франции под названием Costumes de Différents Pays. Все иллюстрации в каталоге тщательно прорисованы и раскрашены вручную. Богатое разнообразие коллекции Грассе де Сен-Совера напоминает нам о том, насколько отличными друг от друга были культурные традиции городов и регионов мира всего 200 лет назад. Изолированные друг от друга люди говорили на разных диалектах и языках. Встретив человека на улице, по его одежде легко было определить, где он живет, чем зарабатывает на жизнь или какое положение в обществе занимает.

С тех пор стиль одежды сильно изменился, исчезло разнообразие, характеризующее различные области и страны. В настоящее время трудно различить по одежде даже жителей разных континентов, не говоря уже о жителях разных городов, регионов или стран. Мы заменили культурное многообразие более разнообразной личной жизнью и, безусловно, более разнообразной и интересной интеллектуальной жизнью.

Мы в издательстве Manning славим изобретательность и предприимчивость компьютерного бизнеса обложками книг, изображающими богатство региональных различий двухвековой давности, оживших благодаря иллюстрациям Грассе де Сен-Совера.

1. Математика в программном коде

В этой главе

• Решение финансовых задач с помощью математики и программного обеспечения.

• Как избежать распространенных ошибок при изучении математики.

• От программирования к пониманию математики, основываясь на интуиции.

• Python как мощный и расширяемый калькулятор.

Математика подобна бейсболу, поэзии или хорошему вину. Одни настолько увлечены этой наукой, что посвящают ей всю свою жизнь, другим же кажется, что они просто не понимают ее. Вероятно, после 11 лет изучения математики в школе вы уже причислили себя к той или иной группе людей.

Представьте, что в школе вы бы изучали виноделие подобно тому, как изучали математику. Мне бы не понравилось, если бы мне читали лекции о сортах винограда и методах ферментации по часу в день шесть дней в неделю. Будь такой предмет в школе, то, может быть, мне приходилось бы выпивать по три-четыре стакана, чтобы выполнить домашнее задание. С одной стороны, это мог бы быть восхитительный образовательный опыт, но с другой — идти следующим утром на занятия с тяжелой головой — сомнительное удовольствие. Опыт, который я получил на уроках математики, был примерно таким же, и это на какое-то время отталкивало меня от предмета.

Проще всего решить, что вы либо созданы для математики, либо нет. Если вы уже верите в себя и хотите начать учиться — здорово! В остальном эта глава предназначена для тех, кто настроен менее оптимистично. Страх перед математикой настолько распространен, что даже назван математической тревожностью (math anxiety). Я надеюсь рассеять ваше беспокойство и показать, что математика может быть очень интересным увлечением. Все, что вам нужно, — это правильные инструменты и правильный настрой.

Основным инструментом обучения в этой книге станет язык программирования Python. Полагаю, что когда вы изучали математику в школе, то учились по формулам, написанным на доске, а не по компьютерному коду. Это беда, потому что язык программирования высокого уровня намного мощнее школьной доски и намного универсальнее любого дорогого калькулятора, который вы могли бы использовать. Преимущество изучения математики на примерах в программном коде состоит в том, что идеи в этом случае выражаются достаточно точно, чтобы их мог понять компьютер, и нет необходимости спорить по поводу значений новых символов.

Как и при изучении любого нового предмета, лучший способ настроиться на успех — захотеть учиться. Тому может быть множество причин. Вас может заинтриговать красота математических понятий, или вам может доставлять удовольствие решение головоломных математических задач. Возможно, вы мечтаете создать приложение или игру, а для этого нужно реализовать математические вычисления в коде. Но я оставлю все эти причины в стороне и сосредоточусь на более прагматичной мотивации — решение математических задач с помощью программного обеспечения может принести вам много денег.

1.1. Решение финансовых задач с помощью математики и программного обеспечения

На уроках математики от нерадивых учеников часто можно услышать вопрос: «Где в реальной жизни мне могут пригодиться эти знания?» Когда я учился в школе, учителя говорили нам, что математика поможет добиться профессионального успеха и заработать деньги. Я думаю, что они были правы, хотя иногда и приводили неправильные примеры. Например, я не рассчитываю банковские проценты вручную, как и мой банк. Может быть, если бы я стал геодезистом на стройплощадке, как предположил мой учитель тригонометрии, то использовал бы синусы и косинусы каждый день, чтобы заслужить свою зарплату.

Как оказалось, примеры из школьных учебников не так уж и практичны. И все же в реальной жизни есть примеры ошеломляюще прибыльного применения математики. Многие из них заключаются в воплощении правильной математической идеи в пригодном для использования программном обеспечении. Некоторыми из таких примеров я хочу с вами поделиться.

1.1.1. Прогнозирование движения финансового рынка

Все мы слышали легенды о биржевых трейдерах, которые зарабатывают миллионы долларов и умудряются покупать и продавать нужные акции в нужное время. По фильмам, которые я видел, у меня сложился стереотипный образ трейдера как мужчины средних лет в костюме, который кричит на своего брокера по мобильному телефону и разъезжает на спортивной машине. Возможно, когда-то это и соответствовало действительности, но сейчас все изменилось.

В офисах, разбросанных по всему Манхэттену, скрываются тысячи людей, которых называют биржевыми аналитиками. Они разрабатывают математические алгоритмы для автоматизации торговли акциями и получения прибыли. Они не носят костюмы и не кричат в мобильные телефоны, но я уверен, что у многих из них очень хорошие спортивные автомобили.

Но как биржевой аналитик может написать программу, которая автоматически зарабатывает деньги? Ответы на этот вопрос охраняются как самые ценные коммерческие секреты, но можете быть уверены: в них много математики. Рассмотрим короткий пример, чтобы понять, как может работать автоматизированная стратегия торговли.

Акции — это разновидность финансовых активов, представляющих доли участия в компаниях. Когда рынок понимает, что дела у компании идут хорошо, ее акции растут в цене — их покупка становится более дорогостоящей, а продажа — более прибыльной. Цены на акции меняются постоянно и хаотично. На рис. 1.1 показано, как может выглядеть график изменения цены акции в течение торгового дня.

 

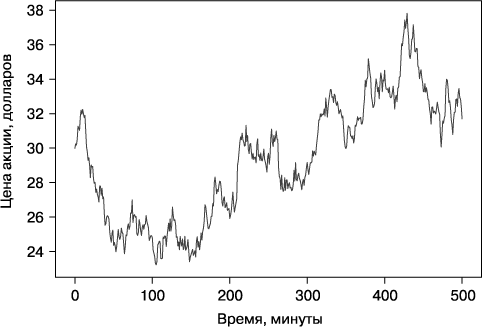
Рис. 1.1. Типичный график изменения цены акции с течением времени

Если купить 1000 этих акций по 24 доллара примерно на 100-й минуте и продать по 38 долларов на 400-й минуте, то можно заработать 14 000 долларов всего за один день. Неплохо! Однако проблема в том, что для этого нужно заранее знать, что акции вырастут и что 100-я и 400-я минуты являются лучшими моментами для покупки и продажи соответственно. Конечно, никто не сможет точно предсказать моменты, когда цена будет минимальной или максимальной, но можно попробовать найти относительно хорошее время для покупки и продажи в течение дня. Посмотрим, как эту задачу решить математически.

Мы могли бы определить, движется ли цена акций вверх или вниз, найдя линию наилучшего соответствия, которая примерно соответствует направлению движения цены. Этот процесс называется линейной регрессией, и мы рассмотрим его в части III. Основываясь на изменчивости данных, можно рассчитать еще две линии выше и ниже линии наилучшего соответствия, которые ограничивают область колебания цены. Как показано на рис. 1.2, эти три линии, наложенные на график колебания цены, довольно хорошо отражают общий тренд.

 

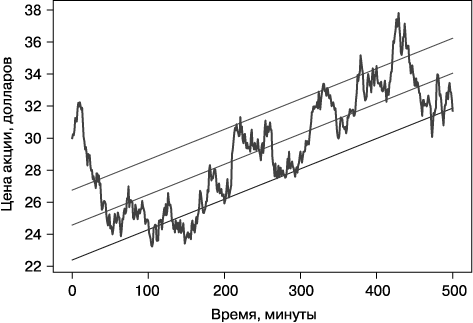
Рис. 1.2. Использование линейной регрессии для выявления тренда изменения цены на акции

Получив математическое понимание движения цены, можно написать код для автоматической покупки, когда цена колеблется возле нижней точки тренда, и продажи, когда она возвращается вверх. В частности, программа может подключаться к фондовой бирже по сети и покупать 100 акций, когда цена пересекает нижнюю линию, и продавать 100 акций, когда цена пересекает верхнюю линию. Рисунок 1.3 иллюстрирует одну из таких прибыльных сделок: покупка по цене около 27,8 доллара и продажа по цене около 32,6 доллара дают заработок 480 долларов в час.

 

Рис. 1.3. Покупка и продажа в соответствии с установленными нами правилами обеспечивают прибыль

Я не берусь утверждать, что продемонстрировал полноценную или хотя бы жизнеспособную стратегию, но дело в том, что, имея правильную математическую модель, можно автоматически получать прибыль. Сейчас множество программ строят и обновляют модели, оценивающие прогнозируемую динамику изменения стоимости акций и других финансовых инструментов. Если вы напишете такую программу, то сможете наслаждаться отдыхом, в то время как она будет приносить вам деньги!

1.1.2. Поиск выгодной сделки

Наверняка у вас не настолько туго набитые карманы, чтобы пускаться в рискованные операции с акциями. Но математика все равно может помочь заработать и сэкономить деньги в других сферах, таких, например, как покупка подержанного автомобиля. С новой машиной все просто: если два дилера продают одинаковые автомобили, то вы, очевидно, пойдете к тому, который предложит наименьшую цену. Однако при покупке подержанного автомобиля приходится оценивать больше факторов — не только цену, но также пробег и год выпуска. Вы можете учитывать даже продолжительность нахождения конкретного подер­жанного автомобиля на рынке как косвенную оценку его качества: чем дольше он продается, тем более подозрительным кажется.

В математике объекты, которые можно описать с помощью упорядоченных списков чисел, называются векторами, и существует целая область математики, называемая линейной алгеброй, посвященная их изучению. Например, подержанный автомобиль может характеризоваться четырехмерным вектором, то есть четверкой чисел (2015, 41 429, 22,27, 16 980). Этот вектор содержит год выпуска модели, пробег, количество дней на рынке и запрашиваемую цену соответственно. У моего друга есть сайт CarGraph.com, на котором собраны данные о выставленных на продажу подержанных автомобилях. На момент написания этих строк в списке насчитывался 101 автомобиль Toyota Prius, выставленный на продажу, и для каждого были предоставлены некоторые или все четыре элемента данных. Кроме того, оправдывая свое название, сайт предлагает визуальное представление данных в виде графика (рис. 1.4). Визуализировать четырехмерные объекты трудно, но если выбрать два измерения, такие как цена и пробег, то их можно изобразить в виде точек на точечной диаграмме.

 

Рис. 1.4. Соотношение «цена/пробег» для автомобилей Toyota Prius, выставленных на продажу на сайте CarGraph.com

Было бы интересно попробовать построить линию тренда. Каждая точка на этом графике представляет чье-то мнение о справедливой цене, поэтому линия тренда объединит эти мнения в более надежную цену при любом пробеге. На рис. 1.5 я использовал экспоненциальную кривую вместо прямой и исключил из расчетов некоторые почти новые автомобили, продающиеся по цене ниже розничной.

 

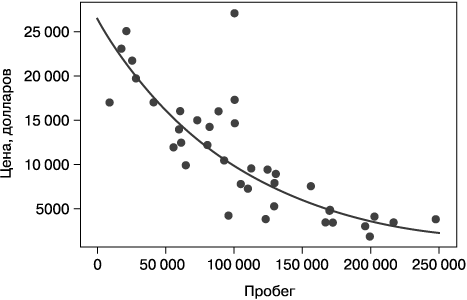
Рис. 1.5. Аппроксимация экспоненциальной кривой соотношения «цена/пробег» для подержанных автомобилей Toyota Prius

Для большего удобства я преобразовал значения пробега в десятки тысяч миль, поэтому пробег 5 соответствует 50 000 миль. Обозначив цену p, а пробег m, я вывел уравнение кривой наилучшего приближения:

p = 26 500 · 0,905m.                (1.1)

Как показывает уравнение (1.1), в среднем цена подержанного автомобиля равна 26 500 долларов, умноженных на 0,905 в степени величины пробега. Подставив значения в уравнение, я выяснил, что, располагая 10 000 долларов, могу купить Prius с пробегом около 97 000 миль (рис. 1.6). Если считать эту кривую отражением справедливой цены, то автомобили ниже этой линии можно рассматривать как выгодные предложения.

 

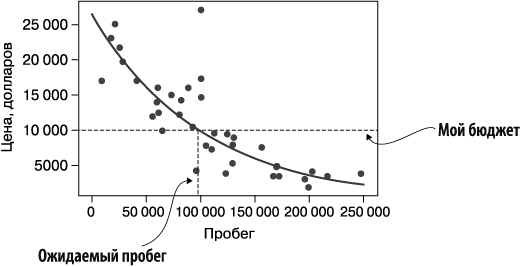
Рис. 1.6. Определение пробега автомобиля Prius, который можно приобрести при бюджете 10 000 долларов

Но уравнение (1.1) не только позволяет определить выгодность сделки. Оно рассказывает о том, как обесцениваются автомобили. Первое число в уравнении — 26 500 долларов — соответствует цене автомобиля с нулевым пробегом. Она удивительно близка к розничной цене нового Prius. Если бы наилучшей аппроксимацией тренда была прямая линия, то это означало бы, что стоимость Prius уменьшается на фиксированную сумму с каждой пройденной милей. Однако экспоненциальная форма кривой говорит о том, что стоимость уменьшается на фиксированный процент. Согласно этому уравнению, проехав 10 000 миль, Prius будет стоить 0,905, или 90,5 %, от первоначальной цены. После 50 000 миль пробега его цену нужно умножить на коэффициент 0,9055 = 0,607, то есть стоимость автомобиля составит 61 % от первоначальной цены.

Чтобы построить график, изображенный на рис. 1.6, я реализовал функцию price(mileage) на Python, которая принимает величину пробега (в десятках тысяч миль) и возвращает наиболее вероятную цену. Результаты вычислений price(0) - price(5) и price(5) - price(10) говорят мне, что первые и вторые 50 000 миль снижают стоимость примерно на 10 000 и 6300 долларов соответственно.

Аппроксимация тренда прямой линией означала бы, что стоимость автомобиля уменьшается на фиксированную величину 0,1 доллара за милю. То есть через каждые 50 000 миль пробега стоимость должна уменьшаться на одни и те же 5000 долларов. Но здравый смысл подсказывает, что первые мили пробега новой машины — самые дорогие, и экспоненциальная функция (уравнение (1.1)) хорошо согласуется с этим, а линейная модель — нет.

Но давайте не будем забывать, что это лишь двухмерный анализ. Мы построили математическую модель, использующую две характеристики из четырех, описывающих каждый автомобиль. В части I вы познакомитесь с векторами различных размерностей и узнаете, как манипулировать многомерными данными. В части II мы рассмотрим различные виды функций, такие как линейные и экспоненциальные, и сравним их, проанализировав скорости изменения. Наконец, в части III вы узнаете, как строить математические модели, которые включают все измерения, имеющиеся в наборе данных, и позволяют получить более точную картину.

1.1.3. Трехмерная графика и анимация

Многие из самых известных и финансово успешных программных проектов так или иначе обрабатывают многомерные данные, часто трехмерные. Здесь я имею в виду трехмерные анимационные фильмы и видеоигры, кассовые сборы которых исчисляются миллиардами долларов. Например, программное обеспечение Pixar для трехмерной анимации помогло заработать более 13 млрд долларов. Серия трехмерных экшен-игр Call of Duty, выпущенных компанией Activision, принесла ей более 16 млрд долларов, а Grand Theft Auto V, выпущенная компанией Rockstar, — 6 млрд долларов.

Каждый из этих проектов основан на вычислениях с трехмерными векторами, или тройками чисел, вида v = (x, y, z). Тройки чисел достаточно, чтобы найти точку в трехмерном пространстве относительно контрольной точки, называемой началом координат. Как показано на рис. 1.7, каждое из трех чисел говорит, как далеко нужно пройти в одном из трех перпендикулярных направлений, чтобы достичь заданной точки.

 

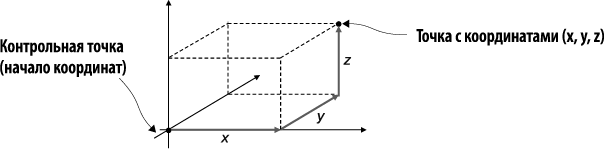
Рис. 1.7. Определение точки в трехмерном пространстве с помощью вектора из трех чисел: x, y и z

Любой трехмерный объект, от рыбы-клоуна в игре «В поисках Немо» до авианосца в Call of Duty, можно определить в компьютере как набор трехмерных векторов. В программе каждый из этих объектов выглядит как список троек чисел типа float. Три тройки чисел определяют три точки в пространстве, которые могут представлять треугольник (рис. 1.8), например:

triangle = [(2.3,1.1,0.9), (4.5,3.3,2.0), (1.0,3.5,3.9)]

 

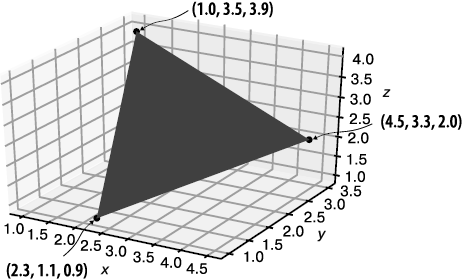
Рис. 1.8. Трехмерный треугольник, образованный тремя тройками чисел, обозначающими координаты вершин

Комбинируя множество треугольников, можно определить поверхность трехмерного объекта, и чем больше треугольников меньшего размера использовать, тем более гладким получится объект. На рис. 1.9 показаны варианты определения трехмерной сферы с помощью все большего числа треугольников все меньшего и меньшего размера.

 

Рис. 1.9. Трехмерные сферы, образованные разным количеством треугольников

В главах 3 и 4 вы узнаете, как использовать трехмерную векторную математику для преобразования трехмерных моделей в двухмерные изображения с тенями, как на рис. 1.9. Кроме того, трехмерные модели должны быть гладкими, чтобы иметь реалистичный вид в игре или фильме, и должны двигаться и изменяться реалистичным образом. Это означает, что рисованные объекты должны подчиняться законам физики, которые тоже выражаются в терминах трехмерных векторов.

Предположим, что вы программист, занимающийся разработкой Grand Theft Auto V, и хотите включить в игру поддержку, например, стрельбы из базуки по вертолету. Снаряд, вылетающий из базуки, начинает полет в точке местоположения главного героя, затем его позиция меняется со временем. Для обозначения различных позиций, которые занимает снаряд на протяжении полета, можно использовать числовые индексы, начиная с v0 = (x0, y0, z0). С течением времени снаряд достигает новых позиций, обозначаемых векторами v1 = (x1, y1, z1), v2 = (x2, y2, z2) и т.д. Скорость изменения значений x, y и z определяется направлением выстрела и скоростью движения снаряда. Кроме того, скорость может меняться со временем — снаряд увеличивает свою позицию по оси z с уменьшающейся скоростью из-за непрерывного действия силы тяжести, направленной вертикально вниз (рис. 1.10).

 

Рис. 1.10. Вектор, описывающий положение снаряда, изменяется с течением времени и определяется начальной скоростью снаряда и силой тяжести

Любой опытный геймер скажет вам, что нужно целиться немного выше вертолета, чтобы попасть в него! Для моделирования физики необходимо знать, какие силы воздействуют на объекты и какие изменения с течением времени они вызывают. Математика непрерывных изменений называется математическим анализом, а законы физики обычно выражаются в терминах объектов матанализа, называемых дифференциальными уравнениями. Подробнее об анимации трехмерных объектов вы узнаете в главах 4 и 5, а о моделировании физических законов с использованием матанализа — в части II.

1.1.4. Моделирование физического мира

Заявление о том, что математическое программное обеспечение создает реальную финансовую ценность, — не просто предположение, доказательством может служить моя карьера. В 2013 году я основал компанию Tachyus, которая занимается разработкой программного обеспечения для оптимизации добычи нефти и газа. Наше программное обеспечение использует математические модели потоков нефти и газа под землей, помогающие добывать их более эффективно и прибыльно. С помощью полученной информации наши клиенты смогли сэкономить миллионы долларов за счет снижения затрат и увеличения добычи.

Чтобы объяснить, как работает наше программное обеспечение, необходимо знать хотя бы основные термины нефтедобычи. В земле бурят отверстия, называемые скважинами, пока не будет достигнут слой пористой породы, содержащей нефть. Этот слой породы, богатый нефтью, называется резервуаром. Нефть выкачивается на поверхность, а затем продается нефтеперерабатывающим предприятиям, превращающим ее в нефтепродукты, которые мы используем каждый день. На рис. 1.11 показана упрощенная схема нефтяного месторождения.

 

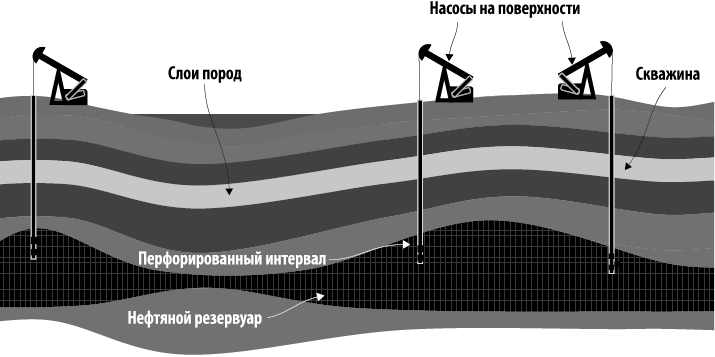
Рис. 1.11. Упрощенная схема нефтяного месторождения

В последние несколько лет наблюдались значительные колебания цен на нефть, но для цели дальнейшего обсуждения допустим, что нефть стоит 50 долларов за баррель, где баррель — это единица объема, равная 42 галлонам, или примерно 159 литрам. Если предположить, что в результате бурения скважин и эффективной откачки компания способна добывать 1000 баррелей нефти в день (объем нескольких плавательных бассейнов на заднем дворе), то ее годовой доход будет исчисляться десятками миллионов долларов и увеличение эффективности даже на несколько процентов может приносить значительную дополнительную прибыль.

Основной вопрос, волнующий нефтедобытчиков: что происходит под землей, как движется нефть? Это сложный вопрос, но на него можно ответить более или менее точно, решая дифференциальные уравнения. Роль переменной здесь играет не положение снаряда, а расположение, давление и дебит жидкостей в пласте. Дебит жидкостей — это функция особого вида, которая возвращает вектор, называемый векторным полем. Текучая среда может распространяться с любой скоростью в любом из направлений в трехмерном пространстве, и эти направление и скорость могут различаться в разных местах внутри резервуара.

Подбирая наиболее вероятные значения для некоторых из этих параметров, мы можем прогнозировать скорость потока жидкостей через пористую горную породу, например песчаник, используя дифференциальное уравнение, называемое законом Дарси. На рис. 1.12 показана формула, выражающая закон Дарси, — не волнуйтесь, если какие-то символы окажутся вам незнакомыми! Функция q, представляющая скорость потока, выделена жирным, чтобы показать, что она возвращает векторное значение.

 

Рис. 1.12. Формула, выражающая закон Дарси, который описывает течение жидкостей через пористые горные породы

Наиболее важная часть этого уравнения — символ в виде треугольника, обращенного вершиной вниз, который представляет оператор градиента в векторном анализе. Градиент функции давления p(x, y, z) в данной пространственной точке (x, y, z) — это трехмерный вектор q(x, y, z), указывающий направление и скорость увеличения давления в этой точке. Знак «минус» обозначает, что трехмерный вектор скорости потока имеет противоположное направление. Это уравнение говорит языком математики, что жидкость течет из областей с высоким давлением в области с низким давлением.

Отрицательные градиенты часто встречаются в физике. Их можно рассматривать как свидетельство того, что природа всегда стремится перейти в состояние с более низкой потенциальной энергией. Потенциальная энергия мяча на холме зависит от высоты холма h в любой его точке x. Если представить, что высота холма задана функцией h(x), то ее градиент направлен вверх, а мяч будет стремиться скатиться вниз — в прямо противоположном направлении (рис. 1.13).

В главе 11 вы узнаете, как вычислять градиенты. Там я покажу, как применять их для моделирования законов физики, а также для решения других математических задач. Кроме того, градиент — одно из самых важных математических понятий в машинном обучении.

 

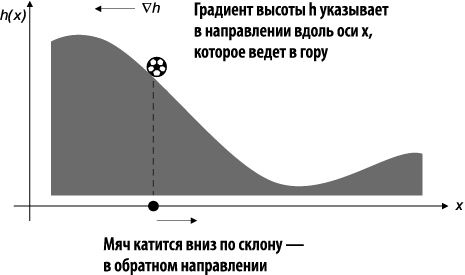
Рис. 1.13. Положительный градиент направлен вверх, а отрицательный — вниз

Я надеюсь, что эти примеры показались вам более убедительными и реалистичными, чем примеры, приводившиеся на уроках математики в школе. Возможно, сейчас вы убедились, что эти математические понятия достойны изучения, но беспокоитесь, что они могут оказаться слишком сложными для вас. Изучение математики — трудная задача, особенно в одиночку. Поэтому, чтобы упростить ее, поговорим о некоторых возможных ловушках, и о том, как я помогу вам избежать их в этой книге.

1.2. Как не надо учить математику

На рынке есть много книг по математике, но не все они одинаково полезны. У меня есть немало друзей-программистов, которые пытались изучать математические концепции, подобные описанным в предыдущем разделе, просто из любопытства или из-за стремления продвинуться по карьерной лестнице. Так вот, используя традиционные учебники по математике в качестве основного ресурса, они часто оказывались в тупике и сдавались. Вот как выглядит типичная история неудачного изучения математики.

1.2.1. Джейн решила подучить математику

Моя (вымышленная) подруга Джейн, веб-разработчик полного цикла, трудится в небольшой технологической компании в Сан-Франциско. В колледже Джейн изучала информатику и математику по самой обычной программе и начинала карьеру как менеджер по продукту. За последние 10 лет она изучила программирование на Python и JavaScript и смогла перейти в отдел разработки программного обеспечения. На новой работе она считается одним из самых способных программистов, так как умеет создавать базы данных, веб-сервисы и пользовательские интерфейсы для обслуживания клиентов. Как видите, она большая умница!

Постепенно Джейн поняла, что изучение науки о данных поможет ей разрабатывать и внедрять новые возможности и улучшить качество обслуживания клиентов. Большую часть времени по пути на работу Джейн читает блоги и статьи о новых технологиях, а недавно ее поразили несколько статей на тему глубокого обучения. В одной из них рассказывалось о модели глубокого обучения AlphaGo, созданной в Google, сумевшей обыграть в настольную игру го лучших игроков в мире. В другой статье были показаны потрясающие картины в технике импрессионистов, созданные из обычных изображений, опять же с использованием модели глубокого обучения.

Прочитав эти статьи, Джейн услышала, что Маркус, друг ее друга, получил работу по исследованию технологий глубокого обучения в крупной технологической компании. Маркус якобы получает более 400 000 долларов в год в виде зарплаты и акций. Тогда Джейн задумалась о следующей ступени в своей карьере: разве может быть что-то лучше, чем увлекательная и прибыльная работа?

Немного покопавшись в Интернете, Джейн нашла авторитетный (и бесплатный!) ресурс — книгу «Глубокое обучение» Яна Гудфеллоу и др.1. Введение было очень похоже на технические статьи в блоге, к которым она привыкла, и это еще больше привлекло ее к изучению темы. Но постепенно читать книгу становилось все труднее. В первой главе авторы представили все необходимые математические понятия и ввели множество терминов и обозначений, которых Джейн раньше никогда не видела. Она пробежала глазами эту главу и попыталась перейти к сути, но ей становилось все сложнее.

Джейн решила, что нужно отложить изучение искусственного интеллекта (ИИ) и глубокого обучения до тех пор, пока она не поднатореет в математике. К счастью, в главе, посвященной математике, среди прочего был рекомендован учебник по линейной алгебре для студентов, которые никогда раньше не изучали этот предмет. Она разыскала этот учебник Георгия Шилова (Georgi Shilov) Linear Algebra (Dover, 1977) и обнаружила, что все его 400 страниц так же густо усеяны незнакомыми ей понятиями, как и книга «Глубокое обучение».

Проведя день за чтением заумных теорем о таких понятиях, как числовые поля, определители и алгебраические дополнения, она решила отказаться от своей затеи. Она не могла понять, как эти концепции помогут ей написать программу, способную выиграть у человека в настольную игру или нарисовать картину, и ей больше не хотелось тратить десятки часов на изучение этого сухого материала.

Спустя какое-то время мы с Джейн встретились, чтобы поболтать за чашечкой кофе. Она рассказала мне о трудностях, с которыми столкнулась при чтении литературы по ИИ из-за того, что не знала линейной алгебры. В последнее время я часто слышу похожие жалобы: «Я пытаюсь читать о [новой технологии], но, похоже, сначала мне нужно изучить [тему по математике]».

Она предприняла замечательную попытку: нашла лучший ресурс по предмету, который хотела изучить, и искала ресурсы для получения необходимых начальных знаний, которых ей не хватало. Но доведя этот подход до логического завершения, она оказалась в изматывающем «прочесывании» технической литературы.

1.2.2. Кропотливое изучение учебников по математике

Учебники по математике для вузов, такие как учебник по линейной алгебре, который подобрала Джейн, как правило, однотипны. Все разделы соответствуют одному формату: вводят новую терминологию, обозначают некоторые факты, называемые теоремами, с использованием этой терминологии, а затем доказывают верность этих теорем.

С виду как будто все логично: вы вводите понятие, о котором пойдет речь дальше, формулируете какие-то выводы, а затем обосновываете их. Но почему тогда так трудно читать учебники по математике?

Проблема в том, что сама математика развивается совсем не так. Когда исследователь придумывает новую математическую идею, ему может потребоваться время на эксперименты, прежде чем он найдет правильные определения. Я думаю, что большинство профессиональных математиков описали бы свои шаги так.

1. Придумай игру. Например, начни играть с некоторыми математическими объектами, пытаясь перечислить их все, найти общие закономерности или объект с определенным свойством.

2. Сформулируй некоторые гипотезы. Подумай об общих фактах, которые можно сообщить об игре, и убеди хотя бы себя в том, что они верны.

3. Разработай точный язык для описания игры и предположений. В конце концов, предположения ничего не значат, пока их нельзя высказать.

4. Наконец, добавив немного решимости и удачи, найди доказательство своей гипотезы, показывающее, почему она верна.

Главный урок, который можно вынести из этого процесса, заключается в том, что развитие глобальных идей начинается с их осмысления, а формализация откладывается на потом. Как только вы получите общее представление о развиваемой идее, словарный запас и обозначения станут для вас преимуществом, а не отвлекающим фактором. Учебники по математике обычно написаны иначе, поэтому я рекомендую использовать их как справочники, а не для знакомства с новыми предметами.

Лучший способ изучения математики — не чтение традиционных учебников, а исследование идей и формулировка собственных выводов. Однако вам не хватит часов в сутках, чтобы самому все заново изобрести. Так как лучше поступить? Я выскажу вам свое скромное мнение, которым руководствовался, работая над этой нестандартной книгой по математике.

1.3. Использование натренированного левого полушария

Эта книга адресована опытным программистам или желающим изучать программирование в процессе работы. Писать о математике для программистов — здорово, потому что тот, кто умеет писать код, уже натренировал левое полушарие, отвечающее за аналитическое мышление. Как мне кажется, лучший способ изучать математику — использовать язык программирования высокого уровня, и я полагаю, что в недалеком будущем это станет нормой в математических классах.

Есть несколько причин считать программистов хорошо подготовленными к изучению математики. Я перечисляю их здесь, не только чтобы польстить вам, но и чтобы напомнить, на какие из имеющихся у вас навыков можно опереться в своих математических исследованиях.

1.3.1. Использование формального языка

Один из первых сложных уроков, которые вы усвоили в программировании: код пишется совсем не так, как предложения на обычном языке. Если вы немного ошибетесь в грамматике, когда пишете записку другу, то вас почти наверняка поймут правильно. Но любая синтаксическая ошибка или неправильно написанный идентификатор в коде влекут за собой сбой в работе программы. В некоторых языках даже отсутствие точки с запятой в конце оператора, который в остальном верен, не позволяет запустить программу. В качестве еще одного примера рассмотрим два утверждения:

x = 5

5 = x

Любое из них можно прочитать как означающее, что символ x имеет значение 5. Но на языке Python эти два утверждения имеют неодинаковые значения и синтаксически верным считается только первое. Оператор x = 5 на языке Python — это инструкция присваивания значения 5 переменной x. А оператор 5 = x интерпретируется как попытка присвоить значение x числу 5, что в принципе невозможно. Такая интерпретация может показаться чересчур формализованной, но это совершенно необходимо, чтобы написать правильную программу.

Еще один пример, сбивающий с толку начинающих программистов (да и опытных тоже!), — равенство ссылок. Если определить новый класс на языке Python и создать два идентичных экземпляра, они не будут равны:

>>> class A(): pass

...

>>> A() == A()

False

Казалось бы, два одинаковых выражения должны быть равны, но это правило не действует в языке Python, так как в сравнении участвуют разные экземпляры класса А, которые не считаются равными.

Будьте внимательны, работая с новыми математическими объектами, которые выглядят как известные вам, но ведут себя иначе. Например, если буквы A и B обозначают числа, то AB = BA. Но как вы узнаете в главе 5, это правило не всегда верно, если A и B не являются числами. Если буквами A и B обозначить матрицы, то произведения AB и BA будут иметь разные результаты. Может случиться так, что действительным может быть только одно из произведений или даже ни одного.

Чтобы написать код, недостаточно написать операторы с правильным синтаксисом. Положения, которые представляют операторы, должны иметь смысл. Если вы проявите такую же осторожность при написании математических утверждений, то быстрее будете находить свои ошибки. Еще лучше, если станете записывать свои математические утверждения в коде, тогда часть работы по их проверке возьмет на себя компьютер.

1.3.2. Создайте свой калькулятор

Калькуляторы активно используют на уроках математики, потому что они помогают проверить результаты, вычисленные вручную. Вы должны знать, сколько будет 6 · 7, без калькулятора, но нелишним будет убедиться, что ответ 42 — правильный, сверившись с калькулятором. Калькулятор поможет сэкономить время и позднее, когда математические понятия уже будут освоены. Если вы занимаетесь тригонометрией и вам нужно найти результат 3,14159 / 6, то калькулятор поможет быстро получить его, а вы можете лишние секунды поразмыслить над тем, что означает ответ. Чем шире возможности калькулятора, тем, теоретически, он должен быть полезнее.

Но иногда калькуляторы оказываются слишком сложными. Когда я перешел в старшие классы, мне понадобился графический калькулятор, и я получил TI-84. У него было около 40 кнопок, каждая из которых имела 2–3 режима. Я знал, как использовать от силы 20 из них, так что для меня это был слишком громоздкий инструмент. То же самое было, когда в первом классе я получил свой первый калькулятор. На нем было всего 15 кнопок, но я не знал, что делают некоторые из них. Если бы мне довелось создавать первый калькулятор для школьников, я бы сделал его похожим на изображенный на рис. 1.14.

Этот калькулятор имеет всего две кнопки. Одна из них вводит начальное значение 1, а другая выполняет переход к следующему числу. Такой калькулятор был бы подходящим инструментом для детей, которые учатся считать. (Мой пример может показаться смешным, но такие калькуляторы действительно можно купить! Обычно они механические и продаются под видом счетчиков-шагомеров.)

Освоив счет, вы захотите попрактиковаться в написании чисел и их сложении. Идеальный калькулятор на этом этапе обучения может иметь несколько дополнительных кнопок (рис. 1.15).

Рис. 1.14. Калькулятор для школьников, которые учатся считать	Рис. 1.15. Калькулятор, позволяющий вводить целые числа и складывать их

На этом этапе вам не нужны такие кнопки, как –, × или ÷. Даже решая задачи на вычитание, такие как 5 – 2, вы все равно сможете проверить свой ответ 3, вычислив с помощью калькулятора сумму 3 + 2 = 5. Точно так же сможете решать задачи на умножение, многократно складывая числа. Закончив изучение арифметических операций, можете перейти к использованию калькулятора, выполняющего все арифметические операции.

Я думаю, что идеальный калькулятор должен быть расширяемым, то есть давать возможность добавлять в него дополнительные функции по мере необходимости. Например, изучая новую математическую операцию, вы можете добавить на свой калькулятор соответствующую кнопку. Добравшись до алгебры, сможете заставить калькулятор понимать такие символы, как x или y, в дополнение к числам. Освоив матанализ, сможете научить калькулятор понимать другие математические функции.

Расширяемые калькуляторы, способные обрабатывать данные самых разных типов, кажутся выдумкой, но это именно то, что вы получаете в виде языка программирования высокого уровня. Python поддерживает все арифметические операции, имеет модуль math и множество сторонних математических библиотек, позволяющих расширять среду программирования по мере необходимости. Поскольку Python является полным по Тьюрингу, с его помощью можно (в принципе) вычислить все, что может быть вычислено. Вам нужен только достаточно мощный компьютер, достаточно умная реализация или и то и другое.

В этой книге мы реализуем каждую новую математическую концепцию в виде кода на Python, пригодного для повторного использования. Самостоятельная работа станет для вас отличным способом закрепить понимание новых концепций и добавить в личную библиотеку новый инструмент. Проделав весь путь самостоятельно, вы сможете заменить отточенную популярную библиотеку, если захотите. В любом случае новые инструменты, созданные или заимствованные вами, позволят заложить основу для реализации еще более масштабных идей.

1.3.3. Создание абстракций с помощью функций

Процесс, который я только что описал, в программировании называется абстракцией. Например, чтобы не повторять утомительный счет по порядку, вы используете абстракцию сложения. Чтобы не повторять сложение, применяете абстракцию умножения и т.д.

Из всех способов создания абстракций в программировании наиболее важна для математики функция. Функция в Python — это способ повторного решения некоторой задачи. Функция может принимать входные данные и производить выходные данные. Например,

def greet(name):

    print("Hello %s!" % name)

позволяет поприветствовать нескольких человек с помощью короткого и выразительного кода:

>>> for name in ["John","Paul","George","Ringo"]:

...     greet(name)

...

Hello John!

Hello Paul!

Hello George!

Hello Ringo!

Эта функция несет определенную пользу, но она не похожа на математическую функцию. Математические функции всегда принимают входные значения, всегда возвращают выходные значения и не имеют побочных эффектов.

Функции, которые ведут себя подобно математическим, в программировании называются чистыми функциями. Например, квадратичная функция f(x) = x2 принимает число и возвращает произведение числа на самого себя. Вычис­ляя f(3), вы получаете в результате 9. Это не означает, что число 3 теперь изменилось и превратилось в 9. Это означает, что 9 является соответствующим выходом для входа 3 в функции f. Функцию возведения в квадрат можно представить как машину, которая получает числа через входное окно и выдает результаты (числа) через выходное окно (рис. 1.16).

 

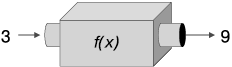
Рис. 1.16. Функция как машина с входным и выходным окнами

Это простая и полезная мысленная модель, и я буду возвращаться к ней на протяжении всей книги. Больше всего в ней мне нравится возможность представить функцию как объект. В математике, как и в Python, функции — это данные, которыми можно манипулировать независимо и которые можно даже передавать другим функциям.

Математика может казаться пугающей, потому что она абстрактна. Помните, что, как и в любой хорошо написанной программе, абстракции вводятся в рассуждения не просто так — они помогают организовывать и передавать более крупные и емкие положения. Когда вы поймете их и воплотите в код, перед вами откроются захватывающие возможности.

Я надеюсь, теперь вы поверите в то, что математика может применяться в разработке программного обеспечения во многих областях. У вас, как у программиста, уже сложился правильный образ мышления и имеются начальные знания, необходимые для изучения новых математических положений. Материал, представленный в этой книге, обогащает меня как в профессиональном, так и в личном плане, и я надеюсь, что обогатит и вас. Давайте начнем!

Краткие итоги главы

• Существуют интересные и перспективные области разработки программного обеспечения с применением математики.

• Математика может помочь количественно оценить тенденции, наблюдающиеся в данных и меняющиеся со временем, чтобы, например, предсказать изменение цен на акции.

• Разные типы функций передают разные виды качественного поведения. Например, функция экспоненциального уменьшения отражает динамику снижения стоимости подержанного автомобиля с каждой пройденной милей.

• Наборы чисел, называемые векторами, представляют многомерные данные. В частности, трехмерные векторы, выражающиеся тройками чисел, могут представлять точки в пространстве. Манипулируя треугольниками, заданными векторами, можно создавать сложную трехмерную графику.

• Математический анализ — это область математики, занимающаяся исследованием непрерывных изменений, и многие законы физики записаны в терминах уравнений счисления, которые называют дифференциальными уравнениями.

• Трудно учить математику по традиционным учебникам! Математику следует учить, исследуя ее, а не просто знакомясь с определениями и теоремами.

• Как программист, вы умеете мыслить и общаться, используя точные определения. Этот навык поможет вам учить математику.