автордың кітабын онлайн тегін оқу Глубокое обучение с подкреплением: теория и практика на языке Python
Переводчик К. Синица
Лаура Грессер, Ван Лун Кенг
Глубокое обучение с подкреплением: теория и практика на языке Python . — СПб.: Питер, 2022.
ISBN 978-5-4461-1699-7
© ООО Издательство "Питер", 2022
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.
Отзывы о книге
Эта книга — доступное введение в глубокое обучение с подкреплением. В ней охвачены как математические концепции, лежащие в основе популярных алгоритмов, так и их практическая реализация. Я считаю ее ценным источником информации для всех, кто интересуется практическим применением глубокого обучения с подкреплением.
Володимир Мних, ведущий разработчик DQN
Отличная книга, прочитав которую вы быстро изучите теорию и язык программирования, а также научитесь на практике реализовывать алгоритмы глубокого обучения с подкреплением. Понятное изложение с использованием привычной нотации, объяснение всех новейших методов проиллюстрировано лаконичным читаемым кодом и ни одной страницы отвлеченных рассуждений — просто идеально для формирования прочных знаний по теме.
Винсент Ванхук, старший научный сотрудник, Google
Как человек, проводящий свои дни в попытках сделать более доступными методы глубокого обучения с подкреплением, могу сказать, что книга Лауры и Кенга — долгожданное пополнение ряда подобной литературы. В ней есть как удобочитаемое введение в основные концепции обучения с подкреплением, так и интуитивно понятные объяснения и код для большинства важных алгоритмов в данной области. Мне кажется, она на долгие годы станет бесценным источником знаний для тех, кто хочет изучать глубокое обучение с подкреплением.
Артур Джулиани, ведущий инженер по машинному обучению, Unity Technologies
До сих пор единственным способом разобраться в глубоком обучении с подкреплением было медленное накопление знаний из десятков разных источников. Наконец-то у нас появилась книга, в которой все это собрано воедино.
Мэтью Ратц, исследователь в области обучения с подкреплением, ETH в Цюрихе
Тем, кто дал мне понять, что возможно все.
Лаура
Моей жене Даниэле.
Кенг
Предисловие
В апреле 2019 года боты, созданные Open AI Five, сыграли в турнире по Dota 2 против команды OG — чемпионов мира 2018 года. Dota 2 — это сложная многопользовательская игра. Игроки в ней могут выбирать разных персонажей. Для победы важны стратегия, работа в команде и быстрое принятие решений. При таком количестве переменных и кажущемся бесконечном просторе для оптимизации, создание конкурентоспособной системы искусственного интеллекта кажется непосильной задачей. И все же боты OpenAI одержали уверенную победу, а немного погодя стали побеждать в 99 % матчей против официальных игроков. В основе этого достижения лежит глубокое обучение с подкреплением.
Несмотря на то что это недавнее событие, исследования в области как обучения с подкреплением, так и глубокого обучения идут не одно десятилетие. Однако значительная часть последних изысканий вкупе с ростом мощности графических процессоров способствовали развитию возможностей современных алгоритмов. В этой книге дано введение в глубокое обучение с подкреплением и сведены в целостную систему результаты работ за последние шесть лет.
Хотя создание системы обучения компьютерной программы для победы в видеоигре, возможно, не самое важное занятие, это только начало. Обучение с подкреплением — это область машинного обучения, занимающаяся задачами последовательного принятия решений, то есть теми, решение которых занимает определенное время. Оно применимо практически в любой ситуации: в видеоиграх, на прогулке по улице или при вождении автомобиля.
Лаура Грессер и Ван Лун Кенг предложили доходчивое введение в сложную тему, играющую ведущую роль в современном машинном обучении. Мало того, что они использовали свои многочисленные публикации об исследованиях на данную тему, они создали библиотеку с открытым исходным кодом SLM Lab, призванную помочь новичкам быстро освоить глубокое машинное обучение. SLM Lab написана на Python с помощью фреймворка PyTorch, но читателям достаточно знать только Python. Эта книга будет полезна и тем, кто собирается применять в качестве фреймворка глубокого обучения другие библиотеки, например TensorFlow. В ней они познакомятся с концепциями и формулировкой задач глубокого обучения с подкреплением.
В издании сведены воедино новейшие исследования в сфере глубокого обучения с подкреплением и даны рабочие примеры и код. Их библиотека также совместима с OpenAI Gym, Roboschool и инструментарием Unity ML-Agents, что делает книгу хорошим стартом для читателей, нацеленных на работу с этими инструментами.
Пол Дикс, редактор серии
Введение
С глубоким обучением с подкреплением (reinforcement learning, RL) мы впервые познакомились, когда DeepMind достиг беспрецедентной производительности в аркадных играх Atari. Используя лишь изображения и не располагая первоначальными знаниями о системе, агенты впервые достигли поведения уровня человека.
Идея искусственного агента, обучающегося методом проб и ошибок, самостоятельно, без учителя, поражала воображение. Это было новым впечатляющим подходом к машинному обучению и несколько отличалось от более привычного обучения с учителем.
Мы решили работать вместе над изучением этой темы. Мы читали книги и статьи, проходили онлайн-курсы, штудировали код и пытались реализовать основные алгоритмы. К нам пришло понимание того, что глубокое обучение с подкреплением сложно не только в концептуальном отношении — реализация любого алгоритма требует таких же усилий, как и большой инженерный проект.
По мере продвижения мы все больше узнавали о характерных чертах глубокого RL — взаимосвязях и различиях между алгоритмами. Формирование целостной картины модели шло с трудом, поскольку глубокое RL — новая область исследований и теоретические знания еще не были оформлены в виде книги. Нам пришлось учиться по исследовательским статьям и онлайн-лекциям.
Другой трудностью был большой разрыв между теорией и реализацией. Зачастую из-за большого количества компонентов и настраиваемых гиперпараметров алгоритмы глубокого RL капризны и ненадежны. Для успеха необходимы корректная совместная работа всех компонентов и подходящие гиперпараметры. Из теории далеко не сразу становятся понятными детали правильной реализации, но они очень важны. Ресурс, объединяющий теорию и практику, был бы неоценим во время нашего обучения.
Нам казалось, что можно найти более простой путь от теории к реализации, который облегчил бы изучение глубокого RL. Данная книга воплощает нашу попытку сделать это. В ней введение в глубокое RL проходит через все стадии: сначала интуитивное понимание, затем объяснение теории и алгоритмов, а в конце реализация и практические рекомендации. В связи с этим к книге прилагается фреймворк SLM Lab, содержащий реализации всех рассматриваемых алгоритмов. Если кратко, это книга, от которой мы не отказались бы в начале своего обучения.
Глубокое RL относится к области обучения с подкреплением. В основе обучения с подкреплением зачастую лежит аппроксимация функции, в глубоком RL аппроксиматоры обучаются посредством глубоких нейронных сетей. Обучение с подкреплением, обучение с учителем и обучение без учителя — три основные методики машинного обучения, каждая из которых отличается формулировкой задач и обучением алгоритмов по данным.
В этой книге мы фокусируемся исключительно на глубоком RL, так как проблемы, с которыми нам приходилось сталкиваться, относятся к данному разделу обучения с подкреплением. Это накладывает на книгу два ограничения. Во-первых, исключаются все прочие методики для обучения аппроксиматоров в обучении с подкреплением. Во-вторых, выделяются исследования между 2013 и 2019 годами, хотя обучение с подкреплением существует с 1950-х годов. Многие современные достижения основаны на более ранних исследованиях, поэтому нам показалось важным проследить развитие основных идей. Однако мы не собираемся описывать всю историю области.
Книга предназначена для студентов, изучающих компьютерные науки, и разработчиков программного обеспечения. Она задумывалась как введение в глубокое RL и не требует предварительных знаний о предмете. Однако предполагается, что читатель имеет базовое представление о машинном обучении и глубоком обучении и программирует на Python на среднем уровне. Опыт работы с PyTorch также полезен, но не обязателен.
Книга организована следующим образом. В главе 1 дается введение в различные аспекты проблем глубокого RL и обзор его алгоритмов.
Часть I книги посвящена алгоритмам, основанным на полезностях и стратегии. В главе 2 рассматривается первый метод градиента стратегии, известный как REINFORCE. В главе 3 описывается первый основанный на полезностях метод под названием SARSA. В главе 4 обсуждаются алгоритмы глубоких Q-сетей (Deep Q-Networks, DQN), а глава 5 сфокусирована на улучшающих их методиках — контрольных сетях (target networks), алгоритмах двойной DQN и приоритизированной памяти прецедентов (Prioritized Experience Replay).
В части II основное внимание уделяется алгоритмам, объединяющим методы, основанные на полезностях и стратегии. В главе 6 представлен алгоритм актора-критика, расширяющий REINFORCE. В главе 7 приведена оптимизация ближайшей стратегии (Proximal Policy Optimization, PPO), которой может быть расширен метод актора-критика. В главе 8 обсуждаются приемы синхронной и асинхронной параллелизации, применимые ко всем алгоритмам в этой книге. В заключение в главе 9 подводятся итоги по всем алгоритмам.
Все главы об алгоритмах построены по одной схеме. Сначала приводятся основные концепции и прорабатываются соответствующие математические формулировки. Затем идет описание алгоритма и обсуждаются реализации на Python. В конце приводится полный алгоритм с подобранными гиперпараметрами, который может быть запущен в SLM Lab, а основные характеристики алгоритма иллюстрируются графиками.
В части III основной упор сделан на практических деталях реализации алгоритмов глубокого RL. В главе 10 описываются практики проектирования и отладки. В нее включены также справочник гиперпараметров и результаты сравнения производительности алгоритмов. В главе 11 представлены основные команды и функции библиотеки SLM Lab, прилагаемой к книге. В главе 12 рассматривается проектирование нейронных сетей, а в главе 13 обсуждается аппаратное оборудование.
В части IV книги речь идет о проектировании среды. В нее входят главы 14, 15, 16 и 17, в которых рассматриваются способы задания состояний, действий, вознаграждений и функций переходов соответственно.
Читать по порядку следует главы с 1-й по 10-ю. В них дано введение во все алгоритмы книги и представлены практические рекомендации, как их запустить. В следующих трех главах, с 11-й по 13-ю, внимание уделяется более специфическим темам, и их можно читать в любом порядке. Для тех, кто не хочет вдаваться в такие подробности, достаточно прочитать главы 1, 2, 3, 4, 6 и 10, в которых последовательно изложены несколько алгоритмов. В конце, в части IV, помещены отдельные главы, предназначенные для читателей, особо заинтересованных в более глубоком понимании использованных сред или построении собственных сред.
Прилагаемая к книге библиотека программного обеспечения SLM Lab — это модульный фреймворк глубокого RL, созданный с помощью PyTorch. SLM — это аббревиатура для Strange Loop Machine (машина на странных петлях), названия, данного в честь знаменитой книги Ховштадтера «Гёдель, Эшер, Бах: эта бесконечная гирлянда»1. Во включенных в книгу примерах из SLM Lab используются синтаксис PyTorch и функции для обучения нейронных сетей. Однако основные принципы реализации алгоритмов глубокого RL применимы и к другим фреймворкам глубокого обучения, таким как TensorFlow.
Для того чтобы новичкам было легче освоить глубокое RL, компоненты SLM Lab разбиты на концептуально понятные части. Кроме того, чтобы упростить переход от теории к коду, они упорядочены в соответствии с изложением глубокого RL в академической литературе.
Другой важный аспект изучения глубокого RL — эксперименты. С этой целью в SLM Lab представлен фреймворк для экспериментов, призванный помочь начинающим в создании и тестировании собственных гипотез.
Библиотека SLM Lab — это проект с открытым исходным кодом на Github. Мы рекомендуем установить ее (на машины с Linux или MacOS) и запустить первое демо, следуя инструкциям, приведенным на сайте репозитория https://github.com/kengz/SLM-Lab. В Git была создана специальная ветка book с версией кода, совместимой с этой книгой. В листинге 0.1 приведена краткая инструкция по установке, скопированная с сайта репозитория.
Листинг 0.1. Установка SLM-Lab с ветки book
1 # клонируйте репозиторий
2 git clone https://github.com/kengz/SLM-Lab.git
3 cd SLM-Lab
4 # переключитесь на специальную ветку для этой книги
5 git checkout book
6 # установите зависимости
7 ./bin/setup
8 # далее следуйте инструкциям, приводимым на сайте репозитория
Рекомендуется сначала задать эти настройки, чтобы можно было обучать агентов по алгоритмам в соответствии с их появлением в книге. Помимо установки и запуска первого примера, необходимости в знакомстве с SLM Lab до прочтения глав об алгоритмах (части I и II) не возникнет: все команды для обучения агентов даны там, где нужно. Кроме того, SLM Lab обсуждается более подробно в главе 11, после перехода от алгоритмов к практическим аспектам глубокого обучения с подкреплением.
1 Go..del, Escher, Bach: An Eternal Golden Braid.
Go..del, Escher, Bach: An Eternal Golden Braid.
Прилагаемая к книге библиотека программного обеспечения SLM Lab — это модульный фреймворк глубокого RL, созданный с помощью PyTorch. SLM — это аббревиатура для Strange Loop Machine (машина на странных петлях), названия, данного в честь знаменитой книги Ховштадтера «Гёдель, Эшер, Бах: эта бесконечная гирлянда»1. Во включенных в книгу примерах из SLM Lab используются синтаксис PyTorch и функции для обучения нейронных сетей. Однако основные принципы реализации алгоритмов глубокого RL применимы и к другим фреймворкам глубокого обучения, таким как TensorFlow.
Благодарности
Завершить этот проект нам помогло немало людей. Спасибо Милану Цвитковичу, Алексу Лидсу, Навдипу Джайтли, Джону Крону, Кате Василаки и Кейтлин Глисон за поддержку и вдохновение. Выражаем благодарность OpenAI, PyTorch, Илье Кострикову и Джамромиру Дженишу за предоставление высококачественной реализации с открытым исходным кодом различных компонентов алгоритмов глубокого RL. Благодарим также Артура Джулиани за предварительные обсуждения структуры сред. Эти ресурсы и обсуждения были бесценны при создании SLM Lab.
Хотелось бы поблагодарить Александра Саблайроллеса, Ананта Гупта, Брендона Стрикланда, Чонга Ли, Джона Крона, Джорди Франка, Кэтрин Джаясурия, Мэтью Ратца, Пидонга Вонга, Раймонда Чуа, Регину Р. Монако, Рико Джоншковски, Софи Табак и Утку Эвси за обстоятельные замечания о ранних набросках этой книги.
Мы очень признательны производственной команде Pearson — Алине Кирсановой, Крису Зану, Дмитрию Кирсанову и Джулии Нахил. Благодаря вашему профессионализму, старанию и вниманию к деталям текст стал гораздо лучше.
Наконец, эта книга не появилась бы на свет без нашего редактора Деборы Вильямс Коли. Благодарим за вашу помощь и терпение.
Об авторах
Лаура Грессер работает разработчиком исследовательского программного обеспечения для робототехнических систем в Google. Получила степень магистра компьютерных наук в Нью-Йоркском университете со специализацией в машинном обучении.
Ван Лун Кенг — разработчик систем искусственного интеллекта в Machine Zone, использует глубокое обучение с подкреплением для решения проблем промышленного производства. Специалист в области теоретической физики и компьютерных наук.
Они вместе разработали две библиотеки программного обеспечения для глубокого обучения с подкреплением и выпустили ряд лекций и учебников по этой теме.
От издательства
Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).
Мы будем рады узнать ваше мнение!
На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах.
О научном редакторе русскоязычного издания
Александр Игоревич Панов, кандидат физико-математических наук, доцент, заведующий отделом ФИЦ ИУ РАН, руководитель Центра когнитивного моделирования МФТИ, ведущий научный сотрудник Института искусственного интеллекта (AIRI), член Научного совета Российской ассоциации искусственного интеллекта. Специалист в области когнитивной робототехники, обучения с подкреплением, общего искусственного интеллекта.
1. Введение в обучение с подкреплением
В этой главе вводятся основные концепции обучения с подкреплением. Сначала рассматриваются простые примеры, которые позволят вам интуитивно понимать основные компоненты, используемые в обучении с подкреплением, — агента и среду.
В частности, мы рассмотрим процесс оптимизации целевой функции посредством взаимодействия агента со средой. Далее дано более формальное определение, а обучение с подкреплением объясняется с помощью понятия марковского процесса принятия решений. Это теоретические основы обучения с подкреплением.
Затем представлены три основные функции, которые должен выучить агент: стратегия, функции полезности и модель среды. Далее показано, как разные варианты обучения этих функций порождают различные семейства алгоритмов глубокого обучения с подкреплением.
В конце дан краткий обзор основного метода глубокого обучения — метода аппроксимации функций, который используется на протяжении всей книги. Также здесь обсуждаются основные различия между обучением с подкреплением и обучением с учителем.
1.1. Обучение с подкреплением
Обучение с подкреплением (reinforcement learning, RL) занимается задачами последовательного принятия решений. Многие реальные проблемы, возникающие в компьютерных играх, спорте, вождении автомобиля, оптимизации товарных запасов, роботизированном управлении, то есть везде, где действуют люди и машины, могут быть представлены в подобном виде.
Решая каждую из этих задач, мы преследуем какую-то цель: победить в игре, безопасно доехать до пункта назначения или минимизировать стоимость строительных материалов. Мы предпринимаем действия и получаем из окружающего мира ответ о том, насколько близки к цели: текущий счет, расстояние до пункта назначения или цену одного изделия. Достижение цели, как правило, подразумевает выполнение ряда действий, каждое из которых изменяет окружающий мир. Мы наблюдаем эти изменения мира, а также получаем обратную информацию, опираясь на которую принимаем решение о следующем шаге.
Представьте, что вы на вечеринке, а ваш друг принес флагшток и предлагает на спор как можно дольше балансировать им, поставив на ладонь. Если вы никогда до сих пор не делали этого, то первоначальные попытки будут не слишком удачными. Вероятно, первые несколько минут вы потратите на то, чтобы методом проб и ошибок почувствовать флагшток, ведь он все время падает.
Эти ошибки позволят накопить полезную информацию и приобрести интуитивное понимание того, как удерживать флагшток в равновесии. Вы узнаете, где находится его центр масс, с какой скоростью он наклоняется, при каком угле наклона падает, как быстро вы может подстроиться и т.д. Вы используете эту информацию, чтобы внести коррективы при следующих попытках, совершенствуетесь и снова корректируете свое поведение. Вы даже не заметите, как начнете удерживать равновесие по 5, 10, 30 с, 1 мин и т.д.
Этот процесс наглядно демонстрирует, как работает обучение с подкреплением. В обучении с подкреплением вас можно назвать агентом, а флагшток и ваше окружение — средой. Фактически первая среда, задачу которой мы научимся решать с помощью обучения с подкреплением, — это игровая версия данного сценария под названием CartPole (рис. 1.1). Агент управляет скользящей вдоль оси тележкой так, чтобы удерживать стержень в вертикальном положении в течение заданного времени. Реальные способности людей гораздо шире, ведь мы можем интуитивно понимать физическую сторону происходящего. А можем и применить навыки выполнения схожих заданий, таких как балансирование подносом, уставленным напитками. Но, по сути, формулировка задачи остается той же самой.
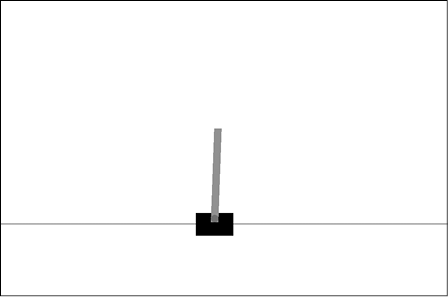
Рис. 1.1. CartPole-v0 — простая игровая среда. Цель — удержание в равновесии стержня на протяжении 200 шагов посредством управления перемещениями тележки вправо и влево
В обучении с подкреплением изучаются подобного рода задачи, а также методы, с помощью которых искусственные агенты учатся их решать. Это область искусственного интеллекта, которая восходит к теории оптимального управления и использует понятие марковского процесса принятия решений (МППР). RL появился в 1950-х годах в контексте динамического программирования и квазилинейных уравнений благодаря Ричарду Беллману. Его имя будет еще не раз упомянуто при изучении получившего известность в обучении с подкреплением уравнения Беллмана.
Задачи RL могут быть представлены как система, состоящая из агента и среды. Среда предоставляет информацию, описывающую состояние системы. Агент взаимодействует со средой, наблюдая состояние и используя данную информацию при выборе действия. Среда принимает действие и переходит в следующее состояние, а затем возвращает агенту следующее состояние и вознаграждение. Когда цикл «состояние→действие→вознаграждение» завершен, предполагается, что сделан один шаг. Цикл повторяется, пока среда не завершится, например, когда задача решена. Полностью этот процесс показан на диаграмме цикла управления (рис. 1.2).

Рис. 1.2. Цикл управления агентом в обучении с подкреплением
Функция, в соответствии с которой агент выбирает действия, называется стратегией. Формально стратегия — это функция, отображающая множество состояний в множество действий. Действие изменяет среду и влияет на то, что агент наблюдает и делает дальше. Обмен информацией между агентом и средой разворачивается во времени, однако его можно рассматривать как процесс последовательного принятия решений.
В задачах RL есть целевая функция, которая является суммой полученных агентом вознаграждений. Задача агента — максимизировать целевую функцию, выбирая наилучшие действия. Он учится этому, взаимодействуя со средой методом проб и ошибок, и использует поощряющие сигналы для подкрепления лучших действий.
Агент и среда определены как взаимоисключающие сущности, чтобы мы могли четко отделить друг от друга состояния, действия и вознаграждения. Среду можно рассматривать как все, что не является агентом. Например, для езды на велосипеде возможны несколько различных, но равнозначных определений агента и среды. Если рассматривать все человеческое тело как агента, который наблюдает свое окружение, а производимые им напряжения мышц — как действия, то среда — это дорога и велосипед. Если считать агентом мыслительный процесс, то средой будут физическое тело, велосипед и дорога, действиями — нервные импульсы, пересылаемые от головного мозга к мускулам, а состояниями — поступающие в мозг сигналы от органов чувств.
По сути, система обучения с подкреплением реализует цикл управления с обратной связью, где агент и среда взаимодействуют и обмениваются сигналами, причем агент пытается максимизировать целевую функцию. Сигналы — это тройка (st, at, rt), что соответствует состоянию, действию и вознаграждению, а индекс t указывает на номер шага (момент времени), на котором возник сигнал. Кортеж (st, at, rt) называется прецедентом или частью получаемого агентом опыта. Цикл управления может повторяться до бесконечности2 или закончиться по достижении либо конечного состояния, либо максимального значения шага t = T. Временной горизонт от t = 0 до момента завершения среды носит название эпизода. Траектория — это последовательность прецедентов, или часть опыта, накопленного в течение эпизода, τ = (s0, a0, r0), (s1, a1, r1)… Обычно агенту для обучения хорошей стратегии требуется от сотен до миллионов эпизодов в зависимости от сложности задачи.
Рассмотрим для обучения с подкреплением три примера сред (рис. 1.3) и определения состояний, действий и вознаграждений. Все эти среды можно получить в OpenAI Gym — библиотеке с открытым исходным кодом, которая предоставляет стандартизованный набор сред.
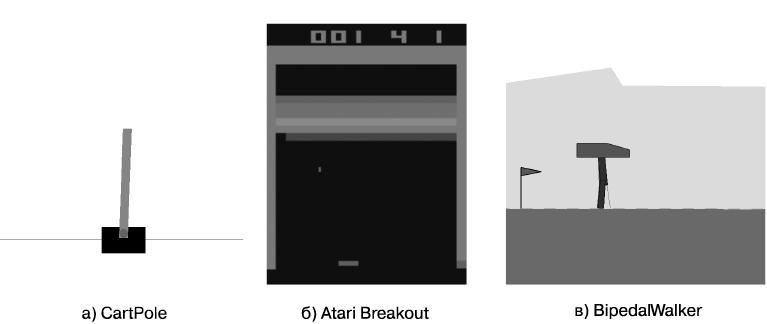
Рис. 1.3. Три примера сред с разными состояниями, действиями и вознаграждениями
CartPole (см. рис. 1.3, а) — одна из простейших сред для обучения с подкреплением, была впервые описана Барто, Саттоном и Андерсоном в 1983 году. В этой среде стержень закреплен на тележке, которая может двигаться по дорожке без трения. Основные особенности среды приведены далее.
1. Цель — удерживать стержень в вертикальном положении в течение 200 шагов.
2. Состояние — массив из четырех элементов: [позиция тележки, скорость тележки; угол наклона стержня; угловая скорость стержня], например [–0,034; 0,032; –0,031; 0,036].
3. Действие — целое число: 0 при перемещении тележки на фиксированное расстояние влево и 1 — при перемещении на фиксированное расстояние вправо.
4. Вознаграждение равно +1 на каждом шаге, на котором стержень остается в вертикальном положении.
5. Среда завершается либо при падении стержня (отклонение от вертикали на угол больше 12°), либо при выходе тележки за пределы экрана, либо при достижении максимального числа шагов, равного 200.
Atari Breakout (см. рис. 1.3, б) — это старая консольная аркадная игра, в которой есть мячик, расположенная внизу экрана платформа и блоки. Цель — попадать в блоки и разрушать их, отбивая мячик платформой. В начале игры у игрока пять жизней, одна из которых теряется, когда мячик попадает мимо платформы.
1. Цель — набрать максимальный счет в игре.
2. Состояние — цифровое изображение в формате RGB с разрешением 160 × 210 пикселов, то есть то, что мы видим на экране игры.
3. Действие — целое число из набора {0, 1, 2, 3}, которое сопоставляется игровым действиям {бездействие, запустить мячик, перемещение вправо, перемещение влево}.
4. Вознаграждение — разность в счете между двумя идущими друг за другом состояниями.
5. Среда завершается, когда все жизни потеряны.
BipedalWalker (см. рис. 1.3, в) — задача непрерывного управления, где агент-робот сканирует окрестности с помощью датчика-лидара и старается удержаться от падения при движении вправо.
1. Цель — идти вправо не падая.
2. Состояние — массив из 24 элементов: [угол наклона корпуса; угловая скорость корпуса; скорость по оси X; скорость по оси Y; угол поворота шарнира бедра 1; скорость шарнира бедра 1; угол поворота шарнира колена 1; скорость шарнира колена 1; есть ли контакт с землей ноги 1; угол поворота шарнира бедра 2; скорость шарнира бедра 2; угол поворота шарнира колена 2; скорость шарнира колена 2; есть ли контакт с землей ноги 2… 10 показаний лидара], например [2,745e–03; 1,180e–05; –1,539e–03; –1,600e–02… 7,091e–01; 8,859e–01; 1,000e+00; 1,000e+00].
3. Действие — вектор из четырех чисел с плавающей запятой со значениями в интервале [–1,0; 1,0], имеющий вид [крутящий момент и скорость бедра 1; крутящий момент и скорость колена 1; крутящий момент и скорость бедра 2; крутящий момент и скорость колена 2], например [0,097; 0,430; 0,205; 0,089].
4. Вознаграждение — за движение вправо максимально до +300 и –100 за падение робота. Кроме того, за каждый шаг дается небольшое отрицательное вознаграждение (плата за движение), пропорциональное приложенному крутящему моменту.
5. Среда завершается, когда тело робота касается земли, либо при достижении цели, расположенной справа, либо после максимального количества шагов, равного 1600.
Эти среды демонстрируют различные варианты того, в каком виде могут быть представлены состояния и действия. В CartPole и BipedalWalker состояния — это векторы, кодирующие свойства, такие как позиции и скорости. В Atari Breakout состояние — это изображение экрана игры. В CartPole и Atari Breakout действия являются одиночными дискретными целыми числами, тогда как в BipedalWalker действие — это вектор из четырех непрерывных вещественных значений. Вознаграждение всегда представлено скалярной величиной, но пределы его значений варьируются в зависимости от задания.
Просмотрев несколько примеров, можно ввести формальные обозначения для состояний, действий и вознаграждений.
Состояние:
st∈S, (1.1)
где S — пространство состояний.
Действие:
at∈A, (1.2)
где A — пространство действий.
Вознаграждение:
rt = R(st, at, st + 1), (1.3)
где R — функция вознаграждения.
Пространство состояний S — это набор из всех возможных в среде состояний. В зависимости от среды оно может быть определено как набор целых или вещественных чисел, векторов, матриц, структурированных или неструктурированных данных. Аналогично пространство действий A — это набор всех возможных действий, определяемых средой. Оно также может иметь разный вид, но чаще всего действие определяется как скалярная величина или вектор. Функция вознаграждения R(st, at, st + 1) присваивает положительное, отрицательное или равное нулю скалярное значение каждому переходу (st, at, st + 1). Пространство состояний, пространство действий и функция вознаграждения задаются средой. Вместе они составляют кортежи (s, a, r), являющиеся основными информационными единицами при описании систем обучения с подкреплением.
1.2. Обучение с подкреплением как МППР
Теперь рассмотрим, как среда переходит из одного состояния в другое с помощью так называемой функции переходов. В обучении с подкреплением функция переходов — это основной компонент марковского процесса принятия решений (МППР), который является математической основой моделирования последовательного принятия решений.
Чтобы понять, как функции переходов связаны с МППР, рассмотрим общую постановку задачи, приведенную в следующем выражении:
st + 1 ~ P(st + 1 | (s0, a0), (s1, a1)… (st, at)). (1.4)
В выражении (1.4) утверждается, что на временном шаге t следующее состояние st + 1 берется из распределения вероятностей P, обусловленного всей историей. Вероятность перехода среды из состояния st в состояние st + 1 зависит от всех предыдущих состояний s и действий a, которые имели место в данном эпизоде до этого момента. Записать функцию переходов в подобной форме сложно, особенно если эпизоды растягиваются на большое количество шагов. При проектировании таких функций переходов нужно учитывать огромное количество комбинаций факторов, возникавших в течение всех предыдущих шагов. Кроме того, в такой формулировке становится очень сложной функция выбора действий агентом — его стратегия. Поскольку для понимания того, как действие может изменить следующее состояние среды, важна вся история состояний и действий, то агенту придется принимать во внимание всю эту информацию, принимая решение о выборе действия.
Чтобы функция переходов среды стала лучше реализуемой на практике, преобразуем ее в МППР. Сделаем такое предположение: переход в следующее состояние st + 1 зависит только от предыдущих значений состояния st и действия at. Данное предположение известно как марковское свойство. С учетом этого функция переходов примет следующий вид:
st + 1 ~ P(st + 1 | st, at). (1.5)
Выражение (1.5) гласит, что следующее состояние st + 1 берется из распределения вероятностей P(st + 1 | st, at). Это упрощенная форма первоначальной функции переходов. Марковское свойство подразумевает, что текущие состояние и действие на шаге t содержат достаточно информации, чтобы в полной мере определить вероятность перехода в следующее состояние на шаге t + 1.
Несмотря на простоту данной формулировки, она довольно эффективна. В подобной форме могут быть выражены многие процессы, такие как игры, управление робототехническими системами и планирование. Это связано с тем, что определение состояния может включать любую информацию, позволяющую сделать функцию переходов марковской.
Рассмотрим пример с последовательностью чисел Фибоначчи, описываемой формулой st + 1 = st + st – 1, где каждый член st рассматривается как состояние. Чтобы эта функция стала марковской, переопределим состояние как ![]()
Примечание 1.1. МППР и частично наблюдаемые МППР
До сих пор понятие состояния применялось в двух случаях. С одной стороны, состояние — это то, что порождается средой и что наблюдает агент. Назовем его наблюдаемым состояниемst. С другой стороны, состояние — это то, что используется функцией переходов. Назовем его внутренним состоянием![]()
В МППР ![]()
Это не всегда верно. Наблюдаемое состояние может отличаться от внутреннего состояния среды, ![]()
В этой книге в большинстве случаев данное различие не учитывается и предполагается, что ![]()
Во-вторых, многие интересные реальные проблемы по своей сути являются частично наблюдаемыми МППР, в их число входят случаи проявления ограниченности датчиков или данных, ошибок моделирования и зашумленности среды. Детальное рассмотрение частично наблюдаемых МППР лежит за пределами этой книги, но они будут вкратце затронуты при обсуждении архитектуры нейронных сетей в главе 12.
Наконец, при рассмотрении структуры состояний в главе 14 различие между st и ![]()
![]()
Теперь можно представить формулировку задачи обучения с подкреплением в виде МППР. МППР определяется кортежем из четырех элементов — S, A, P(.), ![]()
• S — набор состояний;
• A — набор действий;
• P(st + 1 | st, at) — функция перехода состояний среды;
• ![]()
Рассматриваемые в этой книге задачи обучения с подкреплением используют одно важное предположение: функция переходов P(st + 1 | st, at) и функция вознаграждений ![]()
Чтобы формулировка задачи была полной, нужно формализовать понятие максимизируемой агентом целевой функции. Во-первых, определим отдачу3 (return) ![]()
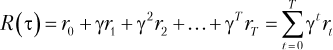
В уравнении (1.6) отдача определена как дисконтированная сумма вознаграждений на траектории, где γ — коэффициент дисконтирования, γ∈ [0, 1].
Тогда целевая функцияJ(τ) становится просто математическим ожиданием отдачи по нескольким траекториям:
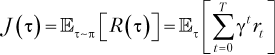
Отдача R(τ) — это сумма дисконтированных вознаграждений γtrt за все временные шаги t = 0… T. Целевая функция J(τ) — это отдача, усредненная по нескольким эпизодам. Математическое ожидание предполагает случайный характер выбора действий и поведения среды, то есть при повторных запусках отдача не всегда будет одинаковой. Максимизация целевой функции — то же самое, что и максимизация отдачи.
Коэффициент дисконтирования γ∈ [0, 1] — важная переменная, влияющая на то, как оцениваются будущие вознаграждения. Чем меньше γ, тем меньший вес имеют будущие вознаграждения, что ведет к «близорукости» агента. В крайнем случае, когда γ = 0, целевая функция рассматривает только начальное вознаграждение r0, как показано в уравнении (1.8):
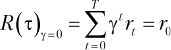
Чем больше значение γ, тем больший вес придается вознаграждениям на будущих временных шагах: агент становится «дальнозорким». Если γ = 1, вознаграждения на всех шагах имеют одинаковый вес, как показано в уравнении (1.9):
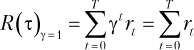
Для задач с бесконечным временным горизонтом нужно устанавливать γ < 1, чтобы целевая функция не стала бесконечной. Для задач с конечным временным горизонтом γ — важный параметр, так как в зависимости от используемого значения коэффициента дисконтирования решение может стать проще или сложнее. Пример этого будет рассмотрен в главе 2.
Определив целевую функцию и представив задачу обучения с подкреплением как МППР, можно выразить цикл управления агентом (рис. 1.2) как цикл управления в МППР (алгоритм 1.1).
Алгоритм 1.1. Цикл управления МППР
1: Считаем, что агент и среда env уже созданы
2: for episode = 0,...,MAX_EPISODEdo
3: state = env.reset()
4: agent.reset()
5: fort = 0,...,Tdo
6: action = agent.act(state)
7: state, reward = env.step(action)
8: agent.update(action, state, reward)
9: if env.done() then
10: break
11: end if
12: end for
13: end for
Алгоритм 1.1 показывает взаимодействие между агентом и средой на протяжении множества эпизодов и некоторого количества шагов. В начале каждого эпизода среда и агент возвращаются к исходным позициям (строки 3 и 4), при этом среда порождает начальное состояние. Затем начинается их взаимодействие: агент выполняет действие, исходя из данного состояния (строка 6), затем, основываясь на этом действии, среда производит следующее состояние и вознаграждение (строка 7), переходя на следующий шаг. Цикл agent.act-env.step длится, пока не будет достигнуто максимальное количество шагов T либо среда не завершится. Здесь появляется новый компонент — agent.update (строка 8), который включает в себя алгоритм обучения агента. На протяжении большого количества шагов и эпизодов этот метод накапливает данные и на внутреннем уровне обучается максимизации целевой функции.
Этот алгоритм общий для всех задач обучения с подкреплением, поскольку он определяет непротиворечивый интерфейс взаимодействия между агентом и средой. Данный интерфейс служит основой для реализации многих алгоритмов обучения с подкреплением, включенных в унифицированный фреймворк, как будет видно в прилагаемой к книге библиотеке SLM Lab.
1.3. Обучаемые функции в обучении с подкреплением
Когда обучение с подкреплением сформулировано как МППР, возникает естественный вопрос: чему должен учиться агент?
Мы видели, что агент может сформировать функцию выбора действий, известную как стратегия. Однако у среды есть и другие свойства, которые могут быть полезны для агента. В частности, существует три основных функции, которые изучаются в обучении с подкреплением.
1. Стратегия π, которая сопоставляет состоянию действие: a ~ π(s).
2. Функция полезности Vπ(s) или Qπ(s, a) для вычисления ожидаемой отдачи ![]()
3. Модель среды4P(s' | s, a).
Стратегия π — это то, каким образом агент производит действия в среде, чтобы максимизировать целевую функцию. Согласно циклу управления агент должен производить действия на каждом шаге после наблюдения состояния s. Стратегия имеет фундаментальное значение для цикла управления, поскольку генерирует действия, которые заставляют его продолжаться.
Стратегия может быть стохастической. Это значит, что она может с определенной вероятностью давать на выходе разные действия для одного состояния. Это может быть записано как π(a | s) и означает вероятность действия a для данного состояния s. Действие, выбранное по стратегии, записывается как a∼π(s).
Функции полезностей представляют информацию о цели. Они помогают агенту понять, насколько хороши состояния и доступные действия с точки зрения ожидаемой отдачи. Они записываются в двух формах:
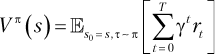
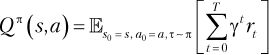
Функция полезности Vπ, приведенная в уравнении (1.10) оценивает, насколько хорошим или плохим является состояние. Vπ дает оценку ожидаемой отдачи от пребывания в положении s, предполагая, что агент продолжает действовать в соответствии со своей текущей стратегией π. Отдача ![]()
Рассмотрим простой пример, который позволит получить представление о функции полезности Vπ. На рис. 1.4 изображена дискретная среда с конечным числом состояний, в которой агент может перемещаться из клетки в клетку по вертикали и горизонтали. Каждая клетка — это состояние, с которым связано вознаграждение, как показано на рис. 1.4, слева. Среда завершается, когда агент попадает в целевое состояние с вознаграждением r = +1.
Справа показаны полезности Vπ(s), рассчитанные для каждого состояния по вознаграждениям с помощью уравнения (1.10) при γ = 0,9. Функция полезности Vπ всегда зависит от конкретной стратегии π. В этом примере взята стратегия π, при которой всегда выбирается кратчайший путь к целевому состоянию. Если стратегия будет другой — к примеру, перемещение только вправо, — то значения полезностей будут иными.
Это показывает, что функция полезности является прогнозной и помогает агенту различать состояния с одинаковым вознаграждением. Чем ближе агент к целевому состоянию, тем выше полезность рассматриваемого состояния.

Рис. 1.4. Вознаграждения r и полезности Vπ(s) для каждого состояния s в простой клеточной среде. Полезность состояния рассчитывается по вознаграждениям с помощью уравнения (1.10) при γ = 0,9. Здесь применяется стратегия π, при которой всегда выбирается кратчайший путь к целевому состоянию с r = +1
Функция полезности Qπ в уравнении (1.11) оценивает, насколько хороша или плоха пара «состояние — действие». Qπ дает оценку ожидаемой отдачи от выбора действия a в состоянии s, предполагая, что агент продолжает действовать в соответствии со своей текущей стратегией π. По аналогии с Vπ отдача подсчитывается, начиная с текущего состояния s и до конца эпизода. Это тоже прогнозная оценка, поскольку не учитываются все вознаграждения, полученные до состояния s.
Функции Vπ и Qπ более подробно рассматриваются в главе 3. А сейчас достаточно знать, что они существуют и могут быть использованы агентом для решения задач обучения с подкреплением.
Функция переходов P(s' | s, a) предоставляет информацию о среде. Сформировав эту функцию, агент обретает способность предсказывать следующее состояние s', в которое перейдет среда после выбора действия a в состоянии s. Применяя полученную функцию переходов, агент может вообразить последствия действий, не вступая в действительное взаимодействие со средой. В дальнейшем он может использовать эту информацию для планирования оптимальных действий.
1.4. Алгоритмы глубокого обучения с подкреплением
В RL агент настраивает функции, которые помогают ему действовать и максимизировать целевую функцию. Эта книга посвящена глубокому обучению сподкреплением (глубокому RL), что означает, что в качестве аппроксимирующего семейства функций будут использоваться глубокие нейронные сети.
В разделе 1.3 были показаны три основные обучаемые функции в обучении с подкреплением. Им соответствуют три больших семейства алгоритмов глубокого обучения с подкреплением — методы, основанные на стратегии, методы, основанные на полезности, и методы, основанные на модели среды. Существуют также комбинированные методы, в которых агенты настраивают несколько этих функций, например функции стратегии и полезности или функцию полезности и модели среды. На рис. 1.5 приведен обзор главных алгоритмов глубокого обучения с подкреплением в каждом из семейств и показаны взаимосвязи между ними.

Рис. 1.5. Семейства алгоритмов глубокого обучения с подкреплением
1.4.1. Алгоритмы, основанные на стратегии
Алгоритмы из этого семейства настраивают стратегию π. Хорошие стратегии должны порождать действия, обеспечивающие траектории τ, которые максимизируют целевую функцию агента ![]()
Главное преимущество основанных на стратегии алгоритмов как класса методов оптимизации — то, что это очень разнообразный класс. Они применимы к задачам с любым типом действий — дискретным, непрерывным или комбинированным. Кроме того, они оптимизируют непосредственно то, что интересует агента больше всего, — целевую функцию J(τ). К тому же Саттоном и другими в теореме о градиенте стратегии было доказано, что этот класс методов гарантированно сходится к локально5 оптимальной политике. Недостатки этих методов — высокая дисперсия и низкая эффективность выборок.
1.4.2. Алгоритмы, основанные на полезности
Агент настраивает либо Vπ(s), либо Qπ(s, a). Настроенная функция полезностей используется им для оценки пар (s, a) и порождения стратегии. Например, стратегия агента может быть такой, что он всегда выбирает действие a в состоянии s с максимальным оценочным значением Qπ(s, a). В подходе, основанном только на полезностях, намного чаще применяется настройка Qπ(s, a), чем Vπ(s), поскольку первую проще преобразовать в стратегию. Это связано с тем, что Qπ(s, a) содержит информацию о парах состояний и действий, тогда как Vπ(s) — лишь сведения о состояниях.
Обсуждаемый в главе 3 метод SARSA — один из старейших алгоритмов обучения с подкреплением. Несмотря на свою простоту, SARSA объединяет многие ключевые идеи методов, основанных на стратегиях, так что с него хорошо начинать изучение этого семейства алгоритмов. Однако он пока не получил широкого распространения из-за высокой дисперсии и низкой эффективности выборок во время обучения. Глубокая Q-сеть (DQN) и ее последователи, такие как двойные DQN и DQN с приоритизированной памятью прецедентов, намного эффективнее и куда популярнее. Это темы глав 4 и 5.
Как правило, основанные на полезности алгоритмы имеют большую эффективность выборок, чем алгоритмы, основанные на стратегии. Это обусловлено тем, что у них меньшая дисперсия и они продуктивнее используют собранные в среде данные. Однако нет гарантии, что эти алгоритмы сойдутся к оптимальным значениям. К тому же в своей стандартной формулировке их можно применять только к средам с дискретным пространством действий. Исторически это было главным ограничением, но последние улучшения, такие как QT-OPT, позволили эффективно применять их к средам с непрерывным пространством действий.
1.4.3. Алгоритмы, основанные на модели среды
Алгоритмы из этого семейства либо занимаются настройкой модели динамики переходов среды, либо задействуют известные динамические модели. Располагая моделью среды P(s' | s, a), агент способен представить, что может случиться в будущем, прогнозируя траекторию на несколько шагов вперед. Пусть среда находится в состоянии s, тогда агент может оценить, насколько состояние изменится, если он предпримет последовательность действий a1, a2… an, повторно применяя P(s' | s, a). При этом он никак не изменяет среду, так что прогнозная траектория появляется у него в результате использования модели. Агент может спрогнозировать несколько разных траекторий с различными последовательностями действий и, оценив их, принять решение о наилучшем выборе действия a.
Исключительно модельный подход широко применяется к играм с известным целевым состоянием, таким как победа либо поражение в шахматах или навигационные задания с целевым состоянием s*. Это связано с тем, что функции переходов в данном случае не моделируют никаких вознаграждений. И чтобы задействовать этот подход для планирования действий, потребуется закодировать информацию о целях агента в самих состояниях.
Поиск по дереву Монте-Карло (Monte Carlo Tree Search, MCTS) — широко распространенный метод, основанный на модели среды. Он применим к задачам с детерминированным дискретным пространством состояний с известными функциями переходов. Под эту категорию подпадают многие настольные игры, такие как шахматы и го, и до недавнего времени многие компьютерные программы для игры в го были основаны на MCTS. В нем не применяется машинное обучение. Для изучения игровых состояний и расчета их полезностей производятся случайные выборки последовательностей действий — случайные симуляции. Этот алгоритм претерпел несколько улучшений, но основная идея осталась неизменной.
Другие методы, такие как итеративный линейно-квадратичный регулятор (iterative Linear Quadratic Regulators, iLQR) или управление на основе прогнозирующих моделей (Model Predictive Control, MPC), включают изучение динамики переходов зачастую с сильно ограничивающими допущениями6. Для изучения динамики агенту нужно действовать в среде, чтобы собрать примеры действительных переходов (s, a, r, s').
Основанные на модели среды алгоритмы весьма интересны тем, что точная модель наделяет агента возможностью предвидения. Он может проигрывать сценарии и понимать последствия своих действий, не производя реальных действий в среде. Это может быть существенным преимуществом, когда накопление опыта из среды очень затратно с точки зрения ресурсов и времени, например, в робототехнике. Кроме того, по сравнению с методами, основанными на стратегии или полезности, этому алгоритму требуется намного меньше примеров данных для обучения оптимальной стратегии. Это обусловлено тем, что наличие модели дает агенту возможность дополнять его реальный опыт воображаемым.
Тем не менее для большинства задач модели среды получить трудно. Многие среды являются стохастическими, и их динамика переходов неизвестна. В таких случаях необходимо настраивать модель. Этот подход все еще находится на ранней стадии разработки, и его реализация сопряжена с рядом проблем. Во-первых, моделирование среды с обширными пространствами состояний и действий может быть очень трудным. Эта задача может даже оказаться неразрешимой, особенно если переходы чрезвычайно сложные. Во-вторых, от моделей есть польза только тогда, когда они могут точно прогнозировать переходы в среде на много шагов вперед. В зависимости от точности модели ошибки прогнозирования могут суммироваться на каждом шаге и быстро расти, что делает модель ненадежной.
На данный момент нехватка хороших моделей — главное ограничение для применения основанного на модели подхода. Однако основанные на модели методы могут быть очень эффективными. Если они работают, то эффективность выборок для них на 1–2 порядка выше, чем у безмодельных методов.
Различие между методами, основанными на модели среды, и безмодельными методами применяется и в классификации алгоритмов обучения с подкреплением. Алгоритм, основанный на модели, — это любой алгоритм, в котором используется динамика переходов среды, как настраиваемая, так и известная заранее. Безмодельные алгоритмы не задействуют динамику переходов среды в явном виде.
1.4.4. Комбинированные методы
Данные алгоритмы настраивают одну или несколько основных функций обучения с подкреплением. Представляется естественным объединить три рассмотренных метода, чтобы воспользоваться преимуществами каждого из них. Широкое распространение приобрела группа алгоритмов, настраивающих стратегию и функцию полезности. Они получили меткое название методов актора-критика, поскольку в них стратегия генерирует действие, а функция полезности критикует действия. Эти алгоритмы рассматриваются в главе 6. Основная их суть в том, что во время обучения настроенная функция полезности может передавать актору обратный сигнал, содержащий больше информации, чем последовательность вознаграждений, доступная из среды. Стратегия настраивается для использования информации, предоставляемой функцией полезности. Затем, как и в методах, основанных на стратегии, стратегия применяется для генерации действий.
Алгоритмы актора-критика — область активных исследований, в которой в последнее время было сделано много интересных усовершенствований. Вот лишь некоторые из них: оптимизация стратегии в доверительной области (Trust Region Policy Optimization, TRPO), оптимизация ближайшей стратегии (Proximal Policy Optimization, PPO), градиенты глубокой детерминированной стратегии (Deep Deterministic Policy Gradients, DDPG), логистический актор-критик (Soft Actor-Critic, SAC). На текущий момент самое широкое распространение получил PPO, он рассматривается в главе 7.
Алгоритмы могут также использовать модель динамики переходов в среде в сочетании с функцией полезности и/или стратегией. В 2016 году исследователи из DeepMind разработали AlphaZero — алгоритм, предназначенный для обучения игре в го. В нем MCTS объединен с настройкой Vπ и стратегии π. Dyna-Q — еще один известный алгоритм, в котором сначала происходит итерационный процесс настройки модели на полученных из среды реальных данных. Затем обученная модель генерирует воображаемые данные и использует их для настройки Q-функции.
Приведенные в этом разделе примеры — лишь малая часть алгоритмов глубокого обучения с подкреплением. Это далеко не исчерпывающий список. Напротив, данный раздел задумывался как обзор главных идей в глубоком обучении с подкреплением и способов применения стратегии, функции полезностей и модели среды как по отдельности, так и в сочетании друг с другом. В области глубокого обучения с подкреплением ведутся активные исследования, и каждые несколько месяцев появляются новые перспективные разработки.
1.4.5. Алгоритмы, которые обсуждаются в этой книге
В этой книге упор сделан на методы, основанные на стратегии и полезности и их комбинациях. Приводится описание методов REINFORCE (см. главу 2), SARSA (см. главу 3), DQN (см. главу 4) и их расширений (см. главу 5), актора-критика (см. главу 6) и PPO (см. главу 7). Глава 8 посвящена методам параллелизации, которые могут применяться ко всем перечисленным алгоритмам.
Эта книга призвана быть практическим руководством, поэтому в ней не затрагиваются алгоритмы, основанные на модели среды. Безмодельные методы значительно лучше исследованы и ввиду своей общности приложимы к более широкому классу задач. Один и тот же алгоритм (например, PPO) с минимальными изменениями может быть применен и к видеоиграм, таким как Dota 2, и к управлению робототехническим манипулятором. По сути, основанным на стратегии или полезности алгоритмам не нужна какая-то дополнительная информация. Их можно просто поместить в среду и позволить обучаться.
Основанным на модели среды методам, напротив, для работы обычно требуются дополнительные знания о среде, то есть модель динамики переходов. Для таких задач, как шахматы или го, модель — это просто правила игры, которые легко запрограммировать. И даже тогда заставить модель работать в связке с алгоритмами обучения с подкреплением — отнюдь не тривиальная задача, как видно по AlphaZero от DeepMind. Зачастую модель среды неизвестна и должна быть настроена, а это само по себе сложная задача.
Алгоритмы, основанные на стратегии и полезности, также не охвачены в полной мере. В книгу вошли алгоритмы, которые получили широкую известность и распространение и при этом иллюстрируют ключевые понятия глубокого обучения с подкреплением. Цель книги — помочь читателям заложить прочные основы знаний в этой области. Надеемся, что приведенное в книге описание алгоритмов подготовит читателей к знакомству с современными исследованиями и их применению в глубоком обучении с подкреплением.
1.4.6. Алгоритмы по актуальному и отложенному опыту
Последнее важное различие между алгоритмами глубокого обучения с подкреплением состоит в том, что они могут работать по актуальному опыту (on-policy) и по отложенному опыту (off-policy). Это влияет на то, как данные используются в цикле обучения.
Алгоритм обучения по актуальному опыту учится по текущей стратегии, то есть для тренировки могут быть задействованы только данные, сгенерированные текущей стратегией π. Это означает, что при обучении в цикле перебираются версии стратегии π1, π2, π3 и т.д., причем на каждой итерации для порождения новых данных используется только текущая стратегия. В результате по окончании обучения все данные должны быть отброшены, поскольку они становятся бесполезными. Это делает методы обучения по актуальному опыту неэффективными с точки зрения выборки прецедентов — им требуется больше обучающих данных. В этой книге обсуждаются следующие методы обучения по актуальному опыту: REINFORCE (см. главу 2), SARSA (см. главу 3), комбинированные методы актора-критика (см. главу 6) и PPO (см. главу 7).
В то же время у алгоритмов обучения по отложенному опыту нет таких требований. Любые накопленные данные могут быть повторно использованы при обучении. Как следствие, у методов обучения по отложенному опыту эффективность выборки прецедентов выше, но хранимые данные могут занимать намного больше памяти. Из методов обучения по отложенному опыту будут рассмотрены DQN (см. главу 4) и его расширения (см. главу 5).
1.4.7. Краткий обзор методов
Мы познакомились с основными семействами алгоритмов глубокого обучения с подкреплением и рассмотрели несколько способов их классификации. В данных подходах упор делается на разные характеристики, и ни один из них не является лучшим. В соответствии с этими различиями все методы могут быть сведены к следующим категориям.
• Основанные на стратегии, полезности, модели среды или комбинированные в зависимости от того, какую из трех основных функций обучения с подкреплением настраивает алгоритм.
• Основанные на модели и безмодельные в зависимости от того, использует алгоритм модель динамики переходов среды или нет.
• Ведущие обучение по актуальному или отложенному опыту в зависимости от того, учится агент на данных, полученных с помощью только текущей стратегии или нет.
1.5. Глубокое обучение для обучения с подкреплением
В этом разделе будут очень кратко рассмотрены глубокое обучение и процесс настройки параметров новой нейронной сети.
Глубокие нейронные сети добились блестящих результатов в аппроксимации сложных нелинейных функций. Их выразительность обусловлена структурой, состоящей из перемежающихся слоев параметров и нелинейных функций активации. В своей нынешней форме нейронные сети существуют с 1980-х годов, когда Ле Кун с коллегами успешно обучили сверточную нейронную сеть распознавать написанные вручную почтовые индексы. Начиная с 2012 года глубокое обучение успешно применялось ко множеству задач. Благодаря ему были достигнуты передовые результаты в целом ряде областей, включая компьютерное зрение, машинный перевод, понимание естественного языка и синтез речи. На момент написания этих строк глубокое обучение — наиболее эффективная из доступных методика аппроксимации функций.
В 1991 году Джеральд Тезауро впервые (и весьма успешно) применил обучение с подкреплением, чтобы научить нейронную сеть играть в нарды на мастерском уровне. Тем не менее лишь в 2015 году DeepMind достигла производительности на уровне человека для многих игр Atari, которые получили широкое распространение в качестве основного метода аппроксимации функций в данной области. С тех пор все крупные успехи в обучении с подкреплением связаны с применением нейронных сетей для аппроксимации функций. Именно поэтому в книге мы сосредоточились исключительно на глубоком обучении с подкреплением.
Нейронные сети настраивают функции, которые являются простым отображением входных данных в выходные. Они выполняют последовательные вычисления на входных данных для получения выходных данных, этот процесс известен как прямой проход. Функция представляется как конкретный набор значений параметров θ сети, говорится, что функция параметризирована θ. Различные наборы параметров соответствуют разным функциям.
Для настройки функции требуются метод, который будет принимать или генерировать достаточно репрезентативный набор входных данных, и способ оценки выходных данных, выдаваемых сетью. Оценить выходные данные можно одним из двух способов. Первый заключается в порождении «корректных» выходных данных, или целевого значения, для всех входных данных и определении функции потерь, которая измеряет ошибку между целевыми и выданными сетью прогнозными выходными значениями. Эти потери должны быть минимизированы. Второй способ — непосредственное предоставление в ответ на все входные данные одного скалярного значения, такого как вознаграждение или отдачи. Эта скалярная величина показывает, насколько хороши или плохи выходные данные сети, и она должна быть максимизирована. Отрицательное значение этой величины может рассматриваться как функция потерь, которую следует минимизировать.
Если задаться функцией потерь, которая оценивает выходные данные сети, то, меняя значения параметров сети, можно минимизировать потери и повысить производительность. Этот процесс известен как градиентный спуск, поскольку параметры изменяются в сторону скорейшего спуска по поверхности функции потерь в поисках глобального минимума.
Процесс изменения параметров сети с целью минимизации потерь известен также как процесс обучения нейронной сети. В качестве примера предположим, что настроенная функция f(x) параметризирована весами сети θ как f(x; θ). Пусть L(f(x; θ), y) — заранее заданная функция потерь, где x и y — это входные и выходные данные соответственно. Процесс обучения может быть описан следующим образом.
1. Из всего набора данных случайным образом выбирается набор (x, y), размер которого значительно меньше, чем размер всего набора данных.
2. При прямом проходе по сети на основе входных значений x вычисляются прогнозные выходные значения yˆ = f(x; θ).
3. По выданным сетью прогнозным значениям yˆ и значениям y из отобранного набора данных рассчитывается функция потерь L(yˆ, y).
4. В соответствии с параметрами сети подсчитываются градиенты (частные производные) функции потерь ∇θL. Современные программные библиотеки для работы с нейронными сетями, такие как PyTorch или TensorFlow, выполняют этот процесс автоматически с применением алгоритма обратного распространения ошибки (что известно также как autograd).
5. Оптимизатор используется для обновления параметров сети с помощью градиентов. Например, оптимизатор на основе стохастического градиентного спуска (stochastic gradient descent, SGD) производит следующее обновление: θ←θ – α∇θL, где α — скалярное значение скорости обучения. Библиотеки для работы с нейронными сетями предоставляют и много других методик оптимизации.
Эти шаги обучения повторяются, пока выходные данные сети не прекратят изменяться или функция потерь не будет минимизирована или стабилизирована, то есть пока сеть не сойдется.
В обучении с подкреплением ни входные данные сети x, ни корректные выходные данные у изначально не даны. Наоборот, эти значения получаются при взаимодействии агента со средой — из наблюдаемых им состояний и вознаграждений. В обучении с подкреплением это представляет особую трудность для обучения нейронных сетей и многократно обсуждается на протяжении всей книги.
Сложность генерации и оценки данных вызвана тем, что настраиваемые функции тесно связаны с циклом МППР. Агент и среда обмениваются интерактивными данными, и в силу своей природы этот процесс ограничен временем, необходимым на то, чтобы агент произвел действие, а среда выполнила переход. Не существует быстрого способа порождения данных для обучения — агент должен приобретать опыт на каждом шаге. Накопление данных и цикл обучения повторяются, на каждом шаге обучения приходится дожидаться, пока новые данные не будут собраны.
Более того, текущее состояние среды и предпринятые агентом действия влияют на последующие состояния, наблюдаемые им. Из-за этого состояния и вознаграждения в любой момент зависят от состояний и вознаграждений на предыдущих шагах. Это нарушает лежащее в основе градиентного спуска предположение о том, что данные независимы и одинаково распределены (i.i.d). Это может, в свою очередь, отрицательно сказаться на скорости, с которой сходится сеть, и качестве конечного результата. Значительные усилия были потрачены на исследования по минимизации данного эффекта, некоторые из методик обсуждаются далее в этой книге.
Невзирая на эти трудности, глубокое обучение — эффективная методика аппроксимации функций. Для преодоления сложности его применения к обучению с подкреплением придется потрудиться, но усилия не пропадут даром, ведь отдача значительно превышает издержки.
1.6. Обучение с подкреплением и обучение с учителем
В основе глубокого обучения с подкреплением лежит аппроксимация функций. Это то, что объединяет его с обучением с учителем (supervised learning, SL7). Однако между обучением с подкреплением и обучением с учителем есть несколько различий. Три основных перечислены далее:
• отсутствие оракула8;
• разреженность обратной связи;
• генерация данных во время обучения.
1.6.1. Отсутствие оракула
Главное различие между обучением с подкреплением и с учителем в том, что в задачах обучения с подкреплением не для всех входных данных модели имеются корректные ответы, тогда как в обучении с учителем для любого примера существует правильный или оптимальный ответ. В обучении с подкреплением аналогом корректного ответа будет доступ к оракулу, сообщающему, выбор какого действия на каждом шаге будет наилучшим для оптимизации целевой функции.
В правильном ответе может быть передано большое количество информации о текущем примере из данных. К примеру, корректный ответ для задач классификации содержит многие биты информации. В нем не только сообщается о правильном классе для каждого примера, но и подразумевается, что этот пример не относится ни к одному другому классу. Если в отдельно взятой задаче классификации есть 1000 классов (как в наборе данных ImageNet), ответ содержит по 1000 бит информации на каждый пример (1 положительное и 999 отрицательных значений). Более того, правильный ответ не обязательно является категорией или вещественным числом. Это может быть как ограничивающий прямоугольник, так и семантическое разбиение — и то и другое содержит большое количество битов информации о рассматриваемом примере.
В обучении с подкреплением агенту после того, как он предпринял действие a в состоянии s, доступно только полученное им вознаграждение. Агенту не сообщается, какое действие оптимальное. Напротив, посредством вознаграждения ему лишь указывается, насколько хорошим или плохим было a. Помимо того что это указание содержит меньше информации, чем правильный ответ, агент учится на вознаграждениях, полученных только в тех состояниях, в которых он побывал. Чтобы получить знания о (s, a, r), ему нужно совершить переход (s, a, r, s'). У агента может отсутствовать информация о важных частях пространств состояний и действий по той простой причине, что он с ними не сталкивался.
Один из способов решения этой проблемы состоит в инициализации эпизодов таким образом, чтобы они начинались с состояний, которые агенту нужно изучить. Однако это не всегда возможно по двум причинам. Во-первых, может отсутствовать полный контроль над средой. Во-вторых, состояния может быть просто описать, но трудно идентифицировать. Рассмотрим ситуацию, когда человекоподобный робот учится делать обратное сальто. Чтобы помочь агенту узнать о вознаграждении за успешное приземление, можно инициализировать среду так, чтобы она запускалась сразу после того, как ноги робота войдут в контакт с полом после удачного сальто. Знание функции вознаграждения в этой части пространства состояний критично, поскольку здесь робот может как удержать равновесие и успешно выполнить сальто, так и упасть. Однако для инициализации робота в данной позиции требуется определить точные угловые координаты и скорости каждого из его суставов или приложенную силу, а это непросто. На практике агенту для достижения данного состояния нужно выполнить очень конкретную длинную последовательность действий, чтобы сделать переворот и почти приземлиться. И нет гарантии, что агент научится делать это, так что данная часть пространства состояний может оказаться так и не исследованной.
1.6.2. Разреженность обратной связи
В обучении с подкреплением функция вознаграждений может быть разреженной, так что скалярная величина вознаграждения часто равна нулю. Это означает, что агент большую часть времени не получает информации о том, как изменить параметры сети, чтобы оптимизировать ее производительность. Снова рассмотрим робота, делающего обратное сальто, и предположим, что агент получает ненулевое вознаграждение +1 только после каждого успешного выполнения прыжка. Почти все предпринимаемые им действия приведут к одному и тому же нулевому вознаграждению от среды. При таких обстоятельствах обучение чрезвычайно затруднено, поскольку агент не получает никаких указаний о том, способствуют ли его промежуточные действия достижению цели. В обучении с учителем нет такой проблемы — всем входным примерам соответствуют желаемые выходные значения, в которых передается информация о том, как сеть должна работать.
Разреженность обратной связи вдобавок к отсутствию оракула означает, что в обучении с подкреплением на каждом шаге из среды будет получено намного меньше информации, чем в тренировочных примерах при обучении с учителем. В результате алгоритмы обучения с подкреплением имеют тенденцию к получению гораздо меньшей эффективности выборки прецедентов из среды.
1.6.3. Генерация данных
В обучении с учителем данные обычно генерируются независимо от обучения алгоритма. Действительно, первым шагом применения обучения с учителем к задаче будет поиск или построение хорошего набора данных. В обучении с подкреплением данные должны порождаться при взаимодействии агента со средой. Эти данные в большинстве случаев генерируются в ходе обучения итеративно, с чередованием периодов накопления данных и обучения. Между получаемыми данными и работой алгоритма существует взаимосвязь. Качество алгоритма влияет на данные, на которых он обучается, а они, в свою очередь, влияют на производительность алгоритма. В обучении с учителем нет этой цикличности и не требуется повторная генерация выборок (bootstrapping).
Кроме того, RL интерактивно: выполненные агентом действия фактически трансформируют среду, которая затем изменяет решения агента, которые преобразуют данные, наблюдаемые агентом, и т.д. Этот цикл обратной связи — отличительная особенность обучения с подкреплением. В задачах обучения с учителем этого цикла нет, как нет и понятия, эквивалентного агенту, способному изменять данные, на которых обучается алгоритм.
Последнее, менее значимое различие между обучением с подкреплением и с учителем состоит в том, что в первом нейронные сети не всегда учатся с применением функции потерь, используемой в распознавании. Получаемые из среды вознаграждения применяются не для того, чтобы минимизировать ошибку, обусловленную разницей между выходными данными среды и желаемыми целевыми значениями, а для построения целевой функции, максимизировать которую затем учится сеть. Тем, кто изучал обучение с учителем, поначалу это может показаться немного странным, но механизм оптимизации, по сути, тот же самый. В обоих случаях параметры сети настраиваются с целью максимизации или минимизации некоторой функции.
1.7. Резюме
В этой главе дано описание задач обучения с подкреплением как работы систем, состоящих из агента и среды, которые взаимодействуют и обмениваются информацией в виде состояний, действий и вознаграждений. Агенты учатся действовать в среде с помощью стратегии так, чтобы максимизировать ожидаемую сумму вознаграждений, которая является их целевой функцией. С применением этих понятий было показано, как обучение с подкреплением может быть сформулировано в виде МППР, в предположении, что функция переходов среды имеет марковское свойство.
Опыт, полученный агентом в среде, может быть использован для настройки функций, которые помогают агенту максимизировать целевую функцию. В частности, были рассмотрены три основные настраиваемые функции в обучении с подкреплением: стратегииπ(s), функции полезностиVπ(S) и Qπ(s, a), а также моделиP(s' | s, a). В зависимости от того, какую из этих функций настраивает агент, алгоритмы глубокого обучения с подкреплением могут быть разделены на основанные на стратегии, полезности или модели среды либо комбинированные. Их можно также разделить на категории в соответствии с тем, как порождаются тренировочные данные. В алгоритмах обучения по актуальному опыту используются только данные, сгенерированные текущей стратегией, в алгоритмах обучения по отложенному опыту могут применяться данные, порожденные любой стратегией.
Вкратце были рассмотрены процесс обучения в глубоком обучении с подкреплением и некоторые из различий между обучением с подкреплением и обучением с учителем.
2 Бесконечные циклы управления существуют в теории, но не на практике. Как правило, для среды устанавливается максимальное количество шагов T.
3 Отдача обозначается R, а ![]()
4 Чтобы сделать нотацию более краткой, принято записывать пару следующих друг за другом кортежей (st, at, rt), (st + 1, at + 1, rt + 1) как (s, a, r), (s', a', r'), где штрих означает следующий шаг. Это обозначение будет встречаться в книге повсеместно.
5 Гарантия глобальной сходимости — все еще открытый вопрос. Не так давно она была доказана для подкласса задач линеаризованного управления. См. статью: Fazel et al. Global Convergence of Policy Gradient Methods for Linearized Control Problems (2018).
6 Например, в iLQR предполагается, что динамика переходов представляет собой линейную функцию от состояний и действий, а функция вознаграждения квадратичная.
7 В сообществе ИИ любят сокращения. Их будет много — почти у всех алгоритмов и названий компонентов есть аббревиатуры.
8 В компьютерных науках оракул — это гипотетический черный ящик, дающий корректные ответы на заданные вопросы.
• отсутствие оракула8;
Чтобы формулировка задачи была полной, нужно формализовать понятие максимизируемой агентом целевой функции. Во-первых, определим отдачу3 (return) 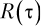 , используя траекторию из эпизода τ = (s0, a0, r0)… (sT, aT, rT):
, используя траекторию из эпизода τ = (s0, a0, r0)… (sT, aT, rT):
По сути, система обучения с подкреплением реализует цикл управления с обратной связью, где агент и среда взаимодействуют и обмениваются сигналами, причем агент пытается максимизировать целевую функцию. Сигналы — это тройка (st, at, rt), что соответствует состоянию, действию и вознаграждению, а индекс t указывает на номер шага (момент времени), на котором возник сигнал. Кортеж (st, at, rt) называется прецедентом или частью получаемого агентом опыта. Цикл управления может повторяться до бесконечности2 или закончиться по достижении либо конечного состояния, либо максимального значения шага t = T. Временной горизонт от t = 0 до момента завершения среды носит название эпизода. Траектория — это последовательность прецедентов, или часть опыта, накопленного в течение эпизода, τ = (s0, a0, r0), (s1, a1, r1)… Обычно агенту для обучения хорошей стратегии требуется от сотен до миллионов эпизодов в зависимости от сложности задачи.
В основе глубокого обучения с подкреплением лежит аппроксимация функций. Это то, что объединяет его с обучением с учителем (supervised learning, SL7). Однако между обучением с подкреплением и обучением с учителем есть несколько различий. Три основных перечислены далее:
Главное преимущество основанных на стратегии алгоритмов как класса методов оптимизации — то, что это очень разнообразный класс. Они применимы к задачам с любым типом действий — дискретным, непрерывным или комбинированным. Кроме того, они оптимизируют непосредственно то, что интересует агента больше всего, — целевую функцию J(τ). К тому же Саттоном и другими в теореме о градиенте стратегии было доказано, что этот класс методов гарантированно сходится к локально5 оптимальной политике. Недостатки этих методов — высокая дисперсия и низкая эффективность выборок.
Другие методы, такие как итеративный линейно-квадратичный регулятор (iterative Linear Quadratic Regulators, iLQR) или управление на основе прогнозирующих моделей (Model Predictive Control, MPC), включают изучение динамики переходов зачастую с сильно ограничивающими допущениями6. Для изучения динамики агенту нужно действовать в среде, чтобы собрать примеры действительных переходов (s, a, r, s').
3. Модель среды4P(s' | s, a).
В компьютерных науках оракул — это гипотетический черный ящик, дающий корректные ответы на заданные вопросы.
В сообществе ИИ любят сокращения. Их будет много — почти у всех алгоритмов и названий компонентов есть аббревиатуры.
Бесконечные циклы управления существуют в теории, но не на практике. Как правило, для среды устанавливается максимальное количество шагов T.
Например, в iLQR предполагается, что динамика переходов представляет собой линейную функцию от состояний и действий, а функция вознаграждения квадратичная.
Гарантия глобальной сходимости — все еще открытый вопрос. Не так давно она была доказана для подкласса задач линеаризованного управления. См. статью: Fazel et al. Global Convergence of Policy Gradient Methods for Linearized Control Problems (2018).
Чтобы сделать нотацию более краткой, принято записывать пару следующих друг за другом кортежей (st, at, rt), (st + 1, at + 1, rt + 1) как (s, a, r), (s', a', r'), где штрих означает следующий шаг. Это обозначение будет встречаться в книге повсеместно.
Отдача обозначается R, а 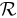 оставлено для функции вознаграждения.
оставлено для функции вознаграждения.
