Введение

Зачем нужна эта книга

Многие из моих знакомых разработчиков пришли в профессию из самых разных областей. У одних — высшее образование в области Computer Science; другие изучали фотографию, математику или даже не окончили университет.

В последние годы я заметил, что программисты все чаще стремятся изучить Compu­ter Science по ряду причин:

• чтобы стать хорошими программистами;

• чтобы на собеседованиях отвечать на вопросы про алгоритмы;

• чтобы удовлетворить свое любопытство в области Com­puter Science или наконец перестать сожалеть о том, что в свое время у них не было возможности освоить этот предмет.

Эта книга для всех вас.

Многие найдут здесь темы, интересные сами по себе. Я попытался показать, в каких реальных (неакадемических) ситуациях эти знания будут полезны. Хочу, чтобы, прочитав эту книгу, вы получили такие же знания, как после изучения базового курса по Computer Science, а также научились их применять.

Проще говоря, цель этой книги — помочь вам стать более квалифицированным и опытным программистом благодаря лучшему пониманию Computer Science. Мне не под силу втиснуть в одну книгу 20-летний стаж преподавания в колледже и профессиональный опыт... однако я постараюсь сделать максимум того, на что способен. Надеюсь, что вы найдете здесь хотя бы одну тему, о которой сможете сказать: «Да, теперь мне это понятно» — и применить знания в своей работе.

Разослав на рассмотрение черновой вариант книги, я получил множество однотипных отзывов. Слишком много материала. Слишком сложно для восприятия. Слишком устрашающе.

Полученные комментарии способствовали внесению нескольких изменений. Текст был сокращен и упрощен; подробности, не имеющие непосредственного отношения к рассматриваемой теме, опущены. Книга была разбита на части, причем самые важные темы идут в первой половине. В результате она получилась менее устрашающей и более понятной.

Чего вы не найдете в издании

Смысл книги состоит в том, чтобы читатель смог лучше понимать Computer Science и применять знания на практике, а вовсе не в том, чтобы полностью заменить четыре года обучения.

В частности, это не книга с доказательствами. Действительно, начиная с части VI, рассмотрены методы доказательства, однако стандартные алгоритмы обычно приводятся здесь без доказательств. Идея в том, чтобы читатель узнал о существовании этих алгоритмов и научился их использовать, не вникая в подробности. В качестве книги с доказательствами, написанной для студентов и аспирантов, я настоятельно рекомендую Introduction to Algorithms1 («Алгоритмы. Вводный курс») Кормена (Cormen), Лейзерсона (Leiserson), Ривеста (Rivest) и Стейна (Stein) (этих авторов обычно объединяют под аббревиатурой CLRS).

Это и не книга по программированию: вы не найдете здесь рекомендаций, когда использовать числа типа int, а ко­гда — double, или объяснений, что такое цикл. Предполагается, что читатель сможет разобраться в листингах на псевдокоде, используемых для описания алго­ритмов2. Цель книги — связать концепции Computer Science с уже знакомыми читателю методами программирования.

Дополнительные ресурсы

Для тех, кто хочет подробнее изучить ту или иную тему, я включил в сноски ссылки на дополнительные материалы. Кроме того, по адресу http://www.whatwil­liamsaid.com/books/ вы найдете тесты для самопроверки к каждой главе.

Что дальше

Я был намеренно краток и старался опускать детали, которые, будучи интересными сами по себе, не требуются для понимания описываемых концепций. В следующих книгах я собираюсь более подробно остановиться на некоторых областях, представляющих особый интерес.

Чтобы предложить тему для следующей книги, подписаться на рассылку или просто задать вопрос, посетите мой сайт: http://www.whatwilliamsaid.com/books. С нетерпением жду ваших сообщений.

От издательства

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства www.piter.com вы найдете по­дробную информацию о наших книгах.

Часть I. Основы Computer Science

1. Асимптотическое время выполнения

1.1. Что такое алгоритм

Предположим, вам нужно научить робота делать бутерброд с арахисовым маслом (рис. 1.1). Ваши инструкции могут быть примерно такими.

1. Открыть верхнюю левую дверцу шкафчика.

2. Взять банку с арахисовым маслом и вынуть ее из шкафчика.

3. Закрыть шкафчик.

4. Держа банку с арахисовым маслом в левой руке, взять крышку в правую руку.

5. Поворачивать правую руку против часовой стрелки, пока крышка не откроется.

6. И так далее...

 

Рис. 1.1. Робот — изготовитель бутербродов

Это программа: вы описали каждый шаг, который компьютер должен выполнить, и указали всю информацию, которая требуется компьютеру для выполнения каждого шага. А теперь представьте, что вы объясняете человеку, как сделать бутерброд с арахисовым маслом. Ваши инструкции будут, скорее всего, такими.

1. Достаньте арахисовое масло, джем и хлеб.

2. Намажьте ножом арахисовое масло на один ломтик хлеба.

3. Намажьте ложкой джем на второй ломтик хлеба.

4. Сложите два ломтика вместе. Приятного аппетита!

Это алгоритм: процесс, которому нужно следовать для получения желаемого результата (в данном случае бутерброда с арахисовым маслом и джемом). Обратите внимание, что алгоритм более абстрактный, чем программа. Программа сообщает роботу, откуда именно нужно взять предметы на конкретной кухне, с точным указанием всех необходимых деталей. Это реализация алгоритма, которая предоставляет все важные детали, но может быть выполнена на любом оборудовании (в данном случае — на кухне), со всеми необходимыми элементами (арахисовое масло, джем, хлеб и столовые приборы).

1.2. Почему скорость имеет значение

Современные компьютеры достаточно быстры, поэтому во многих случаях скорость алгоритма не особенно важна. Когда я нажимаю кнопку и компьютер реагирует за 1/25 секунды, а не за 1/100 секунды, эта разница для меня не имеет значения — с моей точки зрения, компьютер в обоих случаях реагирует мгновенно.

Но во многих приложениях скорость все еще важна, например, при работе с большим количеством объектов. Предположим, что у вас есть список из миллиона элементов, который необходимо отсортировать. Эффективная сортировка занимает одну секунду, а неэффективная может длиться несколько недель. Возможно, пользователь не захочет ждать, пока она закончится.

Мы часто считаем задачу неразрешимой, если не существует известного способа ее решения за разумные сроки, где «разумность» зависит от различных реальных факторов. Например, безопасность шифрования данных часто зависит от сложности разложения на множители (факторизации) больших чисел. Если я отправляю вам зашифрованное сообщение, содержимое которого нужно хранить в секрете в течение недели, то для меня не имеет значения, что злоумышленник перехватит это сообщение и расшифрует его через три года. Задача не является неразрешимой — просто наш любитель подслушивать не знает, как решить ее достаточно быстро, чтобы решение было полезным.

Важным навыком в программировании является уме­ние оптимизировать только те части программы, которые необходимо оптимизировать. Если пользовательский интерфейс работает на 1/1000 секунды медленнее, чем мог бы, это никого не волнует — в данном случае мы предпочли бы незаметному увеличению скорости удобочитаемую программу. А вот код, расположенный внутри цикла, который может выполняться миллионы раз, должен быть написан максимально эффективно.

1.3. Когда секунды (не) считаются

Рассмотрим алгоритм приготовления бутербродов из раздела 1.1. Поскольку мы хотим, чтобы этот алгоритм можно было использовать для любого количества различных роботов — изготовителей бутербродов, мы не хотим измерять количество секунд, затрачиваемое на выполнение алгоритма, поскольку для разных роботов оно будет различаться. Один робот может дольше открывать шкафчик, но быстрее вскрывать банку с арахисовым маслом, а другой — наоборот.

Вместо того чтобы измерять фактическую скорость выполнения каждого шага, которая будет различаться для разных роботов и кухонь, лучше подсчитать (и минимизировать) количество шагов. Например, алгоритм, который требует, чтобы робот сразу брал и нож и ложку, эффективнее, чем алгоритм, в котором робот открывает ящик со столовыми приборами, берет нож, закрывает ящик, кладет нож на стол, снова открывает ящик, достает ложку и т.д.

Измерение времени: алгоритм или программа? Напомню, что алгоритмы являются более обобщенными, чем программы. Для нашего алгоритма приготовления бутербродов мы хотим посчитать число шагов. Если бы мы действительно использовали конкретного робота — изготовителя бутербродов, то нас бы больше интересовало точное время, которое требуется для изготовления каждого бутерброда.

Следует признать, что не все шаги потребуют одинакового времени выполнения; скорее всего, взять нож — быстрее, чем намазать арахисовое масло на хлеб. Поэтому мы хотим не столько узнать точное количество шагов, сколько иметь представление о том, сколько шагов потребуется в зависимости от размера входных данных. В случае с нашим роботом время, необходимое для приготовления бутерброда, при увеличении количества бутербродов не увеличивается (при условии, что нам хватит джема).

Два компьютера могут выполнять алгоритм с разной скоростью. Это зависит от их тактовой частоты, объема доступной памяти, количества тактовых циклов, требуемого для выполнения каждой инструкции, и т.д. Однако обоим компьютерам, как правило, требуется приблизительно одинаковое число инструкций, и мы можем измерить скорость, с которой количество требуемых инструкций увеличивается в зависимости от размера задачи (рис. 1.2). Например, при сортировке массива чисел, если увеличить его размер в тысячу раз, один алгоритм может потребовать в тысячу раз больше команд, а второй — в миллион раз больше3.

 

Рис. 1.2. Более эффективный робот — изготовитель бутербродов

Часто мы хотим измерить скорость алгоритма несколькими способами. В жизненно важных ситуациях — например, при запуске двигателей на зонде, который приземляется на Марсе, — мы хотим знать время выполнения при самом неблагоприятном раскладе. Мы можем выбрать алгоритм, который в среднем работает немного медленнее, но зато гарантирует, что его выполнение никогда не займет больше времени, чем мы считаем приемлемым (и наш зонд не разобьется вместо того, чтобы приземлиться). Для более повседневных сценариев мы можем смириться со случайными всплесками времени выполнения, если при этом среднее время не растет; например, в видеоигре мы бы предпочли генерировать результаты в среднем быстрее, смирившись с необходимостью время от времени прерывать длительные вычисления. А бывают случаи, когда мы хотели бы знать наилучшую производительность. Однако в большинстве ситуаций мы просто рассчитываем наихудшее время выполнения, которое все равно часто совпадает со средним временем выполнения.

1.4. Как мы описываем скорость

Предположим, у нас есть два списка целых чисел, которые мы хотим отсортировать: {1, 2, 3, 4, 5, 6, 7, 8} и {3, 5, 4, 1, 2}. Сортировка какого списка займет меньше времени?

Ответ на вопрос: неизвестно. Для одного алгоритма сортировки тот факт, что первый список уже отсортирован, позволит почти сразу завершить работу. Для другого алгоритма решающим фактором может быть то, что второй список короче. Но обратите внимание, что оба свойства входных данных — размер списка и последовательность расположения чисел — влияют на количество шагов, необходимых для сортировки.

Если некоторое свойство, например «отсортированность», изменяет время выполнения конкретного алгоритма только на постоянную величину, мы можем просто его игнорировать, поскольку его влияние незаметно по сравнению с влиянием размера задачи. Например, робот может делать бутерброды с виноградным или малиновым джемом, но банка с малиновым джемом открывается немного дольше. Если робот делает миллион бутербродов, то влияние выбора джема на время приготовления бутерброда незаметно на фоне количества бутербродов. Поэтому мы можем его игнорировать и просто сказать, что приготовление миллио­на бутербродов занимает примерно в миллион раз больше времени, чем приготовление одного бутерброда.

С точки зрения математики мы вычисляем асимптотическое время выполнения алгоритма, то есть скорость увеличения времени выполнения в зависимости от размера входных данных. Нашему роботу, который делает бутерброды, требуется некоторое постоянное время c для приготовления одного бутерброда и в n раз больше времени, то есть cn, чтобы сделать n бутербродов. Мы отбрасываем константу и говорим, что наш алгоритм приготовления бутербродов занимает время O(n) (произносится как «О большое от n» или просто «О от n»). Это означает, что время выполнения в худшем случае пропорционально количеству бутербродов, которое будет сделано. Нас интересует не точное количество необходимых шагов, а скорость, с которой это число увеличивается по мере роста размера задачи (в данном случае — количества бутербродов).

1.5. Скорость типичных алгоритмов

Сколько бы бутербродов ни делал наш робот, это не увеличивает время, необходимое для изготовления одного бутерброда. Это линейный алгоритм — общее время выполнения пропорционально количеству обрабатываемых элементов. Для большинства задач это лучшее, чего можно добиться4. Типичный пример линейного алгоритма в программировании — чтение списка элементов и выполнение некоторой задачи для каждого элемента списка: время, затрачиваемое на обработку каждого элемента, не зависит от других элементов. Есть цикл, который выполняет постоянный объем работы и осуществляется один раз для каждого из n элементов, поэтому все вместе занимает O(n) времени.

Но чаще количество элементов списка влияет на объем работы, которую необходимо выполнить для отдельного элемента. Алгоритм сортировки может обрабатывать каждый элемент списка, разделяя список на два меньших списка, и повторять это до тех пор, пока все элементы не окажутся в своем собственном списке. На каждой итерации алгоритм выполняет O(n) операций и требует O(lg n) итераций, что в общей сложности составляет O(n) ×O(lg n) = O(n lg n) времени.5

Математическое предупреждение Логарифм описывает, в какую степень необходимо возвести число, указанное в основании, чтобы получить желаемое значение. Например, log10 1000 = 3, так как 103 = 1000. В компьютерах мы часто делим на 2, поэтому обычно используются логарифмы по основанию 2. Сокращенно log2 n обозначается как lg n.2 Таким образом, lg 1 = 0, lg 2 = 1, lg 4 = 2, lg 8 = 3 и т.д.

С этого момента время выполнения начинает ухудшаться. Рассмотрим алгоритм, в котором каждый элемент множества сравнивается со всеми остальными элементами множества, — здесь мы выполняем работу, занимающую O(n) времени, O(n) раз, то есть общее время выполнения алгоритма — O(n2). Это квадратичное время.

Все алгоритмы, у которых время выполнения пропорционально количеству входных данных, возведенному в некоторую степень, называются полиномиальными алгоритмами; такие алгоритмы принято считать быстрыми. Конечно, алгоритм, решение которого пропорционально количеству входных данных в сотой степени, хоть и является полиномиальным, все же не будет считаться быстрым даже при большом воображении! Однако на практике задачи, о которых известно, что они имеют полиномиальное время решения, как правило, решаются за биквадратное (четвертой степени) время или еще быстрее.

Это не означает, что асимптотически более эффективный алгоритм всегда будет работать быстрее, чем асимптотически менее эффективный. Например, ваш жесткий диск вышел из строя и вы потеряли несколько важных файлов. К  счастью, вы сделали их резервную копию в Сети6.

Вы можете загрузить файлы из облака со скоростью 10 Мбит/с (при условии, что у вас хорошее соединение). Это линейное время — количество времени, которое требуется для извлечения всех потерянных файлов, и оно более или менее прямо пропорционально зависит от размера файлов. Служба резервного копирования также предлагает загрузить файлы на внешний диск и отправить их вам — это действие занимает постоянное время, или O(1), потому что время получения этих данных не зависит от их размера7. Если речь идет о восстановлении всего нескольких мегабайтов, то загрузить их напрямую будет намного быстрее. Но, как только файл достигнет такого размера, что его загрузка будет занимать столько же времени, сколько и отправка, удобнее будет использовать внешний диск.

Если полиномиальные алгоритмы быстрые, то какие же алгоритмы медленные? Для некоторых алгоритмов (называемых экспоненциальными) число операций ограничено не размером входных данных, возведенным в некоторую постоянную степень, а константой, возведенной в степень, равную размеру входных данных.

В качестве примера рассмотрим попытку угадать числовой код доступа длиной n символов. Если это десять цифр от 0 до 9, то количество возможных кодов составляет 10n. Обратите внимание, что это число растет намного быстрее, чем n10: если n равно всего 20, полиномиальный алгоритм работает уже почти в 10 миллионов раз быстрее (рис. 1.3)!

 

Рис. 1.3. Даже при небольшом количестве входных данных различия в асимптотическом времени выполнения быстро становятся заметными

1.6. Всегда ли полиномиальное время лучше?

Как правило, специалисты по Computer Science заинтересованы получить полиномиальное решение задачи, особенно если оно выполняется за квадратичное время или еще быстрее. Однако для задач разумного (небольшого) размера экспоненциальные алгоритмы также могут быть приемлемы.

Зачастую мы можем найти приближенное решение задачи за полиномиальное время, однако получить точный (или близкий к точному) ответ можем лишь за экспоненциальное время. Рассмотрим в качестве примера задачу коммивояжера: продавец хотел бы посетить каждый город на своем маршруте ровно один раз и вернуться домой, преодолев минимальное расстояние. (Представьте себе, сколько денег сэкономили бы службы доставки UPS и FedEx, если бы сделали свои маршруты всего лишь немного более эффективными!)

Чтобы получить точный ответ, нужно вычислить все возможные маршруты и сравнить их суммарные расстояния, то есть O(n!) возможных путей. Очень близкое к оптимальному (в пределах до 1 %) решение может быть найдено за экспоненциальное время8. Но возможное «достаточно хорошее» (в пределах 50 % от оптимального) решение может быть найдено за полиномиальное время9. Это обычный компромисс: мы можем быстро получить достаточно хорошее приближение или медленнее — более точный ответ.

1.7. Время выполнения алгоритма

Рассмотрим следующий код:

foreach (name in NameCollection)

{

    Print "Hello, {name}!";

}

Здесь у нас есть коллекция из n строк; для каждой строки выводится короткое сообщение. Вывод сообщения занимает постоянное время10, то есть O(1). Мы делаем это n раз, то есть O(n). Умножив одно на другое, получим результат: время выполнения кода составляет O(n).

А теперь рассмотрим другую функцию:

DoStuff (numbers)

{

    sum = 0;

    foreach (num in numbers)

    {

        sum += num;

    }

    product = 1;

    foreach (num in numbers)

    {

        product *= num;

    }

    Print "The sum is {sum} and the

           product is {product}";

}

Здесь есть два цикла; каждый из них состоит из O(n) итераций и на каждой итерации выполняет постоянную работу, то есть общее время выполнения каждого цикла составляет O(n). Сложив O(n) и O(n) и отбросив константу, мы снова получим не O(2n), а O(n). Представленную выше функцию также можно написать так:

DoStuff (numbers)

{

    sum = 0 , product = 1;

    foreach (num in numbers)

    {

        sum += num;

        product *= num;

    }

    Print "The sum is {sum} and the

           product is {product}";

}

Теперь у нас есть только один цикл, который снова выполняет постоянную работу; просто у него константа больше, чем раньше. Помните, что нас интересует, насколько быстро растет время выполнения задачи при увеличении ее размера, а не точное число операций для данного размера задачи.

Теперь попробуем что-нибудь более сложное. Каково время выполнения этого алгоритма?

CountInventory (stuffToSell, colorList)

{

    totalItems = 0;

    foreach (thing in stuffToSell)

    {

        foreach (color in colorList)

        {

            totalItems += thing[color];

        }

    }

}

Здесь у нас есть два цикла, причем один вложен в другой. Поэтому мы будем умножать их время выполнения, а не складывать. Внешний цикл запускается один раз для каждого элемента каталога, а внутренний — один раз для каждого предоставленного цвета. Для n элементов и m цветов общее время выполнения равно O(nm). Обратите внимание, что это неO(n2); у нас нет оснований полагать, что между n и m существует взаимосвязь.

Рассмотрим еще одну функцию:

doesStartWith47 (numbers)

{

    return (numbers[0] == 47);

}

Эта функция проверяет, равен ли 47 первый элемент целочисленного массива, и возвращает результат. Объем работы, который выполняет функция, не зависит от количества входных данных и поэтому равен O(1)11.

Мы часто пишем программы, которые включают в себя двоичный поиск, следовательно, в нашем анализе будут логарифмы.

Например, рассмотрим следующий код12:

binarySearch (numarray, left, right, x)

{

    if (left > right) { return -1; }

    int mid = 1 + (right - 1)/2;

    if (numarray[mid] == x) { return mid; }

    if (numarray[mid] > x)

        { return binarySearch (numarray, left,

          mid -1, x); }

    return binarySearch (numarray, mid + 1, right, x);

}

Исходя из предположения, что массив отсортирован, мы проверяем, является ли средний элемент массива тем, что мы ищем. Если это так, то возвращаем индекс среднего элемента. Если же нет и средний элемент больше требуемого значения, то мы проделываем то же самое с первой половиной массива, а если больше — то со второй половиной. Для каждого рекурсивного вызова выполняется постоянный объем работы (проверка, что значение left не больше, чем right; это подразумевает, что мы выполнили поиск по всему массиву и искомое значение не было найдено; затем вычисление средней точки и сравнение ее значения с тем, что мы ищем). Мы выполняем O(lg n) вызовов, каждый из которых занимает O(1) времени, поэтому общая сложность двоичного поиска составляет O(lg n).

Углубленные темы Представьте, что у нас есть рекурсивная функция, которая разбивает задачу на две части, размер каждой из них составляет 2/3 от размера оригинала? Формула для вычисления такой рекурсии действительно существует; подробнее о ней и об основной теореме (Master Theorem) вы узнаете в главе 31.

1.8. Насколько сложна задача?

Если есть алгоритм для решения задачи, определить время выполнения этого алгоритма обычно довольно просто. Но что, если у нас еще нет алгоритма, но уже нужно понять, насколько сложно будет решить задачу?

Мы можем это сделать, сравнивая задачу с другими подобными задачами, для которых известно время выполнения. Мы можем разделить задачи на классы — наборы задач, имеющих сходные характеристики. Нас интересуют два основных класса: задачи, которые решаются за полиномиальное время, и задачи, решение которых можно проверить за полиномиальное время. Оба этих класса мы рассмотрим в следующей главе.

2. Структуры данных

2.1. Организация данных

Одно из главных понятий Computer Science — структуры данных. Говоря о времени выполнения алгоритмов, мы предполагаем, что данные хранятся в соответствующей структуре, которая позволяет эффективно их обрабатывать. Какая структура лучше, зависит от типа данных и от того, какой доступ к ним нужен.

• Необходим ли произвольный доступ, или достаточно последовательного?

• Будут ли данные при записи всегда добавляться в конец списка, или нужна возможность вставлять значения в середину?

• Допускаются ли повторяющиеся значения?

• Что важнее: наименьшее возможное время доступа или строгая верхняя граница времени выполнения каждой операции?

Ответы на все эти вопросы определяют то, как должны храниться данные.

2.2. Массивы, очереди и другие способы построиться

Возможно, самая известная структура данных — это массив, набор элементов, проиндексированных ключом. Элементы массива хранятся последовательно, причем ключ имеет форму смещения относительно начальной позиции в памяти, благодаря чему можно вычислить положение любого элемента по его ключу. Именно по­этому индексы массива13 обычно начинаются с нуля; первый элемент массива находится на нулевом расстоянии от начала, следующий — на расстоянии одного элемента от начала и т.д. «На расстоянии одного элемента» может означать один байт, одно слово и т.д., в зависимости от размера данных. Важно, что каждый элемент массива занимает одинаковое количество памяти.

Польза массивов состоит в том, что получение или сохранение любого элемента массива занимает постоянное время, а весь массив занимает O(n) места в памяти14. Если количество элементов заранее известно, то память не расходуется зря; поскольку позиция каждого элемента вычисляется просто по смещению относительно начала, нам не нужно выделять место для указателей. Поскольку элементы массива расположены в смежных областях памяти, перебор значений массива, очевидно, выполняется гораздо быстрее, чем для многих других структур данных из-за меньшего количества неудачных обращений к кэш-памяти15.

Однако требование выделения непрерывного блока памяти может сделать массивы плохим выбором, когда число элементов заранее не известно. С ростом размера массива может понадобиться скопировать его в другое место памяти (при условии, что оно есть). Избежать этой проблемы, предварительно выделив гораздо больше места, чем необходимо, бывает довольно затратно16. Другая проблема — вставка и удаление элементов массива занимает много времени (O(n)), поскольку приходится перемещать все элементы массива.

На практике массивы используются как сами по себе, так и для реализации многих других структур данных, которые накладывают дополнительные ограничения на манипулирование данными. Например, строка может быть реализована в виде массива символов. Очередь — это последовательный список, в котором элементы добавляются только в один конец списка (постановка в очередь), а удаляются из другого (извлечение из очереди); таким образом, очередь может быть реализована как массив, в котором «начало» перемещается вместе с началом очереди при условии, что максимальное количество элементов в очереди никогда не превышает размер массива. Однако очередь неопределенной длины лучше реа­лизовать на основе двусвязного списка (см. раздел 2.3). К другим структурам, реализуемым на основе массивов, относятся списки, стеки и кучи (см. раздел 2.4), очереди с приоритетом (которые часто создаются на основе куч) и хеш-таблицы (см. раздел 2.5).

2.3. Связные списки

Связный список — это структура данных, в которой каждый элемент содержит данные и указатель на следующий элемент списка (а если это двусвязный список, то также ссылку на предыдущий элемент). Указатель на связный список — это просто указатель на первый элемент, или head, списка; поскольку элементы могут размещаться в разных местах выделенной памяти, для поиска указанного элемента необходимо начать с первого элемента и пройтись по всему списку.

Как уже говорилось, многие структуры данных реализованы на основе массивов или связных списков. Во многом связный список является дополнением массива. Если сильная сторона массива — быстрый доступ к любому элементу (по его ключу), то для того, чтобы найти элемент списка, необходимо пройти по всем ссылкам, пока не будет найден нужный элемент, что в худшем случае займет O(n) времени. С другой стороны, массив имеет фиксированный размер, а элементы связного списка могут размещаться в любом месте памяти, и список может произвольно увеличиваться до тех пор, пока не будет исчерпана доступная память. Кроме того, вставка и удаление элементов массива очень затратны, а в связном списке эти операции выполняются за постоянное время, если есть указатель на предыдущий узел (рис. 2.1).

 

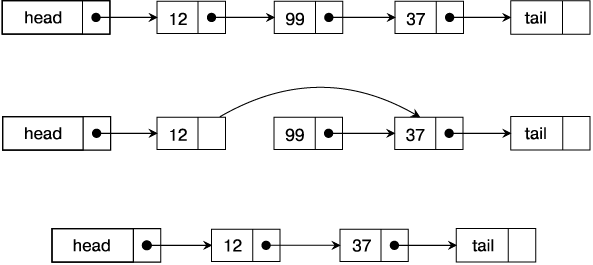
Рис. 2.1. Удаление узла из связного списка

Практическое применение

Представьте себе поезд как пример двусвязного списка: каждый вагон связан с предыдущим и (если он существует) со следу­ющим. В конец поезда можно легко добавить вагоны, но можно вставить вагон и в середину поезда, отсоединив и (пере)присоединив существующие вагоны перед и после добавляемых, или же можно отсоединить вагоны в середине поезда, откатить их на боковой путь и присоединить оставшиеся вагоны. А вот извлечь вагон напрямую не получится; для этого нужно сначала пройти по всему поезду и отделить нужный вагон от предыдущего.

Теоретическая глупость

Как-то мой преподаватель спросил у группы студентов, как определить, содержит ли связный список цикл. Есть несколько классических решений этой задачи. Один из способов — обратить указатели на элементы списка, когда мы их проходим; если цикл существует, то мы в итоге вернемся к началу списка. Другой способ: обходить список с двумя указателями, так что один указатель ссылается на следующий элемент, а второй — через один элемент. Если в списке существует цикл, то в итоге оба указателя когда-нибудь будут ссылаться на один и тот же элемент.

Однако преподаватель добавил условие: он сказал, что ему все равно, сколько времени займет выполнение нашего метода. Я предложил несколько глупый вариант: вычислить объем памяти, необходимый для хранения одного узла списка, и разделить на него общую память системы. Потом вычислить количество посещенных элементов. Если число посещенных элементов превышает количество узлов, которые могут быть сохранены в памяти, список должен содержать цикл.

Преимущество этого решения неоднозначно: оно требует безумно много времени (определяемого размером памяти, а не списка) и является абсолютно правильным.

2.4. Стеки и кучи

2.4.1. Стеки

Стек — это структура данных типа LIFO (Last In, First Out — «последним пришел, первым ушел»), в которой элементы добавляются или удаляются только сверху; это называется «поместить элемент в стек» (push) или «извлечь его из стека» (pop) (рис. 2.2).

Стек можно реализовать на основе массива (отслеживая текущую длину стека) или на основе односвязного списка (отслеживая head списка17). Как и в случае с очередями, реализация на основе массива проще, но она накладывает ограничение на размер стека. Стек, реализованный на основе связного списка, может расти до тех пор, пока хватает памяти.