автордың кітабын онлайн тегін оқу Прикладные структуры данных и алгоритмы. Прокачиваем навыки
Переводчик С. Черников
Джей Венгроу
Прикладные структуры данных и алгоритмы. Прокачиваем навыки . — СПб.: Питер, 2023.
ISBN 978-5-4461-2068-0
© ООО Издательство "Питер", 2023
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.
Отзывы о втором издании
Если вы, как и я, решили заняться кодированием, не имея «традиционного» образования в области информатики, эта книга станет для вас отличным подспорьем. Здесь вы познакомитесь с основами алгоритмов, научитесь использовать и реализовывать распространенные структуры данных. Пособие написано простым языком в легкой и интересной манере! Это отличная книга для тех, кто хочет получить базовые знания в области программирования.
Джон Андерсон, вице-президент по технологическому развитию, Infinity Interactive
Я занимаюсь программированием уже более 30 лет и за это время твердо усвоил, как важно всегда возвращаться к основам. Благодаря книге «Прикладные структуры данных и алгоритмы» я смог удостовериться в предположениях, которые делал в прошлом, и закрепить базовые навыки, которые планирую использовать в будущем. Не стоит покупать эту книгу, чтобы подготовиться к тестовому заданию на собеседовании. Прочтите ее ради развития алгоритмического мышления. Независимо от того, новичок вы в программировании или опытный специалист, вам нужен исчерпывающий набор структур данных и распространенных (и не очень) алгоритмов, которые их дополняют. Ко всему прочему, здесь вы узнаете, как, когда и зачем нужно оптимизировать код, заставите его работать, ускорите и улучшите его, попутно разбираясь с разными тонкостями этой стороны вопроса.
Скотт Хансельман, программист Microsoft, профессор, блогер, автор подкаста
Несмотря на то что я уже пятнадцать лет занимаюсь разработкой программного обеспечения, я многое почерпнул из этого обновленного издания. Хотел бы я прочесть его двадцать лет назад, когда изучал эти концепции в университете. После знакомства с этим пособием я смог по-новому взглянуть на возможности использования хеш-таблиц для улучшения производительности кода. Забудьте все, что вы знали, — это не позволит вам добиться максимальной эффективности!
Найджел Лоури, главный консультант, Lemmata
Во втором издании «Прикладных структур данных и алгоритмов» вы найдете много полезных дополнений к и без того превосходному ресурсу для изучения структур данных и алгоритмов. Объяснение сложных тем вроде динамического программирования простым языком и контрольные вопросы в конце каждой главы делают эту книгу бесценной для всех разработчиков ПО, вне зависимости от наличия у них профильного образования.
Джейсон Пайк, старший инженер-программист, KEYSYS Consulting
Идеальное введение в тему алгоритмов и структур данных для начинающих. Настоятельно рекомендую к прочтению!
Брайан Шо, ведущий программист, Schau Consulting
Предисловие
Структуры данных и алгоритмы — это не просто абстрактные концепции. Освоив их, вы сможете писать эффективный код, благодаря которому программное обеспечение (ПО) работает быстрее и потребляет меньше памяти. Это особенно важно для современных приложений, которые работают на все более мобильных платформах и обрабатывают все больше данных.
Но от большинства ресурсов, посвященных этим темам, мало толку. Как правило, они перегружены специальными терминами, из-за чего тем, кто далек от математики, бывает трудно понять суть. Даже книги, авторы которых обещают «легкое» знакомство с алгоритмами, предполагают наличие у читателя математического образования. Из-за этого многие избегают изучения этих концепций, считая себя недостаточно «умными» для их понимания.
По правде говоря, все, что касается структур данных и алгоритмов, опирается на здравый смысл. Математика — это просто особый язык, и все ее концепции можно объяснить в доступной для любого читателя форме. Чтобы вам было несложно и интересно изучать весь изложенный материал, я использовал только понятную терминологию (и много диаграмм!).
Изучив все приведенные здесь концепции, вы сможете писать качественный, эффективный и быстрый код. Взвесив все плюсы и минусы вариантов кода, вы примете обоснованное решение о том, какой из них лучше всего подходит для конкретной ситуации.
Чтобы сделать все эти концепции максимально доступными и практичными, я привожу в этом пособии идеи, которые вы можете применить уже сегодня. Конечно, по ходу дела вы изучите и кое-какую теорию. Но эта книга посвящена в первую очередь тому, как применять на первый взгляд абстрактные идеи на практике. Если вы хотите писать более качественный код и создавать более быстрое ПО, то обратились по адресу.
Для кого эта книга
Эта книга подойдет для вас, если вы:
• студент-информатик, который нуждается в простом и понятном ресурсе для изучения структур данных и алгоритмов. Эта книга станет хорошим дополнением к любому классическому учебнику, которым вы пользуетесь;
• начинающий разработчик, который знаком с азами программирования, но хочет изучить основы компьютерных наук, чтобы писать более качественный код и расширить свои знания в этой области;
• программист-самоучка, который никогда не изучал информатику формально (или разработчик, который ее изучал, но уже все забыл!), но хочет использовать мощь структур данных и алгоритмов для написания более качественного и масштабируемого кода.
Кем бы вы ни были, я постарался написать книгу так, чтобы она была доступна для понимания людям с любым уровнем подготовки.
Новое во втором издании
Почему второе? С момента публикации первого издания прошли годы, за которые я успел поделиться этим материалом с разными аудиториями. Я немного видоизменил способ подачи информации и нашел дополнительные темы, которые посчитал важными и интересными. Помимо этого, я осознал важность практических упражнений для применения изученных концепций.
Итак, ниже перечислены несколько основных отличий второго издания от первого.
1. Отредактированный материал. Чтобы изложенную в главах информацию было проще понять, я сильно видоизменил текст. В первом издании все термины тоже изложены вполне доступным языком, но я нашел возможность еще сильнее упростить подачу материала.
Я полностью переписал многие разделы исходных глав и добавил ряд совершенно новых. По-моему, этого уже достаточно для публикации нового издания книги.
2. Новые главы и темы. Во второе издание добавлены шесть новых глав, посвященных особенно интересным, на мой взгляд, темам.
В первом издании теория тоже сочеталась с практикой, но в обновленное я добавил еще больше материала, который вы можете сразу же применить. Главы 7 и 20 посвящены только отчетам об ошибках, повседневному кодированию и тому, как знание структур данных и алгоритмов может помочь в написании более эффективного ПО.
В этой книге я постарался максимально доходчиво объяснить тему рекурсии. Я уже посвящал ей одну из глав в прошлом издании, но в это добавил новую — 11-ю, где изложил процесс написания рекурсивного кода, так как знаю, что это может вызвать много сложностей. Я не видел, чтобы этот вопрос рассматривался где-то еще, и считаю такое дополнение уникальным и ценным. Кроме того, я добавил главу 12, где рассказал о динамическом программировании, довольно популярной теме, важной для повышения эффективности рекурсивного кода.
Существующих структур данных довольно много, и бывает трудно выбрать, какие из них добавить в книгу, а какие — нет. Но в последнее время я наблюдаю рост интереса к кучам и префиксным деревьям, которые мне тоже кажутся весьма занимательными. Об этих структурах данных мы поговорим в главах 16 и 17.
3. Упражнения и решения. Теперь в каждой главе вы найдете ряд упражнений для практического закрепления изученных концепций (все подробные решения вы найдете в приложении в конце книги). Благодаря этому улучшению книга превратилась в более полное учебное пособие.
Что вы найдете в этой книге
Как вы уже могли догадаться, бо́льшая часть этой книги посвящена структурам данных и алгоритмам. Пособие состоит из следующих глав.
В главах 1 и 2 мы поговорим о том, что такое структуры данных и алгоритмы, и рассмотрим концепцию временной сложности, которая используется для определения скорости работы алгоритма. По ходу дела мы обсудим массивы, множества и двоичный (бинарный) поиск.
Глава 3 очень важна. В ней я постараюсь максимально доступно объяснить суть нотации «О большое», которая упоминается на протяжении всей книги.
В главах 4, 5 и 6 мы углубимся в эту тему и используем О-нотацию, чтобы заставить код работать быстрее. Попутно я расскажу о разных алгоритмах сортировки, в том числе о сортировке пузырьком, выбором и вставками.
В главе 7 вы примените все полученные ранее знания и оцените эффективность реального фрагмента кода.
В главах 8 и 9 мы обсудим несколько дополнительных структур данных, включая хеш-таблицы, стеки и очереди. Я покажу, как они влияют на скорость работы и простоту кода и как их использовать для решения реальных задач.
Глава 10 посвящена рекурсии — важнейшей концепции в мире информатики. Мы подробно разберем ее и посмотрим, когда она может пригодиться. Глава 11 поможет вам овладеть непростым навыком написания рекурсивного кода.
В главе 12 я покажу, как оптимизировать рекурсивный код и не допустить того, чтобы он вышел из-под контроля. В главе 13 вы узнаете, как использовать рекурсию в качестве основы для сверхбыстрых алгоритмов сортировки и выбора, и усовершенствуете свои навыки разработки алгоритмов.
В главах 14, 15, 16, 17 и 18 мы исследуем структуры данных на основе узлов, включая связный список, двоичное и префиксное дерево, кучу, граф, и узнаем, когда может пригодиться каждая из них.
В главе 19 мы поговорим о пространственной сложности алгоритма, которая имеет большое значение при создании программ для устройств с небольшим объемом дискового пространства или при работе с объемными данными.
В последней главе рассматриваются разные практические приемы оптимизации эффективности кода и предлагаются новые идеи по улучшению кода, который вы пишете каждый день.
Как читать эту книгу
Главы нужно читать по порядку. Есть книги, где некоторые разделы можно пропускать, но эта не относится к их числу: здесь каждая последующая глава основана на информации из предыдущей. Структура книги выстроена так, чтобы вы могли углубляться в материал по мере чтения.
Но во второй половине книги есть главы, которые не вполне отвечают этому принципу. На диаграмме ниже показано, какие из глав взаимосвязаны и должны читаться по порядку.
Например, при желании после чтения главы 10 вы можете перейти сразу к главе 13 (кстати, эта диаграмма основана на структуре данных «дерево», с которой вы познакомитесь в главе 15).
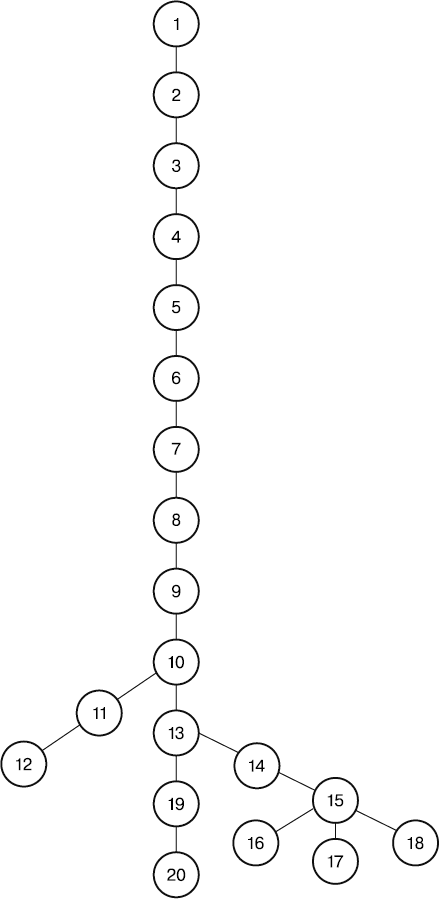
Еще одно важное замечание: чтобы облегчить понимание материала, в книге я не всегда даю всю информацию о каком-то понятии при его первом упоминании. Иногда лучший способ раскрыть суть сложной концепции — сначала объяснить небольшую ее часть и лишь после ее усвоения переходить к следующей. Не воспринимайте первое данное мной определение как общепринятое, пока не закончите чтение раздела по этой теме.
Я пошел на компромисс: чтобы книгу было легче читать, вначале я максимально упрощаю некоторые понятия, углубляясь в них по мере продвижения, вместо того чтобы стремиться к академической точности каждого предложения. Но не беспокойтесь, ближе к концу у вас сформируется четкое представление о пройденном материале.
Примеры кода
Концепции в этой книге не относятся к одному конкретному языку программирования. Поэтому примеры кода, которые вы здесь найдете, написаны на разных языках, в частности Ruby, Python и JavaScript, знакомство с которыми будет весьма кстати.
Разрабатывая примеры, я старался, чтобы все они были понятны даже тому, кто никогда не сталкивался с языком, на котором они написаны. По этой же причине я не использую идиомы, если чувствую, что они могут сбить с толку незнакомого с ними читателя.
Несмотря на то что частое переключение с одного языка программирования на другой может потребовать от читателя некоторых усилий, я считаю, что это позволило сделать книгу независимой от конкретного языка. Опять же, я постарался сделать примеры на всех языках простыми и понятными.
В разделе «Программная реализация» вы найдете несколько длинных фрагментов кода. Я рекомендую вам изучить их, но вам не обязательно понимать каждую строку, чтобы перейти к следующему разделу книги. Если вас утомляет изучение этих объемных фрагментов, просто пропустите их.
Наконец, важно отметить, что не каждый фрагмент кода здесь можно использовать на практике. В первую очередь я старался объяснить конкретные концепции, и, хотя я пытался сделать код полностью рабочим, я вполне мог не учесть некоторые пограничные случаи. У вас есть уйма возможностей для дальнейшей оптимизации приведенного здесь кода — не стесняйтесь!
Интернет-ресурсы
У этой книги есть своя веб-страница (https://pragprog.com/titles/jwdsal2), где вы найдете всю дополнительную информацию. Вы также можете помочь нам, сообщив об ошибках и опечатках, или поделиться предложениями относительно содержания пособия.
Благодарности
Может показаться, что готовая книга — это плод труда одного человека. Но любое издание, в том числе и это, не смогло бы выйти в свет без участия множества людей. Все они поддерживали меня на протяжении процесса ее написания. И я хотел бы лично поблагодарить каждого.
Я хочу сказать спасибо своей замечательной жене Рене за уделенное время и эмоциональную поддержку. За то, что заботилась обо всем, пока я писал, запершись в кабинете, как затворник. Спасибо моим очаровательным детям Туви, Лии, Шайе и Рами за терпение, которое они проявляли, пока я работал над книгой об «алгоритмах». И да — наконец-то все позади.
Спасибо моим родителям, Говарду и Дебби Венгроу, за то, что пробудили во мне интерес к программированию и помогли встать на этот путь. Приглашая репетитора для обучения девятилетнего меня, они и не подозревали, что закладывают фундамент моей будущей карьеры, а теперь еще и этой книги.
Хочу поблагодарить родителей моей жены, Пола и Крейндел Пинкус, за постоянную поддержку, за мудрость и теплоту, которые очень много для меня значат.
Когда я впервые отправил свою рукопись в Pragmatic Bookshelf, я думал, что она и так уже довольно хороша. Но благодаря опыту, конструктивной критике и предложениям замечательных сотрудников издательства книга стала намного лучше. Я хочу поблагодарить своего редактора Брайана Макдональда за то, что он познакомил меня с реальным процессом работы над книгой и поделился идеями, которые сделали лучше каждую главу этого пособия. Я выражаю признательность главному редактору Сюзанне Пфальцер и исполнительному редактору Дэйву Рэнкину. Вы приняли мою рукопись и показали, какой может быть эта книга, превратив ее в ресурс, доступный любому программисту. Спасибо издателям Энди Ханту и Дэйву Томасу за то, что поверили в этот проект и сделали Pragmatic Bookshelf замечательным издательством, с которым хочется сотрудничать.
Хочу поблагодарить чрезвычайно талантливого разработчика ПО и художника Коллин Макгакин за преобразование моих каракулей в красивые цифровые изображения. Это пособие не было бы таким потрясающим без иллюстраций, которые вы создали с присущим вам мастерством и вниманием к деталям.
Мне повезло, что так много экспертов оценили эту книгу. Благодаря их отзывам я смог максимально проработать весь текст, поэтому хотел бы поблагодарить их всех.
Рецензенты первого издания: Алессандро Бахгат, Иво Бальберт, Альберто Боскетти, Хавьер Кольядо, Мохамед Фуад, Дерек Грэхем, Нил Хэйнер, Питер Хэмптон, Род Хилтон, Джефф Холланд, Джессика Янюк, Аарон Калэир, Стефан Кампер, Арун С. Кумар, Шон Линдсей, Найджел Лоури, Джой Маккэффри, Дейвид Морган, Джасдип Наранг, Стивен Орр, Кеннет Парех, Джейсон Пайк, Сэм Роуз, Фрэнк Руис, Брайан Шо, Тибор Симич, Маттео Ваккари, Стивен Вольф и Питер В.А. Вуд.
Рецензенты второго издания: Ринальдо Бонаццо, Майк Браун, Крейг Кастелаз, Джейкоб Че, Зульфикар Дхармаван, Ашиш Диксит, Дэн Дайбас, Эмили Экдал, Дерек Грэхем, Род Хилтон, Джефф Холланд, Грант Казан, Шон Линдсей, Найджел Лоури, Дэри Меркенс, Кевин Митчелл, Нуран Махмуд, Дэвид Морган, Брент Моррис, Эмануэль Ориджи, Джейсон Пайк, Айон Рой, Брайан Шо, Митчелл Фолк и Питер В.А. Вуд.
Помимо рецензентов, я хотел бы поблагодарить и всех читателей бета-версии книги, которые предоставляли отзывы в процессе написания и редактирования ее текста. Ваши предложения, комментарии и вопросы бесценны.
Я хотел бы выразить признательность за оказанную поддержку всем сотрудникам, студентам и выпускникам учебного лагеря по кодированию Actualize, проектом которого изначально и была эта книга. Особую благодарность выражаю Люку Эвансу за то, что он подал мне идею написать ее.
Спасибо вам всем за ваш вклад в реализацию этого проекта.
Обратная связь
Я очень люблю получать обратную связь, поэтому предлагаю вам найти меня в LinkedIn: https://www.linkedin.com/in/jaywengrow. Я с радостью приму ваш запрос на подключение — просто напишите, что вы читатель этой книги. С нетерпением жду ваших сообщений!
Джей Венгроу, jay@actualize.co. Май 2020 года
От издательства
Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).
Мы будем рады узнать ваше мнение!
На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах.
Глава 1. О важности структур данных
Когда человек только учится программировать, его основная цель — обеспечение правильной работы кода, которая оценивается с помощью одного простого критерия — фактической работоспособности.
Но с опытом к разработчикам ПО приходит понимание дополнительных нюансов, влияющих на качество кода. Они узнают, что два разных фрагмента кода могут решать одну задачу, но при этом один из них может быть лучше другого.
Есть много показателей качества кода, но один из важнейших — его сопровождаемость, которая охватывает такие аспекты, как читабельность, структурированность и модульность.
Еще одна отличительная черта качественного кода — его эффективность. Например, у вас может быть два фрагмента кода, решающих одну задачу, но один из них может работать быстрее, чем другой.
Взгляните на следующие две функции, каждая из которых выводит на экран все четные числа от 2 до 100:
def print_numbers_version_one():
number = 2
while number <= 100:
# Если число четное, вывести его на экран:
if number % 2 == 0:
print(number)
number += 1
def print_numbers_version_two():
number = 2
while number <= 100:
print(number)
# Увеличить число на 2, чтобы получить следующее четное число:
number += 2
Как вы думаете, какая из функций работает быстрее?
Если вы выбрали версию 2, то вы правы. Дело в том, что в первой версии цикл выполняется 100 раз, а во второй — только 50. Получается, что версия 1 требует вдвое больше шагов, чем 2.
В этой книге мы будем говорить о написании эффективного кода. Умение писать код, который работает быстро, — один из важнейших навыков хорошего разработчика ПО.
Чтобы развить это умение, сначала нужно разобраться в том, что такое структуры данных и как они влияют на скорость работы создаваемого кода. Итак, начнем.
Структуры данных
Поговорим о данных.
Данные — это обширный термин, охватывающий все типы информации, вплоть до простейших чисел и строк. В классической программе «Hello World!» строка "Hello World!" будет фрагментом данных. По сути, даже самые сложные фрагменты данных обычно состоят из чисел и строк.
Структура данных — это то, как они организованы. Позже вы узнаете, что одни и те же данные могут быть организованы по-разному.
Рассмотрим следующий фрагмент кода:
x = "Hello! "
y = "How are you "
z = "today?"
print x + y + z
Эта простая программа работает с тремя фрагментами данных и выводит три строки для составления одного связного сообщения. Если бы нам потребовалось описать структуру данных в этой программе, мы бы сказали, что у нас есть три независимые строки, каждая из которых содержится в одной переменной.
Но эти же данные могут храниться и в массиве:
array = ["Hello! ", "How are you ", "today?"]
print array[0] + array[1] + array[2]
В этой книге вы узнаете, что организация данных важна не просто сама по себе, — она может значительно повлиять на скорость выполнения вашего кода. В зависимости от выбранного способа организации данных ваша программа может работать быстрее или медленнее, причем разница может быть в несколько порядков. А если вы создаете программу, которой предстоит обрабатывать большие объемы данных, или веб-приложение, используемое одновременно тысячами людей, то от выбранных структур данных может зависеть, будет ваше ПО нормально работать или сбоить из-за чрезмерной нагрузки.
Когда вы разберетесь с влиянием структур данных на производительность программного обеспечения, у вас появятся ключи к написанию быстрого и качественного кода, а вы сами перейдете на совершенно новый уровень как специалист.
В этой главе мы проанализируем две структуры данных: массивы и множества. Несмотря на их похожесть, они по-разному влияют на производительность программы. И проанализировать это влияние нам помогут описанные далее инструменты.
Массив: базовая структура данных
Массив — это одна из простейших структур данных в информатике. Надеюсь, вы уже работали с массивами и знаете, что это — списки элементов. Массив — универсальный инструмент, который может быть полезен во многих ситуациях. Рассмотрим небольшой пример.
В исходном коде приложения, позволяющего пользователям создавать и использовать списки покупок, вам может встретиться такой фрагмент:
array = ["apples", "bananas", "cucumbers", "dates", "elderberries"]
Этот массив включает пять строк, каждая из которых содержит наименование продукта, который я могу купить в супермаркете (вы просто обязаны попробовать ягоды бузины (elderberries)).
При работе с массивами применяется особый технический жаргон.
Под размером массива понимается количество содержащихся в нем элементов. В нашем примере размер массива равен 5, так как он содержит пять значений.
Индекс массива — это число, определяющее позицию элемента в массиве.
В большинстве языков программирования нумерация индексов начинается с 0. Итак, в нашем примере индекс элемента "apples" — 0, а "elderberries" — 4:

Операции над структурами данных
Чтобы оценить производительность структуры данных, например массива, нужно проанализировать способы взаимодействия кода с ней.
Есть четыре основных способа использования структур данных, которые мы называем операциями:
• Чтение — получение элемента из определенного места структуры данных. В случае с массивом это означает поиск значения с определенным индексом. Например, поиск названия продукта с индексом 2 — это чтение массива.
• Поиск — нахождение определенного значения в структуре данных. В случае с массивом это означает выяснение того, есть ли конкретное значение в массиве, и если да, то какой у него индекс. Пример: поиск элемента "dates" в нашем списке продуктов.
• Вставка — добавление нового значения в структуру данных, в нашем случае — в массив. Если бы мы решили добавить инжир ("figs") в список покупок, это было бы примером вставки нового значения в массив.
• Удаление — исключение значения из структуры данных. В случае с массивом это означает удаление из него одного из элементов. Например, если мы решим исключить бананы ("bananas") из списка покупок, это значение будет удалено из массива.
В этой главе мы попробуем разобраться в том, насколько быстро выполняется каждая из этих операций.
Измерение скорости
Итак, как же измерить скорость выполнения операции?
Если вы вынесете из этой книги только один урок, пусть он будет таким: при измерении скорости выполнения операции мы учитываем не количество времени, а число шагов, которое для этого требуется.
Мы уже сталкивались с этим в примере функции, выводящей на экран четные числа от 2 до 100. Вторая версия работала быстрее, потому что требовала вдвое меньше шагов, чем первая.
Почему мы измеряем скорость выполнения кода числом шагов?
Дело в том, что мы никогда не можем однозначно сказать, что какая-то операция занимает, скажем, пять секунд. Выполнение одного и того же фрагмента кода может занять пять секунд на более новом компьютере и гораздо больше времени на старом оборудовании. А, допустим, на суперкомпьютерах будущего этот же код сможет работать еще быстрее. Измерять скорость операции в секундах или минутах ненадежно, поскольку длительность зависит от оборудования, на котором она выполняется.
Но мы можем измерить скорость операции в количестве вычислительных шагов, необходимых для ее выполнения. Если операция A требует 5 шагов, а Б — 500, мы можем предположить, что первая всегда будет выполняться быстрее, чем вторая, на любых компьютерах. Поэтому определение числа шагов — ключевой этап анализа скорости выполнения операции.
Измерение скорости выполнения операции по-другому еще называют измерением ее временной сложности. В книге я буду использовать термины скорость, временная сложность, эффективность, производительность и время выполнения как синонимы. Все они относятся к количеству шагов, необходимых для выполнения операции.
Теперь рассмотрим четыре операции над массивом и определим, сколько шагов нужно для выполнения каждой из них.
Чтение
Начнем с чтения — с определения значения элемента массива с конкретным индексом.
Компьютер может выполнить эту операцию всего за один шаг, потому что может обратиться к любому элементу массива с необходимым индексом и считать его значение. Если бы мы решили найти элемент с индексом 2 в массиве ["apples", "bananas", "cucumbers", "dates", "elderberries"], то компьютер перешел бы прямо к нему и сообщил, что в этой позиции находится значение "cucumbers".
Как компьютеру удается отыскать нужный элемент всего за шаг? Давайте разберемся.
Память компьютера похожа на гигантский набор ячеек. Ниже показана сетка, где некоторые ячейки пустые, а некоторые содержат биты данных.

Хотя это очень упрощенная модель устройства памяти компьютера, она хорошо передает основную идею.
При объявлении массива программа выделяет для него непрерывный блок памяти из пустых ячеек. Так, если вы создаете массив для хранения пяти элементов, ваш компьютер находит группу из пяти пустых ячеек подряд и выделяет ее для использования в качестве массива:

У каждой ячейки есть определенный адрес. От почтового, где содержатся названия улиц и городов, его отличает лишь то, что он представлен числом. Значение адреса каждой последующей ячейки памяти на одну единицу превышает значение предыдущей:

На следующей схеме показан массив из нашего примера со списком покупок с индексами и адресами ячеек памяти.

Когда компьютер считывает значение по определенному индексу массива, он может сразу обратиться к нужному элементу в силу следующих факторов.
1. Компьютер может перейти к любому адресу памяти за один шаг. Например, если вы попросите его проверить значение в ячейке памяти с адресом 1063, он сможет получить к нему доступ без выполнения поиска. Точно так же, если я попрошу вас поднять мизинец правой руки, вам не придется перебирать все пальцы, чтобы определить нужный.
2. Выделяя блок памяти под массив, компьютер отмечает, с какого адреса он начинается. Так, если мы попросим компьютер найти первый элемент массива, он мгновенно обратится к соответствующему адресу памяти.
Теперь мы знаем, как именно компьютер может найти первое значение массива за один шаг. Впрочем, он может найти значение с любым индексом, выполнив простое сложение. Если бы мы попросили компьютер найти значение массива с индексом 3, он просто взял бы адрес памяти, соответствующий индексу 0, и прибавил к нему 3 (в конце концов, у адресов памяти последовательная нумерация).
Применим это к нашему массиву списка продуктов. Он начинается с адреса памяти 1010. Итак, если бы мы велели компьютеру считать значение элемента с индексом 3, он выполнил бы следующую логическую операцию.
1. Массив начинается с индекса 0, который соответствует адресу памяти 1010.
2. Индекс 3 находится ровно через три ячейки после индекса 0.
3. Логично предположить, что элемент с индексом 3 находится в ячейке памяти с адресом 1013, поскольку 1010 + 3 = 1013.
Как только компьютер выяснит, что индекс 3 соответствует адресу памяти 1013, он обратится к соответствующей ячейке и узнает, что в ней содержится значение "dates".
Чтение из массива — довольно эффективная операция, ведь компьютер может обратиться к любому адресу памяти за один шаг. Хотя я разбил мыслительный процесс компьютера на три этапа, сейчас нас интересует его обращение к адресу памяти (в следующих главах мы подробнее поговорим о том, на каких шагах стоит сосредоточиться).
Конечно же, операция, которая выполняется всего за шаг, самая быстрая. Выходит, что массив — это не только основная, но и очень мощная структура данных, потому что мы можем считывать значения в нем с огромной скоростью.
А что, если бы вместо выяснения значения в позиции с индексом 3 мы попросили бы компьютер узнать индекс элемента "dates"? В этом случае речь пойдет об операции поиска, которую мы рассмотрим далее.
Поиск
Как я уже говорил, при поиске в массиве компьютер проверяет, есть ли в нем конкретное значение, и если да, то в позиции с каким индексом.
В каком-то смысле эта операция обратна чтению, при котором мы предоставляем компьютеру индекс и просим возвратить соответствующее ему значение. При поиске же мы даем компьютеру значение и просим возвратить его индекс.
Эти две операции кажутся похожими, но в плане эффективности они сильно разнятся. Чтение выполняется быстро, так как компьютер может сразу обратиться к любому индексу и выяснить значение соответствующего элемента. Поиск требует времени, ведь у компьютера нет возможности сразу перейти к нужному значению.
Важный факт: компьютер может мгновенно получить доступ к любому адресу памяти, но не имеет ни малейшего представления о том, какие значения содержатся в каждой из ячеек.
Вернемся к нашему примеру со списком продуктов. Компьютер не может сразу узнать содержимое каждой ячейки памяти. Для него массив выглядит примерно так:

Чтобы найти нужное значение в массиве, он вынужден проверять все ячейки по очереди.
На следующих изображениях показан процесс, который компьютер будет использовать для поиска значения "dates" в нашем массиве.
Сначала компьютер проверяет элемент с индексом 0:

Поскольку его значение "apples", а не "dates", компьютер переходит к следующему индексу:

В позиции с индексом 1 тоже нет искомого значения "dates", поэтому компьютер переходит к индексу 2:

И снова нам не повезло, и компьютер переходит к следующей ячейке:

Ура! Мы нашли нужное значение и теперь знаем, что его индекс — 3. Компьютеру больше не нужно переходить к следующей ячейке массива, так как он уже нашел то, что мы просили.
В этом примере поиск был выполнен за четыре шага, поскольку компьютеру пришлось проверить четыре ячейки, чтобы обнаружить значение "dates".
В главе 2 вы узнаете о другом способе поиска в массиве, но эта базовая операция поиска, при которой компьютер проверяет каждую ячейку по одной, называется линейным поиском.
Какое же максимальное количество шагов может выполнить компьютер, чтобы провести линейный поиск в массиве?
Если искомое значение окажется в последней ячейке (например, "elderberries"), компьютеру придется перебрать все элементы массива, чтобы его отыскать. Кроме того, если этого значения и вовсе нет в массиве, все равно придется проверить каждую ячейку, чтобы в этом убедиться.
Итак, получается, что при линейном поиске в массиве из пяти элементов максимальное число шагов равно пяти, а в массиве из 500 элементов — 500.
Проще говоря, линейный поиск в массиве из N элементов потребует максимум N шагов. Здесь N — переменная, которую можно заменить любым числом.
В любом случае понятно, что поиск менее эффективен, чем чтение, поскольку может требовать множества шагов, тогда как чтение всегда предполагает только один, вне зависимости от размера массива.
Теперь разберем операцию вставки.
Вставка
Эффективность операции вставки нового фрагмента данных в массив зависит от того, куда именно вы его вставляете.
Допустим, мы хотим добавить значение "figs" в конец нашего списка покупок. На такую вставку у нас уйдет один шаг.
Это обусловлено еще одним фактором: при выделении блока памяти под массив компьютер всегда отслеживает его размер.
Если мы прибавим к этому тот факт, что компьютер знает, с какого адреса памяти массив начинается, то вычислить местонахождение его последнего элемента не составит труда: если массив начинается с адреса памяти 1010, а его размер 5, то его последний элемент хранится в ячейке 1014. Выходит, вставка элемента после него означала бы его добавление к следующему адресу памяти, равному 1015.
После вычисления адреса ячейки, в которую нужно поместить новое значение, компьютер сможет сделать это за один шаг.
Так выглядит вставка значения "figs" в конец массива:

Но есть одна проблема. Поскольку изначально компьютер выделил под массив только пять ячеек памяти, при добавлении шестого элемента ему придется найти дополнительные ячейки. Как правило, это делается автоматически, но каждый язык программирования обрабатывает этот процесс по-своему, поэтому я не буду вдаваться в детали.
Мы рассмотрели процесс вставки нового элемента в конец массива, но вставка в начало или в середину — это совсем другая история. В этих случаях нам приходится сдвигать фрагменты данных, чтобы освободить место для нового значения, а это требует дополнительных шагов.
Допустим, мы хотим добавить значение "figs" в позицию массива с индексом 2:

Чтобы освободить место для нового значения, нам нужно сдвинуть "cucumbers", "dates" и "elderberries" вправо. На это у нас уйдет несколько шагов, так как нам нужно сначала сдвинуть значение "elderberries" на одну позицию вправо, чтобы освободить место для перемещения "dates", а затем сдвинуть значение "dates", чтобы освободить место для "cucumbers".
Рассмотрим этот процесс подробнее.
Шаг 1: сдвигаем вправо значение "elderberries":

Шаг 2: сдвигаем вправо значение "dates":

Шаг 3: сдвигаем вправо значение "cucumbers":
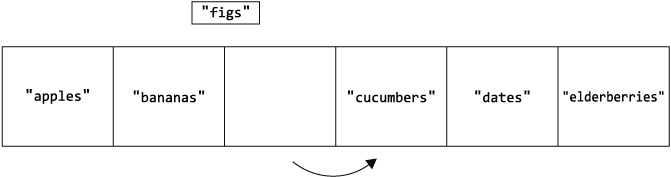
Шаг 4: вставляем значение "figs" в позицию с индексом 2:

Обратите внимание, что в этом примере на операцию вставки ушло четыре шага: три из них заняло передвижение элементов вправо и только один ушел на фактическую вставку нового значения.
Худший сценарий при вставке в массив — тот, на который уйдет больше всего шагов, — вставка значения в начало, ведь нам придется сдвинуть вправо все остальные значения.
Проще говоря, в худшем случае вставка значения в массив из N элементов может потребовать N + 1 шагов, ведь перед вставкой нового значения нам нужно переместить все N элементов.
Теперь рассмотрим последнюю операцию над массивом — удаление элемента.
Удаление
Удаление элемента массива сводится к исключению значения в позиции с определенным индексом.
Давайте удалим из нашего массива значение с индексом 2 — "cucumbers".
Шаг 1: удаляем значение "cucumbers" из массива:

Хотя на удаление значения ушел всего шаг, у нас возникла пустая ячейка в середине массива. Сложно работать с массивом, когда в нем есть пробелы, поэтому для решения этой проблемы нам нужно сдвинуть влево значения "dates" и "elderberries". Это означает, что процесс удаления требует дополнительных шагов.
Шаг 2: сдвигаем влево значение "dates":

Шаг 3: сдвигаем влево значение "elderberries":

Итак, на операцию удаления у нас ушло в общей сложности три шага: первый сводится к фактическому удалению значения, а два других — к сдвигу остальных значений для избавления от пробела.
Как и в случае вставки, худший сценарий при удалении — избавление от первого элемента массива, потому что для избавления от пробела в позиции с индексом 0 нам пришлось бы сдвинуть влево все оставшиеся элементы.
В случае с массивом из пяти элементов удаление первого потребовало бы одного шага, а сдвиг четырех оставшихся — четырех. В случае с массивом из 500 элементов удаление первого потребовало бы одного шага, а сдвиг оставшихся — 499. Следовательно, операция удаления значения из массива, состоящего из N элементов, потребует максимум N шагов.
Поздравляю! Вы проанализировали временну́ю сложность первой структуры данных. Теперь пришло время узнать о том, что у разных структур данных разная эффективность. Это важный аспект, так как выбор структуры данных для использования в коде может сильно повлиять на производительность вашего ПО.
Следующая структура данных — множество — на первый взгляд очень похожа на массив. Но позже вы увидите, что эффективность операций над массивами и множествами разная.
Множества: как одно правило может повлиять на эффективность
Теперь поговорим о множестве. Множество — это структура данных без повторяющихся значений.
Есть разные типы множеств, но мы будем говорить о множестве на базе массива. Это, как и массив, простой список значений. Единственная разница между ним и классическим массивом в том, что множество не допускает вставку повторяющихся значений.
Например, если вы попытаетесь добавить еще одно значение "b" в множество ["a", "b", "c"], компьютер просто не позволит этого сделать — ведь "b" уже есть в этом множестве.
Множества полезны, когда вам нужно гарантировать отсутствие дубликатов.
Например, если вы создаете телефонный онлайн-справочник, вам не нужно, чтобы один и тот же номер встречался в нем более одного раза. На самом деле, я сам столкнулся с такой проблемой: в местной телефонной книге наш домашний номер дублируется — по какой-то ошибке он указан не только рядом с моей фамилией, но и рядом с фамилией Зиркинд (да, это реальная история). Вы даже не представляете, как мне надоело получать телефонные звонки и сообщения от людей, пытающихся дозвониться до Зиркиндов. Я уверен, что и Зиркинды недоумевают, почему им никто не звонит. А когда я звоню Зиркиндам, чтобы сообщить об ошибке, трубку берет моя жена, потому что я набираю свой номер (ладно, последнюю часть я придумал). Если бы только в этой программе использовалось множество…
В любом случае, множество на базе массива — это массив с одним дополнительным ограничением: запретом дубликатов. Хотя этот запрет полезен, он влияет на эффективность одной из четырех основных операций.
Рассмотрим проведение четырех основных операций на базе массива.
Чтение из множества выполняется точно так же, как и из массива — чтобы выяснить значение в позиции с определенным индексом, компьютеру нужен всего один шаг. Как вы уже знаете, это связано с тем, что компьютер может перейти к любому индексу множества, потому что способен с легкостью вычислить соответствующий адрес памяти и обратиться к нему.
Поиск в множестве тоже ничем не отличается от поиска в массиве и требует до N шагов. То же самое касается удаления элемента из множества: чтобы удалить значение и сдвинуть данные влево, нужно до N шагов.
Но, когда дело доходит до вставки, между массивами и множествами появляется различие. Сначала рассмотрим процесс вставки значения в конец множества (лучший сценарий для массива). Как мы уже убедились, компьютер может вставить значение в конец массива за один шаг.
В случае с множеством компьютеру сначала нужно убедиться, что вставляемого значения в нем еще нет, потому что множества используются именно для предотвращения вставки дубликатов.
Как же удостовериться в том, что множество еще не содержит данные, которые мы пытаемся в него добавить? Как вы помните, компьютер не знает, какие значения содержатся в ячейках массива или множества, поэтому ему сначала нужно выполнить поиск и убедиться, что значения, которое мы хотим вставить, нет. Только тогда компьютер разрешит вставку.
Итак, в случае с множеством каждая операция вставки требует предварительного выполнения поиска.
Рассмотрим этот процесс на примере. Представьте, что наш прошлый список продуктов сохранен в виде множества. Это было бы верным решением, ведь мы не хотим дважды покупать один и тот же продукт. Если мы захотим вставить в множество ["apples", "bananas", "cucumbers", "dates", "elderberries"] значение "figs", компьютеру придется выполнить следующие шаги, начиная с поиска вставляемого значения.
Шаг 1: проверка позиции с индексом 0 на предмет наличия значения "figs":

Его там нет, но оно может быть где-то еще. Нужно убедиться, что в этом множестве нет значения "figs", прежде чем мы сможем его вставить.
Шаг 2: проверка позиции с индексом 1:

Шаг 3: проверка позиции с индексом 2:
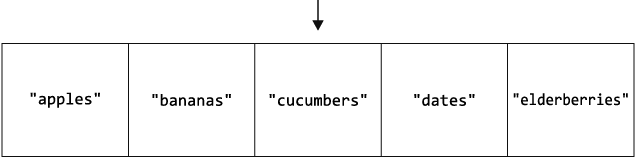
Шаг 4: проверка позиции с индексом 3:

Шаг 5: проверка позиции с индексом 4:

После проверки всего множества мы можем с уверенностью сказать, что в нем нет значения "figs". Теперь мы можем выполнить завершающий шаг операции вставки:
Шаг 6: вставка значения "figs" в конец множества:

Вставка значения в конец множества — это лучший сценарий. Но нам все же пришлось выполнить шесть шагов для множества, изначально содержащего пять элементов, проверив их все перед выполнением вставки.
Иначе говоря, вставка значения в конец множества из N элементов может потребовать до N + 1 шагов: N шагов для поиска, чтобы убедиться в отсутствии вставляемого значения, и один для фактической вставки. Сравните это с обычным массивом, где на вставку значения уходит один шаг.
В худшем случае при вставке значения в начало множества компьютеру придется проверить N ячеек, чтобы убедиться, что множество еще не содержит вставляемого значения, выполнить N шагов, чтобы сдвинуть все значения вправо, и еще один для вставки нового значения. Итого: 2N + 1 шагов. Сравните это со вставкой значения в начало обычного массива, которая требует всего N + 1 шагов.
Означает ли это, что использования множеств нужно избегать лишь потому, что вставка значений в них выполняется медленнее, чем в обычные массивы? Ни в коем случае. Множества очень полезны, когда нужно обеспечить отсутствие дубликатов (надеюсь, однажды ошибка в моей телефонной книге будет исправлена). Но если такой необходимости нет, лучше выбрать массив, поскольку операция вставки для него будет гораздо эффективнее. Важно проанализировать потребности своего приложения и выбрать подходящую для него структуру данных.
Выводы
Подсчет количества шагов для выполнения операций лежит в основе анализа производительности структур данных. От выбора подходящей структуры зависит способность программы справляться с большой нагрузкой. В этой главе вы научились проводить такой анализ для сравнения массива и множества.
Теперь, когда вы познакомились с концепцией временной сложности структур данных, мы можем применить этот анализ для сравнения разных алгоритмов (даже в рамках одной структуры данных), чтобы обеспечить максимальную скорость и производительность кода. Об этом мы и поговорим в следующей главе.
Упражнения
Выполните следующие упражнения, чтобы закрепить знания, полученные из этой главы. Решения вы найдете в приложении в разделе «Глава 1».
1. Для массива из 100 элементов укажите число шагов для выполнения следующих операций:
а) чтение;
б) поиск значения, которого нет в массиве;
в) вставка значения в начало массива;
г) вставка значения в конец массива;
д) удаление первого значения массива;
е) удаление последнего значения массива.
2. Для множества на базе массива из 100 элементов укажите число шагов для выполнения следующих операций:
а) чтение;
б) поиск значения, которого нет в множестве;
в) вставка нового значения в начало множества;
г) вставка нового значения в конец множества;
д) удаление первого значения множества;
е) удаление последнего значения множества.
3. Обычно операция поиска в массиве направлена на нахождение первого экземпляра заданного значения, но иногда нужно найти каждый экземпляр этого значения. Допустим, мы хотим подсчитать, сколько раз в массиве встречается значение "apple". Сколько шагов нам нужно, чтобы найти все его экземпляры? Дайте ответ с точки зрения N.
Глава 2. О важности алгоритмов
Мы уже рассмотрели две структуры данных и увидели, как выбор подходящей может повлиять на производительность кода. Даже такие похожие на первый взгляд структуры данных, как массив и множество, могут обладать разной эффективностью.
В этой главе вы узнаете, что помимо структуры данных на эффективность кода может повлиять и выбор алгоритма.
Вам может показаться, что здесь скрывается какая-то сложная концепция, но это вовсе не так. Алгоритм — это просто набор инструкций для выполнения конкретной задачи.
Даже простой процесс вроде приготовления завтрака — это уже алгоритм, поскольку он подразумевает выполнение определенного набора шагов для решения поставленной задачи. Алгоритм приготовления завтрака (по крайней мере, в моем случае) состоит из четырех шагов.
1. Возьмите тарелку.
2. Насыпьте в тарелку хлопья.
3. Налейте в тарелку молоко.
4. Опустите в тарелку ложку.
Если мы будем четко следовать этой инструкции, то сможем насладиться завтраком.
В случае с вычислениями под алгоритмом понимается набор инструкций, данных компьютеру для выполнения конкретной задачи. Так, когда мы пишем какой-либо код, мы создаем алгоритмы — наборы инструкций, которые должен выполнять компьютер.
Мы можем описывать алгоритмы простым языком, детально излагая инструкции, которые планируем дать компьютеру. Для описания принципа работы разных алгоритмов в книге я буду использовать как обычный язык, так и код.
Иногда для выполнения одной задачи можно использовать два разных алгоритма. Мы уже сталкивались с этим в начале первой главы, когда знакомились с двумя разными способами вывода четных чисел на экран. В том случае один алгоритм предполагал выполнение в два раза большего числа шагов, чем другой.
В этой главе мы познакомимся еще с двумя алгоритмами, решающими одну задачу. Только в этом случае один алгоритм будет на несколько порядков быстрее другого.
Но перед этим нам нужно рассмотреть новую структуру данных.
Упорядоченные массивы
Упорядоченный массив почти идентичен «классическому» из прошлой главы. Единственное отличие в том, что упорядоченные массивы требуют, чтобы значения всегда располагались — как вы уже догадались — по порядку. То есть новое значение нужно вставить так, чтобы в итоге все значения в массиве оставались отсортированными.
Для примера возьмем массив [3, 17, 80, 202]:

Допустим, мы хотим вставить в него число 75. Если бы этот массив был классическим, мы могли бы добавить это значение в конец:

Как мы видели в главе 1, компьютер может сделать это за один шаг.
Но в случае с упорядоченным массивом нам придется вставить число 75 в определенную ячейку, чтобы значения располагались в порядке возрастания:

Но легче сказать, чем сделать. Компьютер не может просто вставить значение 75 в нужное место за один шаг, потому что сначала он должен найти подходящую позицию, а затем сдвинуть другие значения, чтобы освободить место. Рассмотрим этот процесс подробнее.
Начнем с того же упорядоченного массива.

Шаг 1: проверяем значение с индексом 0, чтобы определить, где должно располагаться значение, которое мы хотим вставить (75): слева или справа от него:

Поскольку 75 больше 3, мы знаем, что новое значение должно быть вставлено где-то справа от него. Но мы еще не знаем, в какую именно ячейку, поэтому нам нужно проверить следующее значение.
Мы назовем этот шаг сравнением, ведь мы сравниваем вставляемое значение с числом, присутствующим в упорядоченном массиве.
Шаг 2: проверяем значение в следующей ячейке:

Значение 75 больше 17, поэтому нам нужно двигаться дальше.
Шаг 3: проверяем значение в следующей ячейке:

Значение 80 больше 75, поэтому мы приходим к выводу, что значение 75 нужно вставить слева от 80, чтобы сохранить порядок элементов массива. Чтобы освободить место для вставки значения 75, нам нужно сдвинуть остальные данные.
Шаг 4: сдвигаем последнее значение вправо:

Шаг 5: сдвигаем предпоследнее значение вправо:

Шаг 6: помещаем значение 75 в нужную ячейку:

Как видите, перед помещением значения в упорядоченный массив всегда нужно проводить поиск, чтобы определить правильное место вставки. Это одно из различий в производительности между классическим массивом и упорядоченным.
В этом примере мы видим, что изначально в массиве было четыре элемента, а на вставку ушло шесть шагов. Так, в случае с упорядоченным массивом из N элементов количество шагов для вставки значения равно N + 2.
Интересно, что это количество шагов остается одинаковым вне зависимости от того, в какую именно позицию массива помещается новое значение. При вставке значения в начало мы выполняем меньше сравнений и больше сдвигов, а ближе к концу — больше сравнений, но меньше сдвигов. Меньше всего шагов нужно для вставки нового значения в самый конец, так как эта операция не подразумевает никаких сдвигов. В этом случае мы выполняем N шагов для сравнения нового значения со всеми существующими и один для самой вставки, что в общей сложности дает N + 1 шагов.
Хотя упорядоченный массив проигрывает классическому в эффективности, если речь идет о вставке, он многократно превосходит его, когда дело доходит до поиска.
Поиск в упорядоченном массиве
В прошлой главе я описал процесс поиска определенного значения в классическом массиве: мы проверяем каждую ячейку по одной — слева направо, — пока не найдем искомое значение. Там же я отметил, что этот процесс называется линейным поиском. Посмотрим, чем отличается линейный поиск при работе с классическим и упорядоченным массивами.
Допустим, у нас есть обычный массив [17, 3, 75, 202, 80]. Если бы мы искали значение 22, которого здесь нет, нам пришлось бы проверить каждый элемент, потому что оно может быть где угодно. Учитывая это, мы можем остановить поиск до достижения конца массива, только если нам удастся найти нужное значение до этого момента.
Но в случае с упорядоченным массивом мы можем остановить поиск раньше, даже если искомого значения в массиве нет. Допустим, мы ищем число 22 в упорядоченном массиве [3, 17, 75, 80, 202]. Мы можем остановить поиск, как только дойдем до 75, поскольку 22 никак не может быть справа от него.
Вот так выглядит реализация линейного поиска в упорядоченном массиве на языке Ruby:
def linear_search(array, search_value)
# Перебираем все элементы массива:
array.each_with_index do |element, index|
# Если находим искомое значение, возвращаем его индекс:
if element == search_value
return index
# Если мы обнаружили элемент, значение которого превышает искомое,
# можем выйти из цикла раньше:
elsif element > search_value
break
end
end
# Если искомое значение в массиве не обнаружено, возвращаем nil:
return nil
end
Этот метод принимает два аргумента: array — упорядоченный массив, где мы осуществляем поиск, и search_value — искомое значение.
Вот как можно использовать эту функцию для поиска значения 22 в массиве из нашего примера:
p linear_search([3, 17, 75, 80, 202], 22)
Как видите, метод linear_search перебирает все элементы массива в поисках значения search_value. Процесс останавливается, как только значение обрабатываемого элемента превышает search_value, поскольку мы знаем, что после этого нужного значения в массиве точно не будет.
Учитывая все это, мы можем прийти к выводу, что в определенных ситуациях линейный поиск в упорядоченном массиве может занять меньше шагов, чем в классическом. При этом, если искомое значение превышает значения остальных элементов массива или вообще отсутствует, нам все равно придется проверить каждую ячейку.
Итак, на первый взгляд, стандартные и упорядоченные массивы не сильно различаются в плане эффективности, по крайней мере, в худших сценариях. Для обоих типов, содержащих N элементов, на линейный поиск может уйти до N шагов.
Но далее мы познакомимся с мощным алгоритмом, многократно превосходящим линейный поиск.
До сих пор мы думали, что единственный способ нахождения значения в упорядоченном массиве — линейный поиск. Но это всего лишь один из возможных алгоритмов поиска значения, а не единственный.
Большое преимущество упорядоченного массива по сравнению с классическим в том, что первый позволяет использовать алгоритм бинарного (двоичного) поиска, который работает гораздо быстрее линейного.
Бинарный поиск
Вы наверняка в детстве играли в такую игру: один загадывает число от 1 до 100, а другой пытается его угадать. Каждый раз, когда угадывающий называет число, ему сообщается, больше оно, чем загаданное, или нет.
Принцип этой игры понятен. Скорее всего, вы бы не начали с единицы, а вместо этого первым делом назвали бы число, которое находится ровно посередине. Почему? Потому что, выбрав 50, вне зависимости от полученной подсказки вы сразу исключаете половину возможных чисел!
Если вы называете 50, а вам говорят, что загаданное число больше, вы выбираете 75, исключая половину оставшихся чисел. Если затем вам скажут, что загаданное число меньше 75, вы выберете 62 или 63 и будете продолжать выбирать среднее значение, каждый раз исключая половину оставшихся чисел.
Представьте процесс угадывания числа от 1 до 10. Именно так выглядит принцип работы двоичного (или бинарного) поиска.

Посмотрим, как осуществляется бинарный поиск в упорядоченном массиве. Итак, у нас есть упорядоченный массив из, скажем, девяти элементов. Компьютер не знает, какое значение в каждой из ячеек, поэтому массив можно изобразить так:

Допустим, мы хотим найти значение 7. Вот как будет работать алгоритм двоичного поиска.
Шаг 1: начинаем поиск со средней ячейки. Мы можем обратиться к ней сразу, поскольку для вычисления ее индекса нам достаточно разделить длину массива на 2. Итак, проверяем значение в этой ячейке:

Обнаруженное значение равно 9, поэтому мы можем предположить, что число 7 находится где-то слева от него. Так мы успешно исключили половину ячеек массива — все ячейки справа от той, что содержит 9 (и ее саму):

Шаг 2: проверяем среднюю из оставшихся ячеек. Таких здесь две, и мы произвольно выбираем левую:

В ней мы видим число 4, поэтому искомое значение 7 должно находиться где-то справа от нее. Мы исключаем ячейку с числом 4 и ту, что слева от нее:

Шаг 3: у нас осталось две ячейки для проверки, и мы произвольно выбираем левую:

Шаг 4: проверяем последнюю ячейку (если это не 7, значит, такого значения в упорядоченном массиве вообще нет).

Мы нашли число 7 за четыре шага. Хотя в этом примере столько же шагов ушло бы и на линейный поиск, чуть позже вы сможете оценить истинную мощь двоичного.
Обратите внимание, что алгоритм двоичного поиска можно применить только к упорядоченному массиву. В классическом массиве значения могут располагаться в любом порядке, так что мы никогда не узнаем, где искать нужное значение — слева или справа от выбранной наугад ячейки. В этом и есть одно из преимуществ упорядоченных массивов: они позволяют осуществить бинарный поиск.
Программная реализация
Вот как выглядит реализация бинарного поиска на языке Ruby:
def binary_search(array, search_value)
# Сначала определяем нижнюю и верхнюю границы диапазона, в котором
# может находиться искомое значение. Изначально нижняя граница - это
# первое значение массива, а верхняя - последнее:
lower_bound = 0
upper_bound = array.length - 1
# Запускаем цикл, где последовательно проверяем средние значения диапазона:
while lower_bound <= upper_bound do
# Находим среднее значение между верхней и нижней границами:
# (нам не нужно беспокоиться о том, что результат будет дробным,
# так как в Ruby результат деления целых чисел всегда
# округляется в меньшую сторону до ближайшего целого числа)
midpoint = (upper_bound + lower_bound) / 2
# Проверяем значение в средней ячейке:
value_at_midpoint = array[midpoint]
# Если это значение совпадает с искомым, поиск завершается.
# Если нет, меняем нижнюю или верхнюю границу в зависимости от того,
# превышает ли искомое значение то, которое мы обнаружили, или нет:
if search_value == value_at_midpoint
return midpoint
elsif search_value < value_at_midpoint
upper_bound = midpoint - 1
elsif search_value > value_at_midpoint
lower_bound = midpoint + 1
end
end
# Если мы сузили границы до такой степени, что между ними не осталось
# ячеек, значит, искомого значения в этом массиве нет:
return nil
end
Разберем этот код. Как и метод linear_search, функция binary_search принимает в качестве аргументов массив array и искомое значение search_value.
Вот пример вызова этого метода:
p binary_search([3, 17, 75, 80, 202], 22)
Сначала он задает диапазон индексов ячеек, в которых может быть обнаружено значение search_value:
lower_bound = 0
upper_bound = array.length - 1
Поскольку в самом начале искомое значение search_value может быть обнаружено в любом месте массива, для нижней границы lower_bound мы задаем первый индекс, а для верхней upper_bound — последний.
Сам процесс поиска происходит внутри цикла while:
while lower_bound <= upper_bound do
Этот цикл выполняется, пока у нас остается диапазон ячеек, в которых может находиться искомое значение search_value. Как мы увидим далее, в процессе поиска наш алгоритм будет последовательно сужать этот диапазон, пока между нижней и верхней границами не останется ячеек (lower_bound <= upper_bound). Если за это время искомое значение не будет найдено, мы придем к выводу, что search_value в массиве нет.
В цикле код проверяет значение midpoint, которое находится в середине диапазона:
midpoint = (upper_bound + lower_bound) / 2
value_at_midpoint = array[midpoint]
value_at_midpoint — это элемент в середине диапазона.
Если value_at_midpoint совпадает с искомым значением search_value, мы добились цели и можем возвратить индекс соответствующего элемента:
if search_value == value_at_midpoint
return midpoint
Если search_value меньше, чем value_at_midpoint, значит, нужное значение следует искать левее. Так мы можем сузить диапазон поиска, выбрав в качестве upper_bound индекс слева от средней точки midpoint, поскольку search_value не может находиться справа от нее:
elsif search_value < value_at_midpoint
upper_bound = midpoint - 1
И наоборот, если search_value больше, чем value_at_midpoint, значит, нужное значение следует искать справа от средней точки midpoint, поэтому мы увеличиваем значение lower_bound:
elsif search_value > value_at_midpoint
lower_bound = midpoint + 1
Когда диапазон сужается до 0 элементов, мы возвращаем значение nil. В этом случае мы точно знаем, что search_value в массиве нет.
Сравнение алгоритмов бинарного и линейного поиска
При работе с небольшими упорядоченными массивами алгоритм двоичного поиска не сильно превосходит в эффективности алгоритм линейного поиска. Но посмотрим, что происходит с большими массивами.
Вот максимальное число шагов для выполнения каждого типа поиска в массиве со 100 значениями:
• линейный поиск — 100 шагов;
• двоичный поиск — 7 шагов.
При линейном поиске, если искомое значение находится в последней ячейке или превышает значение в ней, нам придется проверить каждый элемент. В случае с массивом в 100 значений на это уйдет 100 шагов.
Но при использовании двоичного поиска каждое предположение, которое мы делаем, исключает половину ячеек, которые нам иначе пришлось бы проверять. Первое предположение позволяет избавиться сразу от 50 ячеек.
Если мы посмотрим на это с другой стороны, то увидим закономерность.
В случае с массивом из трех элементов двоичный поиск потребовал бы максимум двух шагов.
Если мы удвоим количество ячеек в массиве (и для простоты добавим еще одну, чтобы их общее количество было нечетным), у нас получится семь ячеек. Двоичный поиск в таком массиве потребует максимум трех шагов.
Если мы снова удвоим число ячеек (и добавим еще одну), так чтобы упорядоченный массив содержал 15 элементов, то максимальное количество шагов для выполнения двоичного поиска будет равно четырем.
Закономерность следующая: каждый раз, когда мы удваиваем размер упорядоченного массива, количество шагов для выполнения двоичного поиска увеличивается на единицу. Это логично, так как каждый шаг поиска исключает половину элементов.
Все это говорит о необычайной эффективности такого алгоритма: каждый раз, когда мы удваиваем объем данных, в алгоритм двоичного поиска добавляется всего один шаг.
Сравним его с линейным поиском. Если бы в массиве было три элемента, нам потребовалось бы выполнить до трех шагов. В случае с массивом из семи элементов — до семи, а из 100 — до 100. Итак, при линейном поиске число шагов равно количеству элементов. Поэтому каждый раз, когда мы удваиваем размер массива, мы удваиваем и число шагов, которые нужно выполнить. В случае же с двоичным поиском удвоение размера массива добавляет лишь один шаг.
Посмотрим, как это работает на примере больших массивов. Линейный поиск в массиве из 10 000 элементов может потребовать до 10 000 шагов, а двоичный — всего 13 шагов. Линейный поиск в массиве из миллиона элементов потребует до одного миллиона шагов, а двоичный — 20 шагов.
Разницу в производительности между алгоритмами линейного и двоичного поиска можно показать на графике:

Нам предстоит проанализировать еще много таких графиков, так что давайте потратим немного времени на то, чтобы разобраться в примере. Ось X отражает число элементов в массиве. То есть, двигаясь слева направо, мы имеем дело с возрастающим объемом данных.
Ось Y отражает число шагов алгоритма. То есть, двигаясь снизу вверх, мы имеем дело с возрастающим количеством шагов.
Если вы посмотрите на график производительности линейного поиска, то увидите, что количество шагов возрастает пропорционально росту числа элементов в массиве. По сути, для каждого дополнительного элемента в массиве алгоритм линейного поиска предусматривает один дополнительный шаг. В результате получается прямая диагональная линия.
С другой стороны, при бинарном поиске по мере увеличения объема данных количество шагов алгоритма увеличивается незначительно. Это вполне сочетается с тем, что мы уже знаем: удвоение числа элементов массива добавляет в алгоритм двоичного поиска всего один шаг.
Имейте в виду, что работать с упорядоченными массивами не всегда быстрее. Как вы уже видели, вставка значения в такой массив выполняется медленнее, чем в стандартный. Приходится идти на компромисс: при использовании упорядоченного массива мы готовы мириться с более медленной вставкой ради более быстрого поиска. Опять же, всегда анализируйте потребности своего приложения, чтобы понять, какой из алгоритмов подходит вам больше. Будет ли ваше ПО осуществлять много вставок или, напротив, поиск для него важнее?
Викторина
Чтобы понять, разобрались ли вы с эффективностью двоичного поиска, попробуйте самостоятельно ответить на следующий вопрос (не подглядывайте в ответы).
Вопрос: на двоичный поиск в упорядоченном массиве из 100 элементов уходит семь шагов. Сколько шагов нужно, чтобы осуществить двоичный поиск в упорядоченном массиве из 200 элементов?
Ответ: 8 шагов.
Многие отвечают на этот вопрос интуитивно, говоря, что для этого нужно 14 шагов, но это неверно. Вся прелесть двоичного поиска в том, что каждая проверка значения позволяет исключить половину оставшихся элементов. Поэтому каждый раз, удваивая количество данных, мы добавляем в алгоритм только один шаг. В конце концов, это дублирование данных полностью исключается при первой же проверке!
Стоит отметить, что теперь, когда мы добавили в наш инструментарий бинарный поиск, вставка в упорядоченный массив тоже может стать быстрее. Как мы уже знаем, вставка требует предварительного поиска, но теперь вместо линейного мы можем использовать двоичный. Правда, вставка значения в упорядоченный массив по-прежнему будет медленнее, чем в обычный, поскольку во втором случае для вставки поиск вообще не нужен.
Выводы
Обычно есть несколько способов достижения конкретной вычислительной цели, и выбранный вами алгоритм может серьезно повлиять на скорость выполнения вашего кода.
Важно понимать, что ни одна структура данных и ни один алгоритм не могут идеально подходить для всех ситуаций. Например, то, что упорядоченные массивы позволяют осуществлять двоичный поиск, не означает, что всегда нужно использовать именно их. Если ваша программа в основном будет заниматься не поиском, а добавлением данных, лучше выбрать стандартные массивы, поскольку вставлять значения в них получится гораздо быстрее.
Мы уже изучили способ сравнения алгоритмов, который заключается в подсчете количества шагов, выполняемых каждым из них. В следующей главе мы рассмотрим формальный способ выражения временной сложности конкурирующих структур данных и алгоритмов. Освоив его, мы сможем получать более четкую информацию для принятия взвешенных решений при выборе подходящих алгоритмов.
Упражнения
Выполните следующие упражнения, чтобы закрепить знания, полученные из этой главы. Решения вы найдете в приложении в разделе «Глава 2».
1. Сколько шагов нужно для выполнения линейного поиска числа 8 в упорядоченном массиве [2, 4, 6, 8, 10, 12, 13]?
2. Сколько шагов нужно для выполнения двоичного поиска в примере выше?
3. Какое максимальное число шагов потребуется для выполнения двоичного поиска в массиве из 100 000 элементов?
Глава 3. О да! Нотация «О большое»
Ранее мы с вами говорили о том, что основной фактор, определяющий эффективность алгоритма, — это количество выполняемых им шагов.
Но мы не можем просто сказать, что один алгоритм состоит из 22 шагов, а другой — из 400, потому что количество выполняемых алгоритмом шагов не может быть сведено к конкретному числу. Возьмем, к примеру, линейный поиск. Количество шагов этого алгоритма зависит от числа элементов в массиве. Если массив содержит 22 элемента, алгоритм линейного поиска состоит из 22 шагов, а если 400 — то из 400 шагов.
Поэтому, чтобы количественно оценить эффективность этого алгоритма, мы можем сказать, что для выполнения линейного поиска в массиве из N элементов нужно N шагов. То есть если в массиве содержится N элементов, линейный поиск будет состоять из N шагов. Но такой способ выражения эффективности довольно громоздкий.
Чтобы облегчить обсуждение временной сложности, программисты позаимствовали из мира математики концепцию, благодаря которой можно лаконично и согласованно описывать эффективность структур данных и алгоритмов. Формальный способ выражения этих концепций называется нотацией «О большое» (Big O) или О-нотацией и позволяет легко оценивать эффективность любого алгоритма и сообщать о ней другим.
Разобравшись с О-нотацией, вы научитесь описывать алгоритмы согласованно и лаконично, как профессионалы.
Хотя О-нотация пришла из мира математики, я собираюсь обойтись без сложной терминологии и объяснить ее суть в контексте компьютерных наук. Мы начнем с малого: познакомимся с этой концепцией поверхностно, постепенно углубляясь в ее изучение на протяжении этой и следующих трех глав. Тема несложная, но еще проще ее будет усвоить по частям.
