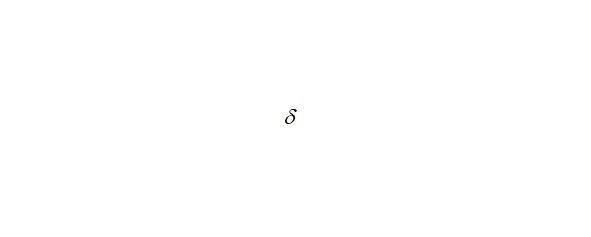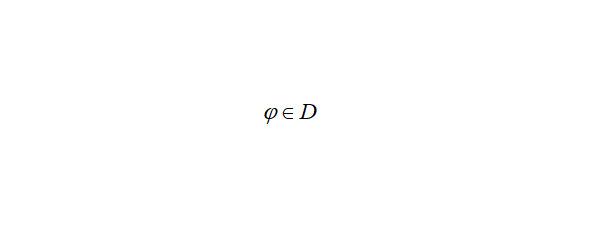О РАССМОТРЕНИИ ЯВЛЕНИЙ ЭЛЕКТРОМАГНЕТИЗМА С ПЕРЕМЕННЫМИ ПОКАЗАТЕЛЯМИ СЕРДЕЧНИКА
УДК 531/534
Юсупова Анора Каримовна
Кандидат физико-математических наук, профессор
Ферганский государственный университет, Фергана, Узбекистан
Алиев Ибратжон Хатамович
Генеральный директор Electron Laboratory LLC, Президент Научной школы «Электрон»
Electron Laboratory LLC, Маргилан, Узбекистан
Аннотация. В настоящем исследовании был рассмотрен метод анализа явлений взаимодействия электромагнита с различными объектами при условии введения в качестве переменной величины размеры его ферромагнитного сердечника. Анализ произведён посредством использования уравнений Максвелла с решением дифференциального уравнения первой степени во множественных переменных относительно электрического поля с учётом векторного оператора Наббла. В результате исследования получена результирующая функция, ранее зависимая от вектора магнитной индукции и, в частности, от индуктивности, в результате зависимая от множественных переменных и непосредственных показателей электромагнита, положения его и зондового объекта в пространстве. А также дано заключение установлена зависимость между величиной силы взаимодействия и переменными размерами сердечника.
Ключевые слова: электромагнит, ферромагнитный сердечник, оператор Наббла, уравнения Максвелла, электромагнитное поле.
Abstract. In this study, a method for analyzing the phenomena of interaction of an electromagnet with various objects was considered, provided that the dimensions of its ferromagnetic core were introduced as a variable. The analysis was performed using Maxwell’s equations with the solution of a differential equation of the first degree in multiple variables relative to the electric field, taking into account the Nabble vector operator. As a result of the study, a resulting function was obtained, previously dependent on the magnetic induction vector and, in particular, on the inductance, as a result dependent on multiple variables and direct indicators of the electromagnet, its position and the probe object in space. A conclusion was also given: a relationship was established between the magnitude of the interaction force and the variable dimensions of the core.
Keywords: electromagnet, ferromagnetic core, Nabble operator, Maxwell’s equations, electromagnetic field.
Annotatsiya. Ushbu tadqiqotda elektromagnitning turli ob’ektlar bilan o’zaro ta’sir qilish hodisalarini tahlil qilish usuli ko’rib chiqildi, agar uning ferromagnit yadrosining o’lchamlari o’zgaruvchan sifatida kiritilgan bo’lsa. Tahlil Nubble vektor operatorini hisobga olgan holda elektr maydoniga nisbatan bir nechta o’zgaruvchilarda birinchi darajali differentsial tenglamaning yechimi bilan Maksvell tenglamalari yordamida amalga oshiriladi. Tadqiqot natijasida ilgari magnit induksiya vektoriga va xususan, induktivlikka bog’liq bo’lgan natijada ko’p o’zgaruvchilarga va elektromagnitning to’g’ridan-to’g’ri ko’rsatkichlariga, uning holatiga va kosmosdagi zond ob’ektiga bog’liq bo’lgan natijaga erishildi.. Shuningdek, xulosa chiqariladi va o’zaro ta’sir kuchining kattaligi va yadroning o’zgaruvchan o’lchamlari o’rtasida bog’liqlik o’rnatildi.
Kalit so’zlar: elektromagnit, ferromagnit yadro, Nubble operatori, Maksvell tenglamalari, elektromagnit maydon.
Введение
Использование электромагнитов в современном мире носит масштабных характер. Большое количество подобных устройств в настоящее время используется для переноса грузов на различные расстояния, благодаря чему создаётся необходимость в организации различного рода конструкции и методов совершенствования каждой из этих конструкций электромагнитов. Заметив, что электромагнитом называется устройство создающее магнитное поле вокруг себя с определяемой индуктивностью и вектором магнитной индукции при прохождении через себя известного электрического тока, важно отметить применение методов совершенствования, основанные на изначальных закономерностях в физике электромагнитов и электромагнетизма.
Наряду с вышеуказанным, укажем некоторую терминологию, а именно факт того, что электромагнит состоит из внешней обмотки, где в качестве сердечника чаще всего выступает ферромагнитных сердечник, что позволяет при прохождении электрического тока принимать свойства магнита. Это явление основывается на том условии, что при прохождении электрического тока через обмотку, каждая часть проволоки заряжается электрическим переменным полем, что приводит к движению зарядов в обмотке. Переменное электрическое поле приводит к образованию переменного магнитного поля, которое поддерживается также и поддерживаемым со стороны разности потенциалом переменным электрическим полем.
К тому же, важно отметить, что при создании переменного магнитного поля, которое по величине меньше электрического поля, переменное электрическое поле в результате вновь организует более малое противоположное первому переменное электрическое поле, которое вновь порождает переменное паразитирующее противоположное магнитное поле, таким образом создавая цепочку из переменных электрических и магнитных полей, чередующиеся между собой и бесконечно убывающие. Объяснение явлений с классическим электромагнитом известны и рассмотрены неоднократно, однако, фактор того, что не рассмотрен вариант с переменными размерами и показателями сердечника делает необходимость рассмотрения настоящего вопроса актуальной.
Материалы и методы
В настоящем исследовании использованы методы анализа, посредством создания физико-математической модели явлений, с последующем выводом функции после решения дифференциальных уравнений в частных производных от многих переменных второго порядка.
Исследование
Во время действия электромагнита начинает действовать при рассмотрении заряда, сила Лоренца (1) и сила Ампера (2), полученные эмпирически.
В данном случае, наглядно можно заметить зависимость обоих сил от вектора магнитной индукции, а также фактор того, что, в частности, выполняется (3).
Поскольку в анализе рассматривается случай с макрообъектами, уместно принять в качестве функции определения силы взаимодействия между электромагнитом и объектом в качестве (2), где принимается некоторое условие. Во время рассмотрения электромагнита, векторы его индукции исходят из одного из полюсов, замыкаясь на втором полюсе, при этом величина вектора магнитной индукции рядом с катушкой изменяется, выражаясь в качестве отдельной функции. Заметив, что полюсом есть точка, из которой расходятся и сходятся векторы магнитной индукции, по своему координатному расположению устремляющаяся к концу ферромагнитного сердечника электромагнита.
Величина вектора магнитной индукции при постоянной величине тока и витков, в центре сердечника составляет (4).
Откуда можно положить зависимость между магнитной проницаемостью сердечника и вектором магнитной индукции, а также над величиной индуктивности (5).
И откуда можно положить выражение для объёма катушки (6).
Заметив в данном случае, что важно учитывать, что противодействовать искомой силе будет и сила, создаваемая электрическим полем и токов Фуко в однородном сердечнике, важные для учёта после нахождения результирующей функции. Из представленных показателей стало очевидно, что необходимо найти функцию для вектора магнитной индукции, зависимая от электрического поля и его показателей, после чего величина для искомой силы в зависимости от расстояния может быть найдена посредством создания математической диаграммы от математического ожидания.
Для нахождения искомой функции достаточно воспользоваться эмпирическим законом электромагнитной индукции Фарадея (7), откуда выводиться второе уравнение Максвелла для зависимости переменного магнитного поля для образования вихревого электрического поля (8).
Что для трёхмерного случая в декартовой системе координат можно представить в виде (9).
Функция для электрического поля является известной и задаваемой (10), откуда левое выражение легко определяемо и может быть задано в качестве некоторой функции (12), откуда легко выражается выражение для вектора магнитной индукции (13) и уже из неё выражение для искомой силы (14).
Откуда уместно заметить для единичного случая (11).
Что можно преобразовать, как (15).
Таким образом была выведена конечная результирующая функция, зависимая от указываемых координат. Исходя из полученных результатов можно представить визуализацию функции в качестве диаграммы и физико-математической трёхмерной и зависимой по времени модели, а также за счёт того, что в описании не были учтены некоторые внешние факторы внешней среды, можно представить вероятностную форму функции (16), с учётом поправок на токи Фуко (17), введя специальную калибровочную-вероятностную функцию, определяемая эмпирически.
Откуда можно легко найти математическое ожидание (18—19) и дисперсию (20) настоящей переменной величины.
Откуда (21).
Таким образом, была получена формула для вычисления силы взаимодействия с учётом абсолютно всех вероятностных случаев и исходов во время анализа, представляясь в качестве результирующей формулы (21).
Заключение
В результате осуществлённого теоретического анализа явления действия электромагнита с учётом различных переменных величин с учётом положения электромагнита, его собственных параметров, величины силы тока и напряжения в обмотке, прочих вероятностных показателей и поправочных констант, была получена результирующая формула. Которая полноценно описывает величину силы взаимодействия между электромагнитом и объектом с переменными размерами ферромагнитного сердечника. Было также показано, что фактор изменения ферромагнитного сердечника электромагнита может обладать переменно величиной размера, что в свою очередь обуславливается изменением области действия электрического поля, организуемая во время прохождения электрического тока в обмотке.
Наряду с прочим, было введено понятие полюсов с их координатными показателями, в результате из полученной формулы наглядно демонстрируя, что увеличение размером сердечника с увеличением степени корреляции с направлением векторов магнитной индукции у полюсов, приводит к увеличению величины силы взаимодействия силы электромагнита с металлическим объектом.
Использованная литература
1. T. Makiuchi, T. Hioki, H. Shimizu, K. Hoshi, M. Elyasi, K. Yamamoto, N. Yokoi, A. A. Serga, B. Hillebrands, G. E. W. Bauer & E. Saitoh. Persistent magnetic coherence in magnets. Nature Materials (2024)
2. Hanan Herzig Sheinfux, Lorenzo Orsini, Minwoo Jung, Iacopo Torre, Matteo Ceccanti, Simone Marconi, Rinu Maniyara, David Barcons Ruiz, Alexander Hötger, Ricardo Bertini, Sebastián Castilla, Niels C. H. Hesp, Eli Janzen, Alexander Holleitner, Valerio Pruneri, James H. Edgar, Gennady Shvets & Frank H. L. Koppens. High-quality nanocavities through multimodal confinement of hyperbolic polaritons in hexagonal boron nitride. Nature Materials (2024)