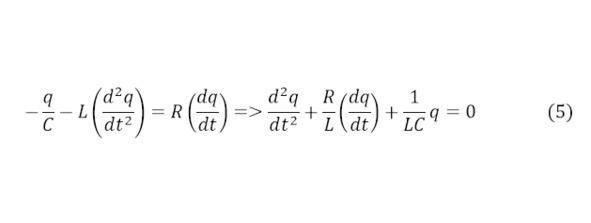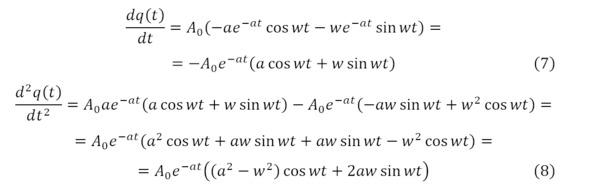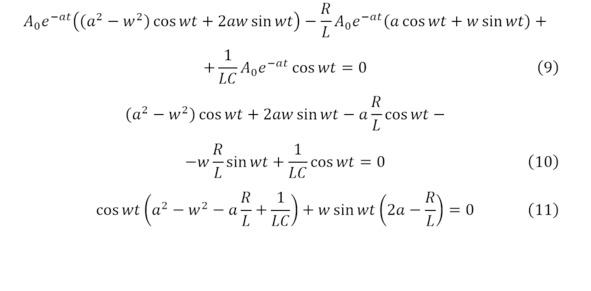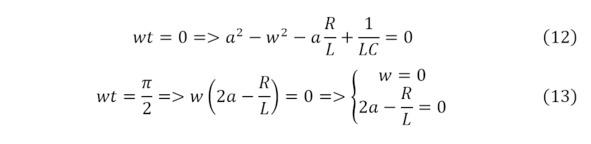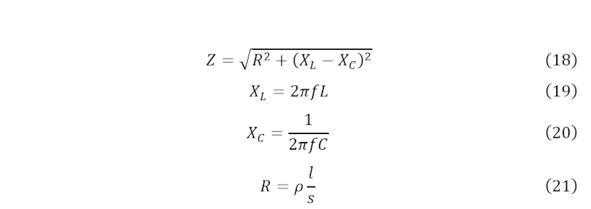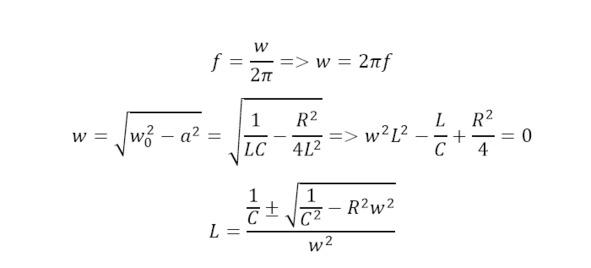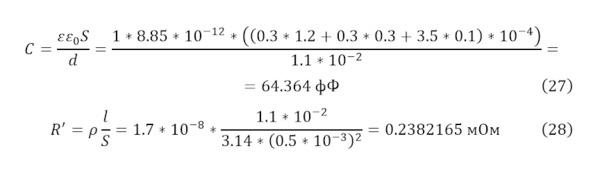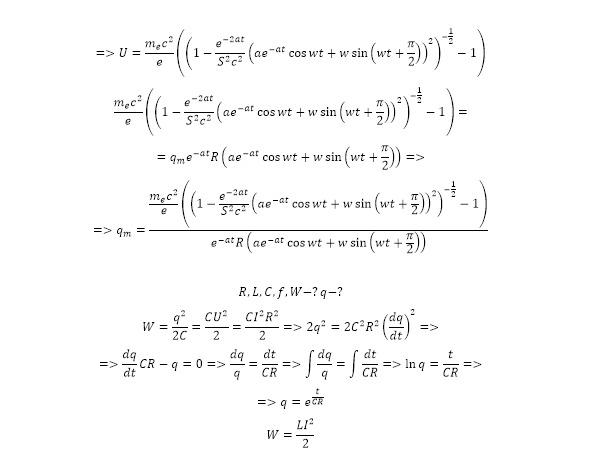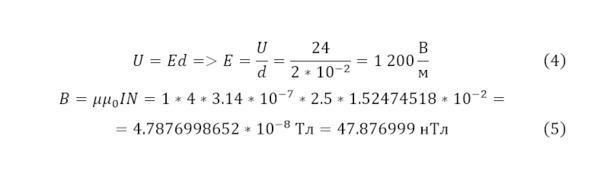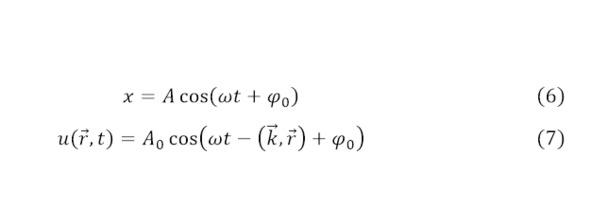ИССЛЕДОВАНИЕ ВЛИЯНИЯ ВНЕШНИХ ПРИРОДНЫХ ВОЗДЕЙСТВИЙ НА ДАЛЬНОСТЬ ДЕЙСТВИЯ СИСТЕМЫ RFID
УДК: 53.06
Хамзаев Дилшод Хамзаевич1, Алиев Ибратжон Хатамович1, Абдурахмонов Султонали Мукарамович3
1Фергана-Азот, 150100, г. Фергана, Ферганская обл., Республика Узбекистан
2Electron Laboratory LLC, 151100, г. Маргилан, Ферганская обл., Республика Узбекистан
3Ферганский Политехнический Институт, 150100, г. Фергана, Ферганская обл., Республика Узбекистан
Аннотация. Исследование основано на анализе явлений направления электромагнитного излучения посредством применения системы двух колебательных контуров ридера и RFID-метки. В ходе анализа установлена зависимость между факторами внешней среды и дальностью действия системы RFID, при помощи создания теоретической модели явления с применением дифференциальных уравнений в частных производных от многих переменных и множественных степеней. Установлен факт анализа посредством модели функции для затухающих электромагнитных периодических колебаний в нулевом случае. В результате выведены две формулы, устанавливающие зависимость от дальности действия RFID-технологии от фактора температуры и влажности среды.
Ключевые слова: фактор влажности, природное воздействие, дифференциальное уравнение в частных производных колебаний тонкой струны, формула Томпсона.
Аннотация. Тадқиқот ўқувчининг иккита тебраниш даври тизими ва РФИД ёрлиғи ёрдамида електромагнит нурланиш йўналиши ҳодисаларини таҳлил қилишга асосланган. Таҳлил давомида атроф-муҳит омиллари ва РФИД тизимининг диапазони ўртасидаги боғлиқлик кўплаб ўзгарувчилар ва кўп даражали қисман дифференциал тенгламалар ёрдамида ҳодисанинг назарий моделини яратиш орқали аниқланди. Нол ҳолатда намланган електромагнит даврий тебранишлар учун функция модели ёрдамида таҳлил қилиш ҳақиқати аниқланди. Натижада, РФИД технологияси диапазонининг атроф-муҳит ҳарорати ва намлиги омилига боғлиқлигини аниқлайдиган иккита формулалар олинган.
Калит сўзлар: намлик омили, табиий таъсир, ингичка симли тебранишларнинг қисман дифференциал тенгламаси, Томпсон формуласи.
Annotation. The study is based on the analysis of the phenomena of the direction of electromagnetic radiation through the use of a system of two oscillatory circuits of the reader and an RFID tag. During the analysis, the dependence between environmental factors and the range of the RFID system was established by creating a theoretical model of the phenomenon using partial differential equations of many variables and multiple degrees. The fact of analysis by means of a function model for damped electromagnetic periodic oscillations in the zero case is established. As a result, two formulas have been derived that establish the dependence of the range of RFID technology on the factor of temperature and humidity of the environment.
Keywords: humidity factor, natural influence, partial differential equation of fine string vibrations, Thompson’s formula.
Введение
Система RFID применяется в различных областях промышленности при учёте и перемещении продукции. В каждом из таких случаев, важно обозначение каждой единицы такой продукции при помощи определённой системы маркировки, к которым относится система идентификации RFID. Технология системы маркировки основана на принципе передачи данных с определённой величиной переменной амплитуды на расстояние через колебательный контур ридера — устройства для передачи и считывания электромагнитного сигнала. Направленное электромагнитное излучение принимается RFID-меткой или RFID-тегом, принимающий при помощи своего колебательного контура электромагнитное излучение и вводящий в него данный из памяти встроенное чипа, после чего сигнал направляется обратно.
Система RFID может действовать в различных моделях с применением дополнительных источников энергии или может обойтись без них. Однако, при передаче данных большую важность имеет характеристика самой волны — уменьшение её энергии при прохождении через определённую среду, чем ограничивается дальность действия RFID-системы. Во время передачи информации электромагнитный сигнал, который затухает по мере отдаления от ридера, преобразуется на этапе возвращения имея переменную амплитуду, оставаясь с постоянной частотой, но при этом переменная величина амплитуды компенсируется на протяжении всей волны. Такое эффект обеспечивает в ходе исследования с целью определения дальности действия RFID-технологии пренебрегать информацией, которую электромагнитная волны заключает в себе.
На основе этого, в дальнейшем проводиться исследование электромагнитной волны с определёнными характеристиками без учёта информации в размере нескольких килобайт, которую она в себе может заключать. Также, исходя из выше указанных параметров определяется масштаб действия RFID-технологии в промышленности, что также приводит к необходимости работы при самых различных внешних погодных и природных условиях с различной степенью температуры среды, влажности воздуха и прочих параметрах. Учёт каждой из переменных является важным, что позволяет говорить, что исследование настоящего эффекта является актуальным.
Исследование
Технология RFID-меток основана на приёме и передаче определённого количества энергии между источником с собственными колебательными контурами и колебательным контуром RFID-метки. При важно заметить, что в структуре ридера имеется единственный конденсатор и множественные катушки, рассчитанные для действия и организации резонанса на различных диапазонах частот.
В данном случае действие осуществляется посредством УВЧ диапазона, за минимальную частоту резонанса в которой принимается величина в 860 МГц, при учёте наличия конденсатора с известной ёмкостью.
Из RFID-ридера сторону RFID-тега направляется электромагнитное излучение, которое необходимо исследовать. Для этого достаточно исходить из закона Ома для колебательного контура (1), установив зависимость через заряд в том же уравнении, учитывая формулу для ЭДС (2), силу тока в цепи (3) и напряжения в системе конденсатора (4), преобразовав до состояния с учётом зарядов в обоих случаях.
Указанные выражения могут быть преобразованы после подстановки в (1) в единую форму (5).
Решение дифференциального уравнения (5), будем искать в форме (6), по причине учёта модели в форме затухающих электромагнитных колебаний.
Для подстановки формы (6) в обыкновенное дифференциальное уравнение второго порядка (5) необходимо определить производные (6) первого порядка (7) и второго порядка (8).
Таким образом можно получить уравнение (9), которое преобразуется в (10—11).
Полученное выражение (11) может принимать нулевое значение только в 2 случаях, рассматриваемые в (12—13) и дающие свои выводы.
Из (13) стало очевидно, что циклическая частота затухающих колебаний не могут быть равны нулю, откуда становиться очевидным формула для степенной константы в формуле затухающих электромагнитных колебаний (14) и которая может быть подставлена в (12).
Таким образом была получена формула для циклической частоты затухающих колебаний, нулевой циклической частоты из закономерностей (15), которую можно подставить в (6), получив формулу для заряда (16), взяв производную, от которой можно получить выражение для силы тока (17).
В результате проведённых вычислений была получена формула, описывающая изменение величие силы тока и заряда в RFID-технологии, включающая в себя показатели индуктивности, ёмкости и сопротивления системы. Уместным является замечание, что каждая из систем может быть выполнена в различной модификации, также уместно использование множественных индуктивностей и единичной ёмкости конденсатора. Для того, чтобы установить дальность действия системы, необходимо определить величину индуктивности, которая может быть вычислена при помощи ёмкости через определённую закономерность.
Для вывода выше указанного выражения, определим выражение для сопротивления системы (18), заметив (19—21).
Определяемое сопротивление необходимо по причине невозможности использования классического выражения формулы Томпсона и выражение для частоты может быть определена из (22), откуда согласно с предыдущими выводами выводится результирующее биквадратное уравнение.
Перед продолжением исследования, укажем действующую частоту УВЧ диапазона в рамках 860—960 МГц, при том, что для статичного случая принимается минимальная величина. При тех же условиях, устанавливается величина ёмкости конденсатора (27) и первоначальная величина сопротивления (28).
Исходя из полученных величин можно получить величину индуктивности (29), нулевой частоты (30), сопротивление ёмкости (31) и сопротивление индуктивности (32).
В результате полученных выражений можно получить значения
Что также можно представить в виде (18—19).
— 860 МГц, это позволяет при диаметре пластины конденсатора ридера в 5,2 см и расстоянии между пластинами в 2 см определить ёмкость такого плоского конденсатора (1), а также индуктивность катушки (2).
Откуда при напряжении 24 В и 2,5 А или 60 Вт, можно легко вычислить количество катушек (3).
Что говорит о том, что в ридере, не произведён и один оборот катушки, при имеющихся расстояниях и проволока, играющая роль катушки совершает оборот вокруг центра обоих пластин всего лишь на 5,489 градуса, что приводит к представляемым данным, без учёта дополнительных схем, изменяющие параметры как конденсатора и катушки, во время передачи информации. Но в статичном состоянии сохраняются именно эти параметры, при выведении волны с затухающими колебаниями.
При этом, в настоящем случае образуется электрическое и магнитное поле, которое в каждый период частоты доходит до своего максимального положительного значения и уменьшается до минимального отрицательного значения. В модуле, максимальная величина электрического поля определена в промежутке между пластинами и может быть определена, как (4), когда же максимальное магнитное поле в центре соленоида в (5).
В результате настоящих вычислений, были определены показатели для электрического и магнитного поля, которые также являются величинами амплитуды электромагнитных колебаний. Настоящая электромагнитная волна распространяется с различными характеристиками, так чаще всего настоящая волна подчиняется описанию, которые в идеальном случае могли быть заданы в качестве (6), в качестве затухающих электромагнитных колебаний задаются согласно (7).
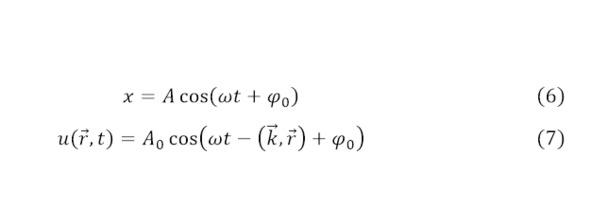
В настоящей форме наглядно видно, что даже при максимальном значении электрического и магнитного поля, величина электрического поля значительно превышает величину магнитного поля. Также, когда электромагнитная волна дойдёт до RFID-метки, то электрическое поле приведёт к включению конденсатора, а магнитное — катушек. Используя это утверждение, можно вывести выражение для силы тока метки, зависимая от величины вектора магнитной индукции, зависимая от координат и времени (8), что приводит также к определению такой же зависимости между индуктивностью и вектором магнитной индукции (9).
В (8—9) был введён показатель вектора магнитной индукции, представляющий собой минимальную величину, которую она примет в момент дохода электромагнитной волны до метки. Однако, эти показатели могут быть констатированы благодаря прямому определению, в силу возможности определения ёмкости конденсатора метки (10), размеры которой также известны.