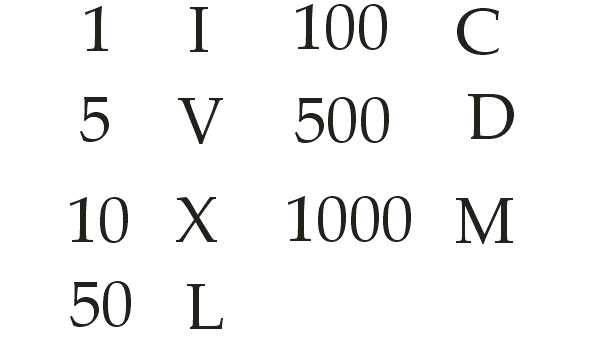автордың кітабын онлайн тегін оқу Системы счисления
Дмитрий Кудрец

Кітап туралы Қазір оқып жатыр57 Тегін фрагмент

Дмитрий Кудрец

Системы счисления

Шрифты предоставлены компанией «ПараТайп»

В книге рассказывается о позиционных и не позиционных системах счисления, приводятся примеры вычислений в разных системах и задания для самостоятельной работы.

Книга адресуется учащимся школ, гимназий, лицеев, а также широкому кругу читателей.

12+

Системы счисления
Введение
Непозиционные системы счисления
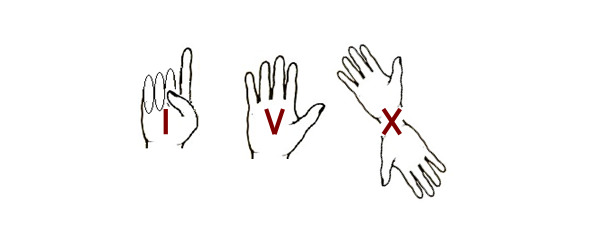
Римские числа
1. Задания для самостоятельной работы
Греческие числа
1. Задания для самостоятельной работы
Старославянская система счисления
1. Задания для самостоятельной работы
Египетские числа
1. Сложение египетских чисел
2. Умножение египетских чисел
3. Задания для самостоятельной работы
Числа Майя и Ацтеков
Вавилонские числа
Мультипликативные системы счисления
1. Задания для самостоятельной работы
Позиционные системы счисления
Системы счисления с заданным основанием
1. Задания для самостоятельной работы
Десятичная система счисления
1. Задания для самостоятельной работы
Двоичная система счисления
1. Перевод из двоичной системы счисления в десятичную
2. Перевод из десятичной системы счисления в двоичную
3. Задания для самостоятельной работы
4. Сложение двоичных чисел
5. Умножение двоичных чисел
6. Вычитание двоичных чисел
7. Деление двоичных чисел
8. Задания для самостоятельной работы
Шестнадцатеричная система счисления
1. Перевод из двоичной системы счисления в шестнадцатеричную и обратно
2. Перевод из шестнадцатеричной системы счисления в десятичную и обратно
3. Задания для самостоятельной работы
Использованная литература

Введение

С давних времен человечество сталкивалось с проблемой подсчёта и записи количества собранного урожая, накопленных богатств, и т. д. Каждые народы решали эту проблему по-разному — одни использовали узелки на верёвках, другие — зарубки на палочках, камешки или ракушки.

С возникновением письменности одновременно возникали и развивались новые системы счёта и правила выполнения операций над числами.

Известно множество способов представления чисел. В одних случаях для обозначения чисел использовались буквы алфавита, в других — применялись специальные символы. Такие символы называются цифрами.

Система обозначения, записи и правила операций над числами называется системой счисления или системой счёта.

За историю человечества существовало множество различных систем счисления. Некоторые из них до сих пор используются, другие системы не получили широкого распространения.

В зависимости от способа изображения чисел с помощью цифр системы счисления делятся на позиционные и непозиционные.

Наиболее распространёнными непозиционными системами счисления являются римские числа, греческие числа, старославянская система счета, египетские и вавилонские числа. В таких системах значение числа не зависит от положения цифры в записи.

Самой распространенной позиционной системой счисления является десятичная система (арабские или десятичные числа). Этой системой мы пользуемся в повседневной жизни. В этой системе значение числа зависит от положения цифры в записи. Например, в записи числа 152 в десятичной системе цифра 5 — обозначает число десятков. Если переставить цифры местами, то изменится и числовое значение. Так в записи 125 — цифра пять будет обозначать число единиц.

Существовали также и мультипликативные системы счисления, которые несут в себе признаки как непозиционных, так и позиционных систем. Примером таких систем являются китайские числа.

Непозиционные системы счисления

В самой простейшей системе счисления для записи чисел используется только одна цифра. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака (единицы), которую можно изобразить в виде палочки, кружочка или любой другой фигуры.

Числа в этой системе будут записываться примерно так:

Такая система счисления в основном использовалась народами, не имеющими письменности. Иногда подобной системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками или точками в тетради количество проданных товаров.

Единичная система — не самый удобный способ записи чисел. Запись больших чисел получается очень длинной и неудобной. С течением времени возникли другие, более удобные, системы счисления.

В непозиционной системе счисления абсолютно неважно, где стоит цифра — на первом или последнем месте. Для определения значения числа нужно сложить (или отнять) все числовые значения. Арифметические действия в непозиционных системах счисления очень неудобны и сложны.

Для обозначения чисел многие народы использовали существующие алфавиты. Такие системы счисления называются алфавитными. Алфавитные системы счисления использовались в Древней Греции, Руси, Риме.

Древние египтяне, Ацтеки и племена Майя для записи чисел использовали специальные символы (цифры). Разные цифры обозначались различными символами. Такие системы называются аддитивными.

Несмотря на то, что непозиционные системы счисления использовались человечеством на протяжении длительного периода, они были далеки от совершенства и имели ряд существенных недостатков: с их помощью нельзя было представлять дробные и отрицательные числа; возникали проблемы при записи очень больших чисел и самый главный недостаток — сложность выполнения арифметических операций.

Римские числа

Достоверных сведений о происхождении римских цифр нет. Скорее всего, эти цифры были заимствованы римлянами у этрусков или других народов.

Числа в римской системе счисления обозначают буквами латинского алфавита I, V, X, L, C, D и M.

Такие обозначения частично произошли от рисунков, изображавших некогда соответствующие числительные (I — палец, V — пятерня с расставленными пальцами, X — две пятерни), а частично являются сокращениями латинских слов (centum — сто, demimille — пятьсот, mille — тысяча).