Переводчики , Е. Матвеев, С. Черников

Литературные редакторы А. Потапова , А. Руденко

Художник В. Мостипан

Корректоры С. Беляева, Г. Шкатова

 

Уилл Курт

Байесовская статистика: Star Wars, LEGO, резиновые уточки и многое другое. — СПб.: Питер, 2021.

 

ISBN 978-5-4461-1655-3

© ООО Издательство "Питер", 2021

 

Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

 

Мелани, которая пробудила во мне страсть к писательству

Об авторе

Уилл Курт (Will Kurt) — специалист по данным в Wayfair, уже больше пяти лет использует байесовскую статистику для решения реальных задач бизнеса. Он часто пишет о вероятности на своем веб-сайте CountBayesie.com. Курт является автором «Программируй на Haskell» (изд. «ДМК Пресс»), в настоящее время живет в Бостоне, штат Массачусетс.

О научном редакторе

Челси Парлетт-Пеллерити (Chelsea Parlett-Pelleriti) — аспирантка в области науки о вычислениях и data science и давняя любительница всего забавного и статистического. Автор текстов о статистике, участница различных проектов, включая серию «Краткий курс статистики» (Crash Course Statistics) на YouTube и «Подготовка к экзамену по статистике (углубленная программа)» (Cracking the AP Statistics Exam) в The Princeton Review. В настоящее время живет в Южной Калифорнии.

Благодарности

Написание книги — это действительно невероятное усилие, которое складывается из труда многих людей. Ниже я упомянул лишь некоторых людей, благодаря которым появилась эта книга. Хотел бы начать с благодарности сыну Арчеру за то, что он всегда сохранял во мне любопытство и вдохновлял меня.

Я очень люблю книги No Starch, и для меня большая честь поработать вместе с удивительной командой, которая теперь издает и мою книгу. Я очень благодарен своим редакторам, рецензентам и невероятной команде No Starch. Лиз Чедвик (Liz Chadwick) в самом начале обратилась ко мне с просьбой о создании этой книги и давала рекомендации на протяжении всего процесса ее написания. Лорел Чан (Laurel Chun) позаботилась о том, чтобы весь процесс перехода от черновых записей с заметками по R к полноценной книге прошел гладко. Челси Парлетт-Пеллерити вышла далеко за рамки требований научного редактора и постаралась сделать эту книгу как можно лучше. Фрэнсис Соу (Frances Saux) добавила много важных комментариев к последующим главам.

Отдельная благодарность Биллу Поллоку (Bill Pollock) за создание такого восхитительного издательства.

Будучи специалистом по английской литературе, я и представить себе не мог, что напишу книгу, связанную с математикой. Хотел бы упомянуть нескольких людей, которые помогли мне увидеть чудо математики. Я всегда буду благодарен моему соседу по комнате в колледже Грегу Мюллеру (Greg Muller), который показал сумасшедшему знатоку английской филологии, насколько захватывающим и интересным может быть мир математики. Профессор Анатолий Темкин (Anatoly Temkin) из Бостонского университета открыл мне двери в математическое мышление, научив меня всегда отвечать на вопрос «что это значит». И, конечно же, огромное спасибо Ричарду Келли (Richard Kelley), который, когда я потерялся в пустыне, стал оазисом математических разговоров и подсказок. Также хотел бы поблагодарить команду по науке о данных в Bombora, особенно Патрика Келли (Patrick Kelley) — с ним мы провели множество увлекательных бесед, и некоторые из них нашли свое отражение в книге. Я также всегда буду благодарен читателям своего блога Count Bayesie, которые подбрасывали замечательные вопросы и идеи. Среди читателей я особенно хотел бы поблагодарить комментатора под ником Nevin, который помог исправить некоторые недоразумения, возникшие вначале.

Наконец хочу поблагодарить выдающихся авторов текстов о байесовской статистике, книги которых во многом способствовали моему собственному развитию в этой области. «Doing Bayesian Data Analysis» Джона Крушке (John Kruschke) и «Bayesian Data Analysis» Эндрю Гельмана (Andrew Gelman) — отличные книги, которые стоит прочитать каждому. Безусловно, книга, которая больше всего повлияла на мое мышление, — это феноменальная «Probability Theory: The Logic of Science» Э.Т. Джейнса (E. T. Jaynes). И еще я хотел бы поблагодарить Обри Клейтона (Aubrey Clayton) за серию лекций об этой сложной книге, которая действительно помогла мне разобраться в непонятных темах.

Введение

Практически все в жизни в некоторой степени неопределенно. Это может показаться преувеличением, но чтобы в этом убедиться, проведите быстрый эксперимент. В начале дня запишите то, что, по вашему мнению, произойдет в следующие полчаса, час, три часа и шесть часов. Затем проверьте, какие из этих пунктов осуществились именно так, как вы себе представляли. Вы быстро поймете, что ваш день полон неопределенностей. Даже что-то такое предсказуемое, как «я почищу зубы» или «я выпью чашку кофе», может по тем или иным причинам не произойти, вне зависимости от ваших ожиданий.

В большинстве случаев, даже несмотря на неопределенность, мы можем достаточно хорошо спланировать свой день. Например, даже если из-за пробок вы будете добираться на работу дольше, чем обычно, то можете довольно точно оценить, во сколько нужно выходить из дома, чтобы успеть. Если у вас очень важная утренняя встреча, можете выйти раньше, чтобы учесть возможные задержки. У всех нас есть врожденное чувство того, как справляться с неопределенными ситуациями и рассуждать о неопределенности. Когда вы думаете так, вы думаете вероятностно.

Зачем изучать статистику?

Байесовская статистика помогает лучше рассуждать о неопределенности, так же как изучение логики в школе помогает увидеть ошибки в повседневном логическом мышлении. Учитывая, что практически каждый имеет дело с неопределенностью в жизни, о чем мы только что говорили, аудитория читателей этой книги становится довольно широкой. Специалисты по работе с данными и исследователи, уже использующие статистику, извлекут выгоду из более глубокого понимания и интуиции насчет работы этих инструментов. Инженеры и программисты узнают много нового о том, как лучше количественно оценивать решения, которые им приходится принимать (я даже использовал байесовский анализ для определения причин ошибок программного обеспечения!). Маркетологи и продавцы могут применять идеи, изложенные в этой книге, при проведении A/B-тестов, пытаясь понять свою аудиторию и лучше оценить возможные сделки. Любой, кто принимает решения на высоком уровне, должен иметь хотя бы базовое чувство вероятности, чтобы можно было быстро сделать предварительные оценки затрат и выгод от неопределенных решений. Я бы хотел, чтобы генеральный директор мог изучить эту книгу во время полета. К моменту приземления у него будет прочный фундамент в статистике, позволяющий лучше оценивать варианты, связанные с вероятностями и неопределенностью.

Я искренне верю, что всем будет полезно думать о проблемах байесовским способом. С помощью байесовской статистики вы можете использовать математику для моделирования неопределенности, чтобы сделать лучший выбор, учитывая ограниченную информацию. Допустим, вам нужно вовремя прийти на работу к особенно важной встрече и вы можете выбрать два разных маршрута. Первый маршрут обычно более короткий, но из-за оживленного движения могут возникнуть пробки. Второй маршрут в целом занимает больше времени, но пробок там не предвидится. Какой маршрут выбрать? Какого типа информация понадобится, чтобы принять решение? И насколько вы можете быть уверены в своем выборе? Даже небольшая добавленная сложность требует дополнительных размышлений и техники. Обычно, когда люди думают о статистике, они думают об ученых, работающих над новым лекарством, экономистах, следящих за тенденциями на рынке, аналитиках, предсказывающих следующие выборы, менеджерах по бейсболу, пытающихся создать лучшую команду, и т.д. Хотя все это, безусловно, увлекательное использование статистики, понимание основ байесовских рассуждений поможет в гораздо большем количестве областей жизни. Если вы когда-нибудь сомневались в новостях, не спали ночами и шерстили интернет в поисках ответа на вопрос «есть ли у вас редкое заболевание» или спорили с родственником по поводу их иррациональных убеждений о мире, изучение байесовской статистики поможет рассуждать лучше.

Что такое байесовская статистика?

Что это за байесовский метод? Если вы когда-либо посещали занятия по статистике, скорее всего, они основывались на частотной статистике. Частотная статистика базируется на идее, что вероятность представляет собой частоту, с которой что-то происходит. Если вероятность выпадения орла при броске одной монетки равна 1 к 2, это означает, что после броска одной монетки мы можем получить половину орла (после двух бросков мы можем получить целого орла, что имеет больше смысла).

Байесовская статистика, с другой стороны, связана с тем, как вероятности отражают неопределенность полученной нами информации. С точки зрения Байеса, если вероятность выпадения орла при подбрасывании монетки равна 0,5, это означает, что мы в равной степени не уверены в том, получим мы орла или решку. Для таких проблем, как подбрасывание монеток, и частотный, и байесовский подходы кажутся разумными, но при выражении уверенности в том, что ваш кандидат победит на следующих выборах, байесовская интерпретация имеет гораздо больший смысл. В конце концов, выборы всего одни, поэтому говорить о том, как часто будет побеждать этот кандидат, не имеет смысла. При проведении байесовской статистики мы просто пытаемся точно описать, что мы думаем об окружающем мире, учитывая имеющуюся у нас информацию.

Поскольку мы можем рассматривать байесовскую статистику просто как рассуждение о неопределенных вещах, то все инструменты и методы имеют интуитивный смысл. Байесовская статистика — это поиск проблемы, с которой вы столкнулись, выяснение того, как можно описать ее математически, а затем использование причины возникновения проблемы для ее решения. Нет никаких загадочных тестов, дающих результаты, в которых вы не совсем уверены, нет распределений, которые нужно запомнить, и нет традиционных экспериментов, которые вы должны идеально воспроизвести. Хотите ли вы выяснить вероятность того, что новый дизайн сайта привлечет больше клиентов, что ваша любимая команда победит в следующей игре или что мы действительно одни во Вселенной, байесовская статистика позволит начать рассуждать об этом математически, используя всего несколько простых правил и новый взгляд на проблемы.

Структура книги

Вот краткое описание книги.

Часть I. Введение в теорию вероятностей

Глава 1. Байесовские рассуждения в обычной жизни

Первая глава знакомит вас с байесовскими рассуждениями и показывает, насколько они схожи с критическим мышлением. Основываясь на своих знаниях о мире, мы рассмотрим вероятность того, что яркий свет в окне ночью — это НЛО.

Глава 2. Измеряем неопределенность

В этой главе будем подбрасывать монетку, чтобы выразить фактические значения неопределенности в виде вероятностей: это будут числа в интервале 0 и 1, которые показывают степень уверенности в своем мнении относительно чего-либо.

Глава 3. Логика неопределенности

В логике для объединения истинных и ложных выражений используются операторы И, НЕ и ИЛИ. Оказывается, для этих операторов вероятность имеет схожие понятия. Мы рассмотрим, как обосновать выбор транспорта, чтобы добраться до места встречи, и шансы на получение штрафа.

Глава 4. Как получить биноминальное распределение вероятностей

Используя правила для вероятностей как логику, в этой главе вы построите свое собственное распределение вероятностей — биномиальное распределение, которое можно будет применить ко многим вероятностным задачам, имеющим схожую структуру. Мы попытаемся предсказать вероятность получения определенной известной коллекционной карточки из игры «гача»1.

Глава 5. Бета-распределение

Здесь вы впервые столкнетесь с непрерывным распределением вероятностей и узнаете, чем статистика отличается от теории вероятности. Практическая часть статистики включает в себя попытки выяснить, какие неизвестные вероятности могут быть основаны на данных. Мы рассмотрим загадочную коробочку для раздачи монет и шансы заработать денег больше, чем потерять.

Часть II. Байесовские и априорные вероятности

Глава 6. Условная вероятность

В этой главе определим вероятности на основе имеющейся информации. Например, если мы знаем, мужчина перед нами или женщина, это позволяет предположить, страдает ли этот человек дальтонизмом. Вы также познакомитесь с теоремой Байеса, которая позволяет «обратить» условные вероятности.

Глава 7. Теорема Байеса и Lego

Здесь визуализируем теорему Байеса на примерах деталек Lego! Эта глава даст вам пространственное представление о том, что теорема Байеса делает математически.

Глава 8. Априорная, апостериорная вероятности и правдоподобие в теореме Байеса

Теорема Байеса обычно разбивается на три части, каждая из которых в байесовских рассуждениях имеет свою цель. В этой главе вы узнаете, как они называются и как их использовать, на примере изучения ограбления со взломом: было ли это преступлением или просто серией совпадений.

Глава 9. Байесовские априорные вероятности и распределение вероятностей

В этой главе посмотрим, как можно использовать теорему Байеса, чтобы лучше понять классическую сцену с астероидом из «Звездных войн: Империя наносит ответный удар». Здесь мы углубимся в априорные вероятности в байесовской статистике. Вы также увидите, как можно использовать целые распределения как априорные вероятности.

Часть III. Оценка параметров

Глава 10. Введение в усреднение и оценку параметров

Оценка параметров — это метод, который применяется для формулирования наилучшего предположения для неопределенного значения. Основной инструмент в оценке параметров — простое усреднение наблюдений. В этой главе мы проанализируем уровни снегопада и увидим, почему это работает.

Глава 11. Измерение разброса данных

Поиск среднего значения — полезный первый шаг в оценке параметров, но нам также нужен способ для учета разброса наблюдений. Здесь вы познакомитесь со средним абсолютным отклонением (Mean Absolute Deviation, MAD), дисперсией и стандартным отклонением как способами измерения разброса наблюдений.

Глава 12. Нормальное распределение

Комбинируя среднее значение и стандартное отклонение, мы получаем очень полезный инструмент для оценки: нормальное распределение. В этой главе вы узнаете, как использовать нормальное распределение, чтобы не только оценить неизвестные значения, но и узнать степень уверенности в оценках. Применим эти новые навыки, чтобы рассчитать время побега при ограблении банка.

Глава 13. Инструменты оценки параметров: PDF, CDF и квантильная функция

Здесь вы узнаете о функции плотности вероятности (PDF), кумулятивной функции распределения (CDF) и квантильной функции, чтобы лучше понять выполняемые вами оценки параметров. С помощью этих инструментов вы оцените коэффициенты конверсии рассылки и увидите, на что они влияют.

Глава 14. Оценка параметров с априорными вероятностями

Хороший способ улучшить оценки параметров — добавить априорную вероятность. В этой главе вы узнаете, как добавление априорной информации об успешном использовании коэффициента переходов в письме поможет лучше оценить реальный коэффициент конверсии для новых рассылок.

Часть IV. Проверка гипотез: сердце статистики

Глава 15. От оценки параметров к проверке гипотез: построение байесовских А/В-тестов

Теперь, когда мы можем оценивать неопределенные значения, нужно найти способ их сравнения для проверки гипотез. Вы создадите A/B-тест, чтобы определить степень уверенности в новом методе электронного маркетинга.

Глава 16. Введение в коэффициент Байеса и апостериорные шансы: конкуренция идей

Было ли у вас такое, что вы не спали полночи, гугля симптомы редкой болезни, которая, как вам кажется, у вас есть? В этой главе мы представим другой подход к проверке идей, который поможет определить, стоит ли волноваться.

Глава 17. Байесовские рассуждения в «Сумеречной зоне»

Вы верите в экстрасенсорные способности? В этой главе будем развивать собственные навыки чтения мыслей, проанализировав ситуацию из эпизода «Сумеречной зоны».

Глава 18. Когда данные не убеждают

Иногда кажется, что данных недостаточно, чтобы изменить чье-то мнение или выиграть спор. Узнайте, как переубедить друга в том, с чем вы не согласны, и почему не стоит тратить время на споры с воинственным дядей!

Глава 19. От проверки гипотез к оценке параметров

Здесь мы вернемся к оценке параметров и узнаем, как сравнить ряд гипотез. Вы рассмотрите первый пример статистики — бета-распределение, используя инструменты, которые мы изучили для простых проверок гипотез, чтобы проанализировать честность конкретной игры.

Приложение A. Краткое введение в язык R

В этом небольшом приложении даны основы языка программирования R.

Приложение Б. Математический минимум

Здесь мы рассмотрим математику на уровне, достаточном для того, чтобы понимать расчеты, приведенные в книге.

Приложение В. Ответы к упражнениям

Здесь вы найдете все упражнения и ответы к ним.

Для некоторых упражнений есть несколько способов решения, поэтому я дам как минимум один вариант.

Что стоит знать, прежде чем приступить к чтению

Единственным требованием к читателю является знание основ алгебры средней школы. Далее в книге вы увидите несколько примеров вычислений, но не особенно сложных. Мы будем использовать немного кода на языке программирования R. Необходимости изучать R заранее нет, я расскажу обо всем по ходу дела. Мы также коснемся высшей математики, но опять же никакого опыта не требуется: в приложениях дано достаточно информации для понимания темы.

Другими словами, эта книга призвана помочь вам начать думать математически, не требуя значительных математических знаний. Когда вы закончите чтение, то сможете даже написать уравнения для описания проблем, с которыми сталкиваетесь в жизни!

Если у вас действительно есть серьезный опыт в статистике (даже в байесовской статистике), думаю, вы все равно весело проведете время с этой книгой. Я считаю, что лучший способ хорошо понять тему — пересматривать основы раз за разом, каждый раз в ином свете. Даже я, автор этой книги, обнаружил в процессе работы много всего нового, что меня удивило!

Отправляемся в приключение!

Вы увидите, что байесовская статистика не только очень полезна, но и может доставлять массу удовольствия! Чтобы изучить байесовские рассуждения, поговорим о Lego, «Сумеречной зоне», «Звездных войнах» и о многом другом. Вскоре вы обнаружите, что начинаете думать о задачах вероятностно и повсюду использовать байесовскую статистику. Эта книга — для быстрого и приятного чтения, поэтому смело переворачивайте страницу и отправляйтесь в путешествие по миру байесовской статистики!

От издательства

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства www.piter.com вы найдете подробную информа­цию о наших книгах.

Часть I. Введение в теорию вероятностей

1. Байесовские рассуждения в обычной жизни

В этой главе мы обсудим байесовские рассуждения — формальный способ уточнить наши представления об окружающем мире, основываясь на наблюдаемых данных. Мы проработаем сценарии и поймем, как связать повседневный опыт с байесовскими рассуждениями.

Хочу вас обрадовать! Все вы уже встречались с байесовскими рассуждениями еще до того, как взяли в руки эту книгу. Байесовская статистика очень хорошо согласуется с тем, как люди рассуждают в обычной жизни, делая выводы из имеющихся сведений. Сложность лишь в том, чтобы разбить этот процесс на шаги и привести к строгой математической форме.

В статистике, чтобы правильно оценивать вероятности, надо строить модели и производить вычисления. Но сейчас мы не будем обращаться к математическим моделям, а просто познакомимся с основными понятиями и узнаем, что такое вероятность, обращаясь к интуиции. Уже потом, в следующих главах, мы присвоим вероятностям точные численные значения. В дальнейшем вы узнаете, как использовать математические методы для построения формальных моделей и для строгих рассуждений о понятиях, вводимых в этой главе.

Рассуждения о странных происшествиях

Как-то ночью вы вдруг просыпаетесь от бьющего в окно яркого света. Вы вскакиваете с кровати, выглядываете на улицу и видите в небе большой объект в форме — да-да — тарелки. Вообще-то, вы скептик и никогда не верили в истории о встречах с инопланетянами, но в растерянности от увиденного и невольно думаете: «А может, это НЛО?!»

Байесовские рассуждения повторяют ход ваших мыслей, когда вы столк­нулись с новой ситуацией — заметить сделанные вероятностные предположения и, основываясь на этих предположениях, обновить представления о мире.

В ситуации с НЛО вы уже прошли весь цикл байесовского анализа, а именно:

1) получили данные;

2) сформулировали гипотезу;

3) пересмотрели свои представления, основываясь на новых данных.

Эти рассуждения обычно происходят так быстро, что вы не успеваете проанализировать собственные мысли. Вы обновили представления о мире, не задаваясь лишними вопросами: хотя до этого вы и не верили в НЛО, после этого происшествия вы пересмотрели свои взгляды и теперь уверены, что увидели летающую тарелку.

В этой главе мы сосредоточимся на том, как упорядочить свои представления о мире, и на том, как возникают новые суждения, чтобы взглянуть на них более строго. К числам мы перейдем в следующих главах.

Рассмотрим все этапы наших рассуждений, начиная с получения данных.

Получение данных

Ключевая идея байесовских рассуждений — делать выводы, исходя из имеющихся данных. Перед тем как сделать какие-либо выводы о ситуации (например, заявить, что вы видели НЛО), нужно понять полученные данные. В нашем случае:

• ослепительный свет за окном;

• висящий в воздухе объект в форме тарелки.

На основании прошлого опыта вы можете описать картину за окном как неожиданную. На вероятностном языке это можно записать так:

P (яркий свет за окном, тарелкообразный объект в небе) = очень низкая,

где P — обозначение для вероятности, а данные перечислены в скобках. Это равенство можно прочитать как: «Вероятность наблюдать яркий свет за окном и тарелкообразный объект в небе очень низкая». Рассматривая совместную вероятность нескольких событий, перечисляем эти события через запятую. Заметим (это важно, как мы увидим дальше!), что в этих данных нет ни слова об НЛО: они состоят только из наблюдений. Можно также рассматривать вероятности отдельных событий, они будут записываться так:

P (дождь) = весьма высокая,

что расшифровывается как: «Вероятность дождя весьма высокая».

В сценарии про НЛО мы должны определить вероятность того, что произойдут одновременно оба события. Вероятность только одного из этих событий будет совсем другой. Например, источником яркого света легко может оказаться проезжающая машина, так что вероятность одного этого события гораздо больше, чем совместно с наблюдением «тарелки» («тарелка» весьма неожиданна сама по себе).

Так как же определить вероятности? Пока обратимся к интуиции — общим представлениям о том, насколько ожидаемы события. В следующей главе мы увидим, как придать вероятностям точные числовые значения.

Априорные предположения и условная вероятность

Встать утром, заварить кофе и поехать на работу — задачи, не требующие от вас аналитических усилий. У вас есть априорные предположения (prior beliefs) о том, как устроен мир. Наши априорные предположения — набор представлений, сформированных за годы жизни (то есть на основе наблюдения за данными!). Вы уверены, что взойдет солнце — оно восходило каждый день, начиная с вашего рождения. Вы можете также предполагать, что если на перекрестке для вас зеленый свет, а для перпендикулярного потока — красный, то можно безопасно проезжать перекресток. Без априорных предположений мы каждый вечер ложились бы спать с ужасом, что завтра солнце может не взойти, а на каждом перекрестке останавливались бы, пристально вглядываясь в приближающиеся машины.

Наши априорные предположения подсказывают, что одновременно увидеть за окном яркий свет и нечто вроде тарелки в небе — весьма редкий случай. По крайней мере, на Земле. Однако живи вы на далекой планете, кишащей летающими тарелками и постоянно посещаемой космическими пришельцами, вероятность увидеть огни и тарелки была бы гораздо выше.

Поэтому мы вводим в формулу наши априорные предположения, отделяя их вертикальной чертой |:

 

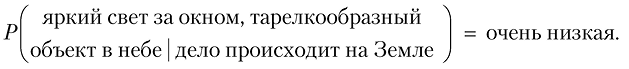
Это равенство читается так: «Вероятность наблюдать яркий свет за окном и тарелкообразный объект в небе при условии, что дело происходит на Земле, очень низкая».

Такая вероятность называется условной — мы оцениваем вероятность события при некотором условии. В данном случае условия — наш прошлый опыт.

Для вероятности использовалось обозначение P. Часто мы также используем короткие обозначения для событий и условий. Если вы не привыкли к уравнениям, они могут казаться слишком сжатыми. Но через некоторое время вы увидите, как короткие названия переменных упрощают чтение и помогают обобщать равенства в целые классы задач.

Так, все наши данные мы будем обозначать одной буквой D:

D= яркий свет за окном, тарелкообразный объект в небе.

С этого момента, когда мы говорим о вероятности нашего набора данных, то пишем просто P (D). Аналогично для априорных предположений мы будем использовать переменную X, например:

X= дело происходит на Земле.

Теперь мы можем обозначать вероятность как P (D | X). Смысл не поменялся, а запись стала намного проще.

Множественные условия

Если на вероятность могут влиять несколько факторов, можно использовать более одного априорного предположения. Допустим, дело происходит под Новый год и ваш опыт говорит вам, что в Новый год часто запускают фейерверки. Если дело происходит на Земле, а на календаре при этом 1 января, увидеть в небе огни уже не так неожиданно, да и сама тарелка может оказаться причудливым фейерверком. Теперь уравнение выглядит так:

 

При учете обоих условий наша условная вероятность превращается из «очень низкой» в просто «низкую».

Априорные предположения на практике

В статистике весь наш прошлый опыт обычно не вводится как явное условие, его существование предполагается неявно. Поэтому здесь мы не будем вводить для этого условия отдельную переменную. Однако в байесовском анализе очень важно помнить, что наше понимание мира всегда обусловлено прошлым опытом. Всю эту главу переменная «дело происходит на Земле» будет сохраняться.

Построение гипотезы

Итак, у нас имеются данные D (мы видели яркий свет и тарелкообразный объект) и наш прошлый опыт X. Чтобы объяснить, что же мы увидели, следует выдвинуть некоторую гипотезу — модель мира, которая даст какое-то предсказание. Гипотезы бывают разными. По сути, все наши основные представления о мире — гипотезы:

• если вы верите, что Земля вертится, вы можете предсказать, что Солнце будет всходить и заходить в определенное время;

• если вы верите, что бейсбольная команда, за которую вы болеете, — самая сильная, то можете предсказать, что они будут выигрывать чаще других команд;

• если вы верите в астрологию, то можете предсказать, что расположение звезд говорит о людях и событиях.

Гипотезы могут быть и более формальными или сложными:

• ученый может строить гипотезу, что некоторое лекарство замедлит развитие рака;

• финансовый аналитик может строить модель ситуации на рынке;

• глубокая нейронная сеть может определять, на каких картинках изображены животные, а на каких — растения.

Все это — примеры гипотез, в них заложен некоторый способ понимания мира, и он используется для предположения о том, что будет происходить. Говоря о гипотезах в байесовской статистике, мы обычно интересуемся, насколько хорошо они предсказывают наблюдаемые нами данные. Когда после увиденного вы думаете: «НЛО!» — то выдвигаете гипотезу. Гипотеза об НЛО, скорее всего, основана на бесчисленных фильмах и телепередачах, просмотренных ранее. Обозначим нашу первую гипотезу так:

H1= НЛО у меня во дворе!

Но что же предсказывает эта гипотеза? «Задним числом» можно спросить: «Что вы ожидали бы увидеть, если бы у вас во дворе приземлилось НЛО?» И ответ был бы таким: «Яркий свет и объект в форме тарелки». Так как гипотеза H1 предсказывает данные D, то, когда мы наблюдаем эти данные при условии верности гипотезы, их вероятность повышается. Формально это записывается как:

P (D | H1, X) >> P (D | X).

Это равенство читается так: «Вероятность увидеть яркий свет за окном и тарелкообразный объект в небе при условии, что это НЛО, и при моем прошлом опыте намного больше (что показано двумя знаками «больше»: >>), чем просто увидеть яркий свет за окном и тарелкообразный объект в небе без объяснений». Здесь используется язык теории вероятностей, чтобы показать, что гипотеза объясняет имеющиеся данные.

Гипотезы в обычной речи

Легко заметить связь вероятности с тем, как мы говорим в обычной жизни. Сказать, что нечто «неожиданно» — это как сказать, что эти данные имеют низкую вероятность на основании нашего прошлого опыта. Слова, что нечто «правдоподобно», могут означать, что данные имеют большую вероятность на основании наших априорных предположений. Сейчас такие переформулировки кажутся очевидными, но суть вероятностных рассуждений — следить, как вы интерпретируете данные, строите гипотезы и меняете представления даже в обычной жизни. Без гипотезы H1 вы были бы в растерянности и не смогли бы объяснить наблюдаемые данные.

Сбор дополнительных доказательств и обновление представлений

Итак, у вас есть данные и гипотеза. Однако с учетом вашего предыдущего опыта (а вы всегда были скептиком) гипотеза все еще смотрится диковато. Чтобы прийти к более надежным выводам, нужно собрать больше данных. Это следующий шаг в статистических рассуждениях (впрочем, в жизни мы интуитивно делаем то же самое). Чтобы собрать больше данных, надо провести новые наблюдения. В нашем сценарии вы выглядываете в окно, чтобы осмотреться.

Вы видите, что источников света вокруг уже несколько, что «тарелка» удерживается канатами, замечаете оператора с камерой, слышите хлопок и крик: «Стоп! Снято!»

Наверняка вы тут же поменяли мнение о том, что случилось. До этого вы думали, что видите НЛО. Но новые данные говорят, что, кажется, рядом снимают кино. Ваш мозг только что за секунды провел сложный байесовский анализ! Разберем подробнее, что же произошло.

Исходная гипотеза:

H1= Приземлилось НЛО!

Сама по себе, при условии вашего прошлого опыта, такая гипотеза крайне маловероятна:

P (H1 | X) = очень-очень низкая.

Но это была единственная толковая гипотеза, которую можно было построить при имеющихся данных. После получения дополнительных данных вы немедленно приходите к другой возможной гипотезе — рядом снимают кино:

H2= За окном снимают кино.

Вероятность этой гипотезы самой по себе также представляется очень низкой (если вы не живете рядом с киностудией):

P (H2 | X) = очень низкая.

Заметим, что мы присвоили H1 «очень-очень низкую» вероятность, а H2 просто «очень низкую». Это согласуется с житейской интуицией. Если бы у вас спросили (без всяких дополнительных данных),  что более правдоподобно: ночное появление рядом НЛО или съемки фильма по соседству, вы бы ответили, что съемки правдоподобнее визита пришельцев.

Теперь нам нужно понять, как учитывать новые данные при пересмотре представлений.

Сравнение гипотез

Сначала вы приняли гипотезу об НЛО, несмотря на ее неправдоподобие, поскольку иных объяснений не было. Но теперь есть другое возможное объяснение — киносъемки, так что появилась альтернативная гипотеза. Рассмотреть альтернативную гипотезу — значит сравнить теории, используя имеющиеся данные.

Когда вы видите канаты, съемочную группу и свет, меняются данные. Обновленные данные выглядят так:

Dобнов.= яркий свет, объект в форме тарелки, канаты, съемочная группа, другие источники света и т.д.

Получив дополнительные данные, вы меняете мнение о том, что происходит.

Разобьем этот процесс на байесовские шаги. Ваша исходная гипотеза, H1, сначала объясняла все данные, но после дополнительных наблюдений H1 уже не может это сделать. Это можно записать так:

P (Dобнов. | H1, X) = очень-очень низкая.

Теперь у вас есть новая гипотеза, H2, объясняющая данные гораздо лучше, то есть:

P (Dобнов. | H2, X) >> P (Dобнов. | H1, X).

Ключевой момент — сравнить, насколько хорошо две гипотезы объясняют наблюдаемые данные. Говоря, что вероятность наших данных при условии второй гипотезы намного больше, чем при условии первой, мы сообщаем, что вторая гипотеза объясняет наблюдения лучше. Это подводит нас к сути байесовского анализа: проверкой убеждений является то, насколько хорошо они объясняют мир. Мы считаем, что некоторые представления правильнее других, поскольку они лучше объясняют наблюдаемые вокруг явления. Математически мы выражаем нашу идею как отношение двух вероятностей:

.

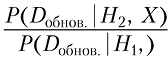
Большое отношение, например 1000, означает, что «H2 объясняет данные в 1000 раз лучше, чем H1». Так как H2 объясняет данные во много раз лучше, чем H1, мы меняем наши представления с H1 на H2. Именно это произошло, когда вы поменяли мнение о наблюдаемом явлении. Теперь вы считаете, что увидели за окном киносъемки, и это более правдоподобное объяснение для имеющихся данных.

Данные влияют на представления, но не наоборот

Напоследок стоит подчеркнуть: абсолютны и неоспоримы во всех наших примерах только данные. Гипотезы меняются, опыт X различен для разных людей, но данные D одинаковы для всех. Рассмотрим две формулы. Первую мы использовали на протяжении всей главы:

P (D | H, X).

Она означает вероятность данных с учетом гипотезы и опыта, проще говоря, «насколько хорошо мои представления объясняют наблюдаемое».

Но можно обратить ее (что мы часто делаем в обычной жизни):

P (H | D, X).

Получим «вероятность моих представлений при условии данных и опыта», то есть «насколько хорошо то, что я вижу, согласуется с моими убеждениями».

В первом случае мы меняем представления о мире в соответствии с собранными данными. Во втором — собираем данные для поддержки имеющихся представлений.

Байесовский стиль мышления основан на пересмотре и изменении представлений о мире. Реальны только данные, а наши представления о мире должны с ними согласовываться. В жизни нужно быть готовым поменять свое мнение. Когда съемочная группа собирается уезжать, вы замечаете, что на всех машинах армейская символика. Группа снимает куртки, под ними — военная форма, и кто-то говорит: «Если кто-то это видел, то мы точно его обдурили. Отличная работа!» С такими новыми данными вы наверняка еще раз поменяете мнение!

Заключение

Повторим, что мы узнали. Наши представления о мире исходно основаны на имеющемся опыте X. Полученные данные D либо согласуются с опытом, P (D | X) = очень высокая, либо оказываются неожиданными, P (D | X) = очень низкая.

Пытаясь объяснить окружающий мир, вы выдвигаете мнение об увиденном, или гипотезу, H. Нередко новая гипотеза позволяет объяснить неожиданные данные, P (D | H, X) >> P (D | X). Получив новые данные или придумав новые идеи, вы можете выдвинуть больше гипотез, H1, H2, H3, … Вы меняете представления о мире, когда новая гипотеза объясняет данные лучше старой:

 

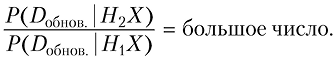
Наконец, важно обращать больше внимания на данные, меняющие представления, а не на поддержку имеющихся представлений, P (H | D).

Итак, мы изучили основы и теперь можем добавить цифры. Далее в части I вы построите математическую модель своих представлений о мире, чтобы точно определить, когда и как их менять.

Упражнения

Попробуйте ответить на эти вопросы, чтобы понять, насколько хорошо вы научились байесовским рассуждениям. Решения можно найти здесь: https://nostarch.com/learnbayes/.

1. Перепишите утверждения ниже, используя математическую нотацию из этой главы:

• вероятность дождя низкая;

• вероятность дождя при условии облачности высокая;

• вероятность, что вы с зонтом при условии дождя, выше, чем просто вероятность, что вы с зонтом.

2. Запишите, используя математические обозначения из этой главы, данные из такой истории. Придумайте гипотезу, объясняющую эти данные.

Вы приходите домой с работы и замечаете, что дверь открыта, а окно разбито. Войдя, вы видите, что вашего ноутбука нет на месте.

3. Дополним историю выше новыми данными. Покажите, как новая информация меняет ваши представления, и придумайте новую гипотезу для объяснения данных. Используйте обозначения из этой главы!

К вам подбегает соседский ребенок и долго извиняется, что случайно попал камнем в ваше окно. Он говорит, что заметил ноутбук и испугался, что его украдут. Открыв дверь, он унес его к себе до вашего прихода.