Ковалев В. В., Уланов В. А.

Курс финансовых вычислений

Учебное издание

Четвертое издание

---

ebooks@prospekt.org

УДК 336.6 : 51 (075.8)
ББК 65.26я73
К56

В. В. Ковалев, В. А. Уланов

В издании представлен обзор основных алгоритмов, используемых при проведении коммерческих и финансовых вычислений. Рассмотрена логика операций дисконтирования и наращения, подробно изложены схемы и алгоритмы оценки денежных потоков, показана эволюция количественных методов оценки финансовых операций. В четвертое издание (1-е изд. — 1999 г.) внесены дополнения в ряд глав, а также существенно расширен библиографический список.

Для преподавателей и студентов экономических вузов, научных и практических работников, специализирующихся в области управления финансами и бухгалтерского учета.

	УДК 336.6 : 51 (075.8)
	ББК 65.26я73

	© В. В. Ковалев, В. А. Уланов, 2013
	© ООО «Проспект», 2013

Не будет преувеличением сказать:

с вычислением коммерсант выступает

на жизненное поприще и с вычислением

сходит в могилу.

Г. Н. Мокеев

Введение

Мы начали книгу словами Григория Николаевича Мокеева – преподавателя одних из лучших в дореволюционной России Высших коммерческих курсов М. В. Побединского. Эти слова, возможно, в гротескной форме, но по сути весьма выпукло и точно подчеркивают значимость методов количественной оценки для успешного ведения бизнеса. Мокеев был не одинок – в начале XX в. многие российские ученые и предприниматели рассматривали меры по совершенствованию финансово-аналитической подготовки будущих коммерсантов как один из факторов, способствующих осуществлению экономических реформ в стране. Профессор Р. Я. Вейцман, один из авторитетнейших теоретиков счетоведения, писал: «Вопрос о постановке преподавания коммерческой арифметики в современной профессиональной школе может считаться вполне актуальным: его следует поставить на очередь и так или иначе разрешить» [I, Вейцман, 1923, с. 3]. Как это ни покажется странным, мысль, высказанная Вейцманом, актуальна и по сей день. Новое издание дополнено тестовыми вопросами для контроля знаний студентов (слушателей). Справедливости ради скажем, что еще в конце 1980-х гг. его слова вряд ли нашли бы отклик не только среди практиков, но и в академической среде; к счастью, в последние годы произошли серьезные изменения в экономике, на которые не могла не прореагировать система образования и подготовки экономических кадров.

Становление рыночных отношений в нашей стране сопровождается появлением относительно новых, по крайней мере для большинства начинающих предпринимателей, навыков и методов, которыми приходится с неизбежностью овладевать при профессиональном занятии бизнесом. К их числу относятся так называемые коммерческие и финансовые вычисления. Суть таких вычислений достаточно очевидна: любая сделка предполагает выполнение расчетов, дающих основание принять решение по поводу целесообразности и эффективности ее проведения. Сложность расчетов может предопределяться различными обстоятельствами, в том числе и уровнем подготовленности участников операции. Многие начинающие бизнесмены, образно говоря, «ощутили на собственной шкуре» последствия необоснованно принятых, непросчитанных решений.

То же самое относится и к обычным гражданам. Финансовая и юридическая безграмотность, правовой нигилизм, незнание базовых законов развития экономики и финансов, неумение и / или нежелание сделать элементарные вычисления, бесцеремонная и, естественно, не всегда корректная реклама, жажда получения сиюминутного «бесплатного» дохода – вот далеко не полный перечень факторов, которые в совокупности могут приводить к весьма печальным последствиям человека, принявшего опрометчивое решение поучаствовать в некоторой операции.

Оказывается, в финансовых вычислениях есть множество вещей, которые только для неискушенного человека очевидны. Например, в финансовом контракте может быть указана некоторая ставка за пользование кредитом, однако фактические расходы по обслуживанию долга могут оказаться существенно выше. Расхожее мнение о том, что схема начисления сложных процентов выгоднее, чем схема начисления простых процентов, справедливо не всегда. Несложно привести и другие примеры подобного рода.

Коммерческие и финансовые вычисления сопровождают нас постоянно; практически нет ни одного человека, который хотя бы раз в жизни не столкнулся с необходимостью сделать какие-то расчеты финансового характера. В последние годы в связи с развитием частного предпринимательства, появлением сети коммерческих банков, свободным ценообразованием, появлением новых финансовых инструментов и инвестиционных возможностей, угрозой инфляции необходимость проведения подобных расчетов становится рутинным делом практически для всех. Из-за финансовой нестабильности в стране даже пенсионеры, никогда прежде не сталкивавшиеся с расчетами рыночного характера, более сложными, нежели расчеты на колхозном рынке, пытаются понять – не лучше ли хранить свои «гробовые» дома в наличной валюте, а не в виде рублевого вклада в каком-то банке.

Как профессиональная область деятельности финансовые расчеты достаточно бурно развиваются в последние десятилетия в связи с появлением новых финансовых инструментов (опционов, фьючерсов, свопов и др.) и, более того, новых направлений деятельности, среди которых следует выделить прежде всего финансовый менеджент и финансовый анализ. Профессия финансового менеджера как специалиста по управлению финансами хозяйствующего субъекта становится все более популярной и востребованной со стороны руководителей компаний. Логика здесь достаточно очевидна, поскольку финансовые потоки в компании представляют собой по сути ее кровеносную систему. Насколько хорошо функционирует эта система, настолько и жизнеспособна компания. Весьма широк и круг, если так можно выразиться, потенциальных соискателей этого звания, в том числе и среди действующих работников аппарата управления предприятий, к которым прежде всего можно отнести значительную часть работников планово-экономической службы, финансового отдела, бухгалтерии.

Относительно экзотичной на современном этапе развития экономики России представляется профессия финансового аналитика как специалиста по рынкам капитала. Эта экзотичность, естественно, носит временный характер и обусловливается относительной неразвитостью рынка ценных бумаг и финансовых институтов. Вместе с тем усилия, предпринимаемые органами власти по развитию этого сектора экономики, безусловно, следует оценить положительно; иными словами, все говорит о том, что в недалеком будущем эта профессия будет в ряду наиболее престижных.

Все эти профессии, равно как и традиционные профессии бухгалтера, финансиста, экономиста, объединяет, в частности, необходимость владения методами финансовых и коммерческих вычислений. Как будет показано в последующих разделах книги, эти методы достаточно просты и не требуют углубленных математических познаний, тем не менее владение ими может иметь далеко идущие последствия для участников сделки. У тех, кто знаком с курсом только по названию, может сложиться впечатление, что описываемые методы нужны лишь банкирам и финансистам, однако это не так, поскольку любая сделка по сути имеет финансовую природу, а значит, должна основываться на некоторых расчетах; кто лучше владеет подобными расчетами, тот и сможет заключить контракт, который по крайней мере не будет ущемлять его интересы.

Приведем несколько вопросов, ответы на которые невозможно дать, не владея некоторыми навыками финансовых вычислений. Предположим, что вы нуждаетесь в банковской ссуде. В одном банке вам предлагают кредит на условиях ежеквартального начисления процентов по ставке α% годовых, в другом – проценты будут начисляться ежегодно, но по ставке β%. Какой вариант предпочтителен? Вы хотите предоставить деньги в долг на девять месяцев своему клиенту. Спрашивается, какую схему начисления процентов целесообразно предусмотреть в договоре? Вы получили долгосрочную ссуду в банке, которую будете гасить частями в течение нескольких лет. Каковы будут ваши расходы по погашению долга, например через два года, и какая часть долга останется к этому времени непогашенной? Вы – держатель векселя и намереваетесь учесть его в банке. Будет ли эта операция доходной или убыточной для вас и можно ли количественно оценить соответствующий доход или убыток? Подобные вопросы можно формулировать десятками, и все они не имеют очевидного ответа, основанного на интуиции. Мы полагаем, что на эти и другие, как более, так и менее сложные вопросы читатель сможет научиться давать ответы после ознакомления с материалами данного пособия.

Книга состоит из шести глав. Первая глава посвящена пояснению логики финансовых операций, введению в терминологию, в том числе и традиционно использовавшуюся в отечественной науке и практике еще в дореволюционное время. Вторая глава посвящена простым процентам и описанию ситуаций, в которых целесообразно их применение. В третьей главе рассмотрены сложные проценты, а также некоторые смежные вопросы, в частности непрерывное наращение, конвертация валюты и др. В четвертой главе рассмотрены денежные потоки, показано, каким образом схемы начисления процентов используются для их оценки. Пятая глава посвящена некоторым приложениям финансовых вычислений. В ней изложены задачи, возникающие при погашении долгосрочной задолженности, при принятии решений по инвестиционным проектам, при оценке акций и облигаций. Методы количественного анализа финансовых операций недетерминированного характера обсуждены на примере страхования. Последняя, шестая, глава представляет собой краткий экскурс в историю становления коммерческих и финансовых вычислений в России, подготовленный в результате обзора доступной литературы XVII – начала XX в.

Следует подчеркнуть особо, что в области финансовых и коммерческих расчетов в нашей стране имеются весьма солидные наработки ученых и практиков, работавших в этой области в дореволюционной России. К сожалению, имена многих из них практически неизвестны современному читателю. Отдавая должное этим специалистам, мы сочли возможным привести достаточно полный библиографический список, включающий по существу все наиболее значимые работы по данной тематике. Любопытный читатель может ознакомиться с некоторыми из этих работ (см. список литературных источников в библиографии в конце книги) и убедиться в том, насколько большое внимание уделялось этой дисциплине в России накануне революции. Часть монографий и пособий по финансовым вычислениям, появившихся в последние годы в нашей стране, также приведена в библиографии. Читатели, заинтересованные в более подробной информации исторического характера, в частности в отношении роли отдельных ученых в становлении данной науки, в оценке взаимосвязи коммерческих вычислений и бухгалтерского учета и т. д., смогут сделать это по первоисточникам из приведенного списка.

Для того чтобы сделать более наглядной приведенную в конце книги библиографию, авторы сочли возможным представить ее в виде двух списков. В первый (список I) включены монографии и учебно-методические пособия, изданные (главным образом) в России и СССР до середины 30-х годов, когда по сути завершается процесс централизации управления бухгалтерским учетом, финансами, банковскими операциями. Во второй (список II) включена литература, вышедшая в нашей стране и за рубежом в послевоенные годы (естественно, в этом списке приведены далеко не все работы, опубликованные по данной тематике). Что касается зарубежной литературы, приведенной в библиографическом списке, то авторы решили ограничиться лишь наиболее доступными российскому читателю изданиями. При ссылке в тексте книги на соответствующий источник номер списка указан римской цифрой перед фамилией автора или названием книги.

В этой книге мы не только попытались обобщить и систематизировать известные методы финансового анализа, но и приводим некоторые расчеты и результаты, либо мало или вообще не освещавшиеся ранее, либо встречавшиеся в других работах в иной интерпретации. В частности, процентная и учетная ставки, дисконт-фактор определяются за период времени, в течение которого осуществляется простейшая финансовая операция, и этот период необязательно равен году. Подробно обсуждаются соотношения между этими показателями, производится качественный анализ процентной ставки. Приведены определения широко применявшихся в довоенной российской (советской) практике таких понятий, как проценты «со 100», «на 100», «во 100». Устанавливается связь величины дохода с введенными понятиями, часто используемыми в тексте для характеристик и пояснений различных способов наращения и дисконтирования. Представлен факторный анализ учета векселя. Тщательно обсуждаются задачи замены платежей и их консолидация при использовании простых ставок, при этом в явном виде приводится ряд формул для решения частных случаев такого рода задач. При анализе процесса наращения сложными процентами за период, отличающийся от целого числа лет, кроме традиционно освещаемых в литературе двух схем (сложных процентов и смешанной) предлагаются и другие способы начисления процентов.

Несмотря на кажущуюся простоту рассматриваемых методов, овладение ими потребует от читателя определенных усилий, поскольку в большинстве случаев в книге приведены выводы и доказательства основных формул. Сделано это не ради собственно доказательств – мы убеждены в том, что лишь понимая сущность той или иной расчетной формулы, читатель сможет эффективно пользоваться ею. К тому же доказательства фактически часто предоставляют методы, позволяющие самостоятельно выводить многочисленные соотношения при решении задач финансового характера, не отраженных в книге. Дело в том, что все разнообразные ситуации, возникающие на практике, невозможно рассмотреть и проанализировать, да в этом и нет необходимости. Поэтому полезно знать не только основные формулы, но и то, как они получены. Однако, чтобы не усложнять изложения курса, авторы опускают доказательства ряда соотношений, поскольку они предполагают достаточно свободное владение математикой (например, доказательства неравенств между множителями наращения простыми и сложными процентами; соотношения между наращенными суммами при применении только сложных процентов и смешанной схемы и т. п.). Тем не менее авторы предлагают читателю выполнить самостоятельно строгое обоснование просто приведенных результатов для лучшего усвоения материала.

Нередко формулы в этой книге приводятся в общем виде (например, для наращения при конвертации, для составления уравнений эквивалентности), что позволяет затем легко получить большое количество соотношений для любых конкретных ситуаций. Причем, несмотря на общность, эти формулы имеют простой и наглядный смысл. При необходимости корректность новой интерпретации тех или иных формул подтверждается соответствующими выводами.

Авторы стремились сделать книгу полезной прежде всего в практическом плане – именно поэтому в ней приведено достаточно много примеров (около 200), позволяющих, с одной стороны, лучше почувствовать логику и смысл предлагаемых методов, а с другой стороны, помочь читателю овладеть навыками в применении тех или иных вычислительных процедур. При этом необходимо иметь в виду следующее предостережение: знак равенства, встречающийся в решении числовых примеров, не надо понимать буквально. В ряде случаев этот знак действительно отражает равенство, но во многих случаях вместо него, строго следуя правилам математики, необходимо было бы писать знак приближенного равенства. Однако в финансовых вычислениях излишняя точность далеко не всегда приносит фактическую пользу, да и точность вычисления часто зависит от используемых таблиц. Как это обычно принято в аналогичных пособиях, мы, как правило, будем писать знак равенства, хотя, возможно, в том или ином случае строгого равенства (с математической точки зрения) и нет. Знак приближенного равенства будет применяться только в тех случаях, когда необходимо специально указать на приближенный характер вычислений или вид формул. В примерах часто использованы условные данные, так как цель авторов – продемонстрировать технику и методы финансовых вычислений. Заметим, что приведенные расчеты не зависят ни от выбора денежной единицы, ни от выбора ставки.

Мы сознательно не приводим примеров выполнения финансовых вычислений с помощью компьютерных технологий. Хотя использование компьютерных программ расчета основных финансовых показателей позволяет без особых размышлений быстро получить искомый результат, главное при этом – не ошибаться в синтаксисе. Однако в этом случае теряется финансовый смысл применяемых формул и решение более сложных задач, не охваченных компьютерными программами, вызывает подчас немалые трудности. Для того чтобы осознанно использовать пакеты многочисленных электронных таблиц, необходимо, по нашему мнению, вначале основательно ознакомиться с основополагающими понятиями и алгоритмами в финансовых вычислениях и овладеть простейшими расчетными схемами. Без этого нельзя правильно и эффективно применять формулы при расчетах (пусть и компьютерных) и грамотно освоить навыки в использовании сравнительно простых, но многочисленных вычислительных процедур.

В последнее время широкое распространение при проведении финансово-экономических расчетов получил табличный процессор Excel. Существует много книг, подробно излагающих как основы работы в Excel, так и осуществление с его помощью всевозможных расчетов, в частности и финансового характера. Среди таких книг мы рекомендуем следующую [II, Пикуза и др.].

При осуществлении финансовых расчетов необходимо активно использовать все средства в равной степени, будь то финансовые таблицы, финансовый калькулятор или персональный компьютер. Многие расчеты можно провести быстро и эффективно с использованием только финансовых таблиц. При решении ряда задач (например, определения внутренней нормы прибыли) несомненную помощь оказывает именно компьютер.

Второе издание книги, которое стало основой для третьего, существенно отличалось от предыдущего. Во-первых, книга реструктурирована, а все ее разделы переработаны и дополнены новыми материалами. Во-вторых, авторы попытались по возможности освободиться от излишней математизации некоторых разделов, иногда пугающей отдельных практиков. Значительно большее внимание уделено финансово-экономическому наполнению излагаемых материалов. В-третьих, для удобства пользователей авторы ввели раздел, описывающий минимум формул, достаточный для выполнения многих финансово-аналитических расчетов. В-четвертых, введена новая глава, в которой систематизированы наиболее важные сферы приложения финансовых вычислений. В-пятых, авторы значительно расширили и реструктурировали исторический раздел, имея в виду дать читателю хотя бы самое общее представление об эволюции той теоретической базы, на которой зиждятся современные финансовые вычисления. В настоящем издании приведены как переработанные, так и новые приложения. В пособие включены также тестовые вопросы для контроля знаний студентов (слушателей). Кроме вопросов качественного характера тесты могут содержать и задачи. Поэтому при составлении тестов приведенные в книге вопросы рекомендуется дополнять несложными в расчетах тестовыми задачами, в качестве которых можно, в частности, использовать задачи из книги [II, Уланов].

В заключение отметим, что значимость рассматриваемых в книге материалов для подготовки экономистов высшей квалификации уже не оспаривается ведущими учеными и практиками. Тем не менее рецидивы скептического отношения к финансовым вычислениям еще встречаются, в частности, в высказываниях либо некоторых «чистых» математиков, пытающихся «прислониться» к прикладным экономическим разработкам путем бездумной их математизации, когда в угоду красоте математических выкладок выхолащивается экономическая природа изучаемого явления, либо отдельных специалистов, работающих в смежных с бухгалтерско-финансовым блоком дисциплинах (автоматизированные системы управления, математическое моделирование экономических процессов и т. п.). Выдвигаемый ими в качестве аргумента тезис, как «заезженная пластинка», повторяет уже не раз слышанное: «В финансовых и коммерческих вычислениях пользуются простым инструментарием, доступным даже школьнику, а потому в университетах следует читать не финансовые вычисления, а финансовую математику»1.

В этой связи прежде всего хочется напомнить, что любые самые сложные вычислительные операции сводятся в известном смысле к четырем элементарным арифметическим действиям. (Вспомним слова Мирабо о том, что «зная только четыре правила арифметики, можно вполне содержать финансы в порядке».) Кроме того, с позиции бухгалтеров и финансистов, не абстрактная финансовая математика, а именно финансовые вычисления представляют практический интерес. Финансовые стохастические модели, безусловно, можно, а для некоторых узких специалистов и следует, рассматривать в спецкурсах, что же касается базового математико-аналитического аппарата, к которому с очевидностью относятся методы, обсуждаемые в курсе финансовых вычислений, то им должен владеть любой экономист высшей квалификации.

По мнению авторов, научность и значимость любой университетской дисциплины в области прикладной экономики отнюдь не определяются одной лишь сложностью используемого в ней математического инструментария, а пробелы в базовом экономическом образовании, да и в математическом тоже, нигде не проявляются так явно, как в необоснованной математизации процесса принятия управленческого решения. Именно поэтому хочется подчеркнуть, что, обосновывая базовые методы финансовой аналитики, во главу угла нужно ставить экономическую, финансовую природу операции; что касается используемого математического аппарата, то он имеет лишь вспомогательное значение.

Иными словами, для менеджера приоритетом является ответственность за возможные последствия принятого им решения. Так, непродуманно составленный договор о некоторой финансовой операции (ставка, частота и схема начисления, поправка на инфляцию и т. п.) может привести к существенным финансовым потерям независимо от того, какой сложности модель была использована, например, для прогнозирования денежного потока. Какими методами обосновано решение – это уже другой вопрос; ясно только одно: обоснование с помощью хитроумной математической модели далеко не всегда минимизирует негативные последствия.

Хотя выполняемые расчеты выглядят несложными, методы финансовых вычислений исключительно важны именно в практической плоскости, и, кроме того, они не приходят к специалисту автоматически вместе с дипломом о высшем или специальном образовании. Невозможно стать финансовым менеджером, лишь читая общетеоретические монографии, учебники и руководства, – нужны рутинная вычислительная практика, умение ориентироваться в методах, привлекаемых для получения ряда оценок, которые можно использовать как формализованное обоснование принимаемого решения в области кредитования и финансирования. Именно этому и посвящено данное пособие – в нем не только объяснена логика количественного обоснования финансовых операций, но и приведено множество примеров и задач, решая которые можно, образно говоря, «набить руку» на исчислении подобных оценок. Большое количество подробно разобранных примеров и задач для самостоятельного решения можно найти в сборнике задач [II, Уланов], который тесно связан с данным пособием и в котором, в частности, поэтому используются такие же обозначения.

Авторы надеются, что книга будет полезна как начинающим финансистам и бухгалтерам, так и опытным специалистам. Наконец, уместно упомянуть о том, что любая конструктивная критика будет воспринята авторами с благодарностью.

Глава 1. Логика финансовых операций в рыночной экономике

1.1. Временная ценность денег

Переход к рыночной экономике сопровождается появлением некоторых видов деятельности, имеющих для финансового менеджера предприятия принципиально новый характер. К их числу относится за дача эффективного вложения денежных средств. В условиях централизованно планируемой экономики на уровне обычного предприятия такой задачи практически не существовало. Причин было несколько.

Прежде всего ни юридические, ни физические лица официально, как правило, не располагали крупными свободными денежными средствами. В частности, денежные ресурсы предприятия жестко лимитировались прямыми или косвенными методами. Так, наличные деньги лимитировались путем установления Государственным банком максимального размера денежных средств, который мог находиться в кассе на конец рабочего дня. Сумма средств на расчетном счете ограничивалась косвенными методами, главным образом, путем изъятия средств в бюджет в конце отчетного периода, а также путем введения довольно жестких нормативов собственных оборотных средств.

Еще одна причина состояла в том, что практически единственный путь использования свободных денег был связан с размещением их под проценты в сберегательном банке. Стабильность экономического развития, оказавшаяся, как теперь принято говорить, застоем, гарантировала в этом случае не только сохранность денежных средств, но и их небольшой рост.

Ситуация резко изменилась в последние годы. Можно выделить как минимум шесть основных моментов. Во-первых, были упразднены многие ограничения, в частности нормирование оборотных средств, что автоматически исключило один из основных регуляторов величины финансовых ресурсов на предприятии.

Во-вторых, кардинально изменился порядок исчисления финансовых результатов и распределения прибыли. С введением новых форм собственности стало невозможным изъятие прибыли в бюджет волевым методом, как это делалось в отношении государственных предприятий, благодаря чему у предприятий появились свободные денежные средства.

В-третьих, как уже упоминалось выше, произошла существенная переоценка роли финансовых ресурсов, т. е. появилась необходимость грамотного управления ими, причем в различных аспектах – по видам, по назначению, во времени и т. д.

В-четвертых, появились принципиально новые виды финансовых ресурсов, в частности возросла роль денежных эквивалентов, в управлении которыми временной аспект имеет решающее значение.

В-пятых, произошли принципиальные изменения в вариантах инвестиционных политики. Переход к рынку открывает новые возможности приложения капитала: вложения в коммерческие банки, участие в различного рода рисковых предприятиях и проектах, приобретение ценных бумаг, недвижимости и т. д. Размещая капитал в одном из выбранных проектов, финансовый менеджер планирует не только со временем вернуть вложенную сумму, но и получить желаемый экономический эффект.

В-шестых, в условиях свойственной переходному периоду финансовой нестабильности, проявляющейся в устойчиво высоких темпах инфляции и снижении объемов производства, стало невыгодным хранить свои деньги даже в государственном банке. Многие предприятия на своем опыте познали простую истину: в условиях инфляции денежные ресурсы, как и любой другой вид активов, должны обращаться и, по возможности, быстрее.

Таким образом, деньги приобретают еще одну характеристику, доселе неведомую широкому кругу людей, но объективно существующую, а именно – временную ценность (time-value of money). Этот параметр можно рассматривать в двух аспектах.

Первый аспект связан с обесценением денежной наличности с течением времени. Представим, что предприятие имеет свободные денежные средства в размере 15 млн руб., а инфляция, т. е. обесценение денег, составляет 20 % в год. Это означает, что уже в следующем году, если хранить деньги «в чулке», они уменьшатся по своей покупательной способности и составят в ценах текущего дня лишь 12,5 млн руб.

Второй аспект связан с обращением капитала (денежных средств). Для понимания существа дела рассмотрим простейший пример.

Пример

Предприятие имеет возможность участвовать в некоторой деловой операции, которая принесет доход в размере 10 млн руб. по истечении двух лет. Предлагается выбрать вариант получения доходов: либо по 5 млн руб. по истечении каждого года, либо единовременное получение всей суммы в конце двухлетнего периода.

Даже на житейском уровне очевидно, что второй вариант получения доходов явно невыгоден по сравнению с первым. Это проистекает из того, что сумма, полученная в конце первого года, может быть вновь пущена в оборот и, таким образом, принести дополнительные доходы. На первый взгляд, такой вывод очевиден и не требует каких-то специальных знаний. Однако проблема выбора моментально усложнится, если немного изменить условие задачи; например, доходы таковы: в первый год – 4 млн руб., а во второй – 5 млн руб. В этом случае уже не очевидно, какой вариант предпочтительнее. Приведенный пример можно усложнять и дальше, вводя дополнительные условия: инфляция, стохастичность величины доходов, выплачиваемых единовременно и периодически, оказание дополнительных услуг и т. п.

Проблема «деньги – время» не нова, поэтому уже разработаны удобные модели и алгоритмы, позволяющие ориентироваться в истинной цене будущих доходов с позиции текущего момента и сравнивать разновременные денежные суммы. Коротко охарактеризуем их в теоретическом и практическом аспектах.

1.2. Операции наращения и дисконтирования

Логика построения основных алгоритмов достаточно проста и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы PV с условием, что через некоторое время t будет возвращена большая сумма FV. Результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя – прироста (FV–PV), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным показателем – ставкой. Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой можно брать либо PV, либо FV. Таким образом, ставка за время t рассчитывается по одной из двух формул:

В финансовых вычислениях первый показатель имеет названия «процентная ставка», «ставка процента» (interest rate, rate of interest), «процент», «рост», «норма прибыли» (rate of return), «доходность», а второй – «учетная ставка» (discount rate), «дисконтная ставка», «дисконт». Очевидно, что обе ставки взаимосвязаны, т. е. зная один показатель, можно рассчитать другой:

Оба показателя могут выражаться либо в десятичных дробях, либо (как правило, на практике) в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения: в формуле (1.1) – исходная сумма, в формуле (1.2) – возвращаемая (ожидаемая) сумма. Из определения показателей следует, что r_t>0 и 0<d_t<1. Случай r_t=0 и d_t=0 не рассматривается, так как тогда FV=PV (сколько дают в долг, столько и получают назад) и можно считать, что финансовой сделки как таковой просто нет. Случаю же d_t=1 соответствует PV=0, т. е. не предоставляя никакой суммы в долг, через некоторое время t получаем FV, тем самым фактически осуществляя грабеж.

Как же соотносятся между собой эти показатели? Очевидно, что всегда d_t<r_t, но поскольку также d_t<1, то d_t<min(r_t,1). Последнее неравенство позволяет по процентной ставке r_t лучше оценить учетную ставку d_t, чем это можно сделать, например, используя неравенство d_t<1. Так при r_t=0,08 (т. е. r_t=8%) из d_t<min(0,08;1) следует d_t<0,08, что является существенно более точной оценкой d_t, чем d_t<1.

Степень расхождения между r_t и d_t зависит от уровня процентных ставок, имеющих место в конкретный момент времени. Так, если r_t=7%, то d_t=6,54%, т. е. расхождение сравнительно невелико; если r_t=70%, то d_t=41,18%, т. е. ставки существенно различаются по величине.

Такой вывод легко обосновать, используя следующие соображения. В силу того что 0<d_t<1, справедливо

Поэтому

Если величина d_t достаточно мала, то, пренебрегая в правой части равенств всеми членами, начиная со второго, получим r_t≈d_t. В частности, если d_t=0,074 (что равносильно d_t=7,4%), то пренебрегаем членами d_t²=0,005476, d_t³=0,0004052 и т. д.

В прогнозных расчетах, например при оценке инвестиционных проектов, как правило, имеют дело с процентной ставкой, хотя обычно это не оговаривается. Объяснение этому может быть, например, таким. Во-первых, анализ инвестиционных проектов, основанный на формализованных алгоритмах, может выполняться лишь в относительно стабильной экономике, когда уровни процентных ставок невелики и сравнительно предсказуемы в том смысле, что их значения не могут измениться в несколько раз или на порядок, как это имело место в России в переходный период от централизованно планируемой экономики к рыночной экономике. Если вероятна значительная вариабельность процентных ставок, должны применяться другие методы анализа и принятия решений, основанные, главным образом, на неформализованных критериях. При разумных значениях ставок расхождения между процентной и дисконтной ставками, как мы видели, относительно невелики и потому в прогнозных расчетах вполне может быть использована любая из них. Во-вторых, прогнозные расчеты не требуют какой-то повышенной точности, поскольку результатами таких расчетов являются ориентиры, а не «точные» оценки. Поэтому, исходя из логики подобных расчетов, предполагающих их многовариантность, а также использование вероятностных оценок и имитационных моделей, излишняя точность не требуется.

Кроме введенных показателей часто используют величину, называемую дисконт-фактором (discount-factor):

Дисконт-фактор показывает, какую часть сумма PV составляет в сумме FV. Очевидно, что 0<v_t<1 и между тремя показателями справедливо соотношение d_t=v_tr_t. Дисконт-фактор v_t может выражаться и в процентах.

Удобной и наглядной характеристикой (особенно при оценке вклада) является индекс роста B_t суммы PV за время t:

Как и прочие введенные показатели, величина B_t выражается либо в десятичных дробях, либо в процентах. Индекс роста показывает, во сколько раз увеличилась первоначальная сумма за время t. Зная B_t, можно вычислить и другие показатели. В частности, из (1.5) следует, что r_t = B_t — 1.

Пример

Сумма PV = 2 тыс. руб. за полтора года возросла до FV = 4,6 тыс. руб. Полагая t =1,5 года, получим

(или 130 %). Таким образом, первоначальная сумма за полтора года возросла в 2,3 раза или, что то же самое, увеличилась на 130 %.

Индекс роста за данный период показывает, во сколько раз выросла величина капитала по отношению к величине капитала в конце предыдущего периода. Поэтому, если известны индексы роста

за соответственно периоды времени t₁,t₂,...,t_k и эти периоды расположены последовательно друг за другом, то индекс роста за время t=t₁+t₂+...+t_k будет равен величине:

Следовательно, если в первый год капитал вырос в 1,2 раза, во второй год общий капитал вырос в 1,7 раза и в третий год вся сумма увеличилась в 1,3 раза, то индекс роста капитала за 3 года составит:

Итак, в любой простейшей финансовой сделке всегда присутствуют три величины, две из которых заданы, а одна является искомой.

Процесс, в котором заданы исходная сумма и ставка, в финансовых вычислениях называется наращением (accumulation, accretion), искомая величина – наращенной суммой (accumulated value, amount), а ставка – ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процессом дисконтирования (discounting), искомая величина – приведенной суммой, а ставка – ставкой дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором – о движении от будущего к настоящему (рис. 1.1).

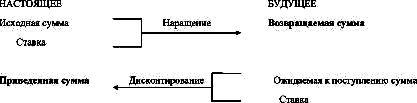
Рис. 1.1. Логика финансовых операций

Экономический смысл финансовой операции, задаваемой формулой (1.1), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (1.1):

то FV>P V (так как 1+r_t>1), т. е. время генерирует деньги.

Естественно, такой же вывод можно сделать, используя формулу (1.2), так как из нее следует, что

и справедливо неравенство 1–d_t<1.

Разность I=FV–PV называется процентом (interest), или процентными деньгами. Это – величина дохода от предоставления в долг денежной суммы PV. (В математике процентом называют сотую долю некоторого числа, что, естественно, отличается от экономического понятия «процент».)

Используя равенство FV=PV+I, формулу (1.7) можно проиллюстрировать таким образом (рис. 1.2):

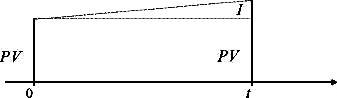
Рис. 1.2. Образование наращенной суммы

В качестве ставки наращения может выступать как процентная, так и учетная ставка. Если наращенная сумма FV находится по формуле (1.7), то ставкой наращения является процентная ставка. С другой стороны, из (1.8) следует, что наращенную сумму можно определять по формуле

, поэтому в этом случае ставкой наращения является учетная ставка. (В качестве примера, когда учетная ставка используется для наращения, является учет векселя в банке, рассматриваемый с позиции банка.)

Аналогичные суждения можно высказать и в связи со ставкой дисконтирования. Если приведенная сумма PV находится по формуле (1.8), то в качестве ставки дисконтирования выступает учетная ставка. С другой стороны, из (1.7) следует, что приведенная сумма определяется также и по формуле

, т. е. в качестве ставки дисконтирования выступает процентная ставка. Ниже будут подробно рассмотрены процессы наращения и дисконтирования, а из полученных формул или из контекста будет ясно, какая ставка и в каком качестве используется в конкретном процессе.

На практике доходность – величина непостоянная, зависящая главным образом от степени риска, ассоциируемого с данным видом бизнеса, в который сделано инвестирование капитала. Связь здесь прямо пропорциональная – чем рисковее бизнес, тем выше значение доходности. Наименее рисковы вложения в государственные ценные бумаги или в государственный банк, однако доходность операции в этом случае относительно невысока.

Величина FV, определяемая по формуле (1.7), показывает как бы будущую стоимость «сегодняшней» величины P V при заданном уровне доходности r_t.

Экономический смысл дисконтирования заключается во временном упорядочении денежных потоков различных временных периодов. Одна из интерпретаций коэффициента дисконтирования 1–d_t в формуле (1.8) показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. В этом случае искомая величина PV показывает как бы текущую, «сегодняшнюю» стоимость будущей величины FV.

Обозначение PV является общепринятым сокращением термина present value (текущая, современная стоимость). Аналогичным образом FV представляет собой сокращение для future value (будущая стоимость).

Пример

Предприятие получило кредит на срок t=1 год в размере PV=50 тыс. долл. с условием возврата FV=80 тыс. долл. В этом случае процентная ставка r₁=0,6 или, что равносильно, r₁=60%; учетная ставка d₁=0,375 или, что равносильно, d₁=37,5%.; а дисконт-фактор v₁=100%–37,5%=62,5%. Если предприятие за взятый кредит через год должно вернуть FV=90 тыс. долл., то при учетной ставке 40 % по формуле (1.8) можно найти величину кредита PV–90•(1–0,4)=54 тыс. долл.

В общем виде процентная ставка r_t может быть представлена как сумма четырех основных компонент, которые определяют величину r_t:

где:

i – норма процента, отражающая компенсацию кредитору за отказ использовать в других целях предоставленную сумму в течение времени t (пока не вернут долг);

f – так называемый фактор риска (эффект Фишера), представляющий собой для кредитора компенсацию за неопределенность (риск) неполучения процентов или всей суммы вообще при наступлении срока возврата долга;

E_p – инфляционная добавка, т. е. компенсация за возможное изменение в уровне цен, за уменьшение покупательной способности денег вследствие инфляции;

g(t) – компенсация, зависящая от продолжительности срока t, на который ссужены деньги, и тем большая, чем длительнее этот срок.

Несколько упрощая для наглядности ситуацию, можно сказать, что процентная ставка представляет собой в определенной степени результат взаимодействия хозяйствующих агентов на рынке ссудного капитала.

Пусть DD является кривой спроса на ссудный капитал, отражающей зависимость между востребуемым объемом денежных средств и величиной процентной ставки (см. рис. 1.3). Естественно, с ростом процентной ставки падает спрос на ссудный капитал. Аналогично пусть SS является кривой предложения ссудного капитала, показывающей, что с ростом процентной ставки растет и объем предлагаемых денежных средств. Величина процентной ставки r определяется точкой пересечения кривых DD и SS, так называемой равновесной точкой, в которой объем спроса равен объему предложения.

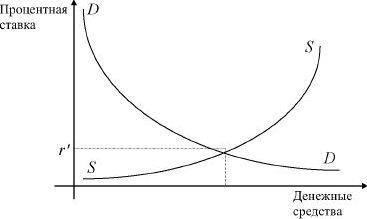
Рис. 1.3. Кривые спроса и предложения

Таким образом, как и на рынке продуктов или ресурсов, пересечение кривых спроса на деньги и предложения денег определяет цену равновесия, которая в данном случае является равновесной процентной ставкой. Иными словами, процентная ставка представляет собой цену, уплачиваемую за использование денег.

1.3. Проценты «со 100», «на 100», «во 100»

Приведем ряд задач, часто возникающих в коммерческих расчетах, а также ряд понятий, связанных с этими задачами, которые ранее широко использовались в российской и советской (до начала 50-х годов) практике, да и в настоящее время представляют определенный интерес.

Пример

Предприятию перечислили сумму, составляющую p% от Q руб. Найти эту сумму.

Обозначая искомую сумму через R, получим

где

(т.е., в отличие от p, выраженного в процентах, p' выражено десятичной дробью).

Формула (1.9) называется формулой вычисления процентов «со 100», а проценты (R), определяемые по формуле (1.9), называются процентами «со 100» (по отношению к числу Q), т.е. проценты определяются по отношению к самому числу. Процентная ставка p (или, что эквивалентно, p') по отношению к числу Q называется процентной ставкой «со 100».

Если сумма, перечисленная предприятию, составляет 60 % от 150 тыс. руб., то, вычисляя проценты «со 100» величины 150 тыс. руб., получим R=150•0,6=90 тыс. руб.

Пример

Фирма реализовала партию товара за S руб., получив при этом p% прибыли. Найти эту прибыль.

Обозначим себестоимость товара через x, тогда S представляет собой сумму себестоимости товара (x) и полученной прибыли

. Поэтому , откуда . И следовательно, прибыль равна величине

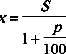
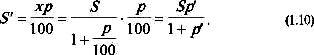
Формула (1.10) называется формулой вычисления процентов «на 100», а проценты ( S'), определяемые по формуле (1.10), называются процентами «на 100» (по отношению к числу S). В этом случае процентная ставка p (или, что эквивалентно, p') по отношению к числу S называется процентной ставкой «на 100».

Если p=20 % и S=120 тыс. руб., то

тыс. руб.

Очевидно, в частности, себестоимость товара определяется из соотношения x=S–S'=120–20=100 тыс. руб.

Проценты «на 100» находят в задачах следующего типа: даны ставка процента и сумма двух слагаемых, одно из которых представляет собой проценты «со 100» другого; требуется найти одно из слагаемых. Так, в предыдущем примере данная величина S была равна сумме себестоимости товара и процентов «со 100» (прибыли).

Запишем (1.7) в виде FV=PV+PV•r_t и выразим второе слагаемое (проценты I), используя FV. Выполняя преобразования, полностью аналогичные тем, которые совершались при решении предыдущего примера, получим

. Таким образом, величина дохода (проценты) от предоставления в долг некоторой денежной суммы является процентами «на 100» по отношению к FV и процентами «со 100» по отношению к PV согласно ставке r_t2.^.

Пример

Фирма реализовала партию товара за K руб., получив при этом p% убытка. Найти этот убыток.

Обозначим себестоимость товара через x, тогда K представляет собой разность между себестоимостью товара (x) и полученного убытка

. Поэтому , откуда . И следовательно, убыток равен величине

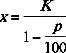
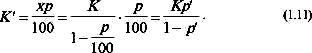
Формула (1.11) называется формулой вычисления процентов «во 100», а проценты (K'), определяемые по формуле (1.11), называются процентами «во 100» (по отношению к числу K). В этом случае процентная ставка p (или p') по отношению к числу K называется процентной ставкой «во 100».

Если p=20% и K=80 тыс. руб., то

тыс. руб.

Очевидно, в частности, себестоимость товара определяется из соотношения x=K+K'=80+20=100 тыс. руб.

Проценты «во 100» находят в задачах следующего типа: даны ставка процента и разность двух слагаемых, одно из которых (вычитаемое) представляет собой проценты «со 100» другого; требуется найти одно из слагаемых. В последнем примере данная величина K была равна разности себестоимости и процентов «со 100» (убытка).

Запишем (1.8) в виде PV=FV–FV•d_t и выразим второе слагаемое (проценты I), используя

. Таким образом, величина дохода (проценты) от предоставления в долг некоторой денежной суммы PV является процентами «во 100» по отношению к PV и процентами «со 100» по отношению к FV согласно ставке d_t.

Из самих определений ясно, что проценты «со 100» вычисляют в так называемых прямых задачах, а проценты «на 100» или «во 100» – в обратных задачах, примеры которых мы еще приведем в дальнейшем3.

Любопытно отметить, что в начале XX в. с помощью формул (1.10) и (1.11) (в отсутствие вычислительных машин и всевозможных калькуляторов) получали правила для составления дробей, упрощающих вычисления процентов.

Если p<1, т. е. p<100%, то вычисление процентов «на 100» и «во 100» в определенном смысле сводится к вычислению процентов «со 100».

Действительно, поскольку в этом случае

то из формулы (1.10) вычисления процентов «на 100» следует

Рассматривая правую часть равенства, делаем вывод, что Sp' – это проценты «со 100» величины S; S(p')²=Sp'•p – проценты «со 100» полученной величины Sp'; S(p')=S(p')³•p – проценты «со 100» величины S(p)² и т. д.

Аналогичный вывод можно сделать, пользуясь соотношением

и преобразуя формулу (1.11) вычисления процентов «во 100»

В заключение сделаем еще одно замечание в связи с различными видами определенными выше процентов. Очевидно, для любого p'>0 справедливо

, а если к тому же p'<1, то справедливо двойное неравенство . Таким образом, при 0<p'<1, т. е. при 0%<p<100%, по отношению к одному числу проценты «на 100» меньше процентов «со 100», которые в свою очередь меньше процентов «во 100».

1.4. Арифметическая и геометрическая прогрессии

Для того чтобы надлежащим образом понимать принципы и методы вычислений, используемых в финансовой математике, необходимо знание таких понятий, как арифметическая и геометрическая прогрессии.

Арифметической прогрессией называется последовательность чисел, в которой каждый член получается из предыдущего путем прибавления к нему одного и того же числа z, называемого разностью этой арифметической прогрессии. Таким образом, арифметическую прогрессию можно записать в виде:

Если z>0, то арифметическая прогрессия называется возрастающей, если z<0, – убывающей. Число членов арифметической прогрессии может быть ограниченным или неограниченным.

Приведем без доказательства две общие формулы при использовании арифметической прогрессии:

• формула для определения n-го члена арифметической прогрессии

• формула для нахождения суммы n первых членов арифметической прогрессии

Характеристическим свойством арифметической прогрессии является тот факт, что каждый ее член, начиная со второго, равен среднему арифметическому его соседних членов, т. е. при n≥2 справедливо

Проиллюстрируем введенное понятие.

Пример

Господин N старается спланировать должным образом приближающийся выход на пенсию. Брокер по инвестиционным ценным бумагам предложил схему, согласно которой господин N платит крупную сумму фирме, а в обмен получает гарантированный ежемесячный доход в 300 руб. Более того, каждый месяц доход будет увеличиваться на 40 руб. Какова будет ситуация через 5 лет?

В этих условиях (выражая деньги в тыс. руб.) a₁=a=0,3, z=0,04, n=60 (умножаем 5 лет на 12 месяцев). По формуле (1.12) находим величину дохода, который через 5 лет господин N получит за месяц:

Используя формулу (1.13), находим общий доход за 5 лет:

Геометрической прогрессией называется последовательность чисел, в которой каждый член получается из предыдущего путем умножения его на одно и то же число q≠0, называемое знаменателем этой геометрической прогрессии. Таким образом, геометрическую прогрессию можно записать в виде:

Число членов геометрической прогрессии может быть ограниченным или неограниченным. Также приведем без доказательства две общие формулы при использовании геометрической прогрессии:

• формула для определения n-го члена геометрической прогрессии

• формула для нахождения суммы n первых членов геометрической прогрессии

Характеристическим свойством геометрической прогрессии с положительными членами является тот факт, что каждый ее член, начиная со второго, равен среднему геометрическому его соседних членов, т. е. при n≥2 справедливо

Если |q|<1, то при неограниченном возрастании числа n сумма S_n стремится к пределу

Это число S называется суммой бесконечно убывающей геометрической прогрессии.

Пример

Господин N, обдумывающий свой выход на пенсию, обратился к другому брокеру и тот предложил схему, по которой за ту же самую крупную инвестиционную сумму обеспечивается гарантированный ежемесячный доход в 300 руб. вместе с увеличением каждый месяц этого дохода на 4 %. Какова будет ситуация через 5 лет?

В этих условиях a₁=a=0,3, q=1,04, n=60. По формулам (1.15), (1.16) получим

На первый взгляд предложенная брокером схема менее предпочтительна для господина N, чем в предыдущем примере. Однако, все зависит от срока. Так, уже через 7 и 8 лет общий доход господина N будет равен: S₈₄=194,738 тыс. руб. и S₉₆=316,289 тыс. руб. В то время как, придерживаясь первоначальной схемы, он получит через 7 и 8 лет соответственно 164,64 тыс. руб. и 211,2 тыс. руб., что гораздо хуже. И чем дальше, тем больше будет ощущаться разница в доходах, доставляемых разными предложенными схемами.

Приведенные формулы нашли широкое применение в финансовой математике, страховом деле и финансовом менеджменте, в частности при оценке акций, облигаций, пенсионных контрактов и др.

Глава 2. Простые проценты

2.1. Наращение простыми процентами

Ссудо-заемные операции, составляющие основу коммерческих вычислений, имеют давнюю историю. Именно в этих операциях и проявляется прежде всего необходимость учета временной ценности денег. Несмотря на то что в основе расчетов при анализе эффективности ссудо-заемных операций заложены простейшие, на первый взгляд, схемы начисления процентов, эти расчеты многообразны ввиду вариабельности условий финансовых контрактов в отношении частоты и способов начисления, а также вариантов предоставления и погашения ссуд.

Предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. При этом выделяется некоторый основной интервал времени, который называется базовым. Поскольку стандартным временным интервалом в финансовых операциях является один год, наиболее распространен вариант, когда этот год берется в качестве базового интервала и процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. В этом случае будем опускать индекс у процентной ставки r₁ (как в дальнейшем и у d₁,v₁ ) и писать просто r (соответственно – d,v). Известны две основные схемы дискретного начисления, т. е. начисления процентов за фиксированные в договоре интервалы времени:

• схема простых процентов (simple interest);

• схема сложных процентов (compound interest).

Схема простых процентов предполагает неизменность величины, с которой происходит начисление. Пусть исходный инвестируемый капитал равен P; требуемая доходность – r (в десятичных дробях). Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину P•r. Таким образом, размер инвестированного капитала F через n лет будет равен:

т. е. проценты начисляются на одну и ту же величину капитала в течение всего срока.

Выражение (2.1) называется формулой наращения по простым процентам, или формулой наращения простыми процентами, а множитель (1+nr) – множителем наращения (accumulation factor), или коэффициентом наращения простых процентов. Очевидно, множитель наращения равен индексу роста капитала P за n лет.

Легко видеть, что приращение капитала

пропорционально сроку ссуды и ставке процента, т. е., в частности, можно сделать вывод, что доход инвестора растет линейно вместе с n. Величина дохода I, как отмечалось в разделе 1.2., называется процентом или, часто, процентным платежом.

На практике процентная ставка r может зависеть от величины исходного капитала P: с увеличением капитала P увеличивается и устанавливаемая ставка r. Например, если инвестируется капитал до 20 тыс. руб., то устанавливается одна ставка процента, если более 20 тыс. руб. – то другая (превышающая предыдущую).

Если ставка r дана в процентах, то при использовании формулы (2.1) ставку нужно выразить в десятичных дробях.

Пример

Найти величину процента и наращенную сумму за трехлетний кредит в 20 тыс. долл., взятый под 9% годовых.

Здесь P=20 тыс. долл., n=3 года, r=0,09. Тогда

Обратим внимание на размерности величин, определяющих процентный платеж (2.2). Так как P измеряется в денежных единицах (например, рублях), n – в единицах времени (годах), то размерностью r является 1/(единица времени) (1/(год)). Иначе говоря, размерности n и r всегда должны быть согласованы. Таким образом, либо n должно измеряться в годах, либо с изменением размерности n (например, не годы, а кварталы), ставка процента должна отражать рост за новую единицу времени (за квартал).

С этих позиций наращение по простым процентам в случае, когда продолжительность n финансовой операции не равна целому числу лет (например, меньше года), определяется по формуле

где:

t – продолжительность финансовой операции в днях;

T – количество дней в году.

Тогда

– продолжительность финансовой операции, уже измеряемая в годах (т. е. в данной ситуации

Для наглядности формулу (2.3) можно записать следующим образом:

, т. е. дробь представляет собой дневную ставку, а произведение– ставку за t дней.

Следует отметить,

что в наших обозначениях r_t,=t'•r является процентной ставкой за время t' и тогда (2,3), естественно, примет вид, аналогичный (1.7):

Так как I=P•r_t,, то наращение по формуле (2.3), и, конечно, по (2.1), происходит процентами «со 100».

Сравнивая (2.1) и (2.3), можно сделать вывод, что формула (2.1) носит общий характер, поскольку в качестве n можно рассматривать любое положительное число, необязательно целое (напомним, что при этом условии формула (2.1) получена). Таким образом, (2.1) представляет собой зависимость наращенной суммы от времени, знание которой, в частности, позволяет на практике установить правила досрочного расторжения договора. Эта зависимость является линейной, и ее график имеет вид прямой линии с тангенсом угла наклона, численно равным процентам P•r за один год (см. рис. 2.1).

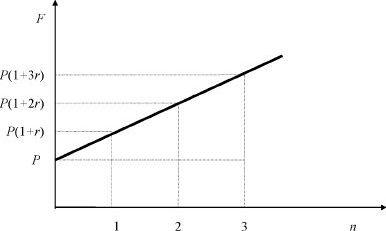
Рис. 2.1. Наращение по простым процентам

Обратим внимание, что предыдущие рассуждения не доказывают справедливость формулы (2.1) для любого положительного n, они лишь показывают естественность применений этой формулы в финансовых расчетах и при нецелых n. По сути, мы соглашаемся со следующим утверждением: поскольку простые проценты начисляются на один и тот же исходный капитал, то логично считать величину начисленных процентов пропорциональной числу периодов, за которые эти проценты начисляются (формула (2.2)) и в том случае, когда число n не является целым. А тогда наращенная сумма определяется по формуле (2.1).

Наращение по простым процентам применяется при обслуживании сберегательных вкладов с ежемесячной выплатой процентов и вообще в тех случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору. Простые проценты применяют и при выдаче широко распространенных краткосрочных ссуд, т.е. ссуд, предоставляемых на срок до одного года с однократным начислением процентов.

Пример

Клиент поместил в банк вклад в сумме 3,5 тыс. руб. под 24 % годовых с ежемесячной выплатой процентов. Какую сумму клиент будет получать каждый месяц?

Так как в этих условиях P=3,5 тыс. руб.,

года, r=0,24, то по формуле (2.2)

Заметим, что если бы клиент не брал деньги, то к его вкладу каждый месяц прибавлялась бы сумма в 0,07 тыс. руб., поскольку начисление происходит по простым процентам. Если обозначить через F_k наращенную сумму через k месяцев, то последовательность F₁,F₂,...,F_k,... образует арифметическую прогрессию с первым членом a₁=3,5 и разностью d=0,07. Естественно, аналогичный результат можно доказать и в общем случае.

Определяя продолжительность финансовой операции, принято день выдачи и день погашения ссуды считать за один день. В зависимости от того, чему берется равной продолжительность года (квартала, месяца), получают два варианта процентов:

• точные проценты (exact interests), определяемые исходя из точного числа дней в году (365 или 366), в квартале (от 89 до 92), в месяце (от 28 до 31);

• обыкновенные проценты (ordinary interests), определяемые исходя из приближенного числа дней в году, квартале и месяце (соответственно 360, 90, 30).

При определении продолжительности периода, на который выдана ссуда, также возможны два варианта:

• принимается в расчет точное число дней ссуды (расчет ведется по дням);

• принимается в расчет приблизительное число дней ссуды (исходя из продолжительности месяца в 30 дней).

Для упрощения процедуры расчета точного числа дней пользуются специальными таблицами (одна для обычного года, вторая для високосного), в которых все дни в году последовательно пронумерованы. Продолжительность финансовой операции определяется вычитанием номера первого дня из номера последнего дня (см. приложение 2).

В том случае, когда в расчетах используются точные проценты, берется и точная величина продолжительности финансовой операции; при использовании обыкновенных процентов может применяться как точное, так и приближенное число дней ссуды. Таким образом, расчет может выполняться одним из трех способов:

• обыкновенные проценты с приближенным числом дней, обозначаемые как 360 / 360 (применяется в Германии, Дании, Швеции);

• обыкновенные проценты с точным числом дней, обозначаемые как 365 / 360 и ли ACT / 360 (Бельги я, Ф ранци я);

• точные проценты с точным числом дней, обозначаемые как 365 / 365 или ACT / ACT (Великобритани я, США)4.

В российской практике можно встретиться с различными схемами начисления процентов. Например, обыкновенные проценты, как правило, применяются в операциях с векселями. Точные проценты используются в официальных методиках Центрального банка и Министерства финансов Российской Федерации для расчета доходности по государственным обязательствам. Эффект же от выбора того или иного способа зависит от значительности суммы, фигурирующей в процессе финансовой операции. Но и так ясно, что использование обыкновенных процентов с точным числом дней ссуды дает больший результат, чем применение точных процентов с точным числом дней ссуды.

Пример

Ссуда в размере 60 тыс. руб. предоставлена 12 марта с погашением 15 августа того же года под процентную ставку 32 % годовых. Рассчитайте различными возможными способами сумму к погашению, если начисляются простые проценты и год високосный.

Величина уплачиваемых за пользование ссудой процентов зависит от числа дней, которое берется в расчет. Точное число дней определяется, например, по табл. 2 в приложении 2: 228–72=156 дн. Приближенное число дней ссуды равно: 18 дней марта (30–12)+120 дней (по 30 дней четырех месяцев: апрель, май, июнь, июль)+15 дней августа=153 дн.

Возможные варианты возврата долга (через F обозначена сумма к погашению):

1. В расчет принимаются точные проценты и точное число дней ссуды:

2. В расчет принимаются обыкновенные проценты и точное число дней:

3. В расчет принимаются обыкновенные проценты и приближенное число дней:

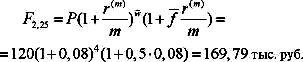
Вообще, как правило, число точных и число приближенных дней ссуды либо очень близки, либо совпадают, что позволяет в банковских расчетах часто пользоваться приближенным числом дней ссуды5.

Пример

Найти величин у процентного платежа за 60-дневный кредит в 20 0 тыс. руб., взятый под 6 % годовых, если расчет ведется способом 360 / 360. По формуле (2.2) получим

Этот пример показывает, как надо применять так называемое правило 6 % – 60 дней (6 % – 60 day rule), которое значительно упрощает вычисление процента. Согласно этому правилу процентный платеж (процент) может быть найден просто делением исходного капитала P на 100.

«Правило 6% – 60 дней» в определенном смысле можно применять и при произвольных значениях r и n, если предварительно преобразовать формулу (2.2), домножая и деля процентный платеж на соответствующие числа следующим образом:

В мировой финансовой практике при расчете процента используют и другие величины. Пусть

в обозначениях формулы (2.3).

Тогда (2.2) можно записать в виде

. Поделив в правой части равенства числитель и знаменатель дроби на r, получим

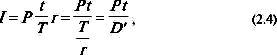
где произведение Pt называется процентным числом, а

– процентным ключом, постоянным делителем или дивизором. Очевидно, что при одной и той же ставке r, но при различном принимаемом количестве дней в году ( T=360 или T=365) будет разным и дивизор.

Дивизор

численно равен такому количеству рублей (или любых других денежных единиц), с которого при ставке процента r получается 1 руб. дохода в день. Это можно пояснить таким образом: rруб. получается с 1 руб. за Tдней, поэтому 1 руб. за то же время получается с капитала , а чтобы иметь 1 руб. дохода каждый день необходимо взять в T раз больше капитала, т. е.

Пример

Вычислить процент с капитала 2,4 тыс. долл., отданного в долг по ставке 20% годовых на срок с 5 марта по 21 сентября того же года, если расчет ведется способом 365/365.

Обозначим P=2,4 тыс. долл. Число дней находим либо прямым подсчетом, либо по таблице: t=200 дней. Так как T=365 и r=0,2, то

и по формуле (2.4) получим тыс. долл., т. е. I=263 долл. Если ставка r выражается в процентах, то, очевидно, дивизор определяется выражением . Именно в таком виде он, как правило, встречается в литературе по коммерческим вычислениям XIX и начала XX в. и называется постоянным делителем.

При вычислении процентного платежа не всегда известна величина капитала P. Возможны такие ситуации (например, в залоговых операциях), что известна либо только величина капитала, увеличенного на процентный платеж (т. е. P+I), либо уменьшенного на процентный платеж (т. е. P–I).

Пусть известна величина F=P+I, годовая ставка r (в виде десятичной дроби) и длительность l (выраженная в годах, необязательно натуральным числом) финансовой операции. Тогда r_l=l•r будет процентной ставкой за время l и для нахождения процентного платежа I пользуемся формулой (1.10) вычисления процентов «на 100»

Если же известна величина K=P–I, то для нахождения процентного платежа I пользуемся формулой (1.11) вычисления процентов «во 100»

Пример

Найти величину дохода кредитора, если за предоставление в долг на полгода некоторой суммы денег он получил от заемщика в совокупности 6,3 тыс. руб. При этом применялась простая процентная ставка в 10% годовых.

Обозначая F=6,3 тыс. руб.; l=0,5 года; r=0,1; по формуле (2.5) получим:

В случае когда срок финансовой операции выражен в днях и обозначен через t, формулы (2.5), (2.6) после простых алгебраических преобразований соответственно примут вид

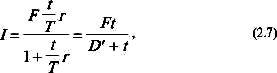
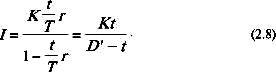
Пример

При обращении 6 июля в банк для получения кредита предприниматель получил 10 тыс. долл. Найти, какую сумму должен будет возвратить предприниматель, если долг необходимо вернуть 14 сентября того же года и начисленные простые проценты по ставке 12% годовых были удержаны банком в момент предоставления кредита. Используется способ 365/360.

Вначале воспользуемся формулой (2.8) для определения процентов, удержанных банком. Так как t=70 дней, T=360 дней, r=0,12

, K=10 тыс. долл., то

Следовательно, предприниматель обязан возвратить долг в размере

В банках при обслуживании текущих счетов для начисления процентов часто используют величины

, которые (так же, как и Pt) называются процентными числами. В этом случае формула для вычисления дивизора остается прежней , но ставка r в ней выражена в процентах.

Обычно сумма на счете часто меняется в результате поступлений или изъятий денежных сумм. Для того чтобы найти общую величину начисленных процентов за некоторый срок, вначале определяют процентные числа за каждый промежуток времени, когда сумма на счете не менялась. Затем все процентные числа складываются и полученное значение делится на D'.

Пример

Сберегательный счет был открыт 15 февраля и на него была положена сумма в 5 тыс. руб. В следующем квартале 10 апреля на счет поступили 3 тыс. руб. Затем 20 мая со счета было снято 2 тыс. руб., 1 сентября добавлена сумма в 1 тыс. руб. и 4 декабря счет был закрыт. Все операции осуществлялись в течение невисокосного года. Определить сумму, полученную владельцем счета, если процентная ставка равнялась 12% годовых и применялся способ 365/360.

Вначале определяем суммы, которые последовательно фиксировались на счете: 5 тыс. руб., 8 (5+3) тыс. руб., 6 (8–2) тыс. руб., 7 (6+1) тыс. руб. Затем находим сроки хранения этих сумм. Они соответственно равны: 54 дня, 40 дней, 104 дня, 94 дня. Сумма процентных чисел составит:

Дивизор в этом случае равен:

. Следовательно, общая величина начисленных процентов составит: тыс. руб., а владелец счета получит 7+0,624=7,624 тыс. руб.

Заметим, что процентные числа можно было вычислять и с несколько иным образом найденными сроками, а именно: для каждого поступления срок хранения определяется исходя из даты поступления и даты закрытия счета. Если происходило изъятие денег, то соответствующее процентное число берется со знаком минус. Тогда: для 5 тыс. руб. – 292 дня, для 3 тыс. руб. – 238 дней, для 2 тыс. руб. – 198 дней и для 1 тыс. руб. – 94 дня. Находим (учитывая знаки) сумму процентных чисел:

т. е. получили такую же величину, как и способом, изложенным ранее.

2.2. Переменные ставки и реинвестирование

Финансовое соглашение может предусматривать не только постоянную процентную ставку на весь период, но и устанавливать изменяющуюся во времени (переменную) ставку. Например, наличие инфляции вынуждает периодически варьировать процентной ставкой. В частности, в соглашении может быть оговорена так называемая плавающая процентная ставка (floating interest rate), когда фиксируется не сама ставка, а изменяющаяся во времени ее база и маржа (margin) – величина надбавки к базе. Величина маржи в течение срока сделки бывает как постоянной, так и переменной, что определяется условиями контракта.

Пусть на период n_k установлена процентная ставка i_k (используем обозначение i_k, а не r_k, так как последнее означает ставку за время k, что может привести к путанице). Тогда приращение капитала за этот период равно величине Pn_ki_k. Если таких периодов m (т. е. k=1, 2,...,m), то наращенная сумма за время

(считая, что все периоды и, следовательно, процентные ставки измеряются в одних и тех же соответствующих единицах) определяется по формуле

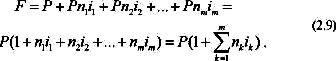
Обозначим

, тогда (2.9) примет вид , т. е. на весь период длительностью n можно установить процентную ставку , доставляющую такой же результат, как и данные переменные ставки, а для определения наращенной суммы можно воспользоваться формулой (2.1). Записывая в виде

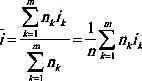
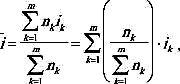
замечаем, что ставка

равна так называемой взвешенной сумме процентных ставок, где весом для каждой ставки i_k служит доля длительности периода n_k, которую он составляет от общей суммы длительностей периодов , причем очевидно, что сумма всех весов равна единице.

Если i₁=i₂=...=i_m=i, т. е. на весь период соглашения установлена постоянная ставка, то

и мы, естественно, из (2.9) получаем первоначальную формулу (2.1) наращения по простым процентам.

Кстати, если n₁=n₂=...=n_m=n', т. е. все периоды равны между собой, то

и опять получаем (2.1), заменяя все процентные ставки их суммой i'.

Конечно, формулой (2.9) можно пользоваться и в тех случаях, когда периоды выражены в различных единицах времени. Главное, чтобы размерность каждого периода n_k была согласована с размерностью процентной ставки i_k. Таким образом, если n_k выражен в годах, то i_k – годовая процентная ставка, если n_k – в днях, то i_k – процентная ставка за один день и т. п.

Пример

Вкладчик поместил в банк 15 тыс. руб. на следующих условиях: в первый год процентная ставка равна 20% годовых, каждые последующие полгода ставка повышается на 3%. Найти наращенную сумму за два года, если проценты начисляются только на первоначальную сумму вклада.

Поскольку P=15, n₁=1,

(периоды начисления измеряем в годах), i₁=0,2, i₂=0,23, i₃=0,26, то по формуле (2.9)

Такую же наращенную сумму можно получить, если простые проценты начисляются за два года (n=2) по ставке

годовых.

Рассматривая

как взвешенную сумму ставок, делаем вывод, что для ставки 20 % весом является дробь 1/2 (так как год составляет половину от двух лет), для каждой последующей ставки весом будет дробь 1/4 (так как половина года составляет четвертую часть от двух лет).

Пусть опять на период n_k установлена процентная ставка i_k, но при изменении (или без изменения) ставки наращенная к этому моменту сумма вкладывается вновь под новый простой процент. Такая финансовая операция называется реинвестированием (reinvestment) или капитализацией полученных на каждом этапе наращения средств.

Предположим для определенности, что период n₁ предшествует периоду n₂, который предшествует периоду n₃ и т. д., что не принципиально, так как в противном случае можно надлежащим образом периоды переобозначить. Тогда через время n ₁ наращенная сумма станет равной величине F₁=P(1+n₁i₁), после чего будет переоформлена на следующий срок (длительностью n₂). Через время n₂ наращенная сумма станет равной величине

и т. д. Рассуждая аналогичным образом, получим формулу для нахождения наращенной суммы за время

при реинвестировании:

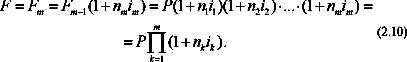
Очевидно, более строго формулу (2.10) можно доказать, используя метод математической индукции. Заметим также, что множитель

представляет собой по существу индекс роста суммы P за время n. Естественно, этот множитель можно определить по формуле (1.6), т. е. как произведение индексов роста за соответствующие периоды.

Если периоды начисления процентов равны друг другу и ставка процента не изменяется с течением времени (т. е. n₁=n₂=...=n_m=n' и i₁=i₂=...=i_m=i), то из (2.10) следует

Пример

По данным предыдущего примера найти наращенную сумму за два года, если одновременно с изменением ставки происходит и капитализация процентного дохода.

В тех же обозначениях из формулы (2.10) следует:

Получили большую наращенную сумму, чем в предыдущем примере, так как после каждого периода начисления осуществлялась операция реинвестирования.