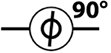Переводчик Е. Матвеев

Литературный редактор Д. Корунцева

Художник В. Мостипан

Корректоры Н. Сидорова, Г. Шкатова

 

Мерседес Химено-Сеговиа, Ник Хэрриган, Эрик Джонстон

Программирование квантовых компьютеров. Базовые алгоритмы и примеры кода. — СПб.: Питер, 2020.

 

ISBN 978-5-4461-1531-0

© ООО Издательство "Питер", 2020

 

Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

 

От издательства

Актуальный список исправлений по книге вы можете найти по адресу: https://github.com/oreilly-qc/oreilly-qc.github.io/blob/master/errata/errata.md.

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства www.piter.com вы найдете подробную информа­цию о наших книгах.

Предисловие

Квантовые компьютеры перестали быть чисто теоретическими устройствами.

Авторы этой книги полагают, что лучшее применение новым технологиям не всегда находят их изобретатели — чаще это делают эксперты в предметной области, экспериментирующие с технологией как с новым инструментом для своей работы. С учетом сказанного эта книга создавалась как практическое руководство по использованию технологии квантовых вычислений для программистов. В дальнейших главах вы освоите условные обозначения и операции вроде тех, что изображены на рис. П.1, и научитесь применять их в тех задачах, которые вас интересуют.

 

Рис. П.1. Квантовая программа немного похожа на нотную запись

Структура книги

Проверенный и надежный подход для практического освоения новых парадигм программирования основан на изучении набора концептуальных примитивов. Например, каждый программист, изучающий программирование для графических процессоров (GPU), должен сначала сосредоточиться на концепции параллелизма, а не на синтаксисе или специфике оборудования.

Главная задача этой книги заключается в формировании интуитивного понимания набора квантовых примитивов — концепций, формирующих инструментарий структурных элементов для решения задач с использованием QPU. Чтобы подготовить вас к этим примитивам, мы сначала представим основные концепции кубитов (правила игры, если хотите). Затем после краткого описания примитивов квантовых процессоров (QPU) мы покажем, как они могут использоваться в качестве структурных элементов в приложениях для QPU.

Книга разделена на три части. Мы рекомендуем читателю сначала ознакомиться с частью I и получить некоторый практический опыт, прежде чем переходить к более сложному материалу.

Часть I. Программирование для QPU

В этой части представлены основные концепции, необходимые для программирования QPU: кубиты, важнейшие команды, суперпозиция и даже квантовая телепортация. Приведенные примеры можно легко запустить в системе моделирования или на физическом QPU.

Часть II. Примитивы QPU

Во второй части книги приводятся описания некоторых алгоритмов и полезных приемов на более высоком уровне. В частности, здесь рассматривается усиление комплексной амплитуды, квантовое преобразование Фурье и оценка фазы. Их можно считать своего рода «библиотечными функциями», которые используются программистами для построения приложений. Без понимания того, как они работают, невозможно стать квалифицированным программистом QPU. Активное сообщество исследователей работает над разработкой новых примитивов QPU, поэтому следует ожидать, что библиотека будет расширяться в будущем.

Часть III. Практическое применение QPU

Мир практических применений QPU — объединяющих примитивы из части II для выполнения полезных реальных задач — развивается так же стремительно, как и сами QPU. В этой части представлены примеры существующих практических применений.

Надеемся, что к концу книги читатель будет понимать, на что способны квантовые приложения, почему они обладают столь мощными возможностями и как распознать типы задач, которые могут решаться с их помощью.

Типографские соглашения

В этой книге приняты следующие типографские соглашения:

Курсив

Используется для обозначения новых терминов.

Моноширинныйшрифт

Применяется для оформления листингов программ и программных элементов внутри обычного текста, таких как имена переменных и функций, баз данных, типов данных, переменных окружения, инструкций и ключевых слов.

Так выделяются советы и предложения.

Так обозначаются советы, предложения и примечания общего характера.

Так обозначаются предупреждения и предостережения.

Благодарности

Эта книга не могла бы выйти без поддержки команды талантливых людей — энтузиастов квантовых вычислений. Авторы хотят поблагодарить Мишель, Майка, Ким, Ребекку, Криса и техническую группу издательства O’Reilly, которые разделили наш энтузиазм и усилили его. Хотя все ошибки и упущения лежат на совести авторов, книга сильно выиграла от невероятно полезной обратной связи и вдохновения от многих научных редакторов, среди которых были Конрад Килинг (Konrad Kieling), Кристиан Соммереггер (Christian Sommeregger), Миншен Инь (Mingsheng Ying), Рич Джонстон (Rich Johnston), Джеймс Уивер (James Weaver), Майк Шапиро (Mike Shapiro), Уайатт Берлиник (Wyatt Berlinic) и Айзек Ким (Isaac Kim).

И-Джей хочет поблагодарить Сью, свою музу. Для него квантовые вычисления начали складываться в осмысленную картину в ту неделю, когда они встретились. И-Джей также передает свою благодарность своим друзьям из Бристольского университета и из SolidAngle, которые уговорили его вый­ти за рамки традиционных представлений.

Ник также благодарит Дерека Хэрригана (Derek Harrigan), когда-то на­учившего его «говорить на двоичном языке», и остальных Хэрриганов за их любовь и поддержку, а также Шеннон Бернс (Shannon Burns) за желание присоединиться к кругу Хэрриганов.

Мерседес благодарит Хосе Марию Химено Блей (José María Gimeno Blay), который разжег ее ранний интерес к компьютерам, и Мехди Ахмади (Mehdi Ahmadi) — постоянного источника поддержки и вдохновения.

Но как бы банально это ни прозвучало, в первую очередь авторы хотят поблагодарить вас — читателей — за любознательность, которая заставила вас взять эту книгу и узнать что-то новое.

1. Введение

Кем бы вы ни были — экспертом в области разработки ПО, компьютерной графики, обработки данных или просто любознательным гиком, — в этой книге на конкретных практических примерах мы постараемся показать, почему тема квантовых вычислений может быть актуальной для вас.

В последующих главах нет подробных объяснений квантовой физики (законов, лежащих в основе квантовых вычислений) или даже квантовой тео­рии информации (возможностей обработки информации, определяемых этими законами). Вместо этого мы приводим работоспособные примеры, формирующие представление о возможностях этой замечательной новой технологии. Что еще важнее, код, представленный в этих примерах, можно будет изменять и адаптировать. Это позволит вам учиться самым эффективным способом из всех возможных: накоплением практического опыта. Попутно базовые концепции поясняются по мере их использования, и только в той степени, в которой они формируют интуитивную основу для написания квантовых программ.

Авторы скромно надеются, что заинтересованные читатели смогут взять на вооружение эти принципы и расширить потенциальные применения квантовых вычислений в областях, о которых некоторые физики даже не слышали. Откровенно говоря, попытки поучаствовать в разжигании квантовой революции — не такая уж скромная задача, но быть среди первопроходцев безусловно интересно.

Необходимая подготовка

Физическая теория, лежащая в основе квантовых вычислений, насыщена сложной математикой. Впрочем, то же самое можно сказать и о физической теории работы транзисторов, однако изучение С++ обходится без единого физического уравнения. В этой книге выбран похожий подход, ориентированный на программистов и не требующий сколько-нибудь значительной математической подготовки. Далее приведен краткий список знаний, которые могут пригодиться для освоения представленных концепций.

• Основные управляющие структуры программирования (if, while и т.д.). Для создания простых примеров, которые могут запускаться в интернете, используется язык JavaScript. Если вы не владеете JavaScript, но у вас есть предшествующий опыт программирования, необходимый уровень подготовки можно набрать менее чем за час. Более подробную информацию о JavaScript можно найти в книге «Learning JavaScript» Тодда Брауна (Todd Brown), опубликованной издательством O’Reilly.

• Некоторые математические концепции уровня программирования, прежде всего:

• понимание использования математических функций;

• знание тригонометрических функций;

• умение работать с двоичными числами и выполнять преобразования между двоичным и десятичным представлением чисел;

• понимание смысла комплексных чисел.

• Элементарное понимание принципов оценки вычислительной сложности алгоритмов (обозначение «O-большое»).

Одной из частей книги, выходящей за рамки этих требований, станет глава 13, в которой будет приведен обзор ряда применений квантовых вычислений в области машинного обучения. Из-за нехватки места в обзоре приводятся очень краткие вводные описания каждого примера машинного обучения, после которых мы показываем, чем в каждом случае вам поможет квантовый компьютер. И хотя мы постарались сделать материал понятным для массового читателя, тем, кто захочет поэкспериментировать с этими примерами, пригодится некоторая подготовка в области машинного обучения.

Книга посвящена программированию квантовых компьютеров (а не их построению или теоретическим обоснованиям), что и позволяет нам обойтись без расширенной математики и квантовой теории. Однако для читателей, пожелавших обратиться к более академической литературе по теме, глава 14 предоставляет полезные источники информации и связывает представленные концепции с математическими принципами, используемыми в научном сообществе квантовых вычислений.

Что такое QPU?

Несмотря на повсеместное использование, термин «квантовый компьютер» может ввести в заблуждение. Он вызывает в воображении образ совершенно нового, чуть ли не инопланетного устройства, заменяющего все существующие программные продукты футуристическими альтернативами.

На момент написания этой книги существовало распространенное, хотя и очень серьезное ошибочное представление. Перспективы квантовых компьютеров связаны не с тем, что они станут «убийцами» традиционных компьютеров, а, скорее, с их способностью радикально расширить набор задач, решаемых вычислительными средствами. Существуют важные вычислительные задачи, легко решаемые на квантовом компьютере, но которые буквально невозможно решить на любом гипотетическом вычислительном устройстве, которые мы когда-либо могли надеяться построить1.

Но принципиально то, что подобное ускорение наблюдается только для определенных задач (многие из которых будут рассмотрены более подробно). И хотя ожидается, что со временем будут обнаружены новые типы таких задач, крайне маловероятно, что все вычисления будет разумно проводить на квантовых компьютерах. При решении большинства задач, на которые расходуются такты процессора вашего ноутбука, квантовый компьютер будет работать не лучше обычного.

Другими словами — с точки зрения программиста — квантовый компьютер в действительности является сопроцессором. В прошлом компьютеры использовали разные виды сопроцессоров, каждый из которых хорошо подходил для своей специализации: арифметических операций с плавающей точкой, обработки сигналов или графического моделирования в реальном времени. С учетом сказанного мы будем использовать термин QPU (Quantum Processor Unit, квантовый процессор) для обозначения устройства, на котором выполняются наши примеры кода. Мы считаем, что это подчеркивает важный контекст, в котором должны представляться квантовые вычисления.

Как и в случае с другими сопроцессорами — например, графическими процессорами (GPU), — программирование для QPU подразумевает написание кода, который будет в основном выполняться на центральном процессоре (CPU) нормального компьютера. Центральный процессор выдает команды QPU-сопроцессора только для инициирования задач, входящих в область его специализации.

Практический подход

Практические примеры образуют основу этой книги. Но на момент ее написания полноценный QPU общего назначения еще не существует — тогда как же вы будете запускать приведенный код? К счастью, даже во время написания книги существовали прототипы QPU, доступные в облаке. Кроме того, для меньших задач поведение QPU можно моделировать на традиционном вычислительном оборудовании. И хотя моделирование больших QPU-программ становится невозможным, для малых фрагментов кода моделирование помогает освоить управление настоящими QPU. Примеры кода в этой книге совместимы с обеими ситуациями, и они останутся полезными и поучительными даже с появлением более совершенных QPU.

Существует много разных библиотек, систем и средств моделирования QPU. Список ссылок на некоторые системы с хорошей поддержкой доступен по адресу http://oreilly-qc.github.io. На этой странице мы приводим примеры кода из книги там, где это возможно, на разных языках. Но чтобы примеры кода не забивали текст, мы приводим примеры только на JavaScript для QCEngine. QCEngine — бесплатная сетевая система моделирования квантовых вычислений, которая позволяет запускать примеры прямо в браузере, без установки какого-либо программного обеспечения. Эта система моделирования была разработана авторами: сначала для личного применения, затем как приложение к книге. Система QCEngine особенно полезна для нас по двум причинам: во-первых, она может работать без загрузки дополнительного кода и, во-вторых, в нее интегрирована система круговых обозначений, которая будет использоваться как средство визуализации в книге.

Учебник QCEngine

Так как материал книги в значительной мере зависит от QCEngine, мы не пожалеем времени и расскажем, как работать с системой моделирования, доступной по адресу http://oreilly-qc.github.io.

Запуск кода

Веб-интерфейс QCEngine, показанный на рис. 1.1, позволяет легко строить различные визуализации, которыми мы будем пользоваться. Чтобы создать эти визуализации, достаточно ввести код в редакторе кода QCEngine.

 

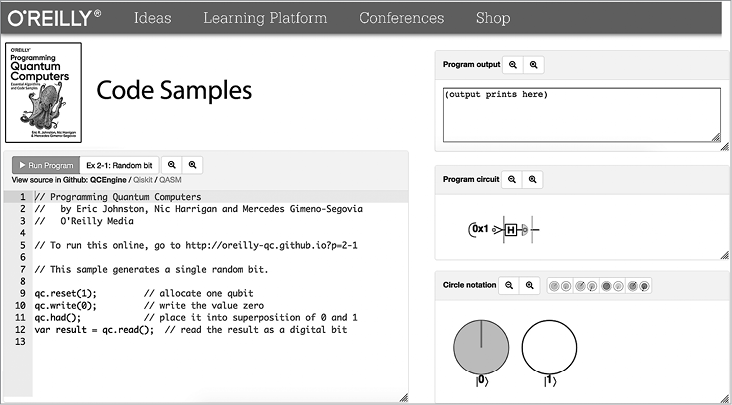
Рис. 1.1. Интерфейс QCEngine

Чтобы запустить один из примеров этой книги, выберите его в раскрывающемся списке в верхней части редактора и щелкните на кнопке RunProgram. На экране появляются новые интерактивные элементы интерфейса для визуализации результатов выполнения кода (рис. 1.2).

• Визуализатор квантовой схемы (Quantumcircuitvisualizer) — элемент выдает визуальное представление схемы, представляющей ваш код. Условные обозначения, используемые в этих схемах, описаны в главах 2 и 3. Это представление также может использоваться для интерактивного пошагового выполнения программы (рис. 1.2).

• Визуализатор круговых обозначений (Circle-notationvisualizer) — визуализация так называемой «круговой записи» регистра QPU (или системы моделирования). В главе 2 мы объясним, как читать и использовать эту запись.

• Консоль вывода QCEngine (QCEngineoutputconsole) — в этом поле появляется весь текст, который выводится вашим кодом (например, в процессе отладки) командой qc.print(). Весь вывод стандартной функции JavaScript console.log() также направляется на консоль браузера JavaScript.

 

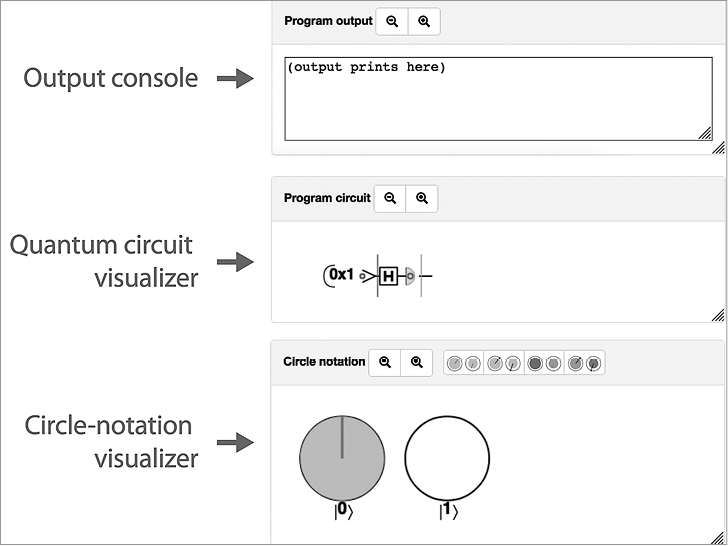
Рис. 1.2. Элементы пользовательского интерфейса QCEnging для визуализации результатов работы QPU

Отладка

Отладка программ для QPU может быть весьма непростым делом. Нередко оказывается, что единственный способ понять, как работает программа, — медленно пройти ее в пошаговом режиме, анализируя визуализации на каждом шаге. Наведя указатель мыши на визуализатор схемы, вы увидите вертикальную оранжевую черту в фиксированной позиции и серую вертикальную черту в той точке схемы, в которой находится ваш курсор. Оранжевая черта обозначает позицию схемы (а следовательно, и программы), представленную визуализатором круговой записи. По умолчанию это конец программы, но, щелкая на других частях схемы, вы сможете просмотреть в визуализаторе круговой записи конфигурацию QPU в соответствующих точках программы. Например, на рис. 1.3 показано, как визуализатор круговой записи изменяется при переходе между двумя шагами программы QCEngine.

Когда у вас появится доступ к системе моделирования QPU, вам наверняка захочется поэкспериментировать. И мы не собираемся вас останавливать! В главе 2 будет рассмотрен код QPU-программ возрастающей сложности.

 

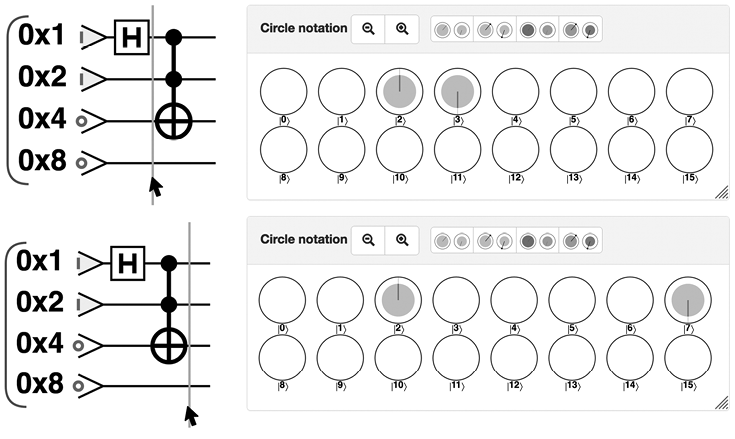
Рис. 1.3. Пошаговое выполнение программы с использованием визуализаторов круговой записи

Низкоуровневые команды QPU

QCEngine — один из нескольких инструментов для запуска и выполнения QPU-кода, но как выглядит сам код, выполняемый QPU? Для управления низкоуровневыми командами QPU обычно используются традиционные языки высокого уровня (как уже было показано с системой QCEngine на базе JavaScript). В этой книге мы будем регулярно пересекать границу между этими уровнями.

Описание программирования QPU с командами машинного уровня, имеющими специфическую квантовую природу, поможет вам освоить принципиально новую логику работы QPU, тогда как умение управлять этими операциями из традиционных высокоуровневых языков (таких как JavaScript, Python или C++) предоставляет более прагматическую парадигму для написания кода. Определение новых языков квантового программирования — одна из активно развивающихся областей. В книге эта тема не описывается, но в главе 14 приведены ссылки для заинтересованных читателей.

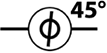
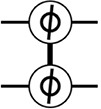
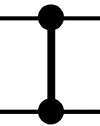
Чтобы немного разжечь ваш интерес к теме, мы приведем сводку некоторых фундаментальных команд QPU в табл. 1.1. Все команды более подробно рассматриваются в последующих главах.

Таблица 1.1. Набор основных команд квантового процессора

Условное обозначение	Название	Применение	Описание
	NOT (также X)	qc.not(t)	Логическое поразрядное отрицание (NOT)
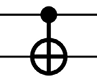
	CNOT	qc.cnot(t,c)	Контролируемое отрицание: if(c) thenNOT(t)
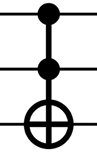
	CCNOT (вентиль Тоффоли)	qc.cnot(t,c1| c2)	if(c1ANDc2)thenNOT(t)
	HAD (вентиль Адамара)	qc.had(t)	Вентиль Адамара
	PHASE	qc.phase(angle,c)	Относительный фазовый сдвиг
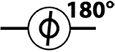
	Z	qc.phase(180,c)	Относительный фазовый сдвиг на 180°
	S	qc.phase(90,c)	Относительный фазовый сдвиг на 90°
	T	qc.phase(45,c)	Относительный фазовый сдвиг на 45°
	CPHASE	qc.cphase(angle,c1| c2)	Условный фазовый сдвиг
	CZ	qc.cphase(180,c1| c2)	Условный фазовый сдвиг на 180°
	READ	val = qc.read(t)	Чтение кубитов с возвращением числовых данных
	WRITE	qc.write(t,val)	Запись традиционных данных в кубиты
	ROOTNOT	qc.rootnot(t)	Корень из отрицания
	SWAP (EXCHANGE)	qc.exchange(t1| t2)	Перестановка двух кубитов
	CSWAP	qc.exchange(t1| t2, c)	Условная перестановка: if(c)thenSWAP(t1,t2)

У каждой из этих операций конкретные команды и хронометраж зависят от производителя и архитектуры QPU. Тем не менее это основной набор базовых операций, которые, как предполагается, будут доступны на всех машинах. Эти операции образуют фундамент QPU-программирования, как команды MOV и ADD для программирования традиционных процессоров.

Ограничения моделирования

Хотя системы моделирования предоставляют потрясающие возможности для прототипизации малых QPU-программ, по сравнению с реальными QPU они безнадежно отстают по производительности. Одной из метрик мощности QPU является количество кубитов, доступных для работы2 (квантовый эквивалент битов, о котором вскоре мы расскажем намного подробнее).

На момент издания книги мировой рекорд моделирования QPU составлял 51 кубит. На практике системы моделирования и оборудование, доступные для большинства читателей книги, справятся с 26 кубитами или около того, прежде чем замедлиться до полной остановки.

Примеры, приведенные в книге, были написаны с учетом этих ограничений. Они могут стать хорошей отправной точкой, но каждый добавляемый кубит удваивает объем памяти, необходимый для моделирования, и снижает скорость вдвое.

Аппаратные ограничения

С другой стороны, наибольшее реальное оборудование QPU, доступное на момент написания книги, составляло около 70 физических кубитов, тогда как наибольший QPU, доступный для массового пользователя через пакет разработки с открытым кодом Qiskit, содержит 16 физических кубитов3. Под физическими кубитами (в отличие от логических) подразумевается, что эти 70 кубитов не имеют механизма исправления ошибок, что делает их слишком зашумленными и ненадежными. Кубиты намного менее устойчивы, чем их традиционные аналоги; слабейшее взаимодействие с окружением может нарушить ход вычислений.

Взаимодействие с логическими кубитами позволяет программисту абстрагироваться от оборудования QPU и реализовать любой алгоритм из учебника, не беспокоясь о конкретных ограничениях физического оборудования. В этой книге мы сосредоточимся исключительно на программировании на уровне логических кубитов. И хотя приводимые примеры достаточно малы для запуска на меньших QPU (таких, как доступные на момент издания), абстрагирование подробностей физического оборудования означает, что навыки и интуитивные представления, которые будут выработаны, останутся исключительно полезными с развитием устройств в будущем.

QPU и GPU: некоторые общие характеристики

Идея программирования совершенно новой разновидности процессоров может показаться устрашающей, даже если она уже сформировала собственное сообщество на Stack Exchange. Ниже перечислены некоторые общие факты, относящиеся к программированию QPU.

• Программы, работающие исключительно на QPU, встречаются очень редко. Обычно программа, выполняемая на процессоре, выдает команды QPU, а потом получает результаты.

• Одни задачи очень хорошо подходят для QPU, а другие нет.

• QPU работает на отдельной тактовой частоте, нежели центральный процессор, и обычно имеет собственные специализированные аппаратные интерфейсы к внешним устройствам (например, оптическим выводам).

• Типичный QPU содержит собственную оперативную память, с которой центральный процессор не может работать эффективно.

• Простой QPU будет представлять собой одну микросхему, с которой работает портативный компьютер (а возможно, даже область внутри другой микросхемы). Более сложный QPU — большое и дорогостоящее устройство, всегда требующее специального охлаждения.

• Первые QPU, даже самые простые, достигали размеров холодильника и требовали специальных источников питания с повышенной мощностью.

• После завершения вычислений центральному процессору возвращается проекция результата, а большая часть внутренних рабочих данных QPU теряется.

• Отладка программ для QPU может быть чрезвычайно сложным делом, требующим специальных инструментов и методов. Пошаговое выполнение программ также усложняется, и часто лучшая тактика заключается во внесении изменений в программу и наблюдении за их влиянием на вывод.

• Оптимизации, ускоряющие один QPU, могут замедлять работу другого.

Звучит довольно пугающе. Но здесь есть один нюанс: замените квантовый процессор графическим, и каждое из этих утверждений останется абсолютно правильным!

Хотя квантовые процессоры представляют собой почти неземную технологию невероятной мощи, в том, что касается проблем, с которыми мы можем столкнуться при освоении их программирования, нет ничего принципиально нового — поколения программистов уже все это видели. Безусловно, в программировании QPU встречаются некоторые нюансы, которые действительно являются принципиально новыми (иначе для чего была бы нужна эта книга?), но очень многие моменты уже нам знакомы, и это должно вас приободрить. Эта задача нам по силам!

Часть I. Программирование для QPU

Что же это такое — кубит? Как наглядно представить его? Какая от него польза? Это короткие вопросы со сложными ответами. В первой части книги мы ответим на них с практической точки зрения. В главе 2 все начнется с описания и использования одного кубита. В главе 3 будет рассмотрена дополнительная сложность систем из многих кубитов. Попутно будут представлены многие одно- и многокубитные операции, а в главе 4 эти темы будут непосредственно использованы: мы опишем, как выполняется квантовая телепортация. Учтите, что примеры кода, демонстрирующие основные темы обсуждения, могут запускаться в системе моделирования QCEngine (см. главу 1) по предоставленным ссылкам.

2. Один кубит

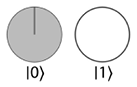
Обычный бит имеет всего один двоичный параметр — бит можно инициализировать в состоянии 0 или в состоянии 1. Математика двоичной логики достаточно проста, а возможные значения 0/1 бита можно наглядно представить двумя кругами (один пустой, а другой заполненный), как показано в табл. 2.1.

Таблица 2.1. Возможные значения традиционного бита — графическое представление

Возможные значения бита	Графическое представление
0
1

А теперь обратимся к кубитам. В каком-то отношении кубиты очень похожи на биты: при чтении значения кубита вы всегда получаете 0 или 1. Таким образом, после чтения кубита его всегда можно описать так, как показано в табл. 2.1. Однако охарактеризовать состояние кубитов до чтения — не столь тривиальная задача, требующая более сложного описания. Перед чтением кубиты могут существовать в суперпозиции состояний.

Вскоре мы попробуем объяснить, что такое суперпозиция. Но чтобы вы имели хотя бы общее представление о том, какие возможности таит эта концепция, следует заметить, что существует бесконечное количество возможных суперпозиций, в которых отдельный кубит может существовать до чтения. В табл. 2.2 перечислены лишь некоторые суперпозиции, в которых может находиться кубит в результате подготовки. И хотя в конечном итоге вы всегда получаете 0 или 1, именно сама доступность этих дополнительных состояний открывает невероятные возможности при вычислениях, хотя для этого придется проявить некоторую изобретательность.

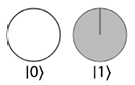
Таблица 2.2. Некоторые возможные значения кубита

Возможные значения кубита	Графическое представление
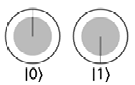
| 0 〉
| 1 〉
0.707| 0 〉 + 0.707| 1 〉
0.95| 0 〉 + 0.35| 1 〉
0.707| 0 〉 – 0.707| 1 〉

В обозначениях из табл. 2.2 метки 0 и 1 были заменены на | 0 〉 и | 1 〉. Эта система обозначений, называемая обозначениями Дирака, или обозначениями бра-кет, часто встречается в квантовых вычислениях. Как правило, числа, заключенные в обозначения бра-кет, представляют значения, в которых может находиться кубит при чтении. Когда речь идет о значении, которое было получено в результате чтения из кубита, мы просто используем число для представления полученного числового результата.

В первых двух строках табл. 2.2 изображены квантовые эквиваленты состояний традиционного бита без какой-либо суперпозиции. Кубит, подготовленный в состоянии | 0 〉, эквивалентен традиционному биту, содержащему 0 (то есть он всегда дает значение 0 при чтении); аналогичным образом дело обстоит с 1. Если бы используемые кубиты находились только в состояниях | 0 〉 или | 1 〉, то, по сути, это были бы самые обычные биты, только очень дорогие.

Но как приступить к освоению более экзотических возможностей суперпозиции, приведенных в других строках? Чтобы получить хотя бы интуитивное представление о запутанных вариантах из табл. 2.2, будет полезно кратко разобраться с тем, что же собой представляет кубит4.

Краткий обзор физических кубитов

Объектом, который легко демонстрирует квантовую суперпозицию, является одиночный фотон. Чтобы продемонстрировать этот факт, отступим на шаг и допустим, что мы попытались использовать местоположение фотона для представления традиционного цифрового бита. В устройстве, показанном на рис. 2.1, переключаемое зеркало (которое может находиться в отражающем или прозрачном состоянии) позволяет управлять тем, на каком из двух путей находится фотон — соответствующему 0 или 1.

Такие устройства действительно существуют в современных технологиях цифровых коммуникаций. Бит из одиночного фотона получится очень капризным (хотя бы потому, что он не способен подолгу находиться на одном месте). Чтобы использовать эту конфигурацию для демонстрации некоторых свойств кубитов, допустим, что переключатель, переводящий фотон в состояние 0 или 1, заменен полупрозрачным зеркалом.

Полупрозрачное зеркало, изображенное на рис. 2.2 (также называемое светоделителем), представляет собой полуотражающую поверхность, которая с вероятностью 50% либо отражает свет на путь, связанный с состоянием 1, либо позволяет ему пройти напрямую на путь, связанный с состоянием 0. Других вариантов нет.

 

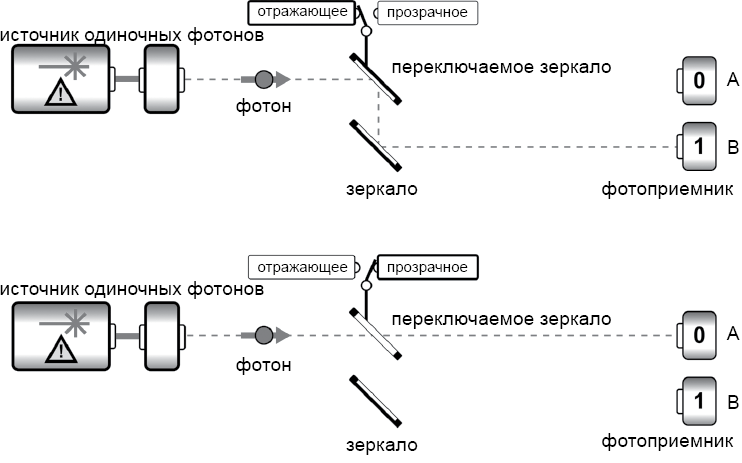
Рис. 2.1. Использование фотона в качестве традиционного бита

 

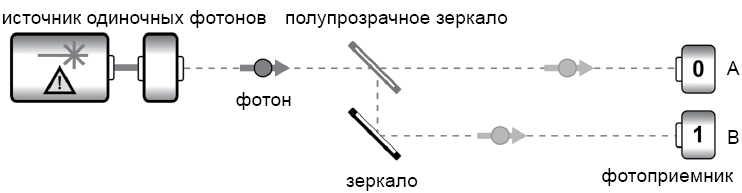
Рис. 2.2. Простая реализация одного фотонного кубита

Когда одиночный неделимый фотон сталкивается с такой поверхностью, он страдает от своеобразного «кризиса идентичности». В результате эффекта, у которого нет традиционных аналогов, он оказывается в состоянии, в котором на него могут воздействовать эффекты как пути 0, так и пути 1. Говорят, что фотон находится в суперпозиции перемещений по всем возможным путям. Другими словами, вместо традиционного бита появляется кубит, который может находиться в суперпозиции состояний, соответствующих значениям 0 и 1.

Природу суперпозиции очень легко понять неправильно (как происходит во многих популярных статьях о квантовых вычислениях). Было бы некорректно утверждать, что фотон находится на путях 0 и 1 одновременно5. Фотон только один, и, если поставить датчики на каждом пути, как показано на рис. 2.2, сработает только один из них. Когда это произойдет, суперпозиция фотона редуцируется в числовой бит и дает определенный результат 0 или 1. Но как вскоре будет показано, существуют полезные (с вычислительной точки зрения) возможности взаимодействия QPU с кубитом в суперпозиции, прежде чем вам потребуется прочитать его.

Разновидность суперпозиции, показанная на рис. 2.2, играет центральную роль в использовании квантовых возможностей QPU. Вследствие этого к описанию и управлению квантовыми суперпозициями также следует подходить с квантовых позиций. Когда фотон находится в суперпозиции путей, мы говорим, что с каждым путем связана некоторая комплексная амплитуда. У комплексных амплитуд есть два важных аспекта — две «ручки переключателя», которые можно подкручивать для изменения конкретной конфигурации суперпозиции кубита.

• Амплитуда (magnitude), связанная с каждым путем суперпозиции фотона, представляет собой аналоговое значение, которое показывает, в какой степени фотон распространился на каждый путь. Амплитуда пути относится к вероятности обнаружения фотона на этом пути. А именно: квадрат амплитуды определяет вероятность того, что фотон будет наблюдаться на заданном пути. На рис. 2.2 можно корректировать комплексную амплитуду, связанную с каждым путем, изменяя степень отражения полупрозрачного зеркала.

• Относительная фаза (relative phase) между разными путями в суперпозиции фотона отражает величину задержки фотона на одном пути относительно другого. Это еще одно аналоговое значение, которым можно управлять за счет различий между перемещениями фотона на путях, соответствующих 0 и 1. Следует заметить, что относительную фазу можно изменить, не влияя на вероятность обнаружения фотона на каждом пути6.

Стоит еще раз подчеркнуть, что термином «комплексная амплитуда» (am­plitude) обозначается совокупность амплитуды и относительной фазы, связанных с некоторым значением из суперпозиции кубита.

Для читателей, интересующихся математикой: комплексные амплитуды, связанные с разными путями в суперпозиции, обычно описываются комплексными числами. Амплитуда, связанная с комплексной амплитудой, соответствует модулю комплексного числа (квадратный корень числа, умноженного на комплексно-сопряженное число), тогда как относительная фаза соответствует углу при выражении комплексного числа в полярной форме. Для читателей, не интересующихся математикой, мы вскоре приведем описание визуальных обозначений, чтобы вам не приходилось отвлекаться на столь сложные материи.

Значения амплитуды и относительной фазы доступны для использования в процессе вычислений; можно считать, что они закодированы в кубите. Но если вы в какой-то момент захотите прочитать из него информацию, то фотон в конечном итоге должен столкнуться с каким-то из датчиков. И в этот момент оба аналоговых значения исчезают — квантовая природа кубита пропадает. И в этом заключается вся суть квантовых вычислений: вы должны каким-то образом использовать эти эфемерные величины, чтобы после разрушающего акта чтения получить некий полезный результат.

Конфигурация на рис. 2.2 эквивалентна примеру кода, который будет приведен в листинге 2.1 для случая, когда фотон используется в качестве кубита.

Впрочем, довольно возни с фотонами! Это руководство для программиста, а не учебник по физике. Давайте абстрагируемся от физики и посмотрим, каким образом описать и наглядно представить кубиты, отдалившись от фотонов и квантовой физики настолько, насколько двоичная логика отдаляется от электронов и физики полупроводников.

Круговая запись

Итак, вы примерно представляете, что такое суперпозиция, но это представление в значительной степени привязано к специфике поведения фотонов. Поищем абстрактный способ описания суперпозиций, который позволял бы сосредоточиться только на абстрактной информации.

Полноценное математическое обоснование квантовой физики предоставляет такую абстракцию, но, как видно из левого столбца табл. 2.2, эта математика куда менее интуитивна и менее удобна, чем простая двоичная логика традиционных битов.

К счастью, эквивалентная графическая система обозначений в правом столбце табл. 2.2 предоставляет более интуитивное описание. Так как мы стремимся сформировать свободное и прагматичное понимание того, что происходит внутри QPU, не углубляясь в малопонятную математику, с этого момента мы будем рассматривать кубиты исключительно в рамках этой круговой записи.

Эксперименты с фотонами показали, что у общего состояния кубита, которое необходимо отслеживать в QPU, есть два аспекта: амплитуда комплексных амплитуд ее суперпозиции и относительная фаза между ними. В круговой записи эти параметры представляются следующим образом:

• величина комплексной амплитуды, связанной с каждым значением, которое может принимать кубит (пока что это | 0 〉 и | 1 〉), описывается радиусом заполненной области, изображенной для каждого из кругов | 0 〉 и | 1 〉;

• относительная фаза между комплексными амплитудами этих значений, обозначается углом поворота круга | 1 〉 относительно круга | 0 〉 (темная линия в кругах делает величину поворота более наглядной).

В этой книге круговая запись используется очень часто, поэтому мы выделим немного времени и разберемся в том, как размеры кругов и углы поворота отражают эти концепции.

Размер круга

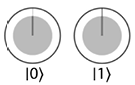
Ранее мы упоминали о том, что квадрат амплитуды, связанный с | 0 〉 или | 1 〉, определяет вероятность получения этого значения при чтении. Так как заполненный радиус в круге представляет амплитуду, это означает, что площадь заполненной области в каждом круге (или в разговорной речи — ее размер) прямо пропорциональна вероятности получить значение этого круга (0 или 1) при чтении кубита. В примерах на рис. 2.3 представлена круговая запись для различных состояний кубитов и вероятность чтения 1 в каждом случае.

 

Рис. 2.3. Вероятность чтения значения 1 для разных суперпозиций, представленных в круговой записи

Чтение из кубита уничтожает информацию. Во всех случаях, представленных на рис. 2.3, при чтении кубита будет получено значение 0 или 1, и когда это произойдет, кубит изменит свое состояние в соответствии с наблюдаемым значением. Таким образом, даже если кубит изначально находился в более сложном состоянии, после того как из него будет прочитано значение 1, при немедленном повторном чтении из него вы всегда будете получать 1.

Следует заметить, что с увеличением заполненной части на круге | 0 〉 вероятность прочитать 0 увеличивается — а это, конечно, означает, что вероятность получить результат 1 уменьшается (до оставшейся величины). В последнем примере на рис. 2.3 существует 90%-ная вероятность получить 0 при чтении из кубита — а следовательно, вероятность прочитать 1 составляет оставшиеся 10%7.

Мы будем часто говорить, что заполненная часть круга в круговой записи представляет амплитуду, связанную с этим значением в суперпозиции. И хотя на первый взгляд это может показаться раздражающей технической подробностью, важно помнить, что амплитуда, связанная с этим значением, в действительности соответствует радиусу круга, хотя часто эти две величины можно без особого вреда приравнять для визуального удобства.

Также легко забыть (хотя и важно помнить), что в круговой записи размер круга, связанный с конкретным результатом, не представляет полной комплексной амплитуды суперпозиции. Отсутствует важная информация: относительная фаза суперпозиции.

Поворот

Некоторые команды QPU также позволяют изменять относительные повороты кругов | 0 〉 и | 1 〉 кубита. Поворот представляет относительную фазу кубита. Относительная фаза состояния кубита может принимать любые значения из диапазона от 0° до 360°; некоторые примеры представлены на рис. 2.4.

По соглашениям, принятым в этой книге, положительный угол поворота соответствует вращению против часовой стрелки, как видно из рис. 2.4.

 

Рис. 2.4. Примеры относительных фаз в одном кубите

Во всех предыдущих примерах поворачивался только круг | 1 〉. Почему не поворачивается круг | 0 〉? Как следует из названия, важна лишь относительная фаза в суперпозиции кубита. Соответственно, нас интересует лишь относительный поворот между двумя кругами8. Если бы операция QPU должна была применить поворот к обоим кругам, то эффект всегда можно заново интерпретировать в эквивалентной форме так, словно повернут был только круг | 1 〉, что делает относительный поворот более очевидным. Пример показан на рис. 2.5.

 

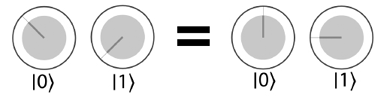
Рис. 2.5. В круговой записи важны только относительные повороты — показанные два состояния эквивалентны, потому что относительные фазы в каждом случае совпадают

Заметим, что относительная фаза может изменяться независимо от амплитуды суперпозиции. Эта независимость также работает и в обратном направлении. При сравнении третьего и четвертого примера на рис. 2.3 становится видно, что относительная фаза между выходными значениями для одного кубита напрямую не влияет на вероятность того, какое именно значение будет прочитано.

Тот факт, что относительная фаза одного кубита не влияет на амплитуды в суперпозиции, означает, что она не оказывает прямого влияния на наблюдаемые результаты чтения. Может показаться, что из-за этого свойство относительной фазы становится несущественным, однако это впечатление невероятно далеко от истины! В квантовых вычислениях с участием нескольких кубитов можно воспользоваться поворотом, чтобы нетривиально и косвенно повлиять на вероятность того, что со временем будут прочитаны разные значения. Более того, хорошо продуманные относительные фазы могут открыть невероятные вычислительные возможности. А теперь мы опишем операции, которые позволят нам это сделать (особенно операции, работающие только с одним кубитом), и наглядно представим их эффект при помощи круговой записи.

В отличие от традиционных битов, имеющих ярко выраженную цифровую природу, амплитуды и относительные фазы относятся к непрерывным степеням свободы. Этот факт породил широко распространенное заблуждение, будто квантовые вычисления чем-то похожи на злосчастные аналоговые вычисления. Однако стоит заметить, что несмотря на возможности манипуляций с разными степенями свободы, ошибки, возникающие в ходе работы QPU, могут исправляться цифровыми методами. Это одна из причин, по которой QPU превосходят аналоговые вычислительные устройства по устойчивости к ошибкам.

Первые операции QPU

Однокубитные операции QPU, как и их аналоги для традиционных процессоров, преобразуют входную информацию в нужный вывод. Только, конечно, в этом случае входные и выходные данные определяются кубитами, а не битами. Многие команды QPU имеют соответствующие обратные операции9, о которых также полезно знать. В таких случаях операция QPU называется обратимой (reversible); по сути, это означает, что ее применение не приводит к потере информации. С другой стороны, некоторые операции QPU являются необратимыми и не имеют обратных операций (то есть они каким-либо образом приводят к потере информации). Как вы вскоре увидите, обратимость или необратимость операции может иметь важные последствия для ее использования.

На первый взгляд некоторые команды QPU выглядят странно, а их полезность далеко не очевидна, но лишь после изучения целой группы таких операций мы быстро найдем им практическое применение.

Команда QPU: NOT

NOT (отрицание) — квантовый эквивалент одноименной традиционной операции. Нуль переходит в единицу, и наоборот. Тем не менее, в отличие от своего традиционного аналога, операция NOT у QPU также может работать с кубитом, находящимся в суперпозиции.

В круговой записи эти результаты представляются очень просто: круги | 0 〉 и | 1 〉 меняются местами, как показано на рис. 2.6.

 

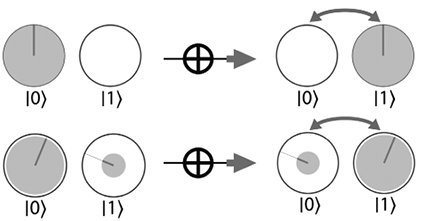
Рис. 2.6. Операция NOT в круговой записи

Обратимость: как и в цифровой логике, операция NOT обратима по отношению к самой себе; ее повторное применение возвращает кубиту исходное значение.

Команда QPU: HAD

Операция HAD (сокращение от фамилии Hadamard) фактически создает равновероятную суперпозицию при ­получении значения | 0 〉 или | 1 〉. Она открывает путь к использованию необычного и тонкого параллелизма квантовой суперпозиции. В отличие от NOT, операция HAD не имеет традиционного аналога.

В круговой записи операция HAD приводит к тому, что выходной кубит имеет одинаковые заполненные площади для | 0 〉 и | 1 〉, как показано на рис. 2.7.

Это позволяет использовать операцию HAD для получения равномерных суперпозиций выходных значений кубита, то есть суперпозиций, в которых оба результата имеют одинаковую вероятность. Также обратите внимание на то, что воздействие HAD на кубиты, изначально находящиеся в состояниях | 0 〉 и | 1