ИНФОРМАЦИЯ О КНИГЕ

УДК 16(075.8)

ББК 87.4я73

И17

Ивлев Ю. В.

Практикум соответствует программе курса логики для высших учебных заведений. В нем учтены последние научные разработки в этой области. При переходе от теории к практике иногда возникают трудности. Для их преодоления в предлагаемой книге даются технологии применения средств логики в познании. Использование данного учебного пособия сократит преподавателям время на проведение консультаций, а студентам позволит успешнее осваивать курс логики.

Для студентов высших учебных заведений, учащихся гимназий, а также для всех желающих изучить логику или усовершенствовать свои познания в этой науке.

УДК 16(075.8)

ББК 87.4я73

© Ю. В. Ивлев, 2013

© ООО «Проспект», 2013

ПРЕДИСЛОВИЕ

Одной из целей, которые предполагается достичь в результате изучения логики, является умение применять ее законы и методологические средства в процессе познания[1].

Как выработать навыки применения логики? Прежде всего, следует выполнять упражнения в процессе изучения теоретического материала. При переходе от теории к практике иногда возникают трудности. Для их преодоления в предлагаемой книге даются технологии применения средств логики в познании. Эти технологии многократно излагались автором при проведении консультаций со студентами и аспирантами, а также практическими работниками.

Использование данного учебного пособия сократит преподавателям время на проведение консультаций, а студентам позволит успешнее осваивать курс логики.

Автор благодарит А. А. Ильина за прочтение рукописи книги и сделанные замечания.

Глава 1.
ПРЕДМЕТ И ЗНАЧЕНИЕ ЛОГИКИ

ЛОГИЧЕСКАЯ ФОРМА МЫСЛИ

Логика называется формальной, поскольку изучает формы мыслей. Форма мысли — это ее особая структура, а именно логическая структура. Покажем, как эта структура выявляется.

Выражения языка, входящие в предложения и не являющиеся предложениями, делятся на два класса — на логические и нелогические выражения. Логическими являются выражения, которые употребляются в процессе рассуждений и утверждений о любых областях человеческой деятельности. Примеры логических выражений: все (ни один, каждый); некоторые (некоторый); суть (есть); не суть (не есть); и; или; если... , то; неверно, что ... ; не; следовательно. В дальнейшем будет показано, что эти выражения — еще не логические термины. Чтобы они стали логическими терминами, их нужно уточнять. Так, грамматический союз «и» может выражать одновременное существование двух ситуаций (идет дождь, и идет снег), может выражать последовательное существование или возникновение двух ситуаций (тучи рассеялись, и засияло солнце). После уточнения эти выражения становятся логическими терминами. Союз «и» в первом смысле называется знаком одновременной конъюнкции и обозначается так: &⁼, а во втором — знаком последовательной конъюнкции (обозначение: &^→). На данном этапе изучения логики будем считать, что приведенные выше выражения русского языка являются логическими терминами.

Логическая форма мысли или процесса мышления выявляется путем частичного отвлечения от смыслов и значений нелогических терминов. Как это делается? Пусть дано предложение «Давид Гильберт — выдающийся математик». Предложение после некоторой реконструкции имеет вид: «Давид

Гильберт есть выдающийся математик». В этом предложении один логический термин — «есть». Выражения «Давид Гильберт» и «выдающийся математик» являются нелогическими терминами. Для выявления логической формы эти выражения можно заменить, например, многоточиями. При этом следует сохранить информацию о типе заменяемых выражений, а также о том, где были разные выражения, а где одно и то же. Получаем: ... есть ... . Очевидно, что выражения «Давид Гильберт» и «выдающийся математик» относятся к разным типам, поскольку Давид Гилберт один, а выдающихся математиков много. Вместо многоточий удобнее использовать символы, называемые переменными. Тогда получаем, например, выражение «s есть P». Так представляется логическая форма исходной мысли.

Еще пример. Рассмотрим рассуждение (процесс мышления) «Москвичи — жители Восточной Европы, поскольку жители Восточной Европы — европейцы, и москвичи — европейцы».

Для выявления логической формы рассуждения нужно рассуждение уточнить. В данном случае уточнение может быть таким:

Каждый житель Восточной Европы есть европеец.

Каждый москвич есть европеец.

Следовательно, каждый москвич есть житель

Восточной Европы.

Вместо слова «следовательно» будем проводить черту. Тогда имеем:

Каждый житель Восточной Европы есть европеец.

Каждый москвич есть европеец.

Каждый москвич есть житель Восточной Европы.

Заменим нелогические термины «житель Восточной Европы», «европеец», «москвич» соответственно символами P, M, S. Получаем:

Каждый P есть M.

Каждый S есть M.

Каждый S есть P.

Этой записью выражается логическая форма исходного рассуждения.

Таким образом, логическая форма мысли (процесса мышления) — это структура этой мысли (этого процесса мышления), которая выявляется путем частичного отвлечения от смыслов и значений нелогических терминов, входящих в словосочетание, выражающее эту мысль (этот процесс мышления).

Упражнение 1

Выявите логические формы мыслей, выраженных следующими предложениями.

1. Некоторые поступки не являются преднамеренными.

2. Каждый студент — учащийся.

3. Если некоторые люди являются талантливыми, то неверно, что ни один человек не является талантливым.

4. Некоторые водные животные являются млекопитающими.

5. Юпитер — планета.

Упражнение 2

Выявите логические формы следующих рассуждений.

1. Поскольку каждый человек, находящийся в здравом уме, может изучить логику, а Иванов находится в здравом уме, то Иванов может изучить логику.

2.

Дельфины — киты.

Рыба — не дельфин.

Рыба — не кит.

ФОРМАЛЬНО-ЛОГИЧЕСКИЕ ЗАКОНЫ

Между мыслями существуют отношения, которые зависят только от логических форм этих мыслей. Например, обвинитель утверждает, что все подсудимые по данному делу виновны, а защита утверждает, что ни один из подсудимых не виновен. Что можно сказать об этих утверждениях, не зная обстоятельств дела? Почти очевидно, что если одна из сторон права, то другая не права, что обе не могут быть правы, а неправы могут быть обе стороны. В случае более сложных утверждений для установления отношений приходится применять специальные методы.

Пример. В каком отношении находятся исходные утверждения (посылки) и результирующее утверждение (заключение) в следующем рассуждении?

Некоторые жители Чикаго не подлежат привлечению

к уголовной ответственности.

Преступники подлежат привлечению

к уголовной ответственности.

Некоторые жители Чикаго — не преступники.

Уточнение рассуждения:

Некоторый житель Чикаго не есть лицо, подлежащее

привлечению к уголовной ответственности.

Каждый преступник есть лицо, подлежащее

привлечению к уголовной ответственности.

Некоторый житель Чикаго не есть преступник.

Логическая форма:

Некоторый R не есть Q.

Каждый F есть Q.

Некоторый R не есть F.

Какие бы выражения (того же типа, в дальнейшем они будут названы общими именами) мы ни брали вместо переменных R, Q и R, всегда окажется, что при истинности посылок заключение является истинным. Такие связи между мыслями называются логическими законами.

Определение: связи между мыслями по формам, при которых истинность одних из этих мыслей обусловливает истинность других, называются формально-логическими законами, или логическими законами.

Чтобы установить, является ли связь между мыслями, выражаемыми посылками, и мыслью, выражаемой заключением, логическим законом, нужно, не изменяя логической формы, вместо нелогических выражений подставлять в посылки и заключение произвольные выражения тех же типов и при этом всякий раз выяснять, окажется ли истинным получаемое высказывание при истинности исходных. Если всегда обнаруживается такая зависимость истинности высказываний, то связь между ними представляет собой логический закон и рассуждение является правильным. Если находится контрпример, то закономерной связи нет и рассуждение не является правильным. Так, рассуждение «Следователь — юрист. Следовательно, хороший следователь — хороший юрист» является неправильным. Контрпримером для него может служить явно неправильное рассуждение:

Мышь — животное. Следовательно,

крупная мышь — крупное животное.

Методом контрпримеров проверим приведенное выше рассуждение:

Каждый житель Восточной Европы есть европеец.

Каждый москвич есть европеец.

Каждый москвич есть житель Восточной Европы.

Логическая форма:

Каждый P есть M.

Каждый S есть M.

Каждый S есть P.

Контрпример:

Каждая курица — птица.

Каждый гусь — птица.

Каждый гусь — курица.

Упражнение 3

Методом контрпримеров установите, являются ли следующие рассуждения правильными.

1. Некоторые биологи не являются философами. Следовательно, некоторые философы не являются биологами.

2.

Некоторые правоведческие произведения —

не философские.

Все философские произведения — мировоззренческие.

Некоторые правоведческие произведения —

не мировоззренческие.

3. Все студенты нашей группы — журналисты. Все студенты нашей группы — члены кружка логики. Следовательно, все члены кружка логики — журналисты.

4. Если философ является дуалистом, то он не идеалист. Если философ не идеалист, то он диалектик или метафизик. Этот философ не метафизик. Следовательно, он диалектик или не дуалист.

5. «Если умер Сократ, то он умер или когда жил, или когда умер. Если когда жил, то он не умер, так как один и тот же человек и жил бы, и был бы мертв; но и не тогда, когда умер, ибо он был бы дважды мертвым. Стало быть, Сократ не умер». (Секст Эмпирик. Соч. в 2 т. М., 1976. Т. 2. С. 289).

6. Некоторые участники этого преступления опознаны потерпевшим. Ни один из членов семьи Петровых не опознан потерпевшим. Следовательно, некоторые члены семьи Петровых не являются участниками этого преступления.

В некоторых случаях можно установить правильность или неправильность рассуждения, не выявляя внутреннюю структуру простых высказываний.

Пример. Дано рассуждение:

«Если не зафиксированы следы преступной деятельности в протоколе осмотра места происшествия, то процессуальный порядок следственного действия не соблюден. Процессуальный порядок следственного действия не соблюден. Следовательно, следы преступной деятельности не зафиксированы в протоколе».

Заменим переменными A, B соответственно высказывания «Следы преступной деятельности не зафиксированы в протоколе», «Процессуальный порядок следственного действия не соблюден». Логическая форма рассуждения:

Если A, то B. B
A

Контрпример: «Если Петров — студент, то он учащийся. Петров — учащийся (школьник). Следовательно, он студент».

Упражнение 4

Не выявляя логической формы следующего рассуждения, установите, является ли оно правильным.

«Если это преступление совершил Петров, то он знал потерпевшего. Петров не знал потерпевшего, но знал его брата. Петрова видели на месте преступления примерно в то время, когда преступление было совершено. У Петрова обнаружены похищенные вещи. Следовательно, Петров не совершал этого преступления».

ОТВЕТЫ И РЕШЕНИЯ

Упражнение 1

1. В предложении «Некоторые поступки не являются преднамеренными» выражения «некоторые» и «не являются» («не суть») — логические термины, слова «поступок» и «преднамеренный» — нелогические термины. Заменяем нелогические термины соответственно символами S и P. Получаем выражение «Некоторые S не суть P», которым представлена логическая форма исходной мысли.

5. В предложении «Юпитер — планета» логическим термином является пропущенное слово «есть». Поскольку термины «Юпитер» и «планета» относятся к разным типам, заменяем их символами разных типов, например s и M. Получаем выражение «s есть M».

Упражнение 2

2. После реконструкции рассуждения имеем:

Каждый дельфин есть кит.

Каждая рыба не есть дельфин.

Каждая рыба не есть кит.

Логическая форма:

Каждый P есть M.

Каждый S не есть P.

Каждый S не есть M.

Упражнение 3

5. В рассуждении «Если умер Сократ, то он умер или когда жил, или когда умер. Если когда жил, то он не умер, так как один и тот же человек и жил бы, и был бы мертв; но и не тогда, когда умер, ибо он был бы дважды мертвым. Стало быть, Сократ не умер» заменим высказывания «Сократ умер», «Он умер, когда жил», «Он умер, когда умер» соответственно символами p, q, r. (В некоторых случаях целесообразно логическую форму выявлять не полностью. Если рассуждение оказывается правильным при не полностью выявленной логической форме, то оно остается правильным и при полностью выявленной логической форме.) Получаем выражение:

«Если p, то q или r. Если q, то не-p. Если r, то не-p. Следовательно, не-p». Контрпримера подобрать не удается. Следовательно, можно с определенной степенью уверенности утверждать, что рассуждение является правильным. Почему же заключение этого рассуждения «Сократ не умер» является ложным? Ложной является посылка «Если умер Сократ, то он умер или когда жил, или когда умер», поскольку человек умирает в процессе перехода от живого состояния к мертвому, а не когда остается живым и не когда является уже мертвым.

6. В рассуждении «Некоторые участники этого преступления опознаны потерпевшим. Ни один из членов семьи Петровых не опознан потерпевшим. Следовательно, некоторые члены семьи Петровых не являются участниками этого преступления» выделим нелогические термины «участник этого преступления», «опознанный потерпевшим», «член семьи Петровых». Обозначим эти термины соответственно символами S, P, Q. Логическая форма представляется выражением «Некоторые S суть P. Ни один Q не суть P. Следовательно, некоторые Q не суть S». Рассуждение не является правильным. Контрпримером может служить рассуждение «Некоторые млекопитающие — водные животные. Ни один волк не является водным животным. Следовательно, некоторые волки не являются млекопитающими». Посылки этого рассуждения истинны, а заключение ложно.

Упражнение 4

Рассуждение является правильным, однако это не очевидно. Преподаватель на этом примере может показать студентам, что у них различная логическая культура, и у многих низкая. Можно, например, попросить студентов ответить на следующие вопросы: «Кто считает, что это рассуждение правильное?», «Кто считает его неправильным?», «Кто не имеет определенного мнения по данному вопросу?». Чаще всего оказывается, что мнения разделяются. Можно, ради шутки, предложить решить вопрос голосованием. Затем полезно отметить, что после изучения логики разногласий по таким вопросам не будет.

Глава 2.
ЛОГИКА И ЯЗЫК

ЯЗЫК КАК ЗНАКОВАЯ СИСТЕМА

Логика, являясь наукой о формах мыслей и отношениях между мыслями по логическим формам, является также наукой о языке, поскольку она изучает способы выражения мыслей в естественных языках и создает особые формализованные языки, позволяющие более точно, чем естественные языки, выражать логические формы мыслей.

Логика рассматривает язык как систему знаков.

Знак — это материальный объект, используемый в процессе познания или общения в качестве представителя какого-либо объекта.

Можно выделить знаки следующих трех типов: (1) знаки-индексы; (2) знаки-образы; (3) знаки-символы.

Знаки-индексы связаны материально с представляемыми ими объектами, например, как следствия с причинами. Так, дым над лесом говорит о наличии там огня, повышенная температура человека — о заболевании, особый цвет ногтей человека — о заболевании внутренних органов, изменение высоты ртутного столба — об изменении атмосферного давления.

Знаками-образами являются те знаки, которые сами по себе несут некоторую информацию о представляемых ими объектах (карта местности, картина, чертеж), поскольку они находятся в отношении подобия с обозначаемыми объектами.

Знаки-символы не связаны материально и не сходны с представляемыми ими объектами. Таковыми, например, являются выражения русского языка «лошадь», «дом», «человек».

Логика исследует знаки последнего вида.

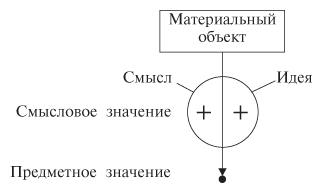
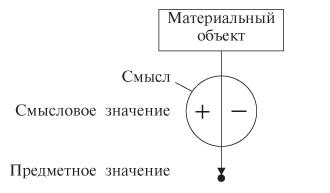
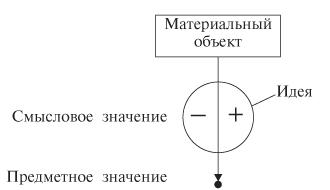
Как правило, знаки имеют предметные и смысловые значения. Предметным значением является тот объект, который представляется (или обозначается) знаком, смысловым значением — выражаемая знаком характеристика объекта, представителем которого является знак (информации об этом объекте, которая позволяет отличать предметы, являющиеся значениями знака, от всех других предметов). Предметное значение часто называют просто значением, а смысловое значение, если оно выражено в языке, — смыслом. Если смысловым значением являются зрительный образ, представление, интуиция и т. д., то смысловое значение называют идеей.

Возможны следующие знаковые ситуации.

Первая. Смысловое значение состоит из смысла и идеи.

Вторая. Смысловое значение состоит только из смысла.

Третья. Смысловое значение состоит только из идеи.

Упражнение 1

Укажите значения и смыслы следующих выражений (знаков-символов).

1. Луна.

2. Студент.

3. Ликург.

4. Автор «Божественной комедии».

5. Омонимы.

6. Синонимы.

7. Ближайшая к Солнечной системе звезда.

8. Вечный двигатель.

9. Человек.

ИМЕНА

Среди знаков-символов выделяют знаки, называемые именами.

Имя — это слово или словосочетание, обозначающее какой-либо предмет. Поскольку имя является знаком, оно имеет смысловое значение (смысл и (или) идею) и (предметное) значение. Значение имени — это предмет, обозначаемый этим именем. Имя обязательно имеет смысловое значение, а предметного значения может не иметь. Смысл — это представленная в языке информация о предметах, которую выражает имя и которая позволяет однозначно выделять предметы, являющиеся значениями имени. Идея — зрительный образ, интуитивное представление о предмете, т. е. то, что изучается психологией, а не логикой.

Различают имена двух типов. Имя, относящееся к первому типу, обозначает один предмет. Имя второго типа является общим для предметов некоторого класса. Имена первого типа называются единичными, а второго — общими. Примеры единичных имен: Луна; столица России; автор романа «Война и мир». Примеры общих имен: животное, имеющее мягкие мочки ушей; государство; ученик. Таким образом, значением единичного имени является единственный предмет. Значениями общего имени являются предметы некоторого класса, содержащего более одного элемента. Класс, который составляют предметы, являющиеся значениями имени, называется объемом имени. Объем единичного имени — класс, состоящий из одного предмета. Объем имени можно представить графически в виде круга, заполненного точками. Каждая точка соответствует предмету, являющемуся значением имени. Точки внутри круга, как правило, опускают.

Общие имена могут быть универсальными. Универсальными называются общие имена, объемом которых является весь универсум рассуждения (вся область предметов, о которых ведется рассуждение). Например, «человек, знающий некоторые иностранные языки или не знающий ни одного иностранного языка». Универсум рассуждения здесь — множество (всех) людей. Объем имени — то же самое множество. Имя «человек, знающий какие-то иностранные языки» — не универсальное, поскольку его объем не совпадает с множеством (всех) людей. Универсум рассуждения определяется контекстом, в котором употребляется имя.

Могут быть имена с разными смыслами и одним и тем же объемом (например, «самый большой город Англии» и «столица Англии»), но не может быть имен с одним и тем же смыслом, но разными объемами.

Имена могут не обозначать ни одного предмета, существующего в универсуме рассуждения. Такие имена являются мнимыми. Примеры: «русалка», «самая удаленная точка Вселенной». Эти имена являются мнимыми, если универсум рассуждения составляют предметы, существующие в объективной реальности. В последнем случае имя является мнимым, если предполагается, что Вселенная бесконечна. Объем мнимого имени — пустое множество.

Имена, значениями которых являются предметы, входящие в универсум рассуждения, называются действительными.

Упражнение 2

Укажите значения, объемы и смыслы следующих имен.

1. Человек.

2. Л. Н. Толстой.

3. Спутник Земли.

4. Естественный спутник Земли.

5. Человек, живущий не по средствам.

6. Первый заместитель Председателя Совета министров.

7. Планета Солнечной системы.

8. Болезнь.

9. Наименьшее натуральное число.

10. Наибольшее натуральное число.

11. Демократия.

12. Человек, живущий подаянием.

13. Предположение, признаваемое истинным, пока не доказано обратное (презумпция).

Упражнение 3

Представьте объемы следующих имен в виде кругов и покажите, в каком отношении эти круги находятся. Круги могут попарно пересекаться, совпадать, один может входить в другой.

1. Стоимость, меновая стоимость, потребительная стоимость.

ОСНОВНЫЕ МЕТОДОЛОГИЧЕСКИЕ ПРИНЦИПЫ УПОТРЕБЛЕНИЯ ИМЕН

Научные языки подчиняются следующим трем методологическим принципам: (1) принципу однозначности; (2) принципу предметности; (3) принципу взаимозаменимости.

Согласно принципу однозначности выражение, используемое в качестве имени, должно быть именем только одного предмета, если это единичное имя, а если это общее имя, то данное выражение должно быть именем, общим для предметов одного класса. В обыденном языке данный принцип не всегда соблюдается. Его соблюдение необходимо в научных языках, особенно при построении искусственных языков, например языка логики предикатов.

Согласно принципу предметности в высказываниях должно утверждаться или отрицаться нечто о значениях имен, входящих в предложения, а не о самих именах. Нужно, конечно, иметь в виду, что значениями некоторых имен являются имена. Такие случаи не противоречат принципу предметности. Например, в предложении «Материя первична, а сознание вторично» «материя» — это имя объективной реальности, а в предложении «“Материя” — философская категория» слово «материя», взятое в кавычки, — это имя имени, имя категории. Такие имена называются кавычковыми именами. Иногда в естественном языке встречаются случаи, когда именем имени является само исходное имя. Например, в предложении «Стол состоит из четырех букв» слово «стол» является именем самого этого слова. Такое употребление имен называется автонимным. Автонимное употребление имен недопустимо в научных языках, поскольку оно приводит к недоразумениям. Так, в известном определении В. И. Ленина: «Материя есть философская категория для обозначения объективной реальности, которая дана человеку в ощущениях его, которая копируется, фотографируется, отображается нашими ощущениями, существуя независимо от них»[2] — имеет место автонимное употребление имени «материя». Это вызывает споры о том, что В. И. Ленин называл материей: объективную реальность или категорию, т. е. мысль, понятие о реальности.

Принцип взаимозаменимости: если в сложном имени заменить часть, в свою очередь являющуюся именем, другим именем с тем же значением, то значение полученного в результате такой замены сложного имени должно быть тем же, что и значение исходного сложного имени. Пусть дано предложение «Земля вращается вокруг Солнца» (будем считать, что предложения тоже являются именами и значением предложения является истина или ложь). Заменим имя «Солнце» в приведенном предложении на имя «центральное тело Солнечной системы». Очевидно, что значения этих имен совпадают. В результате такой замены из истинного предложения получаем истинное.

Принцип взаимозаменимости кажется естественным, однако можно привести примеры подстановки имен, которые, как кажется, ему противоречат. Рассмотрим предложение: «Птолемей считал, что Солнце вращается вокруг Земли». Оно истинно. Заменим имя «Солнце» на имя «центральное тело Солнечной системы», имеющее то же значение. Получим ложное предложение.

Такие несоответствия принципу взаимозаменимости называются антиномиями отношения именования, а контексты, в которых указанная замена не приводит к желаемым результатам, называются интенсиональными, в отличие от экстенсиональных, где замена возможна.

Как сохранить принцип взаимозаменимости и избежать антиномий?

Следует различать два способа употребления имен. Первый — имя просто выделяет предмет (предметы). Второй — предметы, обозначаемые именем, рассматриваются в определенном аспекте. Если имя употребляется во втором смысле, то его можно заменять другим именем с тем же значением, если только во втором имени предметы рассматриваются в том же аспекте. Указанную выше замену можно было бы произвести, если бы Птолемей считал, что значения имен «Солнце» и «центральное тело Солнечной системы» совпадают. Тогда значением предложения «Птолемей считал, что Солнце вращается вокруг Земли» была бы «ложь». Ложным бы оказалось и предложение, получаемое в результате замены: «Птолемей считал, что центральное тело Солнечной системы вращается вокруг Земли».

Упражнение 4

Установите, какие принципы употребления имен нарушены в следующих языковых контекстах.

1. «На первом курсе мы изучаем логику. Мы познакомимся со многими логиками — традиционной и символической, классической и неклассической. После этого для нас не останется тайн ни в логике ребенка, ни в женской логике».

2. Из милицейского протокола: «на полу лежал труп, рядом сидела жена трупа, а брат трупа лежал в другой комнате без сознания».

Упражнение 5

Нарушен ли принцип предметности в следующих утверждениях?

«Как личные, так и неличные формы глагола имеют два залога: действительный и страдательный.

Глаголы в действительном залоге выражают действие, которое производится подлежащим.

Глаголы в страдательном залоге выражают действие, которое испытывает на себе подлежащее» (Маркова Л. С. Краткий грамматический справочник. Английский язык. М., 1972. С. 56).

Упражнение 6

Укажите, какие из следующих выражений — причина, «причина», «“причина”» — можно подставить вместо x в приведенные ниже выражения, чтобы получить истинные предложения.

1. x — философская категория.

2. x — слово русского языка.

3. x — выражение, обозначающее слово.

4. x — озоновой дыры не выявлено.

Упражнение 7

Какие из следующих выражений — Москва, «Москва», «“Москва”», «столица России» — можно подставить вместо x, чтобы получить истинное предложение:

1. x — город, находящийся в Европе.

2. x — название города.

3. x — выражение русского языка.

4. x — выражение, обозначающее слово.

Упражнение 8

Какие из следующих выражений истинны, а какие не истинны:

	1) 2 х 3 = 6;	2) «2 х 3» = 6;
	3) «2 х 3» ≠ «6»;	4) «2 х 3 = 6».

Упражнение 9

Является ли контекст экстенсиональным или интенсиональным:

1. Птолемей считал, что Солнце вращается вокруг Земли. (Относительно терминов «Солнце» и «Птолемей».)

2. Поиск Магелланом пролива из Атлантического океана в Тихий. (Относительно термина «пролив из Атлантического океана в Тихий».)

Упражнение 10

Является ли следующее рассуждение правильным? Если нет, то почему?

1. Все зеленое приятно. Эта картина зеленая. Следовательно, эта картина приятная.