автордың кітабын онлайн тегін оқу Гидравлика
В. А. Зверева, Н. В. Земляная, В. В. Земляной, С. В. Бочаров, О. И. Якушкина, Л. В. Кучерова, А. А. Надежкина
Гидравлика
Учебно-методический комплекс
Информация о книге
УДК 532.(0.76)
ББК 30.123
З-43
Авторы: Зверева В. А., Земляная Н. В., Земляной В. В., Бочаров С. В., Якушкина О. И., Кучерова Л. В., Надежкина А. А.
Рецензенты:
Головин В. Л., зам. директора по научной работе «ФГУП ДальНИИГиМ», ст. научн. сотр., канд. техн. наук;
Гунько Л. М., ст. преподаватель кафедры «Управление судном» Морского института Дальневосточного государственного технического рыбохозяйственного университета.
Учебно-методический комплекс дисциплины «Гидравлика» (УМКД) содержит учебную рабочую программу дисциплины, конспект лекций по дисциплине «Гидравлика», методические указания к практическим занятиям, лабораторный практикум, лабораторный практикум по механике жидкости на портативной лаборатории «Капелька», методические указания к выполнению самостоятельных работ студентов, контрольно-измерительные материалы в виде тестов для текущей и итоговой аттестации.
УМКД предназначен для студентов очной и заочной форм обучения специальности 270112 «Водоснабжение и водоотведение».
УДК 532.(0.76)
ББК 30.123
© Дальневосточный государственный технический университет, 2008
© ДВФУ, 2015
© ООО "Проспект", электронная версия книги, 2015
ПРЕДИСЛОВИЕ
Учебно-методический комплекс дисциплины «Гидравлика» (УМКД) предназначен для студентов очной и заочной форм обучения специальности 270112 «Водоснабжение и водоотведение» и может быть использован для подготовки студентов всех специальностей, обучающихся по направлениям «Строительство», «Горное дело», «Механика», «Охрана окружающей среды», имеющих аналогичные требования к содержанию дисциплины «Гидравлика».
Материал курса «Гидравлика» – неотъемлемая часть комплекса знаний, необходимых для подготовки инженеров по направлению «Строительство». Изучение материала курса направлено на освоение основных законов, действующих в жидкостях, находящихся в состоянии покоя (относительного и абсолютного) и в движущихся жидкостях, основных расчетных зависимостей, необходимых для гидравлического расчета систем, методов и технологий их применения; выработку навыка использования справочной и научной литературы при решении практических задач. Материал подготовлен в соответствии с ГОС ВПО направления подготовки дипломированных специалистов 653500 «Строительство» по специальности 270112 «Водоснабжение и водоотведение», утвержденных Минвузом РФ в 2000 г.
Учебно-методический комплекс дисциплины «Гидравлика» (УМКД) содержит учебную рабочую программу дисциплины, конспект лекций по дисциплине «Гидравлика», методические указания к практическим занятиям, лабораторный практикум, лабораторный практикум по механике жидкости на портативной лаборатории «Капелька», методические указания к выполнению самостоятельных работ студентов, контрольно-измерительные материалы по дисциплине «Гидравлика» для текущего и итогового контроля студентов дневной и заочной форм обучения специальности 270112 «Водоснабжение и водоотведение».
Конспект лекций имеет целью оказать студентам необходимую методическую помощь по изучению дисциплины «Гидравлика».
В материале лекций отражены основные теоретические положения, представлены модели процессов, сопровождающих равновесие и движение жидкостей и газов.
Методические указания к практическим занятиям составлены в помощь студентам специальности 270112 «Водоснабжение водоотведение» для выработки навыков применения теоретических знаний для решения технических задач. Методические указания предусматривают решение задач по наиболее важным разделам дисциплины «Гидравлика».
Методические указания к самостоятельной работе предназначены для приобретения практических навыков гидравлических расчетов при проектировании различных сооружений, систем и устройств, анализа полученных результатов, развитие самостоятельной работы студентов в плане подготовки будущих специалистов строительной отрасли.
Лабораторный практикум составлен на основании государственного стандарта и рабочих учебных программ дисциплины «Гидравлика». Приведены основные теоретические сведения по изучаемым темам дисциплины, расчетные формулы и методика их применения. Каждая глава содержит описание лабораторных работ, порядок их выполнения и оформления, контрольные вопросы. Лабораторный практикум предназначен для студентов, обучающихся по направлениям «Строительство», «Механика», «Горное дело», «Охрана окружающей среды».
Лабораторный практикум на портативных установках «Капелька» составлен на основании ГОС ВПО и рабочих учебных программ дисциплин «Гидравлика» и «Гидромеханика» для усвоения наиболее важных вопросов, предназначен для студентов очной и заочной форм обучения по направлениям «Строительство», «Горное дело», «Механика», «Охрана окружающей среды».
Методические указания содержат основные теоретические сведения по соответствующим темам выполнения лабораторных работ, порядок проведения испытаний и обработки результатов экспериментов. Для проверки знаний, полученных в результате выполнения лабораторных работ, составлены контрольные вопросы.
УМКД разработан сотрудниками кафедры «Гидравлика, Водоснабжение и водоотведение» ДВГТУ. Конспект лекций составлен профессором Н.В. Земляной, рабочая учебная программа и методические указания к практическим занятиям разработаны доцентом В.А. Зверевой; лабораторный практикум – профессором В.В. Земляным, доцентом С.В. Бочаровым и В.А. Зверевой; лабораторный практикум на портативной установке «Капелька» – профессором В.В. Земляным и доцентом В.А. Зверевой, методические указания по выполнению самостоятельной работы студентов – доцентом О.И. Якушкиной, старшими преподавателями Л.В. Кучеровой и А.А. Надежкиной.
РАБОЧАЯ УЧЕБНАЯ ПРОГРАММА
Цели и задачи дисциплины
Гидравлика – прикладная общетехническая наука, целью которой является изучение законов равновесия и движения жидкостей и газов и применение этих законов к решению различных задач инженерной практики в области водоснабжения и водоотведения населенных мест.
Начальные требования к освоению гидравлики (перечень предшествующих дисциплин)
Изучение дисциплины «Гидравлика» осуществляется с помощью и на основании знаний основных общенаучных и общетехнических дисциплин: высшей математики, физики, теоретической механики, сопротивления материалов.
Требования к уровню освоения содержания дисциплины
В результате теоретического изучения дисциплины студент должен знать основные законы, действующие в жидкостях, находящихся в состоянии покоя (относительного и абсолютного) и в движущихся жидкостях, основные расчетные зависимости, необходимые для гидравлического расчета систем, методы и технологию их применения; уметь пользоваться при решении практических задач справочной и научной литературой.
Объем дисциплины и виды учебной работы
Очная форма обучения
| Вид учебной работы | Всего, ч | Распределения по семестрам | |
| IV | |||
| Общая трудоемкость дисциплины | 90 | 90 | |
| Лекции | 18 | 18 | |
| Лабораторные занятия | 18 | 18 | |
| Практические занятия | 18 | 18 | |
| Всего самостоятельная работа | 36 | 36 | |
| В том числе: курсовое проектирование | – | – | |
| Другие виды (РГЗ, рефераты и др.) | – | – | |
| Вид итогового контроля (экзамен, зачет) | зачет | зачет | |
Заочная форма обучения
| Вид учебной работы | Всего, ч | Распределения по семестрам | |
| IV | |||
| Общая трудоемкость дисциплины | 90 | 90 | |
| Лекции | 8 | 8 | |
| Лабораторные занятия | 4 | 4 | |
| Практические занятия | – | – | |
| Всего самостоятельная работа | 78 | 78 | |
| В том числе: курсовое проектирование | – | – | |
| Контрольные работы | 1 | 1 | |
| Вид итогового контроля (экзамен, зачет) | зачет | зачет | |
Содержание дисциплины
Распределение учебного материала по видам занятий
| № п/п | Наименование раздела дисциплины | Распределение по видам (час) | |||
| Лек | ЛЗ | ПЗ | СРС | ||
| 1 | Предмет гидравлики, краткая история ее развития | 1 | |||
| 2 | Физические свойства жидкостей | 1 | 2 | 2 | 2 |
| 3 | Гидростатика | 4 | 4 | 4 | 8 |
| 4 | Относительный покой жидкости. Сила давления жидкости на плоские поверхности | 2 | |||
| 5 | Гидродинамика. Основы кинематики. Уравнения количества движения и момента количества движения | 2 | 2 | ||
| 6 | Гидравлические сопротивления | 3 | 12 | 8 | 18 |
| 7 | Истечение жидкости из отверстий, насадков и из под затворов | 2 | 2 | 4 | |
| 8 | Гидравлический расчет простых трубопроводов | 2 | 2 | ||
| 9 | Основы теории подобия. Численные методы расчета | 1 | 2 | ||
Содержание лекционного курса (наименование раздела, темы, краткое содержание)
Лекция 1. Предмет гидравлики, краткая история ее развития. Область применения гидравлики. Открытия древних ученых в области гидравлики. История развития гидравлики новой эры.
Лекция 2. Физические свойства жидкостей. Жидкости и их главнейшие отличия от твердых и газообразных тел. Плотность и удельный вес однородной жидкости. Упругие свойства жидкостей. Внутреннее трение или вязкость. Капиллярность, поглощение газов жидкостями. Особые свойства воды. Свойства идеального газов.
Лекция 3. Гидростатика. Силы, действующие в жидкостях. Гидростатическое давление и его свойства. Дифференциальные уравнения гидростатики (равновесия). Закон Паскаля.
Лекция 4. Относительный покой жидкости. Сила давления жидкости на плоские поверхности: Геометрическая и физическая интерпретация основного уравнения гидростатики. Относительный покой жидкости. Сила давления жидкости на плоские, произвольно ориентированные поверхности. Давление жидкости на цилиндрическую поверхность. Закон Архимеда и его приложение.
Лекция 5. Гидродинамика. Основы кинематики. Уравнения количества движения и момента количества движения: Основные понятия о движении жидкости. Модель идеальной жидкости. Уравнение количества движения. Уравнение Бернулли для идеальной жидкости. Уравнение Бернулли для реальной жидкости. Измерение скорости потока и расхода жидкости. Уравнение энергии в дифференциальной форме.
Лекция 6. Гидравлические сопротивления. Режимы движения жидкости. Кавитация. Потери напора при ламинарном течении жидкости. Потери напора при турбулентном течении жидкости. Местные гидравлические сопротивления.
Лекция 7. Истечение жидкости из отверстий, насадков и из-под затворов. Истечение через малые отверстия в тонкой стенке при постоянном напоре. Истечение при несовершенном сжатии. Истечение под уровень. Истечение через насадки при постоянном напоре. Истечения через отверстия и насадки при переменном напоре (опорожнение сосудов). Истечение из-под затвора в горизонтальном лотке. Давление струи жидкости на ограждающие поверхности.
Лекция 8. Гидравлический расчет простых трубопроводов. Классификация трубопроводов. Простой трубопровод постоянного сечения. Соединения простых трубопроводов. Сложные трубопроводы. Гидравлический удар. Изменение пропускной способности трубопроводов в процессе их эксплуатации.
Лекция 9. Основы теории подобия. Численные методы расчета.
Содержание практических и лабораторных занятий
Содержание лабораторных занятий
| № п/п | Номер раздела п. 5.1 |
Наименование лабораторной работы |
| 1 | 1 | Изучение основных физических свойств жидкости |
| 2 | 2 | Изучение приборов для измерения давления |
| 3 | 2 | Относительный покой жидкости во вращающемся сосуде |
| 4 | 3 | Приборы и методы измерения гидравлических величин |
| 5 | 5 | Уравнение Д. Бернулли для установившегося движения вязкой несжимаемой жидкости |
| 6 | 5 | Режимы движения жидкости |
| 7 | 5 | Экспериментальное определение коэффициента гидравлического трения |
| 8 | 5 | Экспериментальное определение коэффициентов местных сопротивлений |
| 9 | 5 | Истечение жидкости из отверстий и насадков |
Содержание практических занятий
| № п/п | Номер раздела п. 5.1 |
Наименование темы практического занятия |
| 1 | 1 | Физические свойства жидкостей |
| 2 | 2 | Гидростатическое давление |
| 3 | 2 | Сила гидростатического давления на плоские стенки и цилиндрические поверхности |
| 4 | 2 | Относительный покой жидкости |
| 5 | 5 | Уравнение неразрывности. Уравнение Д. Бернулли |
| 6 | 5 | Режимы движения жидкости |
| 7 | 5 | Гидравлические сопротивления |
| 8 | 5 | Истечение жидкости через отверстия и насадки |
| 9 | 6 | Основы теории подобия и моделирования |
График изучения дисциплины
| Вид учебных занятий | № лекции | |||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| Лекции | + | + | + | + | + | + | + | + | + | |||||||||
| ЛЗ | + | + | + | + | + | + | + | + | + | |||||||||
| ПЗ | + | + | + | + | + | + | + | + | + | |||||||||
| Аттестация | А | А | ||||||||||||||||
Учебно-методическое обеспечение дисциплины (рекомендуемая литература)
Основная литература
1. Штеренлихт Д.В.. Гидравлика: учебник. – В 2-х кн. Кн. 1. 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1991.
2. Большаков В.А., Попов В.И. Гидравлика. Общий курс: учебник. – Киев: Выща шк.: Головное изд-во, 1989.
3. Лаптев Н.Н. Гидравлика: учеб. пособие. – СПб.: Стройиздат, 2006.
4. Чугаев Р.Р. Гидравлика (Техническая механика жидкости). – Л.: Энер-гоиздат; Ленинград. отд-е, 1982.
5. Сборник задач по гидравлике / В.А. Большаков, Ю.М. Константинов, В.Н. Попов и др. / под ред. В.А. Большакова. – Киев: Вища шк.: Головное изд-во, 1979.
6. Земляной В.В., Зверева В.А., Бочаров С.В. Гидравлика: лабораторный практикум. – Владивосток: Изд-во ДВГТУ, 2003.
7. Зверева В.А. Гидравлика: Лабораторный практикум на портативных установках «Капелька». – Владивосток: Изд-во ДВГТУ, 2007.
Дополнительная литература
1. Богомолов А.И., Михайлов К.А. Гидравлика. – М.: Стройиздат, 1972.
2. Киселев П.Г., Альтшуль А.Д. Механика жидкости и газа. – М.: Стройиздат, 1985
Справочная литература
1. Справочник по гидравлике / под ред. В.А. Большакова. 2-е изд., переаб. и доп. – Киев: Вища шк.: Головное изд-во, 1984.
2. Справочник по гидравлическим расчетам / под ред. П. Г. Киселева. Изд. 5-е. – М.: Энергия, 1974.
3. Курганов А.М., Федоров Н.Ф. Гидравлические расчеты систем водоснабжения и водоотведения: справочник. – Л.: Стройиздат, 1986.
Программное обеспечение
1. Контролирующая программа (тесты).
2. Программа для подбора диаметра простого трубопровода на ЭВМ на языке FORTRAN.
3. Программы для построения графика потребного напора на ЭВМ на языке FORTRAN.
8. Технические и электронные средства обучения, иллюстрационные материалы, специализированное и лабораторное оборудование
Список иллюстрационных материалов (плакаты)
1. Физические свойства жидкостей.
2. Уравнение Д. Бернулли.
3. Примеры местных гидравлических сопротивлений структуры течения и расчетные формулы.
4. Графики Никурадзе зависимости
5. Силы давления покоящиеся жидкости на плоские симметричные стенки.
6. Давление на цилиндрические поверхности.
7. Графики Кольбрука-Уайта.
8. Структура потока в насадках разного типа.
9. Истечение через малые отверстия. Коэффициенты скорости, сжатия, расхода.
10. Структура потока в круглых трубах.
11. Основные зависимости для определения параметров свободной струи.
12. Вихревые линии и трубки. Циркуляция.
13. Напряженное состояние жидкой среды.
Специализированное и лабораторное оборудование
Специализированная лаборатория гидравлики
Перечень оборудования
1. Вискозиметр Энглера.
2. Капиллярный вискозиметр ВПЖ-2.
3. Механический манометр, вакуумметр, мановакуумметр.
4. Пьезометр.
5. Трубка Пито (скоростная трубка).
6. Опытная установка ГД-1. «Определение абсолютного, манометрического и вакуумметрического давления».
7. Опытная установка ГД-2. «Относительный покой жидкости во вращающемся сосуде».
8. Опытная установка ГД-3. «Демонстрация уравнения Д. Бернулли».
9. Опытная установка ГД-4. «Демонстрация режимов движения жидкости».
10. Опытная установка ГД-5. «Экспериментальное определение коэффициента трения
11. Опытная установка ГС, позволяющая одновременно определять коэффициенты различных местных гидравлических сопротивлений
Портативная гидравлическая лаборатория «Капелька»
1. Изучение физических свойств жидкости: опытное определение плотности жидкости, коэффициента температурного расширения, коэффициента поверхностного натяжения, вязкости жидкости вискозиметром Стокса и капиллярным вискозиметром.
2. Изучение устройства и принципа действия жидкостных приборов для измерения давления.
3. Измерение гидростатического давления жидкостными приборами.
4. Изучение структуры потоков жидкости.
5. Определение режима течения.
6. Иллюстрация уравнения Бернулли.
7. Определение местных потерь напора.
8. Определение потерь напора по длине.
Текущий и итоговый контроль по дисциплине
Формы и методы текущего контроля
Формами текущего контроля являются выполненные лабораторные работы и задачи практических и домашних заданий. Методы текущего контроля по дисциплине – защита лабораторных работ, задач и определение уровня посещаемости занятий
Контрольные вопросы для определения минимального уровня освоения программы дисциплины
1. Плотность, объёмный вес жидкости, связь между ними, зависимость от температуры и давления.
2. Вязкость жидкости, единицы измерения, зависимость от температуры и давления.
3. Сжимаемость, упругость, температурное расширение жидкостей.
4. Гидростатическое давление и его свойства, единицы измерения давления.
5.Основные уравнения гидростатики, его энергетический смысл и геометрическая интерпретация.
6. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера) и их решение.
7. Сила давления жидкости на плоскую поверхность. Центр давления.
8. Сила давления жидкости на криволинейные цилиндрические поверхности.
9. Виды движения жидкости.
10. Линия тока, элементарная струйка, вихревая трубка.
11. Поток жидкости, живое сечение струйки и потока, расход и средняя скорость, смоченный периметр, гидравлический радиус.
12. Уравнение неразрывности элементарной струйки и потока в случае установившегося движения жидкости.
13. Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера).
14. Уравнение Д. Бернулли для элементарной струйки установившегося движения и его энергетическая интерпретация.
15. Уравнение Д. Бернулли для потока невязкой и вязкой жидкости.
16. Энергетическая интерпретация уравнения Д. Бернулли для потока вязкой жидкости.
17. Геометрическая интерпретация уравнения Д. Бернулли для потока вязкой жидкости.
18. Уравнение количества движения для установившегося потока.
19. Виды потери энергии.
20. Режимы движения жидкости.
21. Критерии Рейнольдса для определения режима движения жидкости.
22. Зависимость потери напора от режима движения жидкости.
23. Распределение местных скоростей по сечению ламинарного потока.
24. Определение потери напора по длине при ламинарном режиме движения и турбулентном.
25. Особенности турбулентного потока.
26. Местные гидравлические сопротивления.
27. Определение потерь напора при внезапном расширении потока.
28. Виды местных потерь напора и их определения.
29. Математическое моделирование гидравлических явлений.
30. Геометрическое, кинематическое и динамическое подобие потоков.
31. Критерии гидродинамического подобия.
32. Основные правила моделирования.
33. Метод анализа размерностей (Пи - теорема).
34. Моделирование течений в напорных водоводах.
Рейтинговая оценка по дисциплине
Распределение баллов по видам учебных работ
| № п/п | Наименование работ | Распределение баллов |
| 1 | Теоретический материал | 15 |
| 2 | Лабораторные работы | 20 |
| 3 | Индивидуальные домашние задания | 20 |
| 4 | Решение задач | 15 |
| 5 | Посещаемость | 10 |
| 6 | Зачет | 20 |
| Итого | 100 |
Перевод баллов в пятибалльную шкалу
| Отлично | 76-100 |
| Хорошо | 51-75 |
| Удовлетворительно | 26-50 |
| Неудовлетворительно | более 25 |
При набранной общей сумме менее 25 баллов по результатам третьей аттестации студент не допускается к итоговой аттестации по дисциплине.
КОНСПЕКТ ЛЕКЦИЙ
Введение
Предлагаемый конспект лекций по дисциплине «Гидравлика» предназначен для студентов специальности «Водоснабжение и водоотведение» и рассчитан на 18 часов лекционных занятий.
Для инженеров по специальности «Водоснабжение и водоотведение» знание законов равновесия и движения жидкостей является необходимым компонентом профессиональной квалификации, т.к. эти законы используются практически во всех технологических процессах, связанных с транспортировкой и очисткой воды. УМКД построен таким образом, что теоретический лекционный материал используется вначале при решении практических задач, а затем закрепляется во время проведения лабораторных работ.
Курс гидравлики, или технической гидромеханики является традиционным предметом технического образования и обеспечен достаточным количеством учебной литературы. Темы лекций, примеры расчетов, иллюстрации в данном конспекте подобраны в соответствии с требованиями Государственного стандарта для строительных специальностей, детализация материала учитывает наличие и объем лабораторных работ по курсу.
При составлении конспекта лекций использованы издания, обозначенные в списке использованной литературы, а также материалы сайтов ИНТЕРНЕТ. Некоторые лекции были переработаны, дополнены, некоторый материал взят из источников без изменения, а некоторые темы написаны полностью авторами.
Цель составления данного конспекта лекций заключалась в том, чтобы из большого объема существующего учебного материала выбрать минимум, необходимый для инженеров по специальности «Водоснабжение и водоотведение» и довести степень освоения его с учетом практических, лабораторных занятий и самостоятельной работы до уровня навыков в гидравлических расчетах. Для специальностей «Водоснабжение и водоотведение», «Теплогазоснабжение и вентиляция» и «Гидротехническое строительство» общий курс гидравлики должен быть дополнен специальными курсами, а также лабораторными и практическими занятиями, в которых должны быть отражены вопросы, характерные для указанных направлений строительства.
Лекция 1. ПРЕДМЕТ ГИДРАВЛИКИ, КРАТКАЯ ИСТОРИЯ ЕЁ РАЗВИТИЯ
1.1. Область применения гидравлики
Гидравликой называется техническая наука, изучающая формы и законы механического (молярного) движения и относительного покоя жидкостей и газов, а также разрабатывающая методы применения этих законов в различных областях производственной деятельности человеческого общества. Название «гидравлика» произошло от сочетания греческих слов «хюдор» – вода и «аулос» – труба, желоб и означало вначале учение о движении воды по трубам. В настоящее время трудно найти какую-либо область техники, в которой так или иначе не применялись бы эти законы. Главнейшими областями применения законов гидравлики являются гидротехника и мелиорация, водоснабжение и канализация, гидроэнергетика и водный транспорт.
1.2. Открытия древних ученых в области гидравлики
Развитие гидравлики исторически обусловлено и тесно связано с историей использования человеческим обществом воды.
Зачаточные, несистематические знания о некоторых вопросах гидравлики, по всей вероятности, возникли еще в доисторические времена, однако до нас дошли сведения лишь о более поздних открытиях.
Первым научным трудом в области гидравлики считают трактат Архимеда (287–212 до н.э.) «О плавающих телах», написанный за 250 лет до н.э. Древние водопроводы и большое количество водяных мельниц, построенных на Руси до XIII в. «водяными людьми», как называли тогда их строителей, доказывают, что многие вопросы практической гидравлики были известны в глубокой древности и русским людям.
На протяжении последующих после открытия Архимеда 17 столетий никаких новых открытии в гидравлике не произошло.
1.3. История развития гидравлики новой эры
Разрушение средневекового феодального строя и замена его капиталистическим строем содействовали развитию в то время многих научных проблем, в том числе и в области гидравлики.
К ранним работам по гидравлике следует отнести работу Леонардо да Винчи (1452–1519) «О движении и измерении воды», опубликованную только в XX в., т.е. через 400 с лишним лет после смерти ученого. Однако «есть основания считать, что с рукописями Леонардо да Винчи были знакомы и Стевин (1548–1620), и Галилей (1564–1612), и Торричелли (1608–1647), и Паскаль (1623–1662), работы которых оказали большое влияние на развитие гидравлики.
В 1586 г. была опубликована работа Стевина «Начала гидростатики», в 1612 г. – работа Галилея «Рассуждении о телах, пребывающих в воде, и о тех, которые в ней движутся»; в 1643 г. Торричелли открыл законы истечения жидкостей из отверстий; в 1650 г. Паскаль открыл закон о передаче давлений в жидкостях, опубликованный в 1683 г. в трактате «О равновесии жидкостей»; в 1685 г. Ньютон (16–52–1727) сформулировал гипотезу о внутреннем трении в жидкостях.
На этом закончился важнейший этап в развитии гидравлики. Несмотря на элементарные приемы, использованные при доказательствах основных законов, они были сформулированы настолько точно, что не претерпели изменений и в наше время.
Повсеместное использование водных сил способствовало накоплению практического опыта в области гидравлики и создавало благоприятные условия для развития ее основ. Этому содействовали успехи ученых в области математики и механики.
Однако теоретические основы гидравлики (гидромеханика) как учения о механическом движении жидкостей и газов были созданы значительно позднее в России трудами академиков Петербургской академии наук: Михаилом Васильевичем Ломоносовым (1711–1765), Даниилом Бернулли (1700–1782) и Леонардом Эйлером (1707–1783).
В замечательной работе Бернулли «Гидродинамика», «академическом труде, выполненном автором во время работы в Петербурге», как значится на титульном листе этой книги, опубликованной в 1738 г., дается фундаментальная теорема гидродинамики, известная под названием «уравнения Бернулли» и устанавливающая общую связь между давлением, высотой и скоростью движения жидкости. С выходом этого трактата связано и появление самого термина «гидродинамика».
Позже уравнение Бернулли было распространено и на газы, а после дополнения его членами, учитывающими влияние сил трения, оно стало основным уравнением современной гидравлики.
В своем трактате «Общие принципы движения жидкости» (1755 г.) Эйлер «первый вывел систему дифференциальных уравнений движения идеальной, т.е. абстрактной, лишенной трения, жидкости», положив тем самым начало аналитической механике сплошной среды. Эйлеру механика жидкостей обязана введением понятия давления в точке движущейся или покоящейся жидкости, а также выводом уравнения сплошности или непрерывности жидкости; формулировкой закона об изменении количества движения и момента количества движения применительно к жидким и газообразным средам; выводом «турбинного уравнения»; первоначальными основами теории корабля, а также выяснением вопроса о происхождении сопротивления жидкости движущимся в ней телам.
Работы основоположников гидродинамики Д. Бернулли и Л. Эйлера возникли на базе расцвета математики и механики в конце XVII в., обусловленного практическими задачами, выдвинутыми развитием производительных сил в эпоху разложения феодализма и рождения капиталистического строя.
Основой для развития гидродинамики явились гениальные естественнонаучные открытия Ломоносова, к которым относится, прежде всего, закон сохранении вещества и движения, впервые сформулированный в диссертации «Рассуждения о твердости и жидкости тела». Развернутое обоснование этого закона было дано Ломоносовым в открытом письме к Эйлеру от 5 июля 1748 г. Ломоносов при этом не только дал неопровержимые научные доказательства открытого им закона, но и поднялся до понимания его как всеобщего закона природы.
Наряду с теоретическими основами гидравлики – классической гидромеханикой - развивалась экспериментальная и практическая гидравлика.
В 1791 г. в Санкт-Петербурге вышла «Карманная книжка для вычисления количества воды, вытекающей через трубы, отверстия или по желобам; также и силы, какою они ударяют, стремясь с данной скоростью; с приложением правил для вычисления трений, производимых в машинах, в пользу находящихся при строении мельниц и проведении вод», написанная А. Колмаковым. Это была первая русская книга по практической гидравлике в современном автору понимании.
В 1836 г. майором корпуса инженеров путей сообщения И.П. Мельниковым (18004–1880) был издан первый общий курс гидравлики под названием «Основания практической гидравлики или о движении воды в различных случаях и действие ее ударом и сопротивлением». Ни в одной стране, кроме Франции, подобных курсов гидравлики еще не существовало. Возникали гидравлические и гидротехнические лаборатории. Первая гидравлическая лаборатория в России была создана еще в 1855 г. Соколовым, при Санкт-Петербургском институте путей сообщения, где был создан отдел гидравлики при кабинете прикладной механики. В 1902 г. И.Г. Есьманом и др. создается гидравлическая лаборатория при Санкт-Петербургском политехническом институте. В 1904 г. вступает в строй лаборатория при Московском техническом училище, развитием которой в дальнейшем занимался И.П. Куколевскому (1878–1960).
В 1903 г. В.Е. Лимонов (1862–1936) создал гидротехническую лабораторию при Санкт-Петербургском институте путей сообщения.
Нужно отметить, однако, что на дальнейшем развитии теоретической базы гидравлики – гидромеханики – сильно сказался механистический характер естествознания XVIII – начала XIX вв., вызвавший попытки универсализации механических воззрений на «природу». В результате этого создавалось противоречие между теоретической и практической частями гидравлики. Преодоление этой ограниченности могло стать возможным, очевидно, только после преодоления во всем естествознании механистической односторонности XVIII в.
«Оставьте трудиться напрасно, – писал знаменитый русский математик Н.И. Лобачевский (1793–1856), – стараясь извлечь из одного разума всю мудрость, опрашивайте природу, она хранит все тайны и на вопросы Ваши будет отвечать Вам непременно и удовлетворительно».
«Нужен, настоятелен и будет решать дело – разумный и твердый опыт, а молодое и неопытное умственное построение пойдет на поводу и в ту, и в другую сторону, пока, приученное опытом к верной дороге, само не станет возить за собой или на себе всю сущность опытного знания». Так писал великий русский ученый Д.И. Менделеев (1834–1907) в своей фундаментальной монографии «О сопротивлении жидкостей и воздухоплавании», опубликованной в 1880 г. В этой монографии не только дано систематическое и критическое изложение существовавших к тому времени работ по теории сопротивления, но и приводятся оригинальные идеи Д.И. Менделеева по этому вопросу. В частности, указывается на важное значение вязкости жидкости при определении сопротивления трения хорошо обтекаемого тела; дается отчетливое разграничение трения жидкости о гладкие и шероховатые стенки; отмечается основная роль «прилипшего» к твердому телу слоя жидкости.
Глубоко анализируя и критикуя современную ему теорию сопротивления трения, Д.И. Менделеев с предельной ясностью устанавливает энергетическую сторону явления, отсутствовавшую в этой теории.
Работа Д.И. Менделеева позволила выдающемуся русскому ученому и инженеру Н.П. Петрову (1836–1920) окончательно установить в 1883–1885 гг. закон внутреннего трения жидкости, ставшей основой всей гидродинамической теории трения, и на его основе разработать знаменитую теорию гидродинамического трения в машинах. В своей трилогии «Трение в машинах и влияние на него смазывающей жидкости», вышедшей в свет в 1883–1889 гг. и удостоенной Академией наук сначала Ломоносовской, а затем Макарьевской премий, Н.П. Петров блестяще сочетал свою теорию с тщательно проведенными опытами, с важнейшими нуждами производства и внедрил ее в практику «русского железнодорожного и бумагопрядильного дела». Н.П. Петрову по праву принадлежит роль создателя современной физической теории ламинарного движения; ему же первому принадлежит указание о том, что установленный им закон внутреннего трения справедлив только для этого движения, что характер гидравлических сопротивлений ламинарных и турбулентных потоков (согласно современной терминологии) совершенно различен.
Бурное развитие естествознания во второй половине XIX в. нашло свое отражение и в механике. Ее гениальный представитель – Н.Е. Жуковский (1847–1921) – «отец русской авиации», как он был назван в подписанном В.И. Лениным постановлении Совета Народных Комиссаров СССР, подняв рациональную механику до уровня естественнонаучной дисциплины, опирающейся в своей теоретической части на наблюдения и эксперимент, внес огромный вклад в развитие не только гидроаэродинамики, но и самых разнообразных областей науки, в том числе и гидравлики.
Н.Е. Жуковский является основоположником русской школы теории фильтрации, его последователи и ученики, среди которых Н.Н. Павловский (1884–1937), Л.С. Лейбензон (1879–1951), достигли в области подземной фильтрации воды, нефти и газов столь значительных успехов, что русским и советским ученым в этой области, несомненно, принадлежит ведущая роль в мировой науке.
Н.Е. Жуковский разработал классическую теорию гидравлического удара в водопроводных трубах, проверенную им с помощью великолепно поставленных опытов на московском водопроводе, создал теорию движения взвешенных наносов в водных потоках и решил ряд других вопросов, способствовавших сближению теоретического и практического направлений в гидравлике.
Самые общие механические и физические идеи, их многочисленные приложения к решению разнообразных частных задач как технической аэромеханики, так и гидравлики и гидротехники, которые были сначала выполнены самим Н.Е. Жуковским, а затем его последователями и учениками – С.А. Чаплыгиным (1869–1942), И.Г. Есьманом (1868–1955), Н.Н. Павловским, Л.С. Лейбензоном, С.А. Христиановичем с их школами, создали мировую славу русской гидротехнике и гидравлике.
Тесная связь гидравлики с запросами техники и практической жизни придала ей исключительную целеустремленность и открыла разнообразнейшие области ее применения.
Большое влияние на развитие гидравлики оказал также замечательный русский гидромеханик И.С. Громека (1851–1889).
Целью этого ученого, как и большинства учеников московской школы теоретической механики, являлось решение определенных реальных задач механики. В своей диссертации «Некоторые случаи движения несжимаемой жидкости» И.С. Громека положил начало новому, особому разделу механики вихревых движений жидкости – теории так называемых винтовых потоков и потоков с поперечной циркуляцией.
Такие потоки возникают, например, на изгибе русла. Особенно большое практическое значение приобрело изучение потоков с поперечной циркуляцией и винтовых потоков в связи с развитием гидротехники.
Теория И.С. Громеки нашла свое дальнейшее развитие в трудах А.Я. Миловича (1874–1958), М.В. Потапова (1887–1949), С.С. Бюшгенса (1882–1963) и других ученых.
Советскими гидротехниками разработан ряд оригинальных инженерных конструкций, основанных на возбуждении и применении поперечной циркуляции потока. Таковы плавучие направляющие системы М.В. Потапова, основоположника этого направления в гидротехнике.
Русские ученые – математики, механики, гидравлики и гидротехники, упорно и настойчиво работают над проблемами, которые ставит перед наукой бурное развитие производительных сил в нашей стране. Важнейшей из этих проблем в области гидравлики является проблема сопротивления жидкостей, оставшаяся после Н.П. Петрова, и до конца не решеной в области турбулентного движения жидкости. Кажущаяся «беспорядочность» движения частичек жидкости при этом режиме порождает большие трудности в экспериментальном и теоретическом их исследовании. Однако и в этой сложной области к настоящему времени достигнут определенный прогресс на основе работ А.Н. Колмогорова с его школой, М.А. Великанова, Л.Е. Лойцянского, Е.Н. Абрамовича и др.
Лекция 2. ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ
2.1. Жидкости и их главнейшие отличия от твердых и газообразных тел
Жидкости – вещества в конденсированном агрегатном состоянии, промежуточном между состояниями газов и твердых тел. При высоких температурах они имеют сходство с газообразным состоянием, а при низких – с твердым. Благодаря этому жидкости обладают свойствами как газов, так и твердых тел.
Так, например, как и в газах, всякое повышение или понижение давления в однородной жидкости распространяется по всем направлениям с одной и той же (звуковой) скоростью, оставаясь в то же время неизменным по своей величине. В отличие от газов, жидкости, как и твердые тела, мало сжимаемы и не распространяются по всему объему, т.е. могут иметь свободную поверхность.
Как и в кристалле, молекулы жидкости колеблются (1013 колебаний в секунду) около временного положения равновесия ничтожно короткий срок (1010 с), но в отличие от кристалла молекулы жидкости несоизмеримо чаще меняют это положение равновесия, переходя из одного места в другое. Если отвлечься от колебательной составляющей движения, молекула жидкости описывает в своем плавном движении траекторию в виде ломаной линии, похожей на траекторию газовых молекул. Вследствие этого, в отличие от твердых тел, жидкости не имеют в конечном объеме кристаллической решетки, т.е. характеризуются неправильным расположением своих молекул.
Как и газы, жидкости характеризуются текучестью, и как твердые тела – упругостью на растяжение и сдвиг. Последняя обычно замаскирована большой текучестью.
2.2. Плотность и удельный вес однородной жидкости
Плотностью ![]()
Жидкость считают однородной, если плотность ее во всех точках одна и та же, для однородной жидкости плотность равняется отношению массы тела М (кг) к его объему W (м3):
![]()
Удельным весом называется физическая величина, характеризующая распределение силы тяжести по объему.
Для однородной жидкости удельный вес можно определить из отношения силы тяжести тела G к его объему:
![]()
Между удельным весом
![]()
Удельный вес и плотность жидкости зависят от температуры. Известно, что удельный вес воды (при нормальном атмосферном давлении) принимает максимальное значение при 4°С и уменьшается при изменениях температуры в любую сторону. Однако изменения удельного веса воды с изменением температуры довольно незначительны, как это видно из табл. 2.1 (все значения
Таблица 2.1
Удельный вес воды при различной температуре
| t° | 0 | 4 | 10 | 20 | 30 | 40 | 60 | 100 |
|
|
9806 | 9807 | 9801 | 9789 | 9764 | 9730 | 9642 | 9399 |
2.3. Упругие свойства жидкостей
Сжимаемость жидкостей характеризуется коэффициентом объемного сжатия ![]()
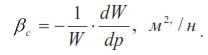
При условии постоянства массы жидкости следует
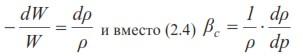
Как видим, коэффициент объемного сжатия определяет также и относительное изменение плотности жидкости при изменении давления на единицу давления.
Отметим, что величина К, обратная коэффициенту объемного сжатия, называется модулем объемной упругости жидкости:
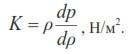
Средние значения К и ![]()
Таблица 2.2
Коэффициент объемного сжатия и модуль объемной упругости воды при различной температуре
| T°С | 0 | 10 | 20 | 30 |
| К, н/м2 | 19,52·108 | 20,30·108 | 21,08·108 | 21,48·108 |
|
|
5,12·10-10 | 4,93·10-10 | 4 · 10-1074 | 4,66·10-10 |
Из табл. 2.2 следует, что сжимаемость воды весьма незначительна, потому в большинстве случаев на практике ею можно пренебречь. Так, например, если взять воду в объеме 0,001 м3 (1 л) при температуре t = 10°С и увеличить действующее на нее первоначальное давление на 20,3 · 104 н/м2, то, согласно формуле (2.4) и данным табл. 2.2, найдем, что первоначальный объем при этом уменьшится на величину 0,1 см3, составляющую всего лишь 0,01 % первоначального объема.
Допущение о несжимаемости жидкости чрезвычайно упрощает аналитические выкладки и позволяет получать вполне приемлемые для большинства решаемых в гидравлике вопросов результаты. Однако не следует при этом забывать, что такое допущение противоречит молекулярно-кинетической природе жидкостей и может привести в некоторых случаях к совершенно неверным результатам.
В самом деле, всякое достаточно малое изменение внешнего давления на жидкость распространяется не мгновенно, а с конечной, хотя и очень большой скоростью, равной скорости звука. Формулу (2.6) можно представить в виде
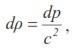
где
Эти обстоятельства приходится учитывать при изучении явлений, происходящих, например, во время закрытия или открытия задвижек в трубопроводах, когда возникает так называемый гидравлический удар, т.е. повышение или понижение давления благодаря изменению скорости движения. Допущение о несжимаемости жидкости в таких случаях приведет к совершенно неверным результатам.
Сжимаемость жидкости необходимо учитывать также в процессах, в которых скорость движения самой жидкости имеет величину близкую к скорости распространения звука. (Такие случаи пока еще не реализованы в гидравлических процессах.)
При допущении несжимаемости жидкости объемный модуль упругости К обращается в бесконечность и уравнение (2.6) заменяется уравнениями
Отметим в заключение, что сжимаемость жидкостей весьма мала по сравнению со сжимаемостью газов, но по сравнению со сжимаемостью твердых тел, например, металлов или других строительных материалов, она сравнительно велика. Например, сжимаемость воды примерно в 100 раз больше сжимаемости стали.
2.4. Внутренне трение, или вязкость
Свойство жидкости оказывать при своем движении сопротивление относительному сдвигу своих частиц известно под названием вязкости, или внутреннего трения жидкости. Вязкость жидкости является одним из наиболее существенных ее свойств. Это свойство обусловливается внутримолекулярным движением жидкости и проявляется в том, что при относительном перемещении одних слоев жидкости по отношению к соседним, вызывающим деформацию объема, в ней возникают силы трения. Огромнейшее влияние на развитие теории вязкости оказали работы русского ученого А.И. Бачинского (1877–1944), еще в 1912 г. впервые установившего связь вязкости жидкости с ее удельным объемом (величиной, обратной удельному весу).
Дальнейшее развитие теория вязкости получила в трудах М.Ф. Широкова, Я.И. Френкеля, Г.М. Панченкова и др.
Силы трения обусловливают то, что слой жидкости, движущийся быстрее, увлекает слой жидкости, движущийся медленнее, и наоборот. Благодаря силам трения происходит преобразование механической энергии движущейся жидкости в тепловую.
Действие сил трения (значит, вязкости) можно наблюдать на следующем примере. Начнем вращать цилиндрический сосуд с жидкостью около вертикальной оси. Через некоторый промежуток времени вся жидкость в сосуде придет во вращение: сначала в движение придут частицы у стенок сосуда, постепенно движение передается благодаря силам трения остальным частицам.
Важно отметить, что после того как вся масса жидкости станет вращаться с одной и той же угловой скоростью, т.е. как твердое тело, силы трения между отдельными слоями обратятся в нуль.
Вязкость жидкости характеризуется коэффициентом вязкости
Пусть dn – расстояние между двумя бесконечно близкими слоями; du – разность скоростей этих слоев. Согласно гипотезе Ньютона, касательное напряжение
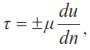
где
Величину
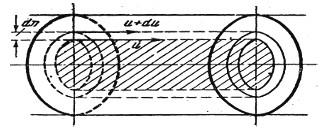
Рис. 2.1. Возникновение силы трения между смежными слоями
Гипотеза Ньютона была подтверждена опытами Кулона (1736–1806) лишь 100 лет спустя, а затем точнейшими опытами основоположника гидродинамической теории смазки Н.П. Петрова и стала, таким образом, законом внутреннего трения жидкости при ламинарном движении. В опытах Кулона не было обнаружено какого-либо влияния давления на величину коэффициента вязкости воды.
Позднейшие опыты, однако, показали, что в действительности это влияние существует, но становится заметным лишь при больших давлениях. Во многих технических задачах с большими давлениями не приходится встречаться, поэтому пренебрежение влиянием давления на вязкость в этих случаях для инженерной практики вполне оправдано.
Коэффициент
Таким образом, динамический коэффициент вязкости
Динамический коэффициент вязкости жидкости изменяется также и с изменением температуры. Так, например, по современным данным для воды
Таблица 2.3
Зависимость
| t° с | 0 | 10 | 20 | 30 |
| 104 |
17,92 | 13,04 | 10,04 | 8,00 |
Как видим, с увеличением температуры коэффициент вязкости значительно уменьшается. Эти значения довольно хорошо укладываются в формулу, данную Пуазейлем в первой половине прошлого столетия:
где t – температура, °С; ![]()
Касательные напряжения в различных жидкостях, движущихся ламинарно с одним и тем же градиентом скорости, относятся как соответствующие значения ![]()
Отношение динамического коэффициента ![]()
![]()
Это название коэффициент v получил благодаря своей размерности, в которую входят только кинематические характеристики.
В табл. 2.4 приведены числовые значения кинематического коэффициента вязкости v для воды при различной температуре.
Таблица 2.4
Значения кинематического коэффициента вязкости
| t,°С | v, см2 /сек | t,°С | v, см2 /сек | t,°С | v, см2 /сек |
| 0 | 0,0178 | 12 | 0,0124 | 30 | 0,0.081 |
| 5 | 0,0152 | 15 | 0,0114 | 40 | 0,0066 |
| 10 | 0,0131 | 20 | 0,0101 | 50 | 0,0055 |
Отметим в заключение, что по мере накопления экспериментального материала по вязкости создавалась и ее теория, преимущественно трудами русских ученых. К настоящему времени мы имеем хорошо согласованные с опытом теоретические формулы для коэффициентов вязкости.
Необходимо, кроме того, отметить, что для случаев движения пульпы, глинистых растворов, гидроторфа, нефти (при температурах, близких к температуре застывания), формула (2.9) должна быть дополнена добавочным членом ![]()
Жидкости, подчиняющиеся закону Ньютона (2.9), называются часто Ньютоновскими жидкостями в отличие от жидкостей, подчиняющихся формуле
2.5. Капиллярность, поглощение газов жидкостями
Известно, что свободная поверхность жидкости, т.е. поверхность жидкости на границе с газом или поверхность на границе двух не перемешивающихся жидкостей, находится в состоянии равномерного поверхностного натяжения. Поверхностное натяжение характеризуется силой поверхностного натяжения, отнесенной к единице длины «образующей линии» свободной поверхности, так называемым коэффициентом поверхностного натяжения
В большинстве гидравлических процессов влиянием поверхностного натяжения ввиду его малости пренебрегают. Необходимость его учета возникает лишь в том случае, если свободная поверхность жидкости приобретает заметную кривизну, т.к. в этом случае силы поверхностного натяжения сказываются на давлении в жидкости. Действием поверхностного натяжения объясняется так называемое капиллярное поднятие жидкости (если жидкость смачивающая) или опускание (если жидкость не смачивающая) в трубках малого диаметра. Способность жидкости подниматься или опускаться в трубках малого диаметра под действием сил поверхностного натяжения называется капиллярностью.
Для воды при t = 20°С зависимость высоты капиллярного поднятия h (мм) в стеклянной трубке от ее диаметра d (мм) определяется формулой
Для ртути при t = 20° С зависимость между величиной опускания h (мм) и диаметром d (мм) дается в виде
Высоту капиллярного поднятия приходится иногда учитывать также при подземной фильтрации жидкости.
Жидкости обладают способностью поглощать и растворять соприкасающиеся с ними газы. Такое явление называется абсорбцией. При этом весовое количество растворенного (абсорбированного) газа изменяется при данной температуре пропорционально давлению жидкости, оставаясь по объему практически постоянным (закон Генри).
Вода в природном состоянии всегда содержит известное количество растворенного воздуха: при обычной температуре и нормальном атмосферном давлении оно составляет около 2 % объема воды. При уменьшении давления соответствующая часть растворенного воздуха выделяется из жидкости. Чем больше снижение давления, тем более бурно происходит выделение воздуха; при этом образуются и пары жидкости. Вода приходит в состояние холодного «кипения», нарушается ее сплошность и образуется своего рода эмульсия, обладающая гораздо большей сжимаемостью и совершенно отличными от прежнего физическими и механическими свойствами. Это явление бывает чаще всего на поверхности быстро движущихся в воде частей механизмов, в тех местах потока жидкости, где давление понижается до некоторого критического, например, у лопастей гребных винтов, лопаток турбин и насосов и известно под названием гидродинамической кавитации, борьба с которой является одной из существенных технических задач. В результате кавитационных явлений происходят механическое разрушение металлических деталей гидромашин (кавитационная эрозия), срыв работы насосов, уменьшение производительности трубопроводов и т.п.
Выделение воздуха и парообразование могут происходить и при давлениях, больших атмосферного, если температура воды увеличивается или вода слишком аэрирована. Это часто служит причиной образования воздушных «пробок» в длинных трубопроводах; выделяемый воздух и пары жидкости накапливаются в их наиболее высоких местах и могут затруднить или даже совсем прекратить движение воды.
К выделению воздуха и паров приводит также внезапное возникновение движения по трубам при очень быстром открытии задвижки или крана, когда происходит так называемый гидравлический удар.
Кавитации подвержены и другие жидкости.
2.6. Особые свойства воды
Кроме описанных свойств вода обладает еще особыми свойствами, называемыми «аномалиями воды», которые в основном заключаются в следующем.
1. В интервале температур от 4 до 0°С объем воды при ее охлаждении не уменьшается, а увеличивается. Плотность ее уменьшается. При замерзании объем воды увеличивается почти на 10 %.
2. Температура замерзания воды с увеличением давления до 2 000 ат понижается, а не повышается.
3. Теплоемкость воды чрезвычайно велика по сравнению с другими телами и имеет минимум примерно при 40°С.
4. Необычайно высокая теплота плавления (скрытая теплота плавления) с повышением давления убывает, а не возрастает, как можно было бы ожидать.
Перечисленные «аномалии» воды свидетельствуют о том, что вода не такое простое соединение, как часто думат. Даже «химически чистая» вода не является простым соединением Н2O. С точки зрения современной молекулярной физики, эту «химически чистую» воду иногда представляют как смесь разного рода ассоциированных молекул (H2O)8, (H2Q)4, (H2O)2 и «простых» молекул Н2O, различными особенностями которых и объясняют аномалии воды.
Еще более сложную ассоциацию представляет собой вода в природной обстановке в условиях искусственных сооружений, устраиваемых для использования ее. В этих условиях вода как «растворитель» не может идти в сравнение ни с каким другим веществом.
Вода как раствор сама по себе может агрессивно действовать на металл и бетон сооружений, приводя к их разрушению. Причиной последнего служит, прежде всего, действие так называемой агрессивной углекислоты, содержащейся в воде. Явление разъедания металлов и бетона под действием воды известно под названием коррозии.
Наконец, присутствие в воде растворенных солей и взвешенных частиц приводит к нежелательным явлениям инкрустации стенок.
2.7. Свойства идеального газа
Уравнение состояния идеального газа объединяет законы Бойля-Мариотта и Гей-Люссака и связывает между собой основные параметры газа – давление, температуру и удельный объем. Для 1 кг газа это уравнение выведено Клайпероном в следующем виде:
где Р – давление газа; V – удельный объем; Т – абсолютная температура; R – газовая постоянная.
Лекция 3. ГИДРОСТАТИКА
3.1. Силы, действующие в жидкостях
Гидростатика – раздел гидравлики, в котором изучаются законы покоящейся жидкости, действующие при этом силы, плавание тела без их перемещения. Все частицы жидкости испытывают действие как вышележащих частиц, так и внешних сил, действующих по поверхности жидкости. Действие этих сил вызывает внутри жидкости напряжение, называемое гидростатическим давлением. Силы могут быть поверхностные и массовые. Поверхностными силами являются силы давления на свободной поверхности – атмосферное или отличное от него, внешнее давление (в случае если жидкость замкнута) или силы давления соседних частиц жидкости. Поверхностные силы распределены по поверхности и пропорциональны ее площади.
Массовыми силами являются силы, пропорциональные массе жидкости: силы тяжести и инерционные силы.
Жидкость, помещенная в резервуар, оказывает давление как на его стенки, так и на дно, зависящее от плотности жидкости и места положения рассматриваемой точки. Так, вода и ртуть при одинаковых прочих условиях будут оказывать разное силовое воздействие на стенки сосуда, а частицы жидкости, находящиеся внизу, будут сжиматься сильнее, чем верхние.
3.2. Гидростатическое давление и его свойства
Рассмотрим резервуар, представленный на рис. 3.1, а. На дно резервуара площадью abcd оказывает воздействие вес налитой жидкости, т.е. Р=![]()
Выделим на боковой поверхности небольшую площадку ![]()
![]()
![]()
![]()
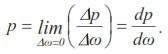
В качестве единицы этой величины применяют Па. Под паскалем понимают давление, создаваемое силой в 1н, равномерно распределенной по нормали к поверхности площадью 1 м2.
Итак, гидростатическое давление в точке является пределом отношения силы гидростатического давления, действующей на элементарную площадку к самой элементарной площадке, если последняя стремится к точке.
Рассмотрим свойства гидростатического давления. На вертикальной левой стенке резервуара (рис. 3.1, а) выделим элементарную площадку ![]()
![]()
![]()
![]()
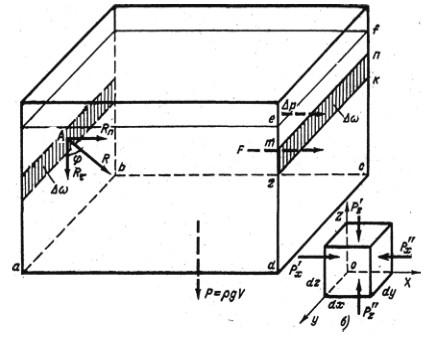
Рис. 3.1. Схема иллюстрирующая первое свойство гидростатического давления
Из вышесказанного следует несколько свойств.
Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Выделим из жидкости, заполняющей объем резервуара (рис. 3.1, а) – элементарный кубик со сторонами dх, dу, dz (рис. 3.1, б). Кубик находится в равновесии, та это значит, что уравновешены поверхностные и массовые силы по всем трем осям:
где dхdуdх – объем кубика.
Сократив равенства, получим
Членом pgdz, бесконечно малым по сравнению с p'zr и p''z, можно принебречь, т.е.
Кубик не деформируется (не вытягивается вдоль одной из осей, жидкость находится в покое), поэтому давления по различным осям одинаковы, а именно:
Свойство 2. Гидростатическое давление неизменно во всех направлениях, гидростатическое давление в любой точке одинаково по всем направлениям.
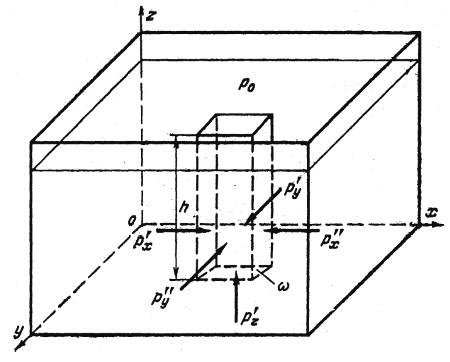
Рис. 3.2. Иллюстрация второго свойства гидростатического давления
Третьим свойством гидростатического давления является зависимость его от координат пространства р=f(х, у, z).
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.
Выясним характер этой зависимости. Выделим из жидкости, заполняющей резервуар (рис. 3.2), параллелепипед с основанием
Разделив полученное равенство на
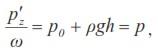
где р – гидростатическое давление жидкости на глубине h.
Это уравнение является основным уравнением гидростатики.
Полученное уравнение означает: полное или абсолютное давление в любой точке покоящейся жидкости складывается из давления на ее свободной поверхности ро и давления рgh, созданного весом выше лежащего слоя жидкости (так называемого столба жидкости).
В открытом резервуаре, находящемся на поверхности земли, первое слагаемое в последнем уравнении равно атмосферному давлению, второе слагаемое рgh называется избыточным давлением
В водоеме на глубине 10 м согласно формуле (3.11)
Таким образом, давление 1 м столба жидкости равно 9,8 кПа.
3.3. Дифференциальные уравнения гидростатики (равновесия). Закон Паскаля
Для выяснения закона распределения гидростатического давления в покоящейся жидкости рассмотрим общий случай равновесия жидкого тела, находящегося в состоянии относительного покоя.
Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед (рис. 3.3) со сторонами ![]()
![]()
![]()
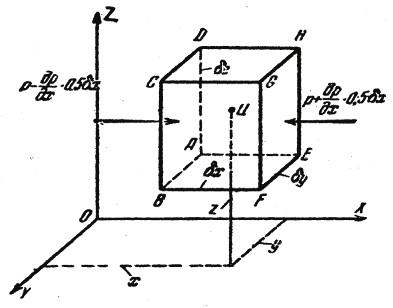
Рис. 3.3. Иллюстрация дифференциального уравнения гидростатики
Пусть р – гидростатическое давление в точке Ц, тогда, учитывая непрерывность изменения напряжения в жидкой среде и пренебрегая величинами бесконечно малыми, стремящимися к нулю при уменьшении параллелепипеда до размеров точки, мы можем определить среднее гидростатическое напряжение на соответствующих гранях параллелепипеда по следующим выражениям:
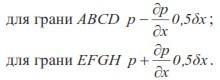
Аналогичные выражения могут быть написаны и для гидростатических напряжений по другим граням.
Равнодействующую массовых сил, действующих на единицу массы жидкости (ускорение массовых сил), обозначим через F, а проекции ее на оси координат – соответственно через Fх, Fу, Fz и на любое направление – через Fn, тогда, условие равновесия сил, действующих на выделенный параллелепипед, заключающееся в равенстве нулю суммы проекций всех сил на избранное направление, можно записать, например, для оси ОХ в виде
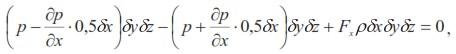
Или
Вообще, очевидно, для любого избранного направления будем иметь:
Система уравнений
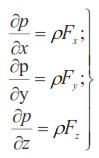
представляет собой общие условия равновесия жидкости, данные Эйлером.
Умножив уравнения Эйлера соответственно на dх, dу, dz и сложив их, получим:
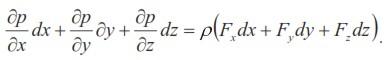
Учитывая, что левая часть уравнения представляет собой полный дифференциал гидростатического давления, получим
Уравнение (3.14) может иметь смысл только при условии, что и выражение в скобках в правой части его также представляет собой полный дифференциал некоторой функции U(х, у, z), которую по аналогии с теоретической механикой назовем силовой функцией. Следовательно, проекции ускорения массовых сил должны определяться следующими соотношениями:
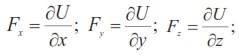
Как известно из теоретической механики, в этом случае должна существовать некоторая функция координат П (х, у, z), называемая потенциальной энергией, равная силовой функции, взятой с обратным знаком. Из этого следует:
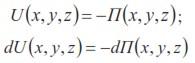
и уравнение (3.14) можно переписать в виде:
Интегрируя уравнение (3.15), получим
или
![]()
где С – произвольная постоянная интегрирования.
В нашем случае потенциальная энергия относится к единице массы, поэтому будем ее называть удельной потенциальной энергией.
В формуле (3.16) удельная потенциальная энергия П и давление р соответствуют одной и той же частичке жидкости, находящейся в относительном покое.
Для двух частиц одного и того же объема одной и той же однородной жидкости уравнение (3.16) можно написать в виде:
Поверхностью равного давления в жидкости называется поверхность, все точки которой испытывают одинаковое давление.
Уравнение такой поверхности мы получим из уравнений (3.14) или (3.17), полагая, что р = const или: dp = 0. При этом
или
Таким образом, все частички жидкости, расположенные на поверхности равного давления, обладают одинаковой удельной потенциальной энергией, соответствующей массовым силам.
Одной из поверхностей равного давления является свободная поверхность жидкости, т.е. поверхность жидкости, граничащая с газовой средой (в гидротехнике обычно с воздухом), т.к. во всех ее точках давление равно внешнему давлению р0.
Уравнение поверхности равного давления (3.18) можно рассматривать как уравнение работы массовых сил при элементарном перемещении по поверхности равного давления. Из равенства нулю этой работы следует: ускорение массовых сил, действующих на жидкость, находящуюся в относительном покое, в любой точке жидкости направлено по нормали к поверхности равного давления, проходящей через эту точку.
В условиях земного притяжения в гидростатике из массовых сил действует только сила тяжести. Принимая положительным направление оси z вертикально вверх и считая для небольших поверхностей силы тяжести параллельными друг другу, будем иметь:
![]()
и, согласно уравнению (3.14),
или
Интегрируя уравнение (3.20), получим:
или (т.к. pg =
где С – произвольная постоянная интегрирования.
Полученное уравнение делением обеих частей на
Для любых двух частиц одного и того же объема жидкости уравнение (3.21) можно представить в виде:
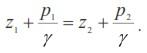
Это уравнение выражает гидростатический закон распределения давления и называется основным уравнением гидростатики.
Основное уравнение гидростатики было получено ранее при помощи анализа действия сил, поделив формулу (3.10) на ![]()
Основное уравнение гидростатики (3.22) может быть использовано для обоснования закона Паскаля.
Возьмем внутри однородной покоящейся жидкости две произвольные точки с отметками z1 и z2 относительно некоторой произвольно выбранной плоскости отсчета. Давления в этих точках равны соответственно р1 и р2 и связаны уравнением (3.22).
Увеличим, не нарушая равновесия, в точке z1 давление на ![]()
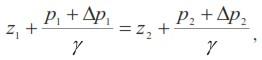
что дает
Отсюда следует закон Паскаля: всякое изменение давления в какой-либо точке покоящейся жидкости, не нарушающее ее равновесия, передается в остальные ее точки без изменений.
Для решения прикладных задач важно уметь определять гидростатическое давление в точке.
Пусть z – координата произвольной точки А (рис. 3.4) внутри покоящейся жидкости, в которой необходимо определить давление р. z 0 – координата точки В того же объема, давление в которой известно и равно р0
Применим основное уравнение гидростатики (22):
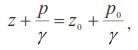
откуда
где z0 – z есть не что иное, как глубина погружения одной точки под другой.
Из этой формулы следует, что чем ниже расположена точка, тем большее давление она испытывает.
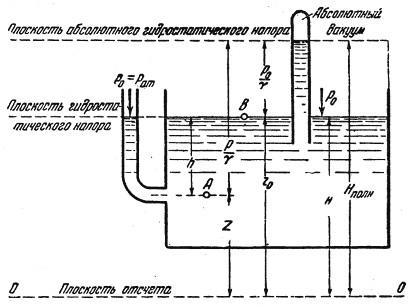
Рис. 3.4. Схема для определения гидростатического давления в точке
Если точка В взята на свободной поверхности (рис. 3.4), то z0 – z есть глубина h погружения точки, а р0 – давление на свободной поверхности и
Формула (3.24) является формулой гидростатического давления в точке на глубине h под свободной поверхностью. Таким образом, гидростатическое давление в данной точке покоящейся жидкости складывается из внешнего давления на поверхности р0 и давления ![]()
![]()
В гидротехнической практике в большинстве случаев внешним давлением является давление атмосферы (р0 = рam).
Эпюра гидростатического давления на наклонную стенку показана на рис. 3.5, а давление в точке поверхности находится по формуле
т.е. в системе координат р, l зависимость p = f (l) изображается прямой линией. Треугольник АВС представляет собой диаграмму давления и называется эпюрой манометрического давления.
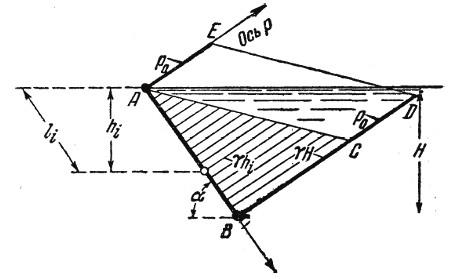
Рис. 3.5. Схема к определению гидростатического давления на стенку
Лекция 4. ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИ. СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКИЕ ПОВЕРХНОСТИ
4.1. Геометрическая и физическая интерпретация основного уравнения гидростатики
Величина
Заметим, что стеклянная трубка может служить для измерения давления в жидкости и поэтому называется пьезометром.
В гидравлике высоту, соответствующую манометрическому давлению, называют пьезометрической высотой и пьезометрическим напором, мы будем называть пьезометрической высотой или напором величину р/
Величину z, отсчитываемую от некоторой произвольной горизонтальной плоскости – плоскости отсчета, называют высотой положения и геометрическим напором.
Сумму двух напоров – геометрического и пьезометрического
Основное уравнение гидростатики (3.21) обычно формулируют в виде так называемого закона гидростатического распределения давлений: гидростатический напор одинаков в любых точках покоящейся однородной жидкости.
С физической точки зрения, гидростатический напор Н есть не что иное, как удельная потенциальная энергия покоящейся жидкости, состоящая из удельной энергии положения z и удельной энергии давления р /
Под удельной энергией при этом подразумевается энергия единицы веса жидкости.
4.2. Относительный покой жидкости
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня, или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением
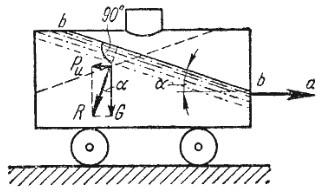
Рис. 4.1. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции РM, равная по величине mа. Равнодействующая
![]()
Свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, поэтому она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол
Рассмотрим еще один частный случай относительного покоя жидкости. Жидкость находится в сосуде, вращающемся равномерно с угловой скоростью вокруг своей вертикальной оси (рис. 4.2). Когда движение установится, жидкость будет вращаться вместе с сосудом и будет относительно последнего находиться в покое.
Из массовых сил на каждую частицу жидкости, например М (рис. 4.2), в данном случае будут действовать сила тяжести и центробежная сила инерции переносного движения, вызванная вращением жидкости вместе с сосудом.
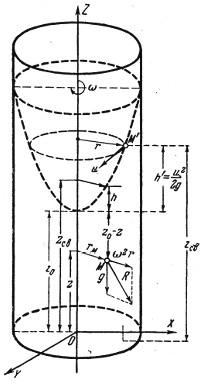
Рис. 4.2. Сосуд, вращающийся равномерно с угловой скоростью вокруг своей вертикальной оси
Для ускорения сил тяжести:
Для ускорения центробежных сил инерции переносного движения:
Прежде всего на основе полученных выражений исследуем форму свободной поверхности жидкости в сосуде, рассматривая ее как поверхность равного давления. Воспользуемся дифференциальным уравнением поверхности равного давления
Подставив значения Fх, Fу, Fz, под которыми следует понимать алгебраическую сумму проекций ускорений силы тяжести и силы инерции, получим
откуда после интегрирования найдем:
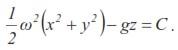
Это уравнение показывает, что поверхности равного давления представляют собой параболоиды вращения. Придавая С различные значения, получим семейство параболоидов вращения. Для того чтобы получить уравнение свободной поверхности, надо определить С0 для нее. Обозначим ординаты свободной поверхности через zCB. Учитывая, что в самой низкой точке свободной поверхности при zCB =z0 х = 0 и у = 0, получим:
![]()
Окончательно, имея в виду, что x2 + у2 = z2, получим:
Из формулы (4.6) следует, что каждая точка свободной поверхности, например, М', находится над уровнем zO на высоте
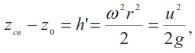
где u = ![]()
Теперь найдем закон распределения давления по объему жидкости. В соответствии с выражением для полного дифференциала гидростатического давления в рассматриваемом случае получим
Интегрируя, найдем
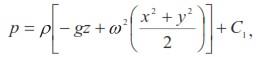
или
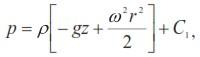
где r – расстояние частицы от оси вращения. Постоянную С1 определим по давлению р0 в точке свободной поверхности, расположенной на оси OZ. При этом r = 0; z = z0 и
Подставляя значение С1 в формулу для р, найдем:
Здесь z – координата любой частинні в объеме жидкости.
В связи с тем, что, согласно уравнению (4.7)
где h – глубина погружения частицы, измеряемая от свободной параболической поверхности. Из уравнения (4.13) видно, что давление распределяется по гидростатическому закону.
4.3. Сила давления жидкости на плоские, произвольно ориентированные поверхности
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом ![]()
Избыточное гидростатическое давление изменяется по линейному закону Р =
