Оглавление

1. Квадратные уравнения
2. ПРЕДИСЛОВИЕ
3. РАЗДЕЛ I. ОПРЕДЕЛЕНИЕ, СТРУКТУРА И ЭЛЕМЕНТЫ КВАДРАТНОГО УРАВНЕНИЯ
   1. §1. Мысли с потолка, ведущие к идее, или Откуда что взялось?
   2. §2. Кто есть кто, или Определение квадратного уравнения
   3. §3. Малочисленная семейка, или Виды квадратных уравнений
   4. §4. Квадратные уравнения и К^о
   5. §5. Всегда ищи первопричину! или Как решить квадратное уравнение?
   6. §6. Важный математический аспект, или Количество…
   7. §7. …и качество, или Теорема Виета
4. РАЗДЕЛ II. МЕТОД, СПОСОБЫ И ПРИЁМЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
   1. §8. От добра добра не ищут? или Основной метод решения квадратного уравнения
   2. §9. Стандартные отступления от «стандарта»
   3. §10. Любимый способ нахождения корней с неправильным названием, или Метод подбора
   4. §11. Вгляжусь в тебя, как в зеркало… или Ещё одна не очевидная, но видимая связь
   5. §12. Выход есть всегда, или Вводим новую неизвестную
   6. §13. Вводим новую неизвестную — 2, или Приёмы с первым коэффициентом
   7. §14. Лучше один раз увидеть, чем семь раз услышать
5. РАЗДЕЛ III. ИССЛЕДОВАНИЯ КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ
   1. §15. Они точно есть! или Их точно нет?
   2. §16. Количество — необходимо и достаточно?
   3. §17. Милые приятные пустячки
   4. §18. И «целого мира» мало
   5. §19. Боже, как страшно жить! или Стечение обстоятельств
   6. §20. Красивые «неудобные» корни
   7. §21. По мотивам одной известной задачи
6. РАЗДЕЛ IV. НЕКОТОРЫЕ ОБОБЩЕНИЯ И ЗАНИМАТЕЛЬНЫЕ ЗАВИСИМОСТИ
   1. §22. Обобщение знакомое и нужное почти всем
   2. §23. Ограничение обобщения, или Трёхчленные уравнения
   3. §24. Обобщение также знакомое, но нужное не всем
   4. §25. Квадратные уравнения и комплексные числа
   5. §26. А что, если брать несколько?
   6. §27 Что ещё придумать? Очень много всего!
   7. §28. Квадратные уравнения и другие числовые конструкции
7. РАЗДЕЛ V. ПРИЛОЖЕНИЯ ТЕОРИИ КВАДРАТНЫХ УРАВНЕНИЙ
   1. §29. Мы с тобой одной крови
   2. §30. Эти приложения учат ещё в школе
   3. §31. Назвался груздем — полезай в кузов
   4. §32. Особые приметы
   5. §33. Не ожидали?
   6. §34. Помощь себе подобным
   7. §35. Ба, знакомые всё лица!
8. ЗАКЛЮЧЕНИЕ
9. КОММЕНТАРИИ
10. ПРИЛОЖЕНИЯ
    1. Некоторые сведения о теории уравнений
    2. Канонические квадратные уравнения

Посвящаю своим ученикам школы №15 
г. Перми, в особенности одноклассникам моего сына (Алексею Макарычеву, Максиму Григорцу, Владимиру Печенкину и другим), с которыми общались незабываемые три с половиной года.

Автор

ПРЕДИСЛОВИЕ

Данная книга является самой первой в серии «Школьная математика ОТ и ДО» и первой в теме «Квадратные уравнения».

Предполагается издать четыре части — квадратные уравнения: от определения до применения; от упражнений до олимпиадных задач; от древности до современности; от начальной школы до выпускных классов.

За несколько лет, которые прошли с момента возникновения общей идеи этой серии, эфемерность замысла оформилась в конкретные разработки, к реализации которых были подключены студенты математического факультета Пермского государственного педагогического, а теперь уже гуманитарно-педагогического университета.

Эти книги помогут школьникам в математическом самообразовании (первые три части), учителям — в методическом. Студентам — как в том, так и в другом. Содержание первых трёх частей можно использовать для создания элективных курсов, курсов по выбору и разнообразных форм дополнительного математического образования, а четвёртая позволит построить оптимальную систему обучения математике в школе.

                                   ***

Казалось бы, что может быть банальней в школьном курсе математики, чем квадратные уравнения? Разве что только таблица умножения.

Нередко «оценочным признаком» низкой математической подготовки школьника служит фраза «он даже квадратные уравнения не умеет решать». Предполагается, что этот процесс должен стать инструментом, применяемым «легко и непринуждённо», а не оставаться самостоятельной задачей, требующей значительных затрат умственных ресурсов.

Однако, обидное пренебрежение этим математическим объектом, на наш взгляд, весьма ошибочно. Квадратные уравнения таят в себе удивительно занимательную теорию, полезную для взрослеющего и пытливого ума. Собственно этими соображениями мы и хотим поделиться.

Не надо думать, что все предложенные теоретические факты необходимо запоминать (хотя некоторые стоило бы). Просто из того минимума, содержащегося в школьном курсе математики, при большом желании можно вытянуть закономерности, позволяющие существенно облегчить жизнь решателям математических задач.

Решать квадратные уравнения — что это?

Наука или искусство?

С первого — математического — взгляда, конечно наука!!!

Квадратные уравнения — это математическое понятие, процесс его решения имеет определённый алгоритм, который применяется для решения других (математических, физических, а порой и жизненных) задач.

А искусство, что оно? Только для души!

Но если решать квадратные уравнения не только для дела, но и для души, то вы с высокой вероятностью увидите красоту в этом привычном процессе.

Для изображения картин тоже необходимы техника рисунка, правила перспективы и т. д. Но каждый художник вкладывает в своё произведение собственное видение жизни.

Так и при решении квадратных уравнений можно не ограничиваться известным алгоритмом, а творчески выбирать приёмы получения корней.

В этой — первой — части саги о квадратных уравнениях мы представляем их математическую теорию, а возможность применить её у читателя будет во второй части «Квадратные уравнения от упражнений до олимпиадных задач».

Между прочим, теория — какая бы она ни была — не берётся из ниоткуда. Когда-то и квадратные уравнения были серьёзным объектом для математических исследований. Поэтому третья часть — «Квадратные уравнения от древности до современности» — ждёт своего часа.

Заранее обговорим те ограничения, которых будем придерживаться в рамках данного изложения. Прежде всего, учитывая, что квадратные уравнения начинают изучаться в восьмом классе, мы без специальных комментариев используем все математические знания «предыдущих лет». Там, где на наш взгляд, появляются спорные с точки зрения последовательности изучения факты, мы отсылаем к приложению или сноскам.

Кроме того, в основном тексте книги опущены строгие математические подробности, которые касаются таких понятий как собственно «уравнение» и его видов, дающих представление о «родословной» квадратного уравнения. Если читатель не знает (или забыл) эти факты, он может обратиться к приложению или комментариям.

Автор благодарит своих выпускниц математического факультета Пермского государственного педагогического университета Марию Волкову (2002 г.), Ольгу Крысову (2003 г.) и Инессу Баранову (2008 г.), фрагменты чьих курсовых и выпускных исследований вошли в эту книгу.

Благодарю всех, кому идея создания подобного рода книг созвучна и тех, кто, ознакомившись с книгой, не найдёт её целесообразной.

РАЗДЕЛ I.
ОПРЕДЕЛЕНИЕ, СТРУКТУРА И ЭЛЕМЕНТЫ КВАДРАТНОГО УРАВНЕНИЯ

§1. Мысли с потолка, ведущие к идее,
или Откуда что взялось?

…Забавное число — ноль. На что ни умножь — само же в результате и получается! Прямо загляденье:

0 × 0 = 0 × 1 = 0 × 2 = 0 × 10 = … = 0, т.е. 0 × a = 0 × 0

Однако, интересно, а будет ли выполняться равенство 0 × a = 0², если вместо нуля поставить произвольное число? Например, какое удвоенное число равно своему квадрату, то есть x × 2 = x²? Или утроенное x × 3 = x²?

Поставим задачу в общем виде: найти число, квадрат которого, равен произведению этого числа на конкретное данное число a. Построим модель: xx = ax или x² = ax.

Так как мы ищем число, отличное от нуля, то, разделив обе части построенного равенства на x, получим, что x = a.

То есть, если удвоенное число равно своему квадрату, то это число 2, а если утроенное, то 3.

Можно этот факт запомнить — вдруг пригодится?..

                                        ***

…Инструктаж судьи на одном из этапов туристической эстафеты:

— Вам необходимо огородить участок прямоугольной формы, площадью 1 ар для стоянки. Дополнительные очки той команде, которая затратит как можно меньше страховочной верёвки. На старт, внимание, начали!

1 ар — это 100 квадратных метров. Участок может иметь размеры 20 × 5 или 25 × 4. Но наша команда знает, что наименьший периметр прямоугольника при его заданной площади будет в том случае, если он — квадрат (теперь и вы это помните!). Отлично! Значит необходимо найти сторону квадрата, если его площадь равна 100. Ну, это легко! Ещё с младших классов, благодаря большой вычислительной практике, помним, что число 10 умноженное на себя даёт сто.

Хорошо, что мы не на уроке математики, а то пришлось бы составлять уравнение x² = 100…

                                   ***

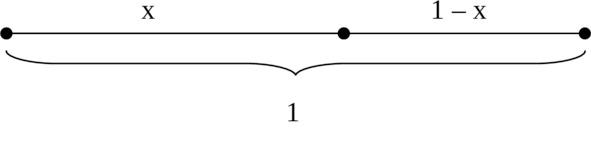
…Не так давно с нами эксперимент проводили: надо было из множества прямоугольников разнообразной формы выбрать один, который покажется самым приятным на вид. Многочисленные повторения этого опыта показали, что чаще всего люди выбирают те прямоугольники, стороны которого относятся как «золотая пропорция». Золотое (или гармоническое) сечение — это такое деление отрезка, при котором отношение всего отрезка к большей части равно отношению большей части к меньшей 1: x = x: (1 — x).

Если воспользоваться свойством пропорции (произведение крайних членов равно произведению средних), то можно получить уравнение, чтобы найти длину большей части этого отрезка: x² = 1 — x.

                                   ***

…В каком прямоугольном треугольнике стороны выражаются тремя последовательными натуральными числами?

Пусть n длина меньшего катета, тогда второй катет и гипотенуза выражаются как (n +1) и (n +2).

По теореме Пифагора все длины увязываем в уравнение:

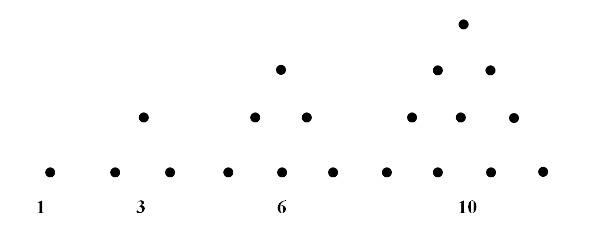
Пифагорейцы исследовали фигурные числа, в частности, треугольные (их можно изобразить в виде треугольника).

Треугольное число с номером n можно найти как половину произведения n× (n+1). Для ответа на вопрос, является ли треугольным число 45 и если да, то каков его номер, надо решить уравнение n× (n+1) = 90…

                                   ***

Задумайте два натуральных числа от 1 до 20. Найдите их сумму и произведение. Сообщите мне. Я отгадаю задуманные вами числа. Вам интересно, как я это сделаю?..

§2. Кто есть кто,
или Определение квадратного уравнения

Квадратным называется уравнение вида ax² + bx + c = 0, где a, b, c — некоторые заданные действительные числа, причём a ≠ 0, а x принимается за неизвестное.

Числа a, b, c называют так:

a — старшим или первым коэффициентом,

b — вторым,

c — свободным или третьим[1].

«Нумерация» коэффициентов зависит не от их реального месторасположения, а от того, при какой степени неизвестной они находятся. Например, число 2 будет первым коэффициентом в любом из трёх уравнений:

А вот число 5 в третьем уравнении является свободным коэффициентом, а в первом уравнении — вторым коэффициентом.

То есть первый (старший) коэффициент — это множитель при квадрате неизвестной, второй — при первой степени. Свободный (третий) коэффициент — это слагаемое без неизвестной, то есть «свободный от неизвестной».

Очевидно, что в качестве неизвестного необязательно брать букву x. Более того, привыкнув за школьные годы к этому неизменному обозначению, среднестатистический ученик начинает испытывать затруднения в восприятии (узнавании, интерпретации) квадратных уравнений, встречающихся при решении более сложных математических (физических и других) задач.

Собственно говоря, и коэффициенты квадратного уравнения не всегда могут обозначаться указанными выше буквами. Одним словом, квадратное уравнение имеет вполне определённую структуру, а как обозначаются элементы этой структуры — дело десятое. Человек со сложившимся математическим стилем мышления понимает, что квадратным уравнением будет являться любое равенство, в правой части которого стоит ноль, а в левой — сумма трёх слагаемых, одно из которых является произвольным числом, другое — произведением произвольного числа на первую степень неизвестного и третье — произведением ненулевого числа на вторую степень неизвестного.

Тогда квадратными будут уравнения:

mx² + nx + k = 0 (относительно x, m ≠ 0),

xa² + ya + z = 0 (относительно a, x ≠ 0).

Уравнение y² + xy + x² = 0 можно рассматривать как квадратное, но только либо относительно x, либо только относительно y.

Пока же договоримся, что теоретические вопросы будем излагать на привычных обозначениях.

Вернёмся к определению. Давайте выделим внешние, «бросающиеся в глаза», черты квадратного уравнения. Во-первых, наличие знака равенства. Отсутствие его с очевидностью снимает вопрос о правомерности называть объект уравнением.

(Любое ли равенство является уравнением — разговор особый и не в рамках этой книги.)

Во-вторых, левая часть нашего равенства представляет собой алгебраическую сумму трёх слагаемых.

Возникает первый вопрос: обязательно трёх?

Другими словами количество слагаемых — это определяющий признак или нет? Давайте посмотрим.

Значения второго и свободного коэффициентов квадратного уравнения в определении никак не ограничиваются (в отличие от первого). Следовательно, они могут быть равными нулю. Тогда под определение квадратного подходят уравнения вида