автордың кітабын онлайн тегін оқу Испытания нефтегазового оборудования и их метрологическое обеспечение
Испытания нефтегазового оборудования и их метрологическое обеспечение
Учебное пособие
Под редакцией
профессора А. И. Владимирова,
профессора В. Я. Кершенбаума
Информация о книге
УДК 658.652/ 614.8/622.32
ББК 34.47
И88
Авторы:
Аванесов В. С., Кершенбаум В. Я., Микаэлян Э. А., Придвижкин В. А., Салащенко В. А., Семин В. И., Скрипка В. Л., Чайковский Г. П.
Рецензенты:
Шарафиев Р. Г., д-р техн. наук, профессор кафедры «Технология нефтяного машиностроения» ФГБОУ ВПО «Уфимский государственный нефтяной технический университет»;
Схиртладзе А. Г., д-р пед. наук, канд. техн. наук, профессор кафедры «Автоматизированные системы обработки информации и управления» ФГБОУ ВПО МГТУ «СТАНКИН».
Под редакцией профессора А. И. Владимирова, профессора В. Я. Кершенбаума.
Учебное пособие состоит из трех частей. В первой части приведены классификация погрешностей измерений, их математические модели и методы обработки результатов измерений. Рассмотрены методы и приборы для измерения температуры, давления, расхода, уровня, геометрических размеров, вибрации, параметров электромагнитной совместимости, а также свойств и состава вещества. Приведены схемы подключения датчиков к программируемым логическим контроллерам (ПЛК).
Во второй части пособия рассмотрены принципы организации испытаний, технологический цикл испытаний, особенности программ испытаний на надежность машиностроительной продукции. Рассмотрены проблемы испытаний на воздействие факторов внешней среды, а также на воздействие внешних механических и гидрогазовых факторов. Описаны также испытания на вибрационные и ударные нагрузки.
В третьей части рассмотрены испытания нефтегазового оборудования: испытания металлоконструкций буровых установок, трубопроводной арматуры, газотурбинных газоперекачивающих агрегатов.
Для бакалавров специальности «Стандартизация, сертификация», изучающих дисциплину «Методы и средства измерений, испытаний и контроля».
УДК 658.652/ 614.8/622.32
ББК 34.47
© Коллектив авторов, 2016
© ООО «Проспект», 2016
Введение
В последние 10–15 лет на предприятиях нефтяной и газовой промышленности происходят значительные изменения. О том, что оборудование в нефтегазовой отрасли должно быть прочным, надежным, известно всем и давно. Действительно, нужно измерять, контролировать основные технологические параметры оборудования, следить за их отклонениями. Нужно иметь возможность дистанционно (из диспетчерского пункта) включать и отключать отдельные агрегаты, открывать и закрывать задвижки; обеспечивать режимы работы установок путем поддержания наиболее важных параметров на заранее рассчитанных значениях. Улучшить ресурс оборудования и продлить срок его эксплуатации можно, если будут правильно организованы испытания, при этом будут учтены условия эксплуатации оборудования.
Реализация испытательных процессов значительно видоизменилась в результате бурного внедрения в промышленности микропроцессоров, персональных компьютеров и прикладного программного обеспечения. Удешевление микропроцессорных устройств и расширение их функций сделало возможным построение так называемых «интеллектуальных систем», которые вычисляют значения косвенных параметров на основе прямых измерений по запрограммированным формулам, показывают значения измеряемых параметров на жидкокристаллических индикаторах, преобразуют измеряемый параметр в стандартный унифицированный сигнал для его передачи по каналам связи.
При всем многообразии новых технических средств автоматизации оператор по добыче нефти и газа наиболее тесно взаимодействует с современными пультами (панелями, станциями) управления, на мониторах которых отображаются мнемосхемы технологических процессов с указанием значений наиболее важных технологических параметров и сопровождением системами сигнализации, блокировок и защит. Оператор имеет возможность вмешиваться в ход технологического процесса в рамках своей ответственности в соответствии с действующими регламентами и инструкциями. Предлагаемое читателю учебное пособие подготовлено в рамках образовательной программы «Развитие инновационных профессиональных компетенций в новой среде обучения – виртуальной среде профессиональной деятельности», реализуемой в Российском государственном университете нефти и газа им. Губкина и имеет цель — познакомить читателя с современным испытательным оборудованием технологических установок и комплексов нефтегазовой отрасли, оснащенных системами контроля и управления.
Учебное пособие состоит из трех частей.
В первой части приведены классификация погрешностей измерений, их математические модели и методы обработки результатов измерений. Рассмотрены методы и приборы для измерения: температуры, давления, расхода, уровня, геометрических размеров, вибрации, параметров электромагнитной совместимости, а также свойств и состава вещества. Приведены схемы подключения датчиков к программируемым логическим контроллерам (ПЛК).
Во второй части пособия рассмотрены принципы организации испытаний, технологический цикл испытаний, особенности программ испытаний на надежность машиностроительной продукции. Рассмотрены проблемы испытаний на воздействие факторов внешней среды, а также на воздействие внешних механических и гидрогазовых факторов, испытаний на вибрационные и ударные нагрузки.
В третьей части рассмотрены испытания нефтегазового оборудования. Ввиду большого разнообразия применяемых в нефтегазовой отрасли технических устройств, авторы ограничились в данном издании рассмотрением методов контроля и испытаний весьма узкого типового ряда изделий — представителей — металлоконструкций, сосудов под давлением, резьбовых соединений, носящих отраслевую специфику, силовых агрегатов. Приведен порядок испытаний и расчет несущей способности металлоконструкций буровых установок. Рассмотрены основные виды испытаний трубопроводной арматуры. Рассмотрены система контроля, взаимозаменяемость и специфика сборки конических резьбовых соединений, проверка элементов профиля резьбы. Приведены методики испытаний резьбовых соединений на усталость, на герметичность и статическую прочность при осевом растяжении и изгибе. Рассмотрены испытания газотурбинных газоперекачивающих агрегатов. Приведены основные параметры испытаний и условия проведения испытаний, требования к испытательным стендам и требования безопасности при проведении испытаний. В последующих работах планируется расширить номенклатуру исследуемых изделий — насосы, компрессоры, турбо- и винтовые двигатели и т. д.
Учебное пособие может быть рекомендовано для студентов обучающихся по направлениям «нефтегазовое дело», «стандартизация и метрология», «управление качеством » и «проектирование технологических машин и комплексов».
ЧАСТЬ 1. МЕТРОЛОГИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОЦЕССОВ ИСПЫТАНИЙ
Глава 1. Метрологическое обеспечение испытательного оборудования
Для контроля и автоматизации технологических операций на испытательных стендах и установках применяются контрольно-измерительные приборы и средства автоматизации (КИПиА).
Испытательные стенды выполняют ряд технологических процессов для целенаправленного определения механических, физико-химических и других характеристик оборудования. Каждый технологический процесс характеризуется определенными технологическими параметрами, которые могут изменяться во времени. Такими параметрами являются химический состав, температура, давление, уровень, вибрация, нагрузка, деформация испытательных образцов, расход материальных и энергетических потоков. Совокупность технологических параметров, полностью характеризующих данный технологический процесс, называется технологическим режимом.
1.1. Методы измерения
Задача измерения (цель) заключается в определении значения измеряемой физической величины с требуемой точностью в заданных условиях.
Метод измерения — это прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерения. Метод измерения должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу их в разряд случайных.
По физическому принципу все методы измерений делятся на электрические, магнитные, акустические, оптические, механические и т. д. По режиму взаимодействия средства и объекта измерений все методы подразделяются на статические и динамические. По виду измерительных сигналов методы измерений делятся на аналоговые и цифровые. По способу взаимодействия средства измерения и объекта измерения методы измерения разделяют на контактные (чувствительный элемент средства измерений приводится в контакт с объектом измерения) и бесконтактные (чувствительный элемент средства измерения не приводится в контакт с объектом измерения).
Наиболее разработанной является классификация методов по совокупности приемов использования принципов и средств измерений. По этой классификации различают метод непосредственной оценки и методы сравнения (рис. 1.1).
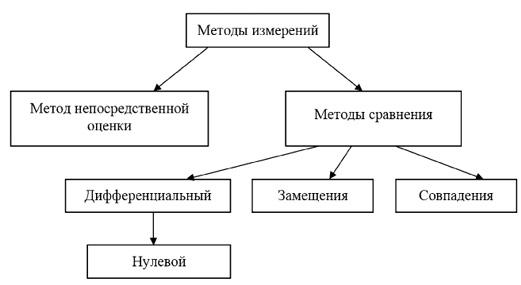
Рис. 1.1. Классификация методов измерений [16]
Сущность метода непосредственной оценки состоит в том, что о значении измеряемой величины судят по показанию одного или нескольких средств измерения, которые заранее градуированы в единицах измеряемой величины или единицах других величин, от которых она зависит. Это наиболее распространенный метод измерения. Его реализуют большинство средств измерения прямого действия.
Другую группу образуют методы сравнения: дифференциальный, нулевой, совпадений, замещения. К ним относятся все те методы, при которых измеряемая величина сравнивается с величиной, воспроизводимой мерой. Следовательно, отличительной особенностью этих методов сравнения является непосредственное участие мер в процессе измерения.
При дифференциальном методе измеряемая величина X сравнивается непосредственно или косвенно с величиной Xм, воспроизводимой мерой. О значении величины X судят по измеряемой приборам разности ∆Х = X — Xм и по известной величине Xм, воспроизводимой мерой. Следовательно, X = Xм + ∆X. При дифференциальном методе производится неполное уравновешивание измеряемой величины. Данному методу свойственна часть признаков метода непосредственной оценки, и он может дать весьма точный результат измерения, если только измеряемая величина и величина, воспроизводимая мерой, мало отличаются друг от друга. Дифференциальный метод позволяет существенно повысить точность измерений. Например, если ∆X = 0,01X и относительная погрешность измерения ∆X составляет 1%, то относительная погрешность результата измерений X равна 0,01% (если не учитывать погрешность меры).
Нулевой метод — разновидность дифференциального метода. Его отличие — в том, что результирующий эффект сравнения двух величин доводится до нуля. Это контролируется нуль-индикатором. В данном случае значение измеряемой величины равно значению, которое воспроизводит мера. Высокая чувствительность нуль-индикаторов, а также выполнение измерения с высокой точностью позволяют получить малую погрешность измерения.
Метод замещения заключается в поочередном измерении прибором искомой величины и выходного сигнала меры, однородного с измеряемой величиной. По результатам этих измерений вычисляется искомая величина. Поскольку оба измерения производятся одним и тем же прибором в одинаковых внешних условиях, а искомая величина определяется по отношению показаний прибора, систематическая погрешность результата измерений в значительной мере уменьшена. Так как погрешность прибора неодинакова в различных точках шкалы, наибольшая точность измерения получается при одинаковых показаниях прибора. В то же время при методе замещения результат измерения отягощают две случайные погрешности измерительного прибора, так как производятся два измерения (измеряемой величины и величины, воспроизводимой мерой). Поэтому, если средство измерения имеет большую случайную погрешность, оно непригодно для использования, например, в качестве компаратора в аналитических измерениях.
Метод совпадения — разность между измеряемой величиной и величиной, воспроизводимой мерой, определяют, используя совпадение отметок шкал или периодических сигналов. Метод широко используется в практике неэлектрических измерений.
Если метод измерений предусматривает разработку основных приемов применения средства измерения, то методика выполнения измерений (МВИ) — это, по сути, технология выполнения измерений с целью наилучшей реализации выбранного метода измерений. Методика измерений — это установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение необходимых результатов измерений с гарантированной точностью в соответствии с принятым методом. Обычно методика измерений регламентируется нормативно-техническим документом (НТД).
Методика измерений предопределяет требования к выбору средств измерения, порядок выполнения операций, необходимость соблюдения установленных условий измерений, числа измерений, способов обработки их результатов. Унификация методик имеет большое значение для обеспечении единства измерений.
1.2. Метрологические характеристики средства измерения
Метрологические характеристики — это характеристики свойств средства измерения, которые оказывают влияние на результат измерений и его погрешности и предназначены для оценки технического уровня и качества средства измерения, а также определения результатов измерений и расчетной оценки характеристик инструментальной составляющей погрешности измерений. Номенклатура метрологических характеристик средств измерения представлена на рис. 1.2.
Средство измерения — техническое средство, предназначенное для измерения и позволяющее решать измерительную задачу путем сравнения измеряемой величины с единицей физической величины (ФВ).
Истинные значения физических величин — значения, идеальным образом отражающие свойства данного объекта, как в количественном,так и в качественном отношении и являющиеся абсолютной истиной.
Действительным значением физических величин называются значения, найденные экспериментально и настолько приближающиеся к истинным, что для данной цели они могут быть использованы вместо них.
Измерение — нахождение значения физической величины опытным путем с помощью специальных технических средств.
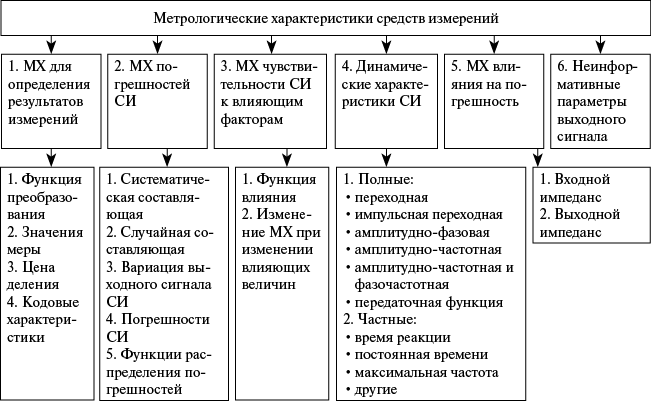
Рис. 1.2. Номенклатура метрологических характеристик средств измерений [16]
Результаты измерений представляют собой приближенные оценки истинных значений величин, найденных опытным путем. Результаты измерений зависят от метода измерения, от технических средств измерения и от восприятия наблюдателя, осуществляющего измерения.
Прямое измерение — измерение, при котором искомое значение величины находят непосредственно из опытных данных.
Косвенное измерение — измерение, при котором искомое значение величин находят на основании зависимости между этими величинами и величинами, подвергаемыми прямым измерениям.
Измерительный прибор — средство измерения, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем (ГОСТ 16263-70).
Измерительная информационная система — совокупность средств измерения (мер, измерительных приборов, измерительных преобразователей и пр.) и вспомогательных устройств, соединенных между собой каналами связи и предназначенных для получения измерительной информации, доступной для наблюдения, обработки и управления объектами.
Условия измерений — совокупность влияющих величин, описывающих состояние окружающей среды и средств измерения.
Влияющая величина — физическая величина, не измеряемая данным средством измерения, но оказывающая влияние на его результаты.
Примеры влияющих величин:
–климатического происхождения — температура окружающей среды, относительная влажность воздуха, атмосферное давление;
–электрического и магнитного происхождения — колебания силы электрического тока, напряжения в электрической сети, частоты переменного электрического тока, постоянные и переменные магнитные поля и т. д.;
–внешних нагрузок — вибрации, ударные нагрузки, внешние касания деталей прибора;
–ионизирующие излучения, газовый состав атмосферы и т. д.
Нормальные условия измерений — это условия, при которых влияющие величины имеют нормальные или находящиеся в пределах нормальной области значения. Нормальная область значений влияющей величины — это область значений, в пределах которой изменением результата измерений под воздействием влияющей величины можно пренебречь в соответствии с установленными нормами точности. Нормальные условия измерений задаются в нормативной документации на средство измерения. При нормальных условиях определяется основная погрешность данного средства измерения. Номинальные значения наиболее распространенных нормальных влияющих величин приведены в табл. 1.1 в соответствии с ГОСТ 8.395-80 «ГСИ. Нормальные условия измерений при поверке. Общие требования».
Таблица 1.1
Номинальные значения наиболее распространенных нормальных влияющих величин (по ГОСТ 8.395-80)
| Влияющая величина | Номинальное значение |
Значение, допускаемое к ограниченному применению в качестве номинального |
|---|---|---|
| Температура: К °С Атмосферное давление: кПа Па мм рт. ст. Относительная влажность, % | 293 20 101,3 – 760 60 | 273; 90; 4,2 23; 25; 27 100 101325 750 0, 55, 58, 65 |
Кроме величин, указанных в табл. 1.1, допускается нормировать номинальные значения других влияющих величин. Допускается устанавливать также интегральные характеристики (например, параметры вибрации, показатели преломления нормального воздуха или его плотность). Номинальные значения магнитной индукции (напряженности магнитного поля) и напряженности электростатического поля должны соответствовать характеристикам поля Земли в данном географическом районе (кроме районов магнитных аномалий).
Рабочими называются условия измерений, при которых влияющие величины находятся в пределах своих рабочих областей. Рабочая область значений влияющей величины — область, в пределах которой нормируется дополнительная погрешность или изменение показаний средства измерения. Предельные условия измерений — условия, характеризуемые экстремальными значениями измеряемой и влияющих величин, которые средство измерения может выдержать без разрушений и ухудшения его метрологических характеристик.
Субъект измерения. Человек принципиально не в состоянии представить себе объект целиком, во всем многообразии его свойств и связей. Вследствие этого взаимодействия субъекта с объектом возможно только на основе математической модели объекта. Субъект измерения — человек — объединяет в себе обе ветви процесса измерения (реальности и отражения), активно воздействует на него и осуществляет:
–постановку измерительной задачи;
–сбор и анализ априорной информации об объекте измерения;
–анализ адекватности объекту измерения выбранной модели;
–обработку результатов измерений.
Результат измерения — значение ФВ, полученное путем ее измерений. Результат измерения представляется именованным или неименованным числом. Совместно с результатом измерения при необходимости приводят данные об условиях измерений.
Достоверность измерений определяется степенью доверия к результату измерения и характеризуется вероятностью того, что истинное значение измеряемой величины находится в указанных пределах. Данная вероятность называется доверительной.
Правильность измерений — это характеристика измерений, отражающая близость к нулю систематических погрешностей результатов измерений.
Повторяемость (сходимость) результата измерений — характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, выполняемых повторно одними и теми же методами и средствами измерения и в одних и тех же условиях. Повторяемость измерений отражает влияние случайных погрешностей на результат измерения.
Воспроизводимость результатов измерений — характеристика качества измерений, отражающая близость друг к другу результатов измерений одной и той же величины, полученных в разных местах, разными методами и средствами измерения, разными операторами, но приведенных к одним и тем же условиям.
Погрешность — это отклонение ∆X результата измерения Xизм от истинного значения Xис измеряемой величины, определяемое по формуле ∆X = Xизм – Xис. Однако истинное значение ФВ найти в принципе невозможно. Но не потому, что оно не существует, — это означает всего лишь непознаваемость истинного значения ФВ, в гносеологическом смысле являющегося аналогом абсолютной истины. Так как получить на практике истинное значение измеряемой величины невозможно, его заменяют действительным. Измерение тем точнее, чем меньше его погрешность. Однако абсолютные погрешности в общем случае зависят от значения измеряемой величины, поэтому не пригодны для количественной характеристики точности измерений. Этого недостатка не имеют относительные погрешности.
Точность измерения — характеристика качества измерения, отражающая близость к нулю погрешности его результата. Точность измерения является величиной качественной. Высокая точность измерения соответствует малым погрешностям и наоборот. По характеристике точности измерения делятся на равноточные и неравноточные.
Равноточные измерения какой-либо ФВ выполнены одинаковыми по точности средствами измерения и в одних и тех же условиях.
Неравноточные измерения физической величины выполнены различными по точности средствами измерения и (или) в разных условиях. Методика обработки результатов равноточных и неравноточных измерений различна.
Способы получения результата: прямые, косвенные, совместные и совокупные измерения.
Прямыми называются измерения, при которых значение величины находят непосредственно по показаниям средства измерения.
Косвенные измерения — это измерения, при которых значение измеряемой величины находят на основании известной зависимости между ней и величинами, подвергаемыми прямым измерениям, которые проводились в одинаковых условиях.
Совместные — одновременно проводимые измерения двух или нескольких неодноименных величин для установления зависимости между ними.
Совокупные измерения — проводимые одновременно измерения нескольких одноименных величин, при которых их искомые значения находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.
В зависимости от числа измерений, проводимых во время эксперимента, различают одно- и многократные измерения (измерения с многократным наблюдением измеряемого параметра).
Однократные измерения выполняются один раз.
Многократные измерения одного и того же размера физической величины следуют друг за другом.
По отношению к изменению измеряемой величины измерения делятся на статические и динамические. Целью данной классификации является возможность принятия решения о том, нужно ли при конкретных измерениях учитывать скорость изменения измеряемой величины. Погрешности, вызываемые влиянием скоростей изменения измеряемой величины, называются динамическими.
К статическим относятся измерения физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
Динамические измерения — это измерения изменяющейся по размеру ФВ. Признаком, по которому измерение относят к статическому или динамическому, является динамическая погрешность при данной скорости или частоте изменения измеряемой величины и заданных динамических свойствах средства измерения. По существу динамическое измерение является измерением функциональной зависимости измеряемой величины от времени.
По метрологическому назначению измерения делятся на технические и метрологические.
Технические измерения производятся рабочими средствами измерения с целью получения информации о свойствах материальных объектов, процессов и явлений окружающего мира. Это самый массовый вид измерений.
Метрологические измерения выполняются при помощи эталонов с целью воспроизведения единиц физической величины для передачи их размера рабочим средствам измерения. Их производят с целью обеспечения единства и требуемой точности технических измерений. К метрологическим измерениям относят:
–воспроизведение единиц и шкал физической величины первичными эталонами и передачу их размеров менее точным эталонам;
–калибровку средств измерения;
–измерения, выполняемые при поверке средств измерения;
–другие измерения, выполняемые с этой целью (например, измерения при взаимных сличениях эталонов одинакового уровня точности) или для удовлетворения других внутренних потребностей метрологии (например, измерения с целью уточнения фундаментальных физических констант и стандартных справочных данных о свойствах веществ и материалов, измерения для подтверждения заявленных измерительных возможностей лабораторий).
При метрологических измерениях в обязательном порядке учитываются погрешности, а при технических принимается наперед заданная погрешность, достаточная для решения данной практической задачи. Поэтому при технических измерениях нет необходимости определять и анализировать погрешности получаемых результатов. В зависимости от выражения результатов измерений последние подразделяются на абсолютные и относительные.
Абсолютное измерение основано на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Понятие «абсолютное измерение» рассматривается как определение величины в ее единицах.
Относительное измерение — это измерение отношения определяемой величины к одноименной. Относительные измерения при прочих равных условиях могут быть выполнены более точно, чем абсолютные, поскольку в суммарную погрешность не входит погрешность меры величины.
1.3. Методы повышения точности средства измерения
Важнейшей задачей при измерении является снижение всех составляющих его погрешности, т. е. повышение точности измерительной процедуры. Причинами возникновения погрешностей измерения являются воздействия:
–внешних влияющих величин (температура окружающей среды, напряженность внешних магнитного и электрического полей, ускорение вибраций, напряжение питающей сети и пр.);
–внутренних влияющих величин (изменение емкости, сопротивлений и индуктивности элементов схемы, напряжение собственных шумов и др.);
–неинформативных параметров входного процесса (частота при измерении эффективного значения переменных сигналов, изменение уровня сигнала при изменении его частоты или периода и пр.).
Методы повышения точности средств изменения можно подразделить на две группы:
–методы предотвращения возникновения данной погрешности. К ним относят конструктивно-технологические методы (использование элементов и узлов наиболее высокого качества с наиболее стабильными параметрами);
–защитно-предохранительные методы (уменьшение влияния внешних влияющих величин за счет уменьшения диапазона их измерения в локализированном пространстве (термостатирование, экранирование, стабилизирование и т. д.).
Методы снижения влияния существующих погрешностей в свою очередь подразделяют на:
–методы коррекции (снижение уровня погрешностей на основе аналитического или экспериментального обнаружения погрешностей, обычно систематических или медленно изменяющихся, случайных);
–методы статистической минимизации погрешностей (снижение предполагаемых, но не обнаруживаемых случайных погрешностей измерительных приборов во время и после измерения).
В процессе эксплуатации любого средства измерения могут возникнуть неисправность или поломка, называемые отказом.
Метрологическая надежность средств измерения — это свойство средств измерения сохранять установленные значения метрологических характеристик в течение определенного времени при нормальных режимах и рабочих условиях эксплуатации. Метрологическая надежность характеризуется интенсивностью отказов, вероятностью безотказной работы и наработкой на отказ.
Межповерочный интервал — это интервал, в течение которого обеспечивается заданная вероятность безотказной работы средства измерения.
В процессе эксплуатации средства измерения может производиться корректировка межповерочного интервала. Выбор оптимального межповерочного интервала осуществляется на основе сравнения межповерочных интервалов, установленных для отечественных и зарубежных аналогов, данных о надежности, данных по результатам периодической поверки.
1.4. Погрешности измерения
Погрешность измерения — оценка отклонения измеренного значения величины от ее истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Простая и логичная концепция точности в ряде зарубежных стран стала подвергаться критике. Основной причиной неудовлетворенности являлся термин «погрешность». В отличие от русского языка, в английском и французском языках понятия «ошибка» (т. е. просчет, неверное действие) и «погрешность» не различаются (the error в английском языке, erreur во французском). Получившая всеобщее признание и повсеместно применяемая в мире идеология управления качеством товаров и услуг на основе стандартов ИСО серии 9000 заключается в обеспечении условий для безошибочного выполнения всех производственных функций и трудовых операций. Похожая проблема стояла в 1927 г. перед физиком В. Гейзенбергом, когда он готовил к публикации свою статью «О наглядном содержании квантово-теоретической кинематики и механики». В этой работе он ввел соотношения, устанавливающие принципиальные ограничения погрешностей измерения импульса силы Δр, координаты Δх, энергии ΔЕ и импульса Δt:
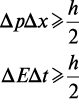
где h = 1,05457266 × 10–34 — постоянная Планка, эрг·с.
Вернер Гейзенберг назвал эти фундаментальные неравенства соотношениями неопределенностей, применив термин «неопределенность» (англ.: uncertainty) как синоним термина «погрешность».
В 1993 г. был выпущен документ ИСО/МЭК «Руководство по выражению неопределенности измерений (англ.: Guide to the Expression of Uncertainty in measurement)», в котором было введено понятие «неопределенность измерений». Руководство приобрело статус международного регламента, обязательного к применению. Оно нацелено, во-первых, на обеспечение потребителей полной информацией о всех составляющих погрешности результатов измерений и, во-вторых, на международную унификацию отчетов об измерениях и оценке их точности, с целью формирования основы для международного сравнения результатов измерений. При этом имеется в виду, что всемирное единство в методах оценки точности измерений обеспечивает правильное использование результатов измерений во всех областях деятельности. Концепция «неопределенность измерения» является необходимой при проведении международных сличений эталонов и составлении калибровочных таблиц.
Для подробного анализа точности полученного результата измерения используется не «анализ погрешности», а расчет неопределенности измерений.
Неопределенность — параметр, связанный с результатом измерения и характеризующий рассеяние значений, которые могли бы быть приписаны измеряемой величине.
Абсолютная неопределенность измерения — неопределенность измерения, выраженная в единицах измеряемой величины.
Относительная неопределенность результата измерений — отношение абсолютной неопределенности к результату измерений.
Стандартная неопределенность — неопределенность, выраженная в виде стандартного отклонения.
Расширенная неопределенность — величина, задающая интервал вокруг результата измерения, в пределах которого, как ожидается, находится большая часть распределения значений, которые с достаточным основанием могут быть приписаны измеряемой величине.
Вероятность охвата — вероятность, которой, по мнению экспериментатора, соответствует расширенная неопределенность результата измерений.
Получение окончательных результатов в классическом подходе погрешности измерения также приписывают результату измерений. Таким образом, обе концепции дополняют друг друга, сливаясь в единую концепцию оценивания точности результатов измерений. При этом, следуя причинно-следственным связям, целесообразно установить следующую последовательность введения основных понятий теории точности измерений: истинное значение величины => действительное значение величины => результат измерения => погрешность измерения => неопределенность результата измерения, как характеристика этой погрешности.
Таким образом, понятия погрешности и неопределенности могут быть гармонично использованы без их взаимного противопоставления. Между характеристиками погрешности измерения и неопределенностью измерения существует определенное соответствие: СКО соответствует стандартной неопределенности, доверительные границы — расширенной неопределенности.
Погрешности измерения классифицируются:
а) по причине возникновения (методические, инструментальные, субъективные);
б) по форме выражения (абсолютная, относительная);
в) по характеру измерения во времени(систематическая, случайная);
Абсолютная погрешность измерения — погрешность измерения, выраженная в единицах измеряемой величины.
ΔX = X – Xи, (1.2)
где: ΔX – абсолютная погрешность измерения;
X – результат измерения;
Хи — истинное значение.
Абсолютная погрешность не может служить мерой точности, так как она не несет информации о соотношении между погрешностью и значением измеряемой физической величины.
Относительная погрешность измерения — погрешность, равная отношению абсолютной погрешности к действительному значению измеряемой величины.
где: δх – относительная погрешность;
ΔX – абсолютная погрешность измерения;
Х – действительное значение измеряемой величины.
Приведенная погрешность измерения –погрешность средства измерения, определяемая как отношение абсолютной погрешности к некоторому нормирующему значению.
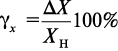
где: γx — приведенная погрешность измерения;
ΔX — абсолютная погрешность измерения;
Xн — нормирующее значение.
Xн выбирается в зависимости от характеристик шкал и характера зависимости абсолютной погрешности от значения измеряемых физических величин.
Основная погрешность — это погрешность измерения при применении средства измерений в нормальных условиях. Предел допускаемой основной погрешности — это наибольшая основная погрешность измерительного прибора, при которой он может быть признан годным и допущен к применению.
Дополнительная погрешность измерения — это составляющая погрешности, возникающая вследствие отклонения какой-либо из влияющих величин от ее номинального значения.
Наибольшее воздействие внешние влияющие величины оказывают на систематическую составляющую погрешности прибора, так как они приводят к однозначным изменениям параметров средства измерений.
Систематическая погрешность Хсист– составляющая погрешности измерения, которая остается постоянной или изменяется закономерно при повторении измерения одной и той же физической величины.
Систематические погрешности измерений подразделяются на аддитивные, не зависящие от X, и мультипликативные — пропорциональные X.
Случайная погрешность Хсл — составляющая погрешности измерения, изменяющаяся во времени случайным образом.
К случайным относятся и грубые погрешности.
Грубая погрешность — погрешность, которая значительно отличается от ожидаемого результата.
1.5. Расчет погрешностей измерения
Основной задачей эксперимента является измерение численных значений наблюдаемых физических величин. Измерением называется операция сравнения величины исследуемого объекта с известной величиной (мерой). Принято различать прямые и косвенные измерения. При прямом измерении производится непосредственное сравнение величины измеряемого объекта с величиной меры. В результате искомая величина находится прямо по показаниям измерительного прибора, например, сила тока — по отклонению стрелки амперметра, вес — по показаниям весов и т. д. Однако, гораздо чаще, измерения проводят косвенно, например, площадь прямоугольника определяют по измерению длин его сторон, электрическое сопротивление — по измерениям силы тока и напряжения и т. д. Во всех этих случаях искомое значение измеряемой величины получается путем соответствующих расчетов. Результат всякого измерения всегда содержит некоторую погрешность.
Поэтому к задаче измерений относится не только нахождение самой величины, но и оценка допущенной при измерении погрешности. Если оценка погрешности результата измерения не сделана, то можно считать, что измеряемая величина вообще неизвестна, поскольку погрешность, вообще говоря, может быть того же порядка, что и сама измеряемая величина или даже больше. В технических измерениях обычно заранее известно, что выбранный измерительный инструмент обеспечивает приемлемую точность, а влияние случайных факторов на результат измерений пренебрежимо мало по сравнению с ценой деления применяемого прибора. Случайные погрешности обязаны своим происхождением ряду причин, действие которых различно в каждом опыте и не может быть учтено. Они имеют разные значения даже для измерений, выполненных одинаковым образом, т. е. носят случайный характер. Допустим, что сделано N повторных измерений одной и той же величины. Если измерения выполнены одним и тем же методом, в одинаковых условиях и с одинаковой степенью тщательности, то такие измерения называются равноточными.
Пусть минимальный интервал значений измеряемой величины, через который ведутся отсчеты (цена деления прибора), будет h, а среднее арифметическое всех результатов измерений будет х. Обозначим через ki число тех результатов, которые отклонились от среднего х на величину Δх = ih. Отложив по оси абсцисс величину абсолютных погрешностей Δхi, а по оси ординат — значения ki, получим ступенчатый график, называемый гистограммой (рис. 1.3).
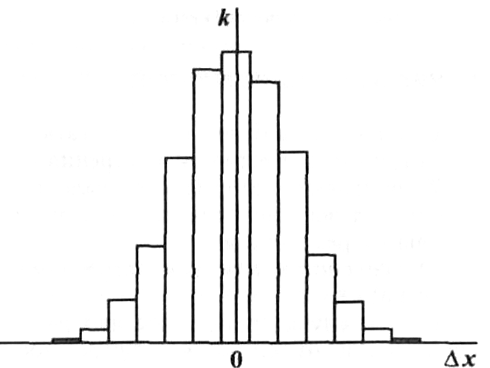
Рис. 1.3. Гистограмма распределения погрешностей [31]
Если устремить число измерений к бесконечности, а интервал h — к нулю, то гистограмма переходит в пределе в непрерывную кривую, которая является кривой функции распределения погрешностей. При условиях, которые обычно выполняются при проведении измерений, эта кривая представляет собой график функции Гаусса, имеющей следующий вид:
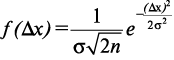
где параметр σ определяет ширину распределения.
Несколько кривых Гаусса для различных значений параметра σ показаны на рис. 1.4.
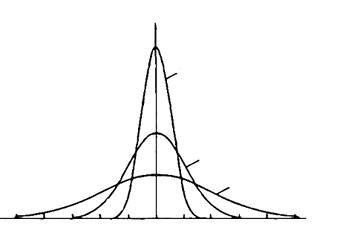
Рис. 1.4. Функция Гаусса [31]
При вычислении погрешностей измерений будем предполагать, что
1) грубые погрешности измерения исключены;
2) поправки, которые следовало определить (например, смещение нулевого деления шкалы), вычислены и внесены в окончательные результаты;
3) все систематические погрешности известны (с точностью до знака).
В этом случае результаты измерений оказываются все же несвободными от случайных погрешностей. Если случайная погрешность окажется меньше систематической, то, очевидно, нет смысла пытаться уменьшить величину случайной погрешности — все равно результаты измерений не станут значительно лучше и, желая получить большую точность, нужно искать пути к уменьшению систематической погрешности. Наоборот, если случайная погрешность больше систематической, то именно случайную погрешность нужно уменьшить в первую очередь и добиться того, чтобы случайная погрешность стала меньше систематической, с тем чтобы последняя опять определяла окончательную погрешность результата.
На практике обычно уменьшают случайную погрешность до тех пор, пока она не станет сравнимой по величине с систематической погрешностью. При увеличении числа измерений случайная погрешность уменьшается.
Поскольку из-за наличия случайных погрешностей результаты измерений по своей природе представляют собой тоже случайные величины, истинного значения Хист измеряемой величины указать нельзя. Однако можно установить некоторый интервал значений измеряемой величины вблизи полученного в результате измерений значения Хизм, в котором с определенной вероятностью содержится Хист. Тогда результат измерений можно представить в следующем виде:
Хизм – ΔХ ≤ Хист ≤ Хизм + ΔХ, (1.6)
где ΔХ — погрешность измерений.
Из-за случайного характера погрешности точно определить ее величину невозможно. Задача получения наилучшей оценки значения Хист и определения пределов интервала (1.6) по результатам измерений является предметом математической статистики.
Пусть проведено n измерений величины X. Тогда за наилучшую оценку истинного значения результата измерений принимается среднее арифметическое значение
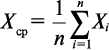
где Хср — среднее арифметическое значение,
Хi — результат i-гo измерения.
Для оценки случайной погрешности измерения существует несколько способов. Наиболее распространена оценка с помощью средней квадратической погрешности σ (ее часто называют стандартной погрешностью, или стандартом измерений), она в качестве параметра входит в функцию распределения Гаусса (1.5), а квадрат этой величины (σ2) называется дисперсией.
Средняя квадратическая погрешность:
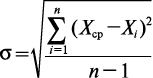
где n — число наблюдений.
Для оценки насколько может уклониться от истинного значения Хист среднее арифметическое Хср, полученное по формуле (1.7) для n повторных равноточных измерений, необходимо среднюю квадратическую погрешность σ разделить на квадратный корень из числа измерений n и получить значение средней квадратической погрешности среднего арифметического измерения:
полученная формула (1.9) показывает, как точность измерения зависит от числа проведенных наблюдений (измерений).
Пусть α является вероятностью того, что результат измерении отличается от истинного значения физической величины на величину, не большую, чем ΔХ. Вероятность α в этом случае носит название доверительной вероятности, а интервал значений измеряемой величины от (Х — ΔХ) до (Х + ΔХ ) называется доверительным интервалом. Определим доверительный интервал. Чем большим будет установлен этот интервал, тем с большей вероятностью Хист попадает в этот интервал. С другой стороны, более широкий интервал дает меньшую информацию относительно величины Хист. Если ограничиться учетом только случайных погрешностей, то при небольшом числе измерений n для уровня доверительной вероятности α полуширина доверительного интервала (1.6) равна:
ΔХсл = t σХср, (1.10)
где ΔХсл — случайная погрешность измерения;
t — коэффициент Стьюдента (см. табл. 1.2).
Смысл понятий «доверительный интервал» и «доверительная вероятность» состоит в следующем: пусть α = 0,95, тогда можно утверждать с надежностью 95%, что истинное значение величины Хист не отличается от оценки (1.7) больше, чем на ± ΔХсл. Значения коэффициентов t в зависимости от α и n табулированы (см. табл. 1.2). Чтобы окончательно установить границы доверительного интервала, необходимо расширить его с учетом систематической погрешности ΔХсист. Систематическая погрешность, как правило, указана в паспорте или на шкале прибора, а в простейших случаях может быть принята равной половине цены деления младшего разряда шкалы.
Таблица 1.2
Коэффициенты Стьюдента
| α = | 0,70 | α = | 0,95 | α = | 0,99 |
|---|---|---|---|---|---|
| n | t | n | t | n | t |
| 1 2 3 4 5 6 7 8 9 10 15 20 30 100 | 1,963 1,386 1,250 1,190 1,156 1,134 1,119 1,108 1,100 1,093 1,074 1,064 1,055 1,036 | 1 2 3 4 5 6 7 8 9 10 15 20 30 100 | 12,706 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,131 2,086 2,042 1,960 | 1 2 3 4 5 6 7 8 9 10 15 20 30 100 | 63,657 9,925 5,841 4,604 4,032 3,707 3,499 3,355 3,250 3,169 2,947 2,845 2,750 2,575 |
1.6. Погрешности прямых и косвенных измерений
Суммарная погрешность определяется как квадратный корень из суммы квадратов случайной и систематической погрешностей:
Вычисленная согласно (1.11) величина ΔХ является абсолютной погрешностью. Очевидно, что при одном и том же значении ΔХ результат может оказаться достаточно точным при измерении некоторой большой величины, тогда как при измерении малой величины его точность будет недостаточной. Например, пусть имеется возможность измерять линейные размеры с погрешностью ΔХ = 1 мм. Ясно, что это заведомо превышает необходимую точность при измерении, например, размеров комнаты, но измерение окажется слишком грубым при определении толщины монеты. Таким образом, становится понятной необходимость введения относительной погрешности, которая определяется из выражения (1.5) и позволяет оценить величину погрешности к самой измеряемой величине.
Обычно случайная погрешность измерений ΔХсл определяется суммой большего числа статистически независимых составляющих с конечными дисперсиями. Практика показала, что в этом случае погрешность подчинена закону, близкому к закону Гаусса, иногда называемому нормальным. Этот результат является следствием центральной предельной теоремы, согласно которой закон распределения суммы независимых случайных величин с конечными дисперсиями независимо от их закона распределения стремится к закону Гаусса при увеличении числа слагаемых. Даже при трех-четырех слагаемых с соизмеримыми дисперсиями закон распределения суммы может быть близок к закону Гаусса, особенно в области больших значений плотности вероятности. Однако в области малых значений плотности вероятности закон распределения суммы сходится к гауссову значительно медленнее. Закон Гаусса часто используют в качестве математической модели неизвестного закона распределения.
Рассмотрим теперь случай, когда при повторении измерений в одних и тех же условиях устойчиво получаются одинаковые значения Х = Х0. В этом случае систематическая погрешность ΔХсист настолько превышает случайную ΔХсл, что влияние случайной погрешности ничтожно мало. Истинное значение Х отнюдь не равно Х0. Оно, по-прежнему, остается неизвестным, и для него можно записать Х = Х0 ± ΔХ, причем погрешность ΔХ определяется в данном случае воспроизводящимися от опыта к опыту ошибками, связанными с неточностью измерительных приборов или метода измерений. Такую погрешность ΔХ , как отмечалось, называют систематической ΔХсист. Для более точного определения физической величины х в данном случае необходимо изменить постановку самого опыта: взять прибор более высокого класса точности, улучшить методику измерений и т. п.
Рассмотрим, каким образом оценить случайную погрешность косвенного измерения величины Y, которая является функцией некоторого числа m непосредственно измеряемых величин Хi, т. е.
y = f (x1, x2 .... xm ). (1.12)
Само среднее значение Yср можно найти из известной функциональной зависимости Y, подставляя в качестве аргументов усредненные по всем проведенным опытам значения непосредственно измеренных величин Хiср Соответствующие вычисления показывают, что абсолютная погрешность ΔY в этом случае определяется по формуле:
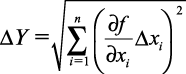
где
Относительная погрешность для косвенных измерений величины Y определяется как:
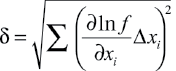
Выражение (1.13) применяют в тех случаях, когда в зависимости (1.12) измеряемые величины Хi, входят, в основном, в виде слагаемых, а формула (1.14) оказывается особенно удобной тогда, когда правая часть (1.12) представляет собой произведение величин Хi .
Учитывая зависимость между абсолютной и относительной погрешностями, легко по известной величине ΔY вычислить относительную погрешность и наоборот. Рассмотрим применение формул (1.13) и (1.14) на примере.
Пусть функциональная зависимость косвенно измеряемой величины Y от непосредственно измеряемых величин Хi имеет следующий простой вид:
Y = αX1 + βX2. (1.15)
Поскольку функция Y представляет собой сумму двух слагаемых, находим частные производные:
,
и подставляем их в формулу (1.13):
причем абсолютные погрешности Δх1 и Δх2 должны быть предварительно определены, по выражениям (1.7)–(1.10).
Рассмотрим теперь функциональную зависимость косвенно измеряемой величины Y от непосредственно измеряемых величин Хi следующего вида:
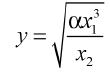
В этом случае для определения погрешности косвенно измеряемой величины Y воспользуемся формулой (1.14). Для этого сначала найдем логарифм, а затем — частные производные:
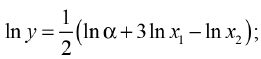
(1.18)
Подставляя в (1.14), найдем
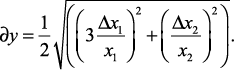
При обработке результатов измерений может быть предложен следующий порядок операций.
При прямых измерениях
Вычисляется среднее арифметическое из n измерений:
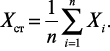
2. Вычисляется средняя квадратическая погрешность из n измерений:
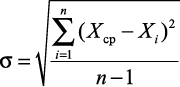
3. Вычисляется значение средней квадратической погрешности среднего арифметического измерения:
4. Для заданного значения α доверительной вероятности и числа n произведенных измерений по таблице (1.2) определяется t и вычисляется случайная погрешность ΔХсл:
ΔХсл = t σХср. (1.23)
5. Оценивается величина систематической погрешности ΔХсист по техническим характеристикам в паспорте или по шкале прибора, а в простейших случаях может быть принята равной половине цены деления младшего разряда шкалы.
6. Вычисляется полуширина доверительного интервала (абсолютная погрешность результата измерения).
7. Вычисляется относительная погрешность результата измерения.
8. Окончательный результат записывается в виде:
X = Xср ± ΔХ. (1.26)
При косвенных измерениях
1.Для каждой серии измерений величин, входящих в определение искомой величины, производится обработка в описанной последовательности по формулам (1.20–1.24). При этом для всех измеряемых величин задают одно и то же значение доверительной вероятности α.
2.Оценивается точность результата косвенных измерений по формуле (1.13), где производные вычисляются при средних значениях величин.
3.Определяется относительная погрешность результата серии косвенных измерений по формуле (1.14).
4.Окончательный результат записывается в виде:
Y = Yср ± ΔY, (1.27)
где Yср = f (Xср1, Xср2, …. Xсрm).
1.7. Классы точности средств измерения
Класс точности — это обобщенная характеристика средств измерения, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. Классы точности регламентируются стандартами на отдельные виды средств измерения с использованием метрологических характеристик и способов их нормирования.
Стандарт не распространяется на средства измерений, для которых предусматриваются раздельные нормы на систематическую и случайные составляющие, а также на средства измерений, для которых нормированы номинальные функции влияния, а измерения проводятся без введения поправок на влияющие величины. Классы точности не устанавливаются и на средства измерений, для которых существенное значение имеет динамическая погрешность.
Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средства измерения.
Пределы допускаемой абсолютной основной погрешности могут задаваться либо в виде одночленной формулы:
Δ = ±α, (1.28)
либо в виде двухчленной формулы:
Δ = ±(α + βх), (1.29)
где Δ и х выражаются одновременно либо в единицах измеряемой величины, либо в делениях шкалы измерительного прибора.
Формула (1.28) описывает чисто аддитивную погрешность (рис. 1.5а), формула (1.29) (рис. 1.5в) описывает сумму аддитивной и мультипликативной погрешностей.
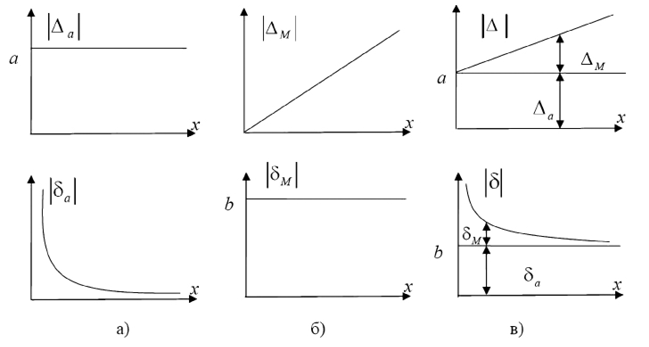
Рис. 1.5. График аддитивной (а), мультипликативной (б), суммарной (в) погрешностей в абсолютной и относительной форме [16]
Более предпочтительным является задание пределов допускаемых погрешностей в форме приведенной или относительной погрешности.
Пределы допускаемой приведенной основной погрешности нормируются в виде одночленной формулы:
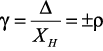
где число
ρ = 1 × 10n; 1,5 × 10n; 2 × 10n; 2,5 × 10n; 4 × 10n; 5 × 10n; 6 × 10n;
(n = 1; 0; –1; –2...).
Пределы допускаемой относительной основной погрешности могут нормироваться либо одночленной формулой:
либо двухчленной формулой:
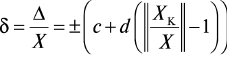
где Xк — конечное значение диапазона измерений или диапазона значений воспроизводимой многозначной мерой величины, а постоянные числа q, с и d выбираются из того же ряда, что и число р.
В обоснованных случаях пределы допускаемых абсолютной или относительной погрешностей можно нормировать по более сложным формулам или даже в форме графиков или таблиц.
Средствам измерения, пределы допускаемой основной погрешности которых задаются относительной погрешностью по одночленной формуле (1.31), присваивают классы точности, выбираемые из ряда чисел р и равные соответствующим пределам в процентах. Так, для средства измерений с δ = 0,002 класс точности обозначается 0,2.
Если пределы допускаемой основной относительной погрешности выражаются двухчленной формулой (1.32), то класс точности обозначается как c/d, где числа c и d выбираются из того же ряда, что и р, но записываются в процентах. Так, измерительный прибор класса точности 0,02/0,01 характеризуется пределами допускаемой основной относительной погрешности:
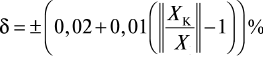
Классы точности средств измерения, для которых пределы допускаемой основной приведенной погрешности нормируются по формуле (1.31), обозначаются одной цифрой, выбираемой из ряда для чисел р и выраженной в процентах. Если, например, γ = ±0,005 = ±0,5%, то класс точности обозначается как 0,5. Обозначения классов точности средств измерения представлены в табл. 1.3.
Обозначение классов точности наносится на циферблат, щиток или корпус прибора. На рис. 1.6 представлены приборы с обозначением классов точности на лицевых панелях. В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают «Класс точности М», а на приборе — буквой «М».
Классы точности обозначаются римскими цифрами или буквами латинского алфавита для средств измерений, пределы допускаемой погрешности которых задаются в форме графиков, таблиц или сложных функций входной, измеряемой или воспроизводимой величины.
К буквам при этом допускается присоединять индексы в виде арабской цифры. Чем меньше пределы допускаемой погрешности, тем ближе к началу алфавита должна быть буква и тем меньше цифра. Недостатком такого обозначения класса точности является его чисто условный характер.
Средство измерения может иметь два и более класса точности, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Таблица 1.3
Обозначения классов точности средств измерения [16]
| Форма выражения |
Предел допускаемо погрешности |
Обозначение |
|---|---|---|
| Абсолютная погрешность | Δ = ±2 Гц | М |
| Абсолютная погрешность | Δ = ±(0 2 + 0,03f )Гц | С |
| Приведенная погрешность, если нормирующее значение выражено в единицах измеряемой величины | γ = ±1,5% | 1,5 |
| Приведенная погрешность, если нормирующее значение принято равным длине шкалы | γ = ±0,5% | 
|
| Относительная погрешность постоянная | δ = ±0,5% | 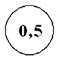
|
| Относительная погрешность, возрастающая с уменьшением измеряемой величины | 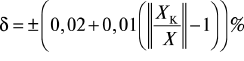
|
0,02/0,01 |
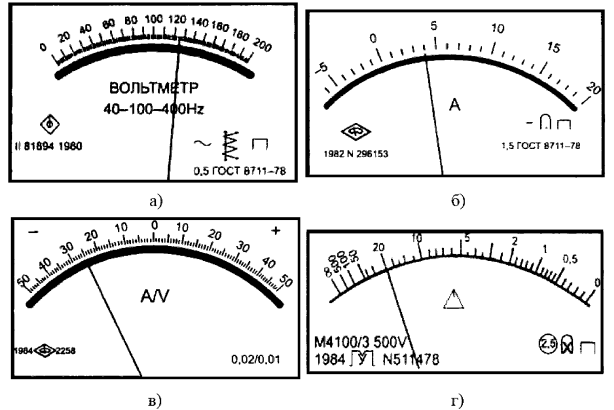
Рис. 1.6. Лицевые панели приборов: а — вольтметра класса точности 0,5; б — амперметра класса точности 1,5; в — амперметра класса точности 0,02/0,01; г — мегомметра класса точности 2,5 с неравномерной шкалой [16]
1.8. Обеспечение единства измерений
При проведении измерений необходимо обеспечить их единство. Задача обеспечения единства измерений возникла одновременно с потребностью в измерениях. Под единством измерений понимается характеристика качества измерений, заключающаяся в том, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам воспроизведенных величин, а погрешности результатов измерений известны с заданной вероятностью и не выходят за установленные пределы. Понятие «единство измерений» довольно емкое. Оно охватывает важнейшие задачи метрологии: унификацию единиц физических величин, разработку систем воспроизведения величин и передачи их размеров рабочим средствам измерения с установленной точностью (рис. 1.7).
На достижение и поддержание на должном уровне единства измерений направлена деятельность государственных и ведомственных метрологических служб, осуществляемая в соответствии с установленными правилами, требованиями и нормами. На государственном уровне деятельность по обеспечению единства измерений регламентируется стандартами государственной системы обеспечения единства измерений (ГСИ) или нормативными документами органов метрологической службы.
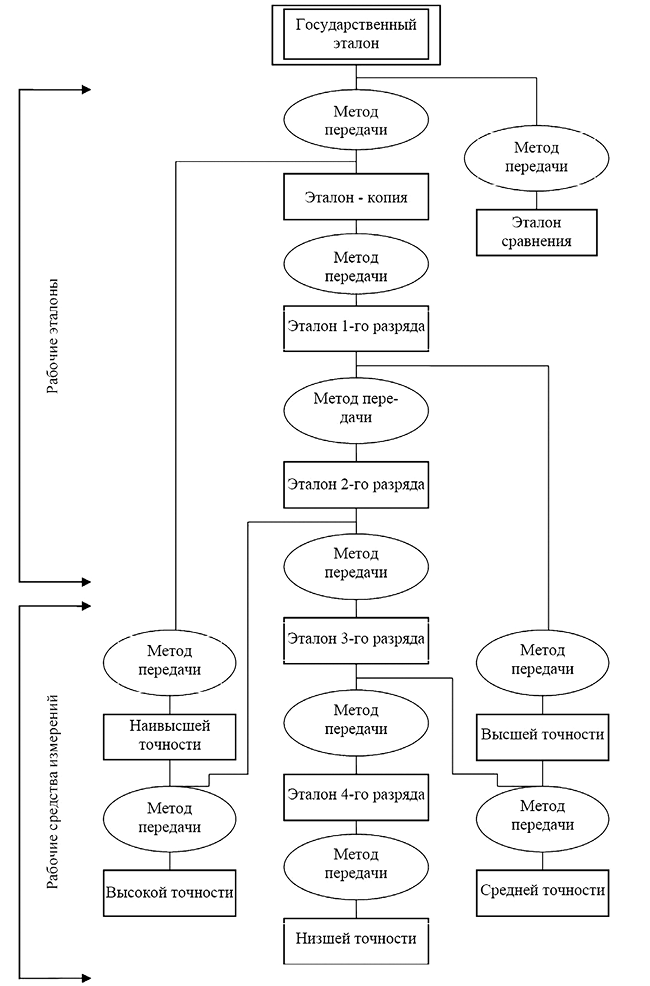
Рис. 1.7. Схема передачи единицы физической величины от эталона рабочим средствам измерений [16]
Государственная эталонная база содержит 126 государственных первичных эталонов, 312 вторичных эталонов, в том числе 52 военных эталона, и около 100 тыс. рабочих эталонов. В настоящее время государственное регулирование процесса обеспечения единства измерений в Российской Федерации осуществляется Ростехрегулированием, в ведении которого находятся 7 федеральных научно-исследовательских метрологических институтов, 86 государственных региональных центров метрологии, 7 межрегиональных территориальных управлений. Всего в стране в эксплуатации находится около 1,0 млрд средств измерения. В сферах, подлежащих государственному регулированию, действуют более 1200 аккредитованных лабораторий в области поверки.
Государственные первичные, а также вторичные и рабочие эталоны образуют эталонную базу системы обеспечения единства измерений. Государственные первичные эталоны, воспроизводя основные и производные единицы величин, передают их размеры с помощью рабочих эталонов средствам измерений посредством многоуровневой и разветвленной системы передач размеров единиц величин. Эта система объединяет (кроме 126 государственных первичных эталонов, 312 государственных вторичных эталонов, 52 военных эталонов) около 100 000 государственных рабочих эталонов, а также около 75 000 эталонов, принадлежащих юридическим лицам, аккредитованным на право поверки средств измерения. Количество средств измерения, подлежащих ежегодно поверке в законодательно установленных сферах, по экспертным оценкам, составляет не менее 150 млн единиц, и около 200 млн средств измерений должно калиброваться. В соответствии с Федеральным законом от 26 июня 2008 г. № 102-ФЗ «Об обеспечении единства измерений» государственное регулирование обеспечения единства измерений осуществляется в формах:
–утверждения типа средств измерения;
–поверки средств измерения;
–аттестации методов (методик) измерений;
–метрологической экспертизы;
–аккредитации;
–государственного метрологического надзора.
В основополагающем российском стандарте ГОСТ Р 8.000-2000 «Государственная система обеспечения единства измерений. Основные положения» установление согласованных требований к совокупности узаконенных единиц величин и шкал измерений отнесено к важнейшим объектам деятельности по обеспечению единства измерений. Одной из важнейших практических функций метрологических служб по обеспечению единства измерений в стране является поверка измерительных средств. Главная цель поверки — выяснение и официальное подтверждение соответствия измерительных средств регламентированным значениям точности и установление их пригодности для дальнейшего использования по назначению. Такое официальное подтверждение служит гарантией достоверности результатов измерений.
В современных условиях виды деятельности метрологической службы весьма разнообразны и носят комплексный характер. Они охватывают установление единиц величин, используемых в стране, создание и хранение государственных эталонов, создание образцовых средств измерений, разработку и унификацию методов и средств измерений высшей точности, создание проверочных схем для всех средств измерения, развитие теоретических исследований в области метрологии, проведение государственных испытаний новых средств измерения, осуществление систематических поверок мер и измерительных приборов, метрологический надзор за работой предприятий и организаций всех ведомств и областей деятельности. Значительная доля этой многоплановой деятельности, направленная на упорядочение измерений, регламентируется комплексом нормативно-технических документов, образующих ГСИ.
Государственные поверочные схемы разрабатываются государственными метрологическими органами в виде государственных стандартов. По каждой единице физических величин они составляются отдельно и охватывают все ступени: государственные эталоны, эталоны-копии, эталоны-свидетели, эталоны сравнения, образцовые и рабочие измерительные средства. Верхняя часть поверочной схемы разработана детально с указанием конкретных эталонов, нижняя часть содержит указания лишь о видах измерительных средств. В схеме также указаны и методы передачи размера единиц по каждой ступени, например:
–непосредственное сличение с мерой;
–сличение меры одного вида с помощью компаратора;
–прямое измерение поверяемым прибором размера, воспроизведенного образцовой мерой;
–прямое измерение образцовым прибором поверяемой меры;
–косвенное измерение величины, воспроизводимой поверяемой мерой и пр.
Ведомственные поверочные схемы разрабатываются ведомственными метрологическими службами и включают те единицы измерений, которые используются на предприятиях и в организациях данного ведомства. Эти схемы должны быть согласованы с государственными поверочными схемами и утверждены органами государственной поверочной службы. Ведомственная поверочная схема начинается с ведомственного рабочего эталона или с образцового прибора с указанием вышестоящего государственного поверяемого средства и содержит более детальный перечень поверяемых измерительных средств.
Локальные поверочные схемы разрабатываются на предприятиях и являются по существу еще более подробным продолжением ведомственных поверочных схем, включающих все средства измерений и контроля, используемые на данном предприятии. Оформляются локальные поверочные схемы в виде нормативно-технического документа предприятия и утверждаются назначенным ведомственным (отраслевым) органом по метрологии. Такая структура служб метрологического обеспечения гарантирует выполнение принципа единства измерений по всем звеньям и уровням.
Глава 2. Методы и приборы для измерения давления
2.1. Единицы измерения давления
Под давлением в общем случае понимают предел отношения нормальной составляющей силы к площади, на которую она действует. При равномерном распределении силы давление на всех участках площади одинаково. В этом случае давление определяют по формуле:
Р = F / S,
где Р — давление; F — сила; S — площадь.
По своей физической природе давление (сила, действующая на единицу площади) не может быть измерена прямыми методами, т. е.непосредственным сравнением с эталоном. Распределенную по поверхности силу надо заменить равнодействующей силой, приложенной к математической точке и преобразовать в физическую величину, доступную для наблюдения. Первым подобное устройство в 1644 г. создал итальянский физик и математик Э. Торричелли (1608–1647). Заполненная ртутью и запаянная с одного конца стеклянная трубка открытым концом погружается в сосуд с ртутью. Ртуть из трубки перетекает в сосуд, но под действием атмосферного давления останавливается на высоте, соответствующей значению этого давления. В день проведения эксперимента эта величина составила 760 мм, что впоследствии было принято за «нормальное значение». Высота столба ртути прямо пропорциональна атмосферному давлению.
Паскаль Блез (1623–1662), французский математик, физик, 15 ноября 1647 г. провел эксперимент на склоне горы Пюи-де-Дом. По мере подъема на гору ртуть понижалась в трубке — и так значительно, что разница на вершине горы и у ее подошвы составила более 3 дюймов. Прибор, который использовался в этом эксперименте, Паскаль назвал барометром. Опыт, проведенный Паскалем, подтвердил предположение Торричелли о существовании атмосферного давления. Именно поэтому первыми единицами для измерения давления были миллиметры ртутного столба и воды. Давление может быть выражено в различных единицах.
В системе СИ за единицу давления принят паскаль (Па) — давление, вызываемое силой 1 Н, равномерно распределенной по поверхности площадью 1 м2, 1 Па = 1 Н/м2, а в системе единиц МКГСС (метр, килограмм-сила, секунда) в качестве основной единицы давления приняты 1 кгс/см2 или внесистемная единица — техническая атмосфера (нормальная, физическая атмосфера) 1 ат = 1 кгс/см2 = 104 кгс/м2.
К внесистемным единицам давления, также допускаемым к применению, относятся миллиметр ртутного столба (мм рт. ст.), равный давлению на горизонтальную поверхность столба ртути высотой 1 мм при 0 °С и ускорении свободного падения 980,665 см/с2, миллиметр водного столба (мм вод. ст.), равный давлению на горизонтальную поверхность столба воды высотой 1 мм при +4 °С и ускорении свободного падения 980,665 см/с2.
1 атм (нормальная, физическая атмосфера) = 760 мм рт. ст. (при t = 0 °С, g = 9,80665 м/с2, p(Hg) — 13 595,08 кг/м3) = 760 Торр (торричелли) = 10 333 мм вод. ст. = 14,696 фунтов (английских) на квадратный дюйм = 15,724 фунтов (русских) на квадратный дюйм = = 1,033227 кгс/см2 = 1,01325 бар;
1 ат (техническая атмосфера) = 1 кгс/м2;
1 бар = 106 дин/см2 = 106 барий = 105 Па;
1 мм рт. ст. = 1,00000014 Торр = 133,3224 Па;
1 фунт/дюйм2 = 0,070307208 кгс/см2 (Великобритания);
1 фунт/дюйм2 = 0,070306682 кгс/см2 (США).
Соотношения между единицами давления различных систем приведены в табл. 2.1.
Таблица 2.1
Единицы давления
| Единица | Па | кгс/см2 | мм вод. ст. | мм рт. ст. |
|---|---|---|---|---|
| 1 Па | 1 | 1,019716×10–5 | 0,1019745 | 0,750061×10–2 |
| 1 кгс/см2 | 98 666,5 | 1 | 10 000,28 | 735,559 |
| 1 мм вод. ст. | 9,80638 | 0,999972×10–4 | 1 | 0,0735539 |
| 1 мм рт. ст. | 133,322 | 1,35951×10–3 | 13,5955 | 1 |
«Пустоты» как полного отсутствия молекул газов достичь невозможно, абсолютной пустоты не существует нигде, даже в космосе.
В зависимости от вида измеряемого давления приборы условно делятся на:
–барометры — для измерения абсолютного давления;
–манометры — для измерения избыточного давления, они показывают на сколько давление в системе превышает атмосферное;
–напоромеры — для измерения избыточного давления до 0,4 × 105 Па;
–вакуумметры — для измерения глубокого разрежения;
–тягомеры — для измерения разрежения до 0,4 × 105 Па;
–мановакуумметры — для измерения избыточного давления и вакуума;
–тягонапоромеры — для измерения избыточного давления до 0,4 × 105 Па и разрежения до 0,4 × 105 Па;
–дифференциальные манометры (дифманометры) — для измерения разности (перепада) давлений.
По принципу действия приборы для измерения давления подразделяются на:
–жидкостные, основанные на уравновешивании измеряемого давления давлением соответствующего столба жидкости;
–деформационные, измеряющие давление по величине деформации различных упругих элементов (мембранные, сильфонные, с трубчатой пружиной Бурдона);
–грузопоршневые, в которых измеряемое давление уравновешивается внешней силой, действующей на поршень;
–электрические, основанные на преобразовании давления в одну из электрических величин, или на изменении электрических свойств материалов под действием давления.
2.2. Жидкостные приборы для измерения давления
Принцип действия жидкостного манометра основан на создании разности высот столбиков жидкости h в коленах U-образной стеклянной трубки под действием разности давлений Ра и Рb (рис. 2.1):
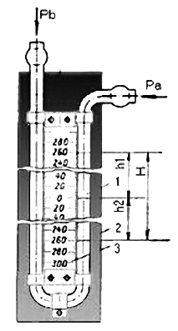
Рис. 2.1. Жидкостный манометр
∆Р = Рb – Рa = gph (Па), (2.1)
где g = 9,81 м/с2 — ускорение свободного падения;
р — плотность жидкости, наполняющей манометр, кг/м3;
h — разность высот жидкости в коленах манометра, м.
При равенстве давлений (Рa = Рb) мы имеем классический случай равенства уровня жидкости в сообщающихся сосудах. Если левое колено манометра запаяно, то давление можно считать равным нулю, а значение h однозначно определит величину Рa.
Показания U-образного манометра не зависят ни от диаметра его трубки, ни от ее формы — теоретически прибор может состоять из сообщающихся сосудов произвольной формы. Во избежание возникновения погрешности измерения прибор следует располагать вертикально. В качестве рабочей жидкости U-образных манометров для работы в вакуумных системах применяют вакуумное масло.
Для более точного определения малых давлений используют жидкостный микроманометр с наклонной трубкой под различными углами (рис. 2.2). При этом определяется по шкале наклонной трубки длина L, заполненная жидкостью, от нулевой точки и переводится в высоту h по вертикали:
h = Lsin (α) (2.3)
Точность отсчетов наклонных манометров повышается по сравнению с вертикальными в 1/sin(α) раз. Так, если α = 5040’, то sin (5040’) = 0,1, тогда h = L/10, т. е. в этом случае представляется возможность произвести отсчет в 10 раз точнее, чем в обычном манометре.
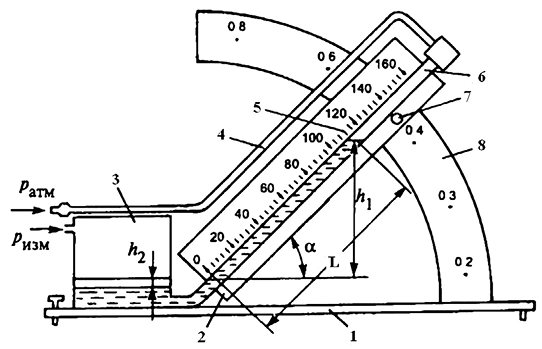
Рис. 2.2. Микроманометр: 1 — платформа, 2 — основание, 3 — бачок-резервуар, 4 — резиновый шланг, 5 — шкала, 6 — стеклянная трубка, 7 — фиксирующий зажим, 8 — наклонный упор
2.3. Грузопоршневые манометры
В грузопоршневых манометрах чувствительным элементом является поршень, с помощью которого давление уравновешивается грузом или каким-либо силоизмерительным устройством (рис. 2.3). Распространение получил манометр с так называемым неуплотненным поршнем, в котором поршень притерт к цилиндру с небольшим зазором и перемещается в нем в осевом направлении. Впервые подобный прибор был создан в 1833 г. русскими учеными Е. И. Парротом и Э. Х. Ленцем; широкое применение поршневые манометры нашли во второй половине XIX в. благодаря работам Е. Рухгольца (Германия) и А. Амага (Франция), которые независимо друг от друга предложили «неуплотненный» поршень.
Основное преимущество поршневых манометров перед жидкостными заключается в возможности измерения ими больших давлений при сохранении высокой точности. Поршневой манометр с относительно небольшими габаритами (высота около 0,5 м) превосходит по пределам измерений и точности 300-метровый ртутный манометр, конструкция которого была разработана французским ученым Л. Кальете. Манометр был смонтирован на Эйфелевой башне в Париже в 1891 г.
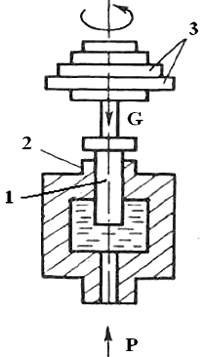
Рис. 2.3. Грузопоршневая колонка: 1 — поршень, 2 — цилиндр, 3 — грузы
Верхний предел измерения поршневых манометров составляет около 3,5 ГН/м2 (3,5×108 мм вод. ст.). При этом высота измерительной установки не превышает 2,5 м. Для измерения такого давления ртутным манометром потребовалось бы довести его высоту до 26,5 км.
Наиболее распространены грузопоршневые манометры с простым неуплотненным поршнем (рис. 2.4). Пространство под поршнем заполнено маслом, которое под давлением поступает в зазор между поршнем и цилиндром, что обеспечивает смазку трущихся поверхностей. Угол отклонения оси поршневой системы от вертикали не должен превышать 5 угловых минут. Вращение поршня относительно цилиндра предотвращает появление контактного трения. Давление определяется весом грузов, уравновешивающих его, и площадью сечения поршня.
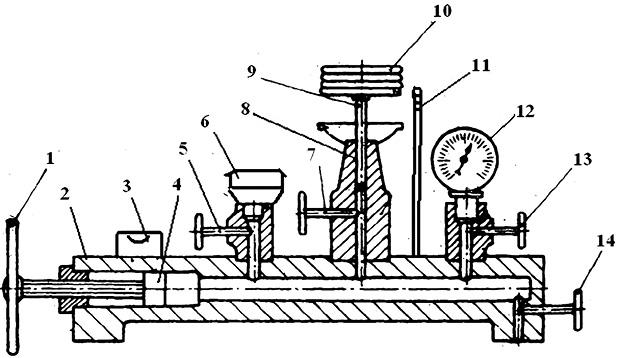
Рис. 2.4. Грузопоршневой манометр с неуплотненным поршнем: 1 — маховик; 2 — корпус; 3 — индикатор уровня; 4 — поршень; 5, 7, 13 — игольчатые вентили; 6 — емкость с маслом; 8 — колонка с каналом; 9 — поршень; 10 — грузы; 11 — репер; 12 — манометр; 14 — вентиль для спуска масла
Изменяя вес грузов и площадь сечения поршня, можно в широком диапазоне менять пределы измерений, которые для манометров. данного типа составляют 0,04–10 МН/м2 (0,4–100 кгс/см2). При этом погрешность наиболее точных эталонных манометров — не более 0,002–0,005%.
При дальнейшем повышении пределов измерений площадь поршня становится столь малой, что для грузов необходимо конструировать специальные устройства (опорные штанги, рычажные устройства). Например, для уменьшения веса грузов в манометрах системы Жоховского (СССР) уравновешивающее усилие создается при помощи гидравлического мультипликатора . В этом случае даже при измерении высоких давлений 2,5 Гн/м2 (2,5 × 104 кгс/см2) измерительная установка предельно компактна и не требует наложения большого числа грузов.
Поршневые манометры специальных конструкций применяются также при измерении небольших избыточных давлений, разрежений, абсолютного и атмосферного давлений. Как правило, поршневые системы таких манометров предварительно уравновешиваются специальным устройством, что позволяет понизить нижний предел измерений практически до нуля. Поршень может быть уравновешен, например, пружинным механизмом. Вращение поршня осуществляется от электродвигателя. При создании разрежения в пространстве над верхней частью поршня избыток атмосферного давлении уравновешивают грузы, накладываемые на его нижнюю часть. Кроме цилиндрических поршней, применяют сферические и конические поршни. В так называемых колокольных манометрах роль поршня выполняет колокол, а в манометрах типа «кольцевых весов» — плоская перегородка внутри полого кольца.
Поршневые манометры применяют для градуировки и поверки манометров других типов, при точных измерениях и контроле давления с выходом показаний на цифровой счетчик или с передачей показаний на расстояние.
2.4. Манометры с трубчатой пружиной
В 1845 г. французский часовщик Этьен Бурдон (1808–1884) наблюдал, как свернутая в кольцо трубка распрямлялась, когда по ней прокачивали воздух. В 1849 г. Э. Бурдон запатентовал изобретение, в котором для измерения давления использовал одновитковую плоскоовальную трубчатую пружину. Трубчатые пружины применяют для измерения избыточного давления или вакуума. Манометрическая пружина Бурдона представляет собой изогнутую по дуге окружности полую трубку (рис. 2.5а) эллиптического или овального сечения (рис. 2.5б). Свободный конец 1 трубки запаян и связан с передаточным механизмом, а другой конец 2 соединен с измеряемой средой. Под действием давления или разрежения кривизна трубки меняется, свободный конец трубки перемещается пропорционально давлению. К трубчатым пружинам относят и винтовую (геликоидальную) пружину (рис. 2.5в) и пружину спиральной формы (рис. 2.5г).
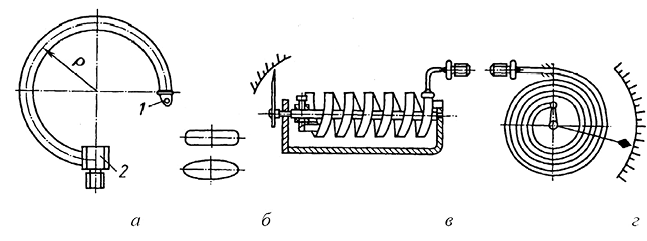
Рис. 2.5. Трубчатые пружины Бурдона: а — трубка Бурдона, б — сечение трубки: эллиптическое, овальное, в — винтовая (геликоидальная) пружина, г — пружина спиральной формы
Многовитковые трубчатые пружины могут без передаточного механизма отклонять стрелку на угол более 360°. По сравнению с одновитковыми пружинами они сложнее в изготовлении и имеют большие температурные погрешности. Изготавливают трубчатые пружины из латуни Л80 или бронзы. Многовитковые трубчатые пружины используются в приборах для измерения давления в скважинах.
Схема манометра с трубчатой пружиной (трубка Бурдона) изображена на рис. 2.6. Под действием давления среды (жидкости или газа), подаваемой во внутреннюю полость через штуцер 8, деформируется чувствительный элемент (упругая трубка Бурдона). Перемещение конца трубки через промежуточный рычаг передается зубчатому сектору, который вращает шестеренку с осью, на которой закреплена стрелка. На корпусе прибора закреплена шкала с оцифрованными делениями, по положению стрелки на шкале определяется давление.
Перемещение конца трубки можно описать выражением
Х = (ратм – р)(А1 – А2) / С, (2.4)
где А1 и А2 — площади наружной и внутренней поверхностей трубки,
С — жесткость трубки.
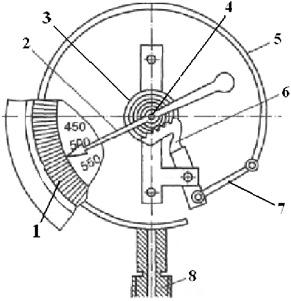
Рис. 2.6. Схема манометра с трубчатой пружиной [31]: 1 — шкала; 2 — стрелка шкалы манометра; 3 — спиральная пружина; 4 — шестеренка с осью; 5 — полая металлическая трубка, запаянная с одного конца (трубка Бурдона); 6 — зубчатая передача; 7 — промежуточный рычаг; 8 — штуцер для подачи давления среды
При сбросе давления трубка должна вернуться в исходное состояние. Величина невозврата называется упругим гистерезисом и является источником неустранимой погрешности прибора. Зазор (люфт) в зубчатой передаче устраняется за счет жесткости пружины, один конец которой закреплен на подвижной опоре в корпусе прибора, а второй — на оси с указательной стрелкой. Вращая подвижную опору, можно установить стрелку на начало отсчета (ноль шкалы). Очевидно, что чем больше величина перемещения, тем больше значение выходного сигнала. Вместе с тем, чем больше перемещение, тем больше упругое последействие материала чувствительного элемента, а значит, и нелинейность, гистерезис, временна`я нестабильность.
Мембраной называют тонкую упругую, чаще всего круглую, плоскую или гофрированную пластину, закрепленную по краям. Она бывает металлической или неметаллической (рис. 2.7). Мембраны применяют в качестве упругих элементов в муфтах, чувствительных элементов систем для измерения давления.
Под действием газа, жидкости или сосредоточенной силы (рис. 2.7а) мембрана прогибается, и в ней возникают деформации изгиба и растяжения. Для уменьшения растягивающих напряжений мембраны выполняют гофрированными. Плоские мембраны имеют большую жесткость и очень малый прогиб. В гофрированных мембранах концентричные волнообразные складки (гофры) могут иметь различный профиль (рис. 2.7б, 2.7в) — синусоидальный, пилообразный, трапецеидальный. Эти мембраны отличаются большей надежностью и чувствительностью, их конструкция допускает значительные деформации.
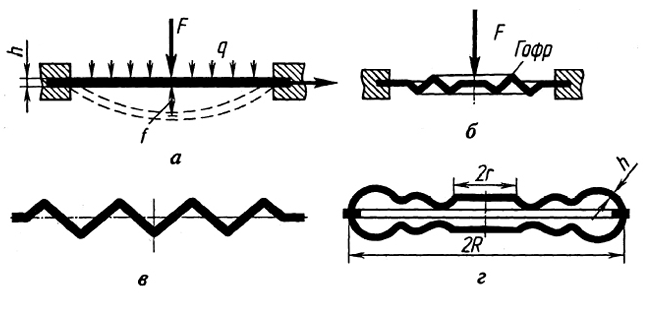
Рис. 2.7. Мембраны: а — плоская мембрана; б — гофрированная мембрана; в — мембрана с пилоабразным профилем; г — мембранная коробка
Две гофрированные мембраны, сваренные или спаянные по буртику, образуют мембранную коробку (рис. 2.7г), которая позволяет увеличить чувствительность упругого элемента. По использованию мембранные коробки делят на манометрические, анероидные и наполненные. Внутренняя полость манометрических коробок соединена со средой, давление в которой (избыточное или вакуум) необходимо измерить. В анероидных коробках из внутренней полости откачивают воздух до разрежения 0,1–0,2 МПа. Они измеряют абсолютное давление воздуха в барометрах и высотомерах. В наполненной мембранной коробке внутренняя полость заполнена азотом или парами эфира. Металлические мембраны изготавливают из нержавеющих сталей, фосфористой и бериллиевой бронз, биметаллов, неметаллические — из резины, кожи, пластмасс, прорезиненного шелка. Толщина металлических мембран составляет 0,06–1,5 мм, неметаллических — 0,1–3,0 мм. Неметаллические мембраны менее долговечны, их свойства сильно зависят от температуры и времени эксплуатации (старение свойств).
Сильфонами называют тонкостенные цилиндрические сосуды, стенки которых имеют волнообразные складки (рис. 2.8). Они применяются для измерения давления, герметизации подвижных соединений, в качестве сосудов переменной вместимости, упругих соединений трубопроводов. Под действием сил F, приложенных к крайним сечениям, либо внутреннего или внешнего давления стенки сильфона деформируются и его длина изменяется.
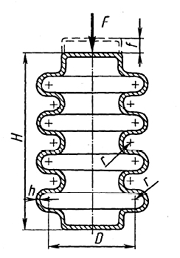
Рис. 2.8. Сильфон
Конструкции, основные параметры и размеры сильфонов определяются ГОСТ. По сравнению с мембраной сильфоны имеют большие габариты и сложнее в изготовлении. Их диаметр равен 8–150 мм, толщина стенок — 0,1–0,5 мм. Сильфоны изготавливаются цельнотянутыми или паянными из латуни Л80, бериллиевых бронз БрБ2, БрБ2,5, нержавеющей стали Х18Н10Т и других материалов.
2.5. Электрические манометры
Тензорезистивные нанометры
Тензорезистор — это элемент, изменяющий свое сопротивление в зависимости от деформирования. Тензорезисторы устанавливают на мембрану, чувствительную к изменению давления. В итоге при давлении на мембрану она изгибается и изгибает тензорезисторы, закрепленные на ней, вследствие чего, сопротивление на них меняется и меняется сила тока в цепи. Тензорезисторы изготовляются из металла или полупроводника, наклеиваются или выращиваются на поверхности мембраны. Технология изготовления тензорезисторов определяет как чувствительность сенсора, так и его стабильность. Металлические тензорезисторы имеют очень низкую чувствительность, так как значения сопротивления изменяются только в соответствии с изменением геометрических размеров. Сопротивление растет пропорционально удлинению резистора и уменьшению его поперечного сечения в результате деформации. У металлов максимальный коэффициент тензочувствительности достигает 2 единиц, обычно — 1,6. Главным достоинством металлических тензорезисторов является простота и низкая стоимость изготовления тензорезисторов из фольги. Однако использование клеев приводит к нестабильности показаний прибора. Кроме того, тонкий слой клея не обеспечивает хорошей изоляции между тензорезисторами и мембраной. Современный уровень технологий позволяет наносить на металлическую мембрану тонкий слой диэлектрика, а затем металлические резисторы. Наиболее ярким представителем этого направления является конструкция датчиков избыточного давления МИДА-ДИ-13П и абсолютного давления МИДА-ДА-13П с разъемом для электрического подключения показаны на рис. 2.9 и 2.10.
Штуцер 1, мембрана 3 с жестко закрепленным кристаллом полупроводникового чувствительного элемента 4, алюминиевые проводники 5, разваренные на кристалл и на выводы коллектора 6, конструктивно образуют тензопреобразователь. Полупроводниковый чувствительный элемент 4 изготовлен из гетероэпитаксиальной структуры «кремний на сапфире» (КНС).
Тензопреобразователь через выводы коллектора 6 электрически подключен к электронному блоку 7, а выход электронного блока — к выходному разъему датчика 8, установленному на основании 9.
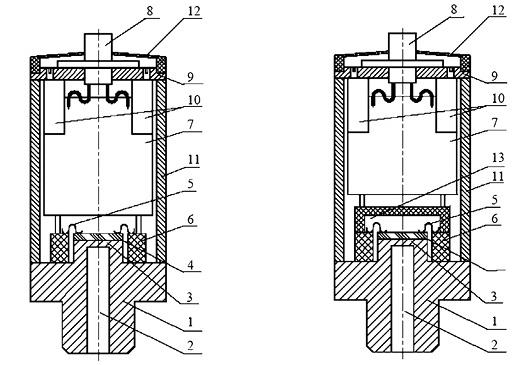
Рис. 2.9. Рис. 2.10.
Датчик давления МИДА-ДИ-13П Датчик давления МИДА-ДА-13П
В состав электронного блока входят корректоры (переменные резисторы) нуля (начального значения выходного сигнала) и диапазона (диапазона изменения выходного сигнала). Электронный блок защищен от внешних воздействий кожухом 11. Дополнительная защита от влаги, воды и пыли осуществляется съемным колпачком 12. Измерение происходит следующим образом. Давление измеряемой среды, находящейся в рабочей полости 2 штуцера 1, воздействует на металлическую мембрану 3 и на полупроводниковый чувствительный элемент 4 с четырьмя тензочувствительными гетероэпитаксиальными кремниевыми резисторами, расположенными на его поверхности. В результате механической деформации чувствительного элемента меняется сопротивление резисторов, соединенных в мостовую схему. Мостовая схема питается стабилизированным напряжением, подаваемым с электронного блока. Изменение сопротивления плеч моста приводит к изменению напряжения, снимаемого с мостовой схемы. Электронный блок усиливает сигнал мостовой схемы и преобразует его в требуемый унифицированный выходной сигнал датчика. Корректоры нуля и диапазона позволяют в небольших пределах регулировать выходной сигнал датчика с тем, чтобы нижние и верхние значения выходного сигнала соответствовали нижнему и верхнему пределам измерения.
Кремниевый механический резонатор
Отличительной особенностью преобразователей серий EJA и EJX, разработанных фирмой Yokogawa является принцип измерения давления: в качестве чувствительного элемента в них используется кремниевый механический резонатор (рис. 2.11), который представляет собой параллелепипед плоской формы, защищенный герметичной капсулой и интегрированный в плоскость кремниевой мембраны. При изготовлении чувствительных элементов применяются самые современные технологии роста кристаллов, благодаря чему вся эта сложная структура получается с единой монокристаллической решеткой. В зависимости от знака приложенного давления резонатор растягивается или сжимается, в результате чего частота его собственных механических колебаний соответственно растет или уменьшается. Колебания механического резонатора в постоянном магнитном поле преобразуются в колебания электрического контура, и, в итоге, на выходе чувствительного элемента получается цифровой (частотный) сигнал, точно отражающий величину измеряемого давления.
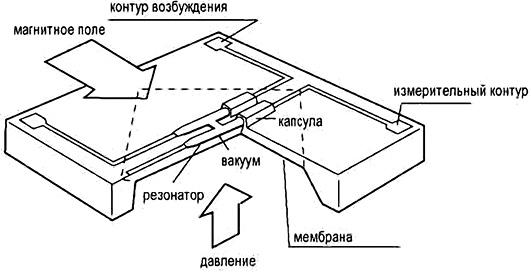
Рис. 2.11. Кремниевый механический резонатор
Погрешность измерений: ±0,04% шкалы.
Стабильность измерения: ±0,1% от верхнего предела измерения в течение 10 лет.
Таблица 2.2
Пределы измерения кремниевого механического резонатора
| Капсула | Диапазон измерения, кПа | Диапазон перенастройки шкалы, кПа |
|---|---|---|
| L M H V | –10…10 –100…100 –500…500 –0.5…14 МПа | 0–0,1…0–10 0–0,5…0–100 0–2,5…0–500 0–0,07…0–14МПА |
Максимальное рабочее давление
–капсула L: 16 МПа;
–капсула M, H: 25 МПа.
Керамический емкостной сенсор
Емкостный сенсор имеет одну из наиболее простых конструкций состоит из двух плоских электродов и зазора между ними. Один из этих электродов представляет собой мембрану, на которую давит измеряемое давление, вследствие чего изменяется величина зазора. То есть по сути этот тип датчиков представляет собой конденсатор с изменяющейся величиной зазора.
Преобразователи давления Cerabar S, производимые Endress+Hauser, предназначены для высокоточного измерения давления газов, пара и жидкостей. В качестве чувствительного элемента используется кремниевый сенсор — сухой чувствительный элемент с прямым воздействием давления процесса на керамическую диафрагму, деформируемую максимум на 0,025 мм. Изменение электрической емкости, измеряемой между электродами на диафрагме и керамической основе, пропорционально изменению давления. Диапазон измерения определяется толщиной керамической диафрагмы.
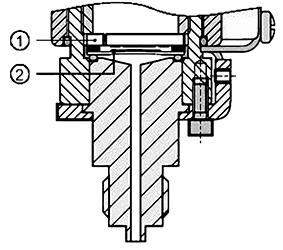
Рис. 2.12. Датчик давления Cerabar S: 1 — керамическое тело; 2 — керамическая диафрагма
Ocoбенности и преимущества:
–высокая точность измерения,
–нелинейность не более ±0,1% от диапазона шкалы,
–дрейф не более ±0,1% в год,
–температурная погрешность не более ±0,1%,
–самодиагностика сенсора и электроники,
–устойчивость к 40-кратной перегрузке,
–высокая химическая стойкость.
Оптические датчики давления
Оптические датчики давления построены на двух принципах измерения: волоконно-оптическом и оптоэлектронном.
Волоконно-оптические датчики
Волоконно-оптические датчики давления являются наиболее точными, и их работа не сильно зависит от колебания температуры. Чувствительным элементом является оптический волновод. Об измеряемой величине давления в таких приборах обычно судят по изменению амплитуды и поляризации проходящего через чувствительный элемент света.
Оптоэлектронные датчики
Датчики этого типа состоят из многослойных прозрачных структур. Через эту структуру пропускают свет. Один из прозрачных слоев может изменять свои параметры в зависимости от давления среды. Есть два параметра, которые могут изменяться: первый — это показатель преломления, второй — это толщина слоя. На рис. 2.13 показаны оба метода, изменение показателя преломления — рис. 2.13а, изменение толщины слоя — рис. 2.13б.
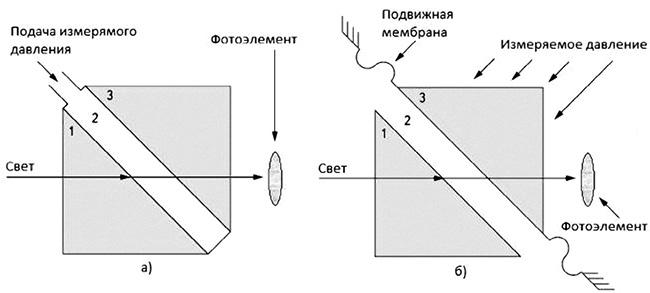
Рис. 2.13. Оптические датчики давления: а — метод изменение показателя преломления; б — метод изменения толщины слоя
При изменении этих параметров будут меняться характеристики проходящего через слои света, это изменение будет регистрироваться фотоэлементом. К достоинствам датчика этого типа можно отнести очень высокую точность. Оптические методы измерений обладают рядом преимуществ перед остальными способами детектирования давления: простотой, низкой температурной чувствительностью, высокой разрешающей способностью и высокой точностью. Особенно перспективными являются оптоэлектронные датчики, реализованные на основе явления интерференции света. Такие преобразователи используют принцип измерения малых перемещений Фабри—Перо. На рис. 2.14 показана упрощенная схема одного из таких датчиков. В состав датчика входят следующие компоненты: пассивный кристалл оптического преобразователя давления с диафрагмой, вытравленной в кремниевой подложке, светоизлучающий диод (СИД) и кристалл детектора.
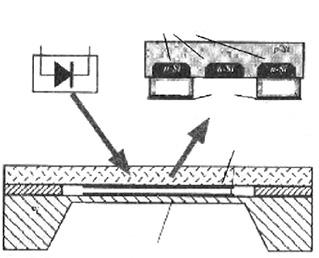
Рис. 2.14. Схема оптоэлектронного интерференционного датчика давления
стекло
СИД
диафрагма
фотодиоды
встроенные фильтрыФабри—Перо
SiO2
интерферометрФабри—Перо
Al
детектора
кристалл
SiO2
Детектор состоит из трех фотодиодов p–n, к двум из которых пристроены оптические фильтры Фабри—Перо, имеющие небольшую разницу по толщине. Эти фильтры представляют собой кремниевые зеркала с отражением от передней поверхности, покрытые слоем из диоксида кремния, на поверхность которых нанесен тонкий слой алюминия. Оптический преобразователь похож на емкостный датчик давления, за исключением того, что в нем конденсатор заменен на интерферометр Фабри—Перо, используемый для измерения отклонения диафрагмы. Диафрагма, сформированная методом травления в подложке из монокристаллического кремния, покрыта тонким слоем металла. На нижнюю сторону стеклянной пластины также нанесено металлическое покрытие. Между стеклянной пластиной и кремниевой подложкой существует зазор, получаемый при помощи двух прокладок. Два слоя металла формируют интерферометр Фабри—Перо с переменным воздушным зазором, в состав которого входят подвижное зеркало, расположенное на мембране, меняющее свое положение при изменении давления, и параллельное ему стационарное полупрозрачное зеркало на стеклянной пластине. Поскольку величина зазора связана с внешним давлением линейной зависимостью, длина волны отраженного излучения меняется при изменении давления. Принцип действия датчика основан на измерении модуляции длины волны, получаемой от сложения падающих и отраженных излучений. Частота периодического интерференционного сигнала определяется шириной рабочей полости интерферометра w, а его период равен 1/2w. Детектор работает как демодулятор, электрический выходной сигнал которого пропорционален приложенному давлению. Он является оптическим компаратором, сравнивающим высоту рабочей камеры датчика давления и толщину виртуальной камеры, сформированной за счет разности высот двух фильтров Фабри—Перо. Когда размеры этих камер равны, ток фотодетектора будет максимальным. При изменении давления происходит косинусная модуляция фототока с периодом, соответствующим половине средней длины волны источника излучения. Фотодиод без фильтра используется в качестве эталонного диода, отслеживающего полную интенсивность света, поступающего на детектор. Его выходное напряжение применяется при последующей обработке сигналов для получения нормированных результатов измерений. Поскольку рассматриваемый датчик давления является нелинейным, он обычно встраивается в микропроцессорную систему, на которую возложены функции его линеаризации.
Манганиновые датчики давления
В манганиновых датчиках под действием давления изменяется электрическое сопротивление тонкой манганиновой проволоки. Эти датчики обычно используют для измерения давления свыше 100 MПа.
Магнитные датчики давления
Для решения проблемы измерения очень низких давлений является применение магнитных датчиков (рис. 2.15). Датчики переменного магнитного сопротивления измеряют изменение магнитного сопротивления дифференциального трансформатора, вызванного перемещением магнитной диафрагмы, возникающего вследствие воздействия на нее внешнего давления. Конструкция, состоящая из Е-образного сердечника и катушки, формирует магнитный поток, силовые линии которого проходят через сердечник, воздушный зазор и диафрагму.
Магнитная проницаемость материала сердечника по крайней мере в 1000 раз выше проницаемости воздушного зазора, поэтому его магнитное сопротивление всегда ниже сопротивления воздуха. В связи с этим величина индуктивности всей этой конструкции определяется шириной зазора. При отклонении диафрагмы величина воздушного зазора либо увеличивается, либо уменьшается в зависимости от направления перемещения, что вызывает модуляцию индуктивности. При возбуждении мостовой схемы высокочастотным сигналом ее выходной сигнал модулируется по амплитуде приложенным давлением. Амплитуда результирующего сигнала пропорциональна разбалансу моста, а его фаза соответствует направлению этого разбаланса. На выходе такого датчика ставят демодулятор для получения постоянного выходного напряжения.
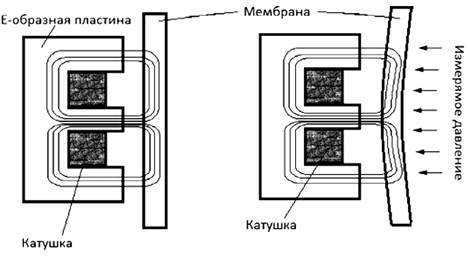
Рис. 2.15. Магнитные датчики давления
Пьезоэлектрические датчики давления
Пьезоэлектрики — это материалы, способные в электрическом поле изменять свои линейные размеры. Это явление называют пьезоэлектрическим эффектом. Впервые пьезоэффект обнаружили Ж. и П. Кюри в 1880 г. на кристаллах кварца. Пьезоэлектрический эффект связан с появлением электростатических зарядов на гранях кристаллов кварца при их деформации вдоль оси перпендикулярно этим граням. Кристаллы выполняют в виде двух пластин, механически соединенных с мембраной, на которую воздействует измеряемое давление.
Для измерения быстропеременных давлений до 100 МПа применяют малоинерционные пьезоэлектрические преобразователи, позволяющие измерять давление в диапазоне частот от 30 до 2000 Гц (рис. 2.16)
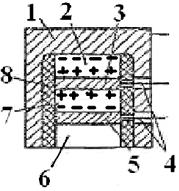
Рис. 2.16. Пьезоэлектрический датчик давления
Датчик состоит из стального корпуса 1, пластин датчика давления, изготовленных из керамики титаната бария 2, стальных электродов 3 и 5, предохранительного стекла 6 и выходных контактов 4. Все перечисленные детали жестко скреплены между собой и с корпусом карбинольным клеем 8. Датчик работает следующим образом. При сжатии пьезопластин за счет изменяемого давления на их обкладках возникают избыточные электрические заряды, которые накапливаются. Чувствительность таких преобразователей можно повысить, используя большее количество кварцевых пластин, увеличивая активную площадь мембраны или удлиняя пластину. Недостатками пьезокварцевых манометров является низкая точность измерения статического давления из-за утечки электрического заряда, а достоинством их — низкая температурная погрешность.
2.6. Промышленные датчики давления
Датчик давления с магнитомодуляционным преобразователем
Для дистанционного измерения давления применяют электрические манометры, в которых происходит непрерывное преобразование избыточного давления в пропорциональный электрический унифицированный сигнал в виде постоянного тока 4–20 мА. Преобразование выполняется следующим образом (рис. 2.17). Измеряемое давление преобразуется одновитковой трубчатой пружиной 1 в перемещение постоянного магнита 6, который создает управляющие воздействия в виде магнитного потока Ф. Этот поток компенсируется магнитным потоком обратной связи Фо.с возникающим при протекании в обмотках обратной связи Wo.с выходного сигнала постоянного тока.
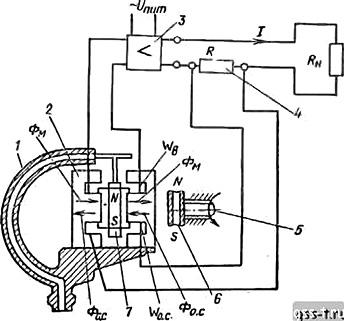
Рис. 2.17. Принципиальная схема манометра МП-Э
При изменении потока Фо.с изменяется намагниченность сердечников магнитомодуляционного преобразователя 2, а в его обмотках возникает сигнал рассогласования. Этот сигнал управляет сигналом усилительного устройства 3, который передается в линию дистанционной передачи и одновременно в обмотку обратной связи. Настройка диапазона измерений осуществляется резистором 4 настройки нуля путем плавного перемещения постоянного магнита 6 при помощи винта 5.
Манометры модели 22364 с дифференциально-трансформаторной передачей
Манометры предназначены для непрерывной выдачи информации в виде унифицированного электрического сигнала. Приборы применяются в качестве первичных в комплекте со вторичными дифференциально-трансформаторными приборами в системах контроля и управления (регулирования, сигнализации и т. п.) различных технологических процессов. Принцип действия приборов (рис. 2.18) основан на уравновешивании измеряемого давления силой упругой деформации чувствительного элемента — одновитковой трубчатой пружины 13, подвижный конец 11, которой соединен резьбовым штоком 9 с плунжером 5 дифференциального трансформатора 7. Перемещение подвижного конца пружины, пропорциональное измеряемому давлению, через резьбовый шток передается плунжеру. Перемещение плунжера вызывает изменение значения взаимной индуктивности от 0 до 10 мГн между первичной обмоткой и двумя секциями вторичной обмотки дифференциального трансформатора, включенными встречно.
Рис. 2.18. Манометр модели 22364 с дифференциально-трансформаторной передачей: 1 — штуцер; 2 — защитный колпачок; 3 — корпус прибора; 4 — планка крепежная; 5 — плунжер; 6 — постоянный резистор; 7 — дифференциальный трансформатор; 8 — катушка дифференциального трансформатора; 9 — резьбовый шток; 10 — контргайка; 11 — подвижный конец пружины; 12 — жгут проводов; 13 — пружина; 14 — штепсельный разъем; 15 — переменный резистор; 16 — держатель
Принципиальная электрическая схема прибора модели 22364 приведена на рис. 2.19. Среда с рабочим давлением Р через присоединительный штуцер 1 поступает в полость манометрической пружины 2 и вызывает ее перемещение, а также перемещения связанного с ней плунжера 3. При воздействии измеряемого давления плунжер перемещается в зазоре трансформаторных катушек: возбуждения 5 и сигнальных 4. Изменение положения плунжера в зазоре дифференциально-трансформаторного преобразователя приводит к изменению взаимной индуктивности между их обмотками и, соответственно, электрических параметров (напряжения и фазы) выходного сигнала.
Катушка возбуждения питается от вторичного прибора переменным током 0,125 А частотой 50 Гц. Сигнальные обмотки формируют выходной сигнал переменного тока, который изменяется по амплитуде и фазе взависимости от перемещения плунжера. Резисторы R1 и R2 предназначены для установки «нуля» прибора и корректировки диапазона измерения.
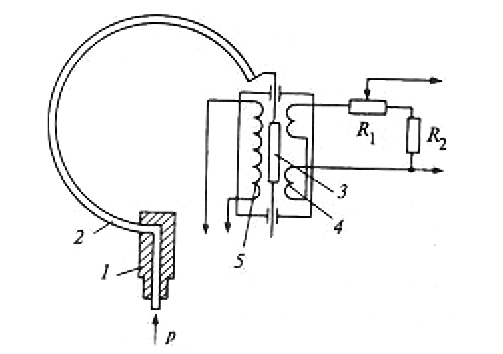
Рис. 2.19. Принципиальная электрическая схема измерителя давления с дифференциально-трансформаторной связью: 1 — присоединительный штуцер; 2 — манометрическая пружина; 3 — плунжер; 4 — сигнальные катушки; 5 — катушка возбуждения; R1 — корректор нуля; R2 — регулятор диапазона
Тензорезистивные датчики «Сапфир»
Комплексы датчиков «Сапфир-22М»; «Сапфир-22МТ» предназначены для пропорционального непрерывного преобразования давления, разрежения и разности давлений жидкостей и газов нейтральных и агрессивных сред в унифицированный токовый выходной сигнал.
Комплексы микропроцессорных датчиков «Сапфир-22МП» предназначены для дискретного пропорционального преобразования. Дискретность преобразования давления 16 bit; период преобразования 0,4 с.
Приборы имеют три исполнения: «Сапфир-22М», «Сапфир-22МП», «Сапфир-22МТ» (рис. 2.20). Электронный блок датчиков позволяет переключать выходной сигнал между режимами (0–5) мА или (4–20) мА — устанавливать прямую или обратную зависимость выходного тока от значения измеряемого давления, не нарушая при этом метрологических и температурных характеристик прибора.

Рис. 2.20. Датчики «Сапфир»: а — «Сапфир-22М»; б — «Сапфир-22МП»; в — «Сапфир-22МT»
Технические характеристики комплексов «Сапфир»
Диапазон измерения давления: 0,16 кПа до 100 МПа.
Выходной сигнал: 4–20/20–4; 0–5/5–0; 0–0/20–0 мА.
Питание датчиков с выходным сигналом: 0–5/5–0; 0–20/20–0 мА- (В) 36 ± 0,72.
Питание датчиков с выходным сигналом: 4–20/20–4 мА — (В) 15… 42.
Сопротивление нагрузки для датчиков с сигналом: 0–5/5–0 мА — (кОм) 2,5.
Сопротивление нагрузки для датчиков с сигналом: 0–20/20–0 мА, (кОм) 1,0.
Предел основной допускаемой погрешности, (γ,%): ±(0,15; 0,25; 0,5).Вариация выходного сигнала: 0,5 γ.
Дополнительная температурная погрешность, (на 10 °С): 0,8 γ.
Диапазон рабочих температур: –40...+80 °С.
Датчик давления Rosemount 3051S
В датчиках давления Rosemount 3051S (рис. 2.21) применяется конструкция SuperModule. Она представляет собой полностью герметичный узел, IP68, обеспечивающий надежную защиту от проникновения пыли и воды. В состав узла входят плата электроники и емкостный преобразователь давления, выполненный по сенсорной технологии Saturn. Емкостная ячейка изолирована механически, электрически и термически от технологической измеряемой среды и окружающей среды. Основной и дублирующий сенсоры емкостной ячейки, выполненные по этой технологии, увеличивают надежность работы датчика и значительно улучшают метрологические характеристики. Особенностью датчиков давления Rosemount 3051S являются малые значения основной приведенной погрешности, дополнительной погрешности от влияния температуры и статического давления, улучшенные показатели нестабильности измерений во времени.

Рис. 2.21. Датчик давления Rosemount 3051S
Применение корпуса датчика типа PlantWeb позволяет встраивать дополнительные платы расширения и модули, что увеличивает функциональность датчика, обеспечивает удобство диагностики, снижает стоимость обслуживания.
Измеряемые среды: жидкости, в том числе нефтепродукты; пар, газ, газовые смеси.
Диапазоны измеряемых давлений:
–минимальный: 0–0,025 кПа;
–максимальный: 0–68,9 MПа.
Диапазон температур:
–окружающей среды от –51...+85 °С;
–измеряемой среды от –73...+205 °С.
Выходные сигналы:
–4-20/HART;
–Foundation Fieldbus;
–Profibus-PA.
Основная приведенная погрешность:
–±0,025% (вариант Ultra);
–±0,055% (вариант Classic).
Основная относительная погрешность: ±0,04% (вариант Ultra for Flow).
Диапазон перенастройки пределов измерений: 200:1, 100:1.
Измерительный преобразователь давления JUMO dTRANS p02
Преобразователи давления JUMO dTRANS p02 предназначены для измерения относительного и абсолютного давлений агрессивных и неагрессивных газов, паров и жидкостей (рис. 2.22). Измерительные преобразователи давления работают по пеезорезистивному или тонкопленочному тензометрическому принципу. Выходной сигнал постоянного тока прямо пропорционален входному давлению.
При взрывозащищенном исполнении «ЕЕх ia IIC» преобразователь давления устанавливается внутри взрывоопасной зоны 1 для соединения с зоной 0.
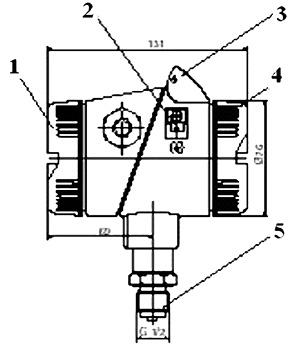

Рис. 2.22. Преобразователь давления JUMO dTRANS p02: 1 — крышка для электрических подключений; 2 — клемма заземления; 3 — защитная откидная крышка (под ней клавиатура); 4 — фронтальное кольцо; 5 – монтаж к технологическому аппарату; 6 — жидкокристаллический дисплей
Дисплей показывает:
–давление с различными, свободно выбираемыми, единицами измерения и в процентах, (возможные единицы измерения, отображаемые на дисплее: м вод. ст., дюймы вод. ст., дюймы рт. ст., футы вод. ст., мм вод. ст., мм рт. ст., фунты/кв. дюйм, бар, мбар, кг/см2, кПа, торр, МПа;
–выходной ток: 4–20 мА;
–температуру в градусах Цельсия или градусах Фаренгейта;
–ошибку измерения, выход за пределы диапазона измерений;
–минимальное и максимальное давление;
–давление и температуру одновременно (в две строки).
Клавиши управления служат для установки:
–начального и конечного значения выходного диапазона с указанием значений давления;
–начального и конечного значения выходного диапазона без указания значений давления (слепая установка);
–демпфирования или постоянной времени;
–функции датчика тока;
–выходного сигнала в случае неисправности;
–блокировки клавиатуры;
–сброса минимального и максимального значений;
–корректировки плотности для различных сред;
–единиц измерения температуры (градусы Цельсия или градусы Фаренгейта).
Преобразователем давления JUMO dTRANS p02 можно управлять с помощью переносного пульта управления (HART®-коммуникатopa) или ПК через HART® модем, используя установочную программу, работающую в среде Windows. После подключения питания измерительный преобразователь давления проводит самотестирование. Установочная программа позволяет с удобством проверять и устанавливать все параметры измерительного преобразователя давления, кроме того, она предоставляет дополнительные функции:
–запись измеряемых значений;
–графическое представление температуры и давления;
–подробные сообщения по диагностике.
Технические характеристики.
Смещение нулевой точки / точность регулирования: ≤ 0,01 мА
Влияние температуры окружающей среды в диапазоне –20...+85 °С
(диапазон температурной компенсации)
–нулевая точка: ≤ 0,005%/К (норма); ≤0,01%/К (максимум);
–интервал: ≤0,005%/К (норма);≤0,01%/К (максимум).
Отклонение характеристики: ≤0,1% верхнего предела номинального диапазона измерений:
Гистерезис:
–для номинальных диапазонов: ≥100 бар;
–≤0,05% конечного значения;
–для номинальных диапазонов ≤25 бар: ≤0,02% конечного значения.
Воспроизводимость:
–для номинальных диапазонов ≤100 бар: ≤0,5% конечного значения;
–для номинальных диапазонов ≤25 бар: ≤0,02% конечного значения.
Постоянная времени: максимум 150 мс, без демпфирования.
Нестабильность за год: ≤0,1% конечного значения.
Давление разрыва:
–10-кратный верхний предел;
–максимум 2 000 бар.
Механические удары: 50 г / 11 мс.
Механические колебания: максимум 5 г при 10–2000 Гц.
Глава 3. Методы и приборы для измерения температуры
Температурой называется степень нагретости вещества.
Немецкий физик Г. Фаренгейт (1686–1736) в 1709 г. изобрел спиртовой, а в 1714 г. — ртутный термометр. Он предложил разделить температуру между точками замерзания и испарения воды на 180 делений.
Французский естествоиспытатель Р. А. Реомюр (1683–1757) в 1730 г. предложил применять водно-спиртовой термометр. Спирт, смешанный в пропорции 5:1 с водой, расширяется в отношении 1000:1080 при изменении температуры от точки замерзания до точки кипения воды, таким образом Реомюр предложил шкалу от 0 до 80°.
Шведский астроном А. Цельсий (1701–1744) в 1742 г. предложил 100-градусную шкалу термометра.
Шотландский инженер и физик У. Дж. М. Ранкин (1820–1872) — один из создателей технической термодинамики. Шкала Ранкина начинается при температуре абсолютного нуля, точка замерзания воды соответствует 491,67 °Ra, точка кипения воды: 671,67 °Ra. Число градусов между точками замерзания и кипения воды по шкале Фаренгейта и Ранкина одинаково и равно 180.
Английский физик У. Т. Кельвин (1824–1907) в 1848 г. предложил совершенно точную и равномерную, не зависящую от свойств рабочего вещества шкалу, получившую название термодинамической температурной шкалы (шкалы Кельвина).
Д. И. Менделеев в 1874 г. впервые научно обосновал целесообразность построения термодинамической температурной шкалы не по двум реперным точкам, а по одной. Такая шкала имеет значительные преимущества и позволяет определять термодинамическую температуру точнее, чем шкала с двумя реперными точками.
В табл. 3.1 представлены реперные точки температурной шкалы МТШ-90.
Таблица 3.1
Реперные точки температурной шкалы МТШ-90
| Реперная точка |
К | °C | |
|---|---|---|---|
| е-Н2 | Тройная точка | 13,8033 | –259,3467 |
| Ne | Тройная точка | 24,5561 | –248,5939 |
| о2 | Тройная точка | 54,3584 | –218,7916 |
| Аг | Тройная точка | 83,8058 | –189,3442 |
| Нg | Тройная точка | 234,3156 | –38,8344 |
| н2о | Тройная точка | 273,16 | +0,01 |
| Ga | Точка плавления | 302,9146 | +29,7646 |
| In | Точка затвердевания | 429,7485 | +156,5985 |
| Sn | Точка затвердевания | 505,078 | +231,928 |
| Zn | Точка затвердевания | 692,677 | +419,527 |
