автордың кітабын онлайн тегін оқу Инструменты финансового рынка
Е.В. Ширшов, Н.И. Петрик, А.Г. Тутыгин
Инструменты финансового рынка
Учебное пособие
Издание второе, исправленное и дополненное
Информация о книге
УДК 681.140
ББК 65.26Я73
Ш64
Авторы:
Ширшов Е. В., Северный (Арктический) федеральный университет, г. Архангельск, Высшая школа экономики, управления и права, профессор кафедры менеджмента; Петрик Н. И., Северный (Арктический) федеральный университет, г. Архангельск, Высшая школа экономики, управления и права, доцент кафедры финансов и кредита; Тутыгин А. Г., Фонд «Архангельский региональный центр микрофинансирования», г. Архангельск, исполнительный директор.
Рецензенты:
Скрипниченко В. А., д-р экон. наук, профессор кафедры финансов и кредита Высшей школы экономики, управления и права САФУ; Дрожжин Д. П., канд. с.-х. наук, доцент, ведущий консультант отдела науки и высшей школы Министерства образования и науки Архангельской области.
Систематизированы основные инструменты финансовых вычислений. Приведены различные математические методы и способы количественного финансового анализа, разнообразных финансовых и кредитных расчетов, определения доходности операций по ценным бумагам. Подробно рассмотрены методы начисления процентов, обобщающие характеристики рентных платежей, методики определения эффективности краткосрочных и долгосрочных финансовых вложений, представлены критерии оценки доходности операций с ценными бумагами.
Учебное пособие прошло многолетнюю апробацию на базе Высшей школы экономики, управления и права Северного (Арктического) федерального университета имени М. В. Ломоносова.
Для студентов экономических вузов, обучающихся по направлениям бакалавриата 38.03.01 «Экономика»; 38.03.02 «Менеджмент»; 38.03.04 «Государственное и муниципальное управление» всех форм обучения, слушателей системы послевузовского образования, преподавателей.
УДК 681.140
ББК 65.26Я73
© Ширшов Е. В., Петрик Н. И., Тутыгин А. Г., 2015
© Ширшов Е. В., Петрик Н. И., Тутыгин А. Г., 2016, с изменениями
© ООО «Проспект», 2016
Введение
В любом из современных курсов экономики и управления используются инструменты финансового рынка. Профессиональное занятие бизнесом требует, прежде всего, умения оценивать все возможные варианты финансовых последствий при совершении любой сделки. Центральная проблема экономики и управления — это проблема рационального выбора, для этого необходимы определенные знания в области финансовых вычислений, оценки принимаемых финансовых и управленческих решений, основанные на теории и практике количественного финансового анализа.
В первом разделе пособия рассмотрены основные понятия финансового количественного анализа, приведены параметры финансовых вычислений — проценты, система процентных ставок, наращение процентов, дисконтирование платежей, финансовая эквивалентность платежей, влияние инфляционных процессов, консолидация платежей, аннуитеты, показана их взаимосвязь.
Во втором разделе уделено внимание вопросам, относящимся к количественному анализу разнообразных потоков платежей. Рассмотрены методы погашения долгов, ипотечное кредитование, операции с ценными бумагами, страхование.
Все разделы пособия содержат типовые примеры, что облегчает восприятие теоретического материала и делает его доступным для самостоятельного освоения и применения в практической деятельности как студентами, так и специалистами различных финансовых институтов. Изложение материала построено от простого к сложному, что позволяет сделать правильный математический расчет в определенной хозяйственной ситуации и сделать оптимальный выбор.
Изучение инструментария финансово-экономических расчетов позволит будущему специалисту сформировать необходимые знания в его профессиональной деятельности.
Учебное пособие прошло многолетнюю апробацию на базе Высшей школы экономики и управления Северного (Арктического) федерального университета имени М. В. Ломоносова.
Пособие представляет интерес не только для студентов экономических вузов, бизнес-школ, колледжей, но и для специалистов — сотрудников банков, инвестиционных компаний, пенсионных фондов и страховых компаний.
Раздел I. Основные понятия финансовых вычислений
1. Виды процентов
Проценты (процентные деньги) — это абсолютная величина дохода (interest) от предоставления капитала в долг в любой ее форме (выдача ссуды, покупка облигации, учет векселя, продажа товара в кредит и т. д.). Проценты обозначаются буквой I. Величина полученного дохода определяется исходя из:
• величины вкладываемого капитала P;
• срока n, на который вкладывается капитал;
• размера и вида процентной ставки (обозначения i, d, j, f, σ).
Наращение основной суммы S происходит за счет присоединения процентных денег к основному капиталу: S = P + I.
Коэффициентом наращения называется безразмерная величина, которая показывает, во сколько раз вырос капитал.
Период начисления — это промежуток времени, за который начисляются проценты. Период начисления может быть разбит на интервалы, по прошествии которых происходит начисление процентов.
Существуют два способа начисления процентов: декурсивный и антисипативный. При декурсивном способе проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из предоставляемого капитала P. Процентная ставка представляет собой отношение суммы начисленного за определенный интервал дохода (процентов) к сумме имеющегося капитала на начало данного интервала. При антисипативном (предварительном) способе проценты начисляются в начале каждого интервала. Сумма процентных денег (дохода) определяется исходя из наращенной суммы. В этом случае процентная ставка представляет собой отношение суммы дохода, выплачиваемой за определенный интервал, к величине наращенной суммы. Такая процентная ставка называется учетной (в широком смысле).
При обоих способах начисления проценты могут быть либо простыми, либо сложными.
1.1. Простые проценты
Величина процентной ставки определяется как
где IГ — сумма процентов за год; P — сумма капитала, предоставляемого в кредит. Процентная ставка выражается десятичной дробью.
Для простых процентов доход за n лет
I = IГ n.
Наращение основной суммы
S = P + I = P + Pin = P(1 + in),
где 1+ in = kн — коэффициент наращения.
Когда срок финансовой сделки не равен целому числу лет, период начисления равен отношению числа дней ∂ функционирования сделки к числу дней в году K, т. е. n =
В этом случае формула наращенной суммы примет вид
На практике применяются три варианта расчета процентов с использованием временной базы К.
1. Точные проценты с точным числом дней ссуды (английская практика). Продолжительность года K (временная база) равна 365 (366) дням. Точное число дней ссуды ∂ определяется путем подсчета числа дней между датой выдачи ссуды и датой ее погашения. Для подсчета числа дней можно воспользоваться Приложением 1.
2. Обыкновенные (коммерческие) проценты с точным числом дней ссуды (французская практика). Величина ∂ рассчитывается, как в предыдущем случае, а временная база принимается равной K = 360 дн.
3. Обыкновенные проценты с приближенным числом дней ссуды (германская практика). В этом случае год делится на 12 месяцев по 30 дней в каждом, и временная база K = 360 дн.
При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимают за 1 день.
Пример 1.1. Банк выдал кредит 50 тыс. руб. 15 января. Срок возврата кредита — 12 сентября. Процентная ставка установлена в размере 10% годовых. Год невисокосный. Определить сумму, подлежащую возврату.
Р е ш е н и е. Наращенную сумму долга S, подлежащую возврату, рассчитаем тремя методами.
1. По формуле точных процентов с точным числом дней ссуды. Точное число дней ссуды определим по Приложению 1. Порядковый номер 15 января — 15, порядковый номер 12 сентября — 255. Точное число дней ссуды ∂ = 255–15 = 240 дн.

2. По формуле обыкновенных процентов с точным числом дней ссуды.
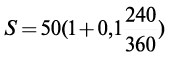
3. По формуле обыкновенных процентов с приближенным числом дней ссуды. Приближенное число дней ссуды: январь — 16 дней, февраль, март, апрель, май, июнь, июль, август — 30 ⋅ 7 дн., сентябрь — 12 дн.
Тогда
∂ = 16 + 30 ⋅ 7 + 12–1 = 237 дней.
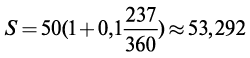
Начиная с 2000 г. в нашей стране для реальных расчетов применяется английская практика (начисление точных процентов).
Рассмотрим случай, когда на различных интервалах начисления процентов применяются различные простые процентные ставки. Наращенная сумма на конец срока определяется следующим образом:
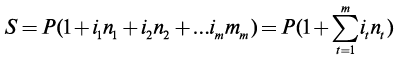
где it — ставка простых процентов в периоде t, t =
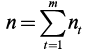
Пример 1.2. Контракт предусматривает следующий порядок начисления процентов: первый год — ставка 10%, в каждом последующем полугодовая ставка повышается на 1%. Необходимо определить коэффициент наращения за два года.
Р е ш е н и е. Находим коэффициент наращения:
kн =  = 1 + 0,1 ⋅ 1 + 0,11 ⋅ 0,5 + 0,12 ⋅ 0,5 = 1,215.
Обычно к наращению по простым процентам прибегают при выдаче краткосрочных ссуд (на срок до одного года) или в случае, когда проценты не присоединяются к сумме долга, а периодически выплачиваются кредитору.
На практике при инвестировании средств в краткосрочные депозиты прибегают к начислению процентов на уже наращенные в предыдущем периоде суммы, т. е. происходит многоразовое наращение, именуемое реинвестированием, или капитализацией процентов. В этом случае наращенная сумма определяется по формуле
Пример 1.3. 200 руб. положены 1 марта на месячный депозит под 12% годовых. Какова наращенная сумма, если операция повторяется три раза?
Р е ш е н и е. Если начисляются точные проценты, то
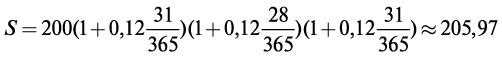
Начисление обыкновенных процентов (германская практика); наращенная сумма
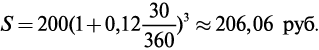
1.2. Простые учетные ставки
Простая учетная ставка — антисипативный способ начисления процентов. Суть его сводится к тому, что проценты начисляются в начале расчетного периода, при этом за базу (100%) принимается сумма погашения долга.
Введем обозначения:
d% — простая годовая учетная ставка;
d — относительная величина этой ставки;
Dг — сумма процентных денег за год;
D — сумма процентных денег за период, равный n.
Тогда простая учетная ставка
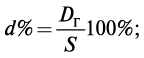
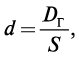
где S — наращенная сумма.
Сумма процентных денег за 1 год составит Dг = dS, а за период nD = Dгn = Sdn. Произведем преобразования:
S = P + D; S = P + Sdn; S — Sdn = P; P = S(1 — dn).
Получаем
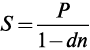
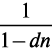
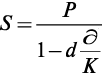
Пример 1.4. Через 180 дней после подписания договора должник уплатит 310 руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что при начислении процентов используется простая учетная ставка и временная база K = 360 дн.?
Р е ш е н и е. Первоначальная сумма долга — это величина P:
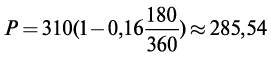
На практике расчеты по простым учетным ставкам чаще всего применяются при учете векселей и других краткосрочных долговых обязательств.
Пример 1.5. Владелец векселя учел его в банке по простой учетной ставке 9% за 30 дней до срока погашения, получив при этом 4963 руб. Определить номинал векселя.
Р е ш е н и е. Номинал векселя — это величина S:
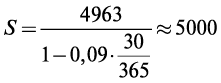
Задачи для самостоятельного решения
Задача 1.1. Сумма процентов, начисленных в период с 10 января по 31 октября, составила 1568 руб. Определить размер первоначального капитала, если банк начисляет проценты по ставке 11% годовых при условии, что год невисокосный.
Задача 1.2. Годовая ставка при начислении обыкновенных процентов по депозитному 30-дневному сертификату номиналом 100 тыс. руб. равна 10%. Год високосный. Определить сумму точных процентов, выплаченных при погашении сертификата.
Задача 1.3. Переводный вексель выдан на сумму 500 тыс. руб. с уплатой 19 декабря. Векселедержатель учел вексель в банке 25 октября по учетной ставке 8%. Определить сумму, полученную векселедержателем, и размер дисконта в пользу банка.
Задача 1.4. Сберегательный сертификат выдан на 186 дней под 16% годовых с погашением 50 тыс. руб. Год невисокосный. Определить доход держателя сертификата.
Задача 1.5. На какой срок должен быть выпущен сберегательный сертификат номиналом 10 тыс. руб., если сумма погашения при 8% годовых составляет 10,5 тыс. руб.? Год невисокосный.
Задача 1.6. Сберегательный сертификат номиналом 10 тыс. руб. выдан на 120 дней с погашением в сумме 12 тыс. руб.
Определить: 1) учетную ставку; 2) процентную ставку.
За временную базу принять 360 дней.
Задача 1.7. По сберегательному сертификату, выданному на 210 дней, начисляется дисконт в размере 12% от суммы погашения. Год невисокосный.
Определить: 1) учетную ставку; 2) процентную ставку.
1.3. Сложные проценты
Основное отличие сложных процентов от простых заключается в том, что база для начисления процентов меняется от одного расчетного периода к другому. Сумма начисленных в каждом периоде процентов добавляется к капиталу предыдущего периода, а начисление процентов в последующем периоде производится на эту, уже наращенную величину первоначального капитала. Механизм наращения первоначального капитала по сложным процентам называется капитализацией.
Как и в случае простых процентов, существуют два способа начисления сложных процентов: антисипативный и декурсивный.
В случае декурсивного способа расчета сложных процентов начисление процентов на первоначальную сумму производится в конце периода наращения.
В конце первого периода (года) наращенная сумма равна:
S1 = P + Pi = P(1 + i).
В конце второго периода (года) проценты начисляются на уже наращенную сумму:
S2 = P(1 + i) + P(1 + i)i = P(1 + i)(1 + i) = P(1 + i)2.
И так далее, в конце n-го периода (года) наращенная сумма будет равна
Sn = P(1 + i)n.
Величина (1 + i)n является коэффициентом наращения сложных процентов (Приложение 2).
Если срок ссуды измеряется дробным числом лет, то наращенную сумму можно найти смешанным методом:
S = P(1 + i)[n](1 + {n}i),
где [n] — целая часть числа n; {n} — дробная часть числа n.
В контрактах на получение кредитов часто предусматривается капитализация процентов по полугодиям, кварталам, иногда помесячно. В этом случае указывается годовая ставка j (номинальная). Тогда для начисления процентов m раз в году используется формула
S = P (1+j/m)mn.
Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена по смешанному методу
S = P(1+ j/m)mn(1+ (j/m{n}),
где mn — число полных периодов начисления процентов, {n} — дробная часть одного периода начисления процентов.
Пример 1.5. На сумму 600 руб. ежеквартально по ставке 12% годовых начисляются сложные проценты в течение 14 месяцев. Определить величину наращенной суммы двумя методами.
Р е ш е н и е. Общее число периодов начисления процентов составит:
mn = 4, {n} = 0,667.
Наращенная сумма
S = 600 (1 + 0,12/4)4,667 = 688,75 руб.
По смешанному методу начисления
S = 600 (1 + 0,12/4)4 ·(1 + 0,667 · 0,12/4) = 688,81 руб.ּ
Нестабильность экономической ситуации вынуждает банки использовать в кредитных сделках изменяющиеся во времени, но заранее фиксированные для каждого периода ставки сложных процентов. В этом случае наращенная сумма может быть определена по формуле:
где it — процентная ставка в периоде t, t =
Способ начисления сложных антисипативных процентов аналогичен методу при использовании простых антисипативных процентов.
В первом периоде наращенная сумма определяется по формуле:
во втором
в n-м
где
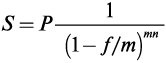
где f — номинальная учетная ставка; m — число период начисления процентов в течение года; n — число лет.
Пример 1.6. Срочный вклад в размере 800 руб. положен в банк на 2,5 года. По условиям договора начисление процентов производится один раз в году по сложной учетной ставке d = 15% годовых. Определить наращенную сумму.
Р е ш е н и е. Наращенная сумма составит
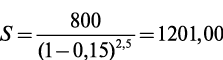
Если наращение по учетной ставке производить не один, а два раза в год (m = 2), то наращенная сумма будет равна:
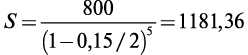
1.4. Непрерывные проценты
Начисление процентов на первоначальный капитал может производиться столь часто, что этот процесс можно рассматривать как непрерывный.
При дискретном начислении процентов m раз в году по номинальной ставке j наращенная сумма
S = P(1 + j/m)mn.
При m → ∞.
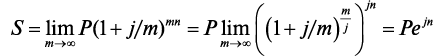
где ejn — коэффициент наращения при непрерывной капитализации процентов.
Если ставку непрерывных процентов j (силу роста) обозначить через σ, то величину наращенной суммы запишем в следующем виде:
Дискретные и непрерывные ставки наращения находятся в функциональной зависимости между собой. Из равенства коэффициентов наращения
(1 + i)n = e σ n
следует, что
σ = ln(1 + i), i = e σ — 1.
Пример 1.7. На первоначальный капитал в сумме 500 руб. начисляются сложные проценты — 8% годовых в течение 4 лет. Определить наращенную сумму, если начисление процентов производится непрерывно.
Р е ш е н и е. Найдем сначала силу роста σ, а потом наращенную сумму S:
σ = ln(1 + i) = ln1,08 = 0,0769611;
S = Pe σ n = 500 · e0,0769611 ≈ 680,25 руб.
В практических финансово-кредитных операциях непрерывные проценты применяются крайне редко. Они имеют теоретическое значение, используются в анализе сложных финансовых проблем при обосновании и выборе инвестиционных проектов.
2. Дисконтирование и его сущность
В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется. Величину P, найденную дисконтированием наращенной суммы S, называют современной стоимостью. С помощью дисконтирования в финансовых операциях учитывается фактор времени. Разность S — P можно рассматривать не только как проценты, начисленные на P, но и как дисконт D с суммы S: D = S — P.
2.1. Математическое дисконтирование
Запишем формулу наращения по простой ставке процентов следующим образом:
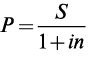
Величина
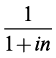
Пример 2.1. Владелец векселя номинальной стоимости 400 руб. и сроком обращения один год предъявил его банку-эмитенту для учета за 90 дней до даты погашения. Банк учел его по ставке 12% годовых (проценты простые). Определить дисконтированную величину и величину дисконта, временная база К = 360.
Р е ш е н и е. Сумма, полученная владельцем векселя в результате его учета:
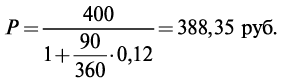
Величина дисконта D = 400 – 388,35 = 11,65 руб.
2.2. Банковское дисконтирование
Банковское дисконтирование основано на использовании учетной ставки d, т. е. проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды.
При банковском дисконтировании современная стоимость P величины S определяется по формуле: P = S(1 — dn), отсюда D = Sdn.
Рассмотрим пример 2.1. По условию S = 400, ∂ = 90, K = 360, возьмем учетную ставку d = 12%. Тогда дисконтированная величина
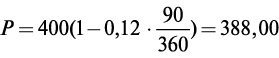
Величина дисконта
D = S — P = 400–388 = 12,00 руб.
В отдельных случаях может возникнуть ситуация, когда совмещают начисление процентов по ставке i и дисконтирование по ставке d. В этом случае наращенная величина ссуды будет определяться по формуле:
S = P(1+in)(1 – dn′),
где n — общий срок платежного обязательства; n′ — срок от момента учета обязательства до даты погашения долга, т. е. n′ < n.
Пример 2.2. Долговое обязательство в сумме 2000 руб. должно быть погашено через 90 дней по ставке 10% годовых. Владелец обязательства учел его в банке за 30 дней до наступления срока по учетной ставке 12%. Найти полученную после учета векселя сумму и величину дисконта.
В соответствии с приведенной выше формулой:
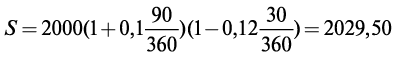
2.3. Дисконтирование по сложной процентной и по сложной учетной ставкам
Современная стоимость P величины S находится в случае сложной процентной ставки по формуле
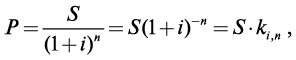
где ki,n = (1 + i)–n — дисконтный коэффициент (коэффициент дисконтирования). Значения этого коэффициента табулированы (см. Приложение 3).
Величина дисконта
D = S — P = S(1 — (1+ i)–n).
При начислении процентов m раз в году получим
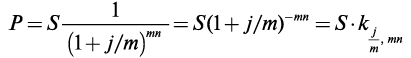
где
