автордың кітабын онлайн тегін оқу Математическое обеспечение финансовых решений
Т.В. Ващенко, Р.О. Восканян
Математическое обеспечение финансовых решений
Учебно-методическое пособие
Информация о книге
УДК 330.4(073)
ББК 65.05я73
В23
Авторы:
Ващенко Т. В. – канд. экон. наук, доцент кафедры финансового менеджмента ФГБОУ ВО «Российский экономический университет имени Г. В. Плеханова»;
Восканян Р. О. – канд. экон. наук, доцент кафедры финансового менеджмента ФГБОУ ВО «Российский экономический университет имени Г. В. Плеханова».
В учебно-методическом пособии излагаются основные вопросы, составляющие сущность и содержание математического обеспечения финансовых решений как учебной дисциплины и как основы принятия эффективных финансово-инвестиционных решений в управлении финансово-хозяйственной деятельностью российских компаний на основе концепций временной стоимости денег, альтернативной доходности, стоимости капитала и т. д. Рассматриваются сущность начисления процентного дохода и различные виды процентных ставок, операции дисконтирования и наращения, показатели доходности и стоимости финансовых операций, методы оценки денежных потоков, конверсия аннуитетов и финансовая эквивалентность платежей.
В пособии приведено большое количество задач для самостоятельного решения, тестов и контрольных вопросов. Для более полного усвоения материала приводятся примеры решения конкретных задач.
Данное пособие будет полезно бакалаврам и магистрам, обучающимся по направлениям 080300 «Финансы и кредит» и 080100 «Экономика» федерального государственного образовательного стандарта 3-го поколения.
Также может быть рекомендовано для самостоятельного изучения всем, кто связывает свою профессиональную деятельность с финансовой сферой.
УДК 330.4(073)
ББК 65.05я73
© Ващенко Т. В., Восканян Р. О., 2017
© ООО «Проспект», 2017
Предисловие
В последнее время актуальность вопросов, связанных с повышением эффективности управления финансами компаний, возрастает в связи с усложняющимися условиями их функционирования под воздействием целого ряда внешних факторов. Постоянно усиливается конкуренция и одновременно ужесточается контроль над деятельностью всех участников финансового рынка, увеличивается количество разнообразных финансовых инструментов и усложняются модели их оценки и управления, мировые финансовые кризисы становятся почти постоянным фоном финансово-хозяйственной деятельности, охватывая все большее количество динамически развивающихся стран и регионов.
Современная рыночная ситуация, характеризующаяся ускоряющейся финансовой глобализацией и интеграцией России в мировое финансовое сообщество, предъявляет особые требования к содержанию и качеству образовательного процесса и уровню подготовки выпускника финансового профиля. В настоящее время российская образовательная система перешла на новый этап развития и новые стандарты обучения, основанные на компетентностном подходе и инновационных методах обучения, направленных на формирование у обучающихся необходимых знаний, умений и навыков, относящихся к области их будущей профессиональной деятельности.
Содержательная и структурная логика представления материала данного учебного пособия полностью учитывает все новые подходы и требования. Последовательно и логично в каждом разделе учебного пособия рассматриваются базовые понятия и определения, лежащие в основе финансовой математики, приводятся необходимые показатели и способы их расчета, дается интерпретация возможных результатов, раскрывается их значимость для принятия обоснованных решений в финансово-инвестиционной сфере.
В первом разделе рассмотрены основные понятия и определения финансовой математики, а также основные формулы, формирующие базовый инструментарий для проведения расчетов и анализа на основе принципа временной стоимости денег: процентные ставки, приведенная и будущая стоимость, операция дисконтирования и наращения.
Второй раздел содержит конкретные приемы и методы расчета основных характеристик денежных потоков различного вида, в том числе не ограниченных по времени потоков и аннуитетов. В третьем разделе рассматриваются вопросы оценки важнейших характеристик финансовых инструментов, используемых для привлечения и вложения капитала, — доходности и стоимости, а также методы учета инфляции в финансовых решениях.
Последний раздел посвящен вопросам практического применения методов финансовой математики для решения наиболее важных задач, базирующихся на анализе денежных потоков — оценке эффективности инвестиционных проектов и оценке стоимости компаний на основе доходного подхода.
Для более полного усвоения изложенного теоретического материала в каждом разделе приводятся примеры решения наиболее типичных задач. Для проверки полученных знаний даны задачи, контрольные вопросы и тесты для самостоятельного решения. Задания учебного пособия не требуют дополнительных знаний и источников информации помимо приведенных в теоретической части.
Практикум, завершающий содержание учебного пособия, содержит кейс с подробным объяснением хода решения, которое основано на принципах оценки денежных потоков, доходности инвестиционных проектов и стоимости финансовых операций с использованием инструментов финансовой математики.
В приложениях приводятся список аббревиатур, используемых при изложении учебного материала, глоссарий, раскрывающий сущность основных используемых понятий, а также наиболее важные формулы и таблицы приведения аннуитетов, необходимые для решения практических задач.
Материалы учебного пособия апробированы авторами при чтении курсов по финансовой математике и математическому обеспечению финансовых решений в Российском экономическом университете имени Г. В. Плеханова и Российской академии народного хозяйства и государственной службы при Президенте РФ.
Введение
Математическое обеспечение финансовых решений (финансовая математика, высшие финансовые вычисления) — специальная область знаний, являющаяся научным фундаментом целого ряда дисциплин, имеющих в своей основе набор базовых принципов или концепций, на которых строится современная финансовая наука и практика, — концепция денежного потока, концепция временной стоимости денег, концепция альтернативной доходности, концепция стоимости капитала, концепция соотношения «риск/доходность».
На этих концепциях базируются анализ денежных потоков компаний и оценка эффективности их финансово-инвестиционной деятельности, управление инвестиционным портфелем, планирование погашения долгосрочных кредитов и займов, расчет важнейших характеристик современных финансовых инструментов, оценка справедливой стоимости ценных бумаг и еще много других практических аспектов финансового управления, являющихся важнейшими задачами в таких дисциплинах, как «Финансовый менеджмент», «Инвестиционный анализ», «Управление денежными потоками», «Финансирование инвестиционных проектов», «Управление стоимостью компании» и др., что и определяет повышенную значимость финансовой математики и необходимость успешного ее освоения в процессе обучения по финансово-экономическим направлениям.
В основе всех перечисленных концепций лежит главный принцип – деньги должны работать и приносить инвесторам доход, который необходимо оценивать с учетом требований к минимально приемлемой доходности, прогнозируемого уровня инфляции и факторов возможного риска. При этом доходность финансовых операций и стоимость финансовых ресурсов являются показателями, используемыми как критерий выбора источников финансирования и целесообразных для реализации инвестиционных проектов.
Необходимым условием эффективности финансово-инвестиционной деятельности компании является соблюдение условия: стоимость инвестируемого капитала не должна быть выше доходности инвестиций. В этом случае вложения капитала принесут достаточный доход, чтобы росли стоимость компании и благосостояние ее собственников, что является важнейшей целью управления в современных условиях.
Таким образом, свободное владение приемами и методами финансовой математики, умение корректно использовать необходимые формулы и алгоритмы расчета, а также верно интерпретировать полученные результаты являются залогом успешного освоения многих финансовых дисциплин и дальнейшей профессиональной деятельности.
Необходимо также отметить, что знание основ финансовых вычислений нередко может быть полезным и в повседневной деятельности, например при выборе банковского вклада, решении вопроса об использовании кредита, при выборе предлагаемых банками инвестиционных продуктов и программ и т. п.
Раздел 1.
Теоретические основы финансовой математики
1.1. Финансовая математика — инструмент реализации в финансовом менеджменте концепции временной стоимости денег
Современный финансовый менеджмент базируется на ряде взаимосвязанных фундаментальных принципов или концепций, представляющих собой методологическую основу для понимания сущности процессов, происходящих на финансовых рынках, логики принятия финансово-инвестиционных решений, выбора методов количественного анализа современных финансовых инструментов.
В соответствии с концепцией денежного потока любая финансовая операция может быть представлена в виде совокупности распределенных во времени поступлений или выплат денежных средств в наличной или безналичной форме. Денежные потоки являются основой для применения различных инструментов анализа и оценки, финансового планирования и прогнозирования, расчета необходимых финансовых показателей, позволяющих разрабатывать эффективную финансовую стратегию и принимать обоснованные финансово-инвестиционные решения. Деление денежных потоков по видам деятельности – инвестиционной, операционной, финансовой – позволяет повысить качество анализа и эффективность управления компанией.
Планирование, оценка и анализ денежных потоков базируется на концепции временной стоимости денег, в соответствии с которой одна и та же денежная сумма имеет разную ценность в разные моменты времени. Это происходит потому, что деньги обязательно должны работать, т. е. вкладываться в различного вида объекты инвестирования, и приносить определенный доход за любой рассматриваемый промежуток времени. Предполагается, что данный доход компенсирует и обесценение денег в результате инфляции, и возможные риски, и альтернативные издержки1.
Поэтому каждый элемент денежного потока строго привязан к конкретному моменту времени, что должно обязательно учитываться в процессе расчета его количественных характеристик.
Временной аспект учитывается при оценке будущих денежных потоков в инвестиционном анализе, при оценке стоимости и доходности различных финансовых инструментов, оценке стоимости бизнеса, планировании погашения кредитов и займов, реструктуризации задолженностей и т. д.
Концепция временной стоимости денег реализуется в финансовом менеджменте через инструментарий финансовой математики, называемой также математическими основами финансового менеджмента или финансовыми вычислениями.
С данной концепцией тесно связана концепция альтернативной доходности, представляющая собой простейший инструмент оценки требуемого дохода на вложенный капитал. Поскольку в условиях рыночной экономики существует большое многообразие финансовых инструментов с различными показателями доходности и риска, у финансового менеджера всегда есть возможность выбора между различными объектами вложения капитала в соответствии с разработанной финансово-инвестиционной стратегией и требованиями к ее результативности. Доход, не полученный в результате отказа от участия в некоторой операции, имеющей минимальный риск и минимальную, но при этом гарантированную доходность, должен учитываться в качестве альтернативных затрат при принятии любых решений, связанных с использованием финансовых ресурсов компании.
Таким образом, ставка альтернативной доходности используется в финансовом менеджменте в двух аспектах:
1) как ставка, характеризующая гарантированную доходность, на которую компания всегда может рассчитывать;
2) как ставка, характеризующая минимально приемлемую доходность инвестиционной деятельности компании.
Ставка альтернативной доходности является субъективной величиной, выбор которой зависит от многих факторов, тем не менее очень часто в качестве ставки альтернативной доходности используется ставка рефинансирования2 Центробанка, если у компании нет оснований выбрать для этой цели какую-либо другую величину.
Концепция стоимости капитала также имеет в своей основе идею о необходимости получения дохода от использования имеющегося капитала. Любая финансово-экономическая деятельность требует постоянных вложений денежных средств. Для поддержания и расширения производственного процесса, повышения его результативности, внедрения новых технологий и освоения новых рынков необходим инвестиционный капитал. Источником инвестиций может быть эмиссионная деятельность компаний (акции и облигации), различного вида кредиты и займы, иностранные инвестиции, собственная прибыль и т. п.
Ни один источник средств не может считаться бесплатным. Стоимость капитала представляет собой цену, которую компания платит за его использование, т. е. годовые расходы по обслуживанию задолженности перед инвесторами и кредиторами. Количественно она выражается в виде процентной ставки, представляющей собой отношение данных расходов к общей сумме используемого капитала. Эта ставка характеризует минимальный уровень доходности инвестиций, который должна обеспечить компания, с тем чтобы не уменьшить свою рыночную стоимость.
Таким образом, процентные ставки, характеризующие стоимость капитала компании и доходность ее инвестиций, являются основой для принятия финансово-инвестиционных решений. Вложения капитала будут приносить компании доход и увеличивать благосостояние ее собственников при условии, что доходность инвестиций окажется не ниже стоимости инвестированного капитала.
1.2. Способы начисления процентов, виды процентных ставок
Для оценки денежных потоков, а также отдельных денежных сумм на основе концепции временной стоимости денег необходимо иметь инструмент приведения элементов денежных потоков к нужному моменту времени. Чаще всего оценка проводится на текущий момент, но это также может быть и любой другой момент в прошлом или в будущем, как в пределах самого денежного потока, так и выходящий за них. Приведение денежного потока к конкретному моменту времени должно учитывать доход, который был получен (или мог бы быть получен) за соответствующий период. Интенсивность получения дохода от вложения капитала в различные направления деятельности характеризуется годовой процентной ставкой, на основе которой выводятся формулы приведения денежных сумм к требуемым моментам времени.
В дальнейшем будут использоваться следующие понятия и обозначения:
Проценты, процентный доход, I (Interest) — доход от предоставления капитала в долг в различной форме (ссуды, кредиты и т. д.), от владения каким-либо финансовым активом либо от инвестиций производственного или финансового характера.
Первоначальная денежная сумма, первоначальный капитал, PV (present value) — величина капитала, имеющегося на начальный момент времени (или величина капитала, вкладываемого в рассматриваемую операцию); либо текущий эквивалент будущей денежной суммы.
Процентная ставка, i (interest rate) — величина, характеризующая интенсивность начисления процентов. Всегда подразумеваются годовые процентные ставки, т. е. ставки, характеризующие возможность получения дохода за год.
Наращение — увеличение первоначальной денежной суммы за счет присоединения начисленных процентов (приведение денежной суммы к будущему моменту времени).
Наращенная (будущая) денежная сумма, FV (future value) — сумма первоначального капитала и начисленных процентов, будущий эквивалент текущей денежной суммы.
Дисконтирование — определение текущего финансового эквивалента будущей денежной суммы (приведение будущей денежной суммы к настоящему моменту времени).
Коэффициент (множитель) наращения — величина, показывающая, во сколько раз изменился первоначальный капитал.
Период начисления, n — период времени, в течение которого начисляются проценты (длительность финансовой операции). Период начисления всегда выражается в годах (так же как процентные ставки всегда задаются годовыми), может являться как целым, так и нецелым числом.
Интервал начисления — минимальный промежуток времени, по прошествии которого начисляются проценты. Период начисления может состоять из одного или нескольких интервалов начисления.
Временная база для расчета процентов, Т — количество дней в году, которое берется для расчета длительности операции n, если изначально она задана в днях. В зависимости от способа определения продолжительности финансовой операции, рассчитываются либо точные, либо приближенные проценты. Приближенные проценты обычно используются для получения промежуточных итогов, когда не требуется абсолютная точность.
Существует несколько способов начисления процентов и, соответственно, несколько видов процентных ставок. В зависимости от применяемого способа начисления финансовые результаты могут достаточно сильно различаться. При этом разница будет тем больше, чем больше величина вкладываемого капитала, применяемая процентная ставка и продолжительность периода начисления.
Общее представление о различных способах начисления процентов дает следующая схема:
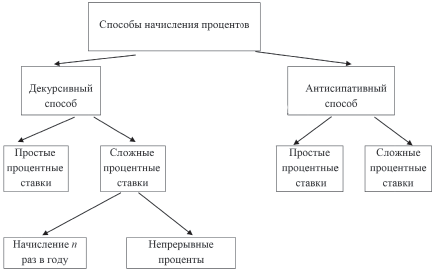
Способы начисления процентов, виды процентных ставок
Декурсивный и антисипативный способы начисления различаются по моменту начисления процентов.
Признаком декурсивного способа является начисление процентов в конце каждого интервала
...