Переводчик А. Логунов

Технический редактор А. Руденко

Литературный редактор А. Руденко

Художники В. Мостипан, А. Руденко

Корректоры М. Молчанова (Котова), Г. Шкатова

Верстка Л. Егорова

 

Тим Рафгарден

Совершенный алгоритм. Алгоритмы для NP-трудных задач. — СПб.: Питер, 2021.

 

ISBN 978-5-4461-1799-4

© ООО Издательство "Питер", 2021

 

Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

 

Предисловие

Перед вами четвертая из серии книг, написанных на базе проводимых мною с 2012 года онлайн-курсов по алгоритмам. Эти курсы, в свою очередь, появились благодаря лекциям для студентов, которые я читал в Стэнфордском университете в течение многих лет. Четвертая часть исходит из того, что читатель уже немного знаком с асимптотическим анализом и О-большим, поиском в графах и алгоритмами кратчайшего пути, жадными алгоритмами и динамическим программированием (все эти темы освещены в предыдущих частях).

О чем эти книги

Четвертая часть серии «Совершенный алгоритм» посвящена NP-трудным1 задачам и работе с ними.

Алгоритмические инструменты для решения NP-трудных задач. Многие реальные задачи являются NP-трудными и кажутся не поддающимися решению теми типами всегда правильных и всегда быстрых алгоритмов, которые были представлены в предыдущих частях. При встрече с NP-трудной задачей придется пойти на компромисс между правильностью и скоростью. Вы увидите старые методы (жадные алгоритмы) и новые (локальный поиск) для разработки быстрых «приближенно правильных» эвристических алгоритмов для работы с приложениями по задачам планирования, максимизации влияния в социальных сетях и задаче коммивояжера. Мы также рассмотрим старые методы (динамическое программирование) и новые (решатели задач смешанного целочисленного программирования и задач выполнимости булевых формул) для улучшения работы алгоритмов исчерпывающего поиска. Приложения будут включать задачу коммивояжера, поиск сигнальных путей в биологических сетях и переупаковку телевизионных станций на аукционе радиочастотного спектра в США.

Распознавание NP-трудных задач. Эта книга научит вас быстро распо­знавать NP-трудную задачу и не тратить время на разработку идеального алгоритма для ее решения. Вы познакомитесь с многочисленными широко известными и базовыми NP-трудными задачами, начиная от задач выполнимости и раскраски графов и заканчивая задачей о гамильтоновом пути. Вы попробуете доказать NP-трудность с помощью редукций.

Для более подробного ознакомления с содержанием книги загляните в разделы «Выводы», где выделены наиболее важные моменты. «Полевое руководство по разработке алгоритмов» на с. 283 даст представление о том, как темы этой книги вписываются в общую алгоритмическую картину.

Разделы книги, помеченные звездочками, — самые продвинутые. Читатели, испытывающие нехватку времени, могут пропустить их при первом чтении без потери непрерывности.

Темы, затронутые в первых трех частях.Первая часть серии «Совершенный алгоритм» охватывает асимптотические обозначения (О-большое и его близких родственников), алгоритмы «разделяй и властвуй» и основной метод, рандомизированные алгоритмы, быструю сортировку и ее анализ, а также линейно-временные алгоритмы отбора. Во второй части рассмотрены различные структуры данных (кучи, сбалансированные деревья поиска, хеш-таблицы, фильтры Блума), графовые примитивы (поиск сначала в ширину и сначала в глубину, связность, кратчайшие пути) и области их применения (от дедупликации до анализа социальных сетей). Третья часть посвящена жадным алгоритмам (задаче планирования, определению минимального остовного дерева графа, кластеризации, кодам Хаффмана), а также динамическому программированию (задаче о рюкзаке, выравниванию рядов, поиску кратчайших путей, построению деревьев оптимального поиска).

Навыки, которые вы приобретете

Освоение алгоритмов требует времени и усилий. Ради чего все это?

Возможность стать более эффективным программистом. Вы изучите несколько невероятно быстрых подпрограмм для обработки данных и несколько полезных структур для организации данных, которые можете применять непосредственно в ваших собственных программах. Реализация и применение этих алгоритмов расширят и улучшат ваши навыки программирования. Вы также узнаете основные приемы разработки алгоритмов, которые актуальны для решения разнообразных задач в широких областях, получите инструменты для прогнозирования производительности этих алгоритмов. Такие шаблоны могут быть вам полезны для разработки новых алгоритмов решения задач, которые возникают в вашей собственной работе.

Развитие аналитических способностей. Алгоритмические описания, мыслительная работа над алгоритмами дают большой опыт. Посредством математического анализа вы получите углубленное понимание конкретных алгоритмов и структур данных, описанных в этой книге. Вы приобретете навыки работы с несколькими математическими методами, которые широко применяются для анализа алгоритмов.

Алгоритмическое мышление. Научившись разбираться в алгоритмах, трудно не заметить, что они окружают нас повсюду, едете ли вы в лифте, наблюдаете ли за стаей птиц, управляете ли вы своим инвестиционным портфелем или даже наблюдаете за тем, как учится ребенок. Алгоритмическое мышление становится все более полезным и распространенным в дисциплинах, не связанных с информатикой, включая биологию, статистику и экономику.

Знакомство с величайшими достижениями информатики. Изучение алгоритмов напоминает просмотр эффектного клипа с многочисленными суперхитами минувших шестидесяти лет развития информатики. Вы больше не будете чувствовать себя чужим на фуршете для специалистов в области computer science, когда кто-то отпустит шутку по поводу алгоритма Дейкстры. Прочитав эти книги, вы будете точно знать, что он имеет в виду.

Успешность при прохождении собеседования. На протяжении многих лет бесчисленные студенты развлекали меня рассказами о том, как знания, почерпнутые из этих книг, позволяли им успешно справляться с любым техническим вопросом, который им задавали во время собеседования.

В чем особенность этой книги

Эта книга предназначена только для одного: постараться научить основам алгоритмизации максимально доступным способом. Воспринимайте ее как конспект лекций, которые опытный наставник по алгоритмам будет давать вам на протяжении серии индивидуальных уроков.

Существует ряд прекрасных, гораздо более традиционных и энциклопедически выверенных учебников по алгоритмам. Любой из них с пользой украсит эту серию книг дополнительными деталями, задачами и темами. Хотелось бы, чтобы вы поискали и нашли что-то полезное среди этих книг для себя. Кроме того, есть книги, которые ориентируются на программистов, ищущих готовые реализации алгоритмов на конкретном языке программирования. Множество соответствующих примеров также находятся в свободном доступе в интернете.

Для кого эта книга?

Весь смысл этой книги, как и онлайн-курсов, на основе которых она создана, — быть широко- и легкодоступной настолько, насколько это возможно. На моих онлайн-курсах широко представлены люди всех возрастов, профессионального опыта и слоев общества, есть немало учащихся и студентов, разработчиков программного обеспечения (как состоявшихся, так и начинающих), ученых и профессионалов со всех уголков мира.

Эта книга не является введением в программирование, и было бы просто идеально, если бы вы уже обладали основными навыками программирования на каком-либо распространенном языке (например, Java, Python, C, Scala, Haskell). Если вам требуется развить свои навыки программирования, то для этих целей есть несколько прекрасных бесплатных онлайн-курсов, обучающих основам программирования.

По мере необходимости мы также используем математический анализ, чтобы разобраться в том, как и почему алгоритмы действительно работают. Свободно доступные конспекты лекций «Математика для Computer Science» Эрика Лемана и Тома Лейтона являются превосходным и освежающим память пособием по системе математических обозначений (например,

и ), основам теории доказательств (метод индукции, доказательство от противного и др.), дискретному распределению вероятностей и многому другому.2

Дополнительные ресурсы

Эта книга основана на онлайн-курсах, которые в настоящее время запущены в рамках проектов Coursera и Stanford Lagunita. Имеется также ряд ресурсов в помощь вам для повторения и закрепления опыта, который можно извлечь из онлайн-курсов.

Видео. Если вы больше настроены смотреть и слушать, чем читать, обратитесь к материалам с «Ютьюба», доступным на сайте www.algorithmsilluminated.org. Эти видео затрагивают все темы этой серии книг. Надеюсь, что они пропитаны тем же заразительным энтузиазмом в отношении алгоритмов, который, увы, невозможно полностью воспроизвести на печатной странице.

Тестовые задания. Как узнать, что вы действительно усваиваете понятия, представленные в этой книге? Тестовые задания с решениями и объяснениями разбросаны по всему тексту; когда вы сталкиваетесь с одним из них, призываю вас остановиться и подумать об ответе, прежде чем читать далее.

Задачи в конце главы. В конце каждой главы вы найдете несколько относительно простых вопросов для проверки усвоения материала (S), а затем более трудные и менее ограниченные по времени сложные задачи (H). Подсказки или решения всех этих задач, отмеченных соответственно знаками (H) и (S), приводятся в конце книги. Читатели могут взаимодействовать со мной и друг с другом по поводу оставшихся задач в конце главы через дискуссионный форум книги (см. ниже).

Задачи по программированию. В конце большинства глав предлагается реализовать программный проект, целью которого является закрепление детального понимания алгоритма путем создания его рабочей реализации. Наборы данных, а также тестовые примеры и их решения можно найти на www.algorithmsilluminated.org.

Форумы. Существенной причиной успеха онлайн-курсов являются реализованные через дискуссионные форумы возможности общения для слушателей. Это позволяет им помогать друг другу лучше понимать материал курса, а также отлаживать свои программы. Читатели этих книг имеют такую же возможность благодаря форумам, доступным на сайте www.algorithmsilluminated.org.

Благодарности

Эти книги не существовали бы без энтузиазма и интеллектуального голода тысяч участников моих курсов по алгоритмам на протяжении многих лет как на кампусе в Стэнфорде, так и на онлайновых платформах. Я особенно благодарен тем, кто предоставлял подробные отзывы на более ранний проект этой книги, среди них: Тоня Бласт, Юань Цао, Лесли Дэймон, Тайлер Дэ Девлин, Роман Гафитню, Бланка Хуэрго, Карлос Гуйя, Джим Хумельсин, Тим Кернс, Владимир Кокшенев, Байрам Кулиев, Клейтон Вонг, Лексин Йе и Даниэль Зингаро. Также благодарю нескольких экспертов, которые предоставили техническую консультацию: Амира Аббуда, Винсента Коницера, Кристиана Коницера, Авиада Рубинштайна и Илайю Сигала.

Я всегда ценю предложения и исправления от читателей. О них лучше всего сообщать через дискуссионные форумы, описанные выше.

Тим Рафгарден Нью-Йорк, штат Нью-Йорк. Апрель 2020

От издательства

Не удивляйтесь, что эта книга начинается с девятнадцатой главы. С одной стороны, она является четвертой частью курса «Совершенный алгоритм» Тима Рафгардена, а с другой — самостоятельным изданием, в котором рассматриваются вопросы NP-трудных задач. Приложения А, Б и В вы можете найти в книге «Совершенный алгоритм. Основы» (часть 1) и «Совершенный алгоритм. Графовые алгоритмы и структуры данных» (часть 2).

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция). Мы будем рады узнать ваше мнение! На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах.

---

19. Что такое NP-трудность?

Вводные книги по алгоритмам, включая предыдущие части этой серии книг, страдают от предвзятости отбора. Они сосредоточены на вычислительных задачах, которые поддаются решению умными быстрыми алгоритмами — в конце концов, что может быть лучше гениального алгоритмического пути напрямик? Хорошая новость: к таким задачам относятся многие фундаментальные и практически значимые задачи (сортировка, графовый поиск, кратчайшие пути, коды Хаффмана, минимальные остовные деревья, выравнивание рядов и т.д.). Но было бы нечестно обучать вас только одной коллекции задач, игнорируя призрак труднорешаемости,3 который появляется возле серьезных проектов. К сожалению, вы встретите много важных вычислительных задач, которые о быстрых алгоритмах не слышали и, по общему мнению специалистов, в ближайшее время не услышат.

Эта суровая реальность вызывает два вопроса. Во-первых, как распознать сложные задачи в своей работе и как на них реагировать, чтобы не тратить время на поиск несуществующего алгоритма? Во-вторых, когда такая задача важна для приложения, как пересмотреть конечные цели и какие алгоритмические инструменты применить для их достижения? Эта книга снабдит вас исчерпывающими ответами на оба вопроса.

19.1. Задача о минимальном остовном дереве и задача коммивояжера: алгоритмическая загадка

Трудные вычислительные задачи могут выглядеть как простые и чтобы различить их, требуется наметанный глаз. Сравните знакомую задачу о минимальном остовном дереве и ее более требовательную двоюродную сестру — задачу коммивояжера.

19.1.1. Задача о минимальном остовном дереве

Одной из известных вычислительных задач, поддающейся решению ослепительно быстрым алгоритмом, является задача о минимальном остовном дереве (MST, minimum spanning tree), рассмотренная в главе 15 Третьей части.4

Задача о минимальном остовном дереве

Вход: связный неориентированный граф G = (V, E) и вещественнозначная (real-valued) стоимость

для каждого ребра

.

Выход: остовное дерево

графа G с минимально возможной суммой реберных стоимостей.

Напомним, что граф G = (V, E) является связным, если для каждой пары

,

вершин граф содержит путь из

в

. Остовное дерево графа G есть подмножество

ребер, позволяющих подграфу (V, T) быть как связным, так и ациклическим. Например, в графе

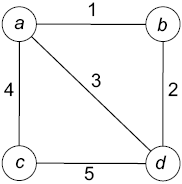
минимальное остовное дерево включает ребра (a; b), (b; d) и (a; c) при совокупной стоимости 7.

Граф может иметь экспоненциально растущее число остовных деревьев, поэтому исчерпывающий поиск возможен только для самых малых графов.5 Но задача о минимальном остовном дереве может быть решена умными быстрыми алгоритмами, такими как алгоритмы Прима и Краскала. Развернув надлежащие структуры данных (кучи и непересекающиеся (дизъюнктивные) множества соответственно), оба алгоритма получают очень быстрые реализации со временем выполнения O((m + n) log n), где m и n — это число ребер и вершин входного графа.

19.1.2. Задача коммивояжера

Другой широко известной задачей, отсутствующей в предыдущих частях, но занимающей видное место в этой книге, является задача коммивояжера (TSP, traveling salesman problem). От задачи о минимальном остовном дереве ее отличают туры — простые циклы, охватывающие все вершины, — которые играют роль остовных деревьев.

Задача: туры коммивояжера

Вход: полный неориентированный граф G = (V, E) и вещественнозначная стоимость ce для каждого ребра

.6

Выход: тур

графа G с минимально возможной суммой реберных стоимостей.

Формально тур — это цикл, который посещает каждую вершину ровно один раз (причем два ребра инцидентны для каждой вершины).

тестовое задание 19.1

Сколько отдельных туров

существует в экземпляре G = (V, E) задачи коммивояжера с

вершинами? (В приведенных ниже ответах

... обозначает факториальную функцию.)

а) 

б) 

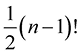
в) (n – 1)!

г) n!

(Ответ и анализ решения см. в разделе 19.1.4.)

Если все остальное не срабатывает, то задачу коммивояжера можно решить, исчерпывающе перечислив все туры (их конечное число) и запомнив наилучший из них. Попробуйте исчерпывающий поиск на небольшом примере.

тестовое задание 19.2

Какова минимальная сумма реберных стоимостей тура в следующем графе? (Каждое ребро помечено своей стоимостью.)

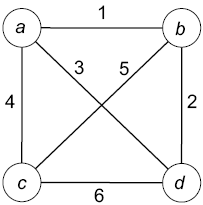
а) 12

б) 13

в) 14

г) 15

(Ответ и анализ решения см. в разделе 19.1.4.)

Задача коммивояжера может быть допустимо решена путем исчерпывающего поиска только для самых малых экземпляров. Можем ли мы добиться лучшего? Может ли существовать, по аналогии с задачей о минимальном остовном дереве, алгоритм, который волшебным образом находит самую дешевую иголку в экспоненциально растущем стоге сена туров коммивояжера? Несмотря на внешнее сходство формулировок этих двух задач, решение задачи коммивояжера представляется гораздо более трудным.

19.1.3. Безуспешные попытки решить задачу коммивояжера

Я мог бы рассказать дурацкую историю о коммивояжере, но не хочу вас запутать. Если увидите серию операций, расположенных в ряде, при том что стоимость или время выполнения операции зависит от предыдущей операции, — это замаскированная задача коммивояжера.

Например, операции могут представлять сборку автомобилей на заводе. Время сборки автомобиля равно сумме фиксированной стоимости сборки и стоимости настройки, которая зависит от разницы заводских конфигураций для этого и предыдущего автомобиля. Максимально быстрая сборка всех автомобилей сводится к минимизации суммы стоимостей настройки, что и составляет задачу коммивояжера.

Возьмем совершенно другое применение. Представьте кучу перекрывающихся фрагментов генома, которые нужно правдоподобно упорядочить. Имея в руках «меру правдоподобия», назначающую стоимость каждой паре фрагментов (например, производную от длины их наибольшей общей подстроки), вы можете свести задачу упорядочения к задаче коммивояжера.7

Соблазненные практическим применением и эстетической привлекательностью задачи коммивояжера, многие величайшие умы в области оптимизации чуть ли не с начала 1950-х годов старались решить ее крупномасштабные экземпляры.8 Но несмотря на десятилетия привлечения интеллектуальной мощи:

Факт

Известного быстрого алгоритма для задачи коммивояжера на момент написания этой книги не существует.

Что мы подразумеваем под быстрым алгоритмом? Еще в Первой части мы согласились с тем, что:

Быстрый алгоритм — это алгоритм, время выполнения которого в наихудшем случае растет медленно вместе с размером входа.

И что мы подразумеваем под «растет медленно»? Для большей части этой серии книг Святым Граалем были алгоритмы, работающие за линейное или почти линейное время. Забудьте о таких алгоритмах — никто не знает алгоритма для задачи коммивояжера, который всегда работает даже за время

на n-вершинных экземплярах или даже за время

.

Есть два конкурирующих объяснения этого мрачного состояния дел: либо быстрый алгоритм для задачи коммивояжера существует, но пока не найден, либо такого алгоритма нет. Большинство экспертов верят во второе.

Умозрительное заключение

Быстрого алгоритма для задачи коммивояжера не существует.

Еще в 1967 году Джек Эдмондс написал:

Я предполагаю, что хорошего алгоритма для задачи коммивояжера не существует. Мои доводы те же, что и для любого математического предположения: (1) это законная математическая возможность, и (2) я не знаю.9

К сожалению, проклятие труднорешаемости не ограничивается задачей коммивояжера. Вы увидите, что многие другие практически релевантные задачи тоже от него страдают.

19.1.4. Решения к тестовым заданиям 19.1–19.2

Решение к тестовому заданию 19.1

Правильный ответ: (б). Существует интуитивное соответствие между упорядочением вершин (которых существует n!) и турами (которые проходят по вершинам по одному разу в некотором порядке), поэтому напрашивается ответ (г). Однако это соответствие подсчитывает каждый тур 2n разными способами: по одному разу для каждого из n вариантов первой вершины и по одному разу для каждого из двух направлений прохождения тура. Таким образом, суммарное число туров равно

. Например, при n = 4 существует три четко различимых тура:

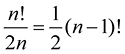
Решение к тестовому заданию 19.2

Правильный ответ: (б). Мы можем перечислить туры, начав с вершины а и пробуя все шесть возможных упорядочений других трех вершин, приняв, что тур заканчивается переходом из последней вершины обратно в а. (На самом деле это перечисление подсчитывает каждый тур дважды, по одному разу в каждом направлении.) Результаты:

Упорядочение вершин	Стоимость соответствующего тура
a, b, c, d или a, d, c, b	15
a, b, d, c или a, c, d, b	13
a, c, b, d или a, d, b, c	14

Самый короткий тур — второй с суммарной стоимостью 13.

19.2. Возможные уровни профессиональной компетенции

Одни вычислительные задачи проще, чем другие. Суть теории NP-трудности состоит в классификации задач — выделении легкорешаемых (подобных задаче о минимальном остовном дереве) и труднорешаемых (подобных задаче коммивояжера). Эта книга нацелена как на читателей, ищущих пособие начального уровня по этой теме, так и на тех, кто стремится к компетенции профессионального уровня. В этом разделе даются рекомендации, как подойти к остальной части книги в зависимости от ваших целей и ограни­чений.

Каковы ваши текущие и желаемые уровни профессиональной компетенции в распознавании и решении NP-трудных задач?10

Уровень 0: «Что такое NP-трудная задача?»

Это полное невежество — вы никогда не слышали об NP-трудности и не знаете, что многие практически релевантные вычислительные задачи считаются не поддающимися решению быстрым алгоритмом. Если я все сделал правильно, то эта книга будет доступной даже читателям уровня 0.

Уровень 1: «О, задача-то NP-трудная? Думаю, что мы должны либо переформулировать задачу (снизить поставленные нами цели), либо вложить больше ресурсов в ее решение».

Это осведомленность на уровне коктейльной вечеринки и, по меньшей мере, владение слухами об NP-трудности.11 Например, управляя своим софтверным проектом, используете ли вы алгоритмическую либо оптимизационную компоненты? Если да, то вам следует приобрести знания уровня 1 на случай, если один из членов вашей команды столкнется с NP-трудной задачей и захочет обсудить с вами возможные дальнейшие шаги. Для этого изучите разделы 19.3, 19.4 и 19.6.

Уровень 2: «О, задача-то NP-трудная? Дайте мне шанс применить мой алгоритмический опыт и посмотрим, насколько далеко я смогу зайти».

Разработчики ПО при достижении уровня 2 приобретают уверенность и богатый инструментарий для разработки практически полезных алгоритмов решения или аппроксимации NP-трудных задач. Серьезные программисты должны быть нацелены на этот уровень (или выше). К счастью, все алгоритмические парадигмы, которые мы развернули в предыдущих частях серии, также полезны для продвижения к NP-трудным задачам. Главы 20 и 21 приведут вас к уровню 2, в разделе 19.4 вы найдете обзор, а в главе 24 — исследование инструментария уровня 2 и его применение.

Уровень 3: «Расскажите поподробнее о задаче. [. . .внимательно слушает. . .] Мои соболезнования, она — NP-трудная».

Вы можете быстро распознавать NP-трудность: знаете несколько известных NP-трудных задач и можете доказать NP-трудность дополнительных задач. Эти навыки позволяют вам консультировать по алгоритмическим вопросам коллег, студентов или инженеров в промышленности. Глава 22 содержит курс молодого бойца для повышения вашего уровня до 3, а раздел 19.5 — обзор.

Уровень 4: «Давайте я вам объясню вот тут на доске предположение, что

».

Самый продвинутый уровень предназначен для начинающих теоретиков и тех, кто ищет строгого математического понимания NP-трудности и рассмотрения вопроса «P против NP». Если этот уровень вас не отпугивает, прочтите дополнительную главу 23.

19.3. «Легкие» и «трудные» задачи

Противопоставление «легкой» и «трудной» задач в теории NP-трудности простыми словами звучит так:

«легкая» может быть решена полиномиально-временным алгоритмом,

«трудная» в худшем случае требует экспоненциального времени.

Это краткое изложение NP-трудности упускает из виду несколько важных тонкостей (см. раздел 19.3.9). Но если через десять лет о смысле NP-трудности вы вспомните только эти несколько слов, то они будут самыми точными.

19.3.1. Полиномиально-временные алгоритмы

Чтобы перейти к определению «легкой» задачи, давайте вспомним время выполнения некоторых известных алгоритмов (из предыдущих частей серии):

Задача	Алгоритм	Время выполнения
Сортировка	MergeSort
Упорядочение сильно связных компонент	Kosaraju
Поиск кратчайшего пути	Dijkstra
Определение минимального остовного дерева	Kruskal
Выравнивание рядов	NW
Поиск кратчайшего пути для всех пар вершин	Floyd-Warshall

Точный смысл n и m зависит от конкретной задачи, но во всех случаях они связаны с размером входных данных.12 Согласно таблице, хотя время выполнения алгоритмов варьируется, все они зависят от размера входных данных в рамках полиномиальной функции. В общем случае:

Полиномиально-временные алгоритмы

Полиномиально-временной алгоритм — это алгоритм с временем выполнения, в наихудшем случае равным

, где n обозначает размер входных данных и d — это константа (независимая от n).

Все шесть алгоритмов являются полиномиально-временными (с достаточно малыми экспонентами d).13 Все ли естественные алгоритмы выполняются за полиномиальное время? Нет. Например, для многих задач исчерпывающий поиск выполняется за время, экспоненциально зависящее от размера входных данных (как указано во второй сноске к задаче о минимальном остовном дереве). В полиномиально-временных алгоритмах, которые мы ранее изучили, есть кое-что особенное.

19.3.2. Полиномиальное время против экспоненциального

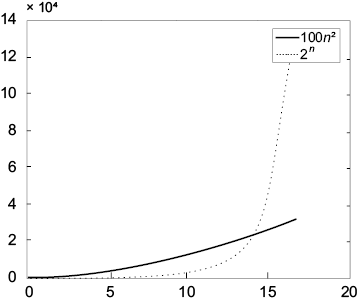
Не забывайте, что любая экспоненциальная функция в конечном счете растет намного быстрее любой полиномиальной функции. Между типичным полиномиальным и экспоненциальным временем выполнения существует огромная разница, даже для очень малых экземпляров. Рассмотрите график, на котором изображены полиномиальная функция 100 n2 и экспоненциальная функция 2n.

Закон Мура утверждает, что вычислительная мощность, доступная по данной цене, удваивается каждые 1–2 года. Означает ли это, что разница между полиномиально- и экспоненциально-временными алгоритмами со временем исчезнет? На самом деле наоборот! Вычислительные амбиции растут вместе с вычислительной мощностью, и с течением времени мы видим все более крупные размеры входных данных и страдаем от все более огромной пропасти между полиномиальным и экспоненциальным периодами выполнения.

Представьте фиксированный бюджет времени, например час или день. Как масштабируется поддающийся решению размер входных данных вместе с добавочной вычислительной мощностью? С полиномиально-временным алгоритмом он увеличивается на постоянный коэффициент (например, с 1 000 000 до 1 414 213) с каждым удвоением вычислительной мощности.14 С алгоритмом, который работает со временем, пропорциональным 2n, где n — это размер входных данных, каждое удвоение вычислительной мощности увеличивает поддающийся решению размер входных данных только на единицу (например, с 1 000 000 до 1 000 001)!

19.3.3. Легкорешаемые задачи

Теория NP-трудности определяет, что «легкие» задачи поддаются решению полиномиально-временным алгоритмом или, что эквивалентно, алгоритмом, для которого поддающийся решению размер входных данных (для фиксированного бюджета времени) масштабируется мультипликативно вместе с увеличением вычислительной мощности:15

Задачи, поддающиеся решению за полиномиальное время

Вычислительная задача поддается решению за полиномиальное время, если существует полиномиально-временной алгоритм, который решает ее правильно для каждого элемента входных данных.

Например, все шесть перечисленных задач поддаются решению за полиномиальное время.

Технически алгоритм (бесполезный на практике), который выполняется за время

на n-размерных входных данных, считается полиномиально-временным, и задача, решенная таким алгоритмом, квалифицируется как поддающаяся решению за полиномиальное время. Если перевернуть это утверждение, окажется, что если задача, такая как задача коммивояжера, не поддается решению за полиномиальное время, то не существует даже

-временного или

-временного алгоритма, который ее решит (!).

Смелость, определения и крайние случаи

Отождествление понятия «легкая» с понятием «поддающаяся решению за полиномиальное время» страдает несовершенством. Задача может быть решена в теории (с помощью алгоритма, который технически выполняется за полиномиальное время), но не в реальности (посредством эмпирически быстрого алгоритма), или наоборот. Любой, у кого хватит смелости написать точное математическое определение (например, полиномиально-временной решаемости), чтобы выразить беспорядочную концепцию реального мира (например, «легко решить посредством компьютера в физическом мире»), должен быть готов к трениям между двоичной природой определения и нечеткостью реальности. Определение неизбежно будет включать или исключать некоторые крайние случаи, которые хочется обойти, но это не повод игнорировать или отклонять хорошее определение. Полиномиально-временная решаемость эффективна16 в разделении задач на «легкие» и «трудные» на эмпирической основе. Имея за плечами полвека свидетельств, мы можем с уверенностью сказать, что естественные задачи, поддающие­ся решению за полиномиальное время, в типичной ситуации могут решаться практическими общецелевыми алгоритмами и что задачи, считающиеся не поддающимися решению за полиномиальное время, в типичной ситуации требуют значительно больше работы и компетенции в предметной области.

19.3.4. Относительная труднорешаемость

Предположим, вы заподозрили, что задача, такая как задача коммивояжера, «не является легкой», имея в виду, что она не поддается решению любым полиномиально-временным алгоритмом (независимо от того, насколько крупным является полином). Как это доказать? Самым убедительным аргументом, конечно, будет герметичное математическое доказательство. Но статус задачи коммивояжера остается в подвешенном состоянии: никто не нашел полиномиально-временного алгоритма, который ее решает, или доказательства, что такого алгоритма не существует.

Как развить теорию, которая с пользой дифференцирует «легкие» и «трудные» задачи при нашем недостаточном понимании всех возможностей алгоритмов? Блестящая идея теории NP-трудности состоит в классификации задач на основе их относительной (а не абсолютной) трудности и объявления задачи «трудной», если она «по меньшей мере так же трудна, как» подавляющее число других нерешенных задач.

19.3.5. Трудные задачи

Безуспешные попытки решить задачу коммивояжера (раздел 19.1.3) дают косвенные свидетельства, что эта задача, возможно, не решается за полиномиальное время.

Слабые доказательства трудности

Полиномиально-временной алгоритм решил бы задачу коммивояжера, которая сопротивлялась усилиям сотен (если не тысяч) умов на протяжении десятилетий.

Есть ли более убедительный аргумент? Основная идея NP-трудности состоит в том, чтобы показать, что такая задача, как задача коммивояжера, по меньшей мере так же трудна, как и огромное количество нерешенных задач из множества различных научных областей. По сути, в этих задачах легко распознаются решения, стоит только вам понять задачу. А значит, гипотетический полиномиально-временной алгоритм для задачи коммивояжера автоматически будет решать и остальные нерешенные задачи!

Сильные доказательства трудности

Полиномиально-временной алгоритм для задачи коммивояжера позволил бы решить тысячи задач, которые на протяжении десятилетий противостояли усилиям десятков (если не сотен)тысяч умов.

В сущности, теория NP-трудности показывает, что тысячи вычислительных задач являются замаскированными вариантами одной и той же задачи, и полиномиально-временной алгоритм для одной из NP-трудных задач решит все остальные.17

Мы называем задачу NP-трудной, если есть веские свидетельства труднорешаемости в указанном выше смысле:

NP-трудность (главная идея)

Задача является NP-трудной, если она по меньшей мере так же трудна, как и любая задача, решения которой вы легко распо­знáете, если поймете ее суть.

Эта идея будет полностью подтверждена в разделе 23.3.4. А пока мы поработаем с предварительным определением NP-трудности в терминах широко известного математического предположения, что

.

19.3.6. Предположение, что P

NP

Возможно, вы слышали о предположении, что

. Что оно собой представляет? Раздел 23.4 содержит его точную математическую формулировку, но на данный момент мы остановимся на неформальной версии, которая звучит как девиз при проверке домашнего задания:

Предположение, что P ≠ NP (неформальная версия)

Проверить предполагаемое решение задачи точно проще, чем создать собственное решение с нуля.

Здесь P и NP относятся соответственно к задачам, которые могут быть решены с нуля за полиномиальное время, и к тем задачам, решения которых могут быть проверены за полиномиальное время (формальные определения P и NP в главе 23).

Конечно, проверка предложенного кем-то решения судоку или кенкен выглядит проще самостоятельного разбора головоломки. Как и легко проверить, что предложенный кем-то тур коммивояжера является хорошим (с суммарной стоимостью, скажем, не более 1000), просуммировав стоимости его ребер. Не ясно, как быстро можно придумать такой тур с нуля. Поэтому пояснение ниже настаивает: предположение, что

, является истинным.18, 19

19.3.7. Предварительное определение NP-трудности

Условно мы будем называть задачу NP-трудной, если, исходя из допущения об истинности неравенства

, она не может быть решена никаким полиномиально-временным алгоритмом.

NP-трудная задача (предварительное определение)

Вычислительная задача является NP-трудной, если полиномиально-временной алгоритм, ее решающий, опровергает предположение, что

.

Таким образом, рабочий полиномиально-временной алгоритм для NP-трудной задачи подразумевает ложность предположения, что

. Полиномиально-временной алгоритм для каждой отдельной задачи, решения для которой могут быть распознаны за полиномиальное время, — это чрезмерная алгоритмическая щедрость. Вероятно, если предположение, что является истинным, то никакая NP-трудная задача не решится за полиномиальное время, даже алгоритмом, работающим за

- или

-е время на n-размерных входных данных.

19.3.8. Рандомизированные и квантовые алгоритмы

Наше определение решаемости за полиномиальное время на с. 31 рассматривает только детерминированные алгоритмы. Как известно, рандомизация бывает мощным инструментом проектирования алгоритмов (например, таких как QuickSort). Могут ли рандомизированные алгоритмы избежать пут NP-трудности?

И как насчет хваленых разрекламированных квантовых алгоритмов? (Ведь рандомизированные алгоритмы можно рассматривать как частный случай квантовых алгоритмов.) Следует признать, что крупномасштабные общецелевые квантовые компьютеры (если бы они были реализованы) изменили бы правила игры для нескольких задач, включая чрезвычайно важную задачу факторизации крупных целых чисел. Однако задача факторизации не признана NP-трудной, и эксперты предполагают, что даже квантовые компьютеры не способны решать NP-трудные задачи за полиномиальное время. Проблемы, связанные с NP-трудностью, в ближайшее время не исчезнут.20

19.3.9. Тонкости

Сверхупрощенное обсуждение на с. 28 наводит на мысль, что решение «трудной» задачи требует экспоненциального времени в худшем случае. Но определение из раздела 19.3.7 говорит нечто другое: NP-трудную задачу при

невозможно решить никаким полиномиально-временным алгоритмом.

Первое расхождение между этими определениями в том, что NP-трудность исключает полиномиально-временную решаемость только в том случае, когда предположение, что

, является истинным. Но вопрос его истинности остается открытым.

Второе несоответствие в том, что даже в случае истинности предположения, что

, для решения NP-трудной задачи в худшем случае требуется сверхполиномиальное (не экспоненциальное) время.21 Однако эксперты полагают, что для большинства естественных NP-трудных задач, включая задачи из этой книги, действительно требуется экспоненциальное время в худшем случае. Это убеждение формализуется «гипотезой об экспоненциальном времени», более сильной формой предположения, что (раздел 23.5).22

Наконец, несмотря на то что 99 % задач, с которыми вы столкнетесь, будут либо «легкими» (поддающимися решению за полиномиальное время), либо «трудными» (NP-трудными), несколько редких примеров окажутся посередине. То есть распределение на две группы охватывает большинство, но не все практически релевантные вычислительные задачи.23

19.4. Алгоритмические стратегии для NP-трудных задач

Предположим, вы определили задачу, от решения которой зависит успех проекта. Возможно, вы несколько недель, почти швыряясь посудой, пробовали все известные вам парадигмы проектирования алгоритмов, каждую структуру данных из книги, все бесплатные примитивы, но ничего не работало. Наконец, вы поняли, что проблема не в недостатке вашей изобретательности, а в том, что задача — NP-трудная. Вам стало легче, но это не умалило значимости задачи для проекта. Что делать?

19.4.1. Универсальный, правильный, быстрый (выбрать два)

Плохая новость: NP-трудные задачи распространены повсеместно. Прямо сейчас одна из них может скрываться в вашем последнем проекте. Хорошая новость: NP-трудность — не смертный приговор. Часто (но не всегда) такие задачи могут быть решены на практике по меньшей мере приближенно путем достаточного вложения ресурсов и алгоритмической изощренности.

NP-трудность бросает вызов разработчику алгоритмов и сообщает ему, чего ждать. Не надейтесь получить общецелевой и всегда быстрый алгоритм для NP-трудной задачи сродни тем, которые используются для сортировки, поиска кратчайшего пути или выравнивания рядов. Если вам не повезет столкнуться с необычно малыми или хорошо структурированными входными данными, придется потрудиться над решением NP-трудной задачи и, возможно, пойти на некоторые компромиссы.

Какого рода компромиссы? NP-трудность исключает алгоритмы, имеющие ­одновременно три свойства (исходя из предположения о том, что

):

Три свойства (одним из них нужно пожертвовать)

1. Универсальный. Алгоритм учитывает все возможные входы вычислительной задачи.

2. Правильный. Для каждого входа алгоритм решает задачу правильно.

3. Быстрый. Для каждого входа алгоритм выполняется за полиномиальное время.

Вы можете выбрать один компромисс: в отношении универсальности, правильности или скорости. Все три стратегии полезны и распространены на практике.

Остальная часть раздела посвящена этим стратегиям. Главы 20 и 21 подробно освещают последние две. Как всегда, обращаем внимание на принципы проектирования мощных и гибких алгоритмов для широкого круга задач. Вооружитесь этими принципами и применяйте их в соответствии с предметной областью задачи.

19.4.2. Компромисс в отношении универсальности

Одна из стратегий достижения прогресса в решении NP-трудной задачи — в отказе от универсальных алгоритмов и сосредоточении на частных случаях задачи, имеющих отношение к проекту. В лучшем случае это позволит определить специфические для предметной области ограничения на входные данные и разработать алгоритм, который всегда будет правильным и быстрым на этом подмножестве входных данных. Выпускники курса молодого бойца по динамическому программированию в Третьей части уже видели два примера этой стратегии.

Задача о взвешенном независимом множестве. На вход подается неориентированный граф G = (V, E) и неотрицательный вес

для каждой вершины

. Цель состоит в вычислении независимого множества

с максимально возможной суммой вершинных весов, где независимое множество — это подмножество

взаимно несмежных вершин (где для каждого

, а

). Например, если ребра представляют конфликты (между людьми, курсами и т.д.), то независимые множества соответствуют бесконфликтным подмножествам. Эта задача является NP-трудной в общем случае (раздел 22.5). Частный случай задачи, в которой G является путевым графом (с вершинами

,

, …,

и ребрами (

,

), (

,

), …, (

,

)), решается за линейное время алгоритмом динамического программирования, который можно расширить за счет размещения всех ациклических графов (см. задачу 16.3 Третьей части).

Задача о рюкзаке. Входные данные задаются 2n + 1 положительными целыми числами: n значениями

,

, …,

предметов, n размерами

,

, …,

предметов и вместимостью C рюкзака. Цель состоит в вычислении подмножества

предметов с максимально возможной суммой значений, при условии наличия суммарного размера , не превышающего C. Другими словами, цель заключается в использовании дефицитного ресурса самым ценным путем.24 Эта задача является NP-трудной, как мы увидим в разделе 22.8 и задаче 22.7. Для нее существует

-временной алгоритм динамического программирования, который является полиномиально-временным в частном случае, когда C ограничена полиномиальной функцией от n.

Полиномиально-временной алгоритм для рюкзака?

Почему

-временной алгоритм для задачи о рюкзаке не опровергает предположение, что ? Потому что это не полиномиально-временной алгоритм. Размер входных данных — число нажатий клавиш, необходимых для ввода этих данных, — масштабируется вместе с количеством цифр в числе, а не с величиной числа. Чтобы передать число «1 000 000», не требуется миллион нажатий клавиш — всего 7 (либо 20, если вы работаете с основанием 2). Например, в экземпляре с n предметами, вместимостью рюкзака 2n и всеми значениями и размерами предметов не более 2n размер входных данных равен

числам с

цифрами каждое, тогда как время выполнения алгоритма динамического программирования экспоненциально более продолжительно (пропорционально n × 2n).

Алгоритмическая стратегия разработки быстрых и правильных алгоритмов (для частных случаев) использует весь алгоритмический инструментарий предыдущих частей. По этой причине ни одна глава этой книги не посвящена данной стратегии. Однако по пути мы столкнемся с примерами частных случаев NP-трудных задач, поддающихся решению за полиномиальное время, включая задачи коммивояжера, выполнимости (булевых формул) и раскраски графов (задачи 19.8 и 21.12).

19.4.3. Компромисс в отношении правильности

Вторая алгоритмическая стратегия, особенно популярная в критичных по времени приложениях, заключается в отказе от правильности. Алгоритмы, которые не всегда являются правильными, иногда называются эвристическими алгоритмами.25

В идеале эвристический алгоритм является «в основном правильным». Это соответствует одному из двух или сразу обоим утверждениям:

Ослабление правильности

1. Алгоритм является правильным на «большинстве» входных данных.26

2. Алгоритм является «почти правильным» на каждом элементе входных данных.

Второе свойство легче всего интерпретировать для задач оптимизации, где вычисляется допустимое решение (например, тур коммивояжера) с наилучшим значением целевой функции (например, минимальной суммарной стоимостью). «Почти правильный» здесь означает, что алгоритм выводит допустимое решение со значением целевой функции, близким к наилучшему из возможных, как тур коммивояжера с суммарной стоимостью ненамного большей, чем у оптимального тура.

Ваш алгоритмический инструментарий для разработки быстрых точных алгоритмов будет полезен и для создания эвристических алгоритмов. В разделах 20.1–20.3 описаны жадные эвристики (для задач от планирования до максимизации влияния в социальных сетях) с доказательствами «приближенной правильности», гарантирующими, что для каждого входа значение целевой функции на выходе находится в пределах скромного постоянного коэффициента ее наилучшего возможного значения.27

Разделы 20.4–20.5 дополнят ваш инструментарий парадигмой проектирования алгоритмов локального поиска. Локальный поиск и его обобщения эффективны на практике при решении многих NP-трудных задач, хотя он редко гарантирует приближенную правильность.

19.4.4. Компромисс в отношении скорости

Заключительная стратегия подходит для приложений, в которых недопустим компромисс в отношении правильности. Каждый правильный алгоритм для NP-трудной задачи должен выполняться за сверхполиномиальное время на некоторых входах (если

). Следовательно, нужен алгоритм, который будет как минимум максимально быстрым, чтобы превзойти исчерпывающий поиск. Это соответствует одному из двух или сразу обоим утверждениям:

Ослабление полиномиального времени выполнения

1. Алгоритм обычно выполняется быстро (например, за полиномиальное время) на входных данных, релевантных для приложения.

2. Алгоритм работает быстрее, чем исчерпывающий поиск на каждом элементе входных данных.

Во втором случае мы все еще ждем, что на некоторых входах алгоритм будет выполняться за экспоненциальное время — в конце концов, задача является NP-трудной. Раздел 21.1 задействует динамическое программирование, чтобы превзойти исчерпывающий поиск для задачи коммивояжера, сократив время выполнения с

до

, где n — это число вершин. Раздел 21.2 совмещает рандомизацию с динамическим программированием, одерживая верх над исчерпывающим поиском для задачи отыскания длинных путей в графах (с временем выполнения

, а не

, где n и m обозначают числа вершин и ребер во входном графе, k — длину целевого пути, и e = 2,718…).

Достижение прогресса на относительно крупных экземплярах NP-трудных задач в типичной ситуации требует дополнительных инструментов, которые не гарантируют победу над скоростью исчерпывающего поиска, но во многих приложениях показали свою эффективность. Разделы 21.3–21.5 описывают многолетний опыт экспертов в разработке мощных решателей для задач смешанного целочисленного программирования (MIP, mixed integer programming) и задач выполнимости булевых формул (SAT, satisfiability). Многие NP-трудные задачи оптимизации (такие как задача коммивояжера) могут быть закодированы как задачи MIP, а задачи о проверке допустимости (такие как проверка бесконфликтного закрепления учебных занятий за учебными аудиториями) легко выражаются как задачи SAT. Конечно, нет гарантии, что решатель задач MIP или SAT решит ваш конкретный экземпляр за разумное время, но для решения NP-трудных задач на практике сегодня ничего лучше вы не найдете.

19.4.5. Ключевые выводы

Если вы нацелены на получение знаний о NP-трудности уровня 1 (раздел 19.2), то самые важные вещи, которые нужно запомнить, таковы:

Три факта об NP-трудных задачах

1. Повсеместность: практически релевантные NP-трудные задачи есть везде.

2. Труднорешаемость: согласно широко распространенному математическому предположению, ни одна NP-трудная задача не может быть решена любым алгоритмом, который всегда является правильным и всегда выполняется за полиномиальное время.

3. Не смертельный приговор: NP-трудные задачи часто (но не всегда) можно решить на практике, по меньшей мере приближенно, путем достаточного вложения ресурсов и алгоритмической изощренности.

19.5. Доказательство NP-трудности: простой рецепт

Как распознать NP-трудную задачу, чтобы скорректировать конечные цели и отказаться от поиска алгоритма, который якобы будет универсальным, правильным и быстрым? Никто не выиграет, если вы будете тратить недели или месяцы на попытки опровергнуть предположение, что

.

Во-первых, имейте под рукой коллекцию простых и распространенных NP-трудных задач (например, 19 задач в главе 22, рис. 22.1) — в самом простом сценарии ваше приложение сводится к одной из них. Во-вторых, оттачивайте умение сводить одну вычислительную задачу к другой. Такая редукция распространит легкорешаемость от второй задачи к первой. Причем труднорешаемость тоже распространится от первой задачи ко второй, поэтому, чтобы показать, что интересующая вас задача является NP-трудной, нужно лишь свести к ней известную NP-трудную задачу.

Остальная часть этого раздела посвящена данной теме и дает один простой пример (подробнее в главе 22).

19.5.1. Редукции

Любая задача B, которая является по меньшей мере такой же трудной, как и NP-трудная задача A, сама по себе является NP-трудной. Фраза «по меньшей мере такой же трудной, как» может быть формализована с помощью редукций.

Редукции

Задача Асводится к задаче В, если алгоритм, решающий задачу В, может быть легко переведен в алгоритм, решающий задачу А (рис. 19.1).

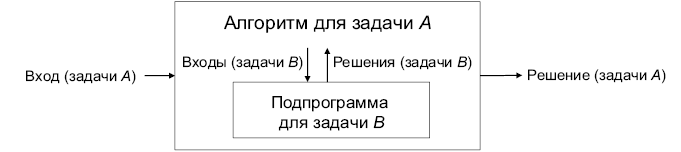
Рис. 19.1. Если задача А сводится к задаче В, то задача А может быть решена с помощью полиномиального (по входному размеру) числа вызовов подпрограммы для В и полиномиального объема дополнительной работы

В контексте NP-трудности словосочетание «легко перевести» означает, что задача А может быть решена за не более чем полиномиальное (по размеру входных данных) число вызовов подпрограммы, решающей задачу В, вместе с полиномиальным объемом дополнительной работы (за пределами вызовов подпрограммы).

19.5.2. Использование упрощений для разработки быстрых алгоритмов

Опытные разработчики алгоритмов всегда ищут редукции, или упрощения, — зачем решать задачу с нуля, если это необязательно? Примеры из предыдущих частей, относящиеся к задачам из раздела 19.3.1, включают:

Знакомые примеры упрощений

1. Поиск медианы кучи целых чисел сводится к сортировке кучи. (После сортировки кучи вернуть срединный элемент.)

2. Поиск кратчайшего пути для всех пар вершин сводится к поиску кратчайшего пути с одним истоком. (Вызвать одноистоковый алгоритм кратчайшего пути один раз с каждым возможным вариантом выбора стартовой вершины во входном графе.)

3. Поиск наибольшей общей подпоследовательности сводится к выравниванию рядов. (Вызвать алгоритм выравнивания рядов с двумя входными строками, штрафом 1 за вставляемый пробел (зазор) и очень большим штрафом за каждое несовпадение двух разных символов.)28

Эти упрощения принимают светлую сторону силы и служат почетной миссии создания новых быстрых алгоритмов из старых, тем самым расширяя границу легкорешаемости. Например, первое упрощение преобразовывает алгоритм MergeSort в O (n log n)-временной алгоритм поиска медианы или, выражаясь шире, превращает любой T (n)-временной алгоритм сортировки в O (T(n))-временной алгоритм поиска медианы, где n — это длина кучи. Второе — преобразовывает любой T (m, n)-временной алгоритм для поиска кратчайшего пути с одним истоком в O (n × T (m, n))-временной алгоритм для поиска кратчайшего пути для всех пар вершин, где m и n обозначают соответственно число ребер и вершин. Третье — превращает T (m, n)-временной алгоритм для выравнивания рядов в O (T (m, n))-временной алгоритм для нахождения наибольшей общей подпоследовательности, где m и n обозначают длины двух входных строк.

Тестовое задание 19.3

Предположим, что задача A может быть решена вызовом подпрограммы для задачи B не более T1(n) раз и выполнением не более T2(n)-й дополнительной работы (вне вызовов подпрограммы), где n обозначает размер входных данных. При наличии подпрограммы, решающей задачу B за время не более T3(n) на n-размерных входных данных, сколько времени нужно для решения задачи A? (Выберите самое сильное истинное утверждение. Считайте, что программа использует по меньшей мере s примитивных операций для построения s-размерных входных данных, чтобы вызвать подпрограмму.)

а) T1(n) + T2(n) + T3(n)

б) T1(n) × T2(n) + T3(n)

в) T1(n) × T3(n) + T2(n)

г) T1(n) × T3(T2(n)) + T2(n)

(Ответ и анализ решения см. в разделе 19.5.5.)

Тестовое задание 19.3 показывает, что при сведении задачи А к задаче В любой полиномиально-временной алгоритм для В может быть переведен в алгоритм для А.29

Упрощения способствуют легкорешаемости

Если задача А сводится к задаче В и В может быть решена полиномиально-временным алгоритмом, то А тоже может быть решена полиномиально-временным алгоритмом (рис. 19.2).

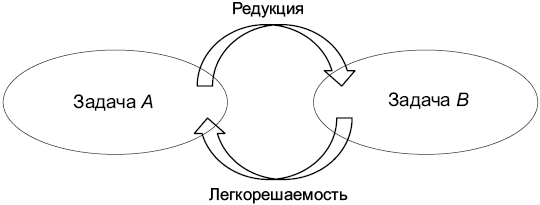
Рис. 19.2. Распространение легкорешаемости от B к А: если задача А сводится к задаче B и B — легкорешаемая задача, то А — тоже легкорешаемая

19.5.3. Использование упрощений для распространения NP-трудности

Теория NP-трудности следует темной стороне силы, часто используя редукции для распространения проклятия труднорешаемости (в противоположность рис. 19.2). Давайте перевернем предыдущее утверждение. Предположим, что задача A сводится к задаче B. Если A является NP-трудной, то полиномиально-временной алгоритм для нее опровергнет предположение, что P ≠ NP. Так вот. Полиномиально-временной алгоритм для B автомати­чески будет приводить к алгоритму для A (потому что A сводится к B) и тоже опровергнет предположение, что P ≠ NP. Это значит, что B тоже NP-трудная!

Упрощения способствуют труднорешаемости

Если задача А сводится к задаче B и является NP-трудной, то B тоже является NP-трудной (рис. 19.3).

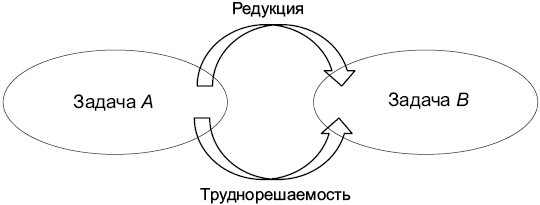
Рис. 19.3. Распространение труднорешаемости в от А к B: если задача А сводится к задаче B и А — труднорешаемая задача, то и B — тоже труднорешаемая

Вот удивительно простой двухшаговый рецепт доказательства NP-труд­ности:

Как доказать, что задача является NP-трудной

Чтобы доказать, что задача B NP-трудная, нужно:

1. Выбрать NP-трудную задачу A.

2. Доказать, что A сводится к B.

Выполнение первого шага требует знания известных NP-трудных задач (см. главу 22). Второй шаг основан на ваших навыках поиска редукций между задачами (снова см. главу 22). Давайте поймем суть этого рецепта и вернемся к задаче о кратчайшем пути с одним истоком, где разрешены отрицательные длины ребер.

19.5.4. NP-трудность бесцикловых кратчайших путей

В задаче о кратчайшем пути с одним истоком входные данные состоят из ориентированного графа G = (V, E), вещественнозначной длины

для каждого ребра

и стартовой вершины

. Длина пути — это сумма длин его ребер. Цель — вычислить для каждой возможной финальной вершины

минимальную длину dist(s,

) ориентированного пути в G из s в

. (Если такого пути не существует, то dist(s,

) определяется как .) Важно отметить, что допускаются отрицательные длины ребер.30, 31 Например, расстояния кратчайшего пути из s в графе

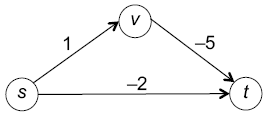
таковы: dist(s, s) = 0, dist(s,

) = 1 и dist(s, t) = −4.

Отрицательные циклы

Как определить расстояния кратчайшего пути в графе, подобном приведенному ниже?

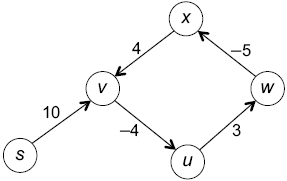
Этот граф имеет отрицательный цикл — ориентированный цикл с отрицательной суммой длин ребер. В нем есть s-

-вершинный путь длиной 10 с одним переходом. Прикрепив циклический обход в конец, мы получим s-

-вершинный путь суммарной длины 8 с пятью переходами. Добавление второго обхода уменьшит совокупную длину до 6 и так далее. Допустив пути с циклами, мы получим граф, не имеющий кратчайшего s-