Переводчик Е. Матвеев

 

Брэдфорд Такфилд

Алгоритмы неформально. Инструкция для начинающих питонистов. — СПб.: Питер, 2022.

 

ISBN 978-5-4461-1919-6

© ООО Издательство "Питер", 2022

 

Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

 

Посвящается моим родителям Дэвиду и Бекки Такфилд, которые когда-то поверили в меня и научили играть в «Точки и квадраты»

Об авторе

Брэдфорд Такфилд (Bradford Tuckfield) — специалист по теории данных и писатель. Руководит фирмой Kmbara (https://kmbara.com/), занимающейся консультациями в области теории данных, а также ведет литературный сайт Dreamtigers (http://thedreamtigers.com/).

О научном редакторе

Алок Малик (Alok Malik) — специалист по теории данных из Нью-Дели (Индия). Занимается созданием моделей глубокого обучения в областях обработки естественного языка и распознавания изображений на Python. Малик разрабатывал такие решения, как языковые модели, классификаторы изображений и текста, системы перевода, модели преобразования речи в текст, системы распознавания именованных сущностей и детекторы объектов. Кроме того, он участвовал в написании книги о машинном обучении. В свободное время любит читать о финансах, преподает на курсах дистанционного обучения и играет на приставке.

Благодарности

«Одно и то же слово по-разному звучит у разных писателей. Один выдирает его из своего нутра. Другой вынимает его из кармана пальто». Так Шарль Пеги (Charles Peguy) сказал о написании отдельных слов. То же относится к главам и целым книгам. В одних случаях мне казалось, что я вынимал эту книгу из кармана пальто. В других все выглядело так, словно я выдирал ее из своего нутра. Будет уместно поблагодарить всех, кто внес свой вклад в этот долгий процесс — либо одалживая мне пальто, либо помогая мне залечить нутро.

Многие хорошие люди помогали мне на долгом пути, который я прошел, чтобы получить опыт и квалификацию, необходимые для написания книги. Мои родители Дэвид и Бекки Такфилд преподнесли мне множество бесценных даров, начиная с жизни и образования, и продолжали верить и вдохновлять меня, а также помогать мне в других отношениях — слишком многочисленных, чтобы я мог их здесь перечислить. Скотт Робертсон (Scott Robertson) дал мне первую работу по написанию кода, хотя моей квалификации было явно недостаточно. Рэнди Дженсон (Randy Jenson) принял меня на первую работу, связанную с теорией данных, — и снова несмотря на мою неопытность и ограниченный опыт. Кумар Кашьяп (Kumar Kashyap) предоставил мне первую возможность руководить группой разработки для реализации алгоритмов. Дэвид Зу (David Zou) стал первым человеком, заплатившим мне за написание статьи (десять долларов за вычетом процента PayPal за десять коротких обзоров фильмов), и это было настолько прекрасно, что я решил более плотно заняться писательской работой. Адитья Дейт (Aditya Date) был первым, кто предложил мне написать книгу и предоставил первую возможность для этого.

Меня также вдохновляли многие учителя и наставники. Дэвид Кардон (David Cardon) предоставил первую возможность участвовать в академических исследованиях и многому научил в процессе работы. Брайан Скелтон (Bryan Skelton) и Леонард Ву (Leonard Woo) стали для меня примерами тех, на кого я бы хотел быть похожим, когда вырасту. Уэс Хатчинсон (Wes Hutchinson) научил важнейшим алгоритмам (таким как кластеризация методом k-средних) и помог лучше понять их работу. Чед Эммет (Chad Emmett) научил думать об истории и культуре, я посвятил ему главу 2. Ури Саймонсон (Uri Simonsohn) показал, как следует подходить к анализу данных.

Некоторые люди помогли мне превратить написание книги в приятное занятие. Сешу Эдала (Seshu Edala) помог отрегулировать мой рабочий график, чтобы высвободить время для работы над книгой, и постоянно подбадривал меня. С Алексом Фридом (Alex Freed) было очень приятно работать на протяжении всего процесса редактирования. Дженнифер Игар (Jennifer Eagar) неофициально стала первым человеком, купившим экземпляр книги за несколько месяцев до ее выхода; это помогало мне в трудные времена. Хланг Хланг Тун (Hlaing Hlaing Tun) была всегда готова поддержать и помочь, оставалась милой и доброжелательной на каждом этапе.

Я не могу вернуть весь долг благодарности, но, по крайней мере, могу сказать спасибо всем, кто мне помогал. Спасибо!

Введение

Алгоритмы встречаются повсюду. Вероятно, вы уже выполнили сегодня как минимум несколько алгоритмов. В книге вы прочтете о десятках алгоритмов: простых и сложных, знаменитых и малоизвестных — но все они интересны и заслуживают вашего внимания. Первый алгоритм в книге также оказывается самым вкусным — он описывает процесс приготовления парфе с гранолой и ягодами; данный алгоритм полностью приведен на рис. 1. Возможно, вы привыкли называть алгоритмы такого типа «рецептами», но он соответствует определению алгоритма у Дональда Кнута: конечный набор правил, определяющий последовательность операций для решения конкретного типа задач.

 

Рис. 1. Алгоритм: конечный набор правил, определяющий последовательность операций для решения конкретного типа задач

Приготовление десертов — не единственная область жизни, управляемая алгоритмами. Ежегодно правительство США требует, чтобы каждый взрослый гражданин выполнял определенный алгоритм, и старается посадить в тюрьму тех, кто делает это неправильно. В 2017 году миллионы американцев выполнили свой долг, завершив алгоритм, показанный на рис. 2, который был взят из формы 1040-EZ.

 

Рис. 2. Инструкции по заполнению налоговой декларации соответствуют определению алгоритма

Что общего у налогов и ягодного десерта? Налоги нужно обязательно платить, они выражаются в числовом виде, рассчитываются по сложным формулам, и люди их обычно терпеть не могут. Десерты встречаются не так часто, являются произведением искусства, и их все обожают. Единственное, что у них есть общего, — при подготовке и того и другого используются алгоритмы.

Великий ученый в области вычислительной теории Дональд Кнут замечал, что термин «алгоритмы» почти синонимичен терминам «рецепт»,«процедура» и «рутина». При декларировании налогов с использованием формы 1040-EZ выполняются 12 шагов (конечный список), определяющих операции (такие как сложение на шаге 4 и вычитание на шаге 6) для решения конкретной задачи: стремления избежать тюремного заключения за уклонение от уплаты налогов. Для приготовления парфе нужны шесть шагов, определяющих операции (такие как добавление ягод на шаге 1 и выкладывание йогурта на шаге 2) для решения конкретной задачи: желания отведать десерт.

Когда вы больше узнаете об алгоритмах, вы начнете видеть их повсеместно и оцените, насколько впечатляющими они могут быть. В главе 1 мы обсудим выдающуюся человеческую способность ловить мяч и ознакомимся с подробностями алгоритма из области подсознания, который позволяет нам это делать. Позднее рассмотрим алгоритмы отладки кода, максимизации доходов, сортировки списков, планирования задач, правки текста, доставки почты и победы в таких играх, как шахматы или судоку. Попутно вы научитесь оценивать алгоритмы по нескольким атрибутам, которые, по мнению профессионалов, важны для алгоритмов. Со временем вы сможете в совершенстве овладеть искусством создания алгоритмов, которое открывает перспективу для творческого подхода и проявления личных качеств в точной и формальной области.

Для кого написана эта книга

В книге доступным языком описываются различные алгоритмы, при этом они сопровождаются кодом на Python. Чтобы извлечь из нее максимум пользы, вам понадобится некоторый опыт в областях, перечисленных ниже.

• Программирование. Все значимые примеры в книге поясняются с помощью кода Python. Я постарался предоставить подробный анализ и объяснения для каждого фрагмента кода, чтобы книга была понятной для читателя, не имеющего опыта программирования на Python и значительного опыта программирования вообще. Тем не менее читатель, обладающий хотя бы базовым пониманием основных концепций программирования — присваивания значений переменным, циклов for, команд if/then и вызовов функций, — будет лучше подготовлен к усвоению материала.

• Школьный курс математики. Алгоритмы часто используются для достижения тех же целей, для которых служат и математические конструкции: решение уравнений, оптимизация и вычисление значений. В алгоритмах также применяются многие принципы, связанные с математическим мышлением, например необходимость использования точных определений. Иногда в своих рассуждениях мы заходим на математическую территорию, включая алгебру, теорему Пифагора, число пи и основы математического анализа. Я постарался избежать хитроумных рассуждений и ограничиться рамками школьного курса математики.

Каждый, кто уверенно чувствует себя в указанных областях, сможет легко усвоить весь материал книги. Она была написана для нескольких групп читателей.

• Учащиеся. Книга подходит для изучения вводного курса алгоритмов, информатики или программирования уровня средней или высшей школы.

• Профессионалы. Практикующие специалисты тоже смогут узнать много полезного из книги. Это и программисты, желающие освоить Python, и разработчики, которые хотят расширить свои знания в области основ информатики и улучшить код за счет алгоритмического мышления.

• Энтузиасты-любители. Они составляют настоящую целевую аудиторию книги. Алгоритмы затрагивают практически каждую часть нашей жизни, поэтому каждый читатель сможет найти в издании что-то интересное, расширяющее границы восприятия окружающего мира.

О книге

В книге не рассматриваются все аспекты всех известных алгоритмов; это лишь вводный курс. Прочитав ее, вы будете четко понимать, что такое алгоритм, как писать код для реализации важных алгоритмов, и оценивать и оптимизировать эффективность алгоритмов. Вы также познакомитесь со многими популярными алгоритмами, которыми пользуются профессионалы. Ниже представлена структура издания.

• В главе 1 «Алгоритмы при решении задач» мы обсудим, как ловим мяч, поищем доказательства существования подсознательного алгоритма, управляющего человеческим поведением, и выясним, как это может нам помочь в практической реализации алгоритмов и их разработке.

• В главе 2 «Алгоритмы в истории» мы совершим путешествие по миру и во времени, чтобы узнать, как древние египтяне и русские крестьяне умножали числа, древние греки находили наибольшие общие делители, а средневековые японские ученые строили магические квадраты.

• В главе 3 «Максимизация и минимизация» представлены методы градиентного подъема и градиентного спуска. Эти простые методы поиска максимумов и минимумов функций используются для оптимизации — важной цели многих алгоритмов.

• В главе 4 «Сортировка и поиск» представлены фундаментальные алгоритмы сортировки списков и поиска в них элементов. Вы также узнаете, как оценивать эффективность и скорость работы алгоритмов.

• В главе 5 «Чистая математика» мы займемся чисто математическими алгоритмами, включая алгоритмы построения непрерывных дробей, вычисления квадратных корней и генерирования псевдослучайных чисел.

• В главе 6 «Расширенная оптимизация» рассматривается нетривиальный метод поиска оптимальных решений: имитация отжига. Кроме того, в ней представлена задача о коммивояжере — одна из стандартных задач современной информатики.

• В главе 7 «Геометрия» рассматривается генерирование диаграмм Вороного, которые находят применение во многих геометрических областях.

• В главе 8 «Язык» речь пойдет об осмысленной расстановке отсутствующих пробелов в тексте и формировании рекомендаций по выбору следующего слова во фразах.

• В главе 9 «Машинное обучение» рассматриваются деревья принятия решений — один из фундаментальных методов машинного обучения.

• В главе 10 «Искусственный интеллект» мы займемся амбициозным проектом: реализацией алгоритма, который может играть против нас и, возможно, выигрывать. Мы начнем с простой игры «Точки и квадраты» и поговорим о том, как можно улучшить быстродействие программы для этой игры.

• В главе 11 «Полный вперед» речь пойдет о том, как перейти к продвинутым задачам, связанным с алгоритмами. Вы узнаете, как построить чат-бот и выиграть миллион долларов, построив алгоритм для головоломки судоку.

Настройка окружения

Алгоритмы, описанные в книге, реализуются на Python. Он распространяется бесплатно, является языком с открытым исходным кодом и работает на всех основных платформах. Ниже описана процедура установки Python для систем Windows, macOS и Linux.

Установка Python в системе Windows

Чтобы установить Python в системе Windows, выполните следующие действия.

1. Откройте страницу с новейшей версией Python для Windows (не забудьте включить завершающую косую черту): https://www.python.org/downloads/windows/.

2. Щелкните на ссылке версии Python, которую хотите скачать. Чтобы скачать новейшую версию, щелкните на ссылке Latest Python 3 Release — 3.X.Y, где 3.X.Y — номер последней версии (например, 3.8.3). Код, приведенный в книге, был протестирован как на Python 3.6, так и на Python 3.8. Если вы захотите скачать более старую версию, то прокрутите страницу до раздела Stable Releases и найдите нужную версию.

3. Ссылка, на которой вы щелкнули на шаге 2, открывает страницу выбранного вами выпуска Python. В разделе Files щелкните на ссылке Windows x86-64 executable installer.

4. Ссылка из шага 3 открывает файл .exe на вашем компьютере. Это установочный файл; щелкните на нем дважды, чтобы открыть. Файл автоматически запускает процесс установки. Установите флажок Add Python 3.X to PATH, где X — номер версии для загруженной установочной программы (например, 8). Затем нажмите кнопку Install Now и выберите настройки по умолчанию.

5. Когда появится сообщение Setup was successful, нажмите кнопку Close, чтобы завершить процесс установки.

На вашем компьютере появилось новое приложение Python 3.X, где X — номер установленной версии Python 3. В поле поиска Windows введите Python. Когда приложение появится на экране, щелкните на нем, чтобы открыть консоль Python. Вводите на консоли команды Python, и они будут выполнены.

Установка Python в macOS

Чтобы установить Python в системе macOS, выполните следующие действия.

1. Откройте страницу с новейшей версией Python для macOS (не забудьте включить завершающую косую черту): https://www.python.org/downloads/mac-osx/.

2. Щелкните на ссылке версии Python, которую хотите скачать. Чтобы скачать новейшую версию, щелкните на ссылке Latest Python 3 Release — 3.X.Y, где 3.X.Y — номер последней версии (например, 3.8.3). Код, приведенный в книге, был протестирован как на Python 3.6, так и на Python 3.8. Если захотите скачать более старую версию, то прокрутите страницу до раздела Stable Releases и найдите нужную версию.

3. Ссылка, на которой вы щелкнули на шаге 2, открывает страницу выбранного вами выпуска Python. В разделе Files щелкните на ссылке macOS 64-bit installer.

4. Ссылка из шага 3 открывает файл .pkg на вашем компьютере. Это установочный файл; дважды щелкните на нем, чтобы открыть. Файл автоматически запускает процесс установки. Выберите настройки по умолчанию.

5. На вашем компьютере создается папка Python 3.X, где X — номер установленной версии Python. В этой папке дважды щелкните на значке IDLE. На экране появляется приложение 3.X.Y Shell, где 3.X.Y — номер новейшей версии. Это консоль Python, из которой можно выполнять любые команды Python.

Установка Python в системе Linux

Чтобы установить Python в системе Linux, выполните следующие действия.

1. Определите, какой менеджер пакетов используется вашей версией Linux. Два типичных варианта — yum и apt-get.

2. Откройте консоль Linux (также называемую терминалом) и выполните следующие две команды:

> sudo apt-get update

> sudo apt-get install python3.8

Если вы используете yum или другой менеджер пакетов, то замените оба упоминания apt-get в этих двух строках именем yum или именем вашего менеджера пакетов. Аналогичным образом, если вы захотите установить более старую версию Python, замените 3.8 (номер последней версии на момент написания книги) другим номером версии (например, 3.6 — одной из версий, которые использовались при тестировании кода книги). Чтобы узнать номер новейшей версии Python, перейдите по адресу https://www.python.org/downloads/source/. Здесь вы найдете ссылку Latest Python 3 Release — 3.X.Y, где 3.X.Y — номер версии; используйте первые две цифры в приведенной выше команде установки.

3. Запустите Python, выполнив следующую команду с консоли Linux:

python3

Консоль Python открывается в консольном окне Linux. Здесь вы можете вводить команды Python.

Установка сторонних модулей

Часть кода, представленного в книге, зависит от модулей Python, которые не входят в базовое программное обеспечение Python, загруженное с официального сайта Python. Чтобы установить сторонние модули на компьютере, выполните инструкции, изложенные на http://automatetheboringstuff.com/2e/appendixa/.

Резюме

В ходе знакомства с алгоритмами мы посетим много разных мест и окунемся в различные исторические эпохи. Вы познакомитесь с открытиями, сделанными в Древнем Египте, Вавилоне, Афинах времен Перикла, Багдаде, средневековой Европе, Японии периода Эдо и Британской Индии, а также с выдающимися достижениями современности и ее ошеломляющими технологиями. Нам придется искать новые решения задач и преодолевать ограничения, которые на первый взгляд кажутся непреодолимыми. При этом мы установим связь не только первопроходцев древней науки, но и всех, кто пользуется компьютером или ловит бейсбольные мячи, с поколениями пользователей алгоритмов, а также их создателей, которые еще не родились, но в отдаленном будущем будут развивать оставленное нами наследие. Эта книга поможет вам сделать первые шаги в мир алгоритмов.

От издательства

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах.

1. Алгоритмы при решении задач

Поймать мяч — на редкость нетривиальное дело. В начале полета мяч может находиться настолько далеко, что будет казаться вам крошечным пятнышком на горизонте. Он может находиться в воздухе всего несколько коротких секунд, а то и меньше. На мяч воздействуют сопротивление воздуха, ветер и, конечно, сила тяготения, из-за чего он двигается по траектории, близкой к параболе. И все броски мяча совершаются с разной силой, под разными углами и в разных средах с разными условиями. Как же бейсболист, находящийся в 100 метрах от подающего, в момент удара узнает, куда нужно бежать, чтобы перехватить мяч, пока тот не коснулся земли?

Этот вопрос, называемый задачей аутфилдера1, продолжает обсуждаться в научных журналах и в наши дни. Мы начинаем с задачи аутфилдера, поскольку она имеет два очень разных решения: аналитическое и алгоритмическое. Сравнение этих решений ярко демонстрирует, что такое алгоритм и чем он отличается от других подходов к решению задач. Кроме того, задача аутфилдера помогает наглядно представить область, которая в основном абстрактна, — наверняка вам уже доводилось что-нибудь бросать и ловить, и данный опыт поможет вам понять теорию, лежащую в основе этой практики.

Чтобы действительно понять, как человек точно определяет, куда упадет мяч, будет полезно понять, как это делает машина. Начнем с аналитического решения задачи аутфилдера. Оно обладает математической точностью, компьютер легко найдет его за долю секунды, и это решение в том или ином виде обычно объясняют во вводном курсе физики. Оно позволит подвижному роботу выполнять функции аутфилдера в бейсбольной команде.

Однако человек не умеет легко решать аналитические уравнения в уме — по крайней мере, не так быстро, как это делает компьютер. Для человеческого мозга лучше подойдет алгоритмическое решение. На его примере мы исследуем, что такое алгоритм и какими преимуществами он обладает по сравнению с другими методами решения задач. Более того, алгоритмическое решение покажет, что алгоритмы естественны для человеческих мыслительных процессов и далеко не всегда выглядят устрашающе. На примере задачи аутфилдера будет представлен новый способ решения задач: алгоритмический подход.

Аналитический подход

Чтобы решить задачу с помощью аналитического метода, необходимо вернуться на несколько столетий назад к ранней модели движения.

Модель Галилея

Уравнения, чаще всего используемые для моделирования перемещения мяча, существуют со времен Галилея. Этот ученый несколько веков назад предложил полиномиальные формулы, связывающие ускорение, скорость и расстояние. Если не учитывать ветер и сопротивление воздуха и предположить, что мяч начинает движение на уровне земли, то, согласно модели Галилея, горизонтальная позиция брошенного мяча в момент времени t определяется формулой:

,

где v1 — начальная скорость мяча по оси x (по горизонтали). Кроме того, высота брошенного мяча (y) в момент времени t по Галилею вычисляется по формуле

,

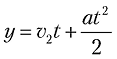
где v2 — начальная скорость мяча по оси y (по вертикали); a — постоянное ускорение свободного падения под воздействием силы тяжести (в метрической системе равно приблизительно –9,81). Подставив первое уравнение во второе, мы находим, что высота брошенного мяча (y) связана с горизонтальной позицией мяча (x) следующей зависимостью:

.

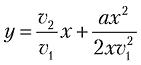
Формулы Галилея можно использовать для моделирования траектории гипотетического мяча на языке Python; соответствующая функция приведена в листинге 1.1. Полиномиальная формула в данном листинге предназначена для мяча, начальная горизонтальная скорость которого составляет приблизительно 0,99 м/с, а начальная вертикальная скорость — около 9,9 м/c. Вы можете поэкспериментировать с другими значениями v1 и v2, чтобы смоделировать бросок с любыми интересующими вас параметрами.

Листинг 1.1. Функция вычисления траектории мяча

def ball_trajectory(x):

    location = 10*x - 5*(x**2)

    return(location)

Построив график функции из листинга 1.1 на языке Python, мы увидим, как приблизительно должна выглядеть траектория мяча (без учета сопротивления воздуха и других незначительных факторов). Средства построения графиков импортируются из модуля matplotlib в первой строке (листинг 1.2). Модуль matplotlib — один из многочисленных сторонних модулей, которые будут импортироваться в коде, приводимом в книге. Прежде чем использовать сторонний модуль, его необходимо установить. Инструкции по установке matplotlib и любых других сторонних модулей доступны на http://automatetheboringstuff.com/2e/appendixa/.

Листинг 1.2. Построение траектории гипотетического мяча между моментом броска (x = 0) и его соприкосновением с землей (x = 2)

import matplotlib.pyplot as plt

xs = [x/100 for x in list(range(201))]

ys = [ball_trajectory(x) for x in xs]

plt.plot(xs,ys)

plt.title('The Trajectory of a Thrown Ball')

plt.xlabel('Horizontal Position of Ball')

plt.ylabel('Vertical Position of Ball')

plt.axhline(y = 0)

plt.show()

На выходе (рис. 1.1) вы получаете красивый график с той траекторией, по которой наш гипотетический мяч должен перемещаться в пространстве. Красивая криволинейная траектория будет похожей для всех движущихся брошенных тел, находящихся под воздействием силы тяготения; писатель Томас Пинчон (Thomas Pynchon) поэтично назвал ее радугой тяготения.

 

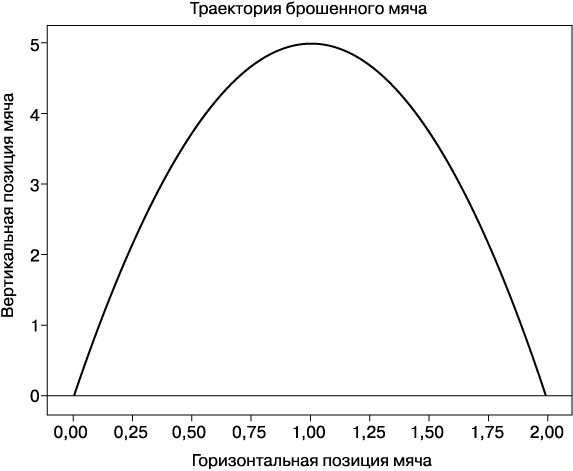
Рис. 1.1. Траектория гипотетического брошенного мяча

Не все мячи будут точно следовать данной траектории, но это один из возможных путей, по которым может перемещаться мяч. Он начинает двигаться в точке 0. Летит вверх, а затем начинает опускаться, перемещаясь от левого края видимой области к правому, как мы не раз видели в жизни.

Стратегия решения для x

Теперь при наличии формулы для вычисления позиции мяча уравнение можно решить для любой интересующей вас точки: когда мяч достигнет наивысшей точки или когда снова опустится до уровня земли — то, что необходимо знать игроку, чтобы поймать его. Студенты, изучающие физику, учатся находить такие решения, и если вы хотите научить робота выполнять функции аутфилдера, то вполне естественно научить его и этим уравнениям. Метод определения итогового положения мяча сводится к тому, что вы берете функцию ball_trajectory(), с которой мы начали, и приравниваете ее к 0:

0 = 10x – 5x2.

Далее уравнение решается для x по формуле квадратного уравнения, которую все мы узнали еще в школе:

 

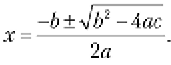
В данном случае мы определяем, что решениями являются x = 0 и x = 2. Первое решение, x = 0, относится к начальной точке движения, где мяч был приведен в движение броском питчера или ударом бьющего. Второе решение x = 2 относится к точке, в которой мяч снова соприкасается с землей после полета.

Использованная нами стратегия была относительно простой. Назовем ее стратегией решения для x. Вы записываете уравнение, описывающее ситуацию, а затем решаете его для интересующей вас переменной. Стратегия решения для x очень часто встречается в естественных науках — как в средней школе, так и в колледже. Студентам предлагается решать уравнения для определения ожидаемой точки падения, идеального уровня экономического производства, пропорции химиката, в которой он должен использоваться в эксперименте, и множества других показателей.

Стратегия решения для x чрезвычайно эффективна. Например, если армия наблюдает, как противник выпускает ракету, то может быстро ввести формулу Галилея в свои вычислительные устройства, почти моментально определить, куда попадет ракета, и вовремя отойти или сбить ее. Это можно легко сделать на обычном ноутбуке, на котором работает Python. Если бы робот играл в защите на бейсбольном поле, то мог бы проделать то же самое и перехватить мяч без малейших усилий.

Стратегия решения для x в данном случае легко реализуется, поскольку мы уже знаем уравнение, которое необходимо решить, и способ его решения. Как упоминалось ранее, уравнение для моделирования траектории брошенного мяча открыл Галилей. Создателем формулы квадратного уравнения был великий Мухаммад ибн Муса аль-Хорезми — первый, кто предложил полное общее решение квадратного уравнения.

Aль-Хорезми — всесторонне образованный ученый, который жил в IX веке и внес свой вклад в астрономию, картографию и тригонометрию. В частности, он ввел термин «алгебра» и научную дисциплину, которая им обозначается. Аль-Хорезми — одна из важнейших фигур, благодаря которым эта книга стала возможной. Мы живем после таких гигантов, как Галилей и аль-Хорезми, поэтому нам не нужно мучиться с выводом уравнений — достаточно просто подставить в них значения и использовать соответствующим образом.

Внутренний физик

Используя уравнения Галилея и аль-Хорезми в сочетании со стратегией решения для x, сложная машина может поймать мяч или сбить ракету. Но можно достаточно уверенно предположить, что большинство бейсболистов не начинают писать уравнения при виде летящего мяча. Надежные источники сообщают, что согласно учебным программам для профессиональных бейсболистов игроки в основном бегают по полю и играют, а не стоят за доской в попытках вывести уравнения Навье — Стокса. Разгадка секрета того, где упадет мяч, не дает четкого ответа на задачу аутфилдера — то есть как человек инстинктивно определяет, где упадет мяч, без обращения к компьютерной программе…

А может быть, и дает. Самое примитивное из возможных решений задачи аутфилдера — предположить, что если компьютеры решают квадратные уравнения для определения того, где упадает мяч, то и человек делает то же самое. Назовем это решение теорией внутреннего физика. Согласно этой теории, «биологический компьютер» нашего мозга способен формулировать и решать квадратные уравнения или рисовать графики и экстраполировать их, причем все это происходит гораздо глубже уровня нашего сознания. Иначе говоря, у каждого из нас где-то глубоко в мозгу обитает «внутренний физик», который может за секунды находить точные уравнения сложных математических задач. Найденное решение передается нашим мускулам, которые приводят в движение наши руки и туловище. Возможно, подсознание позволит сделать это даже тем, кто никогда не посещал уроки физики и не решал уравнения.

У теории внутреннего физика есть свои сторонники. Например, известный математик Кейт Девлин (Keith Devlin) в 2006 году опубликовал книгу, которая называлась «Математический инстинкт: почему вы гениальный математик (наряду с омарами, птицами, кошками и собаками)». На обложке книги изображена собака, которая в прыжке ловит фрисби; стрелками обозначены векторы траектории диска и собаки. Имеется в виду, что собака способна выполнить все сложные вычисления, необходимые для того, чтобы векторы встретились.

Несомненная способность собак ловить фрисби, как и способность людей ловить бейсбольные мячи, вроде бы говорит в пользу теории внутреннего физика. Подсознательное — таинственная и впечатляющая область, глубины которой нам еще только предстоит изучить. Так почему бы ему время от времени не решать уравнения уровня средней школы? Что еще важнее, теорию внутреннего физика сложно опровергнуть, поскольку трудно предложить альтернативу: если собаки не способны решать дифференциальные уравнения в частных производных, чтобы поймать диск, то как они его ловят? Они прыгают высоко в воздух и без малейших усилий хватают фрисби зубами. Если собаки не решают в мозгу какую-то задачу из области физики, то как они (и мы) узнают, как точно перехватить летающий объект?

Еще в 1967 году ни у кого не было хорошего ответа на данный вопрос. В том году инженер Ванневар Буш (Vannevar Bush) написал книгу, в которой описывал научные аспекты бейсбола (так, как понимал их). Однако автор не смог никак объяснить, как аутфилдеры узнают, куда же им нужно бежать, чтобы перехватить летящий мяч. К счастью, физик Севилл Чепмен (Seville Chapman) прочитал книгу Буша и настолько вдохновился ею, что уже в следующем году выдвинул собственную теорию.

Алгоритмический подход

Чепмена как ученого не устраивало, что все списывали на подсознание, и он захотел получить более конкретное объяснение способностей бейсболистов. И вот что он обнаружил.

Как думать шеей

Чепмен начал решать задачу аутфилдера с анализа информации, необходимой для того, чтобы поймать мяч. Хотя человеку может быть трудно оценить точную скорость мяча или траекторию параболической дуги, Чепмен подумал, что нам проще наблюдать за углами. Если кто-то бросает или пинает мяч от земли, а она ровная и плоская, то игрок увидит, как мяч начинает приближаться к уровню его глаз. Представьте угол, образованный двумя линиями: землей и линией видимости мяча игроком. В момент, когда бьющий ударяет по мячу, данный угол составляет (примерно) 0 градусов. После непродолжительного полета мяч окажется выше земли, так что угол между землей и линией видимости мяча игроком увеличится. Даже если игрок не изучал геометрию, он «чувствует» этот угол — например, ощущая, насколько ему приходится задрать голову, чтобы увидеть мяч.

Если предположить, что игрок стоит там, где в конечном итоге упадет мяч (в точке x = 2), то можно получить представление о том, как изменяется угол линии видимости мяча, построив график линии видимости на ранней фазе траектории мяча. Следующий фрагмент кода создает отрезок для графика, построенного в листинге 1.2; предполагается, что он выполняется в том же сеансе Python. Отрезок представляет линию между глазами игрока и мячом после того, как мяч пролетел 0,1 метра по горизонтали.

xs2 = [0.1,2]

ys2 = [ball_trajectory(0.1),0]

Эту линию видимости можно нанести на график вместе с другими линиями, чтобы увидеть, как угол продолжает расти на протяжении траектории мяча. Следующие строки кода добавляют другие отрезки на график, построенный в листинге 1.2. Отрезки представляют линию между глазами игрока и мячом для еще двух точек на пути мяча: точек, в которых мяч переместился на 0,1, 0,2 и 0,3 метра по горизонтали. После создания всех этих отрезков они наносятся на график одновременно.

xs3 = [0.2,2]

ys3 = [ball_trajectory(0.2),0]

xs4 = [0.3,2]

ys4 = [ball_trajectory(0.3),0]

plt.title('The Trajectory of a Thrown Ball - with Lines of Sight')

plt.xlabel('Horizontal Position of Ball')

plt.ylabel('Vertical Position of Ball')

plt.plot(xs,ys,xs2,ys2,xs3,ys3,xs4,ys4)

plt.show()

На полученном графике мы видим несколько линий видимости, которые образуют непрерывно увеличивающиеся углы с уровнем земли (рис. 1.2).

В процессе полета угол линии видимости игрока продолжает расти, и игрок вынужден закидывать голову назад, пока не поймает мяч. Обозначим угол между землей и линией видимости θ. Будем считать, что игрок стоит в точке падения мяча (x = 2). Вспомните из школьного курса геометрии, что тангенс угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. В данном случае тангенс θ равен отношению высоты мяча к его горизонтальному расстоянию от игрока. Следующий фрагмент Python наносит на график стороны, отношение которых определяет тангенс:

xs5 = [0.3,0.3]

ys5 = [0,ball_trajectory(0.3)]

xs6 = [0.3,2]

ys6 = [0,0]

plt.title('The Trajectory of a Thrown Ball - Tangent Calculation')

plt.xlabel('Horizontal Position of Ball')

plt.ylabel('Vertical Position of Ball')

plt.plot(xs,ys,xs4,ys4,xs5,ys5,xs6,ys6)

plt.text(0.31,ball_trajectory(0.3)/2,'A',fontsize = 16)

plt.text((0.3 + 2)/2,0.05,'B',fontsize = 16)

plt.show()

 

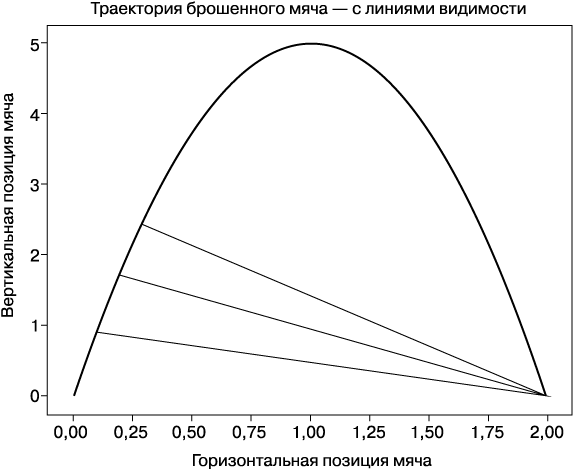
Рис. 1.2. Траектория гипотетического брошенного мяча с отрезками, представляющими линии видимости мяча

Полученный график изображен на рис. 1.3.

Тангенс вычисляется отношением длины стороны A к длине стороны B. Высота A вычисляется по формуле 10x – 5x2, а длина B — по формуле 2 – x. Таким образом, следующее уравнение неявно описывает угол θ для каждой точки полета:

 

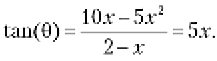
Ситуация в целом достаточно сложна: где-то далеко мяч приходит в движение и быстро летит по параболической кривой, конец которой трудно немедленно спрогнозировать. Но в этой сложной ситуации Чепмен нашел простое отношение:

 

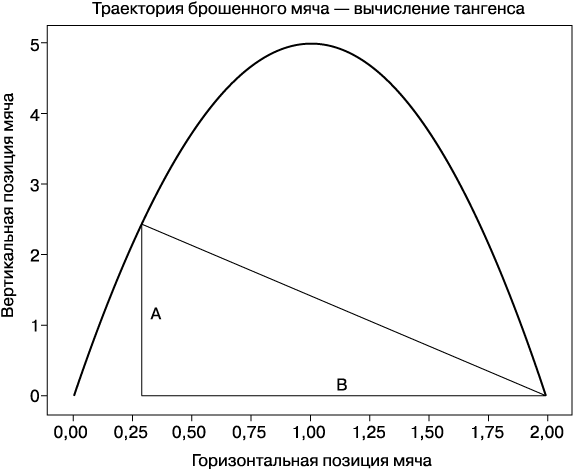
Рис. 1.3. Траектория гипотетического брошенного мяча с отрезками, представляющими линии видимости мяча, и отрезками A и B, отношение длин которых дает интересующий нас тангенс

когда игрок стоит в правильном месте, тангенс θ увеличивается с постоянной скоростью. Вся суть открытия Чепмена заключалась в том, что тангенс θ, угла мяча относительно земли, растет линейно со временем. После того как Чепмен обнаружил эту простую связь, он смог создать элегантное алгоритмическое решение.

Решение опирается на тот факт, что если какая-то характеристика — в данном случае тангенс θ — растет с постоянной скоростью, то ее ускорение равно нулю. Таким образом, стоя точно в том месте, куда падает мяч, вы наблюдаете угол, тангенс которого обладает нулевым ускорением. Если вы стоите слишком близко к исходной позиции мяча, то наблюдаете положительное ускорение, а если слишком далеко — то отрицательное. (При желании вы можете самостоятельно проверить муторные вычисления, на которых основаны эти утверждения.) А это означает, что игрок может понять, в какую сторону ему следует бежать, по тому, насколько равномерно ему приходится задирать голову при наблюдении за подъемом мяча — так сказать, «думать шеей».

Применение алгоритма Чепмена

Не у всех роботов есть шея, так что метод «думать шеей» может оказаться бесполезным для робота-бейсболиста. Не забудьте, что роботы способны моментально решать квадратные уравнения, чтобы понять, где следует ловить мяч, не беспокоясь о скорости роста тангенса θ. Но для людей метод Чепмена может быть в высшей степени полезным. Чтобы оказаться в точке падения мяча, игрок-человек может следовать относительно простому процессу, описанному ниже.

1. Определить ускорение тангенса угла между землей и линией видимости мяча.

2. Если ускорение положительно, то сделать шаг назад.

3. Если ускорение отрицательно, то сделать шаг вперед.

4. Повторять шаги 1–3, пока мяч не окажется прямо перед вами.

5. Поймать его.

Одно серьезное возражение против метода Чепмена из пяти шагов заключается в том, что руководствующиеся им игроки должны на ходу вычислять тангенсы углов, а это означает, что теория внутреннего физика заменяется теорией внутреннего геометра, согласно которой бейсболисты могут мгновенно — и подсознательно — вычислять тангенсы.

Один потенциальный аргумент против этого возражения заключается в том, что для многих углов tan(θ) приблизительно равен θ, поэтому вместо отслеживания ускорения тангенса игроки могут наблюдать за ускорением самого угла. Если ускорение угла можно оценить по воспринимаемому ускорению шейных мышц, которые растягиваются при движении шеи для наблюдения за мячом, и если угол может служить разумным приближением для тангенса, то никакие предположения о великих подсознательных математических или геометрических способностях игроков не нужны — важен только физический навык точной реакции на трудноуловимые ощущения органов чувств.

Когда оценка ускорения остается единственной сложной частью процесса, мы получаем потенциальное решение задачи аутфилдера, которое обладает намного большей психологической достоверностью, чем теория внутреннего физика с подсознательной экстраполяцией парабол. Конечно, психологическая привлекательность решения не означает, что оно может использоваться только людьми. Робот-игрок тоже может быть запрограммирован на следование методу Чепмена и даже может лучше справляться с ловлей мяча, поскольку метод Чепмена позволяет динамически реагировать на изменения из-за ветра или рикошета.

Помимо психологической достоверности, у процесса из пяти шагов, предложенного Чепменом, есть еще одна важнейшая особенность: он не полагается на стратегию решения для x и вообще какое-либо явное уравнение. Вместо этого он предлагает последовательные итерации с простыми наблюдениями и небольшие, постепенные шаги для достижения четко определенной цели. Другими словами, процесс, следующий из теории Чепмена, является алгоритмом.

Решение задач с применением алгоритмов

Слово «алгоритм» также связано с именем великого аль-Хорезми, упоминавшегося ранее. Определить его не так просто — не в последнюю очередь из-за того, что общепринятое определение изменялось со временем. Говоря простым языком, алгоритм представляет собой набор инструкций, который дает четко определенный результат. Это достаточно широкое определение; как было показано во введении, налоговые декларации и рецепты парфе тоже можно с полным основанием считать алгоритмами.

Пожалуй, процесс ловли мяча по Чепмену — или алгоритм Чепмена, как его правильнее называть, — больше похож на алгоритм, чем рецепт парфе, поскольку содержит циклическую структуру, в которой небольшие шаги выполняются многократно до достижения определенного условия. Это типичная алгоритмическая структура, которая неоднократно встречается в данной книге.

Чепмен предложил алгоритмическое решение для задачи аутфилдера, поскольку решение для x было неприемлемо (игроки часто не знают необходимые уравнения). В общем случае алгоритмы оказываются наиболее полезными тогда, когда стратегия решения для x не дает результата. Иногда нужные уравнения неизвестны, но чаще уравнения, которое бы полностью описывало ситуацию, просто не существует, его невозможно решить, или мы сталкиваемся с ограничениями по времени/памяти.

Бытует мнение, что алгоритмы сложны, непостижимы, загадочны, имеют чисто математическую природу и недоступны пониманию, если вы не изучали их много лет. Современная система образования устроена так, что детей начинают учить стратегии решения для x как можно раньше, а алгоритмы в явном виде преподают только на уровне колледжа или магистратуры (если вообще преподают). У многих учащихся на освоение стратегии решения для x уходят годы, и этот метод всегда кажется им чем-то искусственным. Люди с подобным опытом уверены, что алгоритмы будут такими же искусственными и еще более трудно понимаемыми, поскольку они являются «продвинутыми».

Однако я вынес из алгоритма Чепмена важный урок: наше обучение поставлено с ног на голову. Во время перерывов в занятиях ученики узнают и совершенствуют свое владение десятками алгоритмов для ловли, бросков, бега и т.д. Вероятно, есть и другие, намного более сложные и еще не изученные алгоритмы, управляющие социальными взаимодействиями: разговоры, стремление добиться положения в компании, сплетни, формирование альянсов и дружеских отношений. А когда перерыв заканчивается и начинается лекция по математике, мы просим учащихся абстрагироваться от реального мира исследования алгоритмов и заставляем изучать неестественный механистический процесс решения для x — процесс, который не является естественной частью развития личности и даже не является самым эффективным методом решения аналитических задач. Только достаточно продвинувшись в области математики и информатики, ученики возвращаются в естественный мир алгоритмов и эффективных процессов, которые бессознательно и с удовольствием практиковали на перерывах.

Эта книга была задумана как интеллектуальный перерыв для любознательных — перерыв в том смысле, в котором его понимают школьники: конец тяжелой монотонной работы, начало действительно важных дел и продолжение занятий с друзьями в хорошем настроении. Если алгоритмы вызывают у вас трепет, то напомните себе, что мы, люди, алгоритмичны по своей природе, и если вы можете поймать мяч или испечь пирог — значит, можете освоить алгоритм.

В книге мы исследуем много разных алгоритмов. Одни сор­тируют списки или обрабатывают числа. Другие делают возможной обработку естественного языка и искусственный интеллект. Учтите, что алгоритмы не растут на деревьях. Каждый алгоритм до того, как пошел в массы и был представлен для широкого обозрения в этой книге, был кем-то изобретен или найден — как это произошло с Чепменом, который проснулся в мире, где его алгоритм не существовал, а в конце дня лег спать в изменившемся мире. Я постараюсь сделать так, чтобы вы попытались поставить себя на место этих героических изобретателей. Иначе говоря, я рекомендую рассматривать алгоритмы не только как инструменты, но и как трудноразрешимую проблему, которая была успешно решена. Полная карта мира алгоритмов еще не построена — остается еще немало неизученных областей, и я искренне надеюсь, что вы можете стать одним из участников процесса их изучения.

Резюме

В этой главе были представлены два подхода к решению задач: аналитический и алгоритмический. Рассматривая два способа решения задачи аутфилдера, мы исследовали различия этих подходов и в конечном итоге пришли к алгоритму Чепмена. Ученый нашел простую закономерность в сложной ситуации (постоянное ускорение тангенса θ) и использовал ее для разработки концепции итеративного процесса, который получает только один простой ввод (поворот головы за мячом) и приводит к определенной цели (пойманный мяч). Если вы хотите разрабатывать и использовать алгоритмы в своей работе, то можете попытаться встать на путь Чепмена.

В следующей главе мы рассмотрим некоторые примеры алгоритмов в истории. Эти примеры должны углубить ваше понимание алгоритмов; в частности, вы узнаете, что они собой представляют и как работают. Речь пойдет об алгоритмах из истории Древнего Египта, Древней Греции и императорской Японии. Каждый новый изучаемый вами алгоритм можно добавить в арсенал алгоритмов, которыми вы сможете пользоваться в своей работе, пока со временем не дойдете до точки, когда сможете разрабатывать и совершенствовать собственные алгоритмы.