Переводчик Р. Чикин

 

Имран Ахмад

40 алгоритмов, которые должен знать каждый программист на Python. — СПб.: Питер, 2023.

 

ISBN 978-5-4461-1908-0

© ООО Издательство "Питер", 2023

 

Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного разрешения владельцев авторских прав.

 

Моему отцу, Иньятулла Хану, который продолжает мотивировать меня на непрерывное изучение чего-то нового и неизведанного

Об авторе

Имран Ахмад — сертифицированный инструктор Google с многолетним опытом. Преподает такие дисциплины, как программирование на языке Python, машинное обучение (МО), алгоритмы, большие данные (big data) и глубокое обучение. В своей диссертации он разработал новый алгоритм на основе линейного программирования под названием ASTRA. Этот алгоритм применяется для оптимального распределения ресурсов в облачных вычислениях. На протяжении последних четырех лет Имран работает над социально значимым проектом машинного обучения в аналитической лаборатории при Федеральном правительстве Канады. Проект связан с автоматизацией иммиграционных процессов. Имран разрабатывает алгоритмы оптимального использования GPU для обучения сложных моделей МО.

Предисловие

Алгоритмы всегда играли важную роль как в теории, так и в практическом применении вычислительной техники. Эта книга посвящена использованию алгоритмов для решения прикладных задач. Чтобы извлечь максимальную пользу из применения алгоритмов, необходимо глубокое понимание их логики и математики. Мы начнем с введения в алгоритмы и изучим различные методы их проектирования. Двигаясь дальше, мы узнаем о линейном программировании, ранжировании страниц и графах‚ а также поработаем с алгоритмами машинного обучения, пытаясь понять математику и логику, лежащие в их основе. Книга содержит практические примеры, такие как прогноз погоды, кластеризация твитов или рекомендательные механизмы для просмотра фильмов, которые покажут, как наилучшим образом применять алгоритмы. Прочтя эту книгу, вы станете увереннее использовать алгоритмы для решения реальных вычислительных задач.

Для кого эта книга

Эта книга для серьезного программиста! Она подойдет вам, если вы опытный программист и хотите получить более глубокое представление о математических основах алгоритмов. Если вы имеете ограниченные знания в области программирования или обработки данных и хотите узнать больше о том, как пользоваться проверенными в деле алгоритмами для совершенствования методов проектирования и написания кода, то эта книга также будет вам полезна. Опыт программирования на Python вам точно понадобится, а вот знания в области анализа и обработки данных полезны, но не обязательны.

О чем эта книга

В главе 1 «Обзор алгоритмов» кратко излагаются основы алгоритмов. Мы начнем с раздела, посвященного основным концепциям, необходимым для понимания работы алгоритмов. В нем кратко рассказывается о том, как люди начали использовать алгоритмы для математической формулировки определенных классов задач. Речь также пойдет об ограничениях алгоритмов. В следующем разделе будут объяснены различные способы построения логики алгоритма. Поскольку в этой книге для написания алгоритмов используется Python, мы узнаем, как настроить среду для запуска примеров кода. Затем мы обсудим способы количественной оценки производительности алгоритма и ее сравнения с другими алгоритмами. В конце главы нас ждут различные способы проверки работы алгоритма.

Глава 2 «Структуры данных, используемые в алгоритмах» посвящена необходимым структурам, которые содержат временные данные. Алгоритмы могут быть требовательными с точки зрения данных, вычислений или же и того и другого одновременно. Но для оптимальной реализации любого алгоритма ключевое значение имеет выбор подходящей структуры данных. Многие алгоритмы имеют рекурсивную и итеративную логику и требуют специализированных структур данных (которые сами являются итеративными). Поскольку для примеров мы используем Python, эта глава посвящена структурам данных Python, подходящим для реализации обсуждаемых в книге алгоритмов.

В главе 3 «Алгоритмы сортировки и поиска» представлены основные алгоритмы, используемые для сортировки и поиска. Впоследствии они станут основой для изучения более сложных алгоритмов. Мы познакомимся с различными типами алгоритмов сортировки и сравним эффективность разных подходов. Затем рассмотрим алгоритмы поиска, сравним их между собой и количественно оценим их производительность и сложность. Наконец, обсудим области применения этих алгоритмов.

В главе 4 «Разработка алгоритмов» раскрываются основные концепции проектирования алгоритмов. В ней мы рассмотрим различные типы алгоритмов и обсудим их сильные и слабые стороны. Понимание этих концепций важно, когда речь заходит о разработке сложных алгоритмов. Глава начинается с обсуждения различных типов алгоритмических конструкций. Затем представлено решение знаменитой задачи коммивояжера. Далее мы обсудим линейное программирование и его ограничения. Наконец, разберем практический пример, демонстрирующий использование линейного программирования для планирования производственных мощностей.

Глава 5 «Графовые алгоритмы» посвящена алгоритмам решения графовых задач, которые очень распространены в информатике. Существует множество вычислительных задач, которые лучше всего представить в виде графов. Мы познакомимся с методами такого представления и поиска (обхода) на графах. Обход графа означает систематическое прохождение по ребрам графа с целью посещения всех его вершин. Алгоритм поиска может многое рассказать о структуре графа. Многие алгоритмы начинают с обхода входного графа, чтобы получить информацию о его структуре. Несколько других графовых алгоритмов осуществляют более тщательный поиск. Методы поиска лежат в основе графовых алгоритмов. Мы обсудим два наиболее распространенных вычислительных представления графов: в виде списка смежности и в виде матрицы смежности. Далее мы рассмотрим алгоритмы поиска в ширину и поиска в глубину и выясним, в каком порядке они посещают вершины.

В главе 6 «Алгоритмы машинного обучения без учителя» мы узнаем об алгоритмах, которые пытаются изучить внутренние структуры, закономерности и взаимо­связи на основе предоставленных данных без какого-либо контроля. Сначала мы обсудим методы кластеризации. Это методы машинного обучения, которые ищут сходства и взаимосвязи между элементами данных в наборе, а затем объединяют эти элементы в различные группы (кластеры). Данные в каждом кластере имеют некоторое сходство, основанное на присущих им атрибутах или признаках. В следующем разделе нас ждут алгоритмы снижения размерности, которые используются, когда имеется целый ряд признаков. Далее следуют алгоритмы, имеющие дело с обнаружением выбросов (аномалий). Наконец, в главе представлен поиск ассоциативных правил. Это метод анализа, используемый для изучения больших наборов транзакционных данных с целью выявления определенных закономерностей и правил. Эти закономерности отражают интересные взаимосвязи и ассоциации между различными элементами в транзакциях.

Глава 7 «Традиционные алгоритмы обучения с учителем» посвящена алгоритмам, используемым для решения задач с помощью размеченного набора данных с входными признаками (и соответствующими выходными метками или классами). Эти данные затем используются для обучения модели. С ее помощью прогнозируются результаты для ранее неизвестных точек данных. Сначала мы познакомимся с понятием классификации. Затем изучим простейший алгоритм машинного обучения — линейную регрессию — и один из самых значимых алгоритмов — дерево решений. Мы обсудим его слабые и сильные стороны, после чего разберем два важных алгоритма, SVM и XGBoost.

Глава 8 «Алгоритмы нейронных сетей» познакомит нас с основными понятия­ми и компонентами нейронной сети, которая становится все более важным методом машинного обучения. Мы изучим типы нейронных сетей и различные функции активации, используемые для их реализации. Мы подробно обсудим алгоритм обратного распространения ошибки. Он широко применяется для решения проблемы сходимости нейронной сети. Далее познакомимся с переносом обучения, необходимым для значительного упрощения и частичной автоматизации обучения моделей. Наконец, в качестве практического примера мы узнаем, как использовать глубокое обучение для выявления фальшивых документов.

В главе 9 «Алгоритмы обработки естественного языка» представлены алгоритмы NLP. Эта глава построена как переход от теории к практике. В ней рассматриваются главные принципы и математические основы. Мы обсудим широко используемую нейронную сеть для разработки и реализации важных практических задач в области текстовых данных. Также мы разберем ограничения NLP. Наконец, рассмотрим практический пример, в котором модель обучается распознавать эмоциональную окраску отзывов на кинофильмы.

Глава 10 «Рекомендательные системы» посвящена механизмам рекомендаций. Это способ моделирования доступной информации о пользовательских предпочтениях и использования этой информации для предоставления обоснованных рекомендаций. Основой рекомендательной системы всегда является записанное взаимодействие между пользователем и продуктом. В этой главе объясняется основная идея рекомендательных систем и представлены различные типы механизмов рекомендаций. Наконец, демонстрируется пример использования рекомендательной системы для предложения продуктов различным пользователям.

Глава 11 «Алгоритмы обработки данных» посвящена алгоритмам, ориентированным на данные. Глава начинается с краткого обзора таких алгоритмов. Затем рассматриваются критерии классификации данных и описывается применение алгоритмов к приложениям потоковой передачи. Наконец, вашему вниманию будет предложен практический пример извлечения закономерностей из данных Twitter.

Глава 12 «Криптография» познакомит с криптографическими алгоритмами. Глава начинается с истории возникновения криптографии. Затем обсуждаются алгоритмы симметричного шифрования, алгоритмы хеширования MD5 и SHA, а также ограничения и недостатки, связанные с реализацией симметричных алгоритмов. Далее представлены алгоритмы асимметричного шифрования и их использования для создания цифровых сертификатов. В конце нас ждет практический пример, обобщающий все эти методы.

Глава 13 «Крупномасштабные алгоритмы» объяснит, как алгоритмы обрабатывают данные, которые не могут поместиться в память одной ноды и требуют обработки несколькими процессорами. Мы обсудим типы алгоритмов, для которых необходимо параллельное выполнение, а также процесс распараллеливания алгоритмов. Далее будет представлена архитектура CUDA. Мы узнаем, как использовать один или несколько графических процессоров для ускорения алгоритма и как его изменить, чтобы эффективно использовать мощность GPU. Наконец, мы рассмотрим кластерные вычисления и выясним, как Apache Spark создает коллекции данных RDD для чрезвычайно быстрой параллельной реализации стандартных алгоритмов.

Глава 14 «Практические рекомендации» начинается с темы объяснимости алгоритма, которая становится все более важной теперь, когда мы понимаем логику автоматизированного принятия решений. Затем раскрываются проблема этики алгоритмов и возможность возникновения предвзятости при их реализации. Далее подробно обсуждаются методы решения NP-трудных задач. Наконец, кратко изложены способы реализации алгоритмов и связанные с этим сложности.

Что вам потребуется при чтении этой книги

• Требуемое программное обеспечение: Python 3.7.2 или более поздней версии.

• Технические характеристики оборудования: минимум 4 Гбайта оперативной памяти, 8 Гбайт и более (рекомендуется).

• Операционная система: Windows/Linux/Mac.

Вы можете загрузить файлы с примерами кода из репозитория GitHub по адресу https://github.com/PacktPublishing/40-Algorithms-Every-Programmer-Should-Know.

Условные обозначения

В этой книге используется ряд условных обозначений.

Код в тексте

Указывает кодовые слова в тексте, имена таблиц базы данных, имена файлов, расширения файлов, пути, URL-адреса, вводимые пользователем, и аккаунты пользователя в Twitter. Вот пример: «Давайте посмотрим, как добавить новый элемент в стек с помощью push или удалить элемент из стека с помощью pop».

Блоки кода (листинги) выглядят следующим образом:

define swap(x, y)

    buffer = x

    x = y

    y = buffer

Когда мы хотим привлечь ваше внимание к определенной части листинга, соответствующие строки или элементы выделены полужирным шрифтом:

define swap(x, y)

    buffer = x

    x = y

    y = buffer

Любой ввод или вывод командной строки также выделяется полужирным шрифтом:

pip install a_package

Новые термины, важные понятия или слова выделены курсивом. Вот пример: «Один из способов уменьшить сложность алгоритма — это пойти на компромисс в отношении его точности, создав тип алгоритма, называемый приближенным алгоритмом».

Так оформлены предупреждения или важные примечания.

Так оформлены советы и рекомендации.

От издательства

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах.

Часть I. Основы и базовые алгоритмы

В этой части книги мы разберемся, что такое алгоритм, как его создать, какие структуры данных используются в алгоритмах. Кроме того, мы подробно изучим алгоритмы сортировки и поиска, а также применение алгоритмов для решения графических задач. Главы, из которых состоит часть I:

• Глава 1. Обзор алгоритмов.

• Глава 2. Структуры данных, используемые в алгоритмах.

• Глава 3. Алгоритмы сортировки и поиска.

• Глава 4. Разработка алгоритмов.

• Глава 5. Графовые алгоритмы.

1. Обзор алгоритмов

Эта книга содержит информацию, необходимую для понимания, классификации, выбора и реализации важных алгоритмов. Помимо объяснения логики алгоритмов, в ней рассматриваются структуры данных, среды разработки и производственные среды, подходящие для тех или иных классов алгоритмов. Мы сфокусируемся на современных алгоритмах машинного обучения, которые обретают все большее значение. Наряду с теорией мы рассмотрим и практические примеры использования алгоритмов для решения актуальных повседневных задач.

В первой главе дается представление об основах алгоритмов. Она начинается с раздела, посвященного основным концепциям, необходимым для понимания работы разных алгоритмов. В этом разделе кратко рассказывается о том, как люди начали использовать алгоритмы для математической формулировки определенного класса задач. Речь также пойдет об ограничениях различных алгоритмов. В следующем разделе будут объяснены способы построения логики алгоритма. Поскольку в этой книге для написания алгоритмов используется Python, мы объясним, как настроить среду для запуска примеров. Затем обсудим различные способы количественной оценки работы алгоритма и сравнения с другими алгоритмами. В конце главы познакомимся с различными способами проверки конкретной реализации алгоритма.

Если кратко, то в этой главе рассматриваются следующие основные моменты:

• Что такое алгоритм.

• Определение логики алгоритма.

• Введение в пакеты Python.

• Методы разработки алгоритмов.

• Анализ производительности.

• Проверка алгоритма.

Что такое алгоритм

Говоря простым языком, алгоритм — это набор правил для выполнения определенных вычислений‚ направленных на решение определенной задачи. Он предназначен для получения результатов при использовании любых допустимых входных данных в соответствии с точно прописанными командами. Словарь American Heritage дает такое определение:

«Алгоритм — это конечный набор однозначных инструкций, которые при заданном наборе начальных условий могут выполняться в заданной последовательности для достижения определенной цели и имеют определимый набор конечных условий».

Разработка алгоритма — это создание набора математических правил для эффективного решения реальной практической задачи. На основе такого набора правил можно создать более общее математическое решение, многократно применимое к широкому спектру аналогичных задач.

Этапы алгоритма

Различные этапы разработки, развертывания и, наконец, использования алгоритма проиллюстрированы на следующей диаграмме (рис. 1.1).

Как показано на диаграмме, прежде всего нужно сформулировать задачу и подробно описать необходимый результат. Как только задача четко поставлена, мы подходим к этапу разработки.

Разработка состоит из двух этапов.

• Проектирование. На этом этапе разрабатываются и документируются архитектура, логика и детали реализации алгоритма. При разработке алгоритма мы учитываем как точность, так и производительность. Часто для решения одной и той же задачи можно использовать два или несколько разных алгоритмов. Этап проектирования — это итеративный процесс, который включает в себя сравнение различных потенциально пригодных алгоритмов. Некоторые алгоритмы могут давать простые и быстрые решения, но делают это в ущерб точности. Другие могут быть очень точными, но их выполнение занимает значительное время из-за их сложности. Одни сложные алгоритмы эффективнее других. Прежде чем сделать выбор, следует тщательно изучить все компромиссы. Разработка наиболее эффективного алгоритма особенно важна при решении сложной задачи. Правильно разработанный алгоритм приведет к эффективному решению, способному одновременно обеспечить как надлежащую производительность, так и достаточную степень точности.

• Кодирование. Разработанный алгоритм превращается в компьютерную программу. Важно, чтобы программа учитывала всю логику и архитектуру, пре­дусмотренную на этапе проектирования.

 

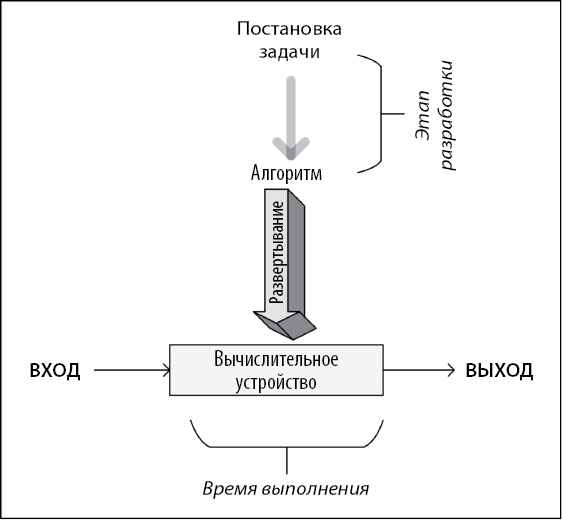
Рис. 1.1

Этапы проектирования и кодирования алгоритма носят итеративный характер. Разработка алгоритма, отвечающего как функциональным, так и нефункциональным требованиям, занимает массу времени и усилий. Функциональные требования определяют то, какими должны быть правильные выходные данные для конкретного набора входных данных. Нефункциональные требования алгоритма в основном касаются производительности для заданного объема данных. Проверку алгоритма и анализ его производительности мы обсудим далее в этой главе. Проверка должна подтвердить, соответствует ли алгоритм его функциональным требованиям. Анализ производительности — подтвердить, соответствует ли алгоритм своему основному нефункциональному требованию: производительности.

После разработки и реализации на выбранном языке программирования код алгоритма готов к развертыванию. Развертывание алгоритма включает в себя разработку реальной производственной среды, в которой будет выполняться код. Производственная среда должна быть спроектирована в соответствии с потребностями алгоритма в данных и обработке. Например, для эффективной работы распараллеливаемых алгоритмов потребуется кластер с соответствующим количеством компьютерных узлов. Для алгоритмов, требующих больших объемов данных, возможно, потребуется разработать конвейер ввода данных и стратегию их кэширования и хранения. Более подробно проектирование производственной среды обсуждается в главах 13 и 14. После разработки и реализации производственной среды происходит развертывание алгоритма, который принимает входные данные, обрабатывает их и генерирует выходные данные в соответствии с требованиями.

Определение логики алгоритма

При разработке алгоритма важно найти различные способы его детализировать. Нам необходимо разработать как его логику, так и архитектуру. Этот процесс можно сравнить с постройкой дома: нужно спроектировать структуру, прежде чем фактически начинать реализацию. Для эффективности итеративного процесса проектирования более сложных распределенных алгоритмов важно предварительно планировать, как их логика будет распределена по нодам кластера во время выполнения алгоритма. Этого можно добиться с помощью псевдокода и планов выполнения‚ о которых мы поговорим в следующем ­разделе.

Псевдокод

Самый простой способ задать логику алгоритма — составить высокоуровневое неформальное описание алгоритма, которое называется псевдокодом. Прежде чем описывать логику в псевдокоде, полезно сформулировать основные шаги на простом человеческом языке. Затем это словесное описание структурируется и преобразуется в псевдокод, точно отражающий логику и последовательность алгоритма. Хорошо написанный псевдокод должен достаточно подробно описывать алгоритм, даже если такая детализация не обязательна для описания основного хода работы и структуры алгоритма. На рис. 1.2 показана последовательность шагов.

 

Рис. 1.2

Как только псевдокод готов (см. следующий раздел), мы можем написать код алгоритма, используя выбранный язык программирования.

Практический пример псевдокода

Ниже представлен псевдокод алгоритма распределения ресурсов, называемого SRPMP. В кластерных вычислениях возможно множество ситуаций, когда параллельные задачи необходимо выполнить на наборе доступных ресурсов, в совокупности называемых пулом ресурсов. Данный алгоритм назначает задачи ресурсу и создает маппинг-сет (mapping set), называемый Ω (омега). Представленный псевдокод отражает логику и последовательность алгоритма, что более подробно объясняется в следующем разделе.

1: BEGIN Mapping_Phase

2: Ω = { }

3: k = 1

4: FOREACH Ti∈T

5:     ωi = A(Δk,Ti)

6:     add {ωi,Ti} to Ω

7:     state_changeTi [STATE 0: Idle/Unmapped] → [STATE 1: Idle/Mapped]

8:     k=k+1

9:     IF (k>q)

10:       k=1

11:    ENDIF

12: END FOREACH

13: END Mapping_Phase

Давайте построчно разберем этот алгоритм.

1. Мы начинаем маппинг с выполнения алгоритма. Маппинг-сет Ω пуст.

2. Первый раздел выбирается в качестве пула ресурсов для задачи T1 (см. строку 3 кода). Целевой телевизионный рейтинг (Television Rating Point, TRPs) итеративно вызывает алгоритм ревматоидного артрита (Rheumatoid Arthritis, RA) для каждой задачи Ti с одним из разделов, выбранным в качестве пула ресурсов.

3. Алгоритм RA возвращает набор ресурсов, выбранных для задачи Ti, представленный посредством ωi (см. строку 5 кода).

4. Ti и ωi добавляются в маппинг-сет (см. строку 6 кода).

5. Состояние Ti меняется со STATE 0:Idle/Mapping на STATE 1:Idle/Mapped (см. строку 7 кода).

6. Обратите внимание, что для первой итерации выбран первый раздел и k=1. Для каждой последующей итерации значение k увеличивается до тех пор, пока не достигнуто k>q.

7. Если переменная k становится больше q, она сбрасывается в 1 (см. строки 9 и 10 кода).

8. Этот процесс повторяется до тех пор, пока каждой задаче не будет присвоен набор используемых ресурсов, что будет отражено в маппинг-сете, называемом Ω.

9. Как только задаче присваивается набор ресурсов на этапе маппинга, она запускается на выполнение.

Использование сниппетов

С ростом популярности такого простого, но мощного языка программирования, как Python, приобретает популярность и альтернативный подход, который заключается в представлении логики алгоритма непосредственно на языке программирования, но в несколько упрощенной версии. Как и псевдокод, такой фрагмент кода отражает основную логику и структуру предлагаемого алгоритма без указания подробностей. Иногда его называют сниппетом. В этой книге сниппеты используются вместо псевдокода везде, где это возможно, поскольку они экономят один дополнительный шаг. Например, давайте рассмотрим простой сниппет для функции Python, которая меняет местами значения двух переменных:

define swap(x, y)

    buffer = x

    x = y

    y = buffer

Обратите внимание, что сниппеты не всегда могут заменить псевдокод. В псевдокоде мы иногда резюмируем много строк кода в виде одной строки псевдокода, отражая логику алгоритма, при этом не отвлекаясь на излишние детали.

Создание плана выполнения

С помощью псевдокода или сниппетов не всегда возможно задать логику более сложных распределенных алгоритмов. Разработку таких алгоритмов можно разбить на этапы, выполняющиеся в определенном порядке. Верная стратегия разделения крупной задачи на оптимальное количество этапов с должной очередностью имеет решающее значение для эффективного исполнения алгоритма.

Нам необходимо и применить эту стратегию, и одновременно полностью отра­зить логику и структуру алгоритма. План выполнения — один из способов детализации того, как алгоритм будет разделен на множество задач. Задача может представлять собой сопоставления или преобразования, которые сгруппированы в блоки, называемые этапами. На следующей диаграмме (рис. 1.3) показан план, который создается средой выполнения Apache Spark перед исполнением алгоритма. В нем подробно описываются задачи времени выполнения, на которые будет разделено задание, созданное для выполнения нашего алгоритма.

 

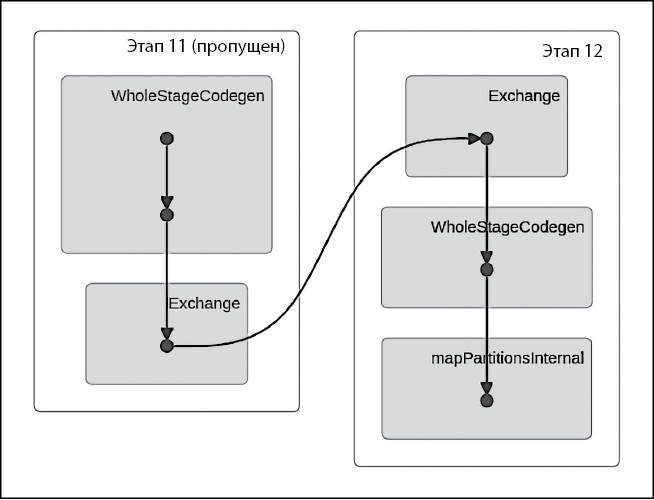
Рис. 1.3

Обратите внимание, что на данной диаграмме представлены пять задач, которые были разделены на два разных этапа: этап 11 и этап 12.

Введение в библиотеки Python

После разработки алгоритм должен быть реализован на языке программирования в соответствии с проектом. Для этой книги я выбрал Python, так как это гибкий язык программирования с открытым исходным кодом. Python также является базовым языком для инфраструктур облачных вычислений, приобретающих все более важное значение, таких как Amazon Web Services (AWS), Microsoft Azure и Google Cloud Platform (GCP).

Официальная домашняя страница Python доступна по адресу https://www.python.org/. Здесь вы найдете инструкции по установке и полезное руководство для начинающих.

Если вы раньше не использовали Python, рекомендуем ознакомиться с этим руководством в целях самообразования. Базовое представление о языке Python поможет лучше понять концепции, представленные в этой книге.

Установите последнюю версию Python 3. На момент написания это версия 3.7.3, которую мы и будем использовать для выполнения упражнений в книге.

Библиотеки Python

Python — это язык общего назначения. Он разработан таким образом, чтобы обеспечить минимальную функциональность. В зависимости от цели использования Python вам придется установить дополнительные библиотеки. Самый простой способ — программа установки pip. Следующая команда pip устанавливает дополнительную библиотеку:

pip install a_package

Установленные ранее библиотеки необходимо периодически обновлять, чтобы иметь возможность использовать новейшие функциональные возможности. Обновление запускается с помощью флага upgrade:

pip install a_package --upgrade

Другим дистрибутивом Python для научных вычислений является Anaconda. Его можно загрузить по адресу https://www.anaconda.com.

В дистрибутиве Anaconda применяется следующая команда для установки новых библиотек:

conda install a_package

Для обновления существующих библиотек дистрибутива Anaconda:

conda update a_package

Существует множество доступных библиотек Python. Некоторые важные биб­лиотеки, имеющие отношение к алгоритмам, описаны далее.

Экосистема SciPy

Scientific Python (SciPy) — произносится как сай пай — это группа библиотек Python, созданных для научного сообщества. Она содержит множество функций, включая широкий спектр генераторов случайных чисел, программ линейной алгебры и оптимизаторов. SciPy — это комплексная библиотека, и со временем специалисты разработали множество расширений для ее настройки и дополнения в соответствии со своими потребностями.

Ниже приведены основные библиотеки, которые являются частью этой экосистемы:

• NumPy. При работе с алгоритмами требуется создание многомерных структур данных, таких как массивы и матрицы. NumPy предлагает набор типов данных для массивов и матриц, которые необходимы для статистики и анализа данных. Подробную информацию о NumPy можно найти по адресу http://www.numpy.org/.

• scikit-learn. Это расширение для машинного обучения является одним из самых популярных расширений SciPy. Scikit-learn предоставляет широкий спектр важных алгоритмов машинного обучения, включая классификацию, регрессию, кластеризацию и проверку моделей. Вы можете найти более подробную информацию о scikit-learn по адресу http://scikit-learn.org/.

• pandas. Библиотека программного обеспечения с открытым исходным кодом. Она содержит сложную табличную структуру данных, которая широко используется для ввода, вывода и обработки табличных данных в различных алгоритмах. Библиотека pandas содержит множество полезных функций, а также обеспечивает высокую производительность с хорошим уровнем оптимизации. Более подробную информацию о pandas можно найти по адресу http://pandas.pydata.org/.

• Matplotlib. Содержит инструменты для создания впечатляющих визуализаций. Данные могут быть представлены в виде линейных графиков, точечных диаграмм, гистограмм, круговых диаграмм и т.д. Более подробную информацию можно найти по адресу https://matplotlib.org/.

• Seaborn. Считается аналогом популярной библиотеки ggplot2 в R. Она основана на Matplotlib и предлагает великолепный расширенный интерфейс для графического отображения статистики. Подробную информацию можно найти по адресу https://seaborn.pydata.org/.

• IPython. Усовершенствованная интерактивная консоль, предназначенная для того, чтобы упростить написание, тестирование и отладку кода Python.

• Запуск Python в интерактивном режиме. Этот режим программирования полезен для обучения и экспериментов с кодом. Программы на Python могут быть сохранены в текстовом файле с расширением .py, и этот файл можно запустить из консоли.

Реализация Python с помощью Jupyter Notebook

Еще один способ запуска программ на Python — через Jupyter Notebook. Jupyter Notebook представляет собой пользовательский интерфейс для разработки на основе браузера. Именно Jupyter Notebook используется для демонстрации примеров кода в этой книге. Возможность комментировать и описывать код с помощью текста и графики делает Jupyter Notebook идеальным инструментом для демонстрации и объяснения любого алгоритма‚ а также отличным инструментом для обучения.

Чтобы запустить программу, вам нужно запустить процесс Jupyter-notebook, а затем открыть свой любимый браузер и перейти по ссылке http://localhost:8888 (рис. 1.4).

 

Рис. 1.4

Обратите внимание, что Jupyter Notebook состоит из ряда блоков, называемых ячейками.

Методы разработки алгоритмов

Алгоритм — это математическое решение реальной проблемы. При разработке и настройке алгоритма мы должны задавать себе следующие вопросы:

• Вопрос 1. Даст ли алгоритм тот результат, который мы ожидаем?

• Вопрос 2. Является ли данный алгоритм оптимальным способом получения этого результата?

• Вопрос 3. Как алгоритм будет работать с большими наборами данных?

Важно оценить сложность задачи, прежде чем искать для нее решение. При разработке подходящего решения полезно охарактеризовать задачу с точки зрения ее требований и сложности. Как правило, алгоритмы можно разделить на следующие типы в зависимости от характеристик задачи:

• Алгоритмы c интенсивным использованием данных. Такие алгоритмы предъявляют относительно простые требования к обработке. Примером является алгоритм сжатия, применяемый к огромному файлу. В таких случаях размер данных обычно намного больше, чем объем памяти процессора (одной ноды или кластера), поэтому для эффективной обработки данных в соответствии с требованиями может потребоваться итеративный подход.

• Вычислительноемкие алгоритмы. Такие алгоритмы предъявляют значительные требования к обработке, но не задействуют больших объемов данных. Пример — алгоритм поиска очень большого простого числа. Чтобы добиться максимальной производительности, нужно найти способ разделить алгоритм на фазы так, чтобы хотя бы некоторые из них были распараллелены.

• Вычислительноемкие алгоритмы с интенсивным использованием данных. Хорошим примером здесь служат алгоритмы, используемые для анализа эмоций в видеотрансляциях. Такие алгоритмы являются наиболее ресурсоемкими алгоритмами и требуют тщательной разработки и разумного распределения доступных ресурсов.

Чтобы определить сложность и ресурсоемкость задачи, необходимо изучить параметры данных и вычислений, чем мы и займемся в следующем разделе.

Параметры данных

Чтобы классифицировать параметры данных задачи, мы рассмотрим ее объем, скорость и разнообразие (часто называемые «три V» — Volume, Velocity, Variety):

• Объем (Volume). Ожидаемый размер данных, которые будет обрабатывать алгоритм.

• Скорость (Velocity). Ожидаемая скорость генерации новых данных при использовании алгоритма. Она может быть равна нулю.

• Разнообразие (Variety). Количество различных типов данных, с которым, как ожидается, будет работать алгоритм.

На рис. 1.5 эти параметры показаны более подробно. В центре диаграммы расположены максимально простые данные с небольшим объемом, малым разнообразием и низкой скоростью. По мере удаления от центра сложность данных возрастает. Она может увеличиваться по одному или нескольким из трех параметров. К примеру, на векторе скорости располагается пакетный процесс как самый простой, за ним следует периодический процесс, а затем процесс, близкий

 

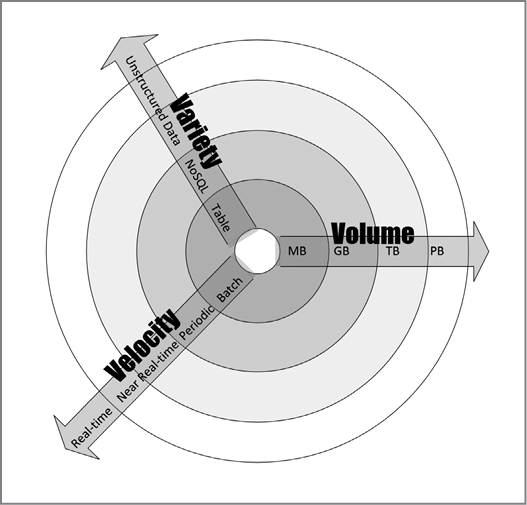
Рис. 1.5

к реальному времени. Наконец, мы видим процесс в реальном времени, который является наиболее сложным для обработки в контексте скорости передачи данных.

Например, если входные данные представляют собой простой csv-файл, то объем, скорость и разнообразие данных будут низкими. С другой стороны, если входные данные представляют собой прямую трансляцию с камеры видеонаблюдения, то объем, скорость и разнообразие данных будут довольно высокими, и эту проблему следует иметь в виду при разработке соответствующего алгоритма.

Параметры вычислений

Параметры вычислений касаются требований к обработке рассматриваемой задачи. От этих требований зависит, какой тип архитектуры лучше всего подойдет для алгоритма. Например, алгоритмы глубокого обучения, как правило, требуют большой вычислительной мощности. Это означает, что для таких алгоритмов важно иметь многоузловую параллельную архитектуру везде, где это возможно.

Практический пример

Предположим, что мы хотим провести анализ эмоциональной окраски в видео­записи. Для этого мы должны отметить на видео человеческие эмоции: печаль, счастье, страх, радость, разочарование и восторг. Это трудоемкий процесс, требующий больших вычислительных мощностей. Как видно на рис. 1.6, для

 

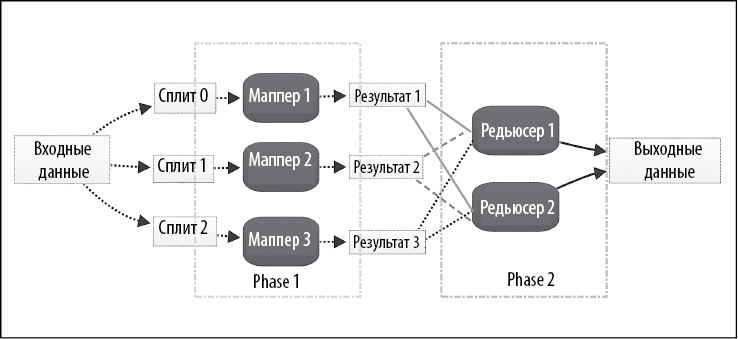
Рис. 1.6

измерения вычислений мы разделили обработку на пять задач, состоящих из двух этапов. Все преобразование и подготовка данных осуществляются в трех мапперах. Для этого мы делим видео на три части, которые называются сплитами. После выполнения маппинга обработанное видео попадает в два агрегатора, которые называются редьюсерами. Чтобы провести анализ эмоциональной окраски, редьюсеры группируют части видео в соответствии с эмоциями. Наконец, результаты объединяются в выводе данных.

Обратите внимание, что количество мапперов напрямую зависит от параллельности выполнения алгоритма. Оптимальное количество мапперов и редьюсеров зависит от характеристик данных, типа алгоритма, который необходимо использовать, и количества доступных ресурсов.

 

Анализ производительности

Анализ производительности алгоритма — важная часть его разработки‚ и одним из способов такой оценки выступает анализ сложности алгоритма.

Теория сложности — это изучение того, насколько сложны алгоритмы. Чтобы быть полезным, алгоритму необходимо обладать тремя ключевыми функциями:

• Он должен быть верным. От алгоритма мало пользы, если он не дает правильных ответов.

• Хороший алгоритм должен быть понятным для компьютера. Лучший алгоритм в мире окажется бесполезным, если его слишком сложно реализовать.

• Хороший алгоритм должен быть эффективным. Невозможно использовать алгоритм, который даст правильный результат, но при этом на его работу уйдет тысяча лет или потребуется 1 миллиард терабайт памяти.

Существуют два типа анализа для количественной оценки сложности алгоритма:

• Анализ пространственной сложности (space complexity analysis) — оценка требований к памяти во время выполнения алгоритма.

• Анализ временной сложности (time complexity analysis) — оценка времени, необходимого для выполнения алгоритма.

Анализ пространственной сложности

При анализе пространственной сложности оценивают объем памяти, необходимый алгоритму для хранения структур временных данных в процессе работы. Способ разработки алгоритма влияет на количество, тип и размер этих структур данных. В эпоху распределенных вычислений и постоянно растущих объемов данных, которые необходимо обрабатывать, анализ пространственной сложности приобретает все большее значение. Размер, тип и количество структур данных определяют требования к памяти для соответствующего оборудования. Современные структуры данных, используемые в распределенных вычислениях, такие как устойчивые распределенные наборы данных (Resilient Distributed Datasets‚ RDDs), должны иметь эффективные механизмы распределения ресурсов, учитывающие требования к памяти на различных этапах выполнения алгоритма.

Анализ пространственной сложности необходим для эффективного проектирования алгоритмов. Если при разработке алгоритма не провести надлежащий анализ, то недостаток памяти для временных структур данных может привести к ненужным перегрузкам диска. Это способно значительно повлиять на производительность и эффективность алгоритма.

В этой главе мы детально рассмотрим временную сложность. Пространственная сложность более подробно будет обсуждаться в главе 13, где мы будем иметь дело с крупномасштабными распределенными алгоритмами со сложными требованиями к памяти во время выполнения.

Анализ временной сложности

Анализ временной сложности позволяет узнать, сколько времени потребуется алгоритму для выполнения задачи, исходя из его структуры. В отличие от пространственной сложности, временная сложность не зависит от оборудования, на котором будет выполняться алгоритм. Она зависит исключительно от структуры алгоритма. Основная цель анализа временной сложности — ответить на ключевые вопросы: будет ли этот алгоритм масштабироваться? Насколько хорошо алгоритм будет обрабатывать большие наборы данных?

Для этого нужно определить влияние увеличения объема данных на производительность алгоритма и убедиться, что алгоритм точен и хорошо масштабируется. Производительность алгоритма становится все более важным показателем в современном мире «больших данных».

Часто мы можем разработать несколько алгоритмов для решения одной и той же задачи. В таком случае нужно проанализировать временную сложность, чтобы ответить на следующий вопрос:

«С учетом обозначенной проблемы какой из нескольких алгоритмов наиболее эффективен с точки зрения экономии времени?»

Существуют два основных подхода к вычислению временной сложности алгоритма:

• Профилирование после реализации. При данном подходе реализуются различные алгоритмы-кандидаты и сравнивается их производительность.

• Теоретический подход до реализации. При этом подходе производительность каждого алгоритма математически аппроксимируется перед запуском алгоритма.

Преимущество теоретического подхода заключается в том, что он зависит лишь от структуры самого алгоритма. Он не зависит от оборудования, на котором будет выполняться выбранный алгоритм, или от языка программирования, используемого для реализации алгоритма.

Оценка эффективности

Производительность алгоритма обычно зависит от типа входных данных. Например, если данные уже отсортированы в соответствии с контекстом задачи, алгоритм может работать невероятно быстро. Если отсортированные входные данные используются для проверки конкретного алгоритма, то он даст неоправданно высокое значение производительности. Это не будет истинным отражением настоящей производительности алгоритма в большинстве сценариев. Чтобы решить проблему зависимости алгоритмов от входных данных, мы должны учитывать различные типы сценариев при проведении анализа производительности.

Наилучший сценарий

При наилучшем сценарии входные данные организованы таким образом, чтобы алгоритм обеспечивал наилучшую производительность. Анализ наилучшего сценария дает верхнюю границу производительности.

Наихудший сценарий

Второй способ оценить производительность алгоритма — попытаться найти максимально возможное время, необходимое для выполнения задачи при заданном наборе условий. Такой анализ алгоритма весьма полезен, поскольку мы при этом гарантируем, что независимо от условий производительность алгоритма всегда будет лучше результатов нашего анализа. Анализ наихудшего сценария лучше всего подходит для оценки производительности при решении сложных проблем с большими наборами данных. Анализ наихудшего сценария дает нижнюю границу производительности алгоритма.

Средний сценарий

Этот подход начинается с разделения всех возможных входных данных на группы. Затем проводится анализ производительности на основе ввода данных от каждой группы. Далее вычисляется среднее значение производительности для каждой из групп.

Анализ среднего сценария не всегда точен, так как он должен учитывать все возможные комбинации входных данных, что не всегда легко сделать.

Выбор алгоритма

Как узнать, какой алгоритм является наилучшим решением? Как узнать, какой алгоритм сработает быстрее? Временная сложность (time complexity) и «О-большое» (обсуждаемые позже в этой главе) — хорошие инструменты для получения ответов на такие вопросы.

Рассмотрим простую задачу сортировки списка чисел. Существует несколько доступных алгоритмов, которые способны выполнить эту работу. Вопрос в том, как выбрать правильный.

Прежде всего следует заметить, что если в списке не слишком много чисел, то не имеет значения, какой алгоритм мы выберем для сортировки. Например, если в списке всего 10 чисел (n = 10), то какой бы алгоритм мы ни выбрали, его выполнение вряд ли займет более нескольких микросекунд, даже при очень плохой разработке. Но как только размер списка достигнет одного миллиона, выбор правильного алгоритма станет важным шагом. Плохой алгоритм может выполняться несколько часов, в то время как хороший способен завершить сортировку списка за пару секунд. Таким образом, в случае большого объема входных данных имеет смысл приложить усилия: выполнить анализ производительности и выбрать алгоритм, который будет эффективно решать требуемую задачу.

«О-большое»

«О-большое» используется для количественной оценки производительности алгоритмов по мере увеличения размера входных данных. Это одна из самых популярных методик, используемых для проведения анализа наихудшего сценария. В этом разделе мы обсудим различные типы «О-большого».

Константная временная сложность (O(1))

Если выполнение алгоритма занимает одинаковое количество времени независимо от размера входных данных, то про него говорят, что он выполняется постоянное время. Такая сложность обозначается как O(1). В качестве примера рассмотрим доступ к n-му элементу массива. Независимо от размера массива для получения результата потребуется одно и то же время. Например, следующая функция вернет первый элемент массива (ее сложность O(1)):

def getFirst(myList):

    return myList[0]

Выходные данные показаны ниже (рис. 1.7):

 

Рис. 1.7

• Добавление нового элемента в стек с помощью push или удаление элемента из стека с помощью pop. Независимо от размера стека добавление или удаление элемента займет одно и то же время.

• Доступ к элементу хеш-таблицы.

• Блочная (иначе называемая корзинная или карманная) сортировка (Bucket sort).

Линейная временная сложность (O(n))

Считается, что алгоритм имеет линейную временную сложность, обозначаемую O(n), если время выполнения прямо пропорционально размеру входных данных. Простой пример — добавление элементов в одномерную структуру данных:

def getSum(myList):

    sum = 0

    for item in myList:

        sum = sum + item

    return sum

Взгляните на основной цикл алгоритма. Число итераций в основном цикле линейно увеличивается с увеличением значения n, что приводит к сложности O(n) на рис. 1.8.

 

Рис. 1.8

Ниже приведены некоторые другие примеры операций с массивами:

• Поиск элемента.

• Нахождение минимального значения среди всех элементов массива.

Квадратичная временная сложность (O(n2))

Считается, что алгоритм выполняется за квадратичное время, если время выполнения алгоритма пропорционально квадрату размера входных данных. Например, простая функция, которая суммирует двумерный массив, выглядит следующим образом:

def getSum(myList):

    sum = 0

    for row in myList:

        for item in row:

            sum += item

    return sum

Обратите внимание на вложенный цикл внутри основного цикла. Этот вложенный цикл и придает коду сложность O(n2) (рис. 1.9).

 

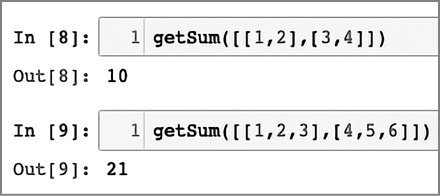
Рис. 1.9

Другим примером квадратичной временной сложности является алгоритм сор­тировки пузырьком (представленный в главе 3).

Логарифмическая временная сложность (O(logn))

Считается, что алгоритм выполняется за логарифмическое время, если время выполнения алгоритма пропорционально логарифму размера входных данных. С каждой итерацией размер входных данных уменьшается в несколько раз. Примером логарифмической временной сложности является бинарный поиск. Алгоритм бинарного поиска используется для поиска определенного элемента в одномерной структуре данных, такой как список в Python. Элементы в структуре данных должны быть отсортированы в порядке убывания. Алгоритм бинарного поиска реализован в функции с именем searchBinary следующим образом:

def searchBinary(myList,item):

    first = 0

    last = len(myList)-1

    foundFlag = False

    while( first<=last and not foundFlag):

        mid = (first + last)//2

        if myList[mid] == item :

            foundFlag = True

        else:

            if item < myList[mid]:

                last = mid - 1

            else:

                first = mid + 1

    return foundFlag

Работа основного цикла подразумевает тот факт, что список упорядочен. На каждой итерации список делится пополам, пока не будет получен результат (рис. 1.10):

 

Рис. 1.10

Определив функцию, мы переходим к поиску определенного элемента в строках 11 и 12. Алгоритм бинарного поиска более подробно обсуждается в главе 3.

Обратите внимание, что среди четырех последних представленных типов временной сложности O(n2) имеет худшую производительность, а O(logn) — лучшую. Фактически производительность O(logn) можно рассматривать как золотой стандарт производительности любого алгоритма (что, однако, не всегда достижимо). С другой стороны, O(n2) не так плох, как O(n3), но все же алгоритмы этого типа нельзя использовать для больших данных, поскольку временная сложность ограничивает объем данных, которые они способны обработать за разумное количество времени.

Чтобы понизить сложность алгоритма, мы можем пожертвовать точностью и использовать приближенный алгоритм.

Весь процесс оценки производительности алгоритмов носит итерационный характер, как показано на рис. 1.11.

 

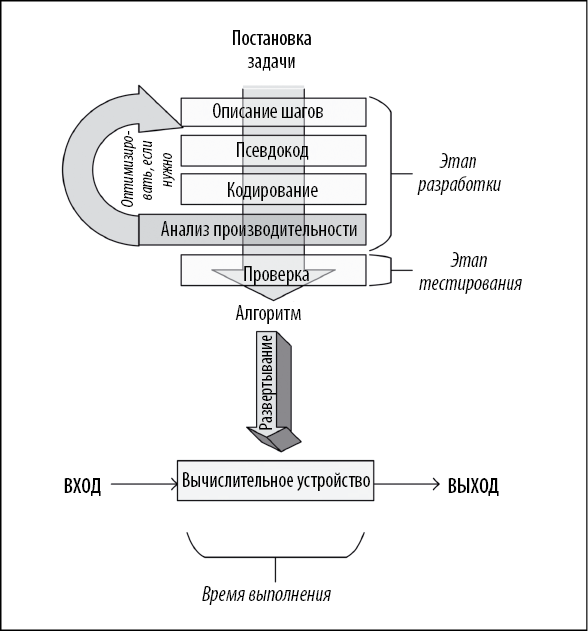
Рис. 1.11

Проверка алгоритма

В процессе проверки алгоритма мы должны убедиться, что он действительно предоставляет математическое решение для нашей задачи. Необходимо проверить результаты для максимального числа возможных значений и типов входных данных.

Точные, приближенные и рандомизированные алгоритмы

Для различных типов алгоритмов используются разные методы тестирования. Сначала выявим различие между детерминированными и рандомизированными алгоритмами.

В случае детерминированных алгоритмов конкретные входные данные всегда порождают одинаковые выходные данные. Но для ряда классов алгоритмов в качестве входных данных используется последовательность случайных чисел, что делает выходные данные разными при каждом запуске алгоритма. Алгоритм k-средних, который подробно описан в главе 6, является хорошим примером (рис. 1.12).

 

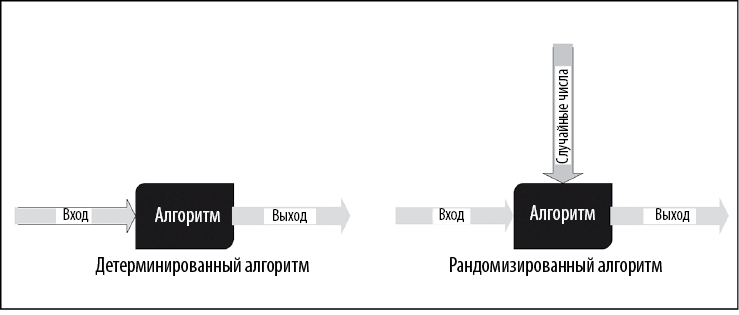
Рис. 1.12

Иногда, чтобы упростить логику и ускорить выполнение алгоритма, используются некоторые допущения. Таким образом, алгоритмы также делятся на два типа:

• Точный алгоритм (exact algorithm). Ожидается, что такой алгоритм даст точное решение без каких-либо допущений или приближений.

• Приближенный алгоритм (approximate algorithm). Когда сложность задачи слишком велика для имеющихся ресурсов, мы упрощаем нашу задачу, делая допущения. Алгоритмы, основанные на этих упрощениях или допущениях, называются приближенными алгоритмами и дают не совсем точное решение.

Чтобы понять разницу между точными и приближенными алгоритмами‚ рассмотрим знаменитую задачу коммивояжера (TSP — travelling salesman problem), впервые представленную в 1930 году. Задача состоит в том‚ чтобы найти кратчайший маршрут для торговца‚ при котором он посетит каждый город из списка, а затем вернется в исходную точку (поэтому она и называется задачей коммивояжера). Для ее решения нужно рассмотреть все возможные комбинации городов и выбрать наименее затратную. Сложность этого подхода составляет O(n!), где n — количество городов. Очевидно, что временная сложность при n > 30 слишком велика.

Если число городов превышает 30, одним из способов снижения сложности является введение ряда приближений и допущений.

При описании требований к приближенному алгоритму важно задать ожидаемую точность. Во время проверки такого алгоритма мы должны убедиться, что погрешность результатов остается в допустимом диапазоне.

Объяснимость алгоритма

Если алгоритм применяется в особо важной ситуации, мы должны иметь возможность объяснить причину того или иного результата. Необходимо убедиться, что вследствие использования алгоритма было принято справедливое решение.

Возможность четко определить признаки, которые прямо или косвенно повлия­ли на конкретное решение, называется объяснимостью алгоритма. Алгоритмы, используемые в жизненно важных ситуациях, оцениваются с точки зрения обоснованности результатов. Этический анализ стал стандартной частью процесса проверки алгоритмов, влияющих на принятие решений, которые касаются жизни людей.

В случае с алгоритмами глубокого обучения достичь объяснимости бывает трудно. Например, если алгоритм используется для отказа в заявлении на ипотеку, важны его прозрачность и возможность объяснить причину.

Алгоритмическая объяснимость — это область активных исследований. Один из эффективных методов LIME (Local Interpretable Model-Agnostic Explanations) был предложен в материалах Ассоциации вычислительной техники (ACM) на 22-й международной конференции по извлечению знаний из данных Special Interest Group on Knowledge Discovery (SIGKDD) в 2016 году. Согласно этому методу, во входные данные каждого экземпляра вносятся небольшие изменения, а затем предпринимается попытка отобразить локальную границу принятия решений для этого экземпляра. После этого можно количественно оценить влияние каждой переменной для этого экземпляра.

Резюме

Эта глава была посвящена изучению основ алгоритмов. Мы узнали об этапах разработки и обсудили различные способы определения логики алгоритма. Далее разобрались, как разработать алгоритм. Наконец, рассмотрели способы анализа производительности и различные аспекты проверки алгоритма.

Прочитав эту главу, мы узнали, что такое псевдокод алгоритма. Нам стали понятны различные этапы разработки и развертывания алгоритма. Мы также узнали, как применять «О-большое» для оценки производительности алгоритма.

Следующая глава посвящена структурам данных, используемым в алгоритмах. А начнем мы с рассмотрения структур данных, представленных в Python. Затем научимся создавать более сложные структуры (стеки, очереди и деревья), необходимые для разработки сложных алгоритмов.

2. Структуры данных, используемые в алгоритмах

Во время работы алгоритму необходима структура данных, чтобы хранить временные данные в памяти. Выбор подходящей структуры имеет ключевое значение для эффективной реализации алгоритма. Определенные классы алгоритмов являются рекурсивными или итеративными по своей логике и нуждаются в специально разработанных структурах данных. Например, добиться хорошей производительности рекурсивного алгоритма проще, если использовать вложенные структуры. Поскольку в книге мы используем Python, эта глава будет посвящена структурам данных Python. Однако эти знания пригодятся и для работы с другими языками, такими как Java и C++.

Прочтя эту главу, вы узнаете, как именно Python обрабатывает сложные структуры данных и какие из них используются для определенного типа данных.

В этой главе нас ждут:

• Структуры данных в Python.

• Абстрактные типы данных.

• Стеки и очереди.

• Деревья.

Структуры данных в Python

В любом языке программирования структуры данных используются для хранения и управления сложными данными. В Python структуры данных — это контейнеры, позволяющие эффективно управлять данными, организовывать их и осуществлять поиск. Они организованы в коллекции — группы элементов данных, которые требуется хранить и обрабатывать совместно. В Python существуют пять различных структур данных для хранения коллекций:

• Список (List). Упорядоченная изменяемая последовательность элементов.

• Кортеж (Tuple). Упорядоченная неизменяемая последовательность элементов.

• Множество (Set). Неупорядоченная последовательность элементов.

• Словарь (Dictionary). Неупорядоченная последовательность пар «ключ — значение».

• DataFrame. Двумерная структура для хранения двумерных данных.

Давайте рассмотрим их более подробно.

Список

В Python список — это основная структура данных, используемая для хранения изменяемой последовательности элементов.

Элементы данных в списке могут быть разных типов.

Чтобы создать список, элементы нужно заключить в квадратные скобки [ ] и разделить запятыми. Ниже представлен пример кода, который создает список из четырех элементов данных разных типов:

>>> aList = ["John", 33,"Toronto", True]

>>> print(aList)

['John', 33, 'Toronto', True]Ex

Список в Python — это удобный способ создания одномерных изменяемых структур данных, необходимых главным образом на различных внутренних этапах алгоритма.

Использование списков

При работе со списками мы получаем полезные инструм