автордың кітабын онлайн тегін оқу Сопротивление материалов. Конспект лекций
Информация о книге
УДК 530.152.1
ББК 30.121
Г67
Автор: Горбачев К. П.
Рецензенты:
Друзь И. Б., д-р техн. наук, проф., зав. каф. теоретической механики и сопротивления материалов МГУ им. Г. И. Невельского;
Лукьянова Г. В., канд. техн. наук, доц., зав. каф. теоретической и прикладной механики Дальрыбвтуза.
В основу конспекта лекций положены требования государственного образовательного стандарта для направления 652900 «Кораблестроение и океанотехника», согласно которому объем лекционного курса «Сопротивление материалов» составляет 54 часа.
Материал полностью соответствует действующим государственным стандартам и учебным программам и в достаточной мере раскрывает содержание разделов, традиционно изучаемых в курсе сопротивления материалов. Кроме того, приводятся решения, устраняющие некоторые методологические неточности, содержащиеся в учебной литературе и отвечающие стандартным представлениям многих авторов учебников и пособий.
Теоретический материал раскрывается с помощью решения типовых задач. Отличительной особенностью изложения решений задач является полное соответствие требованиям выполнения технических расчетов. Единообразное представление материала в ясной и доступной форме облегчит студентам его усвоение.
Усвоению курса способствуют иллюстрации, соответствующие содержанию материала.
В приложении приведен материал для самостоятельного освоения темы «Геометрические характеристики».
УДК 530.152.1
ББК 30.121
© Дальневосточный государственный технический университет, 2007
© ДВФУ, 2015
© ООО "Проспект", электронная версия книги, 2015
Лекция 1. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ В ИНЖЕНЕРНОМ ОБРАЗОВАНИИ
Любое инженерное сооружение (рис. 1.1–1.3) – корабль, самолет, здание, мост, тоннель, автомобиль и т.д. – обязательно имеет несущие элементы.
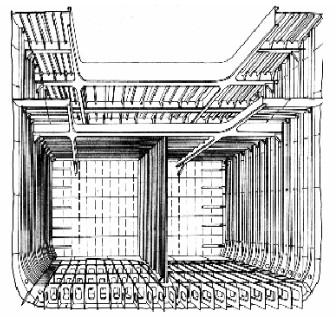
Рис. 1.1. Элементы корпуса грузового судна

Рис. 1.2. Каркас высотного дома и трансляционной вышки

Рис. 1.3. Несущие и опорные элементы моста
Несущие элементы конструкции должны проектироваться и создаваться так, чтобы они были долговечными, т.е. могли воспринимать все силовые воздействия, не разрушаясь в течение эксплуатации конструкции. Кратко говоря, конструкции должны быть прочными.
Конструкция может быть прочной, но излишне деформативной, т.е. недостаточно жесткой. Как следствие, могут возникать колебания, затрудняющие и даже делающие невозможной ее эксплуатацию (рис. 1.1–1.5).
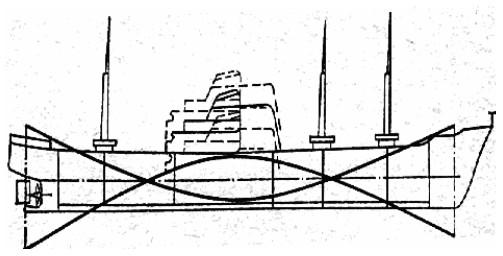
Рис. 1.4. Поперечные колебания корпуса судна

Рис. 1.5. Висячий мост через р. Такома (США). Вскоре после ввода в эксплуатацию мост начал интенсивно раскачиваться под действием ветра и затем рухнул
Сжатая недостаточно жесткая конструкция может изогнуться (выпучиться) от действия сжимающей нагрузки, что приведет к потере ее несущей способности или поломке. Это связано с так называемым явлением потери устойчивости (рис. 1.6).
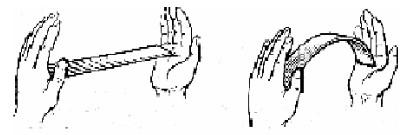
Рис. 1.6. Простейшая иллюстрация явления потери устойчивой формы равновесия
Проблемами расчета различных типов сооружений и их несущих конструкций на прочность, жесткость и устойчивость занимается инженерная наука – строительная механика. Сопротивление материалов является учебной дисциплиной, в которой знакомятся с основными понятиями и принципами, используемыми в строительной механике, и обычно ограничиваются расчетами отдельных элементов конструкций: стержнями, балками или простейшими системами, составленными из них.
В курсе сопротивления материалов последовательно рассматриваются основные виды деформаций: растяжение, сжатие, кручение, изгиб стержней. Наряду с введением соответствующих понятий большое внимание уделяется умению представить работу элемента конструкции с помощью сознательно упрощенной расчетной схемы и соответствующих аналитических зависимостей, что принято называть построением физико-математической модели работы элемента или части конструкции.
Правильно и грамотно построенные расчетные модели позволяют ответить на многие важные инженерные вопросы: дать оценку прочности существующей конструкции; определить предельно допустимые нагрузки; подобрать необходимые размеры элементов и выбрать подходящие материалы, обеспечивающие их прочность и экономичность; провести оптимизацию параметров конструкции, т.е. найти параметры, обеспечивающие в определенном смысле наилучшие свойства этой конструкции.
Изучение сопротивления материалов требует знаний по физике, математике, теоретической механике и базируется на сведениях, изучаемых в курсах этих предметов. Знание основ сопротивления материалов является важнейшим требованием при подготовке инженеров.
Твердые тела и идеализация их свойств.
Допущения о свойствах материалов элементов конструкций
Элементы конструкций изготавливаются из различных материалов – металлов, бетона, дерева, полимеров и др. Их структура и физические свойства могут быть весьма разнообразны. Любой материал состоит из молекул и атомов. Реальные материалы всегда имеют те или иные дефекты в виде неоднородности кристаллической решетки, микротрещин, пор или инородных включений. Расчет конструкций с учетом всего многообразия физико-механических свойств материалов является или невозможным, или в силу своей сложности практически неприемлемым. Кроме того, одновременный учет всех факторов – основных и второстепенных – нецелесообразен с точки зрения влияния каждого из них на окончательный результат.
Для построения логически стройной теории деформирования тел приходится прибегать к определенной идеализации свойств материалов, т.е. возникает необходимость использовать некоторые гипотезы и допущения, идеализирующие реальные материалы.
В связи с этим вводятся соответствующие понятия:
• сплошность;
• однородность или неоднородность;
• изотропность или анизотропность;
Сплошность – полное заполнение материалом всего объема тела без учета конкретной структуры материала (зернистая, кристаллическая и др.) (рис. 1.7).

Рис. 1.7. Структура реального материала с дефектами и включениями и гипотетический сплошной материал
Однородность – отсутствие включений со свойствами, отличными от основного материала, т.е. весь объем материала обладает одинаковыми механическими свойствами (рис. 1.8).
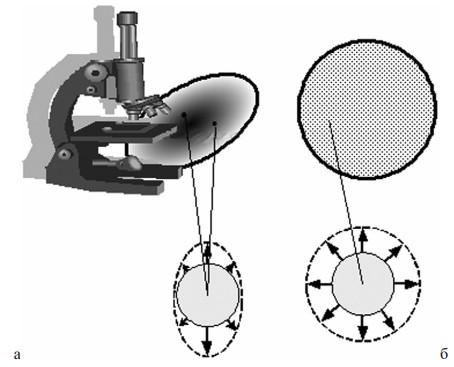
Рис. 1.8. Структура реального материала с инородными включениями и гипотетический однородный материал: а) инородные включения; б) однородный материал
Изотропность – механические свойства материала во всем объеме тела по различным направлениям одинаковы. В противном случае материал называется анизотропным.
Все реальные тела на молекулярном уровне анизотропны. Однако элементарные объемы состоят из большого количества молекул, а если тело кристаллическое, то из большого числа различно ориентированных кристаллов. Такой элементарный объем может быть изотропным в среднем (квазиизотропным), поэтому многие материалы с достаточной точностью можно рассматривать как изотропные. Однако существует много анизотропных материалов, например, слоистые пластики или обыкновенное дерево (вдоль волокон одни свойства, а поперек – другие) (рис. 1.9).
Пример анизотропного материала (дерево)
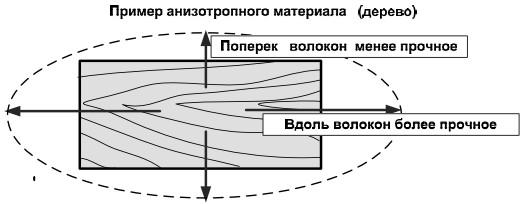
Рис. 1.9. Пример анизотропного материала
Использование некоторой структурной идеализации материала существенно упрощает изучение механики деформирования элементов конструкций.
Соответствие условного материала реальному достигается тем, что в расчет вводятся экспериментально получаемые усредненные характеристики механических свойств реальных материалов.
Не менее важным понятием является понятие деформируемости. С деформируемостью связаны такие понятия как упругость, пластичность и т. д.
Под упругостью понимается свойство тела принимать начальные размеры и форму после устранения причин, вызвавших его деформацию. Наличие остаточных изменений в размерах и форме тела свидетельствует о признаках пластичности и (или) начале процесса разрыхления, предшествующего разрушению.
Деформируемость присуща всем реальным телам. Изменение размеров и формы тела под действием нагрузки называют деформацией тела. Именно в результате деформации тела или конструкции возникают внутренние силы, определяющие прочность материала конструкции. На рис. 1.10 изображены три характерные диаграммы деформирования, связывающие значения силы F и деформации
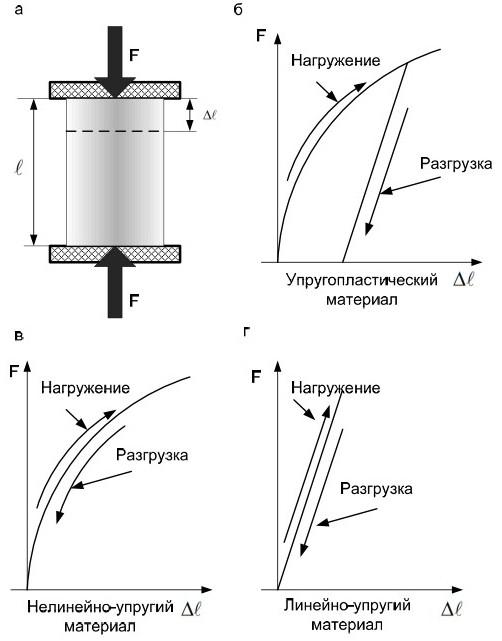
Рис. 1.10. Характерные диаграммы деформирования материалов: а) схема деформирования образца; б) упругопластический материал с нелинейно диаграммой деформирования; в) упругий материал с нелинейной диаграммой деформирования; г) линейно-упругий материал
Материал элементов конструкций будем в дальнейшем считать сплошным, однородным, изотропным и линейно-упругим.
Лекция 2. ВНЕШНИЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ТЕЛА
Сила является мерой механического взаимодействия тела с окружающими телами или средой.
Механика твердого деформируемого тела и сопротивление материалов в частности изучает прочность и деформирование реальных тел (конструкций и их элементов) под действием приложенных к ним внешних сил (рис. 2.1–2.5), температурных, магнитных полей и других воздействий.

Рис. 2.1. Поверхностные внешние сипы, действующие на корпус судна (волновые динамические нагрузки)

Рис. 2.2. Ледовая нагрузка на корпус судна
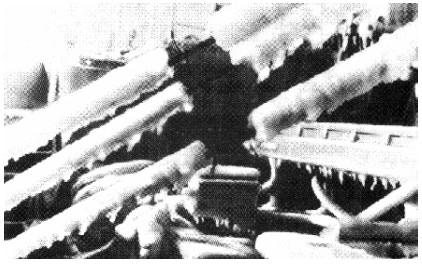
Рис. 2.3. Ледовая нагрузка на такелаж судна при обледенении в море
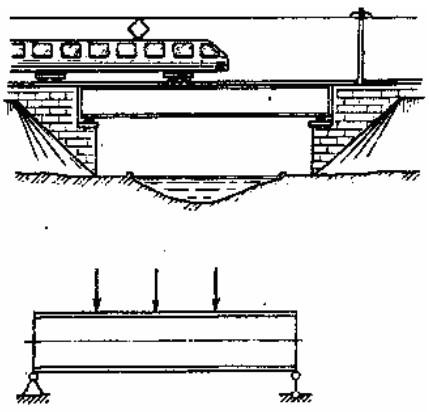
Рис. 2.4. Подвижная нагрузка на несущие элементы моста как результат взаимодействия электровоза и балок моста. Точки приложения зависят от скорости движения электровоза
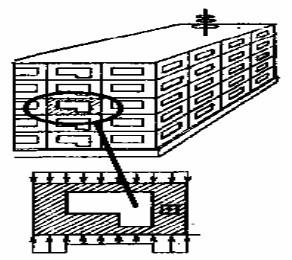
Рис. 2.5. Статические нагрузки, действующие на панель здания (статические нагрузки определяются как результат взаимодействия рассматриваемой панели со смежными панелями с учетом массовых сил и реакций взаимодействия)
При всем многообразии действия сил внешние силы могут быть классифицированы по нескольким признакам.
По способу приложения внешние силы разделяются на объемные, поверхностные и сосредоточенные.
Объемные силы
Объемные силы (силы тяжести, инерции, магнитные и т.д.) непрерывно распределены по объему, занятому телом. Объемную силу, действующую на тело, можно определить как сумму объемных сил, действующих на каждый элементарный объем тела. Например, силу веса элементарного объема
В данном случае произведение
Если в окрестности некоторой точки выделить конечный элементарный объем
Здесь специально оговаривается понятие осредненной интенсивности, так как в пределах конечного объема физический параметр, например, плотность, может быть переменной величиной. Для получения интенсивности объемной силы в каждой точке тела необходимо рассматривать объемы, выражающиеся в объемные точки. Объем таких элементов стремится к нулю и физический параметр, определяющий внешнее воздействие, становится практически постоянной величиной в пределах рассматриваемого элементарного объема, т.е., стягивая объем к точке, получим
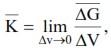
где К – вектор интенсивности объемной силы в рассматриваемой точке.
Вектор интенсивности объемных сил обычно задают в проекциях на координатные оси. Правило знаков обычное, как для проекций. Проекции вектора интенсивности объемной силы на оси 0х, 0у, 0z можно обозначить как
Размерность объемных сил определяется как отношение
Например, средняя интенсивность массовых сил автомобиля при его общей массе m и объеме кузова V (рис. 2.6) будет равна:
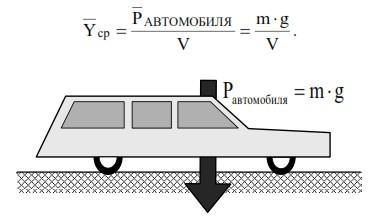
Рис. 2.6. Пример представления объемной силы в виде сосредоточенного силового фактора
Однако в каждой точке объема интенсивность объемных сил будет своя, так как она определяется насыщенностью и положением узлов конструкции кузова, агрегатов двигателя и подвижной части (рис. 2.7).
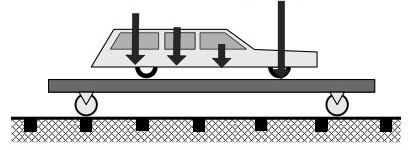
Рис. 2.7. Представление объемных сил в виде дискретного их распределения по длине автомобиля
При детальном анализе, например, анализе прочности кузова автомобиля, это необходимо учитывать, т.е. без формулы (2.2) как основы трудно обойтись.
Важно усвоить, что эти силы, внутренние по своей природе, искусственно относятся к разряду внешних сил. Это можно делать только тогда, когда они определены величинами и направлением действия.
Поверхностные силы
Поверхностные силы могут быть следствием воздействия другого соприкасающегося с ним тела – твердого, жидкого или газообразного. Поверхностные силы – это силы взаимодействия между соседними телами или между рассматриваемым элементом конструкции и окружающей средой. Например, на рис. 2.8, а показана некоторая система взаимодействующих тел – груз массой m транспортируется на платформе, которая, в свою очередь, через шаровые опоры взаимодействует с грунтовым основанием.
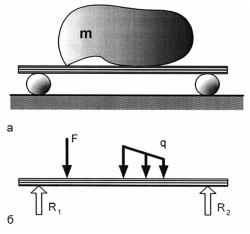
Рис. 2.8. Поверхностные силы: а) расчетная схема; б) основная схема
Объектом расчета является платформа, поэтому необходимо определить нагрузки, действующие на нее как результат взаимодействия платформы с взаимодействующими телами:
1) внешние усилия от взаимодействия платформы с массой перевозимого груза. В данном случае особенностью взаимодействия является то, что часть груза контактирует с платформой в пределах малой площадки (практически взаимодействие сосредоточено в точке), а другая часть поверхности груза соприкасается с платформой в пределах площадки конечных размеров;
2) внешние усилия от взаимодействия платформы с грунтовым основанием. В данном случае взаимодействие осуществляется через шаровые опоры.
Характер взаимодействия тел (рис. 2.8, б) в расчетных схемах отражается в виде векторов (R, F, q и т.д.), по виду которых можно оценить характер соприкосновения.
Обычно используют следующие обозначения:
R – для реакций оснований;
F – для результирующих внешних сил;
Q, q – для распределенной нагрузки.
Поскольку соприкосновение реальных деформируемых тел всегда происходит не в точке, а по некоторой площадке, поверхностные нагрузки являются распределенными. Имея некоторое тело (рис. 2.9), рассмотрим элементарную площадку
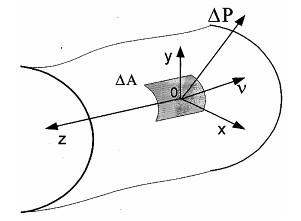
Рис. 2.9. Схема определения интенсивности поверхностной нагрузки
Поверхностную нагрузку, действующую на эту площадку, обозначим
Интенсивность переменной поверхностной нагрузки задается для каждой точки поверхности. В этом случае площадка стягивается к точке, т.е. необходимо перейти к пределу:
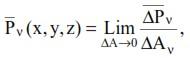
где
Также как и интенсивность объемной силы, интенсивность поверхностной нагрузки проецируется на координатные оси. Обозначим эти проекции на оси 0х, 0у, 0z соответственно
Размерность интенсивности поверхностной нагрузки Н/м2 = Па.
Сосредоточенные силы
В тех случаях, когда площадка контакта пренебрежимо мала по сравнению с размерами нагружаемой поверхности, вводят понятие сосредоточенной силы Р как равнодействующей нагрузки по указанной площадке (рис. 2.10). Размерность сосредоточенной силы – Н (ньютон).
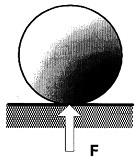
Рис. 2.10. Пример сосредоточенной силы
В практических расчетах часто встречается нагрузка, распределенная по длине элемента конструкции. Так, если на верхний поясок балки действует нагрузка интенсивностью Рv (рис 2.11), то вводится понятие погонной интенсивности Q = Pvb, где b – ширина верхнего пояска.
Погонная интенсивность нагрузки выражается в единицах силы, отнесенных к единице длины (Н/м, кН/м и т.д.).
Таким образом, интенсивность поверхностной нагрузки в общем случае определяется как предел отношения равнодействующей сил, действующих на площадку, к ее площади, стремящейся к нулю.
Для интенсивности нагрузки применимо следующее правило знаков: компонента вектора интенсивности положительна, если она совпадает с направлением соответствующей оси координат.
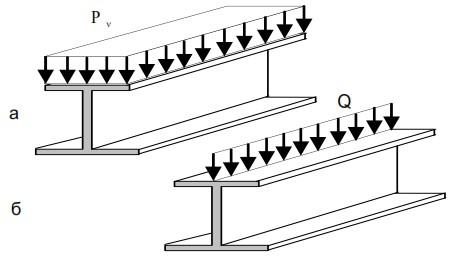
Рис. 2.11. Внешняя нагрузка: а) распределенная; б) погонная
Возможны и моментные воздействия в виде сосредоточенных и распределенных по длине моментов (рис. 2.12).
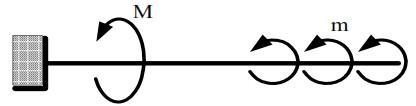
Рис. 2.12. Сосредоточенный и распределенный моменты
Сосредоточенные моменты выражаются в единицах сил, умноженных на единицу длины (Н·м, кН·м и т.д.).
Распределенный по длине момент имеет размерность силы (Н), т.к. определяет величину момента, приходящегося на единицу длины (Н·м/м = Н).
По характеру изменения в процессе действия нагрузки делятся на статические (рис. 2.13, а), динамические и повторно-переменные (2.13, б, в).
К статическим относятся нагрузки, при действии которых силами инерции массы тела, возникающими в процессе нагружения, можно пренебречь.
Динамические нагрузки, в отличие от статических, вызывают большие ускорения и силы инерции, что приводит к колебаниям конструкций, сооружений и их элементов.
Повторно-переменными называются нагрузки, многократно (до нескольких миллионов раз) изменяющие со временем значение и знак. Разрушение материала под действием таких нагрузок называется усталостным.
Схема определения внешних сил, действующих на конструкцию
Если конструкция рассматривается изолированно от окружающих тел, а практически это неизбежно, то их действие на рассматриваемую конструкцию заменяется силами, которые мы называем внешними. Их величина и характер распределения зависят в первую очередь от того, где проходит граница между рассматриваемым объектом и окружающими его телами.
Положим, нас интересует прочность железнодорожной платформы (рис. 2.13, а). Это – объект нашего исследования. Если этот объект рассматривается изолированно, то его взаимодействие с окружающими телами заменяется системой сил (рис. 2.13, в).
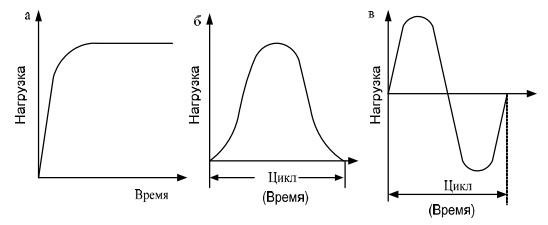
Рис. 2.13. Виды нагружения: а) статическое; б) динамическое; в) повторно-динамическое
Эти силы для нашего объекта – внешние. В их число включается не только сила тяжести платформы Р2, но также реакции взаимодействия автомобиля и платформы R1, R2 и реакции опор R3, R4, дополняющие систему внешних сил до равновесной.
Реакции R1, R2 можно заменить силой веса автомобиля Р1, которую они уравновешивают. Но при оценке прочности платформы положение и величины реакций могут иметь принципиальное значение, поэтому решение задачи целесообразно начинать с определения значений реакций R1, R2 (рис. 2.13, б). При найденных значениях R1, R2 решается задача прочности платформы в заданных границах объекта (рис. 2.13, в).
Таким образом, взаимодействие рассматриваемого объекта с телами, расположенными за пределами условно очерченной границы объекта, характеризуются силами, которые называем внешними (рис. 2.14).
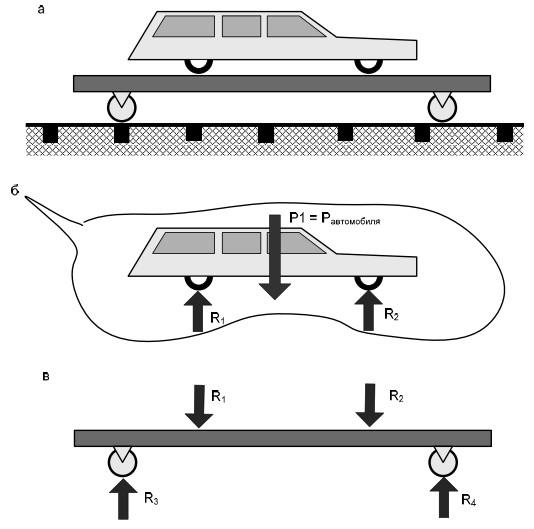
Рис. 2.14. Внешние сипы, действующие на платформу (конструкцию)
На рис. 2.15 приведены условия для определения соответствующих реакций взаимодействия между теми или иными частями рассматриваемого объекта. Такими условиями могут служить уравнения равновесия, которые принимают тот или иной вид в соответствии с расчетной схемой.
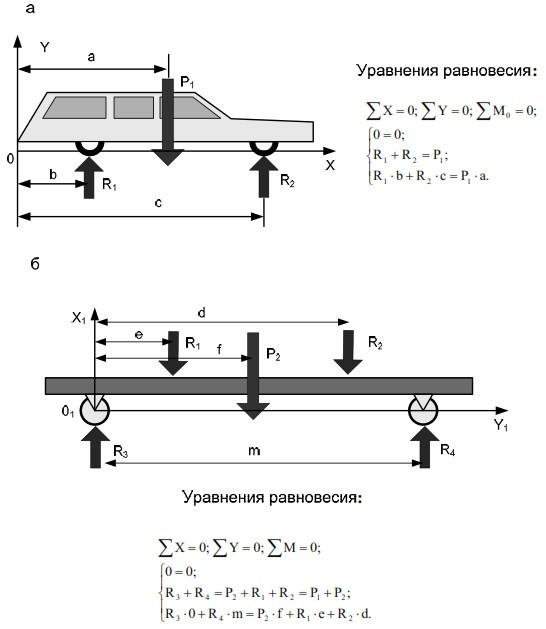
Рис. 2.15. Схемы определения компонентов внешней нагрузки: а) определение реакций взаимодействия автомобиля с платформой; б) определение реакций взаимодействия груженной платформы с полотном дороги
Лекция 3. ВНУТРЕННИЕ СИЛЫ. НАПРЯЖЕНИЯ
Внутренние силы
Между частицами твердого тела до приложения внешних нагрузок действуют внутренние силы, обеспечивающие неизменность его формы. Под влиянием приложенных нагрузок силы взаимодействия получают приращения, между частицами тела несколько изменяются расстояния и тело деформируется.
В сопротивлении материалов под внутренними силами понимаются приращения сил взаимодействия между частицами, возникающими при его нагружении.
В условном материале (сплошном и однородном) внутренние силы передаются сплошным потоком от одной части тела к другой через разделяющую эти части воображаемую поверхность (рис. 3.1).
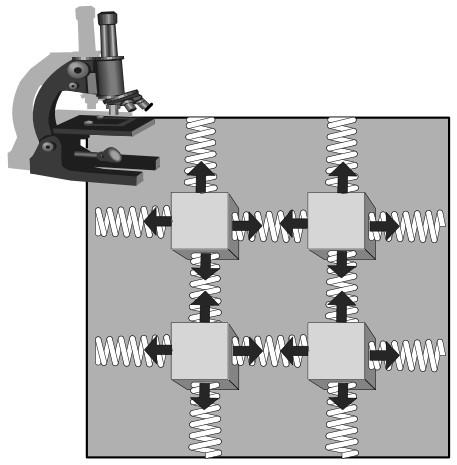
Рис. 3.1. Условное отражение потоков внутренних сип через разделяющие поверхности (грани микрообъемов)
Таким образом, в недеформированном состоянии, т.е. при отсутствии внешних воздействий, связанность частиц тела обусловлена силами их взаимодействия. Эти силы стремятся сохранить тело как единое целое, препятствуя любой попытке изменить взаимное расположение микро- и макрочастиц и таким образом деформировать его. Внешние воздействия, наоборот, стремятся вызвать деформирование тела путем изменения положения частиц и сил их взаимодействия.
Если бы механика деформируемого твердого тела ставила перед собой задачу изучать силы, действующие на каждый атом или даже кристалл в отдельности, пользоваться ее аппаратом было бы чрезвычайно трудно, поэтому механика деформируемого твердого тела рассматривает поведение микрообъемов, основываясь на принятых гипотезах сплошности и однородности. Сплошное однородное тело не имеет в своем составе взаимодействующих дискретных частиц, и целостность объема обеспечивают внутренние связи.
Из теоретической механики известна так называемая аксиома связей, согласно которой равновесие тела сохраняется, если действие связей, закрепляющих тело в пространстве, заменить их реакциями. Применяя эту аксиому к деформированному телу, можно мысленно рассечь его, отделить одну часть от другой и вместо нарушенных связей приложить к каждой части силы, равные усилиям связей. Такие силы называются внутренними.
Для определения этих сил используется специальный прием – метод сечений. В механике деформируемого твердого тела метод сечений применяют для выделения сечений (рис. 3.2, а), микрообъемов (рис. 3.2, б) и вывода уравнений равновесия сил, действующих на них.
Внутренние силы непрерывно распределяются по образовавшемуся сечению вследствие допущения о сплошности материала. Так как внутренние силы
Если силы распределяются по сплошному сечению непрерывно, то их проекции также будут распределены непрерывно. Учитывая это, на рис. 3.2, в приведен график, показывающий распределение проекций внутренних сил на ось У. Показаны только силы, действующие на элементарные площадки, центры тяжести которых лежат на линии m – m.
Каждая проекция представляет собой проекцию главного вектора сил, действующих на элементарную площадку.
По своей природе (согласно гипотезе сплошности и идее метода сечений) внутренние силы являются поверхностными, так как они действуют на поверхности граней бесконечно малых элементов, из которых складывается объем тела.
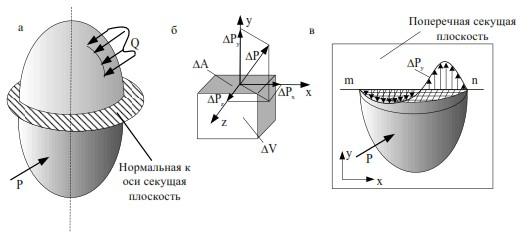
Рис. 3.2. Графическая схема метода сечений и эпюра распределения проекций внутренних сил, действующих по линии т – п на ось У
Напряжения
Воспользовавшись методом сечений, выделим в окрестности некоторой точки элементарную призму, на грани которой действуют внутренние силы (рис.3.3,а).
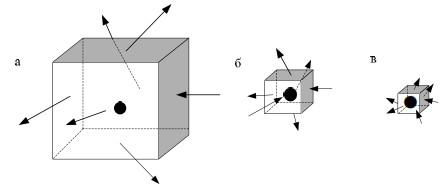
Рис. 3.3. Силовое поле в окрестности точки
Если уменьшить объем элементарной призмы, силовое поле будет более точно отражать действительную напряженность в окрестности точки. При этом силы, действующие на грани этой призмы, в общем случае будут отличны как по величине, так и по направлению от сил, действующих на грани первой призмы. Уменьшая объем (рис. 3.3,6, в), мы в предельном случае сведем его к объему бесконечно малой призмы, на грани которой действуют внутренние силы. Так как внутренние силы, в соответствии с гипотезой сплошности, рассматриваются как распределенные по поверхности, то величина этих сил может быть определена только в том случае, если известна их интенсивность. Размерность интенсивности равна
Интенсивности внутренних поверхностных сил называются напряжениями. Понятие интенсивности внутренних сил, передающихся через проведенное сечение от одной части тела к другой и наоборот (действие и противодействие равны и противоположно направлены), впервые было введено французским математиком и механиком Огюстеном Луи Коши (1789–1857).
Напряжение, как и интенсивность поверхностной нагрузки, выражается в единицах силы, отнесенной к единице площади. В международной системе единиц измерений оно выражается как давление в Па (паскалях). В технических расчетах используют кратную единицу – (мегапаскаль): 1МПа = 106 Па:
Рассмотрим некоторое тело (рис. 3.4, а), внутри которого выделим точку В. Мысленно рассечем его плоскостью, проходящей через эту точку. Отбросим одну из частей тела.
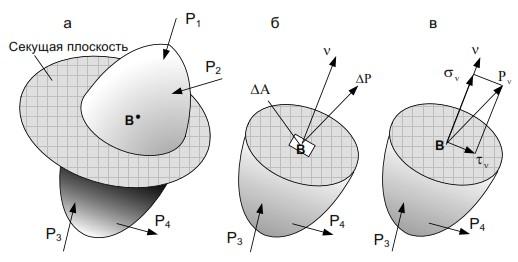
Рис. 3.4. Процедура метода сечений для определения внутренних сил: а) сечение тела плоскостью; б) внутреннее усилие; в) полное напряжение и его составляющие
Согласно аксиоме связей, действие отброшенной части необходимо заменить усилиями, которые в соответствии с гипотезой о сплошности распределены по всему сечению. Положение сечения определяется направлением внешней нормали v (обычно задаются косинусы углов между нормалью и координатными осями, т.е. так называемые направляющие косинусы). Через малую площадку
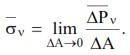
Эта векторная величина является мерой интенсивности внутренних сил.
Как следует из рис. 3.4, в общем случае на площадке могут возникать два вида напряжений: нормальное
Понятие напряжения является фундаментальным для механики деформируемого тела.
Во многих случаях прочность материала в окрестности данной точки определяется именно напряжением, поэтому очень важно уметь вычислять напряжения в точках деформируемого тела.
Напряжение в твердом теле напоминает давление в жидкости или газе. Однако нужно иметь в виду, что давление действует в любом направлении внутри жидкости, тогда как напряжение является величиной, характеризующейся определенными направлениями действия. Напряжение, в частности, может действовать в одном-единственном направлении.
Рассмотрим несколько частных случаев нагружения простейших элементов деталей машин или оборудования.
Предположим, что стержень с поперечным сечением А [м2] (рис. 3.5) нагружен силой Р. Такая схема нагружения отвечает растяжению стержня. На закрепленном конце стержня возникает реакция R, уравновешивающая силу Р. Обе силы действуют по оси бруса. Рассмотрим участок стержня длиной X. Этот участок, также как и все тело, находится в состоянии равновесия, поэтому в поперечном сечении на каждой элементарной площадке dA = A / n, где n → ∞, должно возникнуть внутреннее сопротивление dR =
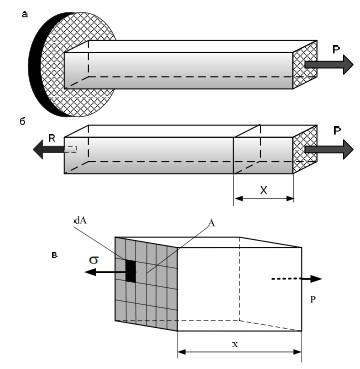
Рис. 3.5. Растяжение стержня постоянной силой: а) расчетная схема; б) основная схема; в) элемент стержня
Здесь
Предположим, что все элементы площади сечения равномерно участвуют в передаче действия силы Р. Тогда для рассматриваемого случая
Откуда следует, что интенсивность внутреннего сопротивления для данного случая может быть определена с помощью формулы
В данном случае интенсивность внутреннего сопротивления
Реакция внутреннего сопротивления R представляет собой внутреннюю силу, действующую в рассматриваемом поперечном сечении, которая в общем случае может принимать от сечения к сечению различные значения, поэтому вместо символа R, который обычно используется для отражения силового взаимодействия между конструкцией и опорными устройствами, будем использовать символ N, определяющий значение внутреннего сопротивления в произвольном поперечном сечении стержня. Тогда формула для определения нормального напряжения в рассматриваемом случае примет вид:
Величина напряжения, как показывает формула (3.2), не зависит от свойств материала, а определяется только внутренней силой N и площадью поперечного сечения А.
Если представить нормальные напряжения отрезками, отложенными вдоль оси стержня от каждой точки его поперечного сечения, то эти отрезки заполнят пространственную область, называемую телом напряжений. Объем тела напряжений составляет
Проекция тела напряжений на плоскость называется эпюрой напряжений.
В качестве второго примера рассмотрим расчетную схему (рис. 3.6), отвечающую другому виду сопротивления – сдвигу или срезу заклепки.
Мысленно рассечем заклепку поперечным сечением, совпадающим с плоскостью стыковки листов, и разведем обе части соединения на некоторое расстояние.
Для того чтобы каждая из частей находилась в равновесии, также как и все соединение, необходимо в плоскости поперечных сечений приложить внутренние силы S, уравновешивающие действие внешних сил Р (рис. 3.6, б). Обе силы действуют поперек оси заклепки, поэтому их называют поперечными силами.
Рассмотрим любую из частей рассматриваемого соединения, находящихся в равновесии. Повторим рассуждения, приведенные выше.
На каждой элементарной площадке площади поперечного сечения заклепки dA = А / n, где n → ∞, должно возникнуть внутреннее сопротивление dS = tdА. Здесь
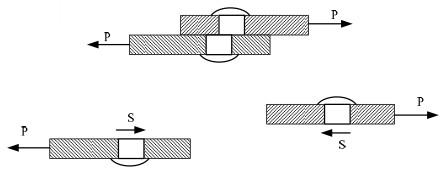
Рис. 3.6. Сдвиг. поперечные силы.
Предположим, как и выше, что все элементы площади сечения равномерно участвуют в передаче действия силы Р. Тогда для рассматриваемого случая
Откуда следует, что интенсивность внутреннего сопротивления для случая сдвига или среза может быть определено с помощью формулы
Напряжение, определяемое последней формулой, называется средним касательным напряжением.
Полное напряжение и его компоненты
Выше приведены простейшие случаи оценки напряженного состояния деталей. В общем случае для определения компонентов напряженного состояния используется аппарат сопротивления материалов, теории упругости, текучести, ползучести и т.д.
Полное напряжение характеризует поверхностную плотность внутренней силы взаимодействия между частями тела на данной площадке. Напряжение играет важнейшую роль в расчетах на прочность. Непременно предполагается, что рассчитываемый элемент, согласно принятому выше допущению, выполнен из сплошного материала. Для материалов, имеющих молекулярную структуру, невозможно связать элемент площадки с силой, действующей на этот элемент. Иначе говоря, для дискретной механики деформируемого твердого тела указанная выше формулировка напряжения неприемлема.
Разложим вектор напряжения
Если разложить на составляющие не напряжение, а саму силу
для нормального напряжения
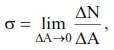
для касательного
Следовательно, напряжение
Через любую точку можно провести бесчисленное множество сечений. В каждом сечении получим свое полное напряжение. Совокупность напряжений по всем площадкам, проходящим через рассматриваемую точку, определяет напряженное состояние в точке.
Если известны напряжения в трех площадках, проходящих через точку тела, то легко найти напряжение в любой четвертой площадке, проходящей через эту точку. Для этого необходимо у рассматриваемой точки четырьмя сечениями выделить бесконечно малый элемент (рис. 3.7). Чаще всего три сечения проводят перпендикулярно координатным осям, а четвертое – наклонно. Полученная фигура называется тетраэдр.
Если известны векторы P1, P2, P3, то из уравнений равновесия выделенного тетраэдра нетрудно найти вектор
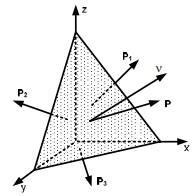
Рис. 3.7. Напряжения в четырех площадках в окрестности точки
Такими сечениями обычно являются сечения, перпендикулярные координатным осям. Если рассматривается наклонное сечение, то происходит как бы поворот координатных осей таким образом, чтобы одна из осей оказалась перпендикулярной этому сечению.
На рис. 3.7 наклонное сечение не проходит через точку В. Однако элемент бесконечно малый и при предельном переходе сечение пройдет через точку В.
Каждый вектор определяется тремя компонентами (проекции вектора на координатные оси) и представляет собой тензор первого ранга. Напряженное состояние в точке определяется тремя векторами (значениями напряжений в трех площадках), то есть девятью компонентами, и представляет собой тензор второго рода.
Не трудно показать, что при повороте площадки конец вектора полного напряжения перемещается по поверхности эллипсоида, т.е. каждому напряженному состоянию в точке соответствует свой эллипсоид напряжений – эллипсоид Ламе (Lame Gabriel (1795–1870) выдающийся французский инженер).
Обозначения компонентов напряжений.
Тензор напряжений (в декартовых координатах)
Выше указывалось, что напряжения в трех сечениях, проходящих через рассматриваемую точку, определяют напряженное состояние в точке. Рассмотрим напряженное состояние в точке В (рис. 3.8, а). Через точку В проведем сечение, перпендикулярное оси 0х (рис. 3.8, г), и оставим ту часть элемента, внешняя нормаль к сечению которой направлена в положительную сторону оси 0х. В точке В этого сечения действует напряжение, которое можно обозначить Рх.
Разложим этот вектор на составляющие вдоль координатных осей. Каждую составляющую обозначим буквой
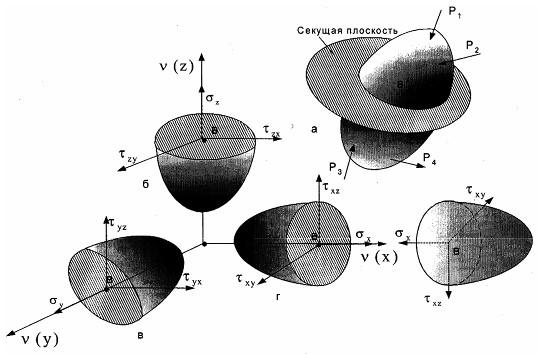
Рис. 3.8. Обозначения напряжений в сечениях, перпендикулярных координатным осям: а) сечение тела плоскостью; б) плоскость сечения, перпендикулярная оси 0у; в) плоскость сечения, перпендикулярная оси 0z; г) плоскость сечения, перпендикулярная оси 0х
В результате получаем напряжение
В этом случае у нормального напряжения можно опустить второй индекс, т.к. ясно, что нормальное напряжение в сечении, перпендикулярном оси 0х, направлено вдоль этой оси. При такой замене получим
Эти напряжения определяют усилия, которые передаются через единичную площадку от одной части элемента конструкции к другой. Действие и противодействие равны и противоположно направлены, поэтому от одной части к другой передаются такие же усилия, но противоположного направления (см. правую часть рис. 3.8, г).
На рис. 3.8, б изображены напряжения в точке В сечения, перпендикулярного оси 0z. Напряжения численно равны усилиям, передающимся через единичную площадку, поэтому по своему характеру они не должны отличаться от внутренних силовых факторов (нормальных и поперечных сил), значит правило знаков для напряжений логично принять таким же, как и для внутренних силовых факторов. Показанные на рис. 3.8 направления векторов напряжений принято считать положительными
Следовательно, если внешняя нормаль к сечению совпадает с положительным направлением координатной оси, то положительные компоненты напряжений (нормальное и касательные) направлены в положительные стороны соответствующих координатных осей. И наоборот (см. правую часть рис. 3.8, г), если внешняя нормаль направлена в отрицательную сторону координатной оси, то положительные компоненты напряжений направлены в отрицательные стороны соответствующих координатных осей.
При этом положительное нормальное напряжение (также как и положительная нормальная сила в поперечном сечении бруса) всегда направлено по внешней нормали к сечению, что соответствует растяжению в рассматриваемом направлении.
Итак, напряженное состояние в точке определяется значениями напряжений в трех сечениях.
Следовательно, рассмотренные напряжения в координатных плоскостях определяют напряженное состояние в точке.
Обозначая полное напряжение для точки как Рv, а нормаль к данной площадке через v, будем иметь очевидное равенство: Р2v =
Расположим все напряжения, определяющие напряженное состояние в рассматриваемой точке, в виде следующей матрицы:
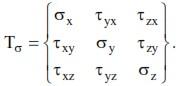
Эта матрица называется тензором напряжений. Напряженное состояние в точке вполне определено, если задан тензор напряжений для этой точки.
Главные площадки. Главные напряжения
Полуоси эллипсоида напряжений определяют значения полных напряжений в трех взаимно перпендикулярных площадках, которые равны нормальным напряжениям в этих площадках. Таким образом, в каждой точке элемента конструкции можно провести не менее трех сечений (площадок), в которых отсутствуют касательные напряжения.
Площадки, на которых касательные напряжения равны нулю, называются главными. Нормальные напряжения, действующие на главных площадках, называются главными нормальными напряжениями. Они обозначаются
Виды напряженного состояния
В общем случае напряженное состояние в теле неоднородно, оно различно в разных точках, поэтому в любом сечении тела напряжения распределены неравномерно. Для изучения напряженного состояния в точке рассматриваются элементарные объемы в ее окрестности. Форма этих объемов (элементов) зависит от вида секущих плоскостей, которые, в свою очередь, определяются принятой системой координат.
Наиболее распространенными являются прямоугольная и цилиндрическая формы. Выбор системы координат зависит от особенностей геометрии исследуемого тела. Удачно выбранная система координат способствует минимуму затрат при решении конкретной задачи. Существуют различные виды классификации напряженного состояния.
В зависимости от значений главных напряжений предлагается следующая классификация напряженного состояния:
объемное состояние (ни одно из главных напряжений не равно нулю);
плоское состояние (два главных напряжения не равны нулю, а одно главное напряжение равно нулю);
одноосное (линейное) состояние (только одно из главных напряжений не равно нулю).
Следует отметить, что при изучении пластического деформирования и разрушения материалов предлагаемая классификация видов напряженного состояния неудобна. В этих случаях вместо главных напряжений для классификации вида напряженного состояния принимаются другие инвариантные параметры.
Говоря о том или ином напряженном состоянии, следует иметь в виду, что эта классификация в общем случае условна. Она предполагает, что те компоненты напряженного состояния, которыми мы пренебрегли по сравнению с рассматриваемыми в данном случае напряжениями, тождественно равны нулю. В действительности они отличны от нуля, но их учет в расчетной схеме не приводит к заметным поправкам решения, а только усложняет его.
Изменение величин и направлений главных напряжений при переходе от одной точки тела в другую происходит непрерывно. Может случиться, что в некоторой точке В напряженного тела одно главное напряжение равно нулю, в таком случае напряженное состояние в этой точке называется плоским. Уже в соседних точках тела напряженное состояние может быть пространственным (объемным), при котором ни одно из главных напряжений не равняется нулю.
Наряду с этим встречаются и такие случаи, которые характеризуются тем, что во всех точках тела напряженное состояние плоское, и при этом главные площадки с нулевым главным напряжением во всех точках тела параллельны друг другу. В таком случае можно сказать, что все тело в целом испытывает плоское напряженное состояние.
Линейное напряженное состояние в точке возникает в двух случаях.
В первом случае, когда в отдельных точках пространственно или плоско напряженного тела два из трех главных напряжений равны нулю.
Во втором случае, когда во всех точках тела наблюдается однородное напряженное состояние, которое можно представить как равномерное, возникает одинаковое по величине растяжение или сжатие в параллельных для всех точек направлениях.
Лекция 4. ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ТОЧКЕ СПЛОШНОЙ СРЕДЫ
Обозначения компонентов перемещения
Рассмотрим произвольное тело при определенной температуре окружающей среды, которое не подвергается воздействию внешних сил. Выделим в пределах объема этого тела точку В (рис. 4.1, а).
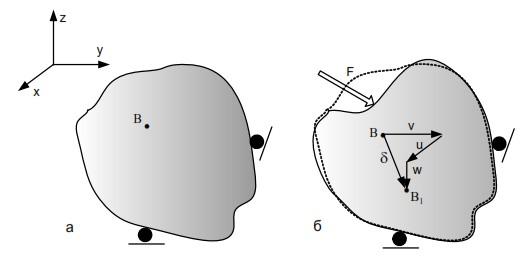
Рис. 4.1. Компоненты смещения точек тела: а) тело до деформации; б) тело после деформации
После приложения внешних сил, а также изменения температуры тело может изменить форму и размеры, а каждая его точка получит соответствующее перемещение. Точка В перейдет в новое положение В1 (рис. 4.1, б).
Полное перемещение точки определяется как
Деформации
Силы, как основной фактор взаимодействия между телами, представляют собой меру механического действия тел друг на друга и взаимодействия частей одного тела между собой.
В результате силового взаимодействия материальные частицы тела приходят в движение и расстояния между ними изменяются, что приводит к деформации формы тела и изменению его объема.
Существует, по крайней мере, два понятия о деформациях. Первое, назовем его "обобщенное", используется в обыденном общении и связанно с нашими представлениями о видимых изменениях формы и размеров некоторого объекта. Например, изменение объема велосипедной камеры.
Второе определяется с учетом основ механики деформируемого твердого тела, теории, которая построена на представлении материала как сплошного и непрерывного массива. Разрушение начинается тогда, когда в пределах некоторого микрообъема создается определенная ситуация, приводящая к микроразрушениям, их росту и объединению и, наконец, к критической ситуации, предшествующей разрушению.
Таким образом, анализ состояния конструкции надо начинать с анализа напряженно-деформированного состояния некоторой точки или области этой точки, поэтому, рассуждая выше о напряжениях, мы говорили, что они представляют интенсивность внутренних сил (реакций), действующих на бесконечно малых площадках. Точно также общие деформации тела складываются из суммы деформаций бесконечно малых объемов. Если эти объемы представить как совокупность бесконечно малых призм или тетраэдров, то изменение формы и объема тела будет связано с изменением длин граней элементарных объемов и их перекашиванием (сдвигом).
Деформации принято делить на линейные, связанные с изменением длин граней бесконечно малых объемов, и угловые, возникающие при изменениях первоначально существующих углов между гранями. Линейные деформации приводят к изменению объема, а угловые – к изменению формы.
При изучении курсов, имеющих прикладное направление, например, сопротивления материалов, с понятиями линейных деформаций часто знакомят студентов на примере растяжения или сжатия образца или стержня. При этом у некоторых студентов создается представление, что под линейной деформацией понимается отношение приращения (в алгебраическом смысле) длины образца или стержня к его первоначальной длине. Так можно рассуждать только в частном случае, когда рассматривается стержень, находящийся в условиях одноосного и однородного напряженно-деформированного состояния. Рассмотрим два примера (рис. 4.2).
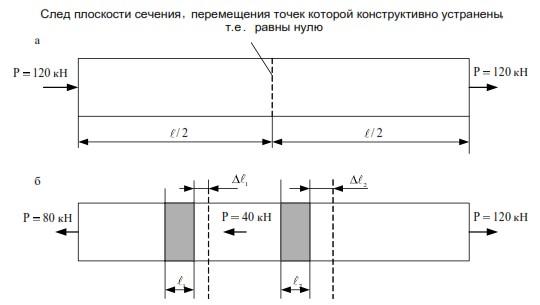
Рис. 4.2. К определению линейных деформаций по длине стержня
Рассмотрим стержень (рис. 4.2, а), растягиваемый силами Р. Среднее сечение с помощью некоторых конструктивных решений не смещается и остается плоским. Тогда одна половина стержня удлиняется на некоторую величину
Если стержень разбить на малые участки, в пределах которых реализуется однородное напряженно-деформированное состояние (рис. 4.2, б), то средние линейные деформации в пределах этих участков можно с достаточной точностью для практики определять по формуле:
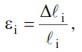
где
В частном случае, когда по длине рассматриваемого стержня сохраняется однородное напряженное состояние, для определения деформаций можно пользоваться формулой
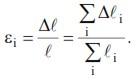
В механике деформируемого твердого тела под термином "деформация" обычно понимают локальную деформацию, связанную с изменением расстояния между близкими материальными точками тела, и изменение взаимной ориентации отдельных волокон тела малой длины.
Для изучения деформации тела представим его рассеченным на множество элементов, которые будут изменять свою форму и объем при действии внешних сил или температурных полей (рис. 4.3).
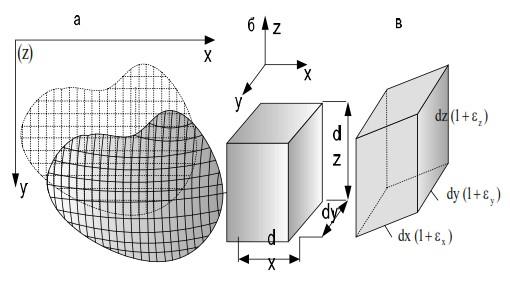
Рис. 4.3. Деформация тела и его элементов: а) тело до деформации и после; б) элементарный параллелепипед до деформации; в) элементарный параллелепипед после деформации
Пунктиром изображено тело в свободном состоянии (до приложения внешних сил и изменения температуры). Ось 0х перпендикулярна плоскости чертежа. Оси 0у и 0z расположены в плоскости чертежа.
Рассмотрим изменение формы и размеров одного из параллелепипедов в результате действия на тело внешней нагрузки. До деформирования тела одна из вершин параллелепипеда находилась в точке В. Длины его ребер были равны соответственно dх, dу и dz, а углы между гранями – 90°. В результате действия внешних сил (на рис. 4.3 они не показаны) бесконечно малый параллелепипед изменяет форму и объем. Вершина В переходит в точку В1. Форма и объем любого деформированного параллелепипеда вполне определяется удлинением (укорочением) его ребер и искажением первоначально прямых углов между гранями. Возможными искривлениями ребер и граней элемента пренебрегаем, так как его размеры могут быть сколь угодно малыми.
Введем понятие деформаций в точке тела как количественную меру деформирования микрообъема в окрестности рассматриваемой точки.
До нагружения, как уже указывалось, длины ребер параллелепипеда равны dх, dу и dz (рис. 4.2, б). После нагружения, а также в результате изменения температуры длины ребер изменились на величины
В соответствии с этим получим:
где
Если принять dx, dy, dz равными единице, то линейную деформацию можно отождествить с изменением длины единичного отрезка. Линейная деформация — величина безразмерная.
Если длина отрезка была равна dх, то она изменется на величину
Линейная деформация считается положительной при увеличении и отрицательной при уменьшении длины отрезка.
Бесконечно малые параллелепипеды определяются положением их вершин в координатных плоскостях, поэтому изменение углов между гранями (угловые деформации) следует рассматривать в той или иной координатной плоскости (рис. 4.4).
Угловой деформацией называется изменение первоначально прямого угла между гранями элемента.
Если угол между положительными направлениями координатных осей уменьшается, то угловая деформация считается положительной. Первоначально прямой угол
Аналогично можно провести перпендикуляр к ребру В1С1 и измерить угол уху между ним и ребром В1D1.
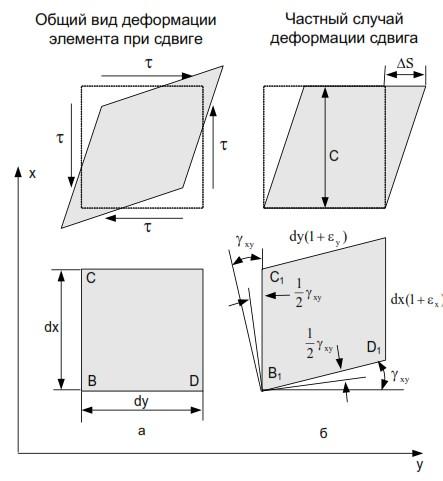
Рис. 4.4. Угловая деформация в плоскости хОу: а) вид элемента до деформации; 6) элемент в деформированном состоянии
Угловую деформацию в плоскости х0у определяют, суммируя углы –
