автордың кітабын онлайн тегін оқу Логика. Краткое пособие по общему курсу
Информация о книге
УДК 16(075.8)
ББК 87.4я73
К89
Автор:
Кузина Е. Б., кандидат философских наук, доцент кафедры логики философского факультета Московского государственного университета имени М. В. Ломоносова.
Предлагаемое пособие предназначено для экспресс-подготовки к экзамену по семестровому курсу логики, в котором обычно излагаются основные разделы без использования современного логического аппарата. Пособие не может заменить учебник – оно предназначено для систематизации перед экзаменом уже полученных в семестре знаний. С этой целью его разделы и главы сопровождаются схемами, в которых отражена структура и даны определения ключевых терминов соответствующего раздела.
УДК 16(075.8)
ББК 87.4я73
© Кузина Е. Б., 2025
© ООО «Проспект», 2025
ПРЕДМЕТ ЛОГИКИ
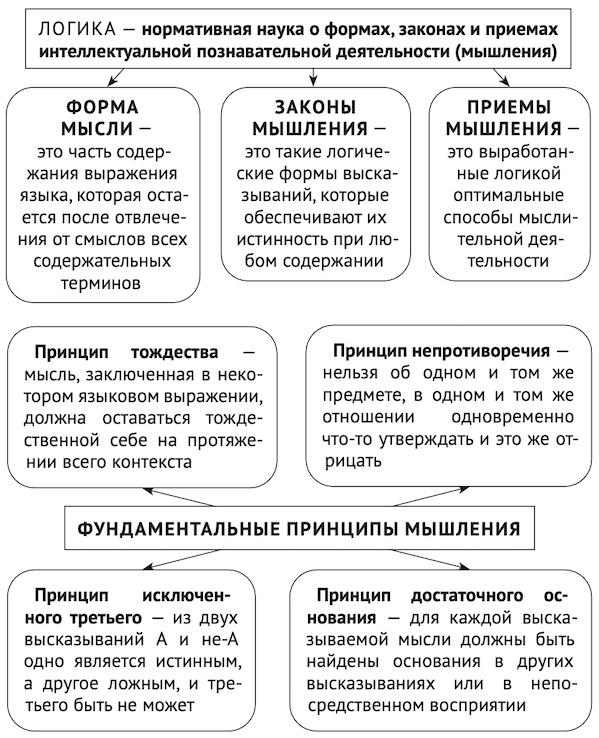
Логику обычно определяют как нормативную науку о формах, законах и приемах мышления. Мышление является второй (после чувственной) рациональной ступенью познания. Мышление осуществляется посредством языка: сам процесс рационального познания невозможен без языка, и его результат непременно выражается в языке.
Мысль имеет содержание и форму. Содержание мысли составляет отражаемая действительность. Например, содержанием мысли, выраженной предложением «Каждый студент сдает какие-нибудь экзамены», является утверждение об отношении между любым студентом и какими-то экзаменами, а его форма может быть описана как утверждение об отношении между любым предметом одного класса и некоторым предметом другого класса. Такую же форму имеют мысли: «Любое нечетное число больше какого-нибудь четного числа», «Каждый штангист сильнее какого-нибудь легкоатлета» и множество других мыслей.
Форма мысли (логическая форма) — это та часть содержания мысли, которая остается после отвлечения от смыслов всех содержательных (дескриптивных, нелогических) терминов. Можно сказать, что формой мысли является ее структура, то общее, что могут иметь различные по содержанию мысли.
Формы мысли тоже очень разнообразны: одни мысли отражают действительность, фиксируя общие признаки предметов некоторого класса и тем самым обобщая эти предметы, выделяя их из всех прочих. В других мыслях утверждается или отрицается присущность признака предмету или отношение между предметами, в-третьих — совершается переход от имеющихся знаний (выраженных в высказываниях) к новому знанию.
Законами мышления (логическими законами) называются такие логические формы высказываний, которые обеспечивают их истинность при любом содержании. Например, высказывания: «Если делимость числа на 6 является достаточным условием его делимости на 2, то неделимость числа на 2 является достаточным условием его неделимости на 6», «Если вода, будучи нагрета до 100° (в нормальных условиях), кипит, то если вода не кипит (в нормальных условиях), значит, она не нагрета до 100°». Эти и любые другие высказывания той же формы не могут оказаться ложными просто в силу их логической формы: Если А влечет В, то не-В обусловливает не-А. Эта форма является логическим законом.
Существует бесконечное множество логических законов, каждый из которых выражает некоторую необходимую и устойчивую связь между мыслями, обеспечивая в процессе мышления переходы от истинных утверждений к истинным. Все они не что иное, как формы всегда истинных (логически истинных) высказываний.
В традиционной логике в качестве законов рассматривались лишь некоторые наиболее фундаментальные принципы, которым должно следовать мышление: тождества, непротиворечия, исключенного третьего и достаточного основания. Первые три, будучи выраженными в виде формул, являются логическими законами в современном смысле: тождества (если А, то А), непротиворечия (неверно, что А и не-А), исключенного третьего (А или не-А). Принцип же достаточного основания представляет только методологический принцип научного познания и речевого общения.
Содержательно смыслы четырех упомянутых принципов можно выразить так:
Принцип тождества предписывает, чтобы на протяжении всего процесса рассуждения или обсуждения какого-либо предмета выражения языка употреблялись в одном и том же смысле, иначе говоря, чтобы предмет обсуждения не подменялся.
Принцип непротиворечия говорит о том, что нельзя об одном и том же предмете, в одно и то же время, в одном и том же отношении нечто утверждать и отрицать, иначе говоря, невозможно, высказывать одновременно А и не-А.
Согласно принципу исключенного третьего, из высказываний А и не-А (в одно и то же время, в одном и том же отношении) одно обязательно является истинным, а другое ложным, и ничего третьего быть не может.
Принцип достаточного основания требует, чтобы каждая высказанная мысль имела обоснование другими мыслями или чувственными данными.
Приемы мышления — это выработанные логикой правильные и целесообразные способы оперирования с мыслями, с результатами рационального познания. Это и выработка определений, и осуществление классификаций, и установление отношений между понятиями или высказываниями, и переходы от данного понятия к более общему или к менее общему, и отрицание различных видов высказываний, выведение следствий из имеющихся знаний и многие другие мыслительные операции.
ЯЗЫК — ИНСТРУМЕНТ МЫШЛЕНИЯ И ПОЗНАНИЯ
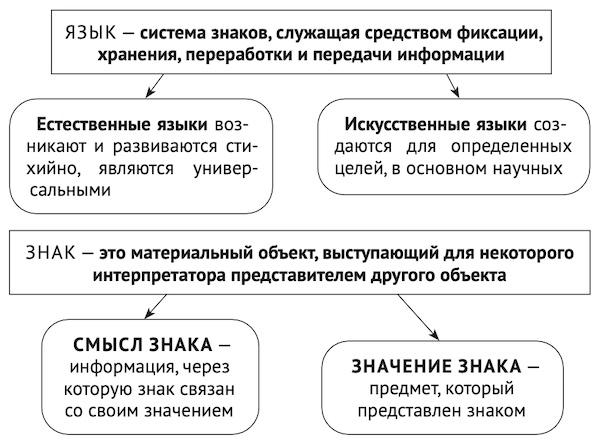
Мышление осуществляется в языке и без языка невозможно. Языком называется система знаков, служащая средством фиксации, хранения, переработки и передачи информации. А знак — это чувственно воспринимаемый предмет, выступающий для некоторого интерпретатора представителем какого-либо объекта, ситуации, любой характеристики предметов, событий, вообще чего угодно. То есть знак представляет все, о чем можно говорить. Предмет, который представлен знаком, называется значением знака. Знак связывается со своим значением посредством информации, иногда заключенной в самом знаке, а чаще приписываемой знаку. Эта информация называется смыслом знака. Именно смысл позволяет связать знак с его значением, иначе говоря, смысл — это то, что понимает человек, употребляющий или воспринимающий знак. Любая система знаков называется языком.
Язык может быть естественным, возникшим стихийно в процессе общения, или искусственным, созданным специально для каких-то практических или познавательных целей, чаще всего для работы в той или иной науке, где информация должна быть зафиксирована, обработана и передана однозначно и точно.
Искусственные языки логики (поскольку она изучает мышление с точки зрения его форм) предназначены прежде всего для выявления и фиксации логических форм мыслей, которые изначально выражены в естественном языке.
Не вдаваясь в подробности особенностей различных выражений естественного языка, отметим лишь, что для наших целей важно выделить два основных типа выражений естественного языка: предложения (в которых что-то утверждается или отрицается о чем-то) и их части, не являющиеся предложениями, — термины. Среди терминов, в свою очередь, важно выделить логические и нелогические. Логические термины определяют форму мысли, ее структуру, а нелогические представляют содержание мысли.
Для пояснения рассмотрим два выражения: «число, которое делится на 3, но не делится на 6» и «человек, который читает, а не пишет». Логические термины в них — соединительный союз («и», «но») и отрицание. Остальные термины в этих примерах являются нелогическими. Общая структура приведенных выражений, определяемая только логическими терминами, такова: предмет, имеющий одну характеристику и не имеющий другой характеристики. Если же учитывать и типы нелогических терминов, то формы этих выражений различаются. Первое имеет форму: предмет, находящийся в некотором отношении с одним конкретным предметом и не находящийся в этом же отношении с другим конкретным предметом. Второе имеет форму: предмет, имеющий один признак и не имеющий другого признака.
В логике существует много различных языков, созданных для научных целей разных областей и направлений современной логики. В кратком курсе классической логики используются главным образом два языка: язык логики высказываний и язык традиционной силлогистики. Язык логики высказываний будет представлен в разделе «Логический анализ высказываний», в главе «Сложные высказывания», а язык традиционной силлогистики — в том же разделе, главе «Отношения между высказываниями».
ПОНЯТИЕ
1. Понятие, его основные логические характеристики
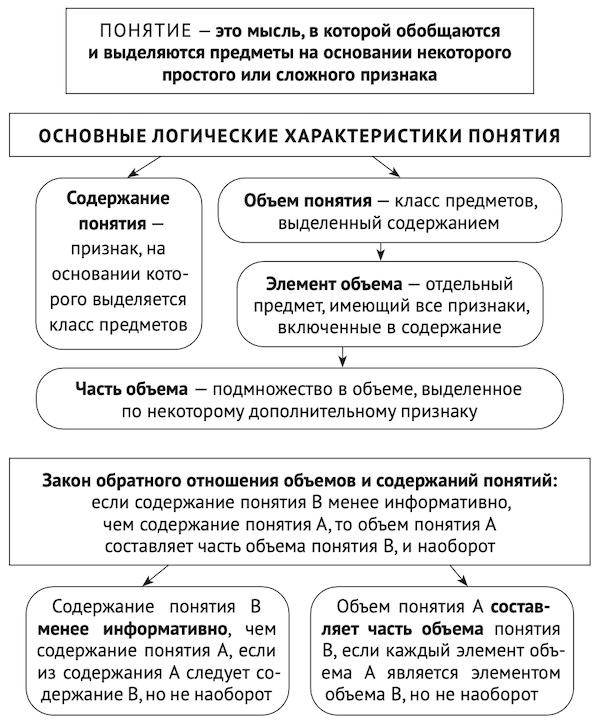
Понятие — это мысль о классе предметов, обобщенных и выделенных по некоторому признаку (простому или сложному). Признаком называется все то, в чем предметы могут быть сходны друг с другом или отличны один от другого.
Понятие выражается в языке особой лингвистической конструкцией, называемой универсалией. Самый общий вид универсалии — α А(α), где α представляет универсум, в рамках которого выделяется класс мыслимых в понятии предметов, и А(α) — признак, по которому выделяется этот класс в универсуме.
Например, понятие, связываемое обычно с термином «квадрат», выражается универсалией: «прямоугольник, в котором все стороны равны», где «прямоугольник» указывает универсум (род), а «равносторонний» — признак, выделяющий квадраты в универсуме прямоугольников. Понятие, которое связывается с термином «супруги», выражается универсалией: «пара людей, которые состоят в браке друг с другом». Здесь «пара людей» указывает универсум, а «состоящие друг с другом в браке» — отличительный признак супругов в данном универсуме. В понятии, формой выражения которого является универсалия «отношение двух прямых на плоскости, при котором они не имеют общих точек или все их точки — общие», указан универсум «отношение двух прямых на плоскости», а затем дан отличительный признак параллельности.
Понятие как форма мысли имеет две основные характеристики — содержание и объем.
Содержание понятия, связываемого с определенным термином, — это признак (информация), на основании которого выделяются и обобщаются в класс предметы, обозначаемые этим термином. В той универсалии, которой выражается понятие, это А(α).
Объемом понятия называется класс (множество) обобщенных в понятии предметов. Каждый отдельный предмет, имеющий тот признак, который составляет содержание понятия, называется элементом объема. А любое подмножество этого класса, которое можно выделить каким-то дополнительным признаком, добавленным в содержание, называется частью объема.
Например, в данном выше понятии «квадрат» мыслятся (обобщаются) те прямоугольники, у которых все стороны равны, т. е. объем этого понятия — множество всех квадратов, а элементом объема является любой из них. Часть объема можно выделить, указав длину стороны квадрата (квадрат со стороной 5–7 сантиметров).
Объемом понятия, связанного с термином «супруги», является множество всех тех пар людей, которые состоят друг с другом в браке, элементом объема — любая такая пара, частью объема, например, — супруги, состоящие в браке более 20 лет.
Объем сформулированного выше понятия «параллельность» — это множество отношений прямых, лежащих в одной плоскости, при котором они не пересекаются. Множество одноэлементное, потому что так характеризуется только одно отношение между прямыми на плоскости. Это отношение и является элементом объема. Собственную часть в одноэлементном объеме выделить нельзя.
Различают логическое и фактическое содержание и, соответственно, логический и фактический объемы понятия. Определения содержания и объема, данные выше, являются, строго говоря, определениями фактического содержания и фактического объема. Тогда как логическим содержанием называется информация, заключенная в логической форме понятия, без учета смыслов нелогических терминов. Логическое содержание задает логический объем понятия.
Например, логическая форма понятия «прямоугольник, у которого все стороны равны» обычно записывают так: x P(x), где х в данном случае обозначает «прямоугольник», а Р(х) — принадлежность прямоугольнику свойства «иметь равные стороны». А в общем случае х P(x) означает: предмет (из какого-то универсума), обладающий некоторым свойством. «Р(х)» — логическое содержание этого понятия, а его логический объем — множество предметов, выделяемых из универсума некоторым простым признаком-свойством. Такое же логическое содержание и такой же логический объем имеют понятия: «человек ростом 180 сантиметров», «козленок, умеющий считать до 10» и многие другие.
Понятие «пара людей, которые состоят в браке друг с другом» имеет форму <x, y> R (x, y), и, значит, логическое содержание его: пара предметов (из некоторого универсума), состоящих один с другим в каком-то отношении. Таково же логическое содержание понятий: «пара чисел таких, что первое больше второго», «пара городов, находящихся друг от друга на расстоянии не более 50 километров» и многих других понятий, а логический объем — множество пар предметов, выделяемых из универсума некоторым простым признаком-отношением.
2. Закон обратного отношения между объемами и содержаниями понятий
Между объемами и содержаниями любых двух понятий, относящихся к одному универсуму, существует устойчивая необходимая связь, отражаемая так называемым законом обратного отношения: если содержание понятия В менее информативно, чем содержание понятия А, то объем понятия А составляет часть объема понятия В, и наоборот.
Содержание одного понятия (В) менее информативно, чем содержание другого понятия (А) означает, что из содержания второго (А) можно извлечь информацию содержания первого (В), но не наоборот. Например, из того, что человек знает 3 иностранных языка, следует, что человек знает несколько иностранных языков. Но в обратную сторону это не проходит: из того, что некто знает несколько иностранных языков, не следует, что он знает именно 3 иностранных языка. Значит, содержание понятия «человек, знающий несколько иностранных языков» менее информативно, чем содержание
...