Предисловие

Если вы уже пытались узнать что-то о нейронных сетях и глубоком обу­чении, то, скорее всего, столкнулись с изобилием ресурсов, от блогов до массовых открытых онлайн-курсов различного качества и даже книг. У меня было именно так, когда я начал изучать эту тему несколько лет назад. Однако если вы читаете это предисловие, вполне вероятно, что вы нигде не нашли достаточно полноценного описания нейронных сетей. Все эти ресурсы напоминают попытку нескольких слепцов описать слона (https://oreil.ly/r5YxS). Вот что привело меня к написанию этой книги.

Ресурсы по нейронным сетям обычно делятся на две категории. Некоторые из них касаются в основном концептуальной и математической части и содержат как рисунки, которые, как правило, встречаются в объяснениях нейронных сетей, так и круги, соединенные линиями со стрелками на концах, а также подробные математические объяснения того, что происходит, чтобы вы могли «вникнуть в матчасть». Пример этого — очень хорошая книга Яна Гудфеллоу и др. «Deep Learning»1.

На других ресурсах — много кода, запустив который вы видите, как снижается ошибка и «обучается» нейронная сеть. Например, следующий пример из документации PyTorch действительно задает и обучает простую нейронную сеть случайными данными:

# N - размер партии; D_in - входной размер;

# H - скрытое измерение; D_out - размер вывода.

N, D_in, H, D_out = 64, 1000, 100, 10

# Создать случайные входные и выходные данные

x = torch.randn(N, D_in, device=device, dtype=dtype)

y = torch.randn(N, D_out, device=device, dtype=dtype)

# Произвольно инициализировать веса

w1 = torch.randn(D_in, H, device=device, dtype=dtype)

w2 = torch.randn(H, D_out, device=device, dtype=dtype)

learning_rate = 1e-6

for t in range(500):

    # Прямой проход: вычислить прогнозируемое y

    h = x.mm(w1)

    h_relu = h.clamp(min=0)

    y_pred = h_relu.mm(w2)

    # Вычислить и вывести потери

    loss = (y_pred — y).pow(2).sum().item()

    print(t, loss)

    # Backprop для вычисления градиентов w1 и w2 относительно потерь

    grad_y_pred = 2.0 * (y_pred — y)

    grad_w2 = h_relu.t().mm(grad_y_pred)

    grad_h_relu = grad_y_pred.mm(w2.t())

    grad_h = grad_h_relu.clone()

    grad_h[h < 0] = 0

    grad_w1 = x.t().mm(grad_h)

    # Обновить веса с помощью градиентного спуска

    w1 -= learning_rate * grad_w1

    w2 -= learning_rate * grad_w2

Очевидно, что такие объяснения не дают понимания того, что на самом деле происходит: лежащих в основе математических принципов, отдельных компонентов нейронной сети, как они работают вместе и т.д.2

А каким должно быть хорошее объяснение? Тут полезно посмотреть, как объясняются другие концепции информатики: например, если вы хотите узнать об алгоритмах сортировки, то в учебнике найдется:

• объяснение принципа работы алгоритма простыми словами;

• визуальное объяснение работы алгоритма — схема, график;

• математическое объяснение почему алгоритм работает3;

• псевдокод, реализующий алгоритм.

Эти элементы объяснения нейронных сетей редко (или никогда) объединяются, хотя мне кажется очевидным, что правильное объяснение нейронных сетей должно быть именно таким. Эта книга — попытка восполнить этот пробел.

Для понимания нейронных сетей нужно несколько мысленных моделей

Я не исследователь и не доктор наук. Но я профессионально преподавал Data Science: провел пару буткемпов по Data Science в компании Metis, а затем в течение года путешествовал по всему миру с Metis, проводя однодневные семинары для компаний из разных отраслей. На этих семинарах я рассказывал о машинном обучении и основных концепциях разработки программного обеспечения. Мне всегда нравилось преподавать, и в последнее время, занимаясь в основном машинным обучением и статистикой, меня интересует вопрос, как лучше всего объяснить технические понятия. Что касается нейронных сетей, я обнаружил, что наиболее сложной задачей является создание правильной «мысленной модели» того, что представляет собой нейронная сеть, тем более что для понимания нейронных сетей полностью требуется не одна, а несколько ментальных моделей и все они освещают различные (но все же важные) аспекты работы нейронных сетей. Следующие четыре предложения являются правильными ответами на вопрос: «Что такое нейронная сеть?»

• Нейронная сеть — это математическая функция, которая принимает входные и производит выходные данные.

• Нейронная сеть — это вычислительный граф, через который протекают многомерные массивы.

• Нейронная сеть состоит из слоев, каждый из которых может рассматриваться как ряд «нейронов».

• Нейронная сеть — это универсальный аппроксиматор функций, который теоретически может представить решение любой контролируемой проблемы обучения.

Не сомневаюсь, что читатели уже слышали одно или несколько из этих понятий раньше и в целом понимают, для чего нужны нейронные сети. Однако для полного понимания нужно осознать их все и показать, как они связаны. Как тот факт, что нейронная сеть может быть представлена в виде вычислительного графа, сопоставить, например, с понятием слоя? Для более точного понимания мы реализуем все эти концепции с нуля в Python и соединим их, создавая рабочие нейронные сети, которые вы можете обучать на своем компьютере дома. Несмотря на то что мы уделим немало времени деталям реализации, целью реализации этих моделей в Python будет укрепление и уточнение нашего понимания концепций. Здесь спешка не нужна.

Я хотел бы, чтобы после прочтения этой книги у вас было такое глубокое понимание всех этих мысленных моделей и результатов их работы, чтобы понимать, каким образом нейронные сети должны быть реализованы. После этого все концепции, связанные с обучением в будущих проектах, станут для вас проще.

Структура книги

Первые три главы наиболее важные и сами по себе достойны отдельных книг.

1. В главе 1 я покажу, как представлять математические функции в виде последовательности операций, связанных вместе, чтобы сформировать вычислительный граф. Также я покажу, как это представление позволяет нам вычислять производные выходов этих функций по отношению к их входам, используя правило цепи. В конце главы расскажу об очень важной операции — умножении матрицы — и покажу, как она может вписаться в математическую функцию и в то же время позволит нам вычислить производные, которые понадобятся для глубокого обучения.

2. В главе 2 мы будем использовать строительные блоки, которые сделали в главе 1 с целью создания и обучения модели для решения реальных проблем: в частности, мы будем использовать их для построения моделей линейной регрессии и нейронных сетей для прогнозирования цен на жилье на основе реальных данных. Я покажу, что нейронная сеть работает лучше, чем линейная регрессия, и попытаюсь объяснить почему. Подход к построению моделей «сначала суть» в этой главе должен дать вам очень хорошее представление о том, как работают нейронные сети, а также покажет ограниченные возможности пошагового подхода для определения моделей глубокого обучения. И тут на сцену выходит глава 3.

3. В главе 3 мы возьмем строительные блоки из подхода «сначала суть» из первых двух глав и используем их для построения компонентов более высокого уровня, которые составляют все модели глубокого обучения: слои, модели, оптимизаторы и т.д. Мы закончим эту главу обучением модели глубокого обучения, заданной с нуля, на наборе данных из главы 2 и покажем, что она работает лучше, чем простая нейронная сеть.

4. Как выясняется, существует несколько теоретических предпосылок того, что нейронная сеть с заданной архитектурой действительно найдет хорошее решение для данного набора данных при обучении с использованием стандартных методов обучения, которые мы будем использовать в этой книге. В главе 4 мы поговорим о хитростях, применяемых в процессе обучения, которые обычно увеличивают вероятность того, что нейронная сеть найдет хорошее решение, и по возможности дадим математическое описание, почему они работают.

5. В главе 5 мы обсудим фундаментальные идеи, лежащие в основе сверточных нейронных сетей (CNN), разновидности архитектуры нейронных сетей, специализирующихся на распознавании изображений. Существует множество объяснений принципов работы CNN, поэтому я сосредоточусь на самых основных понятиях о CNN и их отличиях от обычных нейронных сетей: в частности, как CNN делают так, что каждый слой нейронов превращается в «карты признаков», и как два из этих слоев (каждый из которых состоит из нескольких карт объектов) связываются друг с другом посредством сверточных фильтров. Кроме того, что мы будем писать обычные слои в нейронной сети с нуля, а также сверточные слои с нуля, чтобы укрепить понимание того, как они работают.

6. В первых пяти главах мы создадим миниатюрную библиотеку нейронных сетей, которая определяет нейронные сети как серию слоев, которые сами состоят из серии операций, которые передают входные данные вперед и градиенты назад. Но большинство нейронных сетей реализуются на практике не так. Вместо этого используется техника, называемая автоматическим дифференцированием. Я приведу краткий обзор автоматического дифференцирования в начале главы 6 и далее использую его для основной темы главы: рекуррентных нейронных сетей (RNN), архитектуры нейронных сетей, обычно используемых для анализа данных, в которых точки данных появляются последовательно, например временнˆых данных или естественного языка. Я объясню работу «классических RNN» и двух вариантов: GRU и LSTM (и конечно, мы реализуем все их с нуля). Далее мы опишем элементы, которые являются общими для всех этих вариантов RNN, и некоторые различия между этими вариантами.

7. В заключение, в главе 7, я покажу, как все, что мы делали с нуля в главах 1–6, может быть реализовано с использованием высокопроизводительной библиотеки с открытым исходным кодом PyTorch. Изучение такой структуры очень важно для развития вашего знания нейронных сетей; но погружение и изучение структуры без предварительного понимания того, как и почему работают нейронные сети, серьезно ограничит ваше обучение в долгосрочной перспективе. Цель такого порядка глав в этой книге — дать вам возможность писать чрезвычайно высокопроизводительные нейронные сети (с помощью PyTorch), настраивая при этом вас на долгосрочное об­учение и успех (через изучение основ). В конце мы приведем краткую иллюстрацию того, как нейронные сети могут использоваться для обучения без учителя.

Моя идея состояла в том, чтобы написать книгу, которую я сам бы хотел почитать, когда только начинал изучать эту тему несколько лет назад. Надеюсь, книга будем вам полезна. Вперед!

Условные обозначения

В книге используются следующие типографские обозначения:

Курсив

Используется для обозначения новых терминов.

Моноширинныйшрифт

Применяется для оформления листингов программ и программных элементов внутри обычного текста, таких как имена переменных и функций, баз данных, типов данных, переменных среды, операторов и ключевых слов.

Моноширинныйжирный

Обозначает команды или другой текст, который должен вводиться пользователем.

Моноширинныйкурсив

Обозначает текст, который должен замещаться фактическими значениями, вводимыми пользователем или определяемыми из контекста.

Теорема Пифагора: a2 + b2 = c2.

Так обозначаются советы, предложения и примечания общего характера.

Использование примеров кода

Дополнительный материал (примеры кода, упражнения и т.д.) можно скачать по адресу репозитория книги на GitHub по адресу oreil.ly/deep-learning-github.

Благодарности

Благодарю своего редактора Мелиссу Поттер вместе с командой из O'Reilly, которые были внимательны и отвечали на мои вопросы на протяжении всего процесса.

Выражаю особую благодарность нескольким людям, чья работа по созданию технических концепций в области машинного обучения, доступная для более широкой аудитории, вдохновила меня, и тем, кого мне посчастливилось узнать лично: это, в частности, Брэндон Рорер, Джоэл Грус, Джереми Уотт и Эндрю Траск.

Благодарю своего босса в Metis и директора в Facebook, которые поддерживали меня, когда я пытался выкроить время на работу над этим проектом.

Благодарю Мэта Леонарда, который недолгое время был моим соавтором, после чего наши пути разошлись. Мэт помог организовать код в минималистичном стиле — lincoln — и дал очень полезную обратную связь по поводу сырых вариантов первых двух глав, написав свои собственные версии больших разделов этих глав.

Наконец, благодарю своих друзей Еву и Джона, которые вдохновили меня на решительный шаг и фактически заставили меня начать писать. Я также хотел бы поблагодарить моих многочисленных друзей в Сан-Франциско, которые терпели мое волнение, переживали вместе со мной по поводу книги и оказывали всяческую поддержку, хотя в течение многих месяцев я не мог найти время потусоваться с ними.

От издательства

Некоторые иллюстрации снабжены QR-кодом. Перейдя по ссылке, вы сможете посмотреть их цветную версию.

Ваши замечания, предложения, вопросы отправляйте по адресу comp@piter.com (издательство «Питер», компьютерная редакция).

Мы будем рады узнать ваше мнение!

На веб-сайте издательства  вы найдете подробную информа­цию о наших книгах.

---

Глава 1. Математическая база

Не нужно запоминать эти формулы. Если вы поймете принципы, по которым они строятся, то сможете придумать собственную систему обозначений.

Джон Кохран, методическое пособие Investments Notes, 2006

В этой главе будет заложен фундамент для понимания работы нейронных сетей — вложенные математические функции и их производные. Мы пройдем весь путь от простейших строительных блоков до «цепочек» составных функций, вплоть до функции многих переменных, внутри которой происходит умножение матриц. Умение находить частные производные таких функций поможет вам понять принципы работы нейронных сетей, речь о которых пойдет в следующей главе.

Каждую концепцию мы будем рассматривать с трех сторон:

• математическое представление в виде формулы или набора уравнений;

• код, по возможности содержащий минимальное количество дополнительного синтаксиса (для этой цели идеально подходит язык Python);

• рисунок или схема, иллюстрирующие происходящий процесс.

Благодаря такому подходу мы сможем исчерпывающе понять, как и почему работают вложенные математические функции. С моей точки зрения, любая попытка объяснить, из чего состоят нейронные сети, не раскрывая все три аспекта, будет неудачной.

И начнем мы с такой простой, но очень важной математической концепции, как функция.

Функции

Как описать, что такое функция? Разумеется, я мог бы ограничиться формальным определением, но давайте рассмотрим эту концепцию с разных сторон, как ощупывающие слона слепцы из притчи.

Математическое представление

Вот два примера функций в математической форме записи:

•

.

•

.

Записи означают, что функция f1 преобразует входное значение x в x2, а функция f2 возвращает наибольшее значение из набора (x, 0).

Визуализация

Вот еще один способ представления функций:

1. Нарисовать плоскость xy (где x соответствует горизонтальной оси, а y — вертикальной).

2. Нарисовать на этой плоскости набор точек, x-координаты которых (обычно равномерно распределенные) соответствуют входным значениям функции, а y-координаты — ее выходным значениям.

3. Соединить эти точки друг с другом.

Французский философ и математик Рене Декарт первым использовал подобное представление, и его начали активно применять во многих областях математики, в частности в математическом анализе. Пример графиков функций показан на рис. 1.1.

Есть и другой способ графического представления функций, который почти не используется в матанализе, но удобен, когда речь заходит о моделях глубокого обучения. Функцию можно сравнить с черным ящиком, который принимает значение на вход, преобразует его внутри по каким-то правилам и возвращает новое значение. На рис. 1.2 показаны две уже знакомые нам функции как в общем виде, так и для отдельных входных значений.

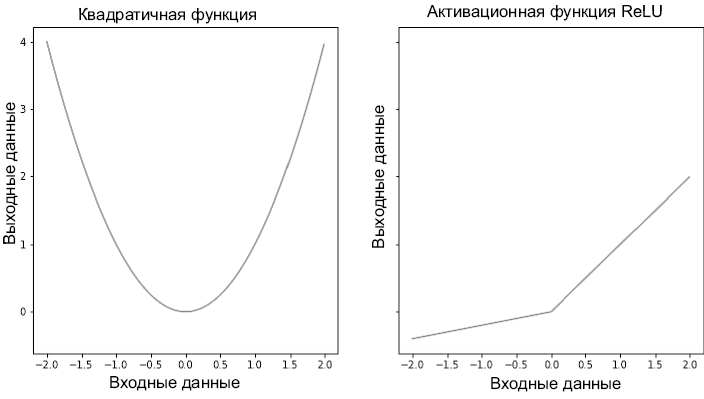
Рис. 1.1. Две непрерывные дифференцируемые функции

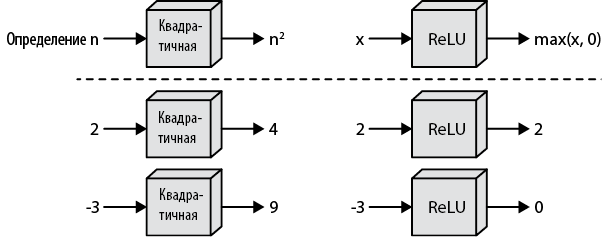
Рис. 1.2. Другой способ представления тех же функций

Код

Наконец, можно описать наши функции с помощью программного кода. Но для начала я скажу пару слов о библиотеке NumPy, которой мы воспользуемся.

Примечание № 1. NumPy

Библиотека NumPy для Python содержит реализации вычислительных алгоритмов, по большей части написанные на языке C и оптимизированные для работы с многомерными массивами. Данные, с которыми работают нейронные сети, всегда хранятся в многомерных массивах, чаще всего в дву- или трехмерных. Объекты ndarray из библиотеки NumPy дают возможность интуитивно и быстро работать с этими массивами. Например, если сохранить данные в виде обычного или многомерного списка, обычный синтаксис языка Python не позволит выполнить поэлементное сложение или умножение списков, зато эти операции прекрасно реализуются с помощью объектов ndarray:

print("операции со списками на языке Python:")

a = [1,2,3]

b = [4,5,6]

print("a+b:", a+b)

try:

    print(a*b)

except TypeError:

    print("a*b не имеет смысла для списков в языке Python")

print()

print("операции с массивами из библиотеки numpy:")

a = np.array([1,2,3])

b = np.array([4,5,6])

print("a+b:", a+b)

print("a*b:", a*b)

операции со списками на языке Python:

a+b: [1, 2, 3, 4, 5, 6]

a*b не имеет смысла для списков в языке Python

операции с массивами из библиотеки numpy:

a+b: [5 7 9]

a*b: [ 4 10 18]

Объект ndarray обладает и таким важным для работы с многомерными массивами атрибутом, как количество измерений. Измерения еще называют осями. Их нумерация начинается с 0, соответственно первая ось будет иметь индекс 0, вторая — 1 и т.д. В частном случае двумерного массива нулевую ось можно сопоставить строкам, а первую — столбцам, как показано на рис. 1.3.

Эти объекты позволяют интуитивно понятным способом совершать различные операции с элементами осей. Например, суммирование строки или столбца двумерного массива приводит к «свертке» вдоль соответствующей оси, возвращая массив на одно измерение меньше исходного:

print('a:')

print(a)

print('a.sum(axis=0):', a.sum(axis=0))

print('a.sum(axis=1):', a.sum(axis=1))

a:

[[1 2]

[3 4]]

a.sum(axis=0): [4 6]

a.sum(axis=1): [3 7]

Рис. 1.3. Двумерный массив из библиотеки NumPy, в котором ось с индексом 0 соответствует строкам, а ось с индексом 1 — столбцам

Наконец, объект ndarray поддерживает такую операцию, как сложение с одномерным массивом. Например, к двумерному массиву a, состоящему из R строк и C столбцов, можно прибавить одномерный массив b длиной C, и библиотека NumPy выполнит сложение для элементов каждой строки массива a4:

a = np.array([[1,2,3],

              [4,5,6]])

b = np.array([10,20,30])

print("a+b:\n", a+b)

a+b:

[[11 22 33]

[14 25 36]]

Примечание № 2. Функции с аннотациями типов

Как я уже упоминал, код в этой книге приводится как дополнительная иллюстрация, позволяющая более наглядно представить объясняемые концепции. Постепенно эта задача будет усложняться, так как функции с несколькими аргументами придется писать как часть сложных классов. Для повышения информативности такого кода мы будем добавлять в определение функций аннотации типов; например, в главе 3 нейронные сети будут инициализироваться вот так:

def __init__(self,

             layers: List[Layer],     

             loss: Loss, learning_rate: float = 0.01) -> None:

Такое определение сразу дает представление о назначении класса. Вот для сравнения функция operation:

def operation(x1, x2):

Чтобы понять назначение этой функции, потребуется вывести тип каждого объекта и посмотреть, какие операции с ними выполняются. А теперь переопределим эту функцию следующим образом:

def operation(x1: ndarray, x2: ndarray) -> ndarray:

Сразу понятно, что функция берет два объекта ndarray, вероятно, каким-то способом комбинирует и выводит результат этой комбинации. В дальнейшем мы будем снабжать аннотациями типов все определения функций.

Простые функции в библиотеке NumPy

Теперь мы готовы написать код определенных нами функций средствами библиотеки NumPy:

def square(x: ndarray) -> ndarray:

    '''

    Возведение в квадрат каждого элемента объекта ndarray.

    '''

    return np.power(x, 2)

def leaky_relu(x: ndarray) -> ndarray:

    '''

    Применение функции "Leaky ReLU" к каждому элементу ndarray.

    '''

    return np.maximum(0.2 * x, x)

Библиотека NumPy позволяет применять многие функции к объектам ndarray двумя способами: np.function_name(ndarray) или ndarray.function_name. Например, функцию relu можно было написать как x.clip(min = 0). В дальнейшем мы будем пользоваться записью вида np.function_name(ndarray). И даже когда альтернативная запись короче, как, например, в случае транспонирования двумерного объекта ndarray, мы будем писать не ndarray.T, а np.transpose(ndarray,(1,0)).

Постепенно вы привыкнете к трем способам представления концепций, и это поможет по-настоящему понять, как происходит глубокое обучение.

Производные

Понятие производной функции, скорее всего, многим из вас уже знакомо. Производную можно определить как скорость изменения функции в рассматриваемой точке. Мы подробно рассмотрим это понятие с разных сторон.

Математическое представление

Математически производная определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю:

.

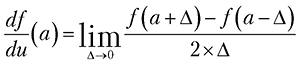
Можно численно оценить этот предел, присвоив переменной Δ маленькое значение, например 0.001:

.

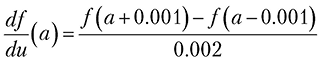
Теперь посмотрим на графическое представление нашей производной.

Визуализация

Начнем с общеизвестного способа: если нарисовать касательную к декартову представлению функции f, производная функции в точке касания будет равна угловому коэффициенту касательной. Вычислить этот коэффициент, или тангенс угла наклона прямой, можно, взяв разность значений функции f при a – 0.001 и a + 0.001 и поделив на величину приращения, как показано на рис. 1.4.

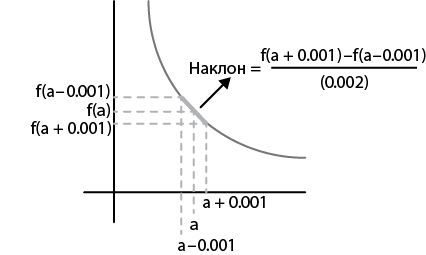
Рис. 1.4. Производная как угловой коэффициент

На рисунке производную можно представить в виде множителя, кратно которому меняется выходное значение функции при небольшом изменении подаваемого на вход значения. Фактически мы меняем значение входного параметра на очень маленькую величину и смотрим, как при этом поменялось значение на выходе. Схематично это представлено на рис. 1.5.

Рис. 1.5. Альтернативный способ визуализации концепции производной

Со временем вы увидите, что для понимания глубокого обучения второе представление оказывается важнее первого.

Код

И наконец, код для вычисления приблизительного значения производной:

from typing import Callable

def deriv(func: Callable[[ndarray], ndarray], input_: ndarray,

                        delta: float = 0.001) -> ndarray:

    '''

    Вычисление производной функции "func" в каждом элементе массива

    "input_".

    '''

    return (func(input_ + delta) — func(input_ — delta)) / (2 * delta)

Выражение «P — это функция E» (я намеренно использую тут случайные символы) означает, что некая функция f берет объекты E и превращает в объекты P, как показано на рисунке. Другими словами, P — это результат применения функции f к объектам E:

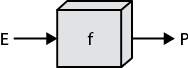
А вот так выглядит соответствующий код:

def f(input_: ndarray) -> ndarray:

    # Какое-то преобразование

    return output

P = f(E)

Вложенные функции

Вот мы и дошли до концепции, которая станет фундаментом для понимания нейронных сетей. Это вложенные, или составные, функции. Дело в том, что две функции f1 и f2 можно связать друг с другом таким образом, что выходные данные одной функции станут входными для другой.

Визуализация

Наглядно представить концепцию вложенной функции можно с помощью рисунка.

На рис. 1.6 мы видим, что данные подаются в первую функцию, преобразуются, выводятся и становятся входными данными для второй функции, которая и дает окончательный результат.

Рис. 1.6. Вложенные функции

Математическое представление

В математической нотации вложенная функция выглядит так:

.

Такое представление уже сложно назвать интуитивно понятным, потому что читать эту запись нужно не по порядку, а изнутри наружу. Хотя, казалось бы, это должно читаться как «функция f2 функции f1 переменной x», но на самом деле мы вычисляем f1 от переменной x, а затем — f2 от полученного результата.

Код

Чтобы представить вложенные функции в виде кода, для них первым делом нужно определить тип данных:

from typing import List

# Function принимает в качестве аргумента объекты ndarray и выводит

# объекты ndarray

Array_Function = Callable[[ndarray], ndarray]

# Chain — список функций

Chain = List[Array_Function]

Теперь определим прохождение данных по цепочке из двух функций:

def chain_length_2(chain: Chain, a: ndarray) -> ndarray:

    '''

    Вычисляет подряд значение двух функций в объекте "Chain".

    '''

    assert len(chain) == 2, \

    "Длина объекта 'chain' должна быть равна 2"

    f1 = chain[0]

    f2 = chain[1]

    return f2(f1(x))

Еще одна визуализация

Так как составная функция, по сути, представляет собой один объект, ее можно представить в виде f1 f2, как показано на рис. 1.7.

Рис. 1.7. Альтернативное представление вложенных функций

Из математического анализа известно, что если все функции, из которых состоит составная функция, дифференцируемы в рассматриваемой точке, то и составная функция, как правило, дифференцируема в этой точке! То есть функция f1 f2 — это просто обычная функция, от которой можно взять производную, — а именно производные составных функций лежат в основе моделей глубокого обучения.

Для вычисления производных сложных функций нам потребуется формула, чем мы и займемся далее.

Цепное правило

Цепное правило (или правило дифференцирования сложной функции)в математическом анализе позволяет вычислять производную композиции двух и более функций на основе индивидуальных производных. С математической точки зрения модели глубокого обучения представляют собой составные функции, а в следующих главах вы увидите, что понимание того, каким способом берутся производные таких функций, потребуется для обучения этих моделей.

Математическое представление

В математической нотации теорема утверждает, что для значения x

,

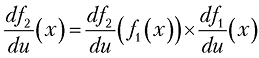
где u — вспомогательная переменная, представляющая собой входное значение функции.

Производную функции f одной переменной можно обозначить как

. Вспомогательная переменная в данном случае может быть любой, ведь запись и означает одно и то же. Я обозначил эту переменную u.

Но позднее нам придется иметь дело с функциями нескольких переменных, например x и y. И в этом случае между

и уже будет принципиальная разница.

Именно поэтому в начале раздела мы записали производные с помощью вспомогательной переменной u и будем в дальнейшем использовать ее для производных функций одной переменной.

Визуализация

Формула из предыдущего раздела не слишком помогает понять суть цепного правила. Давайте посмотрим на рис. 8, иллюстрирующий, что же такое производная в простом случае f1 f2.

Из рисунка интуитивно понятно, что производная составной функции должна представлять собой произведение производных входящих в нее функций. Предположим, что производная первой функции при u = 5 дает значение 3, то есть

.

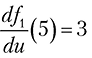
Затем предположим, что значение первой функции при величине входного параметра 5 равно 1, то есть

. Производную этой функции при u = 1 приравняем к –2, то есть .

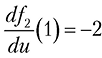
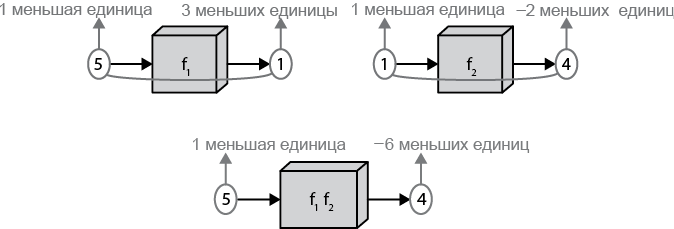
Рис. 1.8. Цепное правило

Теперь вспомним, что эти функции связаны друг с другом. Соответственно если при изменении входного значения второго черного ящика на 1 мы получим на выходе значение –2, то изменение входного значения до 3 даст нам изменение выходного значения на величину –2

3 = –6. Именно поэтому в формуле для цепного правила фигурирует произведение:

.

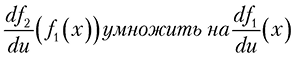
Как видите, рассмотрение математической записи цепного правила с рисунком позволяет определить выходное значение вложенной функции по ее входному значению. Теперь посмотрим, как может выглядеть код, вычисляющий значение такой производной.

Код

Первым делом напишем код, а потом покажем, что он корректно вычисляет производную вложенной функции. В качестве примера рассмотрим уже знакомые квадратичную функцию и сигмоиду, которая применяется в нейронных сетях в качестве функции активации:

def sigmoid(x: ndarray) -> ndarray:

    '''

    Применение сигмоидной функции к каждому элементу объекта ndarray.

    '''

    return 1 / (1 + np.exp(-x))

А этот код использует цепное правило:

def chain_deriv_2(chain: Chain,

                  input_range: ndarray) -> ndarray:

    '''

    Вычисление производной двух вложенных функций:

    (f2(f1(x))' = f2'(f1(x)) * f1'(x) с помощью цепного правила

    '''

    assert len(chain) == 2, \

    "Для этой функции нужны объекты 'Chain' длиной 2"

    assert input_range.ndim == 1, \

    "Диапазон входных данных функции задает 1-мерный объект ndarray"

    f1 = chain[0]

    f2 = chain[1]

    # df1/dx

    f1_of_x = f1(input_range)

    # df1/du

    df1dx = deriv(f1, input_range)

    # df2/du(f1(x))

    df2du = deriv(f2, f1(input_range))

    # Поэлементно перемножаем полученные значения

    return df1dx * df2du

На рис. 1.9 показан результат применения цепного правила:

PLOT_RANGE = np.arange(-3, 3, 0.01)

chain_1 = [square, sigmoid]

chain_2 = [sigmoid, square]

plot_chain(chain_1, PLOT_RANGE)

plot_chain_deriv(chain_1, PLOT_RANGE)

plot_chain(chain_2, PLOT_RANGE)

plot_chain_deriv(chain_2, PLOT_RANGE)

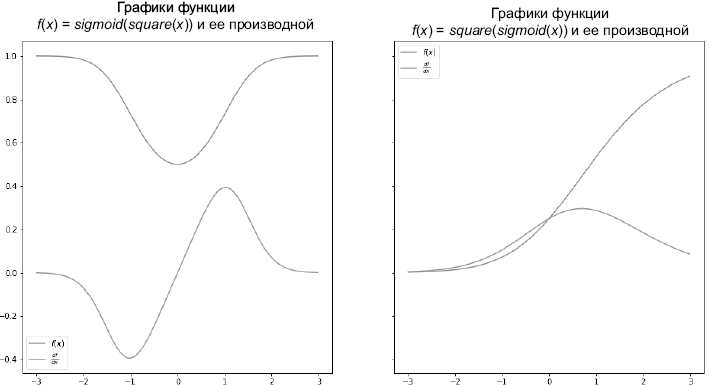
Рис. 1.9. Результат применения цепного правила. (См. иллюстрацию в цвете: https://storage.piter.com/upload/new_folder/978544611675/0109.png)

Кажется, цепное правило работает. Там, где функция наклонена вверх, ее производная положительна, там, где она параллельна оси абсцисс, производная равна нулю; при наклоне функции вниз ее производная отрицательна.

Как математически, так и с помощью кода мы можем вычислять производную «составных» функций, таких как f1 f2, если обе эти функции дифференцируемы.

С математической точки зрения модели глубокого обучения представляют собой цепочки из функций. Поэтому сейчас мы рассмотрим более длинный пример, чтобы в дальнейшем вы смогли экстраполировать эти знания на более сложные модели.

Более длинная цепочка

Возьмем три дифференцируемых функции f1, f2 и f3 и попробуем вычислить производную f1 f2 f3. Мы уже знаем, что функция, составленная из любого конечного числа дифференцируемых функций, тоже дифференцируема.

Математическое представление

Дифференцирование происходит по следующей формуле: